A theory of constrained swelling of a pH-sensitive hydrogel†‡
Romain
Marcombe
ab,
Shengqiang
Cai
a,
Wei
Hong
c,
Xuanhe
Zhao
a,
Yuri
Lapusta
b and
Zhigang
Suo
*a
aSchool of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA. E-mail: suo@seas.harvard.edu
bIFMA-LAMI, French Institute of Advanced Mechanics, Campus de Clermont-Ferrand/Les Cézeaux, 63175 Aubière, France
cDepartment of Aerospace Engineering, Iowa State University, Ames, IA 50011, USA
First published on 26th January 2010
Abstract
Many engineering devices and natural phenomena involve gels that swell under the constraint of hard materials. The constraint causes a field of stress in a gel, and often makes the swelling inhomogeneous even when the gel reaches a state of equilibrium. This paper develops a theory of constrained swelling of a pH-sensitive hydrogel, a network of polymers bearing acidic groups, in equilibrium with an aqueous solution and mechanical forces. The condition of equilibrium is expressed as a variational statement of the inhomogeneous field. A free-energy function accounts for the stretching of the network, mixing of the network with the solution, and dissociation of the acidic groups. Within a Legendre transformation, the condition of equilibrium for the pH-sensitive hydrogel is equivalent to that for a hyperelastic solid. The theory is first used to compare several cases of homogenous swelling: a free gel, a gel attached to a rigid substrate, and a gel confined in three directions. To analyze inhomogeneous swelling, we implement a finite element method in the commercial software ABAQUS, and illustrate the method with a layer of the gel coated on a spherical rigid particle, and a pH-sensitive valve in microfluidics.
1. Introduction
Immersed in an aqueous solution, a network of covalently crosslinked polymers imbibes the solution and swells, resulting in a hydrogel. The amount of swelling is affected by mechanical forces, pH, salt, temperature, light, and electric field.1,2 Gels are being developed for diverse applications as actuators, converting non-mechanical stimulations to large displacements and appreciable forces.3–6 Many applications require that the gels swell against the constraint of hard materials. For example, a microfluidic valve involves a gel anchored by a rigid pillar, and the gel swells in response to a change in the pH, blocking the flow.7 Analogous mechanisms have been used by plants to regulate microscopic flow,8 and in oilfields to enhance production.9 As another example, an array of rigid rods embedded in a gel rotate when the humidity in the environment drops below a critical value.10,11 It has also been appreciated that, in a spinal disc, the swelling of the nucleus pulposus is constrained by the annulus fibrosus, and that understanding this constrained swelling is central to developing a synthetic hydrogel to replace damaged nucleus pulposus.12Despite the ubiquity of constrained swelling in practice, the theory of constrained swelling requires substantial work to be broadly useful in analyzing engineering devices and natural phenomena. Developers of methods of analysis face two essential challenges. First, swelling of a gel is affected by a large number of stimuli. It is unrealistic to expect any single material model to describe the behavior of many gels. Second, when a gel is constrained by a hard material, the swelling often induces in the gel an inhomogeneous field of stress and large deformation. The magnitude of the stress is of central importance to applications such as valves and actuators. The large deformation, in addition to being important to applications, may also lead to cavities, creases, buckles, and other intriguing patterns that are hard to analyze.13–17
Following a recent trend in the study of inhomogeneous deformation of complex materials, we have been pursuing a modular approach, which in effect meets the two challenges separately. As an example, we have shown that the swelling of a neutral network in equilibrium is equivalent to the deformation of a hyperelastic material.18 The latter can be readily analyzed by adding a material model to commercial finite element software like ABAQUS. This approach is applicable to a neutral network characterized by a free-energy function of any form. Commercial software like ABAQUS is widely used in many fields of engineering, and has been developed to analyze large deformation of extraordinary complexity. Consequently, this approach has enabled researchers to use the commercial software to analyze complex phenomena in gels.19,20
The present paper goes beyond the neutral network, and develops a theory for a pH-sensitive hydrogel, a network of polymers bearing acidic groups, in equilibrium with an aqueous solution and a set of mechanical forces. Following our recent work on polyelectrolyte gels,21 we express the condition of equilibrium as a variational statement. For a pH-sensitive gel, the variational statement includes the following fields: the displacement of the network, the concentrations of the solvent and ions, and the degree of acidic dissociation. The variations are subject to auxiliary conditions of several types, including the conservation of various species, incompressibility of molecules, and electroneutrality in the gel and in the external solution.
Our task in the present paper is greatly simplified by the assumption of electroneutrality. To appreciate this assumption, consider a highly charged network immersed in a dilute solution of ions, so that the concentration of the counterions in the gel exceeds that in the external solution. At the interface between the gel and the external solution, the counterions in the gel spill into the external solution, and the region near the interface is no longer neutral, leading to an electric double layer of a thickness scaled by the Debye length. Outside the electric double layer, electroneutrality is nearly maintained in the gel and in the external solution. In many applications, the Debye length is much smaller than other lengths of interest. This paper will not be concerned with the electric double layer, and will assume that the gel is electroneutral. This assumption will miss phenomena at the size scale comparable to the Debye length, but will capture the overall behavior of the gel.21
As a model material, the gel is characterized by a free-energy function developed by Flory,22 Recke and Tanaka,23 Brannon-Peppas and Peppas,24 and others. (Incidentally, these authors also assumed electroneutrality.) The free-energy function accounts for the stretching of the network, mixing of the network and the solution, and dissociation of the acidic groups. The model is used to compare several cases of homogeneous swelling: a free gel, a gel attached to a rigid substrate, and a gel confined in three directions.
Inhomogeneous swelling is then studied by developing a finite element method. Inhomogeneous swelling of pH-sensitive gels has been studied in several recent papers,25–27 but the existing methods have not been demonstrated for the analysis of complex phenomena of large deformation. In this paper, we represent the free energy as a functional of the field of deformation by using a Legendre transformation. Within this representation, the inhomogeneous field in a pH-sensitive hydrogel in equilibrium is again equivalent to the field in a hyperelastic solid. We implement the finite element method by writing a user-supplied subroutine in the commercial software ABAQUS, and illustrate the method with a layer of the gel coated on a spherical rigid particle, and a pH-sensitive valve in microfluidics. We hope that this work will enable other researchers to study complex phenomena in pH-sensitive hydrogels. To this end, we have made our code freely accessible online.28
2. The condition of equilibrium for inhomogeneous swelling
Fig. 1 sketches a model system: a network of covalently crosslinked polymers bearing acidic groups AH. When the network imbibes the solvent, some of the acidic groups dissociate into hydrogen ions H+ mobile in the solvent, and conjugate bases A− attached to the network. Once dissociated, the conjugate base A− gives rise to a network-attached charge, i.e., a fixed charge. The reaction is reversible:| AH ↔ A− + H+ | (2.1) |
 | ||
| Fig. 1 A network of polymers imbibes a solution and swells, resulting in a gel. The polymers are covalently crosslinked and bear acidic groups, some of which dissociate into hydrogen ions mobile in the solvent, and fixed charges attached to the network. The external solution is composed of four mobile species: solvent molecules, hydrogen ions, counterions, and co-ions. | ||
The three species equilibrate when their concentrations satisfy
 | (2.2) |
The external solution is composed of four species: solvent molecules (i.e., water), hydrogen ions, counterions that bear charges of the sign opposite to the fixed charges (e.g., sodium ions), and co-ions that bear charges of the same sign as the fixed charges (e.g., chloride ions). To describe essentials of the method of analysis, we neglect the dissociation of water, and assume that counterions and co-ions are monovalent. Let ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) S,
S, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,
H+, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) + and
+ and ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) − be the numbers of particles of the four species in the external solution. When these numbers change by small amounts, the free energy of the external solution changes by
− be the numbers of particles of the four species in the external solution. When these numbers change by small amounts, the free energy of the external solution changes by
μSδ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) S + μH+δ S + μH+δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ + μ+δ H+ + μ+δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) + + μ−δ + + μ−δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) − − | (2.3) |
Fig. 2 illustrates a gel undergoing inhomogeneous swelling. We take the stress-free dry network as the state of reference. A small part of the network is named after the coordinate of the part, X, when the network is in the state of reference. Let dV(X) be an element of volume, dA(X) be an element of area, and NK(X) be the unit vector normal to the element of area.
 | ||
| Fig. 2 A dry network is taken to be the state of reference. In the current state, the network is immersed in an aqueous solution and subject to a set of mechanical forces. | ||
In the current state, the part of the network X moves to a place with coordinate x. The function
| xi = xi(X) | (2.4) |
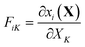 | (2.5) |
In the current state, let Bi(X)dV(X) be the external mechanical force applied on the element of volume, and Ti(X)dA(X) be the external mechanical force applied on the element of area. When the network deforms by a small amount, δxi(X), the field of mechanical force does work
| ∫BiδxidV + ∫TiδxidA | (2.6) |
Following a common practice in formulating a field theory, we stipulate that an inhomogeneously swollen gel can be divided into many small volumes, and each small volume is locally in a state of homogeneous swelling, characterized by a nominal density of free energy W as a function of various thermodynamic variables. Consequently, the Helmholtz free energy of the gel in the current state is given by
| ∫WdV | (2.7) |
The gel, the external solution, and the mechanical forces together constitute a thermodynamic system, held at a fixed temperature. The Helmholtz free energy of the system is the sum of the free energy of the gel, the free energy of the external solution, and the potential energy of the mechanical forces. When the system is in equilibrium, associated with small variations of the fields, the variation of the Helmholtz free energy vanishes. Consequently, the condition of equilibrium is
∫δWdV + μSδ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) S + μH+δ S + μH+δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ + μ+δ H+ + μ+δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) + + μ−δ + + μ−δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) − − ∫BiδxidV − ∫TiδxidA = 0 − − ∫BiδxidV − ∫TiδxidA = 0 | (2.8) |
Note that W is a function of various thermodynamic variables, so that the variational statement (2.8) includes variations of the following inhomogeneous fields: the displacement of the network, the concentrations of the solvent and ions, and the degree of acidic dissociation. The variations are subject to auxiliary conditions of several types, including the conservation of various species, incompressibility of molecules, and electroneutrality in the gel and in the external solution. These auxiliary conditions are discussed below.
Denote the nominal concentration of species α by Cα(X). That is, Cα(X)dV(X) is the number of particles of species α in the element of the network when the gel is in the current state. Of the four mobile species, the solvent molecules, the counterions, and the co-ions are each conserved. The gel gains these particles at the expense of the external solution:
∫δCS(X)dV + δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) S = 0 S = 0 | (2.9) |
∫δC+(X)dV + δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) + = 0 + = 0 | (2.10) |
∫δC−(X)dV + δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) − = 0 − = 0 | (2.11) |
The mobile hydrogen ions, however, are not conserved, but are produced as the acidic groups dissociate. The change in the total number of the hydrogen ions in the system equals the change in the number of the fixed charges:
∫δCH+(X)dV + δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ = ∫δCA−(X)dV H+ = ∫δCA−(X)dV | (2.12) |
The sum of the number of the associated acidic groups AH and that of the fixed charges A− equal the total number of the acidic groups:
| CAH(X) + CA−(X) = f/v | (2.13) |
As discussed in Introduction, we assume that electroneutrality prevails both in the gel and in the external solution, so that
| CH+(X) + C+(X) = CA−(X) + C−(X) | (2.14) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ + H+ + ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) + = + = ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) − − | (2.15) |
Because typically the stress in a gel is small and the amount of swelling is large, we assume that individual polymers and solvent molecules are incompressible. Furthermore, the concentrations of ions are assumed to be low, so that their contributions to the volume of the gel are negligible. Under these simplifications, when the dry network of unit volume imbibes CS number of solvent molecules and swells to a gel of volume detF, these volumes satisfy the condition
| 1 + vSCS = detF | (2.16) |
Subject to the auxiliary conditions (2.9)–(2.16), the state of the inhomogeneously swollen gel is specified by the following independent fields: xi(X), C+(X), C−(X), and CH+(X). We stipulate that the nominal density of free energy is a function:
| W = W(F,C+,C−,CH+). | (2.17) |
Using the auxiliary conditions (2.9)–(2.16), we rewrite the condition of equilibrium (2.8) in terms of variations of the independent fields, namely,
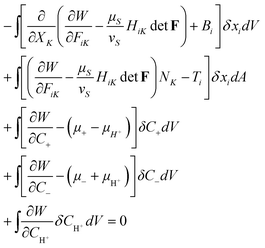 | (2.18) |
In writing (2.18), we have used the divergence theorem, as well as an identity ∂detF/∂FiK = HiKdetF, where HiK is the transpose of the inverse of the deformation gradient, namely, HiKFiL = δKL and HiKFjK = δij.
Inspecting (2.18), we write
 | (2.19) |
The quantity siK is known as the tensor of nominal stress. The term containing μs is due to the assumed molecular incompressibility.
The statement (2.18) holds for arbitrary variations of the independent fields, xi(X), C+ (X), C−(X), and CH+ (X). Consequently, each line of (2.18) leads to the condition of a partial equilibrium with respect to the variation of a single independent field. The first line of (2.18) leads to
 | (2.20) |
| siKNK = Ti | (2.21) |
The next two lines of (2.18) lead to
 | (2.22) |
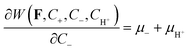 | (2.23) |
These equations are the conditions of ionic equilibrium with respect to the variations in the concentrations of the counterions and co-ions in the gel. The combinations μ+ − μH+ and μ− + μH+ are due to the assumed electroneutrality.
The last line of (2.18) leads to
 | (2.24) |
This equations is the condition of chemical equilibrium with respect to the dissociation of the acidic groups, a condition that reproduces (2.2), as shown in the next section.
3. A specific material model
The conditions of equilibrium described in the previous section are independent of models of the external solution and gel. This section applies the conditions of equilibrium to a commonly used material model.External solution
Let![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) +,
+, ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) − and
− and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+ be the true concentration of the three species of ions in the external solution. We assume that the external solution is dilute, so that the electrochemical potentials of the ions relate to the concentrations as21
H+ be the true concentration of the three species of ions in the external solution. We assume that the external solution is dilute, so that the electrochemical potentials of the ions relate to the concentrations as21 | (3.1) |
 | (3.2) |
Imagine that the solution is separated from a reservoir of pure solvent by a membrane, which allows solvent molecules to pass through, but not the ions. The solvent molecules will permeate from the reservoir into the solution, until the solution is under a pressure, the osmotic pressure, kT(![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+ +
H+ + ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + +
+ + ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) −. Consequently, relative to the pure solvent, the solvent molecules in the ionic solution has the chemical potential
−. Consequently, relative to the pure solvent, the solvent molecules in the ionic solution has the chemical potential
μS = −kTvS(![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+ + H+ + ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + + + + ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) −). −). | (3.3) |
Eqn (3.1)–(3.3) express the electrochemical potential in terms of the concentrations of the four mobile species.
pH-sensitive gel
Following Flory,22 Ricke and Tanaka,23 Brannon-Peppas and Peppas,24 and many others, we adopt an idealized model, assuming that the free-energy density of the gel is a sum of several contributions:| W = Wnet + Wsol + Wion + Wdis | (3.4) |
The free energy of stretching the network is taken to be
| Wnet = ½NkT[FiKFiK − 3 − 2log(detF)] | (3.5) |
The free energy of mixing the polymers and the solvent takes the form:
 | (3.6) |
This contribution consists of the entropy of mixing of the polymers and the solvent molecules, as well as the enthalpy of mixing, characterized by a dimensionless parameter χ.
The concentrations of the mobile ions are taken to be low, so that their contribution to the free energy is due to the entropy of mixing, namely,
 | (3.7) |
The contribution due to the dissociation of the acidic groups is taken to be
 | (3.8) |
The expression consists of the entropy of dissociation and the enthalpy of dissociation, where γ is the increase in the enthalpy when an acidic group dissociates. Note that CA− and CAH are the nominal concentration of the fixed charges and of associated acidic groups, respectively. They are not among the independent variables chosen to represent the free-energy function, (2.17). Using (2.13) and (2.14), however, we can express them in terms of the chosen independent variables, CA− = CH+ + C+ − C−, CAH = f/v − (CH+ + C+ − C−).
Equilibrium between the gel, external solution, and mechanical forces
Recall that the number of particles of species α in the gel in the current state divided by the volume of the dry network defines the nominal concentration of the species, Cα. The same number divided by the volume of the gel in the current state defines the true concentration of the species, cα. The two definitions are related as Cα = cαdetF. Recall that when the number of particles is counted in units of the Avogadro number, NA = 6.023 × 1023, the molar concentration of the species α is designated by [α]; for example, cH+ = NA[H+].Recall a relation in continuum mechanics connecting the true stress σij and the nominal stress: σij = siKFjK/detF, so that (2.19) can be written as
 | (3.9) |
Using the function W(F,C+,C−,CH+) specified above, (3.9) becomes that
 | (3.10) |
Πion = kT(cH+ + c+ + c− − ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+ − H+ − ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + − + − ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) −) −) | (3.11) |
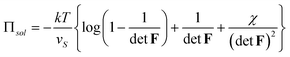 | (3.12) |
Here Πion is the osmotic pressure due to the imbalance of the number of ions in the gel and in the external solution, and Πsol is the osmotic pressure due to mixing the network and the solvent. Condition (3.9) is readily interpreted: in equilibrium, the applied stress σij equals the contractile stress of the network minus the osmotic pressure.
The conditions of ionic equilibrium (2.22) and (2.23) become
c+/![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + = cH+/ + = cH+/![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+ H+ | (3.13) |
c−/![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) − = (cH+/ − = (cH+/![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+)−1 H+)−1 | (3.14) |
These conditions are known as the Donnan equations. The condition of chemical equilibrium with respect to acidic dissociation (2.24) becomes that
 | (3.15) |
This condition reproduces (1.2), with the identification
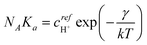 | (3.16) |
Parameters used in numerical calculations
In numerical calculations, we assume that the volume per monomer equals the volume per solvent molecule, v = vS. Electroneutrality in the external solution requires that![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) − =
− = ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + +
+ + ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+ Consequently, the composition of the external solution is specified by two independent numbers, say, the concentration of the counterions
H+ Consequently, the composition of the external solution is specified by two independent numbers, say, the concentration of the counterions ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + and the concentration of the hydrogen ions
+ and the concentration of the hydrogen ions ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+. The later relates to the pH of the external solution,
H+. The later relates to the pH of the external solution,  .
.
The polymers are specified by several parameters. Recall that N is the number of polymer chains per unit volume of the dry network, so that 1/Nv is the number of monomers per polymer chain. The dimensionless parameter χ measures the enthalpy of mixing the polymers and the solvent. The number f is the number of acidic groups on a polymer chain divided by the total number of monomers on the chain. For applications that prefer gels with large swelling ratios, materials with low values of Nv and χ and high value of f are used. In numerical calculations, we set Nv = 10−3, χ = 0.1, and f = 0.05. The constant of acidic dissociation, Ka, has the same dimension as the concentration (in the unit mol L−1). We set pKa = −log10Ka = 4.3, a commonly accepted value for the dissociation of carboxylic acids.
We will normalize the chemical potential by kT, and normalize the stresses by kT/v. A representative value of the volume per molecule is v = 10−28 m3. At room temperature, kT = 4 × 10−21 J and kT/v = 4 × 107 Pa. The elastic modulus of the dry network is NkT. For Nv = 10−3, the elastic modulus is NkT = 4 × 104 Pa.
4. Several cases of homogenous swelling
The material model described above is now applied to several cases of homogeneous swelling (Fig. 3). In each case, the conditions of equilibrium (3.10)–(3.15) form a set of simultaneous nonlinear algebraic equations. Their solutions illustrate the basic behavior of a gel with or without constraint. These cases of homogeneous swelling also provide tests for the finite element program to be developed in the following section.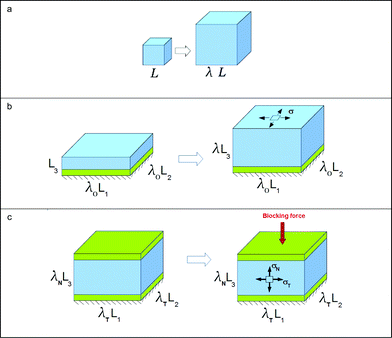 | ||
| Fig. 3 Several cases of homogeneous swelling. (a) Free swelling. (b) Swelling subject to biaxial constraint. (c) Swelling under triaxial constraint. | ||
In the case of a free gel, Fig. 3a, all components of stress vanish, and the swelling is isotropic: F = λδiK. Fig. 4a plots the swelling ratio of the gel, λ3, as a function of the composition of external solution. The latter is specified by  , and the molar concentration of the counterions,
, and the molar concentration of the counterions, ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) +/NA. The gel swells more when the external solution has low concentrations of both the hydrogen ions and the counterions, but swells less when the external solution is concentrated with either species. These trends are considered in some detail below.
+/NA. The gel swells more when the external solution has low concentrations of both the hydrogen ions and the counterions, but swells less when the external solution is concentrated with either species. These trends are considered in some detail below.
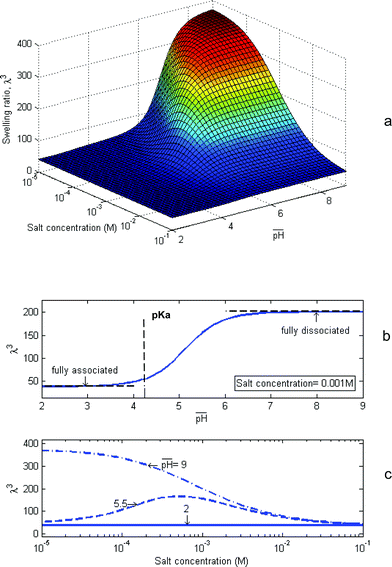 | ||
Fig. 4 Numerical results for a free swelling gel. (a) The swelling ratio is plotted as a function of the two variables that specify the composition of the external solution: the  and the salt concentration (i.e., molar concentration of the counterions). (b) The swelling ratio is plotted as a function of and the salt concentration (i.e., molar concentration of the counterions). (b) The swelling ratio is plotted as a function of  for a fixed salt concentration. (c) The swelling ratio is plotted as a function of the salt concentration at several values of for a fixed salt concentration. (c) The swelling ratio is plotted as a function of the salt concentration at several values of  . . | ||
Fig. 4b plots the swelling ratio as a function of  at a fixed concentration of the counterions. The trend can be understood in terms of the two limits: fully-associated limit and fully-dissociated limit. When
at a fixed concentration of the counterions. The trend can be understood in terms of the two limits: fully-associated limit and fully-dissociated limit. When  , the abundance of hydrogen ions causes all the acidic groups to be associated, namely,
, the abundance of hydrogen ions causes all the acidic groups to be associated, namely,
| CAH = f/v, CA− = 0. | (4.1) |
Consequently, the network is neutral, and ions of every species are equally distributed in the gel and the external solution:
cH+ = ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+, c+ = H+, c+ = ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) +, c− = +, c− = ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) −. −. | (4.2) |
The balanced ions do not contribute to osmosis, Πion = 0.
When 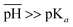 , the scarcity of hydrogen ions causes all the acidic groups to be dissociated, namely,
, the scarcity of hydrogen ions causes all the acidic groups to be dissociated, namely,
| CAH = 0, CA− = f/v | (4.3) |
Consequently, the network bears a known number of fixed charges. These fixed charges must be neutralized by counterions, as dictated by electroneutrality. Consequently, mobile ions will be more concentrated in the gel than in the external solution. These unbalanced ions contribute to osmosis, Πion > 0, so that the network in the fully-dissociated limit will imbibe more solvent than the network in the fully-associated limit.
Fig. 4c plots the swelling ratio as a function of the molar concentration of the counterions in the external solution, ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + /NA, at several values of
+ /NA, at several values of 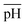 . When
. When  , the hydrogen ions are abundant, and the gel approaches the fully-associated limit. When
, the hydrogen ions are abundant, and the gel approaches the fully-associated limit. When  , the hydrogen ions are scarce, and the gel approaches the fully-dissociated limit. These two limits have been discussed above. The external solution with an intermediate value,
, the hydrogen ions are scarce, and the gel approaches the fully-dissociated limit. These two limits have been discussed above. The external solution with an intermediate value,  , deserves additional comments.20 The Donnan equation, c+/
, deserves additional comments.20 The Donnan equation, c+/![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + = cH+/
+ = cH+/![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+, requires that the two species of positive ions in the gel and in the external solution be distributed proportionally. When
H+, requires that the two species of positive ions in the gel and in the external solution be distributed proportionally. When ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + <
+ < ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+ in the external solution, c+ < cH+ in the gel. The abundance of hydrogen ions in the gel causes the acidic groups to be mostly associated, so that the network is nearly neutral. As
H+ in the external solution, c+ < cH+ in the gel. The abundance of hydrogen ions in the gel causes the acidic groups to be mostly associated, so that the network is nearly neutral. As ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + increases while
+ increases while ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+ is fixed, more counterions will be available in the gel, and more acidic group will dissociate. This process of ion exchange causes the swelling ratio to increase with the concentration of the counterions in the external solution. When the external solution has a very high concentration of the counterions, however, the gel behaves like a neutral gel, and the swelling ratio drops.
H+ is fixed, more counterions will be available in the gel, and more acidic group will dissociate. This process of ion exchange causes the swelling ratio to increase with the concentration of the counterions in the external solution. When the external solution has a very high concentration of the counterions, however, the gel behaves like a neutral gel, and the swelling ratio drops.
Fig. 3b illustrates a layer of a gel attached to a rigid substrate. The substrate is flat, and the thickness of the gel is much smaller than the length and the width of the gel, so that the deformation of the gel is homogeneous. The two stretches in the plane of the layer is prescribed to be λ0. When the gel is brought into contact with the external solution, the two in-plane stretches remain fixed, but the gel swells in the direction normal to the layer, with stretch λ. The swelling ratio of the substrate-attached gel varies with the composition of the external solution, with the trends similar to that of the unconstrained gel. However, the amount of swelling of the free gel is significantly larger than that of the substrate-attached gel (Fig. 5). Consequently, the amount of swelling cannot be specified as a material property, but must be solved as a part of the boundary-value problem.
 | ||
| Fig. 5 The swelling ratio of a free gel and a substrate-attached gel as a function of the pH of the external solution. | ||
Fig. 3c illustrates a layer of a gel attached to a rigid substrate, with equal stretches prescribed in the plane, λT. The layer is also constrained in the normal direction, but with a different level of stretch λN. The gel develops a state of triaxial stress, σT and σN. As mentioned in the Introduction, in many applications of the pH-sensitive hydrogels, the gel has to exert a pressure on the constraining hard material. In such applications, various ways to change the blocking stress σN are important. Fig. 6 plots the blocking stress as a function of the pH of the external solution at several values of the lateral stretch. The blocking stress also exhibits two limits. When the pH value in the external solution is low, the abundant hydrogen ions cause the acidic groups on the network approach the fully associated limit, and the magnitude of the blocking stress is small. When the pH value in the external solution is high, the scarce hydrogen ions cause the acidic groups on the network approach the fully dissociated limit, and the magnitude of the blocking stress is large. The magnitude of the blocking stress can be changed by prescribing a different value of the in-plane stretch. As expected, the magnitude of the blocking stress increases when the lateral stretch decreases.
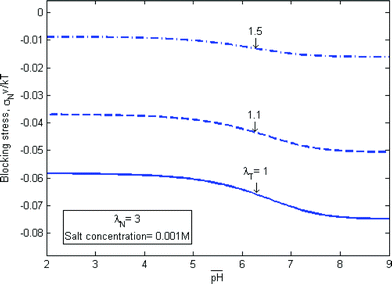 | ||
| Fig. 6 The blocking stress as a function of the pH of the external solution at several values of the lateral stretch. | ||
The theory outlined in this paper describes many of the qualitative trends observed experimentally. However, a quantitative comparison between the theory and experiments is difficult for several reasons. First, to highlight the essential ideas of the theory, we have used relatively simple models of solutions. Most experiments are carried out using more complex systems, such as copolymers and solutions of multiple species. Second, the existing experiments often report insufficient details, leaving many parameters to fit. With these difficulties in mind, we leave more extensive comparison to future work, and restrict ourselves here to a comparison between the theory and one set of experiments, as follows.
Eichenbaum et al.28 have done a series of experiments to study the effect of crosslink density on the swelling behavior of pH-sensitive hydrogels. Ref. 28 provided all material parameters except f in our model. The comparison is plotted in Fig. 7. The theoretical predictions fit well with Eichenbaum's experimental data for poly(methacrylic acid-co-acrylic acid) gels with four different crosslink density with one fitting parameter f = 0.35. Both the theoretical predictions and experimental results show swelling ratio induced by the change of the pH value in outer solution is reduced as the crosslink density increases.
 | ||
| Fig. 7 Comparison between theoretical predictions and experimental results. The scattered dots are experimental data and different lines are the calculation results. Material parameters are given in ref. 28: salt concentration is 0.03M, χ = 0.45 + 0.489φ, Ka = 10−4.7. The mole fraction of pH sensitive monomers f = 0.35 is used by fitting the calculation with experimental data. | ||
5. Finite element method
The condition of equilibrium of a pH-sensitive hydrogel is expressed as the variational statement (2.8), which governs the following independent inhomogeneous fields: xi(X), C+(X), C−(X), and CH+(X). This variational statement has a form different from that used in commonly available commercial finite element software. In this section, we transform this variational statement into a different form, which can be readily implemented in commercial finite element software.Following a commonly used approach in thermodynamics, we introduce another free-energy function Ŵ by a Legendre transformation:
| Ŵ = W − (μ+ − μH+)C+ − (μ− + μH+)C− − μSCS | (5.1) |
We can solve the nonlinear algebraic eqn (3.13)–(3.15), and express CH+, C+ and C− in terms of ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+,
H+, ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) + and detF; see part A in the ESI.‡ Consequently, Ŵ can be expressed as a function of the following independent variables:
+ and detF; see part A in the ESI.‡ Consequently, Ŵ can be expressed as a function of the following independent variables:
Ŵ = Ŵ(F,![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+,cİ+). H+,cİ+). | (5.2) |
The physical significance of this change of variables is understood as follows. When a network is immersed in a solution, so long as the amount of the gel is small compared to the amount of the external solution, the composition of the external solution remains unchanged as the gel swells. Consequently, concentrations of the hydrogen ions and counterions in the external solution, cİH+ and cİ+, remain fixed, and so do the electrochemical potentials of all the species. Inserting (5.1) into (2.18), the condition of equilibrium (2.18) becomes that
| ∫δŴdV = ∫BiδxidV + ∫TiδxidA | (5.3) |
The variational statement (5.3) takes the same form as that of a hyperelastic solid. That is, the work done by the mechanical forces equals the variation in the free energy. Because the composition of the external solution, ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+ and
H+ and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) +, remain fixed when the mechanical forces do work, the variation in the free energy Ŵ = Ŵ(F,
+, remain fixed when the mechanical forces do work, the variation in the free energy Ŵ = Ŵ(F,![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+,
H+,![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) +) is entirely due to the variation of the deformation gradient. Consequently, the variational statement (5.3) can be readily implemented in commercial finite element software.
+) is entirely due to the variation of the deformation gradient. Consequently, the variational statement (5.3) can be readily implemented in commercial finite element software.
We have implemented the above theory in the commercial finite element software, ABAQUS, by coding the function Ŵ = Ŵ(F,![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) H+,
H+,![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) +) into a user-defined subroutine for a hyperelastic material. Details in implementing the finite element method may be found in our paper on neutral gels,18 and part A of the ESI‡ of the present paper. The subroutine is given in the part C of the ESI‡ and posted online.29
+) into a user-defined subroutine for a hyperelastic material. Details in implementing the finite element method may be found in our paper on neutral gels,18 and part A of the ESI‡ of the present paper. The subroutine is given in the part C of the ESI‡ and posted online.29
We first test our finite element program against the cases of homogeneous swelling. For example, Fig. 5 plots the swelling ratios of a free gel and a substrate-attached gel. We have also tested other cases of homogeneous swelling. In all cases, the results obtained by the finite element method agree well with those of the analytical solutions.
We then test the finite element program using a case of inhomogeneous swelling: a layer of a gel coated on a rigid spherical particle (Fig. 8). The core–shell structure is immersed in a solution. When the pH of the external solution changes, the gel swells or deswells, but the rigid particle remains inert. In this particular calculation, when  , the gel is taken to be stress-free, and the ratio of the outer radius of the gel to the radius of the rigid particle is set to be B/A = 1.5. When
, the gel is taken to be stress-free, and the ratio of the outer radius of the gel to the radius of the rigid particle is set to be B/A = 1.5. When  , the gel swells subject to the constraint of the rigid particle. Consequently, a field of stress develops in the gel and the amount of swelling is inhomogeneous, even when the gel reaches a state of equilibrium. To compare with the finite element solution, Part B of the ESI‡ lists the differential equations for this spherical symmetric boundary-value problem. These equations are solved by using a finite difference method. The results are compared with those obtained by using the finite element method.
, the gel swells subject to the constraint of the rigid particle. Consequently, a field of stress develops in the gel and the amount of swelling is inhomogeneous, even when the gel reaches a state of equilibrium. To compare with the finite element solution, Part B of the ESI‡ lists the differential equations for this spherical symmetric boundary-value problem. These equations are solved by using a finite difference method. The results are compared with those obtained by using the finite element method.
 | ||
| Fig. 8 Swelling of a gel coated on a rigid spherical particle. (a) Distribution of the concentration of water in the gel. (b) Distribution of the radial stress and hoop stress in the gel. | ||
Fig. 8a plots the distribution of the swelling ratio in the gel. Due to the constraint of the rigid particle, the gel swells inhomogeneously. Near the outer surface, the gel is nearly unconstrained, and the swelling ratio approaches that of a free gel. Near the interface between the gel and the core, however, the gel is constrained, and the swelling ratio is much below of that of the free gel.
The constraint of the rigid particle also causes in the gel a field of stress. Fig. 8b plots the distribution of the stress in the gel. Near the outer surface of the gel, the radial stress vanishes because of the boundary condition, and the magnitude of the hoop stress is small because the gel is nearly free. Near the interface between the gel and the rigid core, the radial stress is tensile and the hoop stress is compressive. These trends can be readily understood. If the rigid particle were removed, the gel would swell homogeneously and stress-free, and both the inner radius and outer radius would increase. In the presence of the rigid particle, however, the inner radius is constrained to be of the original size, leading to the tensile radial stress and compressive hoop stress. As shown in Fig. 8b, the results obtained by using finite element method agree well with those obtained by solving the ordinary differential equations.
As another illustration of the finite element method, consider the microfluidic valve7 mentioned in the Introduction. Fig. 9 illustrates a gel coated on a rigid pillar in a microfluidic channel. The gel is taken to deform under the plane strain conditions. When  , the gel is in a stress-free state, and the channel is open. When
, the gel is in a stress-free state, and the channel is open. When  , the gel swells to push against the walls of the channel, and the channel is closed. In the open state, the outer radius of the gel should be small to ease the flow. In the closed state, the size of the contact between the gel and a wall, as well as the pressure in the contact, should be large to block the flow. In this case, the calculation needs to deal with the inhomogeneous deformation of the gel, as well as the contact between the gel and the walls. An analytical solution too this problem is unavailable. However, by implementing our subroutine in ABAQUS, we can use almost all the functions already embedded in this commercial software.
, the gel swells to push against the walls of the channel, and the channel is closed. In the open state, the outer radius of the gel should be small to ease the flow. In the closed state, the size of the contact between the gel and a wall, as well as the pressure in the contact, should be large to block the flow. In this case, the calculation needs to deal with the inhomogeneous deformation of the gel, as well as the contact between the gel and the walls. An analytical solution too this problem is unavailable. However, by implementing our subroutine in ABAQUS, we can use almost all the functions already embedded in this commercial software.
 | ||
Fig. 9 In a microfluidic channel, a gel is anchored by a rigid pillar. When  , the gel shrinks, and the channel is open. When , the gel shrinks, and the channel is open. When  , the gel swells, and the channel is closed. As the outer radius of the gel increases, both the size of the contact and the pressure in the contact increase. , the gel swells, and the channel is closed. As the outer radius of the gel increases, both the size of the contact and the pressure in the contact increase. | ||
Fig. 9 plots the deformed configuration of the valve, as well as the size of the contact and the distribution of the pressure. We fix the radius of the pillar, A/D = 0.1. As the outer radius of the gel increases, both the size of the contact and the pressure in the contact increase. The size of the contact and the pressure may be crucial for such a design for valves. In the original design of the valve, several pillars were placed across the width of the channel.7 In such a design, the pillars form a periodic array, and the above analysis remains valid. The finite element program may be used to explore other patterns of pillars, or other designs of pH-sensitive valves.
6. Concluding remarks
This paper develops a theory of a network of covalently crosslinked polymers bearing acidic groups, in equilibrium with an aqueous solution and a set of mechanical forces. The inhomogeneous swelling is affected by the pH and salinity of the external solution, as well as by the geometry of the constraint. The condition of equilibrium is expressed as a variational statement that governs the following independent fields: the displacement of the network, and the concentrations of the hydrogen ions, counterions and co-ions. By using the Legendre transformation, the variational statement is cast into a form such that a swollen gel in equilibrium is governed by the same equations as those for an equivalent hyperelastic material. The theory is implemented as a finite element method in the commercial software ABAQUS, and is illustrated with cases of homogeneous and inhomogeneous swelling. It is hoped that this work will enable other researchers to study complex phenomena in pH-sensitive hydrogels. To this end, we have made our code freely accessible online.29Acknowledgements
This work was supported by the NSF through a grant on Soft Active Materials (CMMI–0800161), by the DARPA through a contract on Programmable Matter (W911NF-08- 1-0143), and by Schlumberger through a contract on Swelling Elastomers for Applications in Oilfields.References
- Y. Li and T. Tanaka, Annu. Rev. Mater. Sci., 1992, 22, 243–277 CrossRef CAS.
- Y. Osada and J. P. Gong, Adv. Mater., 1998, 10, 827–837 CrossRef CAS.
- F. Carpi and E. Smela, Biological Applications of Electroactive Polymer Actuators. Wiley, 2009 Search PubMed.
- A. Richter, G. Paschew, S. Klatt, J. Lienig, K. Arndt and H. P. Adler, Sensors, 2008, 8, 561–581 CAS.
- Y.-J. Lee and P. V. Braun, Adv. Mater., 2003, 15, 563–566 CrossRef CAS.
- L. Dong, A. K. Agarwal, D. J. Beebe and H. R. Jiang, Nature, 2006, 442, 551–554 CrossRef CAS.
- D. J. Beebe, J. S. Moore, J. M. Bauer, Q. Yu, R. H. Liu, C. Devadoss and B. H. Jo, Nature, 2000, 404, 588–590 CrossRef CAS.
- M. A. Zwieniecki, P. J. Melcher and N. M. Holbrook, Science, 2001, 291, 1059–1062 CrossRef CAS.
- M. Kleverlaan, R. H. van Noort, and I. Jones, Paper 92346, SPE/IADC Drilling Conference held in Amsterdam, The Netherlands, 23–25 February 2005 Search PubMed.
- A. Sidorenko, T. Krupenkin, A. Taylor, P. Fratzl and J. Aizenberg, Science, 2007, 315, 487–490 CrossRef CAS.
- W. Hong, X. Zhao and Z. Suo, J. Appl. Phys., 2008, 104, 084905 CrossRef.
- R. N. Natarajan, J. R. Williams and G. B. J. Anderson, Spine, 2004, 29, 2733–2741 CrossRef.
- T. Tanaka, S.-T. Sun, Y. Hirokawa, S. Katayama, J. Kucera, Y. Hirose and T. Amiya, Nature, 1987, 325, 796–798 CrossRef CAS.
- V. Trujillo, J. Kim and R. C. Hayward, Soft Matter, 2008, 4, 564–569 RSC.
- Y. Klein, E. Efrati and E. Sharon, Science, 2007, 315, 1116–1120 CrossRef CAS.
- E. S. Matsuo and T. Tanaka, Nature, 1992, 358, 482–485 CrossRef CAS.
- Y. Zhang, E. A. Matsumoto, A. Peter, P. C. Lin, R. D. Kamien and S. Yang, Nano Lett., 2008, 8, 1192–1196 CrossRef CAS.
- W. Hong, Z. S. Liu and Z. G. Suo, Int. J. Solids Struct., 2009, 46, 3282–3289 CrossRef CAS.
- J. Kim, J. Yoon and R. C. Hayward, Nat. Mater., 2009, 9, 159–164.
- M. K. Kang and R. Huang, A variational approach and finite element implementation for swelling of polymeric hydrogels under geometric constraints. Submitted for publication, 2009. Preprint available, http://imechanica.org/node/6594 Search PubMed.
- W. Hong, X. H. Zhao, and Z. G. Suo, Large deformation and electrochemistry of polyelectrolyte gels. Submitted for publication, 2009. Preprint available, http://imechanica.org/node/5960 Search PubMed.
- P. J. Flory, Principles of Polymer Chemistry. Cornell University Press, Ithaca, 1953 Search PubMed.
- J. Ricka and T. Tanaka, Macromolecules, 1984, 17, 2916–2921 CrossRef CAS.
- L. Brannon-Peppas and N. A. Peppas, Chem. Eng. Sci., 1991, 46, 715–722 CrossRef CAS.
- S. Baek and A. R. Srinivasa, Int. J. Non-linear Mech., 2004, 39, 1301–1318 CrossRef.
- S. K. De, N. R. Aluru, B. Johnson, W. C. Crone, W. C. Beebe and J. Moore, J. Microelectromech. Syst., 2002, 11, 544–555 CrossRef CAS.
- H. Li, R. Luo, E. Birgersson and K. Y. Lam, J. Appl. Phys., 2007, 101, 114905 CrossRef.
- G. M. Eichenbaum, P. F. Kiser, A. V. Dobrynin, S. A. Simon and D. Needman, Macromolecules, 1999, 32, 4867–4878 CrossRef CAS.
- S. Q. Cai, a user-supplied subroutine in ABAQUS for the analysis of pH-sensitive hydrogels, http://imechanica.org/node/6661 Search PubMed.
Footnotes |
| † This paper is part of a Soft Matter themed issue on Emerging Themes in Soft Matter: Responsive and Active Soft Materials. Guest Editors: Anna C. Balazs and Julia Yeomans. |
| ‡ Electronic supplementary information (ESI) available: Further equations and the code of user subroutine for pH-sensitive hydrogels. See DOI: 10.1039/b917211d |
| This journal is © The Royal Society of Chemistry 2010 |
