Evolution of block-copolymer order through a moving thermal zone

Abstract

We investigate block-copolymer (BCP) thin film ordering kinetics during annealing across a moving in-plane temperature gradient. We operate in the so-called cold zone annealing (CZA) regime, where ordering temperatures are above the glass-transition, but well below the order-disorder transition. By measuring the order through the in-plane gradient, using atomic force microscopy and grazing-incidence small-angle X-ray scattering (GISAXS), we confirm that CZA greatly enhances ordering kinetics, as compared to uniform oven annealing. The maximal ordering occurs over a narrow range of the heating-up phase, and not during the subsequent cooling phase. The large grain sizes obtained using CZA are due to enhanced kinetics, and not the preferential formation of certain grain orientations. Kinetic enhancement is apparent even below the bulk glass-transition temperature. We suggest that the in-plane temperature gradient drives enhanced kinetics.

---

Introduction

Block-copolymers (BCP) are self-assembling polymeric systems which microphase-separate during annealing due to the chemical incompatibility of the blocks. These systems form nanostructures of a variety of morphologies (e.g., cylinders, lamellae, gyroids) with periodicity in the 5 nm to 100 nm regime,¹ making them attractive candidates for high-density patterning and nano-manufacturing. However, there are challenges in achieving defect-free control of the order and orientation of structures. A variety of strategies have been presented, including application of electric fields,^2–4 solvent annealing,^5,6 topographic^7–12 and chemical^13,14 patterning, and tuning the substrate surface energy^15–17 and/or roughness.^18–21

Moving thermal zones are an established processing method for metals and semiconductors, where recrystallization and oriented grain growth occur on the planar front formed by the cooling-edge of the zone. Such methods are routinely applied to generate macrostructures with single-crystal orientation (e.g., silicon ingots). Thermal zones have also been applied to organic systems,^22–24 including block-copolymers.^25–33 We have recently demonstrated that annealing a BCP thin film with a moving thermal zone whose maximum temperature (T_hot) is below the order–disorder transition temperature (T_ODT) can lead to greatly enhanced ordering kinetics, and preferential alignment of the microstructure.³⁴ This ‘cold zone annealing’ (CZA) does not disorder the material during the processing, which makes it of fundamental interest in understanding BCP ordering physics. CZA is also of technological interest since both control of orientation and the ability to rapidly order systems are critically necessary. Moreover, many self-assembling systems have a practically inaccessible T_ODT (e.g., it may be above the material's degradation temperature). Because CZA does not drive the system into a disordered state, the origin of alignment and ordering is qualitatively different from conventional thermal zone refinement or ‘hot zone annealing’ (HZA) techniques. Here, we investigate the origin of enhanced kinetics in thin films processed using CZA by measuring the structure of a cylinder-forming block-copolymer throughout the thermal zone itself. By combining grain-size estimation from atomic force microscopy (AFM) and structural information from grazing-incidence small-angle X-ray scattering (GISAXS), we quantify the evolution of structure as it passes through different regimes of the thermal zone, in an effort to understand the mechanism of cold zone annealing.

Experimental

Samples were thin films of asymmetric poly(styrene-block-methyl methacrylate) (PS-b-PMMA) with total molar mass 47.7 kg mol⁻¹ and a polydispersity index of 1.04 (Polymer Source, Inc.).³⁵ The mass fraction of PS was 0.74, leading to the formation of hexagonally-packed cylinders upon phase separation (repeat distance ≈ 24 nm). Films were cast from toluene solution onto cleaned (via ultraviolet-ozone treatment) silicon wafers (≈ 500 μm thick) using either spin-coating or flow-coating,³⁶ and were baked at 60 °C for 15 h prior to any annealing steps. Film thickness was determined using interferometry (uncertainty of ±1 nm).

The zone annealing apparatus has been described previously.³⁴ Briefly, we establish an in-plane temperature gradient using a temperature-controlled hot block (250 W Watlow heating cartridge) flanked by two water-cooled cold blocks. A 1 mm air gap is used to thermally isolate the blocks. Samples are translated across this thermal gradient, at a constant speed of 1.20 μm s⁻¹, using a robotic arm (Bioprecision Microscope Stage Model 99S021) with computer control (LEP Mac5000 controller interfaced with LabView). To ensure thermal contact with the sample, the cold and hot blocks are coated with a thermally conductive paste (Dow Corning 340 Silicone Heat Sink compound). In order to study the zone in detail, a series of ‘frozen zone’ samples were prepared by rapidly removing the sample from the hot block midway through the zone annealing process. By pushing the sample onto the cold block, it is quenched and the annealing process arrested. The quench translation is sufficiently fast (20 mm s⁻¹) that we expect no effects from the hot zone during this step. These films represent a combinatorial library, where each sample position corresponds to a different subset of the zone annealing history.

Surfaces were imaged using atomic force microscopy (AFM) in the intermittent contact (‘tapping’) mode of an Asylum MFP3D instrument. AFM phase images were analyzed using established methods.^33,34,37,38 Spatial derivatives are used to compute vector orientations throughout the image. For visualization, the angles of these vectors are mapped onto a false-colour scale. The orientation vectors are also used to compute a local two-fold symmetric order parameter:

ψ(r) = e^2iθ(r) (1)

where r is a position vector, and θ is the angle of the cylinders at that location. The orientational correlation function is then calculated using:

g(r) = 〈ψ(0)ψ(r)〉 (2)

where the angled brackets denote averaging over all angles for a given distance. Finally, we compute a correlation length, ξ, by fitting g(r) to an exponential function of the form e^−r/ξ. We use this correlation length as a metric of average grain size.

Grazing-incidence small-angle X-ray scattering (GISAXS) measurements were performed under vacuum at the Advanced Photon Source (Argonne National Laboratory) using the 8-ID-E beamline. Two-dimensional scattering images were measured using a charge-coupled device (CCD) detector at a distance of 1.945 m or 1.975 m, and an X-ray wavelength of 0.169 nm (photon energy of 7.35 keV). The images presented in this paper were obtained at a grazing angle of 0.20°, which is above the critical angle of the polymer–vacuum interface. The sample stage incorporated heat control (via a combination resistive heater and Peltier element), allowing scattering measurements in situ during hot-plate heating.

Results and discussion

Frozen zone

Cold zone annealing (CZA) is a film-processing technique where the sample is pushed across a temperature gradient at a constant speed (see Fig. 1). Our previous work³⁴ has demonstrated that CZA of block-copolymer thin films produces ordering kinetics that are considerably faster than conventional oven annealing at comparable temperatures. Moreover the directionality of CZA (the push direction and/or the direction of the temperature gradient) generates a preferential alignment of the mesophases. In order to understand the origin of these unique properties, we measured the ordering of a cylinder-forming block-copolymer at various stages within the thermal zone. To do so, we prepared ‘frozen zone’ samples by rapidly pushing the sample off of the heating block midway through the zone annealing process. By pushing the sample onto the cooling block, we quench the entire annealing process. The resultant sample is essentially a combinatorial library, where each position along the sample has experienced a subset of the full annealing curve.

Fig. 1 Schematic of the cold zone annealing (CZA) apparatus. The thin film, cast on a silicon substrate, is mounted to a moveable arm. A thermocouple reads the sample temperature during the run, and presses the sample onto the stage. The sample is moved across a temperature-controlled hot block (red) which is flanked on either side by a water-cooled cold block (blue). The three blocks thus form an in-plane temperature gradient. The computer-controlled arm pushes the sample across this in-plane gradient at a prescribed velocity. Each position on the sample thus experiences a Gaussian-like annealing history with a peak temperature of T_hot.

Fig. 2 shows representative AFM images for various positions through the thermal zone. The sample, a 151 nm film annealed up to a maximum temperature of T_hot = 221 °C (refer to Fig. 3a for the associated annealing curve), phase separates into hexagonally-packed cylinders that are ultimately oriented parallel (laying horizontally on the substrate). The false-colour orientation maps allow easy identification of grains and grain boundaries. The orientational correlation length, ξ, is used as a metric of grain size. From Fig. 2 a–d, it is evident that the system phase separates into a large number of small randomly-oriented grains, with subsequent grain coarsening. From the GISAXS data, we see that early in the annealing process, the film phase-separates into a well-defined morphology but with a three-dimensionally random orientation distribution (which leads to the isotropic ring seen in the scattering data of Fig. 2a). As the zone annealing proceeds, this isotropic state converts to a state with cylinders well-aligned parallel to the substrate interface, as seen in Fig. 2c. The peaks at |Q_y| = 0.23 nm⁻¹ (and double that value), as well as the higher-order peaks along +Q_z, are consistent with hexagonally-packed cylinders with their lattice-planes aligned with the substrate interface (but isotropic in-plane). The last stages of zone annealing (Fig. 2d) show decreasing peak widths and intensification of the higher-order reflections, which suggest better ordering and larger grain sizes. We note that AFM is a surface technique probing small areas, whereas GISAXS can measure the entire film thickness, and averages over a large area. However, the present AFM and scattering data agree well on the stages of the ordering process, including the region where maximum ordering occurs. Quantitative ordering data (Fig. 3) further establish the strong agreement between the two techniques.

Fig. 2 Representative AFM and GISAXS data across the thermal zone of a 151 nm sample annealed using T_hot = 221 °C. The four columns (a–d) present data progressively further through the annealing history (the time and temperature are indicated; refer to Fig. 3a for the full temperature profile). The top row are the AFM phase images (scale bar is 500 nm); the center row are the corresponding false-color orientation maps (the color scale below the images indicates grain orientations, the zone-annealing direction is 0°); and the bottom row are GISAXS detector images. The three boxed-in areas in the scattering data (d) denote the regions used for further analysis (e.g., Fig. 3b): 1, the diffuse scattering; 2, the isotropic population; 3, the well-ordered population.

Fig. 3 (a) Correlation length (black circles; left axis) as measured by AFM, and sample temperature at quench (grey line; right axis) across a 151 nm CZA sample heated up to T_hot = 220 °C (the grey diamonds denote the times at which the sample crossed through the bulk T_g). The sample was rapidly quenched mid-way through a push across the hot-zone: each sample position (upper axis) was thus exposed to a subset of the annealing time history (lower axis; the origin of time is defined to be when the sample crosses T_g). The error bars are based upon the standard deviation of replicate AFM images. (b) Intensity of scattering from various portions of the GISAXS detector image (left axis). The diffuse low-Q scattering (red line) decreases as the system orders. The scattering from the isotropic population (orange line) increases after crossing through T_g but then drops as the well-ordered population (blue line) increases. From both the AFM and the scattering data, we see a rapid increase in order over a short span of annealing time.

The grain-size correlation lengths as a function of the zone annealing history (Fig. 3a) indicate that significant phase separation occurs shortly after the sample crosses the glass-transition temperature (T_g ≈ 105 °C). We note that ordering occurs predominantly on the heating edge of the temperature gradient. This differentiates CZA from conventional zone refinement or HZA techniques, which heat the sample into a melted or disordered state, and ordering occurs along the cooling edge.²⁹ In CZA, because we do not cross T_ODT, the system is in the ordered portion of the phase diagram at all times, but mobility is being increased as the sample moves through the heating edge. Thus properties of soft materials related to mobility (e.g., nanoscale dynamic heterogeneities³⁹) are likely crucial to understanding CZA. Another unique feature in Fig. 3a is the rapid increase in grain size across a very narrow range in time and temperature (detailed GISAXS images for this region are shown in Fig. 4). This rapid ordering occurs in the high-slope region of the heating edge, where the in-plane temperature gradient is greatest (▽T ≈ 18 °C mm⁻¹). In fact, the final grain size is achieved prior to reaching the peak of the temperature history. Although higher annealing temperatures lead to larger grain sizes (as will be discussed later), it seems that CZA ordering is not predominantly driven by the maximum temperature, but instead the enhanced kinetics are correlated with the large thermal gradient.

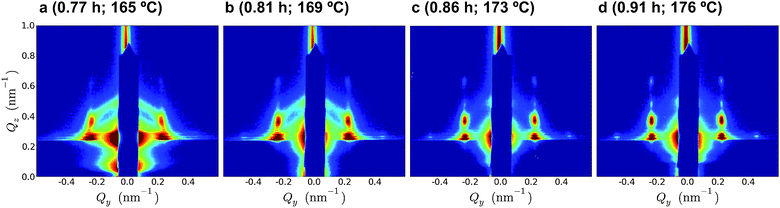Fig. 4 GISAXS images for four locations in the thermal zone of a 151 nm film annealed using T_hot = 221 °C (time above bulk T_g and temperature are indicated; refer to Fig. 3a for the temperature profile). These images are taken in the region demonstrating maximum ordering kinetics, based on AFM grain size and GISAXS scattering. Over a very short span of time and temperature, the film evolves from a nearly isotropic state into having nearly maximal order.

The scattering intensity from the GISAXS data is plotted, as a function of the annealing history, in Fig. 3b. In order to describe the ordering, we have summed the scattering signal from three portions of the GISAXS image (denoted in Fig. 2d): 1, the diffuse low-Q scattering (|Q_r| < 0.20 nm⁻¹, where |Q_r| is the reciprocal-space distance to the centre of the specular beam at (Q_y,Q_z) = (0 nm⁻¹, 0.26 nm⁻¹), behind the beamstop); 2, the ring of scattering at |Q_r| ≈ 0.26 nm⁻¹; and 3, the intense peaks near (|Q_y|, Q_z) = (0.23 nm⁻¹, 0.38 nm⁻¹). These three signals provide a measure of the disordered, the isotropic cylinder, and the parallel-oriented cylinder populations, respectively. This scattering data confirms the AFM measurements: we see a rapid increase in the highly-ordered population across a narrow range of the annealing history, in the region where the in-plane temperature gradient is large, and comparatively little ordering thereafter. The isotropic population appears shortly after crossing through T_g, and disappears as the ordered population grows (the isotropically-distributed grains are being converted into parallel-cylinder domains). We note a quite interesting feature in the diffuse-scattering data: it decreases as the system orders, as expected, but significant diffuse scattering has appeared before the system has crossed the glass-transition. We return to this point below.

Annealing temperature

Because BCP ordering and morphology can depend on annealing temperature and history, we investigated this parameter in detail. Fig. 5 shows AFM and GISAXS data for a 161 nm film. At this thickness, the surface exhibits hexagonally-packed perpendicular-oriented cylinders (standing vertically), as determined by AFM, in certain portions of the annealing curve. Nevertheless, the corresponding GISAXS data suggests that the sub-surface population adopts a parallel orientation (cylinders laying horizontally on the substrate). The surface layer of vertical cylinders exists only during the initial stages of zone annealing; as annealing progresses the surface converts to a mixed morphology (vertical and horizontal cylinders) and finally to a fully horizontal morphology.⁴⁰ A scattering peak at |Q_y| = 0.26 nm⁻¹ appears when some fraction of the film surface is in a vertical orientation (see GISAXS in Fig. 5b). This peak disappears upon further annealing, once the sample converts to a completely parallel orientation. This behaviour is, in fact, consistent with our recent study of the surface morphology diagram for PS-b-PMMA block-copolymers.⁴¹ In particular, a zone annealing experiment appears to trace out a path through the surface morphology diagram, converting from vertical surface structures to horizontal surface structures as the temperature increases (although it may be that zone annealing shifts the boundaries of the phase diagram). The structure of this diagram may also explain the sensitivity to film thickness: for the thicknesses and temperatures studied here, we may be in a ‘high-slope’ region, where small changes in either parameter can push across the vertical-horizontal transition line. The formation of a vertically-oriented surface layer is consistent with our previous work in CZA in the sense that this state is transient; the final state is of horizontally-oriented cylinders throughout the thin film. We note that for films annealed at sufficiently high temperature (≥248 °C), the vertical-cylinder morphology can reappear near T_hot. This may be because the weak surface tension mismatch between the blocks has been eliminated, or the sample has crossed a surface phase transition.⁴² The appearance of vertically-oriented surface structures highlights the utility of scattering-based measurements: purely surface measurements (e.g., AFM) would be unable to deconvolute film ordering from this surface reorganization, or would mistakenly attribute the surface structure as being representative of the entire thin film.

Fig. 5 AFM and GISAXS data for a 161 nm BCP thin film annealed using T_hot = 224 °C. The two columns (a and b) represent two different regions within the thermal zone (time above the bulk T_g and temperature as indicated). The upper row AFM phase images (scale bar is 200 nm) show that films of this thickness convert from having perpendicular-oriented cylinders at the free surface to having parallel-oriented cylinders as annealing progresses. The corresponding GISAXS data (bottom row) confirm that there is a large population of parallel cylinders beneath the film surface.

Despite the appearance of perpendicular-cylinders at the film surface, GISAXS analysis can quantify the ordering kinetics within the film (an example is shown in Fig. 6). The same qualitative behaviour is seen for samples annealed at all T_hot that were studied (from 196 °C to 266 °C): the maximum ordering kinetics occur not at the maximum temperature, but rather over a narrow range of the heating phase, where the in-plane gradient is large. There appears to be a small film thickness effect, since some films (≈ 160 nm) exhibit vertical-cylinder orientation early in the annealing process, whereas films ≈ 10 nm thinner do not generate substantial vertical orientations. However the general ordering processes within the film, and in particular the rapid ordering, evidently do not depend on film thickness.

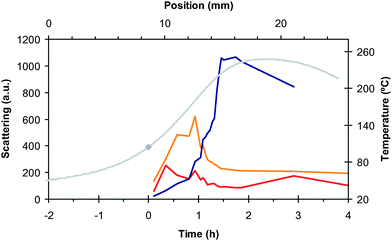Fig. 6 GISAXS scattering intensity for a 161 nm thin film heated to T_hot = 248 °C (the annealing history is denoted by the gray line, which corresponds to the right axis): the diffuse low-Q scattering (red line), the scattering from the isotropic population (orange line), and the well-ordered perpendicular-cylinder population (blue line).

Enhanced kinetics

In order to demonstrate the enhanced kinetics of CZA, we compare the ordering from the T_hot = 221 °C frozen zone sample to a sample heated on a hot-plate using a nominally identically thermal history (the temperature profile is shown in Fig. 7i). This sample experienced a time-variation of temperature identical to the zone-annealed sample, but with the entire sample heated uniformly (hence there are no in-plane thermal gradients). This hot-plate annealing is expected to be similar to conventional oven annealing. GISAXS images, acquired in situ throughout the annealing, are shown in Fig. 7, e–h, and are compared to scattering images from the corresponding CZA sample at similar points through the annealing history (Fig. 7 a–d). The CZA samples have, unmistakably, achieved greater ordering for any given stage in the annealing history. CZA is able to phase separate into an isotropic population earlier in the annealing history, and achieves a final state with better order (as demonstrated by the sharper peaks and higher scattering intensity in Fig. 7 d as compared to h). The final correlation length for the hot-plate sample is⁴³ξ = 450 nm ± 110 nm, whereas the equivalent CZA sample achieves ξ = 810 nm ± 190 nm after the same annealing time. The conversion from the isotropic to aligned state is also not as abrupt as seen in CZA (Fig. 7i). Interestingly, the hot-plate annealed sample shows no significant scattering prior to crossing the glass-transition (Fig. 7e). This would be expected, as a vitrified as-cast sample cannot phase-separate until sufficient mobility is induced. However the equivalent zone-annealed sample (Fig. 7a) shows significant diffuse scattering, and even the appearance of a weak isotropic ring, prior to being heated above the bulk T_g. This suggests that the zone annealing induces sufficient polymer mobility for a small amount of phase separation to occur below the conventional bulk glass-transition temperature. Deviations from bulk T_g are known in thin films,⁴⁴ but expected shifts are insufficient to explain the ordering at T_g −50 °C we observe in films ≳151 nm. Moreover, the same shifts would be expected in both the CZA and hot-plate samples. Our data suggest that CZA generates enhanced kinetics throughout the entire annealing curve (except near the peak, where the in-plane temperature gradient approaches zero).

Fig. 7 GISAXS data for various portions of the thermal history of a 151 nm film heated up to T_hot = 220 °C (the times and temperatures are indicated). (a–d) A film processed using zone annealing (where a thermal front moves through the material). (e–h) A film annealed on a hot-plate using a thermal history nominally identically to the zone-annealed sample (but where there are no in-plane thermal gradients, and no thermal front movement). For any given point along the annealing curve, the zone-annealed samples have markedly greater ordering. Images have been selected to provide a close comparison; the comparison is conservative in the sense that the zone-annealed examples have in fact experienced a slightly shorter thermal history and yet display greater order. (i) Scattering intensity as a function of the annealing history for the hot-plate sample confirms that the extent of ordering, and ordering kinetics, are lower than for zone annealing. Also of note is the absence of significant diffuse scattering prior to crossing the bulk glass-transition. In conventional oven or hot-plate annealing, phase separation is initiated only after crossing T_g.

Activation energy

Fig. 8 shows the correlation length, after a full CZA processing run, for a variety of T_hot. By using this grain size as a measure of kinetics,⁴⁵ we can perform an Arrhenius analysis:

ξ = ξ₀e^−E_a/RT (3)

where R is the universal gas constant, E_a is an activation energy, and ξ₀ is a scaling constant. From the slope in Fig. 8, we calculate E_a = 110 kJ mol⁻¹ ± 40 kJ mol⁻¹. This activation energy for grain growth is lower than the reported values of 270 kJ mol⁻¹ for defect density⁴⁶ and 377 kJ mol⁻¹ for defect motion,⁴⁷ for monolayers of cylinder-forming PS-b-PMMA in conventional annealing experiments. This suggests that the zone annealing technique may lower the activation barrier for grain growth. The orientation bias of CZA may arise from a lower energy barrier for grains with preferred orientations.

Fig. 8 Correlation length as a function of the maximum annealing temperature for CZA samples. Plotted in an Arrhenius fashion, we can estimate an activation energy for the grain growth of 110 kJ mol⁻¹ ± 40 kJ mol⁻¹.

Ordering process

From the AFM and GISAXS data, it is obvious that CZA does not operate by nucleating a preferred population of grains (e.g., aligned in a particular direction), which grow and coalesce. Instead, the entire film phase-separates into small grains with an isotropic distribution. The action of zone annealing is instead to grow these grains much faster than would be expected for conventional oven annealing: CZA enhances ordering kinetics. The increased mobility may be related to a decrease in the effective energy barrier for grain growth or reorientation. One of the qualitative differences between CZA and hot-plate (or oven) annealing is the presence of an in-plane thermal gradient. Further, we note that maximum ordering occurs where the in-plane thermal gradient is maximized. We thus suggest that temperature gradients are able to enhance the kinetics of self-assembling systems. In zone annealing the temperature gradient is coupled to movement of the thermal field; experiments to deconvolute these two effects would thus be critical to understanding the role of thermal gradients. Preliminary measurements indicate the degree of the kinetic enhancement depends on the magnitude of the thermal gradient. The precise relationship should provide insight into the enhancement mechanism. The movement of the thermal zone may be crucial in inducing preferential alignment of the BCP microstructure. Although the thermal gradient is macroscopic (the temperature is approximately uniform on the scale of self-assembly), its presence would induce a substantial directional flux of heat throughout the film.

It is worth noting that the cooling edge of the CZA annealing history also has a large in-plane thermal gradient, yet does not appear to re-initiate rapid grain growth. However, undoubtedly the growth of grains in CZA, as in oven annealing, is convoluted with saturation effects, where large grains need progressively longer times to annihilate defects, coalesce, and reorient. The fact that for all temperatures measured the maximum (abrupt) ordering was observed prior to T_hot suggests that the thermal gradient dominates the ordering process (rather than T_hot itself).

Finally, it is interesting to note that the detailed progress of a sample through different morphologies may depend on its processing history. For instance some samples produced a transient perpendicular-cylinder surface population during the annealing process. Despite sensitivity to preparation history (e.g., residual solvent, residual stresses) or film properties (e.g., film thickness), it appears that the effect of CZA is generically applicable: kinetics is greatly enhanced. For this reason we suggest that similar enhancements may arise in other self-assembling systems exposed to moving thermal gradients that are below their disordering temperature.

Conclusions

We have investigated in detail the ordering steps which occur during a zone annealing experiment, by quenching a sample mid-anneal and probing by AFM and GISAXS through the thermal zone. Zone annealing generates phase-separation into a state with isotropic grain distribution, which coarsens into larger parallel grains (laying horizontal on substrate), similar to oven annealing. CZA, however, greatly enhances ordering kinetics. The maximum ordering rate occurs on the heating edge (not at the maximum temperature), where the in-plane temperature gradient is maximum. We suggest that thermal gradients can generically lead to enhanced self-assembly kinetics, and that the motion of a thermal zone and/or the directionality of heat flux generate an orientational bias.

Acknowledgements

This work was funded in part by the NIST Office of Microelectronics Programs. K.G.Y. acknowledges the support of NSERC Canada in the form of a Postdoctoral Fellowship. N.J.F. acknowledges the support of the NRC-NIST Postdoctoral Fellowship Program. We also wish to thank Joseph Strzalka for help with X-ray scattering measurements. Use of the Advanced Photon Source was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Science, under Contract No. W-31-109-Eng-38.

Notes and references

1. M. J. Fasolka and A. M. Mayes, Annu. Rev. Mater. Res., 2001, 31, 323–355.
2. B. Ashok, M. Muthukumar and T. P. Russell, J. Chem. Phys., 2001, 115, 1559–1564.
3. G. G. Pereira and D. R. M. Williams, Macromolecules, 1999, 32, 8115–8120.
4. Y. Tsori and D. Andelman, Macromolecules, 2002, 35, 5161–5170.
5. S. H. Kim, M. J. Misner and T. P. Russell, Adv. Mater., 2004, 16, 2119–2123.
6. M. Kimura, M. J. Misner, T. Xu, S. H. Kim and T. P. Russell, Langmuir, 2003, 19, 9910–9913.
7. R. A. Segalman, A. Hexemer and E. J. Kramer, Macromolecules, 2003, 36, 6831–6839.
8. D. Sundrani, S. B. Darling and S. J. Sibener, Nano Lett., 2004, 4, 273–276.
9. D. Sundrani, S. B. Darling and S. J. Sibener, Langmuir, 2004, 20, 5091–5099.
10. M. R. Hammond, E. Cochran, G. H. Fredrickson and E. J. Kramer, Macromolecules, 2005, 38, 6575–6585.
11. R. Ruiz, N. Ruiz, Y. Zhang, R. L. Sandstrom and C. T. Black, Adv. Mater., 2007, 19, 2157–2162.
12. X. Zhang, S. H. De Paoli Lacerda, K. G. Yager, B. C. Berry, J. F. Douglas, R. L. Jones and A. Karim, ACS Nano, 2009, 3, 2115–2120.
13. X. M. Yang, R. D. Peters, P. F. Nealey, H. H. Solak and F. Cerrina, Macromolecules, 2000, 33, 9575–9582.
14. S. Ouk Kim, H. H. Solak, M. P. Stoykovich, N. J. Ferrier, J. J. de Pablo and P. F. Nealey, Nature, 2003, 424, 411.
15. P. Mansky, T. P. Russell, C. J. Hawker, M. Pitsikalis and J. Mays, Macromolecules, 1997, 30, 6810–6813.
16. P. Mansky, T. P. Russell, C. J. Hawker, J. Mays, D. C. Cook and S. K. Satija, Phys. Rev. Lett., 1997, 79, 237.
17. E. Huang, L. Rockford, T. P. Russell and C. J. Hawker, Nature, 1998, 395, 757.
18. E. Sivaniah, Y. Hayashi, M. Iino, T. Hashimoto and K. Fukunaga, Macromolecules, 2003, 36, 5894–5896.
19. E. Sivaniah, Y. Hayashi, S. Matsubara, S. Kiyono, T. Hashimoto, K. Kukunaga, E. J. Kramer and T. Mates, Macromolecules, 2005, 38, 1837–1849.
20. Y. Tsori, E. Sivaniah, D. Andelman and T. Hashimoto, Macromolecules, 2005, 38, 7193–7196.
21. K. G. Yager, B. C. Berry, K. Page, D. Patton, A. Karim and E. J. Amis, Soft Matter, 2009, 5, 622–628.
22. J. Bechhoefer and A. Libchaber, Phys. Rev. B: Condens. Matter, 1987, 35, 1393.
23. D. Stefanescu, A. Moitra, A. Kacar and B. Dhindaw, Metall. Trans. A, 1990, 21, 231–239.
24. C. Misbah and A. Valance, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 1282.
25. J. Bodycomb, Y. Funaki, K. Kimishima and T. Hashimoto, Macromolecules, 1999, 32, 2075–2077.
26. T. Hashimoto, J. Bodycomb, Y. Funaki and K. Kimishima, Macromolecules, 1999, 32, 952–954.
27. K. Mita, H. Tanaka, K. Saijo, M. Takenaka and T. Hashimoto, Macromolecules, 2007, 40, 5923–5933.
28. K. Mita, H. Tanaka, K. Saijo, M. Takenaka and T. Hashimoto, Macromolecules, 2008, 41, 6780–6786.
29. K. Mita, H. Tanaka, K. Saijo, M. Takenaka and T. Hashimoto, Macromolecules, 2008, 41, 6787–6792.
30. K. Mita, M. Takenaka, H. Hasegawa and T. Hashimoto, Macromolecules, 2008, 41, 8789–8799.
31. K. Mita, H. Tanaka, K. Saijo, M. Takenaka and T. Hashimoto, Polymer, 2008, 49, 5146–5157.
32. D. E. Angelescu, J. H. Waller, D. H. Adamson, R. A. Register and P. M. Chaikin, Adv. Mater., 2007, 19, 2687–2690.
33. S. M. Park, B. C. Berry, E. Dobisz and H. C. Kim, Soft Matter, 2009, 5, 957–961.
34. B. C. Berry, A. W. Bosse, J. F. Douglas, R. L. Jones and A. Karim, Nano Lett., 2007, 7, 2789–2794.
35. Certain equipment, instruments or materials are identified in this paper in order to adequately specify the experimental details. Such identification does not imply recommendation by the National Institute of Standards and Technology nor does it imply the materials are necessarily the best available for the purpose.
36. C. M. Stafford, K. E. Roskov, T. H. Epps and M. J. Fasolka, Rev. Sci. Instrum., 2006, 77, 023908.
37. C. Harrison, D. H. Adamson, Z. Cheng, J. M. Sebastian, S. Sethuraman, D. A. Huse, R. A. Register and P. M. Chaikin, Science, 2000, 290, 1558–1560.
38. C. Harrison, Z. Cheng, S. Sethuraman, D. A. Huse, P. M. Chaikin, D. A. Vega, J. M. Sebastian, R. A. Register and D. H. Adamson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011706.
39. A. W. Bosse, J. F. Douglas, B. C. Berry, R. L. Jones and A. Karim, Phys. Rev. Lett., 2007, 99, 216101–216104.
40. H. C. Kim and T. P. Russell, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 663–668.
41. X. Zhang, B. C. Berry, K. G. Yager, S. Kim, R. L. Jones, S. Satija, D. L. Pickel, J. F. Douglas and A. Karim, ACS Nano, 2008, 2, 2331–2341.
42. X. Zhang, K. G. Yager, N. Fredin, H. Ro, J. F. Douglas, R. L. Jones and A. Karim, ACS Nano, 2009 , submitted.
43. The data in this manuscript, and in the figures, are presented along with the standard uncertainty involved in the measurement, where the uncertainty represents one standard deviation of the mean.
44. J. A. Forrest and K. Dalnoki-Veress, Adv. Colloid Interface Sci., 2001, 94, 167–195.
45. L. Gaik Teoh, J. Shieh, W. Hao Lai and M. Hsiung Hon, J. Mater. Res., 2004, 19, 2687–2693.
46. R. Ruiz, J. K. Bosworth and C. T. Black, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 054204–054205.
47. J. Hahm and S. J. Sibener, J. Chem. Phys., 2001, 114, 4730–4740.

---

Footnote

† Official contribution of the National Institute of Standards and Technology; not subject to copyright in the United States.

---