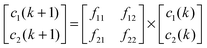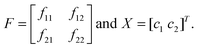Dynamical model for assessment of anti-angiogenic therapy of cancer

Abstract

Different experimental models have substantially established that the anti-angiogenic (AAG) group of drugs are able to control the growth of tumor mass by cutting down the nutritive supply to the cancer cells. The mechanism of action of this group of drugs acts on the cells of the vascular endothelium. Recently, different AAG drugs have been in clinical trials. Initial clinical trials showed that application of AAG drugs produced different sorts of toxicity in patients, so calibration of the doses and drug application schedules are very important at present. Hence, development of analytical models would definitely help in this respect, particularly at the individual level. The analytical model presented here may help to make a judicious choice of drug doses and drug schedule to control the growth of the tumor system under the condition of malignancy.

---

1. Introduction

It has been established that tumor cells survive due to the generation of micro-vessels around it. This process is known as angiogenesis.^1,2 The developed micro-vessels provide the necessary nutrition and oxygen to the tumor cells. Hence a therapy that blocks the process of angiogenesis has been suggested by the oncology researchers. The mode of action of different anti-angiogenic (AAG) drugs like, anti-VEGF (vascular endothelial growth factor) is targeted towards the cells of the vasculature supplying the tumour. Therefore, it prevents the transport of necessary nutrition and oxygen that is necessary for the growth and survival of tumour cells. Consequently the tumour cells die in this manner.

It is interesting to note that at present, different anti-VEGF drugs are in Phase II or Phase III clinical trials.³ Initial clinical trials suggest that there are several forms of discomfort in patients undergoing treatment with AAG drug. Nausea, diarrhea, hypertension are the initial symptoms that are commonly seen in cancer patients treated with AAG drug(s). This may hinder the clinical outcome. Therefore, the present challenge is to formulate a proper drug dosage and drug application schedule for different AAG drugs. Attempts have been made in a conventional manner by screening at the population level. However, development of an analytical model at discrete time intervals may provide a better assessment procedure in scheduling of drug doses and drug application at the individual level.

Recently, using fluid dynamical theories based on probabilistic parameter settings for the movement of endothelial cells in linear equations, a mathematical model has been developed to explain the vascularization (angiogenesis) process during the early events of tumor development.^4,5 In another effort, models for tumor growth and invasion based on multiscale modeling has been developed employing selective variables (which are measured in different scales) across the different levels of hierarchy of the physiological system. Such variables are densities of tumor cells, proliferation and apoptotic rate of the cells, concentrations of vital nutrients, different cytokine concentrations such as VEGF, fibronectin (FNT), and tissue metalloproteinase concentration at the cancer milieu and describe the cells' collective migration and evolving neovasulature. These input variables are integrated in a nonlinear system using multi-grid points to represent the 3D morphology of tumor shape. As different empirically based observations reveal the growth characteristics of tumor; so this sort of model has the capacity to correlate the molecular characteristics to morphological representations. Simulations with these models have been done with different in vivo cell line and ex vivo patients data. The simulated results represent different clinical and experimental autopsied data.^6–10

However, in the models, the considered grid points as well as the probability for the mobilization of the endothelial cells are difficult to implement in the clinical settings and considerations of energy formulation that accounts for different mechanical forces e.g., the cell–cell, cell–matrix adhesion, elastic effects may limit its clinical implications while tracking the system undergoing any therapeutic scheduling. Moreover, the model does not consider the relationship between the vascularization and tumor load. Realistically, in majority of the cancer cases, patients are diagnosed with a substantial load of tumor; that means the process of vascularization is already well developed.

It is also suggested that different chemotherapeutic drugs when applied in low dosage but at frequent interval (metronomic chemotherapy, MCT) has the anti-angiogenic property. It is also argued that tumors at poorly vascularized tissue site survive due to newly formed micro-vasculature. Moreover, angiogenesis plays a role for the development and growth of the connective tissue tumors and hence, are sensitive to anti-angiogenic therapy.^1,3,11 It has been shown that metronomic dosing strategy may induce TSP1, a soluble mediator present in the extracellular matrix, helps to control the tumor growth by binding with CD36 receptors present in the endothelial cells. TSP1 can also bind and sequester VEGF.²

This is the important reason that led the mathematical modeller towards the development of analytical models for MCT treatment. Models developed by several groups have substantially proved that MCT would be equally effective compared to the conventional maximum tolerable dosing strategy. These models considered two types of cells in a tumor system—drug resistant and drug sensitive type with respect to a particular chemotherapeutic drug. Each cell type is considered with a typical doubling time—resistant cell type doubles faster than sensitive type and there exists a conversion rate between the cell types. Therapeutic scheduling is considered to be a 21 day cycle for MTD and for MCT either daily or with a 3 days interval. In MTD total amount of drug has been considered to be applied with six cycles, whereas in the cases of MCT drug application has been considered as a fraction (that corresponds to the amount on each day) of total amount of drug applied. Immunity related cell killing has been established to be advantageous in MCT strategy by imparting an extra controllability to the tumor system.¹²

Development of toxicity in MCT, if any, has also been addressed in such analytical models. Generation of toxicity is assumed to be from two sources—tumor derived (metabolic) and drug induced. The issues of toxicity are solved through fuzzy logic based approach as demonstrated in the model. Analytically it has been proved that MCT does not impose any extra burden of toxicity to the physiological system in spite of prolonged application. In case there is any delay of drug application in MCT due to the pathophysiological constraints (accumulation of toxic metabolites of tumor cells or its debris due to death), MCT still has a better control over the tumor system.¹³ The delay in drug application has been determined and is governed by the clearance rate of toxicity by the excretory system. With higher clearance rate, delay in consecutive drug application is less.¹⁴ However, retention of drug within the physiological system has an advantage of an extra cell killing efficiency.¹⁵ The threshold of toxicity is another determinant factor for the clearance.¹⁶ Thus realistically controllability of tumor growth is governed by the dialectical relationship of the patho-physiological constraint and the presence of drug under the condition.

In these modeling studies, tumor cell death by different therapeutic means say, MCT strategy, immunity related tumor cell killing and antibody based therapy (anti-VEGF)—all are considered as separate subtractive terms operating on the total tumor mass at discrete time interval.¹² Since the growth of micro-vasculature cells around the tumor mass is not monitored in the model, the killing of tumor cells due to death of the micro-vasculature cells has not been considered. Therefore such modeling approaches are not aptly fit for the clinical translations of AAG drugs. Moreover the considered drug sensitivity of the tumor cells in these models would also not be equally applicable when one considers solely anti-angiogenic therapy as in these cases the heterogeneous tumor mass is sensitive to the hypoxia.

For tracking the tumor system in a clinical scenario, fluid dynamics based models have been developed with reduced number of grid points in a 2D matrix to check the probabilistic movement of vessel cells. Reduction in number of grid points has the advantage of tracking the system through CT scan followed by biopsy procedure. Through the same model relationship between angiogenesis and tumor cell growth has been implicated.^17,18 In this model tumor cell growth is dependent on different growth factors concentrations at the cancer milieu and hence, the dependency of tumor cells on angiogenesis is established. Though the tumour system is decoupled from the micro-vasculature system through multi-scale modelling approach, however, the required probabilistic movement of the endothelial cells of the micro-vascular system may not be traceable for the clinical cases.

In the present work, analytical model has been developed to overcome the realistic limitations of the existing analytical models for antiangiogenic therapies. In the following section, development of the analytical model is elaborated and in section 3 simulation results are depicted with the developed model. In section 4, analytical studies for understanding the controllability assessment of the tumor system have been elaborated. Finally, the advantage of the developed model and implementing procedure for its clinical translation is discussed in section 5.

2. System model

2.1 Tumour system

In our earlier model,¹² we have considered two types of cells. Here also two types of tumour cells are taken. Here the similarity of the present tumour growth model with the previous model ends. In the present model, the considered two types of cells are on the basis of sensitivity with respect to anoxia—one is anoxia sensitive (s-type) (c₁) and another is anoxia resistive (r-type) (c₂). This ensures that the cells would respond differentially to AAG treatment. Cell type c₁ and c₂ have an anoxia sensitivity of σ₁ and σ₂, respectively. Each cell type grows exponentially with the multiplication rate of f₁₁ and f₂₂, respectively under conditions of uniform/constant vasculature around the site. Both the cell types can be inter-converted to one another and different inter-conversion rates can be included (f₁₂ and f₂₁). For simplicity these factors may be considered zero. So at discrete time interval (k) the overall system equation can be written as:
For simplicity the above equations can be rewritten as:

X(k + 1) = F·X(k) (1)

where F is a matrix and X is the state vector consisting of the following elements:

2.2 Role of vasculature on tumor growth

In the present work we have considered the full grown tumor system. This tumor systems is dependent on development of the cells of microvasculature (vv) around them. Vasculature cells also grow exponentially with a rate (f_vv). At discrete time interval (k) cell count of microvasculature varies as:

vv(k + 1) = f_vv × vv(k). (2)

If some therapy is applied for killing the micro-vessel cells, then the magnitude of applied drug available in the system is calibrated to a proportion of micro-vessel cells destroyed. At time instant k, let this amount be f_t(k). Then the above eqn (2) gets modified to

vv(k + 1) = f_vv × vv(k) − f_t(k) × vv(k) (3)

Change in vasculature cell count (dv) from k to (k + 1) interval will be:

dv(k) = vv(k + 1) − vv(k)

= f_vv × vv(k) − f_t(k) × vv(k) − vv(k)

= f_vv × vv(k) − vv(k) − f_t(k) × vv(k)

=[f_vv − 1 − f_t(k)]vv(k) (4)

In section 2.1, a full grown tumour system has been considered. Actually, the growth of tumour cells would depend on the availability of the microvasculature around the tumour. With increase or depletion of microvasculature cells around the tumour, the tumour system shifts to a different state. Here, we have considered four states, viz., vigorous, progressive, regressive and dormant. As the quantity of vasculature cells exceeds a threshold, the cells of the tumour double faster and thus, the tumour system progresses gradually to vigorous type. Similarly when the quantity of vasculature cells falls below a threshold, the growth factor stimulation as well as nutrient supply required for the growth of the tumour cells become restricted and thus the tumour system changes to more regressive or dormant type.

In the present model, we have changed f₁₁ and f₂₂ in four different ranges according to the availability of micro-vasculature cells at the cancer milieu. Within each range the selected coefficient remains constant and cell killing depends on the destruction of vasculature cells. Mathematically speaking, we are considering a piece-wise linear approximation of a highly nonlinear system. The simulation scenario is explained later in section 3.

2.3 Effect of anti-angiogenic (AAG) drug

An AAG drug is targeted towards the microvessel cells around the tumor. So an AAG drug kills the cells of the microvessels around the tumor. As a result the connection between the tumor and the systemic circulation is hampered and tumor cells die due to lack of necessary nutrition and oxygen. Hence, death of the tumor cells is indirect. Application of drug dose (f_t) will affect the vasculature cell count as expressed in eqn (4). The change in total tumor cell count (ΔC = Δc₁ + Δc₂) is due to change in vv in the following time interval as follows:

ΔC(k + 1) = cv × dv(k)

The change will be growth if dv(k) is positive and cells decay if dv(k) is negative. Here, cv represents a coefficient that is defined as the number of total tumor cells supported by each micro-vasculature cell. When multiplied with the change in amount of vasculature cells, it translates change in vasculature to change in number of tumor cells. We may take assuming that a full grown tumor requires vv(1) amount of vasculature to support a total tumor cell count [c₁(1) + c₂(1)] at the time of diagnosis and is considered as constant parameter.

Since there are two cell types that respond in different ways to change in vasculature, the cell count change gets modulated using proportion of corresponding cell type (ρ₁, ρ₂) and its sensitivity to anoxia (σ₁, σ₂). Here ρ₁ and ρ₂ are the proportion of a specific type of tumor cells with respect to total tumor cell population (normalized cell count) and may be represented as follows:

andSo the c₁ and c₂ ultimately will change as follows:

Δc₁(k + 1)=σ₁ × cv × ρ₁(k) × [f_vv − 1 − f_t(k)]vv(k) (6a)

Δc₂(k + 1) = σ₂ × cv × ρ₂(k) × [f_vv − 1 − f_t(k)]vv(k). (6b)

Combining Δc₁(k + 1) and Δc₂(k + 1) with eqn (1) after incorporating vv as a third state variable, we get the new 3 × 3 system matrix as represented in eqn (7) Here f_1v = σ₁ × cv × ρ₁(k) × [f_vv − 1 − f_t(k)] and f_2v = σ₁ × cv × ρ₂(k) × [f_vv − 1 − f_t(k)]. Thus the F and X of eqn (1) can be represented as:
This F matrix is time varying and since ρ₁, ρ₂ depend on c₁, c₂, respectively i.e., state variables, the F matrix is essentially nonlinear as well.

2.4 Incorporation of other therapies

It could be also advantageous that therapy with AAG drug could provide an opportunity to include other therapies such as adoptive immunotherapy (cellular therapy) or different immuno-boosting strategies through the use of biological response modifier. To incorporate immunity one has to consider the proportional cell killing corresponding to the immune therapy being used. Since no other state variable is involved, the diagonal terms of each cell type i.e., f₁₁ and f₂₂ are only affected by this immunity related cell killing. Taking the proportion of cells killed to be f_im1(k) and f_im2(k) at kth instant, the F matrix of eqn (7) gets modified to eqn (8):

2.5 Overall system model

We can represent the overall system through a block diagram as shown in Fig. 1. Tumour systems dynamics involves tumour cells along with microvasculature. Similarly, cell killing or growth involves both tumour as well as microvasculature cells. The desired systems state generally implies zero tumour load or a state with a minimum residual disease maintaining a dormant condition under the physiological homeostasis. The controller acts on the difference between actual and desired condition and resembles the therapeutic strategy. The delay block basically implements the delay-differential equation discussed earlier in this section. The adaptive block is responsible for tuning the tumour system parameters to the changing scenario of the pathophysiological system.

Fig. 1 Block diagram depicting the systems model.

3. Simulation results

With the above mentioned model rigorous simulation exercises have been carried out. The following information has been utilized in rationalizing the parametric values for simulation. Our previous simulation exercises established that the tumour system become uncontrollable if the doubling time of the tumour cells is less than three days and similarly, the system works well if the initial tumour load is less than 50 million cells.¹² Moreover, information are available regarding the presence of dormant cells in pre and post vascularization phases, in remission and even in apparently healthy individuals.¹⁹ We assumed that the dormant cells have higher doubling time. It is a general practice to represent data of vasculature through microvascular density (MVD) expressed as percentage vascular area/tumour area.²⁰ The absolute counts for microvessel is also available with wide variations and expressed per field area of (biopsy) tissue section—in one such literature it ranges from 98 to 323 mm⁻².²¹ From this data we have assumed 10 000 microvascular cells around the tumour for our simulation study. For simulation, application of AAG drug is assumed to have 15 days interval (an_cycle = 15 days) and retention of drug (an_ret) is assumed to be 80% of the preceding day—this means that the effect of the drug decays steadily and almost vanishes after two weeks. The amount of vasculature cell killing (f_t) is also translated/calibrated to the percentage of cells. The chosen initial parametric values are summarized in Table 1A and B. Considering the different amount of micro-vascular cells around the tumour, we have chosen a wide range of multiplication rates of the tumour cells (dormant to vigorous) which are depicted in Table 1B. In Table 1B, System II is more dormant type than System I, this may reflect the patient to patient variation found in reality.

Table 1 (A) Initial values for different variables/parameters used for the simulation. (B) Doubling time of the tumour cells depending on the different vasulature ranges used in simulation

Variable/Parameter	Symbol	Unit	Value	Comment
(A)
Tumour cell (sensitive type, s) count	c 1	Number of cells	4 × 10^6	Initial value at time of diagnosis
Tumour cell (resistive type, r) count	c 2	Number of cells	1 × 10^6	Initial value at time of diagnosis
Micro-vasculature cell count around tumour	vv	Number of Cells	1 × 10^4	Initial value at time of diagnosis
Multiplication rate of Micro-vasculature cells	f vv	Cells/day	1.045	Doubles in 15 days (Low)
			1.1045	Doubles in 7 days (High)
Anoxia sensitivity of s-type cells	σ 1	% of cells	1.0	Fully sensitive
Anoxia sensitivity of r-type cells	σ 2	% of cells	0.5	Half of the total cells resist
Duration between two successive drug application	an cycle	Day	15	Once in two weeks interval ref. 22 (Ferrara et al., 2004)
Amount of each drug dose	f t	cells day^−1	0.2 to 0.3	Fraction of microvessel cells destroyed on the day of drug application
Amount of drug retention on the subsequent day of drug application	an ret	% of drug of the preceding day	80%	Effectiveness decays, reaches almost 0 after 10 days
Coefficient denoting both type of tumour cells supported by one micro-vessel cell	cv	C cells/vv cell	500	Derived from initial values supplied for c1, c2, vv

---

Vasculature range (in cell number) [tumour type]	System-I		System-II
	Doubling time in days (f11)	Doubling time in days (f22)	Doubling time in days (f11)	Doubling time in days (f22)
(B)
0–500 [dormant]	25 (1.02811)	20 (1.03526)	90 (1.00775)	75 (1.0093)
501–5000 [regressive]	15 (1.04729)	12 (1.0542)	60 (1.0116)	45 (1.016)
5001–20 000 [progressive]	10 (1.0718)	6 (1.1225)	30 (1.024)	15 (1.048)
20 001–Above [vigorous]	5 (1.1487)	3 (1.2599)	10 (1.072)	7 (1.1045)

---

3.1 Role of the vasculature

Model has been developed with an assumption that in vivo situation the exponential growth of the micro-vasculature cells facilitates the growth of both the sensitive and resistive type of cells. Slope in the semi-log plotting denotes the change in doubling time of each type cells (Fig. 2). With decrease in vasculature cell multiplication rate (f_vv) there will be decrease in cell count of each type of tumour cell over a certain period of time (Table 2). So vasculature cell multiplication rate, in turn, denotes the vigorosity of the tumour type. Micro-vasculature cell growth dynamics is shown in Fig. 3. In both the figures steady vasculature (f_vv = 1) actually represent the cellular growth dynamics of our earlier model.¹²

Fig. 2 Role of micro-vasculature on tumour cell growth and its therapy—(a) sensitive type cell, and (b) resistive type cell. Slope denotes the change in doubling time of sensitive (c) and resistive type cell (d). In the plots, tumour cells are growing with a fixed doubling time of 5 (sensitive type of cells) and 3 (resistive type of cells) days [as shown ‘with steady vasculature’], a varying doubling time with f_vv = 1.045 [as shown ‘when vasculature grows’] and a varying doubling time with f_vv = 1.045 and f_t = 0.25 [as shown ‘when vasculature is treated’].

Fig. 3 Micro-vasculature cell growth dynamics in different condition—with steady vasculature growth rate, multiplying with a growth rate and treated with AAG drug when vasculature cells are growing with a growth rate. Effect of drug on vasculature cells growth dynamics when vasculature cells are multiplying with a rate (b). Corresponding plots [untreated (c) and treated (d)] shows how change in vasculature due to AAG drug treatment are affecting the multiplication rate (doubling time) of both the sensitive and resistive type of cells. In the plots vasculature grows means f_vv = 1.045 and treatment condition is with f_vv = 1.045 and f_t = 0.25.

Table 2 Comparison of cell count of the tumour system after 100 days in untreated (f_t = 0) and treated (f_t = 0.2, f_t = 0.25 and f_t = 0.3) condition with different vasculature growth rates (f_vv) (high and low). The parameters are as mentioned in Table 1A and B

Drug dose (ft)	Growth rate of vasculature cells (fvv)	Number of vasculature cells (vv)	System-I		System-II
			s-type (c1)	r-type (c2)	s-type (c1)	r-type (c2)
f t = 0	High	1.8106 × 10^8	7.5542 × 10^12	6.7749 × 10^15	2.0562 × 10^11	1.1156 × 10^11
	Low	7.8075 × 10^5	2.0709 × 10^12	1.749 × 10^15	6.5319 × 10^9	1.5503 × 10^10
f t = 0.2	High	3.078 × 10^5	1.0633 × 10^12	9.1943 × 10^14	3.3868 × 10^9	1.0003 × 10^10
	Low	904	6.0537 × 10^8	1.459 × 10^9	1.0362 × 10^7	8.4984 × 10^6
f t = 0.25	High	5.5209 × 10^4	1.6144 × 10^11	5.2021 × 10^13	7.165 × 10^8	2.26 × 10^9
	Low	145	2.2911 × 10^8	3.7135 × 10^8	6.126 × 10^6	4.4336 × 10^6
f t = 0.3	High	9.343 × 10^3	4.0805 × 10^9	1.4682 × 10^11	4.1234 × 10^7	1.2194 × 10^8
	Low	21	1.1911 × 10^8	1.6037 × 10^8	4.347 × 10^6	3.0107 × 10^6

---

3.2 Effect of the AAG drug on the system

For the therapeutic assessment simulation exercises are also carried out. The parametric values of different variables are depicted in Table 1. Fig. 2 and 3 show how the multiplication of drug affects both the tumour cell types and vasculature cells when vasculature cells are growing with a multiplication rate. With the change in the vasculature cell number due to application of AAG drug, tumour system is shifted to different state; hence, doubling time of the tumour cells are varying in the time dynamics (Fig. 2 and 3). In Table 2 it is depicted the effect of drug application on the individual cell types of tumour and vasculature cells in different growth conditions of vasculature cells (f_vv). It is observed that keeping the other factors unchanged, therapeutic outcome in response to AAG drug is more efficient with the decrease in the multiplication rate of vasculature cells. An initial phase lag of 5 days is considered before AAG drug is become effective.

Different combinations of anoxia sensitivity have been tested also. This shows that the dynamical trend varies and the tumour load (cell count) is altered as expected. As shown in Fig. 4 the tumour load grows more abruptly when the resistive cell type responds to anoxia with more resistance.

Fig. 4 Tumour cell dynamics with different anoxia sensitivity for the resistive type cells while anoxia sensitivity for other type cells remains unchanged, in (a) behavior of the resistive type cells, and (b) behavior of the total tumour load. In the plots all treatment conditions are shown with f_vv = 1.045 and f_t = 0.25.

4. Analytical studies on the model

When f_vv ≥ 1 but f_t = 0 tumour cells grow. Model is formulated with the assumption that in vivo condition the growth of the vasculature cells provides the necessary growth factors and nutrients for growing of tumour cells and f_t acts as an external forcing function to inhibit the tumour cell growth. When (f_vv − f_t − 1) < 0, f_t is able to control tumour growth and when (f_vv − f_t − 1) > 0, f_t fails to control tumour growth.

The above system is a time varying nonlinear system even within each piece-wise linear state of the tumour system, so determination of controllability criteria at different time points would not be feasible. In the model eqn (7), the F matrix has two nonlinear components: f_1v and f_2v (due to ρ₁ and ρ₂). However, the controllability criteria can be assessed in a better way if the system is linear. By fixing the ρ₁ and ρ₂ to the initial proportions in the iterative process, the system can be approximated to a linear system in each piece-wise linear interval. We have compared the cellular dynamics of the actual nonlinear system with the approximated linear system by keeping the vasculature growth dynamics identical in both cases. Fig. 5 reveals that the approximated linear system is staying above the actual system in terms of cell count. This means that we can consider the linear system as an upper bound to the actual behaviour of the tumour. Therefore from this analysis we can make a comment that the linearized system can give us a caution signal about the actual tumour system. In such a situation, a linearized system can help to make an assessment and characterization of the nonlinear system as the worst case may be manifested through the linear system and can be useful to analyze the controllability.

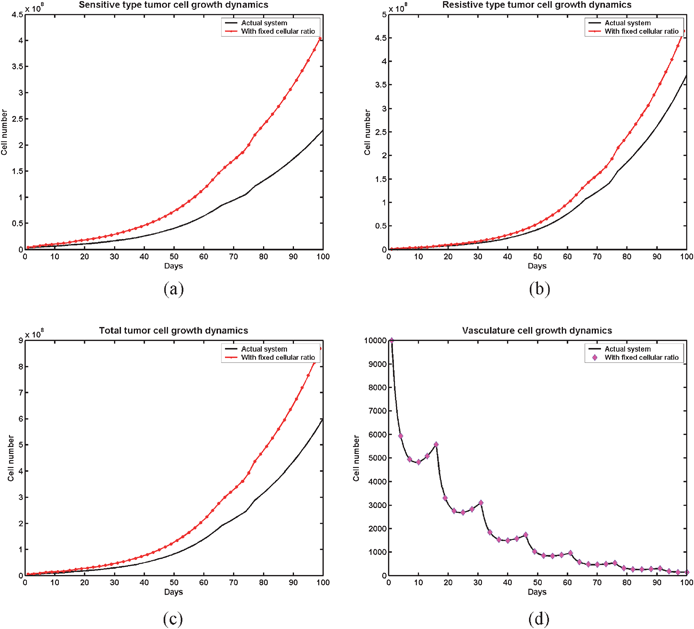Fig. 5 Comparative analysis of the cellular behavior in the actual nonlinear system and in the approximated linearized system during the course of an AAG drug—behaviour of (a) sensitive type cell, (b) resistive type cell, (c) total tumour load and (d) vasculature cell. All the plots are with the condition of f_vv = 1.045 and f_t = 0.25.

With the parameter settings as mentioned in Table 1, Eigenvalue determination reveals that tumour cells are not controllable. To achieve a control over tumour cells, excessive increase in AAG drug dose or frequent dosing strategy is needed. To make the tumour cells controllable immunity factors f_im1 and f_im2 or other sorts of therapeutic intervention which can kill the tumour cells directly should also be in operation (data not shown).

However, here controllability criterion assessment may not be the determinant factor in the assessment of tumour dynamics. As mentioned earlier in section 2, tumour systems model has been developed with the piece-wise linear approximation in terms of microvasculature availability. One main objective of this model is to track how fast the tumour system reaches another state by depletion of the microvasculature cells. Hence, the microvessels dynamics, as its secondary effect, reveal whether or not tumour cell load is manageable (and not unbounded) during the course of a treatment schedule.

5. Discussion

In this work we have attempted to decouple the role of the vasculature in the growth of tumour. Change in the rate of vasculature growth (f_vv) provides the handle to tackle the differential effect of vasculature on the growth of the tumour cells. However, the role of MCT, as mentioned in our earlier modeled version can also be tracked through this model.¹²

Though in an attempt the use of fluid dynamical approach, tumour angiogenesis and blood flow has been modeled during the early process of tumour development, however, discrete changes in the number of vasculature cells and the effect of angiogenesis on the tumour system cannot be assessed.^4,5 Hence, development of analytical model for direct correlation between the change in the number of micro-vasculature cells and the change in tumour cells number would be advantageous for tracking the tumour system at discrete time intervals. This may have an immense implication towards the development of AAG therapy design together with MCT strategy.

It is worthwhile to mention here that during anti-angiogenic treatment free interval MVD at tumour bed can resume their proliferation and support tumour growth. Moreover, disease remission is not always accompanied with the decrease in MVD in different cancer cases. So the therapeutic efficacy of the AAG drug and MVD remains controversial, however, at present, MVD is accepted as a prognostic indicator.¹ We hope that this analytical model will provide the necessary tool to oncologists to reassess, resolve and pin-pointing this issue.

It is difficult to make an assessment and prediction of the controllability criterion if the system is non-linear, hence we have studied the differences in the output by transforming the system to a linear system. Our simulation study shows that the dynamical behavior of the vasculature cells in response to an AAG therapy is same in both the linearized system and nonlinear system though tumour cells behave differently. Hence, we can make a comment that under such condition controllability criteria assessment can make a clue about nonlinear system. However, from our simulation we have observed that under such condition, controllability of the tumour cells cannot be possible (as eigenvalues stay above 1) without increase in drug dose excessively; though slight increase in drug dose make a better controllability for the growth of vasculature cells.

It is reported in literature that AAG drug has also some sorts of toxicity.^3,23 With settings of the parametric values as mentioned in Table 1, simulation study also reveals that with the progress of time as the micro-vasculature cells become less, their effect on the tumour cells diminishes. Under such condition complete removal of tumour cells is not possible. This condition may tend to be more favourable for the tumour system if the multiplication rate of the tumour cells is enhanced. To achieve a control over the tumour cell growth under such condition, incorporation of other therapeutic strategy which can directly kills the tumour cells is becoming a necessity. Such strategy could be immunity mediated cell killing, as pointed earlier.

Clinical trials with several AAG drugs have revealed that there is a large variation of individual’s response to a certain drug. Calibration of dosage along with the therapeutic scheduling is presently a challenge. Conventionally this is done with the population based analysis of snap-shot data after the application of same drug to the patients with same pathological criteria. However, due to variations at several layers—starting from the molecular characteristics of the tumour type to the individual patient’s pathophysiological constraints under the condition of malignancy, therapeutic outcome may differ. So the expected therapeutic outcome at the individual level may be hampered. Moreover, in the majority of the available analytical model of tumour, the system is tracked through tumour diameter or volume. However, it may not represent the actual tumour load as tumour system is consisting of a heterogeneous mass of cells where morphologically normal cells may present also.

The present analytical approach may help in overcoming those limitations. In the arena of systems biology it is necessary to develop a realistic analytical model with respect to its implementation i.e., the measured parameters could easily be fitted into that analytical model for the design of a therapy. Therefore the different variables have been chosen in association with the clinical feasibility of their measurement. The measured parametric values can be adjusted easily in this model by an investigator for individual cases—as the model is flexible in nature. Simulation exercises presented here show the importance of each variable and provide the bounds of the parametric values that would be helpful for its realistic translation.

The parametric comparison of the in vitro growth rate and in vivo growth rate can be easily adjusted. Vasculature cell density, tumour cell number and types can be determined by biopsy examination followed by DCE-MRI. Biopsy samples are subjected to in vitro culture for the determination of the respective cell type growth rate, death rate and conversion rate, if any. Tracking of the system can be done by MRI analysis within a short span of time. Thus the parametric calibration and a correlation can be made through noninvasive technique. Vasculature has the added advantage of tracking the system through DCE-MRI.^24–26 It is to be pointed out that though in literature the data are generally presented as MVD, however, the number of micro-vessels is counted in biopsy samples through immunohistochemistry. Hence, the preparation of single cell suspension of the biopsy sample followed by flow cytometric determination of the ratio of the tumour cells to vascular cells may helpful to calibrate the parameters to fit into this model.

The potentiality of this model is better judged if one follows the predict-observe-correct cycle. This means that before application of a drug the parametric values of different variables are determined. This, in turn, helps in the initial parametric setting of the model. After application of a certain drug for a period of time, the same variables are measured. Thus the deviation, if any, is determined and then again set the model for a long term therapeutic assessment. Thus decision on the calibration of dosage and therapeutic schedule can be formulated. This model along with our earlier model¹² also helps in making a switching decision between different drugs and/or therapies. Thus a better outcome could be expected.

Acknowledgements

Authors acknowledge Dr Sthabir Dasgupta, Consultant Oncologist for his helpful discussion on anti-angiogenic therapy in cancer.

References

1. R. S. Kerbel and J. Folkman, Nat. Rev. Cancer, 2002, 2, 727–739.
2. R. S. Kerbel and B. A. Kamen, Nat. Rev. Cancer, 2004, 4, 423–436.
3. E. A. Donovan and S. Kummar, Curr. Probl. Cancer, 2006, 30, 7–32.
4. S. R. McDougall, A. R. A. Anderson and M. A. J. Chaplain, J. Theor. Biol., 2006, 241, 564–589.
5. A. R. A. Anderson and M. A. J. Chaplain, Bull. Math. Biol., 1998, 60, 857–899.
6. H. B. Frieboes, J. S. Lowengrub, S. Wise, X. Zheng, P. Macklin, E. Bearer and V. Cristini, NeuroImage, 2007, 37, S59–S70.
7. S. M. Wise, J. S. Lowengrub, H. B. Frieboes and V. Cristini, J. Theor. Biol., 2008, 253, 524–543.
8. E. L. Bearer, J. S. Lowengrub, H. B. Frieboes, Y.-L. Chuang, F. Jin, S. M. Wise, M. Ferrari, D. B. Agus and V. Cristini, Math. Oncol., 2009, 69, 4493–4501.
9. V. Cristini, X. Li, J. S. Lowengrub and S. M. Wise, J. Math. Biol., 2009, 58, 723–763.
10. P. Macklin, S. McDougall, A. R. A. Anderson, M. A. J. Chaplin, V. Cristini and J. Lowengrub, J. Math. Biol., 2009, 58, 765–798.
11. D. Ribatti, C. Scavelli, A. M. Roccaro, E. Crivellato, B. Nico and A. Vacca, Stem Cells Dev., 2004, 13, 484–495.
12. A. Mukherjee, D. Majumder and A. Icbal, J. Biol. Syst., 2006, 14, 1–12.
13. D. Majumder and A. Mukherjee, J. Biol. Syst., 2006, 14, 631–650.
14. D. Majumder and A. Mukherjee, Proc 1st Int Conf Comput Syst Biol, Shanghai, China, 2006, pp. 68–73. (presentation detail available in web: http://life.fudan.edu.cn/ICCSB/idates.html).
15. A. Mukherjee and D. Majumder, BioSystems, 2008, 91, 108–116.
16. D. Majumder and A. Mukherjee, IET Syst. Biol., 2007, 1, 298–305.
17. I. Pan and D. Majumder, Int. Conf. Biomed. Imag. & Health Care Engg., IEEE (Madras) & CSI, ID-IC1508, 6–8 Aug., 2009, pp. 19–22.
18. I. Pan and D. Majumder, Int. Conf. Innovat. Tech., IEEE-IMS/EMBS (Delhi), 18–19 June, 2009, P38, pp. 212–216.
19. P. Hahnfeldt, J. Folkman and L. Hlatky, J. Theor. Biol., 2003, 220, 545–554.
20. L. Hlatky, P. Hahnfeldt and J. Folkman, J. Natl. Cancer Inst., 2002, 12, 883–893.
21. P. B. Vermeulen, D. Verhoeven, H. Fierens, G. Hubens, G. Goovaerts, E. Van Marck, E. A. De Bruijn, A. T. Van Oosterom and L. Y. Dirix, Br. J. Cancer, 1997, 76, 40–43.
22. N. Ferrara, K. Hillan, H.-P. Gerber and W. Novotny, Nat. Rev. Drug Discovery, 2004, 3, 391–400.
23. S. Banerjee, M. Dowsett, A. Ashworth and L.-A. Martin, Nat. Clin. Pract. Oncol., 2007, 4, 536–550.
24. A. R. Padhani, J. Magn. Reson. Imaging, 2002, 16, 407–422.
25. E. Furman-Haran, F. Kelcz and H. Degani, J. Exp. Clin. Cancer Res., 2002, 21(3), 47–54.
26. H. Degani, M. Chetrit-Dadiani, L. Bogin and E. Furman-Haran, Thromb. Haemost., 2003, 89, 25–33.

---