The European bathing water directive: application and consequences in quality monitoring programs†
Iago
López Martínez
*,
César
Álvarez Díaz
,
José Luis
Gil Díaz
,
José A.
Revilla Cortezón
and
José A.
Juanes
Submarine Outfall and Environmental Hydraulics Group (GESHA), Environmental Hydraulics Institute (IH Cantabria), Universidad de Cantabria, Avda. de los Castros, s/n., 39005, Santander, Spain. E-mail: lopezy@unican.es; alvarezc@unican.es; giljl@unican.es; revillaj@unican.es; juanesj@unican.es; Fax: +34 942201714; Tel: +34 942201704
First published on 11th August 2009
Abstract
The calculation of percentiles proposed in the Directive 2006/7/EC (parametric approach) to evaluate bathing water quality uses two parameters: mean (µ) and standard deviation (σ). These two parameters are good descriptors of data populations only when data are log normally distributed. Several previous studies have shown that a log transformation is sufficient to achieve normality, while other studies suggest that log normality in bathing water quality datasets is seldom attained. In our study, log normality was achieved in 59.6% of the cases. In order to try to obtain a transformation parameter for Box-Cox (λ) that provides the best fit and perhaps normality in bathing water datasets, the maximum likelihood estimation (MLE) method was applied to 40.4% of the remaining (non log normal) datasets. Results show that there is no transformation parameter that ensures normality for all datasets. In fact, normality is only reached in 10.3% of these datasets but, in these cases, the parametric approach seems to be a good one to evaluate bathing water quality. In cases where normality was not fulfilled even by application of the MLE method, a non-parametric approach to calculate percentiles is considered the most appropriate one. When percentile values obtained through the parametric and non-parametric Hazen approaches are compared, it is shown that the percentage of bathing waters changing their classification is low (12.3%). In these cases, the Hazen approach provides the worst classification in a vast majority of cases (90.6%), being this change important in some cases, in which classification is downgraded from having “Excellent” to “Sufficient” quality. Therefore, the Hazen approach is more appropriate for calculating percentiles, since it provides better estimators of percentile values. Furthermore, this method involves a more conservative approach for the classification of bathing water quality, providing an additional security for bathers’ health. The fact that normality is not fulfilled and that classification of bathing waters could change must be considered by policymakers in order to adopt an alternative method for evaluating bathing waters quality.
Environmental impactThe selection of an appropriate method to evaluate bathing water quality is an important issue that could help the management of these areas. In this sense, the method established in the Directive 2006/7/EC seems to be inappropriate in several cases, as they do not represent adequately the bacteriological quality state of bathing waters. The paper shows a procedure to be applied in these areas in order to select the most appropriate method to evaluate bacteriological quality that can be used for European managers to, firstly, correct the quality evaluation method, due to the close relation between bacteriological concentrations and adverse health outcomes for bathers, and secondly, to gain a better knowledge of water quality state. |
1. Introduction
The Directive 76/160/EEC was the first legislative approach that established a set of quality criteria to be fulfilled for bathing waters in Europe. Hence, it improved bathing water quality through implementation of different Quality Monitoring and Assessment Programs. However, the technical and social advances during the last decades have forced authorities to review the criteria and methods used to classify bathing waters.As a result of these advances, a new Directive (Directive 2006/7/EC) was approved with the general goal of protecting public health through the improvement of the bacteriological quality state of bathing waters. This new approach included several changes, the most important relating to the method used to evaluate bathing water quality, which was based on a percentile calculation, subject to the fulfilment of the parametric condition of normality of the data.
In bathing water quality data, difficulties often arise because the raw data are strongly asymmetric. A transformation to alter the shape of the distribution of the raw data might help to alleviate this problem. Apart from the fact that a symmetric dataset is easier to analyse, many statistical procedures require data to be approximately normal. Hence, a transformation that allows the dataset to achieve normality is often used1 in several research fields, such as hydrology,2 finances,3 environment4,5 and many others. Several former studies show that normality is not always fulfilled by bathing water quality data,6 even after applying the log-transformation proposed by the Directive 2006/7/EC for non-normal data sets, while other authors have proved differently.7
To obtain normality is usual to transform raw datasets through the application of a parameter transformation value (λ), generating a transformed dataset. Transformations are commonly applied because they are assumed to remove heteroscedasticity from the data and, hence, they induce symmetry and perhaps normality to the probability distribution of the variable in question8 ensuring that transformed data are, approximately, Gaussian.9,10 Changing the scale of measurement is natural because it provides an alternative way of reporting the information.5
Nevertheless, transformations do not ensure achievement of normality and, therefore, parameters that define populations with normal distributions: the mean (µ) and the standard deviation (σ), do not represent populations in cases where normality is not fulfilled. As a matter of fact, these parameters are used to calculate percentile values following the Directive 2006/7/EC and, consequently, to evaluate bathing water quality.11
At this point, two aspects must be considered. First, when a normal distribution is achieved with a specific parameter transformation value (λ), the parametric approach is an appropriate method for evaluating bathing water quality. Nevertheless, the original dataset should be transformed according to the parameter value obtained and percentiles calculation should be carried out accordingly.
The second aspect to take into account is that in those cases in which the normality hypothesis is not fulfilled, a non-parametric method can be applied for evaluating bathing water quality. This has the advantage that non-parametric methods don't need a specific data distribution to be applied and, therefore, data do not have to be transformed. These methods generally have greater power than a parametric approach applied on non-normal data,12 since this results in a skewed dataset and, hence, renders the parametric approach with a higher degree of statistical errors than the non-parametric one.6
In both cases, a new problem will be presented when bathing water quality is evaluated. In the first case, although the parametric approach may be adequate, it should be carried out considering the λ optimum based transformation used to achieve normality and not the log transformation established in the Directive 2006/7/EC. In the second case, the aforementioned Directive establishes that percentile values should be calculated according to a parametric method, even in cases where normality is not achieved. This can lead to obtaining percentile values different to those provided by a non-parametric approach. Consequently, it is possible that bathing water classifications may vary depending on the evaluation method employed or even on the type of transformation used.
All these factors have been poorly studied leading to shortcomings in bathing water quality management, especially in the socio-economic impact produced by these inaccuracies. Such limitations must be taken into account by authorities to provide a better and more precise knowledge of the bathing water environment. This paper provides help for the management of bathing water areas.
Therefore, the goals of this paper are the following: firstly, to analyse the log normality distribution of bathing water datasets in order to determine if the parametric approach established in Directive 2006/7/EC is an appropriate method to assess bathing water quality; secondly, to find a transformation parameter that provides a normal distribution in those datasets in which the log transformation does not achieve it, in order to consider a different approach than the one established in the Directive; finally, to analyse the impact on the bathing water classification using a parametric and a non-parametric approach in those datasets that are not normally distributed.
2. Materials and methods
2.1. Source data and study area
The study was conducted in the Balearic Islands (Spain), that are an archipelago formed by 5 principal islands and many islets located in the Mediterranean Sea. Representing 0.16% of the European Union's area and 0.24% of its population, the islands receive more than 10 million visitors in the summer,13 which makes them an important touristic and economic resource. The study area and the location of the sampling points are shown below (Fig. 1). | ||
| Fig. 1 Location of the study area and sampling points (black dots). | ||
Microbiological water quality data were collected in 188 bathing waters in the Balearic Islands, during the bathing seasons from year 2001 to 2005. Datasets of each sampling point have been constructed considering samples of 4 consecutive bathing seasons, 2001–2004 and 2002–2005.
Since 8 of these sampling points didn't have enough data, only 180 were analysed. Hence, 4 datasets were constructed for each sampling point, 2 for the Escherichia coli (E. coli) indicator and 2 for the faecal streptococci (FS) indicator (both indicators being evaluated during the two aforementioned periods, 2001–2004 and 2002–2005). Therefore, 720 bathing water quality datasets were constructed for the 180 sampling points.
In order to comply with the indicators proposed by the Directive 2006/7/EC (E. coli and intestinal enterococci (IE)), it is necessary to establish the relationship between the FS and IE concentrations. For this reason, the Directive allows to apply a ratio of 1:1 to bacteriological samples of FS providing, consequently, bacteriological datasets of IE.
When data were plotted as histograms, these were more or less asymmetric but, in all cases, a positive skew was shown. An example of the different levels of asymmetry observed in the datasets is shown in Fig. 2.
 | ||
| Fig. 2 Different levels of asymmetry observed in bathing water quality datasets from the Balearic Islands, for the E. coli indicator. | ||
In order to appreciate the nature of the data, a statistical description of bathing water quality data is shown for 180 of the 360 datasets corresponding to the E. coli indicator, from the 2001 to 2004 period (Fig. 3).
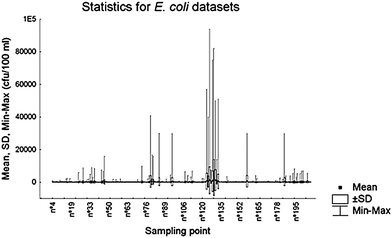 | ||
| Fig. 3 Statistics (mean, standard deviation (SD) and maximum and minimums) for 180 E. coli datasets from the 2001 to 2004 period. | ||
2.2. Maximum likelihood estimation (MLE) method
Given a data vector y = (y1, y2, …, yn) and a parameter value, λ, it is possible to generate a probability distribution function. Integrating this function, the probability density function (PDF) is obtained, which specifies the probability of observing a data vector given a transformation parameter value. The transformation parameter is multidimensional in space, λ = (λ1, λ2, …, λn), so it is possible to generate a PDF for each value of the λ parameter.14 Therefore, the PDF for the data vector y, given the parameter vector λ, can be expressed as a multiplication of the PDFs for individual observations:| f (y) = (y1, y2, …, yn|λ) = f1 (y1|λ)·f2 (y2|λ)…fn (yn|λ) |
The goal of this procedure is to seek the transformation parameter value that best fits the given data. An easier method to reach this goal is based on the likelihood function, reversing the roles of the data vector, y, and the parameter vector, λ.14
| L(λ|y) = f(y|λ) |
Thus, L(λ|y) represents the likelihood of the parameter λ given the observed data, y, and as such, it is a function of λ.14 Once data have been collected and the likelihood function of a model determined, it is possible to make statistical inferences about the population, that is, the probability distribution that underlies the data. In this sense, the aforementioned parameter value can be found in several ways. One of the best approaches is to use the maximum likelihood estimation (MLE) method, which provides a change of scale depending on the transformation parameter value. This method provides a consistent approach to parameter estimation problems and has desirable mathematical and optimality properties, the main one being that it minimizes the variance of the data, narrowing the confidence interval of the estimator value.15
By focusing on the MLE method, we have to take into account that the principle of MLE16 states that the desired probability distribution is the one that makes the observed data “most likely”, which means that one must seek for the value of parameter λ that maximizes the likelihood function, i.e., the one that provides the best fit, in a procedure called parameter estimation. Such λ value, which is found by searching the multi-dimensional parameter space (the whole range of parameter values), is called the MLE estimate.14 This procedure has been used in many environmental fields, such as air quality studies,17 in order to provide transformed datasets with the best fit to a normal distribution and to obtain the aforementioned normal distribution.
2.3. Application of the MLE method to bathing water quality datasets
First, log normality of 720 datasets was analyzed using the Kolmogorov–Smirnov test (α = 0.05). In the cases in which log normality was not fulfilled, the MLE method was applied, in order to analyse the parameter value λ that provides the best fit for bathing water quality datasets.Therefore, it is necessary to transform the data. One of the most important methods of transformation is the Box-Cox transformation,18 which allows the transformation of raw data, y, into transformed data, depending on λ, as follows (1):
 | (1) |
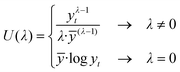 | (2) |
 | (3) |
 | (4) |
 | (5) |
As we mentioned above, this procedure was applied to those datasets that did not achieve log normality. The statistics software MATLAB® R2007a was used to calculate the optimum λ for each dataset and to analyze the normality of the transformed datasets.
2.4. Impact of the parametric approach in bathing water classifications
As a result of the application of the MLE method and the analysis of normality, the transformed datasets can, or not, reach normality. In the cases of datasets that did fulfil normality, the results of percentile considering the parametric approach by application of the λ optimum based transformation and those following the suggestion of the Directive were compared.In the remaining cases, we analysed the impact of the implementation of the parametric method on bathing water quality. So, the percentile values were calculated through the application of the parametric method established in the Directive 2006/7/EC and a non-parametric method.
Non-parametric methods are based on ranked data in ascending order and then, using a formula, determining which point gives the desired percentile. There are several non-parametric methods and, consequently, each one provides different percentile values because the interpolation formula is different for each method. The Hazen method20 was chosen as it is the one that gives the best non-parametric estimate of the percentile value.21 The interpolation formula of the Hazen method is described as follows (6):
 | (6) |
Percentile values obtained for each bathing water quality indicator were classified within the standards established in the Directive 2006/7/EC in order to determine the incidence of both methods in the percentile values and, therefore, in the bathing water quality classification. These standards are shown in Table 1.
As shown in Table 1, the 95th percentile values should be always calculated; the use of the 90th percentile should be considered only in those cases in which “Excellent” or “Good” quality standards are not reached.
3. Results
3.1. Log normality analysis
Table 2 shows the results of the Kolmogorov–Smirnov test conducted on the 720 bathing water quality datasets after log transformation (λ = 0).| E. coli datasets | IE datasets | Total datasets | ||||
|---|---|---|---|---|---|---|
| 2001–2004 | 2002–2005 | 2001–2004 | 2002–2005 | 2001–2004 | 2002–2005 | |
| Log normal datasets | 106 | 105 | 115 | 103 | 221 | 208 |
| Non log normal datasets | 74 | 75 | 65 | 77 | 139 | 152 |
| Total datasets | 180 | 180 | 180 | 180 | 360 | 360 |
429 out of the 720 datasets (59.6%) fulfilled log normality, 221 during the period 2001–2004 and 208 in the 2002–2005 one. This percentage was similar for both E. coli and intestinal enterococci (IE), for which normality was achieved in 211 out of 360 datasets (58.7%) and 218 out of 360 datasets (60.6%), respectively. In these cases, the parametric approach established in the Directive 2006/7/EC is appropriate as the data fulfil the normality hypothesis.
The percentage of non log normality fulfilment (40.4%) in our study is much lower than the one found by other authors, i.e. non log normality in 85% of cases.6
3.2. Application of the MLE method for non log normal datasets
To obtain the optimum λ value through the MLE method, plots were generated for each bathing water quality dataset. An example for sampling point no. 70 is shown in Fig. 4. | ||
| Fig. 4 Example of optimum λ value obtention using the maximum likelihood estimation method for sampling point no. 70. This value is the one that maximizes the log L(λ) function. | ||
In the case of the Box-Cox transformation, the optimum λ value of a sample distribution was calculated. The optimum value of sampling point no. 70 is at λ = −0.4, which is the one that maximizes the log-likelihood function (log L(λ)).
Table 3 shows the number of datasets in which different λ values provide the best fit to a Gaussian distribution (λ optimum) and the number of these datasets that fulfil the condition of normality (normality).
| E. coli datasets | IE datasets | Total datasets | ||||
|---|---|---|---|---|---|---|
| λ optimum | Normality | λ optimum | Normality | λ optimum | Normality | |
| 0 < λ < 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| −0.5 < λ < 0 | 17 | 5 | 25 | 6 | 42 | 11 |
| λ = −0.5 | 99 | 11 | 79 | 8 | 178 | 19 |
| −1 < λ < −0.5 | 1 | 0 | 9 | 0 | 10 | 0 |
| λ = −1 | 21 | 0 | 24 | 0 | 45 | 0 |
| λ < −1 | 11 | 0 | 5 | 0 | 16 | 0 |
| Total | 149 | 16 | 142 | 14 | 291 | 30 |
The λ value that provides the best fit to bathing water data is −0.5, which provides the best fit in 178 out of the 291 datasets (61.1%). Other λ values, such as −1 and the range between −0.5 and 0, provide the best fit for several datasets, but percentages are much lower in both cases, 15.4 and 14.4%, respectively.
The number of datasets that fulfilled normality after performing transformation with the optimum λ value was 30 out of 291 (10.3%). This percentage was similar for the E. coli (10.7%) and IE (9.9%) datasets. The highest percentage of normality fulfilment was obtained for those datasets that use a λ value between 0 and −0.5 as a parameter transformation, and that achieved normality in 11 out of 42 datasets (26.2%). Whereas datasets that employ λ = −0.5 as a parameter transformation achieved normality in 19 out of 178 datasets (10.7%). It is important to note that, in those cases where normality was fulfilled, one should have calculated the percentile values using the λ optimum based transformation instead of the log transformation suggested by the Directive (λ = 0).
3.3. Impact of the evaluation method in bathing water classification
The impact on the bathing water classification was analysed for the 291 datasets that did not fulfil log normality. As it was mentioned above, we compared the results considering the parametric approach by application of the λ optimum based transformation and those following the suggestion of the Directive in those datasets that achieve normality (n = 30). In the remaining cases, where normality was not fulfilled, we compared the Directive's approach with the non-parametric Hazen method.In the first case, no differences between classifications were found (results not tabulated), probably because percentile values are very different from those that are used as a limit between classifications.
Regarding those cases in which normality was not fulfilled, Table 4 shows the classification obtained for each dataset considering both the parametric and the Hazen approaches. In the case of E. coli, 116 datasets achieved the “Excellent” quality classification with both the parametric and the Hazen approaches, while 6 datasets got the “Excellent” classification with the parametric approach but only “Good” with the Hazen method.
| Parametric method | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E. coli datasets | IE datasets | Total datasets | |||||||||||
| Excellent | Good | Sufficient | Insufficient | Excellent | Good | Sufficient | Insufficient | Excellent | Good | Sufficient | Insufficient | ||
| Hazen method | Excellent | 116 | 0 | 2 | 0 | 108 | 1 | 0 | 0 | 224 | 1 | 2 | 0 |
| Good | 6 | 3 | 0 | 0 | 15 | 2 | 0 | 0 | 21 | 5 | 0 | 0 | |
| Sufficient | 5 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 6 | 1 | 0 | 0 | |
| Insufficient | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |
| Total number of datasets | 133 | 128 | 261 | ||||||||||
Table 4 shows that 32 out of the 261 bathing waters analyzed (12.3%) got different a classification level when comparing both methods to evaluate percentiles. In 29 out of 32 bathing waters (90.6%), the classification level became worse with the Hazen (non-parametric) method, whereas the remaining 3 bathing waters (9.4%) improved their classification level with the aforementioned method.
Of those 32 datasets that had different classification level between methods, 14 belonged to the E. coli indicator and the remaining 18 to the IE indicator. For E. coli, 12 out of 14 datasets (85.7%) of bathing water classification became worse when the Hazen method was applied. In the case of IE, the same occurred with 17 out of 18 datasets (94.4%).
Although the application of non-parametric methods affects the quality of a low percentage of bathing waters, and according to Chawla and Hunter (2005),6 it is interesting to note that, in some cases, this change in classification can be dramatic: in our study, 6 beaches were downgraded from having “Excellent” to “Sufficient” quality.
Fig. 5 shows the bathing water classification of the Balearic beaches under study using the parametric and the Hazen approach, both for the E. coli and the IE datasets, for the period 2002–2005. During this time, the classification of 17 datasets (8 for E. coli and 9 for IE) was affected by changes in the evaluation method (Fig. 5).
 | ||
| Fig. 5 Bathing water classification of 17 Balearic beaches considering the parametric (left maps) and the Hazen (right maps) approach for E. coli (upper maps) and IE (lower maps), during the evaluation period 2002–2005. ■, □ and ▲ markers stand for “Excellent”, “Good” and “Sufficient” quality, respectively. | ||
Similarly, the classification status of 16 out of 17 bathing water datasets (94.1%) obtained worse results, while only one improved using the Hazen approach.
4. Discussion
When bathing water quality datasets from the Balearic Island were analysed, log normality was achieved in 59.6% of cases. In these cases, the parametric approach established in the Directive 2006/7/EC is appropriate to calculate percentile values and, consequently, to evaluate bathing water quality. In these cases, mean (µ) and standard deviation (σ), the parameters used to evaluate percentiles, are good descriptors of the dataset.Nevertheless, in the remaining cases (40.4%), log normality was not fulfilled. In these instances, the mean value is not a good estimate of the central value of data22 and, therefore, the parametric method established by the Directive 2006/7/EC is not an appropriate method to assess bathing water quality. In these cases, the transformed datasets were obtained by application of the optimum λ value through the maximum likelihood estimation (MLE) method. All λ parameters obtained were negative, resulting in a positive skew, which is common in environmental quality data.23,24 Only 10.3% of the cases attained a normal distribution when λ optimum based transformation was applied.
The comparison of the results considering the parametric approach by application of the λ optimum based transformation and those following the suggestion of the Directive did not show differences in bathing waters classification. This suggests that the log transformation established by the Directive 2006/7/EC is a suitable transformation and, therefore, the parametric approach is an appropriate method for evaluating bathing water quality, whenever the normal distribution of the data is reached, a fact that cannot be known a priori.
However, although differences in the classification were not found, these can be present in other places. For this reason, the parametric method is still a good approach for evaluating bathing water quality, but considering percentile calculation with the λ optimum instead of the logarithm transformation established in the Directive 2006/7/EC.
In the remaining 89.7% of the cases (36.2% considering all datasets), regardless of the transformation type, a normal distribution of the data was not achieved. In these cases, a non-parametric method seems to be more adequate as they provide alternative measures of central value parameters, such as the median and interquartile ranges (IQR), in which percentiles are included. Consequently, non-parametric methods provide a more stable measure of central value for those datasets that are not normally distributed, because such values are not affected by outliers observations.22
Other authors consider that non-parametric methods are more appropriate than parametric ones, even when normality is fulfilled, especially when the data points are few.25 Nevertheless, in our case, the minimum number of samples in a dataset (n = 44) was enough to obtain tighter confidence intervals in order to apply the parametric method, whenever the normality hypothesis was fulfilled.
The application of the non-parametric approach to bathing water quality datasets that were not normally distributed caused a modification in the quality classification in 12.3% of the cases considered. In the 90.6% of such cases, the application of the Hazen method provided higher values of percentile, resulting in worse water quality classifications. The subsequent application of a non-parametric method can provide a safer approach to classify bathing water quality from a sanitary point of view.
Since there are several studies that show a positive relationship between increasing bacteriological concentrations in the water and the acquisition of health problems by the potential bathers,26 the knowledge of accurate percentile values should be a priority goal for their use in the quality evaluation processes and, therefore, in bathing water management.
In Spain and in other European countries, Quality Monitoring Assessment Programs are developed and carried out by the different Regional Health Departments, practically with two goals. Firstly, that bathing waters reach the highest bacteriological quality standards and secondly, and more importantly, to ensure protection of bathers. Obviously, both facts are closely related, but the use of a specific method of evaluation has advantages and disadvantages; but while the application of the method established in the current legislation will provide, in general, a better classification than those provided by the non-parametric methods, at the same time it provides the worst approach for the protection of the bathers’ health.
This should encourage an open discussion among European authorities concerning the best method to be used in bathing water bacteriological quality evaluation, considering the distribution characteristics of quality datasets and the associated consequences that an inappropriate method of percentile calculation may have on quality status classifications.
5. Conclusions
The results of the study of bacteriological data distribution of 720 datasets belonging to 180 beaches in the Balearic Island suggests that the evaluation method established in the Directive 2006/7/EC should be reviewed, since it is not appropriate for all bathing waters due to the particular characteristics of bacteriological quality data distributions in the aquatic environment.- When the log normality condition is fulfilled, the parametric method established in the Directive 2006/7/EC is appropriate to evaluate bathing water quality.
- When log normality is not satisfied, transformations can be carried out. If any transformation provides normality, parametric methods are appropriate, but performing the λ optimum based transformation to calculate percentiles instead of the log transformation established in Directive 2006/7/EC.
- In those cases in which normality is not fulfilled whatever the transformation employed (more than 36% of the datasets), a non-parametric approach seems to be more adequate.
- The calculation of accurate percentile values is a task that should be analysed and corrected by European authorities, due to the close relation between bacteriological concentrations and adverse health outcomes for bathers.
6.Acknowledgements
The authors wish to express their gratitude to the Mediterranean Institute for Advanced Studies (IMEDEA (UIB-CSIC)), and especially to Guillermo Vizoso, for their invaluable support in the realization of this paper as a part of the collaboration project “Study of bathing water quality control in the Balearic Islands”, and to the Health Regional Department of the Balearic Islands (Conselleria de Salut de les Illes Balears) for providing the bacteriological quality data used in the analysis. Moreover, the authors wish to thank Dr. Fernando Méndez for his helpful contribution and comments.7.References
- W. D. Tan, F. F. Gan and T. C. Chang, Using normal quantile plot to select an appropriate transformation to achieve normality, Computational Statistics & Data Analysis, 2004, 45, 609–619 Search PubMed.
- M. Thyer, G. Kuczera and Q. J. Wang, Quantifying parameter uncertainty in stochastic models using the Box-Cox transformation, Journal of Hydrology, 2002, 265, 246–257 CrossRef.
- G. Tsiotas, On the use of the Box-Cox transformation on conditional variables models, Finance Research Letters, 2007, 4, 28–32 Search PubMed.
- D. McGrath, C. Zhang and O. T. Carton, Geostatistical analyses and hazard assessment on soil lead in Silvermines areas, Ireland, Environ. Pollut., 2004, 127, 239–248 CrossRef CAS.
- M. Meloun, M. Sánka, P. Némec, S. Krítková and K. Kupka, The analysis of soil cores polluted with certain metals using the Box-Cox transformation, Environ. Pollut., 2005, 137, 273–280 CrossRef CAS.
- R. Chawla and P. R. Hunter, Classification of bathing water quality based on the parametric calculation of percentiles is unsound, Water Res., 2005, 39, 4552–4558 CrossRef CAS.
- J. Bartram, G. Rees, 2000, Monitoring Bathing Waters, E & FN SPON, London Search PubMed.
- P. H. Franses and P. de Bruin, On data transformations and evidence of nonlinearity, Computational Statistics & Data Analysis, 2002, 40, 621–632 Search PubMed.
- R. M. Hirsch, Synthetic hydrology and water supply reliability, Water Resour. Res., 1979, 15(6), 1603–1615 CrossRef.
- D. Jain and V. P. Singh, A comparison of transformation methods for flood frequency analysis, Water Resources Bulletin, 1986, 22(6), 903–912 Search PubMed.
- EEC., Directive 2006/7/CE concerning the management of bathing water quality and repealing 76/160/EEC, Official Journal of the European Union. L64/37, 2006 Search PubMed.
- R. C. Blair and J. J. Higgins, A comparison of the power of Wilcoxon's rank-sum statistic to that of Student's statistic under various non-normal distributions, Journal of Educational Statistics, 1980, 5, 309–335 Search PubMed.
- INE, 2007, National Statistics Institute (Instituto Nacional de Estadística). Available: http://www.ine.es/ Search PubMed.
- I. J. Myung, Tutorial on maximum likelihood estimation, J. Math. Psychol., 2003, 47, 90–100 CrossRef.
- NIST, 2006, e-Handbook of Statistical Methods. Available: http://www.itl.nist.gov/div898/handbook/index.htm Search PubMed.
- R. A. Fisher, On an absolute criterion for fitting frequency curves, Messenger of Mathematics, 1912, 41, 155–160 Search PubMed.
- W. J. Owen and T. A. DeRouen, Estimation of the mean for lognormal containing zeroes and left-censored values, with applications to the measurement of worker exposure to air contaminants, Biometrics, 1980, 36, 707–719 CrossRef.
- G. E. P. Box and D. R. Cox, An analysis of transformations, Journal of the Royal Statistical Society, Series B(26), 1964, 211–246 Search PubMed.
- M. J. Gurka, L. J. Edwards, K. E. Muller and L. L. Kupper, Extending the Box-Cox transformation to the linear mixed model, Journal Of the Royal Statistical Society: Series A., 2006, 169(2), 273–288 Search PubMed.
- A. Hazen, Storage to be provided in the impounding reservoirs for municipal water supply, Transactions of the American Society of Civil Engineers., 1914, 77, 1547–1550 Search PubMed.
- P. R. Hunter, Does calculation of the 95th percentile of microbiological results offer any advantage over percentage exceedence in determining compliance with bathing water quality standards?, Lett. Appl. Microbiol., 2002, 34, 283–286 CrossRef CAS.
- D. R. Helsel, Less than obvious. Statistical treatment of data below the detection limit, Environ. Sci. Technol., 1990, 24(12), 1766–1774 CAS.
- R. E. Luna and H. W. Church, Estimation of long-term concentrations using a “universal” wind speed distribution, J. Appl. Meteorol., 1974, 13, 910–916 Search PubMed.
- R. J. Gilliom and D. R. Helsel, Estimation of distributional parameters for censored trace level water quality data 1. Estimation techniques, Water Resour. Res., 1986, 22(2), 135–146 CrossRef.
- P. M. Berthoeux and I. Hau, Difficulties related to using extreme percentiles for water quality regulations, Res. J. WPCF, 1991, 63(6), 873–879 Search PubMed.
- D. Kay, F. Jones, M. D. Wyer, J. M. Fleisher, R. L. Salmon, A. F. Godfree, A. Zelenauch-Jacquotte and R. Shore, Predicting likelihood of gastroenteritis from sea bathing: results for randomized exposure, Lancet, 1994, 344, 905–909 CrossRef CAS.
Footnote |
| † Part of a themed issue dealing with water and water related issues. |
| This journal is © The Royal Society of Chemistry 2010 |
