Calcium binding environments probed by ⁴³Ca NMR spectroscopy

Abstract

Calcium is an important component of materials, metalloproteins, minerals, glasses, and small inorganic and organic complexes. However, NMR spectroscopy of the quadrupolar ⁴³Ca nuclide remains difficult primarily due to its low natural abundance and low resonance frequency. In this Perspective, experimental challenges and recent successes in the field are highlighted, with a focus on solid-state ⁴³Ca NMR spectroscopy. Solution ⁴³Ca NMR studies of calcium-binding biomolecules are also presented. The structural insights afforded from quadrupolar and chemical shift parameters are examined. For example: isotropic chemical shifts have been shown to correlate with the mean Ca–O distance and also with calcium coordination number; quadrupolar coupling constants and chemical shift tensor spans have been shown to be useful probes of polymorphism; and, distance measurements involving ⁴³Ca have been recently demonstrated. Lastly, challenges and opportunities for the future are considered.

---

David L. Bryce

David L. Bryce is an Associate Professor at the University of Ottawa. He obtained his B.Sc. (Honours) degree from Queen's University (1998). His Ph.D. thesis work (Dalhousie, 2002) was carried out in the group of Rod Wasylishen at Dalhousie University and the University of Alberta. This was followed by an NSERC postdoctoral fellowship with Ad Bax at the NIH (2003–04). Research interests include solid-state NMR of quadrupolar and low-receptivity nuclides, quantum chemical calculations of NMR parameters, and biomolecular NMR. He currently serves as the Chair of the Steering Committee for Canada's National Ultrahigh-Field NMR Facility for Solids.

---

1. Introduction

Calcium is an important element in diverse areas of science ranging from biochemistry to materials chemistry to geology. For instance, calcium-binding proteins such as calbindin and calmodulin play essential roles in calcium transport and in the regulation of various cellular processes.¹ Calcium ion transport protein mutations can disrupt channel function and are implicated in various diseases. A recent review of calcium in biological systems is a useful source of information.² Calcium is one of the most abundant elements in the earth's crust, and is found in numerous minerals. For example, hydroxyapatite is a naturally-occurring calcium-containing mineral which is a key constituent of bone.³ In materials chemistry, calcium finds many uses including bio-implant⁴ and battery applications.⁵ Regardless of whether one is concerned with inorganic compounds or biochemical systems, calcium is most often found in its doubly charged cationic form, i.e., Ca²⁺. All discussion in the present article refers to Ca²⁺.

The nuclear magnetic resonance (NMR) properties of the only spin-active calcium isotope, ⁴³Ca, are presented in Table 1.^6,7 This isotope has a quadrupolar nucleus, meaning that the nuclear spin quantum number (I) is greater than 1/2; for ⁴³Ca, I = 7/2. Therefore, in addition to the magnetic shielding interaction which leads to chemical shifts, the NMR spectra of ⁴³Ca will additionally be affected by the nuclear electric quadrupolar interaction. In this Perspective, the primary focus will be on solid-state nuclear magnetic resonance (SSNMR) studies; however, important solution ⁴³Ca NMR studies of calcium-binding biomolecules will also be addressed.

Table 1 NMR properties of ⁴³Ca and some other nuclides^6,7

Nuclide	Natural abundance/%	Nuclear spin quantum number	Quadrupole moment/fm^2	Frequency ratio Ξ/%	Linewidth factor/fm^4	Receptivity relative to ^1H
^43Ca	0.135	7/2	−4.08	6.730029	2.3	8.68 × 10^−6
^11B	80.1	3/2	4.059	32.083974	22	1.32 × 10^−1
^25Mg	10.00	5/2	19.94	6.121635	130	2.68 × 10^−4
^51V	99.75	7/2	−5.2	26.302948	3.7	3.83 × 10^−1
^59Co	100.0	7/2	42.0	23.727074	240	2.78 × 10^−1

---

The magnetic shielding interaction and chemical shifts

The magnetic shielding interaction may be described by a second-rank tensor (σ). Experimentally, one measures chemical shifts rather than magnetic shielding with NMR spectroscopy. Elements of the magnetic shielding tensor (σ_ii) and the chemical shift (CS) tensor (δ_ii) are related as follows: δ_ii = (σ_ref−σ_ii)/(1 −σ_ref). The following expressions will be of use in discussing experimental chemical shift data for ⁴³Ca: the isotropic chemical shift, δ_iso = (1/3)(δ₁₁ + δ₂₂ + δ₃₃); the span, Ω≈δ₁₁−δ₃₃; the skew, κ = 3(δ₂₂–δ_iso)/Ω, where δ₁₁≥δ₂₂≥δ₃₃. Typically only the isotropic chemical shift is accessible from solution NMR experiments; however, the anisotropy, if large enough, may play a role in nuclear spin relaxation. In the solid state, it is possible in principle to measure the three principal elements of the CS tensor. Measuring the elements of the CS tensor has the potential to provide information on the local bonding environment of the calcium cation (e.g., geometry, symmetry, electronic structure). Furthermore, the orientation of the CS tensor principal axis system (PAS) with respect to an external frame (e.g., another interaction frame or the molecular frame) offers further opportunity to understand the calcium binding environment.

Electric field gradients and the nuclear electric quadrupolar interaction

Classically, the nuclear quadrupole moment, Q, quantifies the non-spherical charge distribution in the ⁴³Ca nucleus. The electric field gradient (EFG) at the nucleus due to the surrounding crystal lattice is described by a symmetric, traceless second-rank tensor (V), and this couples with the quadrupole moment. In the PAS of the EFG tensor, the diagonal elements are |V₃₃| ≥ |V₂₂| ≥ |V₁₁|. Typically this nuclear electric quadrupolar interaction is described by the quadrupolar coupling constant, C_Q, and the asymmetry parameter, η:

C_Q = eV₃₃Q/h

η = (V₁₁−V₂₂)/V₃₃

where e is the fundamental charge and h is the Planck constant.

The ⁴³Ca quadrupolar parameters, measured either through line shape fitting of SSNMR powder patterns or through relaxation studies in solution, offer information which is complementary to that obtained from chemical shift measurements. Since Ca²⁺ features a closed-shell electronic configuration, an isolated Ca²⁺ ion, or one which sits on a site of high symmetry (e.g., O_h), will experience no electric field gradient and the quadrupolar coupling constant will be zero. As the EFG deviates from zero, second-order quadrupolar broadening is manifested in the SSNMR spectrum and lineshape simulations will yield the value of C_Q. This value is therefore indicative of the symmetry and distribution of electric charge in the surrounding crystal lattice.

Typical chemical shifts and quadrupolar parameters obtained from ⁴³Ca SSNMR studies are presented in Table 2. The total known range of isotropic chemical shifts covers about 200 ppm, CS tensor spans range from zero to 70 ppm,⁸ and quadrupolar coupling constants range from zero to about 4.3 MHz.⁹

Table 2 Representative experimental calcium-43 chemical shifts and quadrupolar parameters obtained from solid-state NMR spectroscopy^a

Compound	δiso/ppm^b	CQ/MHz	η	Reference
a Experimental errors may be found in the original literature.b Chemical shifts are with respect to 1.0 M CaCl2(aq) at 0 ppm. Some values were adjusted according to reference 20 to account for different chemical shift standards.c The following chemical shift tensor spans are also known: 8 ± 2 ppm (calcite);^8 57 ± 4 ppm (aragonite);^27 70 ± 20 ppm (vaterite);^8 22.4 ± 1.0 ppm (calcium benzoate trihydrate).^34
CaO	136.0	0.0	n/a	20,27
Ca(OH)2	70.5	2.49	0.1	17
CaCO3 calcite^c	21.6	1.39	< 0.05	8
CaCO3 aragonite^c	−26.0	< 0.68	n/a	20,27
CaCO3 vaterite^c	12.6	3.7	0.55	8
CaAl4O7 grossite	54	3.5	0.1	20,30
Ca10(PO4)6(OH)2 (hydroxyapatite) site 1	4.5	2.6	0.4	20,43
Ca10(PO4)6(OH)2 (hydroxyapatite) site 2	17.5	2.6	0.6	20,43
β-C2S site 1	33.7	2.41	0.65	17
β-C2S site 2	53.8	2.98	0.7	17
Calcium benzoate trihydrate^c	−2.5	1.10	0.7	34

---

Relaxation of ⁴³Ca in solution

Solution ⁴³Ca NMR studies of calcium-binding proteins in particular have relied upon interpreting the relaxation of ⁴³Ca to extract information concerning the ⁴³Ca quadrupolar coupling constants, binding constants (K_D), rate constants, and rotational correlation times (τ_C). It is assumed that the quadrupolar mechanism dominates relaxation. The reader is referred to the reviews by Drakenberg¹⁰ and by Aramini and Vogel¹¹ for further details. For relatively small proteins studied in standard magnetic field strengths, ⁴³Ca relaxation falls in the “near-extreme narrowing” condition (ω₀τ_C≈ 1, where ω₀ is the Larmor angular frequency). For example, at B₀ = 11.75 T, ω₀(⁴³Ca) = 211.83 × 10⁶ rad s⁻¹ and so for a protein with τ_C = 6.0 ns (e.g., equine lysosyme¹²), ω₀τ_C = 1.27. In this regime, the relaxation rate constants R₁ and R₂ are related to C_Q and τ_C as shown below. Here, the asymmetry of the EFG tensor is assumed to be negligible.

2. Experimental considerations

Why is ⁴³Ca NMR spectroscopy challenging?

Great advances have been made in recent years in the SSNMR spectroscopy of quadrupolar nuclei and of low-frequency nuclei. The two most important advances are: (i) the availability of spectrometers with increasing magnetic fields, and (ii) the development of radio frequency pulse sequences which provide signal enhancement. Higher magnetic fields increase the Boltzmann population difference across the central transition (CT; m_I = +1/2 ↔−1/2) and therefore increase the sensitivity of the NMR experiment. Radio frequency pulses may be used to accomplish this same goal of increasing sensitivity by increasing the population difference across the CT. In short, a shaped pulse or pulse sequence is typically used to saturate or invert the satellite transition populations, which results in an increase in the population difference across the CT. For example, MacKenzie et al. have applied the rotor-assisted population transfer (RAPT) method recently to acquire ⁴³Ca magic-angle spinning (MAS) NMR spectra of calcium-containing inorganic polymers.¹³ In principle, appropriate inversions of the various satellite populations should lead to a signal enhancement of 7 for the ⁴³Ca CT. However, signal enhancement methods for spin-7/2 nuclei like ⁴³Ca have not been widely applied in part because under MAS conditions it can be difficult to invert the various satellite transition populations in a predictable manner and order.¹⁴ It will likely be difficult to achieve maximum signal enhancement on an unknown sample since the frequencies associated with each of the satellite transitions are unknown a priori. Furthermore, examination of signal enhancement factors reported for various half-integer spins using population transfer experiments suggests that indeed it is more difficult to achieve reliable results with higher-spin nuclides.¹⁵

While studies of traditionally difficult low-frequency and quadrupolar nuclei have substantially expanded, ⁴³Ca remains as one of the more challenging, yet still accessible, nuclides to study by NMR. The reasons for this may be understood by examining the properties of the ⁴³Ca nuclide relative to other comparable nuclides (Table 1). The other nuclides presented have at least one property which is comparable to ⁴³Ca, yet they are all easier to observe using NMR spectroscopy. The receptivity of ⁴³Ca relative to ¹H is 8.68 × 10⁻⁶, i.e., it is almost a million times less receptive than ¹H! This means that the time required to record a ⁴³Ca NMR spectrum with a usable signal-to-noise ratio is very long compared to NMR studies which are familiar to most synthetic chemists. The main contributing factor is the low natural abundance of ⁴³Ca, 0.135%. There are simply not enough NMR-active calcium nuclei in a given sample to give a reasonable NMR spectrum in a short time. The relatively low frequency of ⁴³Ca (about 61 MHz in a 21.1 T magnet where protons resonate at 900 MHz) is an additional problem, both due to the Boltzmann distribution and due to technical issues associated with acoustic ringing in the probes used to receive the NMR signal. Often, specialized probes are required. As mentioned by Drakenberg in the context of solution ⁴³Ca NMR, “there seem to be no probes for this purpose available from the NMR vendors”.¹⁰ For our own ⁴³Ca NMR studies of solids, we have had specialized probes built by Bruker Biospin or built in-house at the National Ultrahigh-Field NMR Facility for Solids (www.nmr900.ca).

Hundreds of milligrams are desirable to obtain usable ⁴³Ca NMR spectra of powdered samples at natural abundance. The signal increases linearly with the number of spins in the sample, and the time required to obtain a useful signal-to-noise ratio will additionally depend on the applied magnetic field strength and the relaxation time constant T₁ of ⁴³Ca. Means to improve the feasibility of ⁴³Ca SSNMR experiments therefore include: running the experiments in the highest possible magnetic field, decreasing the T₁, increasing the sample volume, and/or ⁴³Ca isotopic enrichment.

For example, at 8.46 T, with a sample volume of 2.4 mL, several days of signal averaging with up to 750 000 transients were required in the first study of compounds at natural abundance.²⁷ Wong et al. report experimental times on the order of 12–48 h for other natural abundance powdered samples at 8.45 and 14.1 T, with 9.5 mm outer diameter rotors.¹⁶ Compounds giving rise to narrower resonances will afford spectra of a given signal-to-noise ratio in less time. At ultrahigh-fields, e.g., 21.1 T, the situation can be improved somewhat;^8,17 however, one must be aware that T₁ will also typically be longer at higher field. Calcium-43 has a small quadrupole moment relative to most other quadrupolar nuclides, and quadrupolar relaxation is often not as rapid as for some of these other nuclides. Most studies use recycle delays on the order of 1–5 s; however, it is clear that T₁ is often longer than this, as shown in Fig. 1 for calcite where even 10 s likely does not afford complete relaxation. Decreasing T₁ could be achieved in a few different ways, though this does not appear to have been actively pursued to date. For example, cross-polarization from the proton spin reservoir would allow the experiment to be repeated in accordance with the T₁ of the protons. One could also envisage doping samples with a paramagnetic impurity, as done for example by Ellis and co-workers in their ⁶⁷Zn SSNMR studies.¹⁸ This idea has been pursued in the ⁴³Ca MAS NMR study of Angeli et al. of glasses, wherein < 0.1 wt% Gd₂O₃ was added during sample preparation.⁹ A general approach for observing dilute half-integer spin quadrupolar nuclei has been presented by Lipton, Sears, and Ellis.¹⁹ In addition to some of the above-mentioned points, their report also describes in detail the practical aspects and advantages of working at cryogenic temperatures to boost the population difference across the CT.

Fig. 1 Natural abundance ⁴³Ca magic-angle-spinning NMR spectra of powdered calcite collected at 21.1 T with different recycle delays. Each spectrum is the sum of 5120 scans. The breadth and shape of the resonance are due to second-order quadrupolar effects. A best-fit simulated spectrum is shown above. Reproduced with permission from reference 8.

Isotopic enrichment with ⁴³Ca has the potential to provide the most drastic increase in signal-to-noise; however, this option remains quite expensive in most instances. One recent quotation I have received is for $220/mg of elemental calcium enriched to 62% in ⁴³Ca. In the case of solution NMR studies of calcium-binding proteins, the use of isotopic enrichment is somewhat more feasible since a stock solution can simply be prepared from a source such as ⁴³CaCO₃. This is typical in such studies. For systematic studies of series of small molecules, where synthesis may be required, the expense of ⁴³Ca isotopic enrichment can become prohibitive.

Chemical shift referencing

The IUPAC-recommended chemical shift reference for ⁴³Ca is a 0.1 M solution of CaCl₂ in D₂O.⁶ Amusingly, this sample is too dilute to be useful as a reference and it has been reported that 8 h are required to obtain a useable signal at 8.45 T with a 9.5 mm diameter rotor!²⁰ This would be enough to discourage anyone from pursuing further ⁴³Ca NMR studies. Recent observations from my group,^8,21 as well as from Moudrakovski²² (National Research Council, Ottawa) and from the group of Smith^20,23 (University of Warwick, UK) brought to light some of the difficulties with chemical shift referencing, particularly in the solid state. Gervais et al. summarize the state of affairs in their 2008 paper (Fig. 2).²⁰ It had been proposed that a saturated CaCl₂ solution be used as a chemical shift reference; however, it soon became apparent that “saturated” or highly concentrated solutions prepared in different labs or on different days could yield substantially different chemical shifts (a range of several ppm). In light of the 1981 report of Farmer and Popov²⁴ which describes the dependence of the ⁴³Ca resonance frequency on solute concentration for a series of calcium salts, the variation is not surprising. As a result, one must use caution when comparing chemical shifts reported by different research groups. The current consensus within the SSNMR community is to use a 1.0 M solution of CaCl₂ in H₂O as the chemical shift reference at 0 ppm. On this scale, solid CaO, which provides a convenient secondary reference due to the sharpness of its ⁴³Ca resonance, appears at 136 ppm.²⁰

Fig. 2 Natural abundance ⁴³Ca NMR spectra of CaCl₂ solutions in H₂O, and a magic-angle-spinning NMR spectrum of solid powdered CaO (top). All spectra were acquired at 14.1 T. The shaded bar highlights the range of peak positions observed for various preparations of a “saturated” solution (see main text for discussion). Reproduced with permission from reference 20.

3. Survey of data and discussion

Calcium-43 NMR has been used to study diverse compounds including simple salts,^24–26 small inorganic molecules and materials,^20,27–31 organic complexes,^32–34 protein-calcium complexes,^11,35–39 a calcium-nucleic acid complex,⁴⁰ hydroxyapatites,^41–44 minerals of importance to cement science,^17,45,46 superconductors,⁴⁷ amorphous slags and glasses,^9,48–50 polymorphs,^8,27 and inorganic polymers.⁵¹ Smith and MacKenzie have presented an overview of ⁴³Ca SSNMR studies of inorganic materials up to 2001.⁵² In 2002, Drakenberg summarized the information available from ⁴³Ca NMR studies of calcium-binding proteins in solution.¹⁰ Discussed below are some recent highlights and important papers which elucidate the development of the field.

Solid-state ⁴³Ca NMR Studies

The first ⁴³Ca NMR study of a solid sample appears to be that of Bryant et al., which appeared in 1987.³² In this study, an impure calcium acetate sample enriched to 50% in ⁴³Ca was analyzed by MAS and cross-polarization MAS (CP/MAS) NMR. Cross-polarization from ¹H is a common method for enhancing the sensitivity of a dilute spin-1/2 nucleus (e.g., ¹³C, ²⁹Si), but there can be complications for quadrupolar nuclei, particularly those of higher spin quantum number. Long contact times (e.g. up to 70 ms)³² are anticipated for ⁴³Ca due to its small magnetic moment. It is somewhat surprising then that this first study endeavoured to apply these methods, given that CP/MAS is still not a common experiment for ⁴³Ca studies some 23 years later. In fact, in the seminal application of ¹H-⁴³Ca CP/MAS, the sample and the stator were destroyed in a “catastrophe apparently [resulting] from very severe heating from the rf load”.³²

It took ten years for a follow-up study on solid compounds of natural abundance in ⁴³Ca.²⁷ The pioneering study by Dupree et al. described a linear correlation between the ⁴³Ca isotropic chemical shift and the mean Ca–O bond length of the first coordination shell of calcium. This trend was observed for oxides, silicates, and carbonates, with each set of data described by a common slope of approximately −280 ppm/Å, but with differing intercepts. The correlations were based on the limited data available at the time. Since then, several studies have further investigated this relationship in inorganics,^8,20 organics,^16,33 and biomaterials.¹⁶ Presented in Fig. 3 is a summary of experimental ⁴³Ca chemical shifts vs. mean Ca–O distances for organic and inorganic solids. The chemical shifts were obtained for powdered samples, typically under MAS conditions, and the Ca–O distances are taken from X-ray crystal structures. There is clearly a trend of increasing chemical shift with decreasing Ca–O distance, and this trend becomes more clear when the compounds are separated into particular classes (e.g., organics, aluminates and silicates, other inorganics).

Fig. 3 Correlation between ⁴³Ca isotropic chemical shifts and mean Ca–O distance in inorganic and organic solids. The dashed line indicates the sum of the Ca²⁺ and O²⁻ Pauling ionic radii. Organics: solid circles; aluminates and silicates: open diamonds; other inorganics: open triangles. Reproduced with permission from reference 16.

The relationship between δ_iso and mean Ca–O distance has been investigated computationally as well. The scatter in the data prompted us to study, and confirm, via systematic gauge-including projector-augmented wave (GIPAW) DFT calculations^53,54 that the average Ca–O distance was indeed the dominant structural feature correlated with the value of δ_iso.⁸ Gervais et al. applied the PARATEC code to calculate magnetic shielding constants for various inorganic compounds.²⁰ The ⁴³Ca chemical shifts were found to be correlated to the mean Ca–O distance with slopes as follows: −300 ppm/Å for silicates, −190 ppm/Å for phosphates, −310 ppm/Å for aluminates, and −810 ppm/Å for borates. Wong et al. presented HF/6-31G* calculations on a series of organic calcium complexes as well as calcium-bound proteins.³³ The slope they obtained is −154 ppm/Å. This work also reported a correlation between computed chemical shifts and the Ca–O coordination number and between δ_iso and the number of inner shell water molecules (Fig. 4).

Fig. 4 Calculated ⁴³Ca isotropic chemical shifts (HF/6-31G*) for various organic calcium complexes plotted against (a) mean Ca–O distance and (b) Ca–O coordination number. Solid squares: complexes for which experimental NMR data are not available; solid circles: complexes for which experimental SSNMR data are available; open circles: calcium-binding proteins. Reproduced with permission from reference 33.

Due to the quadrupolar nature of ⁴³Ca, a residual second-order quadrupolar broadening of the CT exists even under MAS conditions (Fig. 1). The two-dimensional multiple-quantum magic-angle spinning (MQMAS) NMR experiment removes this broadening and therefore increases spectral resolution in the indirectly detected dimension.⁵⁵ MQMAS is known to be a relatively low-sensitivity method; nevertheless, ⁴³Ca MQMAS spectra have been presented over the past few years, and applied to address important structural questions.^{42,44,48–50} All reports to date unsurprisingly rely on material which has been isotopically enriched in ⁴³Ca. Triple-quantum, 5Q, and 7Q versions of the experiment have all been implemented. Shimoda and co-workers have applied these methods to understand the calcium sites in amorphous slags and silicate glasses.^48–50 The septuple-quantum experiment, performed at 21.8 T, impressively enabled resolution of three calcium sites in CaSiO₃ glass (see Fig. 5).⁴⁹ While this 7Q experiment provides lower signal-to-noise than the 3Q and 5Q versions, the former was key to resolving these three sites. On the basis of comparisons with literature data for crystalline compounds, it was suggested that the calcium ions are mainly in 7- and 8-fold coordination sites. Similar conclusions, with evidence also for six-coordinate sites, were reached for amorphous silicate slags.^48,50

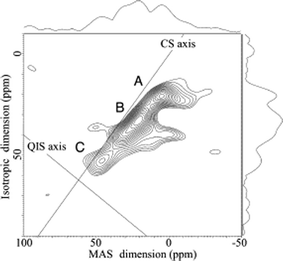Fig. 5 Calcium-43 septuple-quantum magic-angle-spinning NMR spectrum of CaSiO₃ glass at 21.8 T. Pure chemical shift (CS) and quadrupolar-induced shift (QIS) axes are indicated. Three sites, labelled A, B, and C, are resolved. Reproduced with permission from reference 49.

Triple-quantum MAS has also been applied to provide insight into the calcium binding sites of hydroxyapatite.^42,44 These experiments form part of a detailed ⁴³Ca SSNMR study of this material by Laurencin, Smith, and co-workers.^42–44,56 Two crystallographically distinct calcium binding sites were resolved both by ⁴³Ca 3QMAS and by deconvolution of a one-dimensional MAS spectrum obtained at 18.8 T. The spectral parameters were successfully assigned to specific sites in the crystal structure mainly on the basis of the relative intensities of the two signals. Site Ca(I) is characterized by a chemical shift of 4.5 ± 0.8 ppm relative to 1.0 M CaCl₂(aq) while for site Ca(II) δ_iso(⁴³Ca) = 17.5 ± 0.8 ppm. For both sites, C_Q = 2.6 ± 0.4 MHz. Subsequently, ¹H-⁴³Ca rotational-echo double resonance (REDOR) spectroscopy was used to verify the site assignments. This experiment is sensitive to the dipolar coupling between ¹H and ⁴³Ca, which itself depends on <1/r³>, where r is the distance between the spins and the angular brackets indicate a motional average. Details of two-dimensional ¹H-⁴³Ca SSNMR correlation experiments may be found in the article by Wong et al., including the implementation of a rotary-resonance-recoupling (R³)-HMQC experiment.⁴² This paper also highlights an application to an unknown oxy-hydroxyapatite, for which three calcium binding sites are resolved.

Moudrakovski et al. have recently presented a systematic analysis of the feasibility and utility of natural-abundance ⁴³Ca SSNMR for the study of cement-based materials.¹⁷ The results support the idea of using layered crystalline calcium silicate hydrates as models for the calcium silicate hydrates which form during the hydration of Portland cement. At 21.1 T, using a 7 mm o.d. rotor, MAS NMR experiments were performed on powdered samples of anhydrous beta di-calcium silicate (β-C₂S), triclinic and monoclinic tri-calcium silicate (C₃S), hydrated tri-calcium silicate, and a series of synthetic calcium silicate hydrates of different composition. For β-C₂S, two crystallographic sites were resolved and lineshape fitting provided the following parameters: Ca(1), δ_iso = 33.7 ppm, C_Q = 2.41 MHz, η = 0.65; Ca(2), δ_iso = 53.8 ppm, C_Q = 2.98 MHz, η = 0.7. Results from GIPAW DFT calculations implemented in the CASTEP program^53,54 were in good agreement with these data, and supported the assignments to specific crystallographic sites. The trend noted above, that higher chemical shifts correlate with shorter average Ca–O distances, is qualitatively followed in β-C₂S. Tricalcium aluminate (C₃A) presents a challenge in that there are six crystallographically unique calcium sites and so six resonances are expected in the SSNMR spectrum. Notably, four of these sites were resolved in the 1D ⁴³Ca MAS NMR spectrum at 21.1 T. The triclinic and monoclinic polymorphs of C₃S pose an even more daunting challenge as there are 29 and 36 calcium resonances expected, respectively. Although this large number of sites was not fully resolved, the spectra very clearly differentiate between the two polymorphs. The applicability of ⁴³Ca SSNMR to distinguish between polymorphs will be further discussed below.

The sensitivity of ⁴³Ca SSNMR spectra to polymorphism was noted in Dupree's 1997 study.²⁷ The isotropic chemical shifts and quadrupolar coupling constants for the calcite and aragonite polymorphs of calcium carbonate were shown to be substantially different from each other (Table 2). In general, SSNMR spectroscopy is sensitive to polymorphism because the different crystal packing effects for different polymorphs generally have different effects on the magnetic shielding and EFG tensors. The issue of polymorphism in CaCO₃ was further probed by my group in a study where calcite and the metastable polymorph vaterite were characterized in natural abundance at 21.1 T.⁸ In the case of calcite, we were able to completely characterize the calcium binding site in terms of the quadrupolar parameters, the chemical shift tensor, and the relative orientation of the two PASs (see Fig. 6). Because of the S₆ symmetry at the calcium in calcite, it was possible to infer the absolute orientation of the CS tensor with respect to the molecular framework. Interestingly, for the three polymorphs, substantially different chemical shifts, quadrupolar coupling constants, and CS tensor spans were obtained. The value of δ_iso ranges from −26 ppm for aragonite to 12.6 ppm for vaterite to 21.6 ppm for calcite. This is remarkable given that the total known chemical shift range for calcium in all compounds is only on the order of 200 ppm. The value of C_Q(⁴³Ca) ranges from less than 0.68 MHz (aragonite) to 1.39 MHz (calcite) to 3.7 MHz (vaterite) while the CS tensor span ranges from 8 ppm (calcite) to 57 ppm (aragonite) to about 70 ppm (vaterite). The trends differ for the different NMR interactions, indicative of the fact that they report on different aspects of molecular and crystal structures.

Fig. 6 Natural-abundance ⁴³Ca NMR spectrum of solid powdered calcite obtained at 21.1 T under stationary conditions. Simulated spectra in each case are based on a CS tensor skew of 0.9, a quadrupolar coupling constant of 1.39 MHz and a quadrupolar asymmetry parameter of 0. In parts (a), (b), and (c), the angle β between the largest components of the EFG and magnetic shielding tensor is varied to produce simulated spectra; the best fit is obtained for β = 0°. In parts (d), (e), and (f), the CS tensor span is varied in the simulations from 0 to 8 to 16 ppm; the best fit is obtained for Ω = 8 ppm. Reproduced with permission from reference 8.

Another issue addressed in the study of vaterite was the question of the most appropriate space group in which to represent its crystal structure.⁸ Hexagonal P6₃/mmc and orthorhombic Pbnm space groups had been proposed. To address this question by ⁴³Ca NMR spectroscopy, GIPAW DFT calculations were performed on compounds with known crystal structures and with available ⁴³Ca NMR parameters (e.g., δ_iso and C_Q). In this manner, the reliability of the calculations was established. The same computational method was then applied to cross-validate various possible structures for vaterite: orthorhombic, hexagonal, as well as some computationally-optimized structures from the literature. The results clearly showed that the experimental data agreed best with a hexagonal P6₃/mmc space group (Fig. 7). This combined experimental and computational approach to obtaining structural information is powerful, and represents a qualitative example of the sort of information one can glean from “NMR crystallography” approaches.⁵⁷

Fig. 7 Experimental and simulated natural abundance ⁴³Ca SSNMR spectra of vaterite obtained with magic-angle spinning at 21.1 T. Simulations are based on GIPAW DFT-computed parameters for structural models based on (a) the Pbnm space group, (b) DFT-optimized orthorhombic space groups, (c) the hexagonal P6₃/mmc space group. The simulation in (d) is the best fit (i.e., based on experimental data). Reproduced with permission from reference 8.

Laurencin et al. have further pursued the application of ⁴³Ca SSNMR methods to extract semi-quantitative structural information.³⁴ Ca-43 enriched (60%) calcium benzoate trihydrate was used as a model organic calcium complex for which the calcium binding environment resembles that found in calcium-binding proteins. A combination of ⁴³Ca NMR of MAS and static powder samples, GIPAW DFT calculations, and experiments to measure ⁴³Ca-¹³C distances and connectivity (transferred-echo adiabatic-passage double-resonance (TRAPDOR) and heteronuclear J-spin-echoes) were successfully applied to demonstrate the wealth of structural information which is available, despite the ever-present challenges associated with ⁴³Ca NMR spectroscopy. Shown in Fig. 8 are the results of the TRAPDOR experiments which enabled qualitative distance measurements involving ¹³C spins over 5.6 Å away.

Fig. 8 Results of ¹H-¹³C-⁴³Ca TRAPDOR experiments performed on ⁴³Ca-enriched calcium benzoate trihydrate at 9.4 T. (a) Control and double-resonance one-dimensional ¹³C NMR spectra (i.e., without and with ⁴³Ca irradiation). (b) Evolution of magnetization transfer to ¹³C spins which are near (e.g., C₇) and farther (e.g., C₁₇) from the calcium ion. Points are experimental data; solid lines are simulations. Reproduced with permission from reference 34.

The small quadrupole moment of ⁴³Ca can be considered a boon or a bane in SSNMR studies. On the one hand, this results in relatively narrow resonances which get narrower at higher magnetic field. On the other hand, the increased sensitivity and resolution at higher field is concomitant with a loss of the second-order line shape under MAS conditions. This means that it is more challenging to determine the quadrupolar parameters from a standard MAS NMR experiment at a single high applied magnetic field. Multi-field studies or nutation spectroscopy allow one to recover the quadrupolar information. However, for challenging cases where only the highest fields will provide the sensitivity required, quadrupolar information becomes more and more difficult to extract. Fortunately, in high magnetic fields the anisotropy in the CS tensor becomes more feasible to measure, and the span and skew may become more frequently measured spectroscopic parameters as commercially available magnetic fields continue to increase.

Calcium-43 NMR studies of calcium-binding biomolecules

Published calcium-43 NMR studies of calcium-binding proteins have been carried out exclusively in solution; however, conference reports by Ellis and Lipton⁵⁸ as well as a computational study by Smith and co-workers³³ suggest that studies in the solid state are feasible. Andersson et al. reported the observation of ⁴³Ca NMR signals for calcium ions bound to proteins in 1982.³⁸ Through relaxation studies, they determined the ⁴³Ca quadrupolar coupling constants and rotational correlation times for parvalbumin (C_Q = 1.3 ± 0.2 MHz; τ_C = 4.0 ± 1 ns), calmodulin (C_Q = 1.15 ± 0.05 MHz; τ_C = 8.2 ± 2 ns), and troponin C (C_Q = 1.05 ± 0.05 MHz; τ_C = 11.0 ± 2 ns). As has been observed generally from ⁴³Ca relaxation studies, the correlation times are in agreement with those derived from other methods for the entire protein, indicating that the calcium ions are bound rather rigidly. Aramini et al. studied a series of calcium-binding lysozymes and α-lactalbumins and conclude, on the basis of ⁴³Ca NMR data, that there is an evolutionary link between these two classes of protein.¹² The ranges for ⁴³Ca chemical shifts and quadrupolar coupling constants for calcium ions bound to β-trypsin, lysozymes and α-lactalbumins, calbindin D_9K, and EF-hand proteins are depicted in Fig. 9.¹¹ One can clearly see from this summary how ⁴³Ca NMR can rapidly provide qualitative information on the calcium binding site of a protein, given the chemical shift resolution between the different types of proteins. A quantum chemical study of ⁴³Ca NMR parameters for calcium binding sites in organic complexes and metalloproteins shows that the HF/6-31G* level of theory provides good agreement with experiment for chemical shifts and quadrupolar coupling constants.³³ A combined experimental-computational approach making use of these results should prove to be useful in future SSNMR studies aiming to characterize unknown Ca²⁺ binding sites.

Fig. 9 Schematic representation of the ⁴³Ca chemical shifts and quadrupolar coupling constants measured in solution for calcium-binding proteins. Adapted with permission from reference 11.

Kwan et al. recently presented direct ⁴³Ca NMR evidence for Ca²⁺ binding to guanosine quartets (G-quartets) in solution. G-quartets have generated attention for the important role they play in molecular biology and nanotechnology. Their study is an excellent combined application of standard ¹H NMR experiments, along with ⁴³Ca NMR and quantum chemical calculations of the calcium magnetic shielding tensors. Mass spectrometry confirmed that the complex formed was the calcium complex of the 2′,3′,5′-O-triacetylguanosine octamer (TAG₈Ca²⁺). Four models of the calcium complex were used as the basis for the calculations. The models were based on the geometries about calcium from known crystal structures, or on a purely quantum chemically-optimized model. The experimental ⁴³Ca chemical shift of −43 ppm (60 mM in CDCl₃) for TAG₈Ca²⁺ was best reproduced by quantum chemical methods using a HF/6-311++G** calculation on a model built from the crystal structure of a Sr²⁺ complex of 5′-silyl-2′,3′-O-isopropylidene guanosine⁵⁹ (where the Sr²⁺ was replaced with Ca²⁺). On the basis of computed results for the four models, a correlation between ⁴³Ca chemical shifts and the average Ca–O distance was seen, in agreement with correlations presented previously (vide supra). For the TAG₈Ca²⁺ complex, it was predicted that the average Ca–O bond distance is 2.70 ± 0.05 Å. It has been shown previously that calcium ions may play an important role in the polymorphism of DNA complexes,⁶⁰ and therefore ⁴³Ca NMR could make significant contributions to future studies of such complexes.

4. Concluding remarks

The field of ⁴³Ca NMR spectroscopy, particularly in the solid state, has expanded swiftly over the past decade. Overall, the number of applications is still relatively small. Probing calcium binding environments in biomolecules and materials has always been and continues to be important, but it is only recently that ⁴³Ca SSNMR experiments have begun to consistently yield useful spectra and new insights. The traditional difficulties in obtaining ⁴³Ca SSNMR spectra, namely the low natural abundance of ⁴³Ca and its low resonance frequency, have been addressed in a significant way by the availability of stronger magnetic fields in commercial spectrometers, and, to a lesser extent thus far, the development of pulse sequences affording enhanced signal-to-noise. Nevertheless, ⁴³Ca NMR spectroscopy generally remains a challenging endeavour. The brute force approach of isotopic enrichment will yield the most substantial gains in signal-to-noise; however, general application of this method often remains prohibitively expensive. It seems imperative then that further application, and perhaps development and fine-tuning, of pulse sequences optimized specifically for spin-7/2 nuclei be pursued.

Characterizing calcium binding sites in solid metalloproteins is one of the next frontiers in ⁴³Ca SSNMR. Solution NMR as well as computational work suggests that the spectra will be of reasonable breadth and that the spectra will be sensitive to the calcium coordination number and local geometry. Applications in geology, glass science, cement science, and in studying small inorganic and organic complexes will continue to provide important structural insights. As higher magnetic fields continue to play a role in ⁴³Ca SSNMR studies, one may anticipate increased spectral resolution under MAS conditions. Concomitantly, quadrupolar parameters may become less accessible. Under stationary conditions, chemical shift tensor parameters will become more accessible and this tensor may become a generally applicable probe of structure as has already been demonstrated in a few cases.^8,27,34 Quantitative and semi-quantitative distance measurements involving ⁴³Ca³⁴ will also create new opportunities for structure elucidation.

Acknowledgements

D. L. B. is grateful to the Natural Sciences and Engineering Research Council (NSERC) of Canada for continued support, thanks Igor Moudrakovski for a preprint of reference 17, and thanks the SSNMR group at the University of Ottawa for helpful comments. For our work reported in reference 8 and our ongoing studies, access to the 900 MHz NMR spectrometer was provided by the National Ultrahigh-Field NMR Facility for Solids (Ottawa, Canada), a national research facility funded by the Canada Foundation for Innovation, the Ontario Innovation Trust, Recherche Québec, the National Research Council Canada, and Bruker BioSpin and managed by the University of Ottawa (www.nmr900.ca). NSERC is acknowledged for a Major Resources Support grant.

References

1. J. Krebs and M. Michalak, ed., Calcium: A Matter of Life or Death, Elsevier, Amsterdam, 2007.
2. J. Burgess and E. Raven, “Calcium in Biological Systems”, in Advances in Inorganic Chemistry, ed. R. van Eldik and C. D. Hubbard, Elsevier, Amsterdam, 2009, Vol. 61, pp. 251–366.
3. D. McConnell, Apatite: its crystal chemistry, mineralogy, utilization, and geologic and biologic occurrences, Springer-Verlag, New York, 1973.
4. S. R. Paital and N. B. Dahotre, Mater. Sci. Eng., R, 2009, 66, 1.
5. R. Sathiyamoorthi, P. Shakkthivel and T. Vasudevan, Mater. Lett., 2007, 61, 3746.
6. R. K. Harris, E. D. Becker, S. M. Cabral de Menezes, R. Goodfellow and P. Granger, Pure Appl. Chem., 2001, 73, 1795.
7. P. Pyykkö, Mol. Phys., 2008, 106, 1965.
8. D. L. Bryce, E. B. Bultz and D. Aebi, J. Am. Chem. Soc., 2008, 130, 9282.
9. F. Angeli, M. Gaillard, P. Jollivet and T. Charpentier, Chem. Phys. Lett., 2007, 440, 324.
10. T. Drakenberg, in Calcium-Binding Protein Protocols, Volume 2: Methods and Techniques, H. J. Vogel, Ed., Humana Press, Totowa, NJ, USA, 2002, Chapter 18.
11. J. M. Aramini and H. J. Vogel, Biochem. Cell Biol., 1998, 76, 210.
12. J. M. Aramini, T. Drakenberg, T. Hiraoki, Y. Ke, K. Nitta and H. J. Vogel, Biochemistry, 1992, 31, 6761.
13. K. J. D. MacKenzie, N. Rahner, M. E. Smith and A. Wong, J. Mater. Sci., 2010, 45, 999.
14. T. T. Nakashima, R. E. Wasylishen, R. Siegel and K. J. Ooms, Chem. Phys. Lett., 2008, 450, 417.
15. R. Siegel, T. T. Nakashima and R. E. Wasylishen, J. Magn. Reson., 2007, 184, 85.
16. A. Wong, A. P. Howes, R. Dupree and M. E. Smith, Chem. Phys. Lett., 2006, 427, 201.
17. I. L. Moudrakovski, R. Alizadeh and J. J. Beaudoin, Phys. Chem. Chem. Phys., 2010 10.1039/c000353k.
18. A. S. Lipton, T. A. Wright, M. K. Bowman, D. L. Reger and P. D. Ellis, J. Am. Chem. Soc., 2002, 124, 5850.
19. A. S. Lipton, J. A. Sears and P. D. Ellis, J. Magn. Reson., 2001, 151, 48.
20. C. Gervais, D. Laurencin, A. Wong, F. Pourpoint, J. Labram, B. Woodward, A. P. Howes, K. J. Pike, R. Dupree, F. Mauri, C. Bonhomme and M. E. Smith, Chem. Phys. Lett., 2008, 464, 42.
21. D. L. Bryce, “Recent Insights from Solid-State NMR Spectroscopy of Quadrupolar Nuclei at 21.1 T”, 50th Rocky Mountain Conference on Analytical Chemistry, 2008, Breckenridge, CO, USA; abstract #416.
22. I. L. Moudrakovski, private communication, 2008.
23. M. E. Smith, “Recent Developments and Applications in Solid-State NMR for Characterisation of Materials”, 50th Rocky Mountain Conference on Analytical Chemistry, 2008, Breckenridge, CO, USA; abstract #410.
24. R. M. Farmer and A. I. Popov, Inorg. Nucl. Chem. Lett., 1981, 17, 51.
25. J. W. Akitt, in Multinuclear NMR, J. Mason, Ed., Plenum Press, New York, 1987, chapter 7.
26. R. E. Youngman and C. M. Smith, Phys. Rev. B, 2008, 78, 014112.
27. R. Dupree, A. P. Howes and S. C. Kohn, Chem. Phys. Lett., 1997, 276, 399.
28. A. Trokiner, A. Bessière, R. Thouvenot, D. Hau, J. Marko, V. Nardello, C. Pierlot and J.-M. Aubry, Solid State Nucl. Magn. Reson., 2004, 25, 209.
29. D. Padro, V. Jennings, M. E. Smith, R. Hoppe, P. A. Thomas and R. Dupree, J. Phys. Chem. B, 2002, 106, 13176.
30. K. J. D. MacKenzie, M. Schmücker, M. E. Smith, I. J. F. Poplett and T. Kemmitt, Thermochim. Acta, 2000, 363, 181.
31. Z. Lin, M. E. Smith, F. E. Sowrey and R. J. Newport, Phys. Rev. B, 2004, 69, 224107.
32. R. G. Bryant, S. Ganapathy and S. D. Kennedy, J. Magn. Reson., 1987, 72, 376.
33. A. Wong, D. Laurencin, G. Wu, R. Dupree and M. E. Smith, J. Phys. Chem. A, 2008, 112, 9807.
34. D. Laurencin, C. Gervais, A. Wong, C. Coelho, F. Mauri, D. Massiot, M. E. Smith and C. Bonhomme, J. Am. Chem. Soc., 2009, 131, 13430.
35. J. Parello, H. Lilja, A. Cave and B. Lindman, FEBS Lett., 1978, 87, 191.
36. T. Andersson, T. Drakenberg, S. Forsén, T. Wieloch and M. Lindström, FEBS Lett., 1981, 123, 115.
37. T. Shimizu, M. Hatano, S. Nagao and Y. Nozawa, Biochem. Biophys. Res. Commun., 1982, 106, 1112.
38. T. Andersson, T. Drakenberg, S. Forsén, E. Thulin and M. Swärd, J. Am. Chem. Soc., 1982, 104, 576.
39. S. R. Martin, S. Linse, C. Johansson, P. M. Bayley and S. Forsén, Biochemistry, 1990, 29, 4188.
40. I. C. M. Kwan, A. Wong, Y.-M. She, M. E. Smith and G. Wu, Chem. Commun., 2008, 682.
41. H. Pizzala, S. Caldarelli, J.-G. Eon, A. M. Rossi, R. A. S. San Gil, D. Laurencin and M. E. Smith, J. Am. Chem. Soc., 2009, 131, 5145 ; J. Am. Chem. Soc., 2010, 132, 6862.
42. A. Wong, D. Laurencin, R. Dupree and M. E. Smith, Solid State Nucl. Magn. Reson., 2009, 35, 32.
43. D. Laurencin, A. Wong, R. Dupree and M. E. Smith, Magn. Reson. Chem., 2008, 46, 347.
44. D. Laurencin, A. Wong, J. V. Hanna, R. Dupree and M. E. Smith, J. Am. Chem. Soc., 2008, 130, 2412.
45. G. M. Bowers and R. J. Kirkpatrick, J. Am. Ceram. Soc., 2009, 92, 545.
46. H. Zanni, R. Rassem-Bertolo, S. Masse, L. Fernandez, P. Nieto and B. Bresson, Magn. Reson. Imaging, 1996, 14, 827.
47. S. Marchand, A. Trokiner, A. Yakubovsky, A. Knizhnik and Y. Eckstein, Physica C, 2004, 408–410, 826.
48. K. Shimoda, Y. Tobu, K. Kanehashi, K. Saito and T. Nemoto, Solid State Nucl. Magn. Reson., 2006, 30, 198.
49. K. Shimoda, Y. Tobu, Y. Shimoikeda, T. Nemoto and K. Saito, J. Magn. Reson., 2007, 186, 156.
50. K. Shimoda, Y. Tobu, K. Kanehashi, T. Nemoto and K. Saito, J. Non-Cryst. Solids, 2008, 354, 1036.
51. K. J. D. MacKenzie, M. E. Smith and A. Wong, J. Mater. Chem., 2007, 17, 5090.
52. K. J. D. MacKenzie and M. E. Smith, Multinuclear Solid-State NMR of Inorganic Materials, Pergamon, New York, 2002.
53. (a) C. J. Pickard and F. Mauri, Phys. Rev. B, 2001, 63, 245101; (b) J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B, 2007, 76, 024401; (c) M. Profeta, F. Mauri and C. J. Pickard, J. Am. Chem. Soc., 2003, 125, 541.
54. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
55. A. Medek, J. S. Harwood and L. Frydman, J. Am. Chem. Soc., 1995, 117, 12779.
56. D. Laurencin, A. Wong, W. Chrzanowski, J. C. Knowles, D. Qiu, D. M. Pickup, R. J. Newport, Z. Gan, M. J. Duer and M. E. Smith, Phys. Chem. Chem. Phys., 2010, 12, 1081.
57. NMR Crystallography, R. K. Harris, R. E. Wasylishen and M. J. Duer, ed., Wiley, UK, 2009.
58. P. D. Ellis and A. S. Lipton, “Experimental Approaches to the Solid-State NMR Spectroscopic Observation of Metal Nuclides in Proteins”, presented at the “NMR of Metals in Biological Systems and in Materials” symposium, Newark, Delaware, USA, 2007.
59. X. Shi, J. C. Fettinger and J. T. Davis, Angew. Chem., Int. Ed., 2001, 40, 2827.
60. D. Miyoshi, A. Nakao and N. Sugimoto, Nucleic Acids Res., 2003, 31, 1156.

---