Vibration–rotation-tunneling states of the benzene dimer: an ab initio study

Abstract

An improved intermolecular potential surface for the benzene dimer is constructed from interaction energies computed by symmetry-adapted perturbation theory, SAPT(DFT), with the inclusion of third-order contributions. Twelve characteristic points on the surface have been investigated also using the coupled-cluster method with single, double, and perturbative triple excitations, CCSD(T), and triple-zeta quality basis sets with midbond functions. The SAPT and CCSD(T) results are in close agreement and provide the best representation of these points to date. The potential was used in calculations of vibration–rotation-tunneling (VRT) levels of the dimer by a method appropriate for large amplitude intermolecular motions and tunneling between multiple equivalent minima in the potential. The resulting VRT levels were analyzed with the use of the permutation-inversion full cluster tunneling (FCT) group G₅₇₆ and a chain of subgroups that starts from the molecular symmetry group C_s(M) of the rigid dimer at its equilibrium C_s geometry and leads to G₅₇₆ if all possible intermolecular tunneling mechanisms are feasible. Further information was extracted from the calculated wave functions. It was found, in agreement with the experimental data, that for all of the 54 G₅₇₆ symmetry species (with different nuclear spin statistical weights) the lower VRT states have a tilted T-shape (TT) structure; states with the parallel-displaced structure are higher in energy than the ground state of A⁺₁ symmetry by at least 30 cm⁻¹. The dissociation energy D₀ equals 870 cm⁻¹, while the depth D_e of the TT minimum in the potential is 975 cm⁻¹. Hindered rotation of the cap in the TT structure and tilt tunneling lead to level splittings on the order of 1 cm⁻¹. Also intermolecular vibrations with excitation energies starting at a few cm⁻¹ were identified. A further small, but probably significant, level splitting was assigned to cap turnover, although in scans of the potential surface we could not find a plausible ‘reaction path’ for this process. Rotational constants were extracted from energy levels calculated for total angular momentum J = 0 and 1, and from expectation values of the inertia tensor. Although the end-over-end rotational constant B + C agrees well with the measured microwave spectra, there is disagreement with the measurements concerning the (a)symmetric rotor character of the benzene dimer. It is concluded from calculations for the 54 nuclear spin species that the microwave spectrum should show overlapping contributions from many different species. Another interesting conclusion regards the role of the quantum number K, for a prolate near-symmetric rotor the projection of the total angular momentum on the prolate axis. For the benzene dimer, K has a substantial effect on the energy levels associated with the intermolecular motions of the complex.

---

I. Introduction

Just as the water dimer has served as a prototype for hydrogen bonding, the benzene dimer is a prototypical example of London (dispersion) forces between nonpolar molecules. The interactions between aromatic systems are of special interest, since they can play an important role in determining protein and DNA stability^1–4 and DNA–protein interaction.^5,6 The benzene dimer has received much attention both from experimentalists^7–24 and theorists.^25–48 Theorists have been challenged in particular by the subtle binding energy difference between two equilibrium structures of the benzene dimer, a T-shaped one and a parallel-displaced one. The relative stability of such edge-to-face and face-to-face structures can be important in determining the conformation adopted by some proteins.^1–3

Dispersion forces, which are so important especially for the bonding between π-systems, are a nonlocal electron correlation effect. Since the accurate accounting for electron correlation is an important issue in electronic structure calculations, the benzene dimer has become a benchmark system for electronic structure methods. The investigation of which of the two benzene dimer structures is more stable has been the focus of a series of calculations using more and more advanced methods.^{30,32–35,38,41,42} When it was discovered^38,42,49 that the T-shape structure is further stabilized by a slight tilt of the monomers, it became clear that the (tilted) T-shaped structure is lower in energy than the parallel-displaced structure. The experimental evidence^17,19–23 confirms this conclusion. Although the energy difference between the two structures is small, the parallel-displaced structure is not observed in experiments due to collisions with the carrier gases used.^22,50 Also in density functional theory (DFT), the benzene dimer has been used as a benchmark system. DFT, as it is commonly implemented, does not include nonlocal electron correlation effects. It completely fails in describing van der Waals binding between (stacked) π-systems. Authors who tried to account for this deficiency, either by a first-principles approach,⁴⁰ or by fitting functionals to interaction energies,⁵¹ or by DFT + dispersion (DFT-D) methods,^45,46,52 have often included the benzene dimer in their training and/or validation sets.

From the calculations it has become clear that the benzene dimer is a floppy system with low barriers to internal rotation. Quantum mechanical tunneling can occur between various equivalent minima in the potential surface that are separated by these low barriers. Hence, if one wants to understand the properties of the benzene dimer and make comparisons with experimental data, a theoretical description of the benzene dimer cannot be limited to the usual treatment of determining the equilibrium structure, the binding energy, and the harmonic vibrational frequencies; one should use a treatment that properly accounts for the large amplitude internal motions. Moreover, one cannot use the point symmetry group of the equilibrium geometry, because the system is delocalized over many equivalent equilibrium structures (minima in the potential surface). One-dimensional model studies of some tunneling processes in the benzene dimer and a harmonic (normal mode) calculation of the intermolecular vibrations have been made by Spirko et al.³¹

A quantum mechanical method applicable to weakly bound dimers that includes all six (coupled) intermolecular degrees of freedom has been developed^53–56 and successfully applied, for example, to the ammonia dimer⁵³ and the water dimer.^56–62 A global six-dimensional intermolecular potential surface is needed in such a treatment. This has led to a useful understanding of the nature of the internal motions in these systems and to an interpretation of the experimental spectra. At the same time, the comparison of the calculated vibration–rotation-tunneling (VRT) levels with high-resolution spectroscopic data provided a very critical test of the quality of the global potential surface used in the calculations. Making similar calculations for the benzene dimer is very difficult. The benzene dimer potential has 288 equivalent tilted T-shaped minima and 144 equivalent (less deep) parallel-displaced minima. The permutation-inversion (PI) symmetry group that should be used for such weakly bound systems has 576 elements in this case, and is called G₅₇₆.^25,26 What makes the calculations particularly demanding is that some of the barriers between the minima are very low and allow delocalization by tunneling between equivalent minima, whereas the barriers in other degrees of freedom are much higher so that the internal states are localized in these directions. This implies that the internal rotor basis used in the calculations must be extremely large, in order to allow sufficient localization and converge the smaller tunneling splittings.

A global intermolecular potential energy surface for the benzene dimer is available from ab initio calculations for a large number of geometries, combined with analytical fitting of the computed data points.³⁸ The ab initio method used was SAPT(DFT): symmetry-adapted perturbation theory (SAPT) based on monomer wave functions, orbital energies, and response properties obtained from (time-dependent) DFT calculations. This method, initially proposed by Williams and Chabalowski,⁶³ was later extended and implemented by Misquitta et al.^64–66 and by Heßelmann et al.^37,67,68 It is much more economical than the regular SAPT⁶⁹ or the coupled-cluster method using single, double, and perturbative triple excitations, CCSD(T), the two approaches that have established themselves currently as the most accurate of practically applicable methods for obtaining intermolecular interaction potentials. Both groups have shown that SAPT(DFT) results for the benzene dimer are about as accurate as the results from CCSD(T). The benzene dimer potential of ref. 38 gave the second virial coefficient in excellent agreement with experiment, and produced the best estimate of the lattice energy of the benzene crystal.⁷⁰ Also for polycyclic aromatic hydrocarbons, the SAPT(DFT) method was successful.^50,71 The potential surface used in the present study is partly based on the SAPT(DFT) interaction energies calculated in ref. 38. These calculations were extended by adding third-order SAPT terms and slightly increasing the number of grid points. We have also made a new analytic fit of the data points that is more accurate in the low-energy region. In ref. 72, it was shown that the third-order SAPT corrections based on the Hartree–Fock description of the monomers improve the interaction energies for nonpolar systems. We will show here that the third-order terms also improve the accuracy of the SAPT(DFT) benzene dimer potential. We used this improved potential to compute converged VRT levels of the benzene dimer for all the 54 irreducible representations of the group G₅₇₆. Furthermore, to understand the nature of the calculated VRT states, we computed some of their properties and plotted various two-dimensional cuts of the six-dimensional global wave functions. A symmetry analysis provides the selection rules for allowed transitions and tells us how the different VRT levels relate to different tunneling mechanisms and to the intermolecular vibrations.

II. Potential surface

The benzene dimer potential in ref. 38 was based on SAPT(DFT) calculations for 491 intermolecular geometries of the benzene dimer, followed by an analytic fit of the calculated interaction energies. We will denote this fit as ‘pot1’. The main reason for the present modification of pot1 was that it did not sufficiently accurately reproduce the data points in the region of the potential minima. It was found, in particular, that the binding energies for the global minimum, the tilted T-shape (TT) structure, and the local minimum, the parallel-displaced (PD) structure, were nearly the same in the analytic fit, whereas the TT structure was more stable than the PD structure by 10 cm⁻¹ in the SAPT(DFT) calculations and by 34 cm⁻¹ in CCSD(T) calculations. In calculations of the VRT states of the benzene dimer, as described here, this would have led to unphysical results.

We have obtained two new potentials for the benzene dimer. First, we fitted the set of SAPT(DFT) interaction energies from ref. 38 supplemented by a few extra points computed at the same level of theory as in ref. 38. We used the same analytic functional form as in ref. 38, but with larger weights in the low-energy region. This led to ‘pot2’. Second, we performed calculations of the third-order SAPT(DFT) induction and exchange-induction energies and added these to the first- and second-order terms already included. In SAPT(DFT), these third-order energies are calculated by replacing Hartree–Fock orbitals and orbital energies by their Kohn–Sham (KS) counterparts in the regular SAPT formulas for the E⁽³⁰⁾_ind and E⁽³⁰⁾_exch−ind corrections developed in ref. 72. We will denote the KS-level corrections as E⁽³⁾_ind (KS) and E⁽³⁾_exch−ind (KS), respectively. Also, one more grid point was added at this stage. The fit of this data set, done in the same way as the fit of pot2, will be called ‘pot3’.

The SAPT(DFT) calculations were performed using the methodology of ref. 66 extended by our implementation of third-order terms. Similarly to ref. 38, the density-fitting SAPT(DFT) implementation was used.⁷³ The density fitting was shown to provide significant computational savings with only a negligible loss of accuracy.^37,73,74 We have applied the aug-cc-pVTZ basis set⁷⁵ in the “monomer-centered plus” approach.⁷⁶ The basis set was supplemented by midbond (mb) functions with exponents and a position-placement algorithm described in ref. 38. The auxiliary basis sets required for the density-fitting approach were taken from ref. 77 (for all terms except electrostatics) and from ref. 78 (electrostatics). The midbond auxiliary functions were taken from ref. 74. The monomer DFT calculations with the PBE0 functional⁷⁹ were done using the DALTON⁸⁰ program. We applied the Fermi–Amaldi–Tozer–Handy asymptotic correction⁸¹ with an experimental ionization potential of benzene of 0.3397 a.u.⁸² The SAPT(DFT) calculations used the SAPT2008 code.⁸³

During the fitting process, it turned out that the total potential became divergent in the region of the repulsive wall. One of the main reasons for this was that E⁽³⁾_exch−ind(KS) is calculated with the S² approximation, where S is a typical intermolecular overlap integral between monomer orbitals. Since the absolute values of E⁽³⁾_ind(KS) and E⁽³⁾_exch−ind(KS) are large while their sum is very small, small errors in E⁽³⁾_exch−ind(KS) result in significant errors in the sum. To correct this behavior, we have scaled the third-order exchange-induction term analogously to the formula proposed in ref. 84

Ẽ⁽³⁾_exch−ind(KS) = E⁽³⁾_exch−ind(KS)(S²) E⁽¹⁾_exch(KS)/E⁽¹⁾_exch(KS)(S²), (1)

where E⁽¹⁾_exch(KS) is the first-order exchange energy calculated to infinite order in S and E⁽¹⁾_exch(KS)(S²) is the first-order exchange energy calculated in the S² approximation. Such a procedure was important in the repulsive region and had a negligible effect near the minima.

A. Analytic fit

The fitting site–site formulawas the same as in ref. 38. The summation runs over all sites a (on and off the nuclei) of monomer A and sites b of monomer B, while r_ab denotes the distance between two such sites. The function u_ab given by³⁸may be considered a generalization of the popular Buckingham-type exp-6 potential. The exponential terms model both the exchange-repulsion contributions (first-, second- and third-order) and part of the short-range overlap (penetration) effects in the Rayleigh-Schrödinger contributions (electrostatic, induction, and dispersion). The 1/r_ab Coulomb term involving the charges q_a and q_b models the electrostatic interactions, and the 1/rⁿ_ab terms involving the van der Waals coefficients C^ab_n model the long-range dispersion and induction interactions. The latter two terms in eqn (3) are multiplied by the Tang–Toennies damping functions⁸⁵that become unity for large r, and continuously go to zero when r decreases. These functions are necessary to damp the 1/rⁿ_ab divergent character of the latter two terms in eqn (3) at short intermolecular distances.

The sites used in the summation of eqn (2) are the same as in ref. 38 and include the C and H nuclear positions and 13 off-atomic sites on each benzene monomer. Six of the latter sites are placed on the C–H bonds, 0.752214 Å away from the C atoms. Another six of the sites are located on the bisectors between the C atoms, 1.45129 Å from the geometric center of the molecule. The last off-atomic site is at the geometric center of the molecule. Thus, there are five symmetry-distinct sites per monomer. Not all of the components of eqn (3) are utilized on all the sites. Only the C and H sites have nonvanishing C^ab_n and δ^ab_n, n = 6, 8, 10 parameters. The central site carries only the exponential terms of eqn (3) and the other off-atomic sites have exponential terms and charges.

Out of the total of 92 fit parameters, the 4 charges q_a and the 9 asymptotic coefficients C^ab_n were taken from ref. 38. The 15 α_ab parameters, 15 β_ab parameters, 19 damping parameters δ^ab_n, and 30 polynomial coefficients a^ab_m were found here by least-square fitting of the SAPT(DFT) interaction energies. The use of the C^ab_n coefficients from ref. 38 neglects the E⁽³⁾_ind(KS) contribution to the asymptotic dependence. However, since this contribution decays as R⁻¹¹ such an approximation should have a negligible effect on our potential.

We fitted our potentials to 479 out of the 491 SAPT(DFT) interaction energies computed on a set of grid points in ref. 38, plus to a number of additional interaction energies (21 for pot2 and 22 for pot3) computed here. The additional points were placed at and near the characteristic points of pot1. The 12 points from ref. 38 not used in the present fits were utilized as a testing set. The points of ref. 38 were corrected for a mistake in the energy conversion which resulted in a 0.03% error. The interaction energies and the interaction energy components for these points are given in the ESI.†

Compared to pot1, the important difference in the fitting algorithm was that the weight of a configuration i was taken equal to exp[2(E₀ − E_i)/(kcal mol⁻¹)] if E_i < E₀ and (E₀/E_i)² otherwise, with the parameter E₀ chosen as 3 kcal mol⁻¹. In ref. 38, the E_i < E₀ weight was equal to exp[(E₀ − E_i)/(kcal mol⁻¹)]. In effect, the low-energy regions most relevant for the present application are now weighted more strongly relative to higher-energy regions than in ref. 38. This change significantly improved the accuracy of the fit in the lower-energy region, for instance, the maximum error for E_i < −2 kcal mol⁻¹ was reduced from 0.04 kcal mol⁻¹ for pot1 to 0.02 kcal mol⁻¹ for pot2. At the same time, the unweighted root mean square error (RMSE) of pot2 and pot3 for the points with E_i < 0 kcal mol⁻¹, amounting to 0.020 and 0.019 kcal mol⁻¹, respectively, was virtually unchanged compared to pot1 of ref. 38 (0.019 kcal mol⁻¹). The overall RMSE increased to 0.47 and 0.44 kcal mol⁻¹, respectively, compared to the value of 0.15 kcal mol⁻¹ for pot1. However, this increase was almost exclusively due to several points with E_i > 10 kcal mol⁻¹ that are irrelevant for the present application. The maximum error of pot3 for E_i < −2 kcal mol⁻¹ was again 0.02 kcal mol⁻¹, the same as for pot2. The RMSE for the 12 testing point set increased from 0.033 kcal mol⁻¹ for pot1 to 0.044 kcal mol⁻¹ for pot2 and 0.048 kcal mol⁻¹ for pot3, which is not surprising since these points were included in the fit of pot1, but not in the fits of pot2 and pot3. The parameters of the fits are given in the ESI.†

For the application to the benzene dimer VRT states, the fits were regularized since the original version behaved unphysically for very short intermonomer distances, with the interaction energy becoming strongly negative. We found that the main reason for this behavior was the carbon–carbon function u_ab(r_ab) of eqn (3). Therefore, for r_ab ≤ r_max, where r_max is the point where u_CC reaches its maximum, this function was set to a constant value, equal to its value at r_max ≈ 2.5 Å. This simple regularization removed all unphysical behavior at short distances and changed the potential only in regions with interaction energies above 5 kcal mol⁻¹, not relevant for the present applications.

B. Characteristic points on the potential energy surface

The benzene dimer potential surface pot1 was explored in ref. 38 by localizing, in addition to the TT and PD minima, several other stationary points. Here, we did the same for the new potentials, pot2 and pot3. We present the results for pot3 since it differs most from pot1 and should be more accurate than pot2. The method used to find the stationary points was identical to that of ref. 38; it involved eigenvector-following local optimization⁸⁶ starting from randomly selected configurations. We found three minima, six saddle points of index 1, two stationary points of index 2, and one of index 3. The structures are displayed in Fig. 1–4. The search was extensive for the minima and index 1 saddle points and this list is probably complete for this potential. For the higher-index points, we only searched for the most important configurations. We retained the labeling of ref. 38, even though the energetic ordering of the structures has changed. An additional saddle point, not found in ref. 38, is labeled S3a. Table 1 includes some geometric parameters and the interaction energies at the characteristic points of the fitted potential. The pot3 interaction energies are compared with results from ab initio SAPT(DFT) calculations (with and without third-order energies) and from CCSD(T) calculations. In the CCSD(T) method, we used the aug-cc-pVTZ basis set supplemented by the same midbond functions as in the SAPT(DFT) calculations. The calculations were performed in the frozen-core approximation with the Boys–Bernardi counterpoise correction for the interaction energies,^87,88 using the MOLPRO suite of programs.⁸⁹ The basis set is significantly larger than that used for the CCSD(T) calculations in ref. 38 and therefore provides interaction energies of better quality. In fact, this is the best quality basis applied so far at the CCSD(T) level for geometries of the benzene dimer other than the PD, T-shape, and sandwich structures considered in ref. 41.

Fig. 1 Structures at the minima in the potential surface. For the M1 structure, the Euler angles defined in the text are related to the angles indicated as β_A = 90° − θ_A and β_B = 90° − θ_B. For the M2 structure, β_A = θ_A − 90° and γ_B = 60° − θ_B.

Fig. 2 Structures at the saddle points S1 to S3. For the S1 structure, the Euler angles defined in the text are related to the angles indicated as β_A = θ_A − 90° and γ_B = 60° − θ_B. For the S2 structure, β_A = 90° − θ_A and β_B = 90° − θ_B.

Fig. 3 Structures at the saddle points S3a to S5. For the S3a structure, the Euler angles defined in the text are related to the angles indicated as β_A = θ_A − 90° and β_B = 90° − θ_B. For the S4 structure, β_A = 90° − θ_A and β_B = 90° − θ_B.

Fig. 4 Structures at the saddle points S6 to S8. For the S6 structure, the Euler angles defined in the text are related to the angles indicated as β_A = 90° − θ_A and γ_B = 60° − θ_B.

Table 1 Stationary points on the pot3 potential energy surface. The point group symmetry of the corresponding structures is given in the second column. The geometric parameters R, θ_A, θ_B are marked in Fig. 1–4 and are related there to the Euler angles defined in the text. The remaining columns contain interaction energies (in kcal mol⁻¹) from the pot3 fit and calculated by: SAPT(DFT) with third-order terms included [SAPT], by SAPT(DFT) limited to second order [SAPT2], and by supermolecular CCSD(T). Basis sets are specified in the text. Energies relative to the M2 global minimum (in cm⁻¹) are given in parentheses

	Sym	R/Å	θ A	θ B	pot3		SAPT		SAPT2		CCSD(T)
M1	C 2h	3.937	62.12	62.12	−2.686	(36.1)	−2.683	(39.2)	−2.751	(7.1)	−2.619	(46.4)
M2	Cs	4.944	99.22	11.75	−2.789	(0.0)	−2.795	(0.0)	−2.772	(0.0)	−2.752	(0.0)
M3	D 2d	6.103			−1.796	(347.4)	−1.789	(351.8)	−1.817	(334.0)	−1.785	(338.0)
S1	Cs	4.948	98.37	11.12	−2.773	(5.6)	−2.781	(4.9)	−2.755	(5.6)	−2.740	(4.2)
S2	Cs	3.959	63.91	59.55	−2.666	(43.1)	−2.666	(45.3)	−2.731	(14.0)	−2.601	(52.5)
S3	C 2v	4.970			−2.712	(27.1)	−2.698	(33.9)	−2.661	(38.8)	−2.640	(39.0)
S3a	Cs	4.843	103.29	15.78	−2.719	(24.8)	−2.733	(21.8)	−2.711	(21.3)	−2.669	(28.7)
S4	Cs	4.221	66.65	45.28	−2.634	(54.2)	−2.591	(71.2)	−2.636	(47.3)	−2.474	(97.1)
S5	C 2v	5.009			−2.451	(118.2)	−2.441	(123.8)	−2.419	(123.1)	−2.333	(146.3)
S6	Cs	5.908	29.46	19.27	−1.739	(367.3)	−1.738	(369.7)	−1.760	(353.6)	−1.747	(351.4)
S7	C 6v	3.803			−1.804	(344.7)	−1.788	(352.2)	−1.857	(319.9)	−1.589	(406.6)
S8	D 6h	3.816			−1.772	(355.8)	−1.782	(354.5)	−1.849	(322.7)	−1.593	(405.1)

---

Comparison of Table 1 with Table 1 of ref. 38 shows that the fit of pot3 is significantly more accurate at the characteristic points than the fit of pot1 in ref. 38. Except for the S4 saddle point, where the fitted and calculated SAPT(DFT) energies differ by 0.04 kcal mol⁻¹, the accuracy of the fit is better than 0.02 kcal mol⁻¹ for all structures. This is in contrast to the potential of ref. 38, where the M1, S3, and S4 structures had errors larger than 0.02 kcal mol⁻¹ and, due to inaccuracies of the fit, M1 was the global minimum on the fitted potential instead of M2 (although with a very small energy difference)—opposite to the ordering of the ab initio energies. The lower accuracy of the pot3 fit at S4 is probably the result of a relatively less dense coverage of this region, compared to the vicinities of other characteristic points.

It can be seen in Table 1 that the sum of the third-order induction and exchange-induction terms is not very large compared to the total interaction energies—the largest contribution is 0.068 kcal mol⁻¹ or 2.5%. However, stacked configurations (in particular, the PD minimum M1) are destabilized by the third-order energies, while non-stacked (in particular, the TT (M2) and T-shape (S3) structures) are stabilized. Therefore, the third-order effects become fairly important for the relative interaction energies of these structures. In particular, the M1 structure shifts up from 7 to 36 cm⁻¹ above the M2 structure. This effect, combined with the changes in the fitting procedure that emphasize the low-energy regions, leads to important qualitative differences between pot1 and pot3. The M1 and M2 structures were isoenergetic in pot1 to within 1 cm⁻¹, whereas in pot3 the M2 structure is the global minimum, by 36 cm⁻¹ (0.10 kcal mol⁻¹) lower than M1. This energy gap is very close to the 39 cm⁻¹ in the SAPT(DFT) energies.

The SAPT(DFT) interaction energies with third-order contributions agree very well with the CCSD(T) interaction energies at the characteristic points, with an RMSE for the whole set of only 0.10 kcal mol⁻¹ compared to 0.13 kcal mol⁻¹ for the SAPT(DFT) energies at the second-order level. The discrepancies between the SAPT(DFT) and CCSD(T) energies are largest for the S7 and S8 ‘sandwich’ structures (similar to those in ref. 38), but these are less important, higher-energy structures. The third-order terms improve also the agreement of the SAPT(DFT) and CCSD(T) energies relative to the minimum M2 for almost all the characteristic points. In particular, for the structures M1 and S2, the effect is quite significant: the present SAPT(DFT) relative energy of M1 vs. M2 (39 cm⁻¹) compares very well with the value of 46 cm⁻¹ obtained from CCSD(T) calculations. Exceptions to the favorable effect of the third-order corrections are the M3, S6, and S3 structures, but the relative values of these corrections are very small there. The improvement of the relative energies of the stacked and non-stacked configurations due to the third-order effects is also visible in the S3 vs. M1 energy ordering. SAPT(DFT) calculations predict that S3 is 5 cm⁻¹ below M1, in good agreement with the 7 cm⁻¹ predicted by CCSD(T). The energy difference between S3 and M1 can also be compared to the most accurate calculations for the benzene dimer to date by Janowski and Pulay (JP)⁴¹ (these authors did not include the M2 structure) who used basis sets up to aug-cc-pVQZ, performed extrapolations to the complete basis set limit, and obtained 8 cm⁻¹ for the M1-S3 difference, with S3 lower in energy. Although JP used the quadratic configuration interaction [QCISD(T)] method and different geometries, these factors should introduce only small effects relative to CCSD(T) results and our geometries. Thus, it appears that the relative ordering of the low-energy characteristic points is now established to within a few wave numbers. The potential pot3 gives the correct order of M1 and S3 and 9 cm⁻¹ for the energy difference, whereas in pot1 the order was opposite. Also SAPT(DFT) at the second-order level gives an incorrect order of S3 vs. M1 and, interestingly, the same is true for the CCSD(T) interaction energies calculated in ref. 38. The latter were actually obtained from interaction energies computed by MP2 (second-order supermolecular perturbation theory with the Møller–Plesset partitioning of the Hamiltonian) in the aug-cc-pVTZ+mb basis, with the addition of a CCSD(T)–MP2 contribution computed in the aug-cc-pVDZ+mb basis. Thus, this often-used approach fails in this case. Overall, the closeness of the current SAPT(DFT) and CCSD(T) results as well as the very good reproduction of those results by pot3 suggests that pot3 should be a good model for the benzene dimer spectroscopic properties.

The impact of the third-order energies and of the modified fit procedure is less pronounced for the geometries. The geometric parameters of the characteristic points in pot3 are in most cases similar to those of pot1 in ref. 38. In particular, the structures of the major minima, M1 and M2, are almost identical to the M1 and M2 structures from ref. 38. Also the high-energy M3 minimum is little changed. Bludský et al.⁴⁵ and Gräfenstein and Cremer⁴⁸ suggested that the M3 structure is not a local minimum but a saddle point. The current results on the pot3 surface do not support this suggestion. The most significant geometry change between the pot1 and pot3 surfaces occurs for the saddle point S4. This is not surprising, since this saddle point separates the minima M2 and M1 and the relative energy of these minima is significantly different in pot1 and pot3. Also in pot2, the S4 configuration differs significantly from that of pot1 and, therefore, the change of the S4 geometry is partly due to the modification of the fitting procedure. Another important difference between pot1 and pot3 is found in the region of the T-shape structure S3 of C_2v symmetry that lies midway between two equivalent tilted T-shape minima M2 of symmetry C_s. In pot1, S3 is a saddle point of index 1, in pot3 it has become a stationary point of index 2. A nearby saddle point S3a of index 1 was found in pot3. It is of C_s symmetry, just as the M2 minimum, but it corresponds to a perturbation of the C_2v symmetry structure S3 by ‘sideways’ bending of the stem—rather than tilting it, which yields M2. The point S3a was found as a result of the improved fit, it is not due to the inclusion of the third-order effects, since it is also a saddle point on the pot2 surface (although the energy separation depends on the third-order terms). The importance of the S3a structure is that it has a slightly lower energy (25 cm⁻¹ above M2) than the S3 structure (27 cm⁻¹ above M2) and is probably relevant for tunneling between equivalent M2 structures. The lower energy of the S3a point compared to S3 is also confirmed by the CCSD(T) energies. Interestingly, the S3a structure was also found in ref. 45 and 48, but was interpreted as a S4-type structure. In ref. 45, the energy of this characteristic point was found to be lower than that of the S3 structure, but the importance of this finding for tunneling pathways was not realized. In contrast, in ref. 48 the energy of the S3a point was higher than that of S3, and the S3 saddle point was of index 1 (the authors of ref. 45 did not publish the indices of their stationary points). More detailed information on the stationary points of our potential surface can be found in the ESI.†

One may wonder why the relatively small third-order effects led to such significant improvements in the relative positions of the characteristic points. The reason is that the characteristic points have mostly quite distinct monomer orientations and the sum of the third-order induction and exchange-induction energies is fairly sensitive to the orientation. The third-order dispersion interaction, which we did not include, is much more isotropic and, therefore, should not affect too much the relative energies of the different characteristic points. The third-order dispersion energy is expected to be positive,⁷² and the observation that the aug-cc-pVTZ+mb SAPT(DFT) results for the M1 and S3 structures agree better with the complete basis set QCISD(T) results of ref. 41 than with the aug-cc-pVTZ+mb CCSD(T) results in Table 1 is perhaps due to the fact that the lack of the third-order dispersion energy (and of other, most likely smaller, third-order contributions: exchange-dispersion, induction-dispersion, and exchange-induction-dispersion) partly cancels the basis set incompleteness error.

III. Symmetry

The molecular symmetry group of the benzene molecule is D_6h(M); see Table A-11 in ref. 90. This group is the direct product of the permutation group D₆(M) and the inversion group {E, E*}. The carbon nuclei are labeled C₁ to C₆ consecutively around the ring and the attached protons are similarly labeled H₁ to H₆. The notation used is such that the permutation (1 2), for example, exchanges C₁ with C₂ and also exchanges H₁ with H₂, so that the permutations that generate D₆(M) are (1 2 3 4 5 6) and (2 6)(3 5). If we assume that all internal rotations of the benzene monomers within the dimer are feasible in the sense defined by Longuet-Higgins,⁹¹ then the molecular symmetry group of the benzene dimer is the group G₅₇₆ first described in ref. 25; some misprints in the character table in ref. 25 are corrected in ref. 26. The molecular symmetry group of any complex in which all monomer rotations are feasible is called the full cluster tunneling (FCT) group;⁹⁰ thus G₅₇₆ is the FCT group of the benzene dimer. For the symmetry analysis of the VRT states we consider the group G₅₇₆ and various subgroups of it.

As with the product decomposition of D_6h(M), group G₅₇₆ can also be written as a direct product of its permutation subgroup (which we call G^PSG₅₇₆) and the inversion group {E, E*}. Group G^PSG₅₇₆ is the semi-direct product of D₆(M)^A ⊗ D₆(M)^B with {E, P_AB}. The labels A and B refer to the monomers in the dimer: The CH nuclei in monomer A are labeled from 1 to 6, those in monomer B from 1′ to 6′. The interchange permutation P_AB is defined as (1 1′)(2 2′)(3 3′)(4 4′)(5 5′)(6 6′). The irreducible representations (irreps) of G₅₇₆ and the corresponding nuclear spin statistical weights for (C₆H₆)₂ and (C₆D₆)₂ are listed in Table 2. Also the irreps in the direct product group D₆(M)^A ⊗ D₆(M)^B from which they are induced by the inclusion of P_AB and E* are shown in Table 2. In ref. 26, it is explained how the character table²⁵ of G₅₇₆ and the nuclear spin weights can be computed by means of the program package GAP.⁹² The weights in Table 2 or—if two irreps occur on the same line—their sums, can be obtained by multiplication of the benzene monomer nuclear spin weights.⁹³

Table 2 Irreducible representations Γ of the FCT group G₅₇₆, with their dimension n_Γ, and of the subgroup D₆(M)^A ⊗ D₆(M)^B and the corresponding nuclear spin statistical weights. The superscripts ± refer to the inversion, E*, symmetry

G 576	nΓ	D 6(M)^A ⊗ D6(M)^B	Spin statistical weight
Irrep		Irrep	(C6H6)2	(C6D6)2
A ^±1,2	1	A 1 ⊗ A1	28, 21	4278, 4186
A ^±3,4	1	A 2 ⊗ A2	6, 3	741, 703
B ^±1,2	1	B 1 ⊗ B1	78, 91	2628, 2701
B ^±3,4	1	B 2 ⊗ B2	1, 0	1081, 1035
E ^±1	2	A 1 ⊗ A2	21	3496
E ^±2	2	A 1 ⊗ B1	91	6716
E ^±3	2	A 1 ⊗ B2	7	4232
E ^±4	2	A 2 ⊗ B1	39	2774
E ^±5	2	A 2 ⊗ B2	3	1748
E ^±6	2	B 1 ⊗ B2	13	3358
G ^±1,2	4	E 1 ⊗ E1	66, 55	6786, 6670
G ^±3,4	4	E 2 ⊗ E2	45, 36	7750, 7626
G ^±5	4	A 1 ⊗ E1	77	10672
G ^±6	4	A 1 ⊗ E2	63	11408
G ^±7	4	A 2 ⊗ E1	33	4408
G ^±8	4	A 2 ⊗ E2	27	4712
G ^±9	4	B 1 ⊗ E1	143	8468
G ^±10	4	B 1 ⊗ E2	117	9052
G ^±11	4	B 2 ⊗ E1	11	5336
G ^±12	4	B 2 ⊗ E2	9	5704
K ^±	8	E 1 ⊗ E2	99	14384

---

The tilted T-shape (TT) structure at the global minimum in the potential, see M2 in Fig. 1, has C_s = {E, σ} point group symmetry. This group has an order 2, which implies that there are 288 versions of the TT equilibrium structure between which tunneling could occur in the dimer. If none of the internal rotation tunneling motions were feasible then for a version of the TT structure that has monomer A as the ‘cap’ oriented so that the reflection symmetry plane bisects the bonds 2–3 and 5–6, the molecular symmetry group would be C_s(M) = {E, (1 4)(2 3)(5 6)*}. Since some, but not all, internal rotations in the benzene dimer appear to be feasible, i.e., to give rise to observable tunneling splittings, we considered various group chains connecting the molecular symmetry group C_s(M) of the rigid TT dimer to the FCT group G₅₇₆. As an example with A as the cap, we discuss here the group chain C_s(M) ⊂ C_6v(M) ⊂ G₂₄ ⊂ G₄₈ ⊂ G₂₈₈ ⊂ G₅₇₆ that actually agrees with the splitting pattern of the calculated levels, see section VA. Starting from the group C_s(M) of the rigid TT equilibrium structure, the possible internal motions and the corresponding molecular symmetry groups are:

- Cap C₆ internal rotation: C_s(M) ⇒ C_6v(M),

- Tilt tunneling: C_6v(M) ⇒ G₂₄,

- Cap turnover: G₂₄ ⇒ G₄₈,

- Stem C₆ internal rotation: G₄₈ ⇒ G₂₈₈,

- Cap-stem interchange: G₂₈₈ ⇒ G₅₇₆.

The group G₂₈₈ mentioned here is not G^PSG₅₇₆, the permutation subgroup of G₅₇₆, although these two groups both have order 288. Internal rotation of the cap about its C₆ axis corresponds to the lowest (sixfold) barrier (of about 6 cm⁻¹) in the potential at the saddle point S1, see Fig. 2. This process interconnects six equivalent TT minima in the potential. If we assume it to be feasible, the molecular symmetry group C_s(M) is augmented to C_6v(M) by means of the generator (1 2 3 4 5 6); see Table A-7 in ref. 90. Next, a specific TT structure can be converted into a nearby equivalent structure by undoing the tilt and then tilt to the opposite direction. The ‘untilted’ T-shape structure S3, see Fig. 2, with C_2v symmetry and an energy of 27 cm⁻¹ relative to the TT minimum, is a stationary point of index 2. Two nearby saddle points S3a of index 1 with C_s symmetry, see Fig. 3, have the slightly lower energy of 25 cm⁻¹. The permutation-inversion operation that interconnects the two TT structures involved in this tilt tunneling process is (2 6)(3 5)(2′ 6′)(3′ 5′)* and it leads from C_6v(M) to G₂₄ = C_6v(M)^A ⊗ {E, (2′ 6′)(3′ 5′)}; see Table A-27 in ref. 90 where one should replace the permutation (7 8) by (2′ 6′)(3′ 5′). Then, we found in the analysis of our calculated VRT levels (see below) that cap turnover, an operation that reverses the direction of the cap C₆ symmetry axis, is feasible. This process corresponds to operations such as (2 6)(3 5) or (1 4)(2 3)(56). Both of these types of operation are included because they are converted into each other by the feasible sixfold permutation (1 2 3 4 5 6). Cap turnover increases the PI symmetry group from G₂₄ to G₄₈ = D_6h(M)^A ⊗ {E, (2′ 6′)(3′ 5′)}. The operations that subsequently generate the FCT group G₅₇₆ are the sixfold rotation of the ‘stem’ (1′ 2′ 3′ 4′ 5′ 6′), yielding G₂₈₈ = D_6h(M)^A ⊗ D₆(M)^B = D_6h(M)^cap ⊗ D₆(M)^stem, and the interchange P_AB then producing G₅₇₆.

Our calculated VRT levels, see below, lead us to conclude that only three motions will produce observable splittings: Cap C₆ internal rotation, stem tilt, and cap turnover. In this circumstance the molecular symmetry group would be G₄₈. If stem C₆ internal rotation tunneling were also observed then the molecular symmetry group would be G₂₈₈ = D_6h(M)^cap ⊗ D₆(M)^stem. Of these four tunneling motions, if cap turnover tunneling were not observable, then the molecular symmetry group would be the group G₁₄₄ = C_6v(M)^cap ⊗ D₆(M)^stem considered before by Spirko et al.³¹

The symmetry adaptation of the basis, explained in section IVB, ensures that the calculated VRT states carry the irreps of the FCT group G₅₇₆. The particular molecular symmetry group corresponding to the calculated level splitting pattern, can be determined via subduction of the G₅₇₆ irreps along different subgroup chains. We made such an analysis only for the TT structure, since the PD structure was not observed experimentally and our calculations produced only a limited number of VRT states located near the PD minima, at higher energies. We note, though, that the PD (local minimum) structure has C_2h point group symmetry, of order 4, so there are 144 equivalent PD structures. For one of those PD structures the operations C₂ and σ_h in the group C_2h correspond to the PI operations (1 4)(2 3)(5 6)(1′ 4′)(2′ 3′)(5′ 6′)P_AB and (2 6)(3 5)(2′ 6′)(3′ 5′)*, respectively.

IV. Computational method

A. Formalism

The methods that have been developed^53–57 to compute the VRT states of a weakly bound dimer start from the Hamiltonian of a rotating dimer with two internally rotating (rigid) polyatomic monomers, expressed in body-fixed (BF) dimer coordinates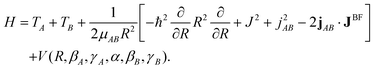The two-angle embedded^94,95 dimer BF frame has its z-axis along the vector R ≡ R_AB that points from the center of mass of monomer A to that of monomer B, R is the length of this vector, ω_A ≡ (α_A, β_A, γ_A) and ω_B ≡ (α_B, β_B, γ_B) are the Euler angles describing the orientations of local coordinate frames (MF) on monomers A and B with respect to the dimer BF frame. The z-axes of the MF frames are chosen parallel to the benzene monomer C₆ axes, the x-axis of the MF frame on monomer A points from the center of this monomer to CH fragment 1, and the x-axis of the MF frame on B from the center of B to CH fragment 1′. The angle α = α_A − α_B is the dihedral angle defined by the monomer z-axes and the dimer z-axis along R.

The operator J^BF represents the total angular momentum with components defined relative to the dimer BF frame, j_AB = j_A + j_B is the sum of the monomer angular momenta with respect to the dimer frame, and μ_AB is the dimer reduced mass. The kinetic energy operator of monomer X ( = A or B) is given by

T_X = A_X(j^MF_Xx)² + B_X(j^MF_Xy)² + C_X(j^MF_Xz)², (6)

with the rotational constants A_X, B_X, and C_X. The superscript MF implies that x, y, and z refer to the components of j_X along the principal axes of monomer X. The Hamiltonian in eqn (5) was derived by Brocks et al.⁹⁴ with the use of the chain rule. An alternative derivation is given in Appendix A-4 of ref. 95. It has been applied in calculations of the VRT levels of the NH₃ dimer^53,95,96 and the water dimer.^{54–57,61,62}

Just as in the earlier work on the NH₃ and water dimers, we introduce a coupled product basis of symmetric rotor functions—Wigner D-functions⁹⁷—for the angular coordinates

in which 〈j_Am_A; j_Bm_B |j_ABK〉 is a Clebsch–Gordan coupling coefficient.⁹⁷ The angles (Θ, Φ) are the polar angles of the intermolecular vector R with respect to the space-fixed frame. The total angular momentum J is a good quantum number and is held fixed. Its projection K on the dimer axis R is a nearly good quantum number and can be used in combination with J to label the dimer VRT states, but there is some mixing between basis functions with different values of K by off-diagonal terms in the Coriolis coupling operator j_AB·J^BF.

In applications to the NH₃, H₂O, and D₂O dimers,^{53,54,56,57,61,62} the basis in eqn (7) could always be truncated at maximum j_A and j_B values of 13, at most. As one will see below, the benzene dimer requires the use of extremely large basis sets with maximum j_A and j_B values of 24 (even 28, in some cases) to obtain sufficiently well converged results. Among the different methods that have been developed, the pseudo-spectral method of Leforestier et al.⁵⁴ is the most efficient one, in terms of computer time and storage. Actually, because of the very high values of j_A and j_B needed, it is the only method that we could apply here. The method is called a split Wigner method, because it employs, in addition to the analytical Wigner function basis of eqn (7), an appropriate numerical grid basis. The lower eigenvalues of the Hamiltonian in eqn (5) are determined iteratively by means of the Lanczos algorithm. The so-called Lanczos vectors in this algorithm are obtained by repeatedly operating with the Hamiltonian on an initial (arbitrary) seed vector. The kinetic energy terms in the Hamiltonian are easily evaluated in the analytical basis, while the potential V is diagonal in the grid basis: its diagonal matrix elements are simply the values of the potential at the grid points. The Lanczos method is applied in the analytical basis, adapted to the irreps of the FCT group G₅₇₆, see section IVB. In the potential energy calculation, one transforms the Lanczos vectors to the grid basis, multiplies with the potential on the grid, and then transforms back to the symmetry-adapted analytical basis. This, together with the fact that these transformations are made in a very efficient manner,⁵⁴ is what makes this method very economical both in the use of storage and in computer time. A potential-optimized⁹⁸ DVR (discrete variable representation) is used for the coordinate R. The calculations were made for total J values of 0 and 1. In the calculations for J = 1 we included the off-diagonal Coriolis coupling between angular basis functions with K = 0 and K = ±1, because without this coupling K would be a good quantum number, the levels with K = ±1 would be degenerate, and we could not compute a possible asymmetry splitting between the |K| = 1 levels of opposite parity.

B. Symmetry adaptation

In order to adapt the basis in eqn (7) to the irreps of the group G₅₇₆, we must first derive how the elements of this group act on the coordinates. We consider the generators of the group: the permutation (1 2 3 4 5 6), the permutation (2 6)(3 5), the interchange P_AB, and inversion E*. It is easily seen that (1 2 3 4 5 6) increases the angle γ_A by 60 degrees. The action of the other generators on the coordinates is less trivial; the results are summarized in Table 3. From the properties of the Wigner D-functions,⁹⁷ it follows then what is the effect on the basis in eqn (7). One finds, in particular, that the Wigner function , and therefore also each basis function, is an eigenfunction of (1 2 3 4 5 6) with eigenvalue exp(2πik_A/6). This property is commonly used to relate the symmetric rotor functions D^(j)_mk(ω)* of a benzene monomer to the irreps of the group D₆(M). Functions with k = 0(mod 6) belong to the D₆ irreps A₁ and A₂, functions with k = ±1(mod 6) carry the E₁ irrep, functions with k = ±2(mod 6) the E₂ irrep, and functions with k = 3(mod 6) the B₁ and B₂ irreps. This can be applied to both monomers A and B and, therefore, it follows immediately from the D₆(M)^A ⊗ D₆(M)^B subduction of the G₅₇₆ irreps, see Table 2, which particular combination of k_A and k_B (modulo 6) values belongs to each G₅₇₆ irrep. The results are included in Table 4.

Table 3 Effect of the G₅₇₆ group generators on the angular coordinates defined in the text

E	(123456)	(26)(35)	P AB	E*
Θ	Θ	Θ	π − Θ	π − Θ
Φ	Φ	Φ	π + Φ	π + Φ
α A	α A	α A + π	−αB	−αA
β A	β A	π − βA	π − βB	π − βA
γ A	γ A +2π/6	−γA	π +γB	γ A
α B	α B	α B	−αA	−αB
β B	β B	β B	π − βA	π − βB
γ B	γ B	γ B	π + γA	γ B

---

Table 4 Projection operators and k_A, k_B values for the G₅₇₆ irreps

G 576 irrep	k A , kB (mod 6)	Projector
A ^±1	0, 0
A ^±2	0, 0
A ^±3	0, 0
A ^±4	0, 0
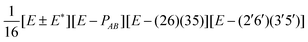
B ^±1	3, 3
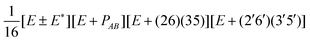
B ^±2	3, 3
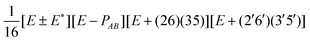
B ^±3	3, 3
B ^±4	3, 3
E ^±1	0, 0	⅛[E ± E*] [E + (26)(35)] [E − (2′ 6′)(3′ 5′)]
E ^±2	0, 3	⅛[E ± E*] [E + (26)(35)] [E + (2′ 6′)(3′ 5′)]
E ^±3	0, 3	⅛[E ± E*] [E + (26)(35)] [E − (2′ 6′)(3′ 5′)]
E ^±4	0, 3	⅛[E ± E*] [E − (26)(35)] [E + (2′ 6′)(3′ 5′)]
E ^±5	0, 3	⅛[E ± E*] [E − (26)(35)] [E − (2′ 6′)(3′ 5′)]
E ^±6	3, 3	⅛[E ± E*] [E + (26)(35)] [E − (2′ 6′)(3′ 5′)]
G ^±1	±1, ±1	¼[E ± E*] [E + PAB]
G ^±2	±1, ±1	¼[E ± E*] [E − PAB]
G ^±3	±2, ±2	¼[E ± E*] [E + PAB]
G ^±4	±2, ±2	¼[E ± E*] [E − PAB]
G ^±5	0, ±1	¼[E ± E*] [E + (26)(35)]
G ^±6	0, ±1	¼[E ± E*] [E + (26)(35)]
G ^±7	3, ±1	¼[E ± E*] [E − (26)(35)]
G ^±8	3, ±1	¼[E ± E*] [E − (26)(35)]
G ^±9	0, ±2	¼[E ± E*] [E + (26)(35)]
G ^±10	0, ±2	¼[E ± E*] [E + (26)(35)]
G ^±11	3, ±2	¼[E ± E*] [E − (26)(35)]
G ^±12	3, ±2	¼[E ± E*] [E − (26)(35)]
K ^±	±1, ±2	½[E ± E*]

---

The twofold symmetry operators have the following effects on the basis

(2 6)(3 5)| j_A, k_A, j_B, k_B, j_AB, J, K, M〉 = (−1)^j_A| j_A, −k_A, j_B, k_B, j_AB, J, K, M〉 (8)

(2′ 6′)(3′ 5′)| j_A, k_A, j_B, k_B, j_AB, J, K, M〉 = (−1)^j_B| j_A, k_A, j_B, −k_B, j_AB, J, K, M〉

P_AB| j_A, k_A, j_B, k_B, j_AB, J, K, M〉 = (−1)^j_A+j_B+J| j_B, k_B, j_A, k_A, j_AB, J, −K, M〉

E*| j_A, k_A, j_B, k_B, j_AB, J, K, M〉 = (−1)^{J−j_AB+k_A+k_B}| j_A, k_A, j_B, k_B, j_AB, J, −K, M〉.

Given the fact that the basis functions in eqn (7) are already adapted to C₆(M)^A ⊗C₆(M)^B by choosing a specific combination of k_A and k_B (modulo 6) values, it is easy to use the relations in eqn (8) to construct a set of projection operators that produce symmetry-adapted basis functions for all irreps of G₅₇₆. We use the so-called Wigner or matrix-element projectors⁹⁹ listed in Table 4. Actually, there are n_Γ of such projectors for an irrep Γ of dimension n_Γ, but we need only one of them per irrep to construct a symmetry-adapted basis for the computation of the VRT levels. The partners in a symmetry-adapted basis carrying a multi-dimensional irrep yield the same energies. If needed, the partner wave functions can be obtained by the action of those generators in eqn (8) that are not contained in the projectors in Table 4. Operating with these projectors on the basis functions of eqn (7), with the application of eqn (8), yields the symmetry-adapted basis functions for all G₅₇₆ irreps. These functions are linear combinations of, at most 16, primitive basis functions. From the properties of the matrix-element projectors,⁹⁹ one can derive that matrix elements of the Hamiltonian can be rewritten such that only the basis functions in the ket need to be symmetry adapted, while one keeps the primitive basis functions in the bra (or vice versa). The calculation of the VRT levels was performed for each G₅₇₆ irrep separately.

C. Computational details

It was already mentioned above that the angular basis had to be very large to obtain sufficiently well converged energy levels. The basis was truncated by choosing maximum values of j_A, j_B, and k_A, k_B. After a series of convergence tests, we used a maximum j_A, j_B value of 24 in most calculations and included all the allowed values of k_A, k_B. In calculations aimed at checking whether the very small interchange tunneling splittings had converged, we even used a maximum j_A, j_B value of 28, while maintaining the highest k_A, k_B at 24. With a maximum j_A, j_B of 24, the corresponding grid contained 27 Gauss–Legendre quadrature points in the angles β_A and β_B, and 54 equidistant points in γ_A, γ_B, and α. When the maximum j_A, j_B was increased to 28, the grid consisted of 32 points in β_A and β_B, and 60 points in γ_A, γ_B, and α. For the radial coordinate, we used 53 equidistant grid points in the range from R = 5.7 to 16 a₀, 50 sine basis functions, and a potential-optimized DVR. The 16 potential-optimized DVR points and weights were determined by solving a one-dimensional eigenvalue problem with an effective radial potential obtained by choosing for each R value the lowest value of the potential on the five-dimensional angular grid.

After some experimentation with different energy thresholds, it was concluded that rejecting all grid points for which the potential (with well depth −975.5 cm⁻¹) was higher than −100 cm⁻¹ had a negligibly small effect on the energy levels. Further checks were made after obtaining converged energy levels and it turned out that less than 0.0001 of the integrated squared amplitude of the wave functions was rejected by using this energy threshold. The final grid for the ‘standard’ basis with a maximum j_A, j_B of 24 contained nearly 0.8 × 10⁹ points and for the extended basis more than 1.5 × 10⁹ points. The number of grid points on which the potential was evaluated was reduced by a factor of 72 through the use of symmetry. With the standard basis, the size of the primitive angular basis set was 9.6 × 10⁶ and 26.3 × 10⁶ for J = 0 and 1, respectively, and with the extended basis it was 20.6 × 10⁶ for J = 0. With the potential-optimized DVR in R, the total basis size is 16 times larger. The largest size of the symmetry-adapted standard basis for J = 0 was nearly 2.2 × 10⁶. It occurs for the K^± irreps of dimension n_Γ = 8; the size of the symmetry-adapted basis is roughly proportional to the dimension of the irrep. Up to 250 Lanczos iterations were needed to converge at least the lowest eight energy levels of a given symmetry to 10⁻⁶ cm⁻¹ or better.

For the benzene monomer rotational constants we used the experimental^100,101 ground state values: A = B = 0.1898 cm⁻¹ and C = 0.0949 cm⁻¹. The atomic masses are 12.0000 u for carbon and 1.0078 u for hydrogen, which yields a dimer reduced mass μ_AB of 39.0235 u.

As explained in section II, we expect that the new potential pot3 which includes third-order induction and exchange-induction terms is the most accurate one. So we used pot3 for the calculation of the VRT levels. In order to check how sensitive the calculated levels are to changes in the potential, we also performed calculations with pot1 and pot2.

D. Convergence, one-dimensional models

In section VA, where we present the calculated VRT levels, we will see that the values of D₀ computed with the standard and extended basis sets, 870.3481 and 870.9526 cm⁻¹, respectively, are still rather different. Hence, we must conclude that the absolute energies of the levels are not converged to better than about 1 cm⁻¹. Fortunately, the energy differences between the levels are converged much better. How much better, depends on the effect that the basis set truncation has for different irreps. In section IVB, it was explained how the different irreps correspond to specific values of k_A and k_B (modulo 6). For irreps with the same values of k_A and k_B, the effect of the basis truncation on the energies is about the same and the energy differences between such levels seem to be converged to about 3 × 10⁻⁴ cm⁻¹ with the standard basis, see below. The energy differences between levels that belong to irreps with different k_A and k_B appear to be converged only to a few tenths of cm⁻¹.

In addition to the symmetry, also the height of the barriers to internal rotation determines how well the energies are converged with a given basis size. We investigated this in one-dimensional models for the internal rotations of the cap and the stem, hindered by sixfold barriers. With the assumption of an ideal T-shaped structure, the reduced rotational constant for internal rotation of the cap is the sum of the monomer rotational constants, A + C. The reduced rotational constant for internal rotation of the stem was assumed to be C + 1/(2μ_ABR_e²), with an equilibrium center-of-mass distance R_e of 9.35 a₀. The height of the sixfold barrier in the model for cap rotation was chosen to be 6 cm⁻¹, which is about the energy difference between the saddle point S1 and the TT equilibrium geometry M2, see section II. In the model for stem rotation we used the value of 118 cm⁻¹ for the height of the sixfold barrier, which is the energy difference between the saddle point S5 and the TT minimum M2. For cap rotation with its very low barrier, a one-dimensional free rotor basis with a maximum k_i of 18 already yields energy levels converged to better than 10⁻⁷ cm⁻¹. For stem rotation with the much higher barrier of 118 cm⁻¹ a basis with maximum k_i of 24 still yields truncation errors of about 0.03 cm⁻¹ in the energies. This should be seen in the perspective of the actual size of the level splittings. Cap rotation with its barrier of 6 cm⁻¹ gives rise to splittings on the order of 1 cm⁻¹, stem rotation hindered by a barrier of 118 cm⁻¹ gives rise to splittings of about 3 × 10⁻⁸ cm⁻¹ ≈ 1 kHz. As a consequence, our results are well converged for tunneling processes leading to relatively large splittings, whereas very small tunneling splittings cannot be converged at all in our full six-dimensional approach.

V. Vibration–rotation-tunneling states

A. Energy levels, properties

The energy levels calculated for J = 0 with the standard basis are listed in Table 5–8. A representative set of levels is shown in Fig. 5(a). As we will explain below, all of these energy levels correspond to the vibrational ground and first excited states localized near the TT equilibrium geometry and the splittings between the levels of a given vibrational state are caused by tunneling between equivalent TT minima in the potential surface. The levels in Fig. 5(a) belong to those G₅₇₆ irreps that are induced from identical irreps on monomers A and B, see Table 2. Therefore, it is not clear whether the tunneling mechanisms causing the splittings between the levels in Fig. 5(a) involve the cap or the stem in the TT structure. Fig. 5(b) displays the levels obtained from the one-dimensional model for the hindered rotation of the cap. If the sixfold barrier to internal rotation of the cap were zero then the levels in Fig. 5(b) would be the |k_i| = 0 through 6 internal rotation energy levels with energies increasing as k²_i. As the sixfold barrier to cap internal rotation is raised, the |k_i| = 3 level splits into two and the energy spacing pattern between the |k_i| = 0, 1, 2 and 3(lower) levels approaches the high barrier 1 : 2 : 1 ratio; these four levels correlate with the ground cap-torsion vibrational state of the high barrier complex which has symmetry A′ in the point group C_s of the TT structure. These levels, with the C₆ irrep labels k_i(mod 6) = 0, ±1, ±2, and 3, have symmetries A₁, E₁, E₂, and B₂, respectively, if we extend the C₆ symmetry of the one-dimensional model to C_6v by inclusion of the reflection. The levels in the upper half of Fig. 5(b) have |k_i| = 3(upper), 4, 5, and 6(lower) in the free internal rotor limit and correlate with the v = 1 first excited cap-torsion vibrational state of the high barrier complex which has symmetry A′′ in C_s. These levels have B₁, E₂, E₁, and A₂ symmetry, respectively, in C_6v. In the high-barrier case, the vibrational excitation energy is large relative to the tunneling splittings. Here, the barrier for cap rotation is low, the ‘vibrationally excited’ state already lies above this barrier, the energy gap between the two ‘vibrational’ states in Fig. 5(b) is of the same magnitude as their ‘tunneling’ splittings, and the latter are far from corresponding to a 1 : 2 : 1 ratio. Still, we will use the designation vibrational ground and excited states for the states that correlate with the vibrational states of A′ and A′′ symmetry in the point group C_s of the TT equilibrium structure. The relation between the levels from the full calculations in Fig. 5(a) and those from the one-dimensional model in Fig. 5(b) can be understood if one realizes that the G₅₇₆ irreps A₁ and A₂ originate from the A₁ irreps on both monomers, the irreps A₃ and A₄ from the monomer A₂ irreps, the irreps G₁ and G₂ from the monomer E₁ irreps, the irreps G₃ and G₄ from the monomer E₂ irreps, the irreps B₁ and B₂ from the monomer B₁ irreps, and the irreps B₃ and B₄ from the monomer B₂ irreps. The similarity between the pictures in Fig. 5(a) and (b) shows that it is the hindered rotation of the cap that is primarily responsible for the energy level pattern.

Fig. 5 (a) Calculated VRT levels for J = 0 for selected irreps, and (b) vibration-tunneling levels from a one-dimensional model for cap rotation.

Table 5 Tilt tunneling ground levels for the ground vibrational state of A′ symmetry calculated for J = 0 with the standard basis, and symmetry with respect to the group chain G₂₄ ⊂ G₄₈ ⊂ G₂₈₈ ⊂ G₅₇₆. The energy zero of the ground level of A⁺₁ symmetry corresponds to a binding energy D₀ of 870.3481 cm⁻¹

k A (mod 6)	G 24	G 48	G 288	G 576	Energy/cm^−1
0	A 1s		A 1g⊗A1	A ^+1, A^+2	0.0000, 0.0003
			A 1g⊗E1	G ^+5	0.3077
			A 1g⊗E2	G ^+6	0.2084
			A 1g⊗B1	E ^+2	0.2239
			A 2u⊗A1	E ^−1	0.2837
			A 2u⊗E1	G ^−7	0.5899
			A 2u⊗E2	G ^−8	0.4923
			A 2u⊗B1	E ^−4	0.5068
±1	E 1a		E 1g⊗A2	G ^−7	0.4018
			E 1g⊗E1	G ^−1,G^−2	0.6569, 0.6569
			E 1g⊗E2	K ^−	0.5916
			E 1g⊗B2	G ^−11	0.5729
			E 1u⊗A2	G ^+7	0.4954
			E 1u⊗E1	G ^+1,G^+2	0.7479, 0.7482
			E 1u⊗E2	K ^+	0.6846
			E 1u⊗B2	G 1 ^+1	0.6647
±2	E 2s		E 2g⊗A1	G ^+6	1.2669
			E 2g⊗E1	K ^+	1.4604
			E 2g⊗E2	G ^+3,G^+4	1.4047, 1.4050
			E 2g⊗B1	G ^+10	1.3762
			E 2u⊗A1	G ^−6	1.2836
			E 2u⊗E1	K ^−	1.4762
			E 2u⊗E2	G ^−3,G^−4	1.4214, 1.4214
			E 2u⊗B1	G ^−10	1.3921
3	B 2a		B 1g⊗A2	E ^−4	2.0840
			B 1g⊗E1	G ^−9	2.2086
			B 1g⊗E2	G ^−10	2.1724
			B 1g⊗B2	E ^−6	2.1235
			B 2u⊗A2	E ^+5	2.0860
			B 2u⊗E1	G ^+11	2.2102
			B 2u⊗E2	G ^+12	2.1744
			B 2u⊗B2	B ^+3,B^+4	2.1250, 2.1253

---

Table 6 Tilt tunneling excited levels for the ground vibrational state of A′ symmetry calculated for J = 0 with the standard basis, and symmetry with respect to the group chain G₂₄ ⊂ G₄₈ ⊂ G₂₈₈ ⊂ G₅₇₆

k A (mod 6)	G 24	G 48	G 288	G 576	Energy/cm^−1
0	A 1a		A 1g⊗A2	E ^+1	0.9130
			A 1g⊗E1	G ^+5	1.3120
			A 1g⊗E2	G ^+6	1.1878
			A 1g⊗B2	E ^+3	1.2070
			A 2u⊗A2	A ^−3,A^−4	1.2214, 1.2217
			A 2u⊗E1	G ^−7	1.6217
			A 2u⊗E2	G ^−8	1.4977
			A 2u⊗B2	E ^−5	1.5169
±1	E 1s		E 1g⊗A1	G ^−5	1.3012
			E 1g⊗E1	G ^−1,G^−2	1.6480, 1.6483
			E 1g⊗E2	K ^−	1.5520
			E 1g⊗B1	G ^−9	1.5430
			E 1u⊗A1	G ^+5	1.4175
			E 1u⊗E1	G ^+1,G^+2	1.7641, 1.7642
			E 1u⊗E2	K ^+	1.6685
			E 1u⊗B1	G ^+9	1.6589
±2	E 2a		E 2g⊗A2	G ^+8	2.1468
			E 2g⊗E1	K ^+	2.3770
			E 2g⊗E2	G ^+3,G^+4	2.3314, 2.3315
			E 2g⊗B2	G ^+12	2.2719
			E 2u⊗A2	G ^−8	2.1675
			E 2u⊗E1	K ^−	2.3978
			E 2u⊗E2	G ^−3, G^−4	2.3522, 2.3525
			E 2u⊗B2	G ^−12	2.2926
3	B 2s		B 1g⊗A1	E ^−2	2.8444
			B 1g⊗E1	G ^−9	3.0250
			B 1g⊗E2	G ^−10	2.9664
			B 1g⊗B1	B ^−1,B^−2	2.9211, 2.9206
			B 2u⊗A1	E ^+3	2.8466
			B 2u⊗E1	G ^+11	3.0276
			B 2u⊗E2	G ^+12	2.9691
			B 2u⊗B1	E ^+6	2.9235

---

Table 7 Tilt tunneling ground levels for the lowest excited vibrational state of A′′ symmetry calculated for J = 0 with the standard basis, and symmetry with respect to the group chain G₂₄ ⊂ G₄₈ ⊂ G₂₈₈ ⊂ G₅₇₆

k A (mod 6)	G 24	G 48	G 288	G 576	Energy/cm^−1
3	B 1a		B 2g⊗A2	E ^−5	4.0534
			B 2g⊗E1	G ^−11	4.1141
			B 2g⊗E2	G ^−12	4.0805
			B 2g⊗B2	B ^−3,B^−4	4.0424, 4.0422
			B 1u⊗A2	E ^+4	4.0567
			B 1u⊗E1	G ^+9	4.1170
			B 1u⊗E2	G ^+10	4.0837
			B 1u⊗B2	E ^+6	4.0452
±2	E 2s		E 2g⊗A1	G ^+6	5.4322
			E 2g⊗E1	K ^+	5.4476
			E 2g⊗E2	G ^+3,G^+4	5.4009, 5.4010
			E 2g⊗B1	G ^+10	5.3773
			E 2u⊗A1	G ^−6	5.4354
			E 2u⊗E1	K ^−	5.4507
			E 2u⊗E2	G ^−3,G^−4	5.4042, 5.4041
			E 2u⊗B1	G ^−10	5.3804
±1	E 1a		E 1g⊗A2	G ^−7	7.9937
			E 1g⊗E1	G ^−1,G^−2	7.9466, 7.9467
			E 1g⊗E2	K ^−	7.8824
			E 1g⊗B2	G ^−11	7.8769
			E 1u⊗A2	G ^+7	8.0006
			E 1u⊗E1	G ^+1,G^+2	7.9532, 7.9533
			E 1u⊗E2	K ^+	7.8892
			E 1u⊗B2	G ^+11	7.8837
0	A 2a		A 1u⊗A2	E ^−1	9.3330
			A 1u⊗E1	G ^−5	9.2392
			A 1u⊗E2	G ^−6	9.2862
			A 1u⊗B2	E ^−3	9.1871
			A 2g⊗A2	A ^+3,A^+4	9.6672, 9.6677
			A 2g⊗E1	G ^+7	9.5711
			A 2g⊗E2	G ^+8	9.6176
			A 2g⊗B2	E ^+5	9.5199

---

Table 8 Tilt tunneling excited levels for the lowest excited vibrational state of A′′ symmetry calculated for J = 0 with the standard basis, and symmetry with respect to the group chain G₂₄ ⊂ G₄₈ ⊂ G₂₈₈ ⊂ G₅₇₆

k A (mod 6)	G 24	G 48	G 288	G 576	Energy/cm^−1
3	B 1s		B 2g⊗A1	E ^−3	5.1728
			B 2g⊗E1	G ^−11	5.2820
			B 2g⊗E2	G ^−12	5.2286
			B 2g⊗B1	E ^−6	5.1855
			B 1u⊗A1	E ^+2	5.1772
			B 1u⊗E1	G ^+9	5.2865
			B 1u⊗E2	G ^+10	5.2333
			B 1u⊗B1	B ^+1,B^+2	5.1904, 5.1898
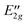
±2	E 2a		E 2g⊗A2	G ^+8	6.4354
			E 2g⊗E1	K ^+	6.4725
			E 2g⊗E2	G ^+3,G^+4	6.4161, 6.4166
			E 2g⊗B2	G ^+12	6.3811
			E 2u⊗A2	G ^−8	6.4406
			E 2u⊗E1	K ^−	6.4778
			E 2u⊗E2	G ^−3,G^−4	6.4217, 6.4220
			E 2u⊗B2	G ^−12	6.3865
±1	E 1s		E 1g⊗A1	G ^−5	8.8366
			E 1g⊗E1	G ^−1,G^−2	8.7917, 8.7920
			E 1g⊗E2	K ^−	8.7180
			E 1g⊗B1	G ^−9	8.7091
			E 1u⊗A1	G ^+5	8.8446
			E 1u⊗E1	G ^+1,G^+2	8.7997, 8.8002
			E 1u⊗E2	K ^+	8.7264
			E 1u⊗B1	G ^+9	8.7173
0	A 2s		A 1u⊗A1	A ^−1,A^−2	10.8577, 10.8583
			A 1u⊗E1	G ^−5	10.7754
			A 1u⊗E2	G ^−6	10.7073
			A 1u⊗B1	E ^−2	10.6763
			A 2g⊗A1	E ^+1	10.9552
			A 2g⊗E1	G ^+7	10.8925
			A 2g⊗E2	G ^+8	10.7914
			A 2g⊗B1	E ^+4	10.7738

---

The splittings between the levels belonging to the same cap hindered rotation quantum number can be interpreted by looking at the full set of levels in Table 5–8 and their symmetries with respect to the group chain C_s(M) ⊂ C_6v(M) ⊂ G₂₄ ⊂ G₄₈ ⊂ G₂₈₈ ⊂ G₅₇₆, see also section III. The C_s symmetry label indicates whether a level correlates with the vibrational ground state, A′, or with the lowest vibrationally excited A′′ state. We also found vibrationally excited states with A′ symmetry, but these have higher energies and are not included in Table 5–8. The splittings of the levels with the same A′ or A′′ symmetry are due to different tunneling mechanisms. We already saw that the splittings between levels belonging to different irreps of C_6v are caused by the sixfold hindered rotation of the cap. The further splittings on the order of 1 cm⁻¹ between the levels in Table 6 and those in Table 5 and between the levels in Table 8 and those in Table 7, see also Fig. 5(a), are caused by tilt tunneling. The levels in each tilt tunneling pair belong to the same C_6v irrep and the same k_A (mod 6), but to different G₂₄ irreps [distinguished by their parity ‘s’ or ‘a’ with respect to the twofold operation (2 6)(3 5)(2′ 6′)(3′ 5′)* that represents tilt tunneling]. The small splittings between levels in the same table with the same G₂₄ irrep and different G₄₈ irreps are caused by cap turnover. These splittings are 0.28, −0.09, 0.016, −0.002 cm⁻¹ for the levels in Table 5 and 0.31, −0.12, 0.021, −0.0025 cm⁻¹ for the levels in Table 6. For the vibrationally excited levels in Table 7 and 8 the corresponding splittings are −0.003, 0.003, −0.007, −0.33 cm⁻¹ and −0.004, 0.005, −0.008, −0.10 cm⁻¹, respectively. Positive values of the splitting imply that the levels of + parity under E* are lower in energy than the levels of − parity, negative values imply the opposite. One observes that this sign is the same as the parity ‘s’ (symmetric) or ‘a’ (antisymmetric) of the G₂₄ irrep to which the levels belong. In view of the convergence problem discussed in section IVD one may wonder whether such small splittings are reliably calculated, but we believe this to be the case. One can verify that these splittings are very nearly equal for different levels belonging to the same G₂₄ irrep. Moreover, the two G₅₇₆ irreps involved in each tunneling level pair always belong to the same values of k_A and k_B (mod 6) so that both levels are equally affected by the basis truncation error. We estimated this truncation error to be about 0.0003 cm⁻¹ in this case, an order of magnitude smaller than the smallest splittings found.

Furthermore, one observes splittings between levels belonging to the same G₄₈ irrep and different G₂₈₈ irreps, but these are rather irregular and do not have any physical meaning. Such irregular splittings are caused by the nonuniform basis set truncation errors for energy levels belonging to irreps with different values of k_A and k_B. The process that would cause such splittings in reality is the sixfold hindered rotation of the stem with a barrier of 118 cm⁻¹; from our one-dimensional model calculations for this process we estimate that the corresponding splittings are on the order of 3 × 10⁻⁸ cm⁻¹ ≈ 1 kHz. Such small splittings cannot be converged with our approach, see section IVD.

Finally, we observe splittings of about 0.0003 cm⁻¹ ≈ 10 MHz between the levels of A^±₁ and A^±₂, A^±₃ and A^±₄, G^±₁ and G^±₂, G^±₃ and G^±₄, B^±₁ and B^±₂, B^±₃ and B^±₄ symmetries. If this splitting is real, it is due to interchange tunneling which, in combination with stem rotation, would increase the feasible PI group from G₄₈ to the FCT group G₅₇₆. In order to check whether interchange is indeed feasible or if the splitting is an artefact due to a basis truncation error (very small, in this case, because these irrep pairs correspond to identical values of k_A and k_B), we increased the basis from a maximum j_A, j_B value of 24 to 28. The basis became so large that this calculation could be done only for the one-dimensional G₅₇₆ irreps. We had already seen in tests with smaller basis sets that the ‘interchange’ splitting systematically decreases when the maximum j_A, j_B value of the basis is increased. Obviously, an increase of the maximum j_A, j_B value allows the wave functions to be more localized and to have smaller overlap (and less tunneling) between different wells in the potential. Since it turned out that the ‘interchange’ splittings decreased by another factor of 10 when the maximum j_A, j_B value was increased to 28, we conclude that this splitting has not yet converged, but that we can set an upper bound of 1 MHz to the actual interchange splitting.

The states shown in Table 5–8 and Fig. 5(a) belong to the vibrational ground state of A′ symmetry and the lowest excited vibrational state of A′′ symmetry in the point group C_s of the TT structure. We also calculated higher states for all irreps, a selection is shown in Table 9. Also the expectation value 〈R〉 of the center-of-mass distance is included in this table, as well as the dimer ‘rotational constants’ A, (B + C)/2, and B − C. The latter were not computed in the standard way, with respect to a body-fixed frame obeying the Eckart conditions,⁹⁰ because this method is only applicable to nearly rigid molecules that exhibit small-amplitude vibrations with respect to a single equilibrium geometry. Here, as already discussed, we have 288 equivalent TT equilibrium structures which are interconnected in sets of 24 by feasible tunneling mechanisms. Instead, we calculated the expectation values of the instantaneous inertia tensor and computed the ‘rotational constants’ from their eigenvalues. Although we realize that this definition of the rotational constants does not allow precise comparison with experimental data, it gives a good idea of the average structure of the dimer. Further on, we will also present rotational constants derived from the energy levels computed for total angular momentum J = 0 and 1.

Table 9 Energy levels (in cm⁻¹) for the A⁺₁, A⁺₂ and A⁺₃, A⁺₄ irreps, relative to the ground A⁺₁ level at −870.3481 cm⁻¹, expectation values 〈R〉 (in a₀), and rotational constants (in MHz) derived from the expectation values of the inertia tensor, see text. The properties of the A⁺₁, A⁺₂ states and those of the A⁺₃, A⁺₄ states are very nearly the same

G 576 irrep	Energy	〈R〉	A	(B+C)/2	B − C
A ^+1/A^+2	0.0000/ 0.0003	9.418	1908.9	423.9	11.2
A ^+1/A^+2	11.2857/11.2864	9.420	1908.3	423.8	12.0
A ^+1/A^+2	15.4264/15.4267	9.320	1895.4	431.7	20.7
A ^+1/A^+2	19.2080/19.2081	9.358	1898.0	428.7	18.4
A ^+1/A^+2	21.0491/21.0495	9.348	1899.4	429.5	18.9
A ^+1/A^+2	28.9401/28.9407	9.252	1889.7	436.9	22.2
A ^+1/A^+2	30.7557/30.7580	9.160	1876.6	444.3	23.9
A ^+1/A^+2	31.4828/31.4812	9.385	1897.9	426.7	17.2
A ^+3/A^+4	9.6672/ 9.6677	9.344	1900.1	429.8	19.9
A ^+3/A^+4	12.1429/12.1434	9.416	1909.3	424.1	11.4
A ^+3/A^+4	20.5728/20.5731	9.338	1899.5	430.3	20.0
A ^+3/A^+4	23.3783/23.3789	9.218	1885.5	439.7	23.7
A ^+3/A^+4	27.4755/27.4760	9.267	1892.0	435.9	22.4
A ^+3/A^+4	30.2274/30.2282	9.294	1889.5	433.8	23.0
A ^+3	32.0419	7.602	1608.8	609.2	29.2
A ^+3/A^+4	37.7031/37.7026	9.133	1872.6	446.6	25.2
TT equil.	−105.2	9.342	1914.5	430.0	31.5
PD equil.	−69.2	7.440	1651.5	626.7	38.3

---

The first observation is that also the higher levels of A⁺₁, A⁺₂ symmetry and almost all of those of A⁺₃, A⁺₄ symmetry are split by about 0.0003 cm⁻¹, just as the lower levels of these symmetries. We already discussed that this splitting is caused by cap-stem interchange tunneling in the TT structure, but that the splitting is exaggerated, perhaps by several orders of magnitude, by the truncation of the basis. The values of 〈R〉, A, (B+C)/2, and B − C are so similar for these pairs of symmetries that these values were not separately given in Table 9, which is another indication that cap-stem interchange is (nearly) quenched. An exception to this rule is the 7th state of A⁺₃ symmetry, which has no A⁺₄ counterpart. Also the properties of this state differ strongly from those of all other states, which are mutually quite similar. The substantially smaller value of 〈R〉 and the values of the rotational constants are close to the values computed for the PD equilibrium geometry, which leads to the conclusion that the 7th state of A⁺₃ symmetry does not have the TT structure, but rather the PD structure. Its energy of 32 cm⁻¹ above the ground level of A⁺₁ symmetry is similar to the energy difference of 36 cm⁻¹ between the local minimum M1 with the PD geometry and the global minimum M2 with the TT geometry, which shows that the zero-point vibrational energy is not very different for the two structures. Also the fact that this A⁺₃ state has no nearly isoenergetic counterpart of A⁺₄ symmetry is explained by the fact that it has the PD structure. The PD equilibrium geometry has point group symmetry C_2h. The element C₂ in this group contains the interchange operation P_AB, see section III. The A⁺₃ state is symmetric with respect to C₂, the A⁺₄ state is antisymmetric. Therefore, the 7th A⁺₄ state, which has the PD structure, is vibrationally excited with respect to the corresponding A⁺₃ state and, accordingly, should have substantially higher energy. The assignment of the 7th state of A⁺₃ symmetry to the PD structure will be confirmed when we look at the wave functions in section VB. Although this state is not the only one among our computed states that has the PD structure, we did not find many because of the limited energy range for which we have converged levels.

A further conclusion from the results in Table 9 is that there are many low lying vibrationally excited levels. Their rotational constants are similar to the values calculated for the TT and PD equilibrium geometries. There are small, but significant, differences between different vibrational states. The zero-point vibrational energy for the most stable isomer with the TT structure, the difference between D_e and D₀, is 105 cm⁻¹.

A theoretically better way to compute the rotational constants for a floppy system as the benzene dimer is to extract them from the energy levels calculated for higher values of J. Due to size limitations, we could only compute the levels for J = 1 and only for the one-dimensional irreps. Results for the A_i^± irreps (i = 1,…,4) for J = 0 and J = 1 are shown in Fig. 6. In order to understand the rotational level pattern of a given vibration-tunneling state, one must first look at the symmetry. From the symmetry of the basis functions discussed in Sec IVB, we derived, for example, that for an A⁺₁ level with J = 0 the corresponding level with J = 1, K = 0 has A⁻₂ symmetry, while the two levels in the asymmetry doublet for J = 1, K = ±1 have A⁺₁ and A⁻₂ symmetry. Similar relations for other irreps can be read from Table 10, which contains the rotational constants extracted from the J = 1 and J = 0 levels. It follows from the standard asymmetric rotor Hamiltonian⁹⁰ that the rotational constant B + C equals the energy difference between the J = 1, K = 0 level and the J = 0 level. The rotational constant A can be extracted from the difference A + (B + C)/2 between the average energy of the two J = 1, K = ±1 levels and the J = 0 energy, and the constant B − C equals the energy difference between the J = 1, K = ±1 levels of opposite parity. The latter difference is on the order of 0.0005 cm⁻¹ and, in view of the basis truncation error, one may wonder whether it is significant. The two irreps involved belong to the same k_A, k_B (mod 6) values and we estimated the basis truncation error to be about 0.0003 cm⁻¹ in this case. With our basis of symmetric rotor functions K is a good quantum number if we neglect off-diagonal Coriolis coupling. We found, indeed, that when we made this approximation, the two J = 1, K = ±1 levels in the asymmetry doublets become exactly degenerate. Hence, the asymmetry doubling from which we extract B − C is due to a small perturbation by the off-diagonal Coriolis terms in the Hamiltonian of eqn (5) and we believe it to be significant, although not very accurate. It is clear from Table 10 that the rotational constants are very similar for irreps that differ only in their parity with respect to interchange P_AB, such as A⁺₁ and A⁺₂, A⁺₃ and A⁺₄, etc.

Fig. 6 VRT levels of A_i^±(i = 1,…,4) symmetry calculated for J = 0 and 1.

Table 10 Energy levels for J = 0 (in cm⁻¹) relative to the ground A⁺₁ level at −870.3481 cm⁻¹ and rotational constants (in MHz) extracted from energy differences between J = 1 and J = 0 levels, see text. The irreps indicated belong to the J = 0 and J = 1, K = 0 levels, respectively, while the J = 1, K = ±1 asymmetry doublets carry both irreps

G 576 irrep	Energy	A	(B + C)/2	B − C
A ^+1, A^−2	0.0000	33744	436.4	28.8
A ^+2, A^−1	0.0003	33731	436.4	28.8
A ^−3, A^+4	1.2214	–21558	440.3	31.9
A ^−4, A^+3	1.2217	–21585	440.3	31.9
A ^+3, A^−4	9.6672	–17250	448.5	5.6
A ^+4, A^−3	9.6677	–17268	448.5	5.6
A ^−1, A^+2	10.8577	–44764	473.6	14.7
A ^−2, A^+1	10.8583	–44791	473.6	14.7

---

In Fig. 6 the levels for J = 1, K = ±1 are compared with the J = 0 levels. The J = 1, K = 0 levels are not shown because on the scale of the figure these levels would overlap with the J = 0 levels. Also the very small asymmetry doubling of the J = 1, K = ±1 levels is not visible. Still, the figure shows an interesting feature, namely that the value of |K| has a significant effect on the vibrational excitation energy and the tilt tunneling splittings. Even the order of the levels in the lower tunneling doublet is reversed for |K| = 1 with respect to K = 0. What looks still stranger for a prolate near-symmetric rotor as the benzene dimer is that the J = 1, K = ±1 levels are often below the corresponding J = 0 levels. This is reflected by the (very large) negative values of the rotational constant A in Table 10, which were extracted from these levels. The value of A for the ground state is positive, but it is also larger by an order of magnitude than the value in Table 9 obtained from the expectation value of the inertia tensor. Obviously, the relative energies of the levels for different values of |K| are not so much determined by the structure of the complex, but rather by its internal motions. In other words, K cannot be considered as a standard rigid rotor quantum number. This is characteristic for weakly bound dimers, see for example the results for the water dimer,^61,62 but the ‘K anomaly’ is stronger here.

One may wonder what is the effect of changing the potential on the calculated VRT level structure, since the (pot3) potential surface used, although we believe it to be of good quality, will certainly be amenable to improvement. We tried to get some idea of this effect by repeating the calculations of the one-dimensional irrep levels for J = 0 with the original potential from ref. 38, pot1, and with the first potential presented in section II, pot2. An idea of the differences between the potentials pot1 and pot3 can be obtained from the comparison of the stationary points in Table 1 and in Table 1 of ref. 38. The results calculated with pot1 and pot2 may be summarized by saying that the picture of vibration, cap hindered rotation, and tilt tunneling splitting of the VRT levels remains quite similar to what we found for pot3. The size of the splittings varies, but not dramatically. The main difference between the results for different potentials is that we found for pot2 and, especially, pot1 that the energies of several states with the PD structure are not much higher than those of the states with the TT structure. We remind the reader that for pot3 almost all the states calculated have the TT structure and the PD states start occurring at about 32 cm⁻¹ above the ground state (cf. the 7th state of A⁺₃ symmetry discussed above). This is consistent with the fact that in pot1 the TT and PD minima are of nearly equal depth, while in pot2 the PD minimum is higher by 6 cm⁻¹, and in pot3 it is higher by 36 cm⁻¹. In the most complete SAPT(DFT) calculations the PD minimum is higher than the TT minimum by about the same amount as in pot3 and in good quality CCSD(T) calculations it is even slightly higher, so we believe that our results with pot3 are the most realistic. To our knowledge, no other potential surface of similar quality is available for the benzene dimer.

B. Wave functions

In order to get more insight in the nature of the internal motions in the benzene dimer we also look at the wave functions. In general these are complex-valued. For the one-dimensional irreps of even parity under E* the wave functions are real-valued, for the odd parity irreps they are purely imaginary. The wave functions depend on six internal coordinates; we show some relevant two-dimensional cuts through the J = 0 wave functions for the one-dimensional irreps. The program already contained efficient transformations from the eigenvectors in the analytic basis to the eigenfunctions on the coordinate grid; this was needed to compute the matrix elements of the potential, see section IVA. The points on the six-dimensional grid used to compute the energy levels and eigenvectors are equidistant in four of the internal coordinates, but not in the polar angles β_A and β_B. For the latter we used a Gauss–Legendre quadrature grid. For plotting the wave functions and properly displaying their symmetry we prefer a grid that is equidistant in all coordinates and includes the end points of the range in each coordinate, so we wrote additional code to compute the wave functions on such a grid. The plot grid included 27 equidistant points for β_A and β_B in the range from 0 to 180 degrees, the same number of points as in the calculation of the energy levels but differently distributed. In all other directions we kept the same grid as defined in section IVC, i.e., 53 points for R in the range from 5.7 to 16 a₀, and 54 points in the range from 0 to 360 degrees for the azimuthal angles α, γ_A, and γ_B. The size of the wave function calculations was reduced by using the sixfold symmetry for both monomers.

In the discussion of Fig. 5 in section VA, we concluded that the cap sixfold rotation tunneling levels of the ground and excited vibrational state with the TT structure should rather be interpreted as a set of cap hindered rotor levels. The levels of the ‘vibrationally excited’ state are in fact above the very low barrier to cap rotation. Fig. 7 shows one of the potential minima as a function of the cap rotation angle γ_A and the stem bend angle β_B. The angle γ_A is limited from 0° to 60°; had we plotted the full range of γ_A from 0 to 360° this minimum would be repeated six times. It is clear from this figure that the potential is quite flat in the direction of γ_A, the barrier at γ_A = 0 and 60° that separates the six equivalent minima is only 6 cm⁻¹. Fig. 8 shows the wave functions for the irreps A⁺₁, A⁻₃, A⁺₃, A⁻₁, those for the A⁺₂, A⁻₄, A⁺₄, A⁻₂ irreps are very similar. First, it is clear from the A⁺₁ wave functions in Fig. 8 that there is considerable tunneling through the cap hindered rotation barrier; the amplitude of the wave function at the barrier is more than half of the amplitude at the minimum of the potential. Second, one observes indeed that both the A⁺₁ and A⁻₃ states belong to the ground vibrational A′ state of the TT structure. The A⁺₃ and A⁻₁ states have a node through γ_A = 30°, β_B = 90°, the potential minimum, and belong to the excited vibrational state of A′′ symmetry. The nodal plane is not vertical, however, which implies that this A′′ ‘vibration’ involves both the cap hindered rotation (around the TT equilibrium value of 30°) and the stem bend (around the equilibrium value of 90°). Fig. 8 shows that these modes mix to a different extent in the A⁺₃ and A⁻₁ states.

Fig. 7 Potential (in cm⁻¹) in the region of one of the TT minima, monomer A is the cap, B the stem. The coordinates β_A, α, and γ_B are fixed close to their values at the minimum: 9, 90, and 48°, respectively, and also R = 9.3 a₀ is close to its equilibrium value.

Fig. 8 Wave functions of the lowest states of different symmetries in the same region as the potential in Fig. 7, with approximately the same values of the fixed coordinates. For all of these symmetries, the wave functions have the same values for γ_A + n × 60° with n = 0,1,…,5.

Fig. 9 shows the wave functions for the irreps B⁺₃, B⁻₁, B⁻₃, B⁺₁, which are very similar to those for the B⁺₄, B⁻₂, B⁻₄, B⁺₂ irreps. The symmetry implies that these wave functions change sign at every 60 degree interval in the cap rotation angle γ_A. The B⁺₃ and B⁻₁ states change sign at the barriers, for γ_A = 0 and 60°, and correlate with the vibrational ground state of A′ symmetry. The B⁻₃ and B⁺₁ states have a node at the potential minimum and correlate with the vibrationally excited state of A′′ symmetry. Here, the nodal plane is almost vertical, so the stem bend mode is less involved in the vibration than for the (higher) A⁺₃ and A⁻₁ states.

Fig. 9 Wave functions of the lowest states of different symmetries in the same region as the potential in Fig. 7, with approximately the same values of the fixed coordinates. For all of these symmetries, the wave functions should be multiplied by (−1)ⁿ for γ_A + n × 60° with n = 0,1,…,5.

Fig. 10 displays the potential surface as a function of the angles β_A and γ_B involved in the tilt of the T-shape structure. The region chosen contains two equivalent TT minima. The barrier between these minima at β_A = 0° and γ_B = 60° in the plot corresponds to the ideal T-shape structure S3 with C_2v symmetry. Actually, S3 is a stationary point of index 2, but the barrier of 27 cm⁻¹ at S3 is only slightly higher than the barrier of 25 cm⁻¹ at the saddle point S3a of C_s symmetry. The ‘reaction path’ from one of the TT minima to the other one via the S3a structure involves the simultaneous change of several coordinates. So, we chose to plot the potential and the wave functions along the simpler path through S3 that involves only two Euler angles. Fig. 11, which shows the wave functions of the lowest A⁺₁ and A⁻₃ states along this path, gives a good impression of tilt tunneling. The A⁺₁ ground state has substantial amplitude at the barrier and the A⁻₃ state is the upper tilt tunneling component that changes sign between the two equivalent minima. One should realize, of course, that the actual tilt tunneling process also involves the S3a saddle point and that the amplitude of the A⁺₁ ground state will be even somewhat larger there.

Fig. 10 Potential (in cm⁻¹) in the region of two of the equivalent TT minima related by tilt tunneling, monomer A is the cap, B the stem. The coordinates γ_A, α, and β_B are fixed to their values at the minimum: 30, 90, and 90°, respectively, and also R = 9.3 a₀ is close to its equilibrium value.

Fig. 11 Wave functions of the ground and excited tilt tunneling states in the same region as the potential in Fig. 10, with approximately the same values of the fixed coordinates.

Finally, Fig. 12 displays a cut of the potential surface that contains two of the PD local minima and the wave function of the 7th state of A⁺₃ symmetry for which we already concluded on the basis of its properties that it is localized near the PD minima. The wave function contour plot shows that this is indeed the case. We checked the amplitude of this state near the TT minima and found that it is very small.

Fig. 12 Potential (in cm⁻¹) in the region of two of the equivalent PD minima and wave function of the 7th state of A⁺₃ symmetry. The coordinates γ_A, α, γ_B are all fixed at 0°, their value at the PD minimum, and R = 7.5 a₀ for the potential plot, 7.6 a₀ for the wave function plot.

We also searched for A⁺₁ states that are excited in the intermolecular stretch mode by looking for a node in the wave functions in the radial coordinate R. In the A⁺₁ state at 48.7 cm⁻¹ above the ground state we found such a node, while the monomer orientations are similar to those in the ground state. So we conclude that the stretch fundamental frequency of the benzene dimer is 48.7 cm⁻¹. A one-dimensional model with a radial cut of the potential obtained by fixing the angular coordinates at the equilibrium values gave a stretch frequency of 54 cm⁻¹. Spirko et al.³¹ in harmonic model calculations on their NEMO potential estimated the stretch fundamental frequency to be about 38 cm⁻¹, but it should be mentioned that this potential has a much shallower well (D_e = 595 cm⁻¹) than ours and a larger value of R_e (9.85 a₀).

C. Discussion

We may conclude from the preceding discussion that both processes, cap hindered rotation and tilt tunneling, that give rise to energy level splittings on the order of 1 cm⁻¹ are now well understood. On the basis of the symmetry of the calculated levels with respect to the group chain C_s(M) ⊂ C_6v(M) ⊂ G₂₄ ⊂ G₄₈ ⊂ G₂₈₈ ⊂ G₅₇₆ , see Table 5–8, we concluded in section VA that also cap turnover produces small, but probably significant, tunneling splittings. Looking at the TT structure it seems, however, that cap turnover by a twofold rotation or must have a high barrier. We made a careful search of the potential energy surface for any low-barrier pathway, but the lowest barrier pathway found involves the saddle point S4 at 54 cm⁻¹ above the TT minimum (18 cm⁻¹ above the PD minimum). This barrier separates the TT minimum from the PD local minimum and, in fact, the lowest energy pathway for cap turnover proceeds from a TT minimum through S4 to a PD local minimum, then again through S4 to an equivalent TT minimum with the cap and stem interchanged. Then, from this cap-stem interchanged TT structure, it proceeds in the same way through S4 (twice) and the PD minimum to a TT structure with the cap turned over with respect to the start structure. Since the cap-stem interchanged TT structure occurs halfway along this cap turnover path, one would think that cap turnover should give rise to smaller tunneling splittings than cap-stem interchange. We found, however, that interchange tunneling produces only very small—and still smaller when we enlarged the basis—energy level splittings, much smaller than the splittings assigned to cap turnover. So, we must conclude that we cannot explain the origin of the ‘cap turnover’ splittings at this stage. One might think of trying to follow the amplitude in some of the wave functions, but such a search is difficult in six dimensions and the wave functions are known only on a grid in coordinate space that may not be sufficiently dense.

Our work on the Ar-benzene complex,^102–104 the ammonia dimer,⁵³ and the water dimer^56–62 has shown that the comparison of calculated VRT levels with experimental (high-resolution) spectroscopic data is an excellent way to check and, if needed, improve the quality of intermolecular potential surfaces. Although much experimental data is available also for the benzene dimer, most of these data consists of UV, Raman, and infrared spectra that address the properties of the (perturbed) monomers. A direct comparison of our calculated intermolecular VRT levels is possible, in principle, with the Raman spectra of Venturo and Felker.²⁰ Low frequency transitions, with two peaks in the ranges of 3.35 to 3.60 and 9.00 to 9.95 cm⁻¹ for different benzene dimer isotopologues, were found in these Raman spectra, which agrees with our finding of low lying intermolecular vibration-tunneling levels. Unfortunately, the low-resolution spectra in ref. 20 did not show sufficient detail to allow a more specific comparison and the peaks are quite broad, so that they may cover many different transitions. Further spectroscopic work in the far-infrared region would be extremely useful.

Microwave spectra of the benzene dimer were taken by Arunan and Gutowski¹⁹ and, later, by Erlekam.²³ Only part of the observed lines was assigned; these lines correspond to a set of symmetric rotor levels. The measured end-over-end rotational constant (B + C)/2 of 427.7 MHz agrees well with our calculated values. In our calculations we found, both from the vibrationally and tunneling averaged inertia tensor and from the asymmetry doubling of the |K| = 1 levels, that the benzene dimer appears to be an asymmetric rotor. Moreover, we found that states exist for many different G₅₇₆ irreps with non-zero nuclear spin statistical weights and slightly different rotational constants. In both experimental papers each of the assigned lines in the microwave spectrum was split into a quartet. The lines in this (probably tunneling) quartet were split by about 60 kHz, with a specific splitting pattern in the ratio of 1 : 2 : 1. As discussed above, such small splittings could not be converged in our full six-dimensional calculations. It is still not clear what is the mechanism that causes this splitting, so further work is still needed also on this feature.

During the work described above, we also derived the selection rules for dipole-allowed transitions. The dipole operator is invariant under all permutations and odd under inversion E*, so it is of symmetry A⁻₁ in the group G₅₇₆. For ΔK = 0 transitions, for example, the parallel component of the dipole moment is of symmetry A⁺₂ in the internal coordinates (and A⁻₂ in the overall rotation). Hence, parallel transitions obey the selection rule: even ↔ odd, where the even/odd in this case refer to the symmetry of the internal states under interchange P_AB. Examples are A^±₁ ↔ A^±₂, A^±₃↔ A^±₄, G^±₁ ↔ G^±₂, and G^±₃ ↔ G^±₄. For all other irreps of dimension higher than one, P_AB interchanges different components of the same irrep and the individual components are localized in the sense that monomer A is the cap and B the stem in one component, and vice versa in another component. Transitions between levels that carry the same internal state irrep are allowed in this case, but it was found for the water dimer¹⁰⁵ that pure tunneling transitions of this type are very weak for complexes with nonequivalent monomers, because of small Frank-Condon overlap. When far-infrared spectra become available, it will be useful to compute transition intensities from our wave functions, as it has been done for the water dimer in ref. 105.

IV. Summary and conclusions

This paper describes an intermolecular potential surface for the benzene dimer from SAPT(DFT) calculations, which is improved compared to the potential in ref. 38, and the calculation of the VRT levels on this potential surface. The potential was obtained with the inclusion of additional, third-order, terms in the interaction energies and in the fitting process the low-energy region was weighted more heavily than in ref. 38. The extended SAPT(DFT) calculations agree better than those of ref. 38 with CCSD(T) interaction energies computed by us in large basis sets at characteristic points of the potential. Also the new fit reproduces the region including these points better than the fit of ref. 38. This is in particular true for the energy difference between the global minimum at the TT geometry and the local minimum at the PD geometry, as well as for the energy barriers at the stationary points.

A coupled-channel type method with a rigid-molecule scattering Hamiltonian in a dimer-fixed coordinate frame was used for the calculation of the VRT states. The channel wave functions consisted of coupled symmetric rotor functions for the internal and overall rotations of the dimer; a potential-optimized DVR method was used for the radial coordinate. Eigenvectors of the Hamiltonian were computed with the iterative Lanczos method. Symmetry adaptation of the channel basis to each of the 54 irreps of the FCT group G₅₇₆, in combination with an efficient calculation of the matrix elements of the potential, made it possible to use extremely large basis sets and obtain rather well converged energy levels. The method correctly includes large amplitude internal motions and tunneling between the multiple equivalent minima in the global six-dimensional potential surface. Very small energy level splittings associated with high-barrier tunneling processes could not be completely converged, however.

Symmetry analysis of the calculated VRT levels, supported by displays of the corresponding wave functions, allowed the assignment of the levels and level splittings to different intermolecular vibration and tunneling mechanisms. In agreement with the experimental data, it was found that almost all of the low lying VRT levels correspond to a tilted T-shape (TT) structure. The global TT minimum (actually 288 equivalent minima) in the potential has a depth D_e of 975 cm⁻¹, the lowest VRT level of A⁺₁ symmetry corresponds to a dissociation energy D₀ of 870 cm⁻¹. States with the parallel displaced (PD) structure were found from about 31 cm⁻¹ upwards. The energy difference between the PD and TT minima in the potential surface is 36 cm⁻¹. The energies of some of the intermolecular vibrations are as low as a few cm⁻¹ above the ground state, which agrees with results from Raman spectroscopy.²⁰ Intermolecular vibrations, which are in fact hindered rotations of the cap in the TT structure, were identified; some of these vibrations also involve the stem bend mode. The lower series of cap hindered rotor levels, with splittings increasing from 0.4 to 0.8 cm⁻¹, is still below the barrier of 6 cm⁻¹ and these levels might be considered as low-sixfold-barrier tunneling levels. These levels correlate with the vibrational ground state of A′ symmetry in the point group C_s of the TT equilibrium structure. The next higher series of levels lies above the sixfold barrier. The wave functions of these states have nodal planes at the minima of the potential and correlate with the lowest A′′ vibrational state of the TT equilibrium structure. So, in that sense, these states may be characterized as vibrationally excited. Another tunneling mechanism is clearly identified: tilt tunneling between nearby TT (tilted T-shape) minima. The energy barrier for this process is about 25 cm⁻¹ and it gives rise to energy level splittings of about 1 cm⁻¹. Extension of the group C_s of the TT equilibrium structure with the additional permutations that become feasible by cap hindered rotation and tilt tunneling yields the PI group G₂₄. Further small, but probably significant, splittings found in the calculated VRT levels would indicate that also cap turnover is feasible, leading to an effective symmetry group G₄₈, but we were not able to find a plausible low-barrier ‘reaction path’ for this process. The sixfold barrier for hindered rotation of the stem is 118 cm⁻¹ in our potential. The tunneling splittings on the order of 1 kHz for this process that we estimated on the basis of one-dimensional model calculations are smaller by many orders of magnitude than the ‘numerical noise’ in the energy levels caused by the fact that the basis size in the full six-dimensional calculations could not be further increased. The splitting caused by cap-stem interchange was calculated to be on the order of 10 MHz with the ‘standard’ basis, but the fact that this splitting systematically decreases when the basis is enlarged indicates that it has not yet converged. The value of about 1 MHz from the largest possible basis may be considered as an upper bound, the interchange splitting may actually be unresolvable even in high-resolution spectra.

For J = 0, the eight lowest energy levels were calculated for each of the 54 G₅₇₆ irreps. For the one-dimensional irreps, the levels were also computed for J = 1, with the inclusion of the Coriolis coupling between the levels with K = ±1 and K = 0. Also some properties of the VRT states were computed from the J = 0 wave functions: expectation values of the intermolecular distance R and of the instantaneous inertia tensor. The resulting end-over-end rotational constant (B + C)/2 agrees well with the value from microwave spectra.^19,23 The small rotational constant B − C extracted from the asymmetry doubling of the calculated J = 1, K = ±1 levels is probably rather inaccurate, since the basis cannot be completely saturated, but we believe that it significantly differs from zero. Also the B − C value obtained from the average inertia tensor indicates that the benzene dimer is an asymmetric rotor. However, the analysis of a series of lines in the microwave spectrum^19,23 led to the conclusion that it is a symmetric rotor. We could not find any plausible explanation for this discrepancy. The C₆H₆ dimer has as many as 53 different symmetry species with non-zero nuclear spin statistical weight. The calculations predict that these species have slightly different rotational constants. The assigned lines in the measured microwave spectra were split into quartets. The components in this (possibly tunneling) quartet may originate from different nuclear spin species, but we could not relate them to our calculated results. Clearly, further work is needed.

Another interesting observation regarding the levels with J = 1, K = ±1 is that these levels are below the corresponding levels with K = 0 in several cases. If the J = 0 and J = 1 levels are considered as those of a prolate, slightly asymmetric rotor, this leads to large negative values of the rotational constant A. In cases where the K = ±1 levels are above the corresponding K = 0 levels, the (positive) value of A extracted from these levels is larger than the expected rigid rotor value by an order of magnitude. Obviously, the (approximate) quantum number K is not just a near-rigid rotor property, but substantially affects the energies associated with the internal motions.

Although there is a large amount of experimental spectroscopic data for different isotopologues of the benzene dimer, further direct comparisons of our results with these data cannot be made because most of the spectra were taken in the UV and infrared regions and concern the (perturbed) monomer transitions. Similar work on the ammonia and water dimers has shown that a comparison of calculated VRT levels with (high-resolution) Terahertz spectra is extremely useful, both to understand the nature of the internal motions in these weakly bound dimers and to check the reliability of the intermolecular potential surface used. We hope that also our theoretical study of the benzene dimer will be followed up by further experimental work. Our wave functions can be applied to compute transition intensities, which might be useful to guide future experiments that adress the intermolecular rovibrational and tunneling motions.

Acknowledgements

We thank Dr Gerrit Groenenboom for his careful reading of the manuscript. A.v.d.A. thanks the Alexander von Humboldt foundation for a Humboldt Research Award. K.S. and R.P. acknowledge support from the NSF grant CHE-0848589. R.P. also acknowledges support by the Polish Science Foundation grant Homing and the Polish Ministry of Science and Higher Education grant No. N N204 123337. R.v.H. thanks the Nederlandse Organisatie voor Wetenschappelijk Onderzoek NWO, gebied Chemische Wetenschappen, for a VENI grant. P.R.B. is very grateful to the Molecular Physics Department of the Fritz Haber Institute for continuing hospitality.

References

1. M. C. Waters, Curr. Opin. Chem. Biol., 2002, 6, 736.
2. L. Serrano, M. Bycroft and A. R. Fersht, J. Mol. Biol., 1991, 218, 465.
3. S. K. Burley and G. A. Petsko, Science, 1985, 229, 23.
4. V. R. Cooper, T. Thonhauser, A. Puzder, E. Schröder, B. I. Lundqvist and D. C. Langreth, J. Am. Chem. Soc., 2008, 130, 1304.
5. X. Huang, D. F. Shullenberger and E. C. Long, Biochem. Biophys. Res. Commun., 1994, 198, 712.
6. L. R. Rutledge, L. S. Campbell-Verduyn and S. D. Wetmore, Chem. Phys. Lett., 2007, 444, 167.
7. K. C. Janda, J. C. Hemminger, J. S. Winn, S. E. Novick, S. J. Harris and W. Klemperer, J. Chem. Phys., 1975, 63, 1419.
8. J. B. Hopkins, D. E. Powers and R. E. Smalley, J. Phys. Chem., 1981, 85, 3739.
9. P. R. R. Langridge-Smith, D. V. Brumbaugh, C. A. Haynam and D. H. Levy, J. Phys. Chem., 1981, 85, 3742.
10. K. H. Fung, H. L. Selzle and E. W. Schlag, J. Phys. Chem., 1983, 87, 5113.
11. K. S. Law, M. Schauer and E. R. Bernstein, J. Chem. Phys., 1984, 81, 4871.
12. K. O. Börnsen, H. L. Selzle and E. W. Schlag, Z. Naturforsch., 1984, 39a, 1255.
13. K. O. Börnsen, H. L. Selzle and E. W. Schlag, J. Chem. Phys., 1986, 85, 1726.
14. J. R. Grover, E. A. Walters and E. T. Hui, J. Phys. Chem., 1987, 91, 3233.
15. R. H. Page, Y. R. Shen and Y. Y. Lee, J. Chem. Phys., 1988, 88, 4621.
16. H. Krause, B. Ernstberger and H. J. Neusser, Chem. Phys. Lett., 1991, 184, 411.
17. B. F. Henson, G. V. Hartland, V. A. Venturo and P. M. Felker, J. Chem. Phys., 1992, 97, 2189.
18. W. Scherzer, O. Krätzschmar, H. L. Selzle and E. W. Schlag, Z. Naturforsch., 1992, 47a, 1248.
19. E. Arunan and H. S. Gutowski, J. Chem. Phys., 1993, 98, 4294.
20. V. A. Venturo and P. M. Felker, J. Chem. Phys., 1993, 99, 748.
21. U. Erlekam, M. Frankowski, G. Meijer and G. von Helden, J. Chem. Phys., 2006, 124, 171101.
22. U. Erlekam, M. Frankowski, G. von Helden and G. Meijer, Phys. Chem. Chem. Phys., 2007, 9, 3786.
23. U. Erlekam, PhD thesis, Humboldt Universität, Berlin, 2008.
24. U. Erlekam, P. R. Bunker, M. Schnell, J.-U. Grabow, G. von Helden and G. Meijer, in preparation.
25. J. A. Odutola, D. L. Alvis, C. W. Curtis and T. R. Dyke, Mol. Phys., 1981, 42, 267.
26. R. Schmied and K. K. Lehman, J. Mol. Spectrosc., 2004, 226, 201.
27. P. Hobza, H. L. Selzle and E. W. Schlag, J. Chem. Phys., 1990, 93, 5893.
28. P. Hobza, H. L. Selzle and E. W. Schlag, J. Phys. Chem., 1993, 97, 3937.
29. R. L. Jaffe and G. D. Smith, J. Chem. Phys., 1996, 105, 2780.
30. P. Hobza, H. L. Selzle and E. W. Schlag, J. Phys. Chem., 1996, 100, 18790.
31. V. Spirko, O. Engkvist, P. Soldan, H. L. Selzle and E. W. Schlag, J. Chem. Phys., 1999, 111, 572.
32. M. O. Sinnokrot, E. F. Valeev and C. D. Sherill, J. Am. Chem. Soc., 2002, 124, 10887.
33. S. Tsuzuki, T. Uchimaru, K. Sugawara and M. Mikami, J. Chem. Phys., 2002, 117, 11216.
34. S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2002, 124, 104.
35. M. O. Sinnokrot and C. D. Sherill, J. Phys. Chem. A, 2004, 108, 10200.
36. T. Sato, T. Tsuneda and K. Hirao, J. Chem. Phys., 2005, 123, 104307.
37. A. Heßelmann, G. Jansen and M. Schütz, J. Chem. Phys., 2005, 122, 014103.
38. R. Podeszwa, R. Bukowski and K. Szalewicz, J. Phys. Chem. A, 2006, 110, 10345.
39. T. Rocha-Rinza, L. D. Vico, V. Veryazov and B. O. Roos, Chem. Phys. Lett., 2006, 426, 268.
40. A. Puzder, M. Dion and D. C. Langreth, J. Chem. Phys., 2006, 124, 164105.
41. T. Janowski and P. Pulay, Chem. Phys. Lett., 2007, 447, 27.
42. R. A. DiStasio, G. von Helden, R. P. Steele and M. Head-Gordon, Chem. Phys. Lett., 2007, 437, 277.
43. E. C. Lee, D. Kim, P. Jurecka, P. Tarakeshwar, P. Hobza and K. S. Kim, J. Phys. Chem. A, 2007, 111, 3446.
44. W. Wang, M. Pitoak and P. Hobza, ChemPhysChem, 2007, 8, 2107.
45. O. Bludsky, M. Rubes, P. Soldan and P. Nachtigall, J. Chem. Phys., 2008, 128, 114102.
46. S. Grimme, C. Mück-Lichtenfeld and J. Anthony, Phys. Chem. Chem. Phys., 2008, 10, 3327.
47. P. R. Bunker, U. Erlekam, M. Schnell, G. von Helden and G. Meijer, unpublished work.
48. J. Gräfenstein and D. Cremer, J. Chem. Phys., 2009, 130, 124105.
49. J. M. Bakker, PhD thesis, Radboud University Nijmegen, 2004.
50. R. Podeszwa and K. Szalewicz, Phys. Chem. Chem. Phys., 2008, 10, 2735.
51. Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364.
52. K. Pernal, R. Podeszwa, K. Patkowski and K. Szalewicz, Phys. Rev. Lett., 2009, 103, 263201.
53. E. H. T. Olthof, A. van der Avoird and P. E. S. Wormer, J. Chem. Phys., 1994, 101, 8430.
54. C. Leforestier, L. B. Braly, K. Liu, M. J. Elrod and R. J. Saykally, J. Chem. Phys., 1997, 106, 8527.
55. H. Chen, S. Liu and J. C. Light, J. Chem. Phys., 1999, 110, 168.
56. G. C. Groenenboom, P. E. S. Wormer, A. van der Avoird, E. M. Mas, R. Bukowski and K. Szalewicz, J. Chem. Phys., 2000, 113, 6702.
57. R. S. Fellers, L. B. Braly, R. J. Saykally and C. Leforestier, J. Chem. Phys., 1999, 110, 6306.
58. R. S. Fellers, C. Leforestier, L. B. Braly, M. G. Brown and R. J. Saykally, Science, 1999, 284, 945.
59. N. Goldman, R. Fellers, M. Brown, L. Braly, C. Keoshian, C. Leforestier and R. Saykally, J. Chem. Phys., 2002, 116, 10148.
60. R. Bukowski, K. Szalewicz, G. C. Groenenboom and A. van der Avoird, Science, 2007, 315, 1249.
61. R. Bukowski, K. Szalewicz, G. C. Groenenboom and A. van der Avoird, J. Chem. Phys., 2008, 128, 094314.
62. W. Cencek, K. Szalewicz, C. Leforestier, R. van Harrevelt and A. van der Avoird, Phys. Chem. Chem. Phys., 2008, 10, 4716.
63. H. L. Williams and C. F. Chabalowski, J. Phys. Chem. A, 2001, 105, 646.
64. A. J. Misquitta and K. Szalewicz, Chem. Phys. Lett., 2002, 357, 301.
65. A. J. Misquitta, B. Jeziorski and K. Szalewicz, Phys. Rev. Lett., 2003, 91, 033201.
66. A. J. Misquitta, R. Podeszwa, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 2005, 123, 214103.
67. A. Heßelmann and G. Jansen, Chem. Phys. Lett., 2002, 357, 464.
68. A. Heßelmann and G. Jansen, Chem. Phys. Lett., 2003, 367, 778.
69. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887.
70. R. Podeszwa, B. M. Rice and K. Szalewicz, Phys. Rev. Lett., 2008, 101, 115503.
71. R. Podeszwa, J. Chem. Phys., 2010, 132, 044704.
72. K. Patkowski, K. Szalewicz and B. Jeziorski, J. Chem. Phys., 2006, 125, 154107.
73. R. Podeszwa, R. Bukowski and K. Szalewicz, J. Chem. Theory Comput., 2006, 2, 400.
74. R. Bukowski, R. Podeszwa and K. Szalewicz, Chem. Phys. Lett., 2005, 414, 111.
75. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796.
76. H. L. Williams, E. M. Mas, K. Szalewicz and B. Jeziorski, J. Chem. Phys., 1995, 103, 7374.
77. F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175.
78. F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285.
79. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
80. DALTON, a molecular electronic structure program, Release 2.0, 2005.
81. D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 10180.
82. S. G. Lias, Ionization Energy Evaluation, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, 2007, http://webbook.nist.gov.
83. R. Bukowski, W. Cencek, P. Jankowski, M. Jeziorska, B. Jeziorski, S. A. Kucharski, V. F. Lotrich, A. J. Misquitta, R. Moszyński, K. Patkowski, R. Podeszwa, S. Rybak, K. Szalewicz, H. L. Williams, R. J. Wheatley, P. E. Wormer and P. S. Żuchowski, SAPT2008: An Ab initio Program for Many-Body Symmetry-Adapted Perturbation Theory Calculations of Intermolecular Interaction Energies, University of Delaware and University of Warsaw, 2008.
84. K. Patkowski, R. Podeszwa and K. Szalewicz, J. Phys. Chem. A, 2007, 111, 12822.
85. K. T. Tang and J. P. Toennies, J. Chem. Phys., 1984, 80, 3726.
86. C. J. Cerjan and W. H. Miller, J. Chem. Phys., 1981, 75, 2800.
87. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
88. K. Szalewicz and B. Jeziorski, J. Chem. Phys., 1998, 109, 1198.
89. H.-J. Werner and P. J. Knowles et al., MOLPRO: a package of ab initio programs, version 2009.1.
90. P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC Research Press, Ottawa, 2nd edn, 1998.
91. H. C. Longuet-Higgins, Mol. Phys., 1963, 6, 445.
92. The GAP Group, GAP—Groups, Algorithms, and Programming, Version 4.4.12, 2008, http://www.gap-system.org.
93. E. B. Wilson, J. Chem. Phys., 1935, 3, 276.
94. G. Brocks, A. van der Avoird, B. T. Sutcliffe and J. Tennyson, Mol. Phys., 1983, 50, 1025.
95. A. van der Avoird, P. E. S. Wormer and R. Moszynski, Chem. Rev., 1994, 94, 1931.
96. J. W. I. van Bladel, A. van der Avoird, P. E. S. Wormer and R. J. Saykally, J. Chem. Phys., 1992, 97, 4750.
97. D. M. Brink and G. R. Satchler, Angular Momentum, Clarendon, Oxford, 3rd edn, 1993.
98. D. O. Harris, G. G. Engerholm and W. D. Gwinn, J. Chem. Phys., 1965, 43, 1515.
99. L. Jansen and M. Boon, Theory of Finite Groups. Applications to Physics, North Holland, Amsterdam, 1967.
100. J. Pliva and A. S. Pine, J. Mol. Spectrosc., 1987, 126, 82.
101. M. Junttila, J. L. Domenech, G. T. Fraser and A. S. Pine, J. Mol. Spectrosc., 1991, 147, 513.
102. A. van der Avoird, J. Chem. Phys., 1993, 98, 5327.
103. E. Riedle and A. van der Avoird, J. Chem. Phys., 1996, 104, 882.
104. R. Neuhauser, J. Braun, H. J. Neusser and A. van der Avoird, J. Chem. Phys., 1998, 108, 8408.
105. M. J. Smit, G. C. Groenenboom, P. E. S. Wormer, A. van der Avoird, R. Bukowski and K. Szalewicz, J. Phys. Chem. A, 2001, 105, 6212.

---

Footnotes

† Electronic supplementary information (ESI) available: Parameters of the analytic benzene–benzene intermolecular potential; geometries and interaction energies from SAPT(DFT) calculations used in the analytic fit; stationary points predicted by the fitted potentials. See DOI: 10.1039/c002653k

‡ Permanent address: Steacie Institute for Molecular Sciences, National Research Council, Ottawa, Canada.

---