 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Study of polycyclic aromatic hydrocarbons adsorbed on graphene using density functional theory with empirical dispersion correction
Olga V.
Ershova
a,
Timothy C.
Lillestolen
b and
Elena
Bichoutskaia
*b
aMoscow Institute of Physics and Technology, 141700, Dolgoprudny, Moscow Region, Russia
bDepartment of Chemistry, University of Nottingham, University Park, Nottingham, UK NG7 2RD. E-mail: elena.bichoutskaia@nottingham.ac.uk
First published on 9th April 2010
Abstract
The interaction of polycyclic aromatic hydrocarbon molecules with hydrogen-terminated graphene is studied using density functional theory with empirical dispersion correction. The effective potential energy surfaces for the interaction of benzene, C6H6, naphthalene, C10H8, coronene, C24H12, and ovalene, C32H14, with hydrogen-terminated graphene are calculated as functions of the molecular displacement along the substrate. The potential energy surfaces are also described analytically using the lowest harmonics of the Fourier expansion. It is shown that inclusion of the dispersive interaction, which is the most important contribution to the binding of these weakly bound systems, does not change the shape of the interaction energy surfaces or the value of the barriers to the motion of polycyclic aromatic hydrocarbon molecules on graphene. The potential energy surfaces are used in the estimation of the friction forces acting on the molecules along the direction of motion. These results underpin the modelling, using density functional theory, of electromechanical devices based on the relative vibrations of graphene layers and telescoping carbon nanotubes.
I. Introduction
The van der Waals (vdW) dispersive interactions between weakly bound systems are notoriously difficult to compute both in gas phase and in periodic solid structures. They are governed purely by long-range electron correlations, which in small non-covalently bound molecular complexes can be taken into account within the framework of standard ab initio wave function theory, reaching benchmark accuracy in computations based on coupled-cluster methods such as coupled-cluster with single, double and perturbative triple excitations, CCSD(T). The CCSD(T) methods become computationally expensive for medium-sized systems, and take prohibitively long times for large complexes. The less-expensive second-order Møller–Plesset perturbation theory (MP2) systematically overestimates the binding energies and underestimates intermolecular distances for dispersive π–π interactions.1,2In condensed matter physics, density functional theory (DFT) is the most widely used approach for calculating electronic structure of medium to large-scale ground-state systems due to its reasonable accuracy and relatively low computational cost. However, a general disadvantage of most commonly used exchange–correlation functionals based on the local (spin) density approximation (LDA) and semi-local generalized gradient approximation (GGA) is that they can not describe long range electron correlations responsible for dispersive interactions.3–5 The reason for this failure is that these density functional approximations are derived from the localized model exchange–correlation holes, whereas the exact exchange–correlation hole is fully nonlocal. Also hybrid functionals, in which DFT is combined with Hartree Fock (HF) theory to incorporate nonlocality of the exchange–correlation hole into the density functional approximations, are unable to describe adequately dispersive interactions.
This can be demonstrated most clearly by calculations of the interlayer cohesive energy in graphite. Graphite is a layered material with highly anisotropic bonding. In-plane, the bonding is dominated by strongly localized covalent sp2 hybridized orbitals, while the interlayer cohesive energy arises from weak nonlocal vdW interactions between the layers. Despite graphite being an abundant material, experiments on the determination of its interlayer cohesion have been scarce. The data are mainly restricted to three experimental values of Benedict et al.6 obtained from the study of radial deformations of multi-walled carbon nanotubes, yielding 35+15−10 meV/atom; of Girifalco7 who reported an exfoliation energy of 43 meV/atom, determined in a heat of wetting experiment; and most recently the result of Zacharia8 who obtained an interlayer cohesive energy of graphite of 52 ± 5 meV/atom in the study of thermal desorption of thin films of polycyclic aromatic hydrocarbon molecules (PAHs) from the surface of graphite.
The computed GGA (PBE) results for graphite give insufficient cohesion energies of as little as 2–5 meV/atom9–12 or even predict graphite to be unbound. The LDA method gives much better results for the cohesion energy, ranging from 20 to 35 meV/atom.9–11,13–16 The latter values are close to the experimental range, however, the apparent success of the LDA predictions for the interlayer binding in graphite is rather fortuitous. Various authors have proposed to supplement the LDA and GGA DFT calculations of the cohesion energy in graphite with an empirical atom–atom vdW interaction term. This term yields an additional long-range attractive potential between layers, incorporating correct long range potentials of the C4D−4 and C3D−3 forms.9–11,17–19 The LDA + vdW and GGA + vdW approaches give consistent results for the interlayer binding energy of graphite in the region of 50 to 65 meV/atom, thus indicating that the weak dispersion forces remain the major contribution to the binding between the layers in graphite.
The investigation of the interlayer interaction in graphite provides a useful starting point not only for the studies of the energetics of other graphitic systems, but also for modelling the relative motion of the components of nested and layered nanomaterials. A number of electromechanical devices have been realised which exploit the remarkable low-friction rotational and sliding capabilities of carbon nanotube walls.20–26 Similarly, self-retracting motion of graphite microflakes has been recently observed, in which small flakes of graphite repeatedly move back-and-forth over large islands of highly oriented pyrolytic graphite.27 If an accurate quantitative description of the interaction between the walls of carbon nanotubes (or layers of graphitic material) is available, the values for the barriers to their relative motion can be extracted from the interlayer interaction energy surfaces, and subsequently used to compute experimentally measurable quantities such as vibrational frequencies,28 threshold and capillary forces, diffusion coefficients and mobilities.29–31
In this paper, it is shown that the dispersion interactions are crucial in determination of the binding energies in layered materials, however they do not significantly affect the values of barriers to the relative motion of PAHs on hydrogen-terminated graphene. Graphene, a single sheet of graphite,32 represents an ideal viewing platform for molecular structures using transmission electron microscopy (TEM) because it provides a robust and low contrast support for molecules and other nanoscale species adsorbed on the surface. Under TEM observation with exposure to an 80 keV electron beam (e-beam) the edges of a graphene sheet continuously change shape, and the high energy of the e-beam transferred to the carbon atoms can cause fragmentation of large sheets of graphene into smaller flake-like graphitic structures.33 The flakes adsorbed on a graphene substrate can be visualised in TEM, and their interaction with the underlying graphene substrate can be exploited in nanoscale sensing applications. The study of adsorption and motion of PAHs on hydrogen-terminated graphene presented in this paper will elucidate the largely unexplored nature of the interaction of graphene flakes with graphene layer.
II. Methodology and tests
In this work, all calculations have been performed using the Q-Chem quantum chemistry package.34 For the binding energies, the counterpoise correction35 was used to correct for basis set superposition error (BSSE). A long-range corrected (LC) hybrid DFT functional with empirical dispersion correction, ωB97X-D,36 was used. The ωB97X-D functional is a new generation of the earlier LC hybrid density functional ωB97X37 which includes an empirical damped atom–atom dispersion correction. The ωB97X functional37 employs 100% exact exchange for long-range electron–electron interactions, approximately 16% short-range exact exchange, a modified B97 exchange density functional for short-range interactions and the B97 correlation density functional38 as follows:| EωB97Xxc = ELR−HFx +cxESR−HFx +ESR−B97x + EB97c | (1) |
| EωB97X−D = EωB97Xxc + Edisp | (2) |
 | (3) |
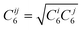 ).39 A damping function of the following form:
).39 A damping function of the following form: | (4) |
In ref. 36, the results of the performance tests can be found in the form of tabulated statistical errors. In this paper, the ωB97X-D functional has been tested in the calculations of the binding energies of the benzene dimer. The binding energies for three conformations of the benzene dimer, T-shaped (T), parallel displaced (PD) and sandwich (S) (see the structures in ref. 40, Fig. 1), calculated using several different density functionals and basis sets are presented and compared with the literature data in Table 1. In the literature, there is no consensus about the global minimum structure of the benzene dimer. The MP2 + ΔCCSD(T) results for the estimated basis set limit interaction energy,40 as well as a DFT-based description,41 show a preference for the PD conformation over the T structure. However, the DFT results with empirical dispersion correction generally predict that the T geometry is most stable. This is consistent with the results for the binding energies obtained with the B97-D and ωB97X-D functionals, as shown in Table 1. The B97-D functional differs from the ωB97X-D functional in the form of the damping function used and in the absence of a short-range Hartree–Fock correction. Within the GGA (BLYP functional42,43) approach, all three conformations of the benzene dimer remain unbound. The LDA (SVWN functional44) predictions for the binding of the benzene dimer are reasonable, similar to the case of the interlayer binding in graphite described in the introduction, however the binding energies for the S and PD conformations are underestimated. The LC hybrid density functional ωB97X significantly underestimates the binding for all three conformations. Hence LDA, GGA and LC hybrid DFT functionals without empirical dispersion corrections should be recognized as inadequate for the description of binding in graphitic structures.
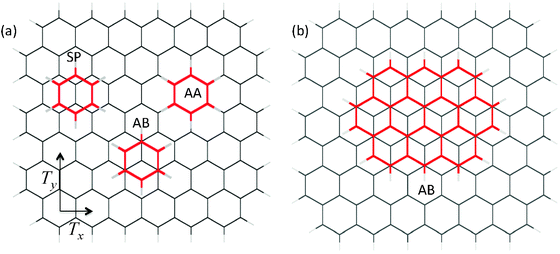 | ||
| Fig. 1 High symmetry positions of PAHs on the hydrogen-terminated graphene showing: (a) the benzene molecule in the AA, AB, and SP positions; (b) the ovalene molecule in the AB position. The translational lengths of the graphene lattice are Tx = 2.46 Å, and Ty = 4.26 Å. | ||
| Method | Basis set | E T | E S | E PD | ΔEPD−S |
|---|---|---|---|---|---|
| MP2 + ΔCCSD(T)40 | CBS limit | 119 | 79 | 121 | 42 |
| B97-D39 | TZV2P | 130 | 77 | 119 | 42 |
| ωB97X-D | TZ(d, p) | 116 | 80 | 107 | 27 |
| ωB97X-D | 6-311++G(3df, 3pd) | 126 | 94 | 115 | 21 |
| ωB97X-D | 6-31G* | 116 | 49 | 80 | 31 |
| ωB97X | TZ(d, p) | 86 | 24 | 55 | 31 |
| LDA(SVWN) | TZ(d, p) | 128 | 37 | 88 | 51 |
| GGA(BLYP) | TZ(d, p) | −73 | −187 | −132 | 55 |
The S conformation is less stable than the PD structure, and the difference in the binding energies, ΔEPD−S, of these two parallel conformations is typically about 30–40 meV. Remarkably, ΔEPD−S does not vary as much as the binding energies with computational method. Even the GGA (BLYP) approach with TZ(d, p) basis set, while giving no binding whatsoever, predicts the value of ΔEPD−S only two times larger than the value obtained with the ωB97X-D functional and the same basis set. ΔEPD−S is essentially analogous to the energy barrier separating two minima of the interaction potential energy surface (PES) calculated as a function of the relative motion of the walls of carbon nanotubes or the layers of graphene. However, while the intermolecular interaction in the benzene dimer tends to zero at large lateral displacement, in ideal infinite graphitic materials the relative motion of neighbouring layers is defined by the oscillatory PES with equivalent minima attributed to the symmetry of the system.
III. Adsorption and motion of polycyclic aromatic hydrocarbons on graphene
A. Binding energy
An atomic cluster description of the interacting system of a PAH with the hydrogen-terminated graphene sheet consisting of 116 carbon atoms (C116H28) has been used. In each case, PAH is initially placed on the substrate in the so-called AB stacking which corresponds to the position at which half of the carbon atoms of PAH are located directly above the carbon atoms of the graphene sheet and the other half are facing the center of hexagons of the substrate. The AB position of PAH on the substrate corresponds to the global minimum in PES, and it is shown in Fig. 1 for the smallest (benzene–hydrogen terminated graphene, Fig. 1a) and the largest (ovalene-hydrogen terminated graphene, Fig. 1b) systems studied. Table 2 presents the comparison between the experimental binding energies of PAHs with the surface of graphite and the theoretical binding energies between PAHs and hydrogen-terminated graphene in the AB position calculated at the ωB97X-D/STO-3G, ωB97X-D/6-31G*, ωB97X/STO-3G, and ωB97X/6-31G* levels of theory. For each interacting system, the geometry in the AB position has been optimized using ωB97X-D/STO-3G approach. The use of larger basis sets was computationally prohibitive for these large systems. The optimized values of the z-separation between PAHs and the C116H28 substrate are tabulated in Table 3, it can be seen that in the minimum AB position the z-separation grows with increase of the molecule size.| PAH | Experiment,8 Redhead analysis45 | Experiment8, Falconer-Madix analysis46 | ωB97X-D/6-31G* | ωB97X-D/STO-3G | ωB97X/6-31G* | ωB97X/STO-3G |
|---|---|---|---|---|---|---|
| C6H6 | 0.50 ± 0.08 | 0.50 ± 0.08 | 0.47 | 0.37 | 0.13 | −0.05 |
| C10H8 | 0.8 ± 0.1 | 0.90 ± 0.07 | 0.76 | 0.59 | 0.21 | −0.07 |
| C24H12 | 1.3 ± 0.2 | 1.5 ± 0.1 | 1.73 | 1.29 | 0.47 | −0.14 |
| C32H14 | 2.2 ± 0.2 | 1.97 ± 0.08 | 2.23 | 1.69 | 0.61 | −0.18 |
| PAH | AB | AA | SP |
|---|---|---|---|
| C6H6 | 3.35 | 3.36 | 3.30 |
| C10H8 | 3.36 | 3.37 | 3.34 |
| C24H12 | 3.38 | 3.40 | 3.31 |
| C32H14 | 3.40 | 3.41 | 3.33 |
The binding energy of the adsorbate to the graphite surface can be identified with the activation energy for desorption, as measured by thermal desorption (TD) spectroscopy.8 The rate of desorption of an adsorbate from a solid surface is commonly described by the Arrhenius equation. Based on the Arrhenius equation, a number of techniques has been proposed that allow the determination of the activation energies for desorption of an adsorbate using the series of the TD spectra. These include an analysis using the Redhead's peak maximum method45 and an isothermal analysis of Falconer and Madix.46 The first numerical column of Table 2 gives estimations of the activation energy for desorption of PAHs on the graphite surface using the Readhead analysis which relates the energy to the temperature at the desorption peak maximum (Tmax) and the heating rate obtained in experiment.8 The second numerical column of Table 2 is the result of an isothermal analysis of the TD spectra using the Falconer-Madix method which employs a linear fit to isothermal desorption data obtained in the experiment8 in the temperature range used.
The next four columns of Table 2 contain the calculated BSSE corrected binding energies. The ωB97X-D/STO-3G results underestimate the experimental values, however in all four cases a sufficient binding is predicted. The improved values obtained at the ωB97X-D/6-31G* level of theory are in good general agreement with experiment. The calculated ωB97X-D/6-31G* values for the binding energies of coronene and ovalene molecules are somewhat greater than the experimental predictions. There could be a number of possible reasons for the discrepancy. The TD spectra of benzene and napthalene exhibit two clearly distinguishable desorption peaks corresponding to monolayer and multilayer desorption allowing unambiguous determination of Tmax. On the other hand, desorption traces of coronene and ovalene exhibit a behaviour indicative of fractional order kinetics, and desorption features of the first monolayer in the TD spectra cannot be clearly distinguished from the multilayer peaks. This leaves considerable uncertainty in the determination of the monolayer desorption maxima and hence desorption temperatures. Additionally, as the data on the density of ovalene (the number of adsorbate molecules per unit area) adsorbed on the graphite surface is not available from low energy electron diffraction or scanning tunneling microscopy experiments, an estimated value was used in ref. 8. It should be also noted that the calculated values correspond to the binding of PAHs to a graphene layer, not bulk graphite.
The binding predicted by the ωB97X functional is poor, indicating that the long-range van der Waals interactions, the dominant contribution to the binding between PAHs and the graphene substrate, cannot be described sufficiently well using this functional. Note that the ωB97X/STO-3G calculations consistently give unbound results. In all considered cases, the values for the binding energy calculated with ωB97X-D/6-31G* are approximately 3.65 times larger than the values predicted by ωB97X/6-31G*.
B. Interaction energy profiles
In addition to global minimum defining the binding energies, PES for the interaction of a PAH with graphene as a function of the molecular displacement along the substrate has two other types of critical points which correspond to the high symmetry orientations of the molecular ring on the substrate. Global maximum corresponds to a position at which all of the atoms in neighbouring layers face each other, so-called AA stacking. Saddle points are associated with the relative orientation lying between the equivalent positions corresponding to the closest minima, which has a similarity with the PD conformation of the benzene dimer, and is called SP stacking. Fig. 1a shows the high symmetry positions of the benzene molecule on graphene which correspond to the critical points of PES. The energy difference in the AA and AB positions defines the largest barrier in the energy profile for the relative sliding of a PAH along the substrate, whereas the energy difference between the AB and SP positions gives a secondary corrugation in PES.Table 4 presents the results for the energy barriers to motion of PAHs along the graphene substrate, calculated at the centre of a large C116H28 flake in order to minimize edge effects. To allow a direct comparison of the energy barriers obtained for different molecules, the values are given in meV per carbon atom of PAH. Similarly to the calculations of the binding energies, for each interacting system geometry optimisation was initially performed using the ωB97X-D/STO-3G level of theory (see Table 3 for the optimized values of z-separation), and the optimised geometries were subsequently used to calculate the barriers to motion of a molecule along the substrate using ωB97X and ωB97X-D functionals with STO-3G and 6-31G* basis sets. The values obtained for the interaction energies are BSSE corrected for each relative position of the interacting system.
| PAH | ωB97X-D/6-31G* | ωB97X-D/STO-3G | ωB97X/6-31G* | ωB97X/STO-3G | ||||
|---|---|---|---|---|---|---|---|---|
| AB-AA | AB-SP | AB-AA | AB-SP | AB-AA | AB-SP | AB-AA | AB-SP | |
| C6H6 | 9.4 | 2.2 | 5.1 | 3.2 | 9.4 | 5.0 | 4.7 | 4.8 |
| C10H8 | 9.5 | 2.4 | 5.3 | 2.1 | 9.3 | 4.1 | 4.8 | 3.3 |
| C24H12 | 11.0 | 3.1 | 5.1 | 3.3 | 10.6 | 6.7 | 5.0 | 5.6 |
| C32H14 | 10.9 | 2.8 | 5.5 | 3.0 | 10.4 | 6.5 | 4.9 | 5.2 |
The values for the largest energy barrier of the AB-AA transition are close for all considered PAHs, regardless of the functional used. Hence, the ωB97X-D energy barrier in the infinite graphene bilayer can be estimated as having the value of approximately ΔVint = 11 meV/atom. Comparison of the values for the barriers calculated with (ωB97X-D) and without (ωB97X) taking into account the dispersion interactions shows that inclusion of the dispersion term does not affect the results obtained for the main barrier. The ratio for the AB-AA barriers obtained with the ωB97X-D and ωB97X functionals using the 6-31G* basis set is 1.00 for C6H6, 1.02 for C10H8, 1.03 for C24H12, and 1.04 for C32H14. It can therefore be concluded that the inclusion of the dispersion interaction correction as an additional empirical term to the DFT treatment does not change the values of the major barrier to the relative motion of PAHs on graphene.
If the graphene substrate is assumed to be a rigid infinite lattice with a multitude of 6-fold axes of symmetry, the interaction between a single carbon atom in PAH and graphene can be approximated using the following analytical potential47
| VCint(x,y,z) = V1(z) − V0(z)[2cos(axx) cos(ayy) + cos(2ayy)], | (5) |
 , where Tx and Ty are the translational lengths of the lattice in the perpendicular x- and y-directions shown in Fig. 1. If the carbon–carbon bond is taken to be 1.42 Å then Tx = 2.46 Å, and Ty = 4.26 Å. If PAH is considered to be a rigid molecule, the interaction potential between the substrate and PAH can be obtained by summation of all contributions from the PAH atoms. The effective potential for the movement of the centre of mass of PAH (CM) on graphene, calculated per carbon atom of PAH, has the following form
, where Tx and Ty are the translational lengths of the lattice in the perpendicular x- and y-directions shown in Fig. 1. If the carbon–carbon bond is taken to be 1.42 Å then Tx = 2.46 Å, and Ty = 4.26 Å. If PAH is considered to be a rigid molecule, the interaction potential between the substrate and PAH can be obtained by summation of all contributions from the PAH atoms. The effective potential for the movement of the centre of mass of PAH (CM) on graphene, calculated per carbon atom of PAH, has the following form | (6) |
To allow a comparison with the analytical profile (6) for the interaction potential energy as a function of the molecular displacement along the substrate, a series of calculations have been produced of the BSSE-corrected ωB97X-D/6-31G* interaction energies between the rigid C6H6 and C116H28 molecules separated by z = 3.35 Å, the value close to the experimental separation in graphite49 and to the distances obtained in the geometry optimisation calculations (see Table 3). The carbon–carbon bond length was fixed at 1.42 Å. The results of such comparison are presented in Fig. 2. The displacement of benzene along the substrate is first calculated by placing the molecule in the AB stacking position in the middle of the fixed graphene flake, and then translating it along the y-direction through the AB-AA-AB-SP-AB path. The interaction potential profile which corresponds to the continuous displacement along the AB-AA-AB-SP-AB path is denoted by triangles in Fig. 2, and the analytical profile obtained with the use of eqn (6) is represented by a solid line.
 | ||
| Fig. 2 The interaction potential energy of the benzene–C116H28 system as a function of the benzene displacement along the AB-AA-AB-SP-AB path (shown in the inset) calculated using ωB97X-D/6-31G* level of theory, as described in the text. Energy (BSSE corrected) is given in meV per carbon atom of the benzene molecule; distance y is given in Å; z separation is fixed at 3.35 Å. The profile obtained using eqn (6) is shown by solid line; the calculated values of the interaction energy along the AB-AA-AB-SP-AB path are depicted by empty triangles showing the edge effects, mainly in the estimation of the empirical dispersion term; the values of the interaction energy calculated at the centre of the C116H28 flake are shown in filled squares. | ||
C. Dispersion contribution to the interaction energy
Fig. 2 shows that for continuous displacement of the benzene molecule along the AB-AA-AB-SP-AB path of the C116H28 flake the small secondary energy barrier corresponding to the AB-SP transition is overestimated compared to the case of motion of the benzene molecule along an infinite graphene layer. The discrepancy can be explained by the edge effects in the interaction with a finite substrate that affect the dispersion contribution to the interaction energy. In order to examine the behaviour of the dispersion energy Edisp as a function of displacement on a surface, the empirical component of the ωB97X-D dispersion energy was calculated using eqn (3) for several series of interactions. The behaviour of the empirical component of the ωB97X-D dispersion energy is qualitatively similar to the one used by Grimme in the DFT-D schemes,39 which only differ by the use of an overall scaling factor and the Wu-Yang50 damping function. Thus, the investigation of the behaviour of Edisp, as given in eqn (3), yields a reliable estimation of the dispersion correction to the DFT energy.The series of dispersion energy profiles containing the benzene molecule interacting with larger molecules is shown in Fig. 3. The displacement, D, is calculated by initially fixing the CM of benzene directly over the CM of the larger molecules (D = 0). For the benzene–coronene system and the benzene–C116H28 substrate system, D = 0 corresponds to the AA stacking position at which the CM of both molecules is located in the centre of a ring. For the benzene–naphthalene and benzene–ovalene systems, D = 0 corresponds to the SP stacking position at which the CM of benzene is in the centre of a ring and the other molecule is bond-centred. The profiles are then calculated by translating the benzene molecule along the y axis by 20 Å in both directions. The profile showing the dispersion energy of the benzene dimer is also included in Fig. 3 for completeness. For the interaction of benzene with the largest molecule considered, C116H28, the dispersion energy profile has an approximately 10 Å wide plateau centred at D = 0, which indicates that the dispersion contribution to the interaction energy does not change significantly in the middle of the large flake compared to the edge (the dimensions of the C116H28 substrate are 17.2 and 15.6 Å in the x- and y- directions, correspondingly, without taking hydrogens into consideration). A similar flat profile of the dispersion energy in the vicinity of D = 0 was obtained for larger PAHs, as shown in Fig. 4, with the plateau being narrowest for the ovalene–C116H28 system. The dispersion energy profiles for the interaction between two identical PAHs, however, show no such feature (Fig. 5).
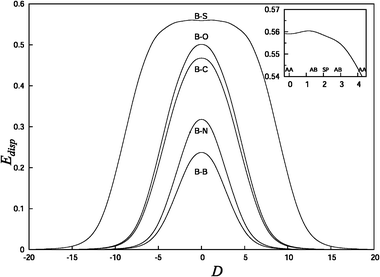 | ||
| Fig. 3 The dispersion energy Edisp (in eV) calculated using formula (3) as a function of the relative displacement of molecules, D (in Å), as described in the text. B–S: benzene–C116H28 substrate; B–O: benzene–ovalene; B–C: benzene–coronene; B–N: benzene–naphthalene; and B–B: benzene dimer. The inset shows the first AA-AB-SP-AB-AA transition for the B–S system. | ||
 | ||
| Fig. 4 The dispersion energy Edisp (in eV) calculated using formula (3) as a function of the relative displacement of molecules, D (in Å), as described in the text. O–S: ovalene–C116H28; C–S: coronene–C116H28; N–S: naphthalene–C116H28; and B–S: benzene–C116H28 molecule. | ||
 | ||
| Fig. 5 The dispersion energy Edisp (in eV) calculated using formula (3) as a function of the relative displacement of molecules, D (in Å), as described in the text. O–O: ovalene dimer; C–C: coronene dimer; N–N: naphthalene dimer; and B–B: benzene dimer. | ||
Even small variations in Edisp affect the value of the secondary energy barrier shown in Fig. 2. From the inset of Fig. 3, it can be estimated that the difference in the dispersion energy values obtained in the AB positions along the AB-SP-AB path is ΔEdisp = 4.7 meV. The energy difference in the total interaction potential energy profile calculated in the equivalent AB positions along the AB-SP-AB path (triangles in Fig. 2) is ΔEωB97X−D = 5.1 meV. This indicates that the difference of 5.1 meV in the values of the interaction potential energy in the equivalent AB positions is a result of the edge effects in estimation of the empirical dispersion term. The edge effects can be eliminated if the interaction energy is calculated not along the continuous path from the centre of the flake towards the edge but in the positions at the centre of the flake which correspond to the same relative orientations of PAH and substrate as those along the AB-SP-AB path. This approach (the profile denoted by squares in Fig. 2) gives the values of the large AB-AA barrier and the small AB-SP barrier of 10.1 meV and 1.1 meV, respectively. The ratio of the barriers is about 9.2 which is very close to the analytical value of 9.
The potential amplitude V0 in eqn (5) describing the interaction of a single carbon atom with graphene was found47 to be in the region between 3.3 and 6.7 meV by fitting to the experimental results on the atomic-scale friction forces between a small flake and graphene.51 In the profile for the interaction potential energy of the benzene–C116H28 system calculated using formula (6) and presented in Fig. 2 by solid line, the value of V0 is 4.5 ± 0.1 meV/atom, which falls well within the estimated experimental range. It follows from eqn (6) that the barrier between the global minimum and global maximum of the potential energy profile is 2.25 V0. Hence, the experimental range for the values of the AB-AA energy barrier for the interaction of PAHs with graphene can be estimated as 7.5–15 meV, and the data presented in Table 4 are in excellent agreement with the experimental range.
D. Friction forces
The calculated PES for the interaction of PAHs on graphene can also be directly used in estimation of the friction forces acting on the molecules along the direction of motion. The frictional mechanisms between small graphene flakes and graphite have been studied experimentally using a frictional force microscope that achieves a resolution in the lateral forces down to 15 pN.51 There was found to be a strong dependence of friction on orientation of the molecules, in which two narrow peaks of high friction were observed at flake-substrate orientation (rotation) angles of 0 and 60°. The first peak had a maximum friction force of 306 ± 40 pN, and the second peak had a maximum of 203 ± 20 pN. Between these peaks, a wide angular range of ultra-low friction close to the detection limit of the microscope was found, thus providing evidence of the superlubricity of graphite. The friction force is maximal when the orientation angle, which defines the mismatch between the lattices of a flake and substrate, is Φ = 0° or 60° (in accordance with 60° rotational symmetry of a graphite sheet), i.e. the flake slides over the graphite surface in commensurate contact47,51. In this geometry, the flake as a whole performs a slip-stick motion due to the binding of a flake to the graphite in the AB stacking relative configuration. The ultra-low friction behaviour and enhanced slipperiness occurs when the flake slides over the graphite surface in incommensurate contact. The flake is then rotated out of perfect registry causing the kinetic friction force to vanish and preventing the collective stick-slip motion of all atoms in the contact. The experimentally observed variation of the lateral friction force with the periodicity of graphene lattice fits very well the theoretical data provided by a modified Tomlinson model.51The effective PES calculated in this paper correspond to the commensurate case of matching lattices (Φ = 0°). If the flake is then moved along the AB-AA-AB and AB-SP-AB pathways on the graphene surface such that the stacking of layers was maintained at Φ = 0°, the frictional force Ff can be simply evaluated as52
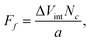 | (7) |
| AB-AA-AB | AB-SP-AB | |
|---|---|---|
| C6H6 | 64 | 30 |
| C10H8 | 107 | 54 |
| C24H12 | 298 | 168 |
| C32H14 | 394 | 202 |
IV. Summary
This study of the interaction of PAHs with a single layer of hydrogen-terminated graphene has been stimulated by recent TEM experiments on fragmentation of graphene sheets into small graphitic flakes,33 whose subsequent interaction with graphene substrate has not yet been investigated in details. The DFT-D method has been chosen as it provides a satisfactory balance between the accuracy of predictions and computational cost. The selected ωB97X-D functional was previously tested on a variety of weakly bound systems,36 and produced results comparable to the common DFT-D functionals B97-D, B3LYP-D, and BLYP-D.39 In this paper, ωB97X-D was used to estimate the binding energies of three conformations of the benzene dimer, and the results obtained with the large TZ(d, p) and 6-311++G(3df, 3pd) basis sets showed a good agreement with the literature data.The potential energy surfaces for the interaction of benzene, C6H6, naphthalene, C10H8, coronene, C24H12, and ovalene, C32H14, with graphene were calculated as functions of the PAH displacement along the hydrogen-terminated graphene substrate. The computed binding energies are in agreement with the experimental data measured by thermal desorption spectroscopy8 and analysed with both Redhead's peak maximum method45 and an isothermal analysis of Falconer and Madix.46 The movement of PAHs on graphene was also described analytically using the lowest harmonics of the Fourier expansion of PES, both computational and analytical results are in excellent agreement. Comparison of the values for the barriers to the movement of PAHs on graphene calculated with and without taking into account the dispersion interactions shows that inclusion of the dispersion term does not change the shape of the interaction energy surfaces or the value of the barriers. For all four considered PAHs, the ratio for the main AB-AA barrier obtained with the ωB97X-D and ωB97X functionals remains consistently close to unity. The potential energy surfaces were further used in the estimation of the friction forces acting on the molecules along the direction of motion, which compares favourably with experiments studying the frictional mechanisms between graphitic flakes and graphite using a frictional force microscopy.51
Acknowledgements
E.B. gratefully acknowledges financial support of an EPSRC Career Acceleration Fellowship. This work was performed during O.E.’s visit to the University of Nottingham funded by Scholarship of the President of Russian Federation for education abroad. O.E. acknowledges financial support of Russian Foundation for basic research (grant 08-02-00685-a), and thanks her supervisors Dr A. M. Popov and Prof. Y. E. Lozovik for useful discussions.References
- S. Grimme, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS
.
- S. Tsuzuki, K. Honda, T. Uchimura and M. Mikami, J. Chem. Phys., 2004, 120, 647 CrossRef CAS
.
- S. Tsuzuki and H. P. J. Luethi, J. Chem. Phys., 2001, 114, 3949 CrossRef CAS
.
- U. Zimmerli, M. Parrinello and P. J. Koumoutsakos, J. Chem. Phys., 2004, 120, 2693 CrossRef CAS
.
- M. Allen and D. J. Tozer, J. Chem. Phys., 2002, 117, 11113 CrossRef CAS
.
- L. X. Benedict, N. G. Chopra, M. L. Cohen, A. Zettl, S. G. Louie and V. H. Crespi, Chem. Phys. Lett., 1998, 286, 490 CrossRef CAS
.
- L. A. Girifalco and R. A. Lad, J. Chem. Phys., 1956, 25, 693 CAS
.
- R. Zacharia, H. Ulbricht and T. Hertel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155406 CrossRef
.
- M. Hasegawa, K. Nishidate and H. Iyetomi, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115424 CrossRef
.
- T. Gould, K. Simpkins and J. F. Dobson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165134 CrossRef
.
- M. Hasegawa and K. Nishidate, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205431 CrossRef
.
- H. Rydberg, N. Jacobson, P. Hyldgaard, S. I. Simak, B. I. Lundqvist and D. C. Langreth, Surf. Sci., 2003, 606, 532
.
- J. C. Charlier, X. Gonze and J. P. Michenaud, Europhys. Lett., 1994, 28, 403 CrossRef CAS
.
- M. C. Schabel and J. L. Martins, Phys. Rev. B: Condens. Matter, 1992, 46, 7185 CrossRef CAS
.
- S. B. Trickey, F. Muller-Plathe, G. H. F. Diercksen and J. C. Boettger, Phys. Rev. B: Condens. Matter, 1992, 45, 4460 CrossRef CAS
.
- R. H. Telling and M. I. Heggie, Philos. Mag. Lett., 2003, 83, 411 CrossRef CAS
.
- H. Rydberg, M. Dion, N. Jacobson, E. Schroder, P. Hyldgaard, S. I. Simak, D. C. Langreth and B. Lundqvist, Phys. Rev. Lett., 2003, 91, 126402 CrossRef CAS
.
- L. A. Girifalco and M. Hodak, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 125404 CrossRef
.
- F. Ortmann, F. Bechstedt and W. G. Schmidt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205101 CrossRef
.
- V. V. Deshpande, H.-Y. Chiu, H. W. Ch. Postma, C. Miko, L. Forro and M. Bockrath, Nano Lett., 2006, 6, 1092 CrossRef CAS
.
- B. Bourlon, D. C. Glattli, C. Miko, L. Forro and A. Bachtold, Nano Lett., 2004, 4, 709 CrossRef CAS
.
- J. Cumings and A. Zettl, Science, 2000, 289, 602 CrossRef
.
- A. Kis, K. Jensen, S. Aloni, W. Mickelson and A. Zettl, Phys. Rev. Lett., 2006, 97, 025501 CrossRef CAS
.
- L. Forro, Science, 2000, 289, 560 CrossRef CAS
.
- A. M. Fennimore, T. D. Yuzvinsky, W.-Q. Han, M. S. Fuhrer, J. Cumings and A. Zettl, Nature, 2003, 424, 408 CrossRef CAS
.
- A. Barreiro, R. Rurali, E. R. Hernandez, J. Moser, T. Pichler, L. Forro and A. Bachtold, Science, 2008, 320, 775 CrossRef CAS
.
- Q. Zheng, B. Jiang, S. Liu, Y. Weng, L. Lu, Q. Xue, J. Zhu, Q. Jiang, S. Wang and L. Peng, Phys. Rev. Lett., 2008, 100, 067205 CrossRef
.
- E. Bichoutskaia, A. M. Popov, Y. E. Lozovik, O. V. Ershova, I. V. Lebedeva and A. A. Knizhnik, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165427 CrossRef
.
- E. Bichoutskaia, Philos. Trans. R. Soc. London, Ser. A, 2007, 365, 2893 CrossRef CAS
.
- E. Bichoutskaia, A. M. Popov, A. El-Barbary, M. I. Heggie and Y. E. Lozovik, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 113403 CrossRef
.
- E. Bichoutskaia, A. M. Popov, M. I. Heggie and Y. E. Lozovik, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045435 CrossRef
.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183 CrossRef CAS
.
- A. Chuvilin, U. Kaiser, E. Bichoutskaia, N. A. Besley and A. N. Khlobystov, Nature Chemistry, 2010 Search PubMed
, in press.
- J. Kong, C. A. White, A. I. Krylov, C. D. Sherrill, R. D. Adamson, T. R. Furlani, M. S. Lee, A. M. Lee, S. R. Gwaltney, T. R. Adams, C. Ochsenfeld, A. T. B. Gilbert, G. S. Kedziora, V. A. Rassolov, D. R. Maurice, N. Nair, Y. Shao, N. A. Besley, P. E. Maslen, J. P. Dombroski, H. Daschel, W. Zhang, P. P. Korambath, J. Baker, E. F. C. Byrd, T. Van Voorhis, M. Oumi, S. Hirata, C.-P. Hsu, N. Ishikawa, J. Florian, A. Warshel, B. G. Johnson, P. M. W. Gill, M. Head-Gordon and J. A. Pople, J. Comput. Chem., 2000, 21, 1532 CrossRef CAS
.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553
.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC
.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef
.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554 CrossRef CAS
.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef
.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2004, 108, 10200 CrossRef CAS
.
- T. Sato, T. Tsuneda and K. Hirao, J. Chem. Phys., 2005, 123, 104307 CrossRef
.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785 CrossRef CAS
.
- S. J. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS
.
- P. A. Redhead, Vacuum, 1962, 12, 203 CrossRef CAS
.
- J. L. Falconer and R. J. Madix, J. Catal., 1977, 48, 262 CrossRef CAS
.
- G. S. Verhoeven, M. Dienwiebel and J. W. M. Frenken, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 165418 CrossRef
.
- W. A. Steele, Surf. Sci., 1973, 36, 317 CrossRef CAS
.
- Y. Baskin and L. Meyer, Phys. Rev., 1955, 100, 544 CrossRef CAS
.
- Q. Wu and W. Yang, J. Chem. Phys., 2002, 116, 515 CrossRef CAS
.
- M. Dienwiebel, G. S. Verhoeven, N. Pradeep, J. W. M. Frenken, J. A. Heinberg and H. W. Zandbergen, Phys. Rev. Lett., 2004, 92, 126101 CrossRef
.
- K. Miura, N. Sasaki and S. Kamiya, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 075420 CrossRef
.
| This journal is © the Owner Societies 2010 |
