The 1,4-phenylenediisocyanide dimer: gas-phase properties and insights into organic self-assembled monolayers†
Ryan P.
Steele‡
a,
Robert A.
DiStasio Jr
a,
Martin
Head-Gordon
*a,
Yan
Li
b and
Giulia
Galli
b
aDepartment of Chemistry, University of California—Berkeley, Berkeley, CA 94720, USA. E-mail: mhg@bastille.cchem.berkeley.edu
bDepartment of Chemistry, University of California—Davis, Davis, CA 9561, USA
First published on 9th November 2009
Abstract
The 1,4-phenylenediisocyanide (PDI) dimer serves as an intriguing case of the substituted benzene dimer, as well as a prototype system for self-assembled monolayers of organic isocyanide complexes. Structures and binding energies are explored using recently developed dual-basis second-order Møller–Plesset perturbation theory energies and gradients. The structures are dictated by a combination of dispersion and electrostatics, a combination not properly treated with local or gradient-corrected density functionals. The PDI dimer binds more than twice as strongly as unsubstituted benzene dimers in several configurations, and greater directional specificity between parallel-displaced and T-shaped structures is observed. A rotated-parallel structure is the predicted lowest-energy, gas-phase configuration, in which the isocyanide ligands are staggered on the monomers. Relevant potential energy curves of the dimer are also presented, and insights into PDI monolayer formation on metal surfaces are explored via simple two-body models. Based on the adsorbate interaction alone, a high-coverage configuration and non-vertical tilt are predicted to be favorable, although the total binding for PDI in these configurations is still insufficient to form ordered monolayers, a result consistent with previous experimental findings. Additional phenyl rings (biphenyldiisocyanide, triphenyldiisocyanide) significantly stabilize the interaction and provide the additional dispersion necessary for an ordered monolayer.
1. Introduction
Non-covalent interactions—encompassing π–π stacking and dispersion forces, hydrogen-bonding, multipole–multipole interactions, and combinations thereof—are ubiquitous in biological systems, and, accordingly, much attention has been paid to prototype systems of biological relevance, such as the benzene dimer.1–7 Substituted benzenes8–10 have received considerably less attention. Yet, one of the underlying motivations for quantifying these non-covalent interactions is the ability to manipulate and control them. Shaping the magnitude, directionality, and specificity of a given interaction is a primary ambition in fields ranging from drug design to materials science. Sinnokrot and Sherrill first reported8 the somewhat surprising result that mono-substituted benzene dimers exhibited slightly increased binding energies, independent of the substituent chosen. Certainly, multiply-substituted dimers with bulky or strongly electrostatic ligands could be constructed to reduce this interaction, but the role of the substituents in dictating the magnitude of this interaction requires further exploration. Here we examine a substituted benzene dimer system with four total substituents.In addition to the inherent interest in controlling the magnitude and selectivity of intermolecular interactions, the results presented herein have direct application to the often-overlooked role these interactions play in other areas of chemistry and materials research, such as molecular assembly.11–16 Self-assembled monolayers (SAMs), for example, are useful in molecular electronics because they provide a directionally uniform surface of adsorbates; this directional uniformity, in turn, is mainly due to stabilizing non-covalent interactions between adsorbate molecules. Indeed, in the classic alkane-thiol [HS–(CH2)(n−1)–CH3] case, for example, sufficiently ordered monolayers do not appear until n ≈ 10.17,18 This result is consistent with the scaling of dispersion interactions with the length of a saturated carbon chain.19,20
We present herein a detailed analysis of the non-covalent dimer of 1,4-phenylenediisocyanide (CN–Ph–NC) dimer, (PDI)2, also known as 1,4-diisocyanobenzene. The motivation for studying this particular system is two-fold:
1. The PDI dimer presents a special, unexplored case of the substituted benzene dimer. In general, substituents may perturb the interaction between the π faces of the phenyl rings and/or provide additional, directly ligand-involved interactions. The para-substituted isocyano ligands of the PDI monomer augment both the extent of π delocalization (the motivation for use in molecular electronics) and charge asymmetry via an enhanced quadrupole, which provide the potential for stronger, more directionally specific interactions in the dimer. Thus, (PDI)2 provides fundamental insight into the degree and specificity of competing intermolecular interactions.
2. The PDI dimer also serves as a model system for SAMs of conjugated organic isocyanide adsorbates. While alkane-thiol compounds have formed the most widely studied SAM, it has been postulated that di-substituted, conjugated isocyanide complexes may have lower barriers to charge injection21 and, thus, serve as better materials for molecular “wires”. A key step in the use of such wires, however, is the preparation of a directionally uniform surface of adsorbates—a subject with interesting questions and applications of its own. The morphology of the SAM, its formation kinetics, its thermal stability, and—crucially—its degree of order are all dictated by non-covalent interactions between adsorbate molecules, such as the alkane dispersion mentioned above. Quantifying the degree and specificity of this interaction for PDI and analogous compounds is the goal of this work.
Unfortunately, these same interactions have proven to be extremely difficult properties to quantitatively predict. Electrostatics alone cannot account for the existence of most of these phenomena, and thus, accurate electron correlation must be included to describe them properly. Kohn–Sham density functional theory (DFT),22 for example, employing the local density approximation (LDA)23 does not account for the inherently non-local effect of dispersion.24 Even gradient-corrected (GGA)25–30 functionals are corrections to the local density and do not treat dispersion forces properly. Empirical dispersion corrections (DFT-D)31–37 have recently gained favor and perform remarkably well for interaction energies—sometimes approaching highly accurate coupled-cluster results. Such terms are purely empirical, however, and have their limitations.
Thus, an ab initio description of electron correlation with the supermolecule approach is still often necessary. Further complicating matters, the methods that properly account for electron correlation are extremely sensitive to the underlying atomic orbital (AO) basis.38 These basis sets typically require functions with high angular momentum to account for polarization within and between molecules, as well as diffuse exponents to properly account for the long-range nature of the interactions. This combination of accurate electron correlation and large basis sets pushes the capability frontiers of modern electronic structure theory and has limited application to small prototype systems. The simplest wavefunction-based treatment of correlation is second-order Møller–Plesset perturbation theory (MP2).39 Coupled with the resolution-of-the-identity (RI) approximation,40–43 MP2 provides an accurate estimate (>90%) of correlation energies at a cost lower than the underlying self-consistent field (SCF) for many systems of interest. Though MP2 is known to over-estimate dispersion interactions,1,2,44–48 it is significantly more economical than its coupled-cluster counterparts and provides a reasonably accurate account of dispersion interactions, particularly when spin-component scaling is introduced.47,49,50–52 It is the fastest wavefunction-based method to qualitatively account for dispersion and will be the method of choice for assessment of the PDI dimer’s properties here. Unfortunately, the same practical shortcoming of all correlated methods also applies to MP2 theory: correlation energies are slowly convergent with respect to the underlying AO basis set.38 In this work, we utilize dual-basis RI-MP2 (DB-RI-MP2)53–59 energies and nuclear gradients as an efficient means of characterizing the (PDI)2 interaction near the basis set limit.
Recently, Li et al.60 explored the interface of a PDI monolayer with the Au(111) surface. Using plane-wave DFT with the PBE functional61 and periodic boundary conditions, several surface morphologies were explored, with a low-coverage configuration conjectured to be most stable. These DFT calculations are currently the only computationally feasible method allowing for a description of the surface interaction; unfortunately, these calculations also wholly ignore dispersion interactions amongst the adsorbates, as mentioned above. While a DFT-D dispersion term was added to the calculations of ref. 60 as an estimate of this favorable interaction, a full characterization of the (PDI)2 interaction was not made. This characterization is the focus of this work. We emphasize that the structures and potential energy curves presented here are gas-phase results in the absence of the metal surface. Such characterizations, however, have proven to be extremely useful for prototype systems, such as the more widely studied benzene dimer.1–7 Optimized dimer structures, relevant potential energy curves, and interaction energies in configurations analogous to SAMs are presented.
2. Computational methods
The aforementioned requirements of accurate electron correlation and extended basis sets make a study of even this prototype system computationally demanding. Without special treatment, a detailed study of the PDI dimer—roughly equivalent cost-wise to the benzene trimer—with MP2 and large basis sets would be prohibitive. The dual-basis (DB) method,53–59 however, has proven to be an accurate alternative to large basis set calculations. Based on a perturbative expansion of basis set relaxation effects, DB methods can produce correlated-electron calculations approaching the AO basis set limit, at a cost savings of roughly an order of magnitude.The DB-SCF method consists of a first-order approximation to basis set relaxation effects and is described in detail in ref. 53 and 56, with available extensions to RI-MP254 and its analytic gradient.57 In short, an iterative SCF calculation is performed to convergence in a subset of the larger, target AO basis set, symbolically represented as 〈target〉 ← 〈small〉, as in 6-311G* ← 6-311G. A single Fock matrix is constructed in the large basis and is subsequently diagonalized. The resulting molecular orbital (MO) coefficients are then used to form the DB energy correction to the SCF energy, as well as the subsequent correlation calculation. We have previously developed—and extensively tested—basis set pairings for target basis sets ranging in size from 6-31G*59 to aug-cc-pVQZ.62 Recently, we have also shown62 that DB errors in binding energies and structures of non-covalent complexes—the quantities most relevant to the current study—are on the order of a few hundredths of a kcal mol−1, relative to target-basis results. These DB errors are orders of magnitude smaller than the intrinsic errors of utilizing the smaller basis set alone, and for this reason, we consider DB methods viable replacements for their single-basis counterparts.
Dual-basis RI-MP2 calculations were carried out utilizing the recently developed DB-RI-MP2 analytical gradient57 in Q-Chem.63 In all cases, SCF calculations were converged to a DIIS64,65 error of at most 10−8 a.u., using integral thresholds of 10−12 a.u. For the RI calculations, the corresponding auxiliary basis sets of Weigend66 were used, and the frozen-core approximation was employed. Linear dependence was handled as described in ref. 62, using a drop tolerance of 10−6. Geometry optimizations were converged to a maximum gradient component of 3 × 10−5 a.u. and either a displacement of 12 × 10−5 or an energy change of 1 × 10−6 a.u.—an order of magnitude tighter than the Q-Chem default tolerances—since the potential energy surfaces involved are often quite flat. No symmetry constraints were applied, aside from the symmetry of the starting structures, and no symmetry was exploited during the calculations. Structures were optimized with the DB pairings for aug-cc-pVDZ and aug-cc-pVTZ; energies were calculated with the dual-basis pairings for aug-cc-pVDZ, aug-cc-pVTZ, aug-cc-pVQZ, and the T → Q extrapolation of Helgaker,67 where, in our case, T and Q refer to aug-cc-pVTZ and aug-cc-pVQZ, respectively. As an estimate of the inherent overbinding of MP2 theory, we have also tabulated spin-component scaled [SCS(MI)]47 energies on the resulting structures (using the spin scalings optimized in ref. 62), as well as ΔCCSD(T)68–70 energies, calculated with the 6-31G* basis for the difference (Δ) between MP2 and CCSD(T) correlation energies. Throughout the remainder of this paper, the DB approximation has been used; given the promising results of ref. 62, basis sets will only hereafter be referred to by the target basis name. For the comparative DFT calculations, the DB approximation has also been utilized. Molecular structures were generated with VMD.71,72
3. Results
3.1 Gas-phase dimer structures
Guided by known structures for the benzene dimer and the potential electrostatic interactions, several dimer configurations were considered. Optimized structures and their respective nomenclature are depicted in Fig. 1 and 2; summarized structural and energetic data is shown in Table 1. Note that some conjectured structures were not found; the absence of these stationary points was confirmed by potential energy scans, included in the ESI.† Properties of the optimized structures are discussed in turn. Unless otherwise specified, binding energies are reported in the text as extrapolated T → Q energies on aug-cc-pVTZ structures.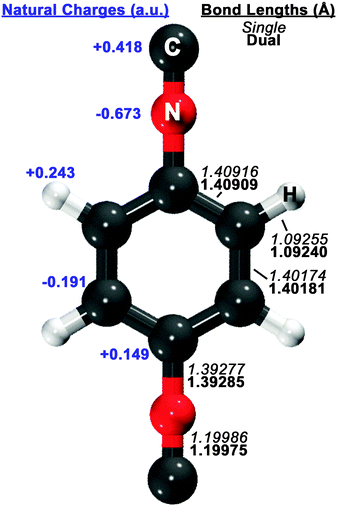 | ||
| Fig. 1 Optimized structure of the 1,4-phenylenediisocyanide (PDI) monomer, computed with RI-MP2/aug-cc-pVDZ. On the right side of the figure, single-basis (italics) and dual-basis (bold) bond lengths are shown for symmetry-unique bonds. The left side of the figure shows HF/aug-cc-pVDZ natural charges, computed with the NBO package,73 for symmetry-unique atoms. | ||
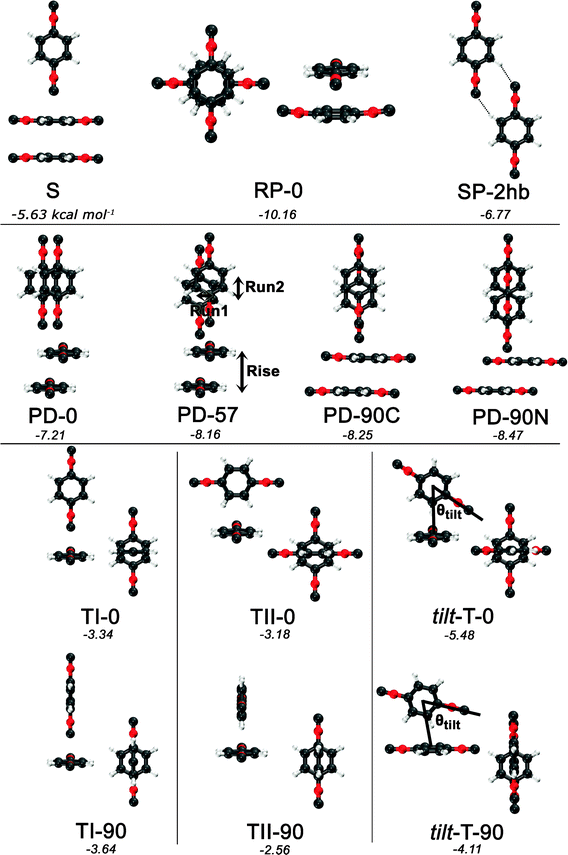 | ||
| Fig. 2 Optimized structures and nomenclature for the PDI dimer using DB-RI-MP2/aug-cc-pVTZ. Except for the planar SP-2hb, side and top views are presented for each structure. Below each structure’s name, the extrapolated and counterpoise-corrected RI-MP2/aug-cc-pVTZ → aug-cc-pVQZ binding energies are shown, in kcal mol−1. | ||
| aug-cc-pVDZ structures | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Geometric parameters | Binding energy/kcal mol−1 | ||||||||||||||
| Structurec | Rd/Å | Risee/Å | Run1/Å | Run2/Å | Tilt angle/degrees | aug-cc-pVDZ | aug-cc-pVTZ | aug-cc-pVQZ | T → Qa | SCS(MI)b | |||||
| Non-CP | CP | Non-CP | CP | Non-CP | CP | Non-CP | CP | CP | |||||||
| S | 3.415 | −10.75 | −4.37 | −7.45 | −5.14 | −6.16 | −5.51 | −5.37 | −5.69 | −2.67 | |||||
| PD-0 | 3.422 | 3.118 | 1.411 | 0.000 | −13.32 | −5.67 | −9.47 | −6.68 | −7.80 | −7.07 | −6.87 | −7.35 | −3.86 | ||
| PD-57 | 3.475 | 3.131 | 0.827 | 1.264 | −14.53 | −6.58 | −10.56 | −7.63 | −8.83 | −8.03 | −7.85 | −8.33 | −4.57 | ||
| PD-90C | 3.473 | 3.156 | 0.000 | 1.449 | −14.54 | −6.59 | −10.58 | −7.65 | −8.86 | −8.05 | −7.89 | −8.34 | −4.48 | ||
| PD-90N | 4.367 | 3.100 | 0.000 | 3.076 | −13.90 | −6.84 | −10.60 | −7.80 | −9.10 | −8.15 | −8.26 | −8.41 | −4.88 | ||
| TI-0 | 7.008 | −5.43 | −2.73 | −4.22 | −2.99 | −3.56 | −3.09 | −3.20 | −3.16 | −1.97 | |||||
| TI-90 | 6.998 | −5.72 | −3.03 | −4.51 | −3.29 | −3.85 | −3.40 | −3.50 | −3.47 | −2.25 | |||||
| TII-0 | 4.745 | −7.08 | −2.54 | −4.75 | −3.00 | −3.58 | −3.14 | −2.91 | −3.24 | −2.05 | |||||
| TII-90 | 4.726 | −6.78 | −1.88 | −4.18 | −2.35 | −2.98 | −2.52 | −2.30 | −2.63 | −1.49 | |||||
| tilt-T-0 | 4.714 | 56.832 | −9.92 | −4.47 | −7.30 | −5.16 | −6.01 | −5.37 | −5.27 | −5.53 | −3.74 | ||||
| tilt-T-90 | 4.658 | 65.991 | −8.74 | −3.08 | −5.92 | −3.80 | −4.57 | −4.02 | −3.80 | −4.18 | −2.64 | ||||
| SP-2hb | 8.133 | 0.000 | 3.634 | 7.276 | −8.23 | −6.05 | −7.57 | −6.53 | −7.02 | −6.66 | −6.73 | −6.75 | −5.56 | ||
| RP-0 | 3.263 | −15.68 | −8.88 | −11.94 | −9.72 | −10.21 | −10.05 | −9.23 | −10.29 | −6.57 | |||||
| aug-cc-pVTZ structures | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Geometric Parameters | Binding Energy/kcal mol−1 | ||||||||||||||
| Structurec | Rd/Å | Risee/Å | Run1/Å | Run2/Å | Tilt angle/degrees | aug-cc-pVTZ | aug-cc-pVQZ | T → Qa | SCS(MI)b | ΔCCSD(T)f | |||||
| Non-CP | CP | Non-CP | CP | Non-CP | CP | CP | CP | ||||||||
| a Extrapolated aug-cc-pVTZ → aug-cc-pVQZ energies, using the extrapolation scheme of Helgaker.67 b Extrapolated aug-cc-pVTZ → aug-cc-pVQZ spin-component-scaled energies, using the SCS(MI) method of DiStasio.47 Scaling parameters for spin components are those of ref. 62. c Refer to Fig. 2 for structure nomenclature. d Center-to-center distance, defined as the distance between the center (averaged coordinates) of the ring carbons. e Rise, run1, run2 and tilt angle are defined as shown in Fig. 2. f Extrapolated aug-cc-pVTZ → aug-cc-pVQZ energies, including the ΔCCSD(T)/6-31G* correction.68–70 | |||||||||||||||
| S | 3.498 | −7.97 | −5.17 | −6.68 | −5.44 | −5.41 | −5.63 | −3.06 | −2.00 | ||||||
| PD-0 | 3.483 | 3.181 | 1.419 | 0.000 | −9.96 | −6.64 | −8.36 | −6.97 | −6.92 | −7.21 | −4.18 | −2.99 | |||
| PD-57 | 3.545 | 3.194 | 0.811 | 1.294 | −11.06 | −7.61 | −9.40 | −7.96 | −7.87 | −8.16 | −4.88 | −3.79 | |||
| PD-90C | 3.549 | 3.227 | 0.000 | 1.477 | −11.08 | −7.65 | −9.44 | −8.00 | −7.96 | −8.25 | −4.87 | −3.85 | |||
| PD-90N | 4.419 | 3.157 | 0.000 | 3.093 | −10.76 | −7.94 | −9.13 | −8.22 | −8.28 | −8.47 | −5.32 | −4.54 | |||
| TI-0 | 7.046 | −4.73 | −3.19 | −4.12 | −3.28 | −3.23 | −3.34 | −2.26 | −1.64 | ||||||
| TI-90 | 7.034 | −4.98 | −3.48 | −4.41 | −3.57 | −3.54 | −3.64 | −2.53 | −1.90 | ||||||
| TII-0 | 4.777 | −5.23 | −2.96 | −4.12 | −3.09 | −2.93 | −3.18 | −2.09 | −1.18 | ||||||
| TII-90 | 4.774 | −4.64 | −2.33 | −3.53 | −2.47 | −2.34 | −2.56 | −1.56 | −0.63 | ||||||
| tilt-T-0 | 4.751 | 56.598 | −7.72 | −5.14 | −6.52 | −5.33 | −5.27 | −5.48 | −3.83 | −3.00 | |||||
| tilt-T-90 | 4.721 | 65.300 | −6.39 | −3.78 | −5.09 | −3.97 | −3.80 | −4.11 | −2.72 | −1.85 | |||||
| SP-2hb | 8.084 | 0.000 | 3.550 | 7.263 | −8.01 | −6.54 | −7.45 | −6.67 | −6.59 | −6.77 | −5.59 | −4.89 | |||
| RP-0 | 3.317 | −12.32 | −9.66 | −10.74 | −9.95 | −9.29 | −10.16 | −6.87 | −5.64 | ||||||
Given these dispersion and electrostatic considerations, the fact that Hartree–Fock (HF) and DFT do not bind this structure is no surprise. At the MP2-optimized geometry, HF is repulsive by 10.95 kcal mol−1, and DFT with the PBE functional61 is repulsive by 5.37 kcal mol−1. Thus, long-range electron correlation, computed at the MP2 level or higher (or with empirical dispersion terms), is necessary for even a qualitatively correct description of the PDI dimer.
The basis set dependence of S is significant. Without the CP correction,75 the aug-cc-pVDZ interaction energy is overbound by nearly a factor of two. While CP-corrected numbers are generally closer to the basis set limit, the elimination of BSSE does not rectify basis set incompleteness errors. As such, the CP-corrected aug-cc-pVDZ result is still in error by 20%, relative to aug-cc-pVQZ. Overall, a common trend is observed: The non-CP-corrected numbers approach the basis set limit from below, whereas the CP-corrected results approach the same limit (more quickly) from above. The geometries are basis set dependent to a lesser extent. The center-to-center distance changes by 0.083 Å between aug-cc-pVDZ and aug-cc-pVTZ, but owing to the flatness of the potential energy surfaces, single-point energies within the same basis set are within 0.1 kcal mol−1 for both structures. Further optimization with aug-cc-pVQZ (a significant computational excursion) appears unnecessary for all structures considered; increasing the level of electron correlation is probably more important1,5–7 since the MP2 structures are most likely too compact. Our best MP2 number for S is the CP-corrected T → Q result of −5.63 kcal mol−1.
Interestingly, two other PD structures were found. The first resides between PD-0 and PD-90, termed PD-57. It is displaced along both the run1 and run2 coordinates (see Fig. 2 for definitions) and, thus, its phenyl ring sits on top of the C1–C2 bond of the paired monomer. A two-dimensional potential energy surface using fixed monomers (see ESI†) indicates that this structure is a saddle point, although it is nearly iso-energetic with PD-90C. This latter fact is a reminder of the flatness of the potential energy surface for these dimer systems. The other PD structure, PD-90N, is a further displacement of PD-90C along the isocyano axis. The phenyl ring of the upper monomer resides above the nitrogen of the lower monomer’s isocyano ligand. The binding energy for PD-90N is noteworthy, since basis set limit MP2 results indicate that it is more strongly bound than any of the other PD structures. It is also most consistent with the experimentally observed74 crystal structure of PDI. This binding strength indicates that electrostatic repulsion from direct contact of the atoms is still significant, and these electrostatic effects can be diminished by slipping one monomer to interact directly with the other monomer’s ligand. Most importantly, however, the dispersion interaction is not significantly deterred in this configuration, despite the fact that the two phenyl rings do not overlap! (The role of dispersion is proven by the unfavorable +9.29 kcal mol−1 interaction energy at the HF level in this configuration.) Dispersion between the phenyl ring and the neighboring ligand is still sufficient to stabilize this complex by −8.47 kcal mol−1, with non-face-to-face dispersion between the phenyl rings probably still significant. This qualitative result may have significance for similar biological systems; direct overlap of aromatic rings is apparently not necessary for a notably stabilizing interaction.
The center-to-center distances are comparable in the first three PD complexes—3.483 Å (PD-0), 3.545 Å (PD-57), and 3.549 Å(PD-90C). With its significantly slipped configuration, PD-90N possesses a much longer center-to-center distance, 4.419 Å. The optimized PD-90C structure exhibits the same out-of-plane bending that was seen in S; the terminal carbon rises 0.066 Å (1.46°) above the ring carbons. The phenyl ring itself, however, displays only a 0.001° dihedral bend. The PD-90N structure shows significantly diminished ligand bending—less than 0.1°.
The same basis set dependence of energies and structures that was observed for S is seen here. Note that aug-cc-pVQZ (or larger) is required for reasonable convergence of energies and elimination of BSSE. Presumably owing to the significant basis set dependence, CP and non-CP T → Q extrapolated numbers still differ by roughly 0.3 kcal mol−1 for three of the PD complexes. Though the CP correction is well-designed for a prototype system such as PDI dimer, it cannot be applied to intramolecular interactions of folded polypeptides77 and other complex systems, which is why the basis set dependence for non-CP results is included in Table 1. As such, the ability to approach the basis set limit without CP correction is a crucial tool.
Both classes of T-shaped structures exhibit slightly less basis set dependence than the PD structures, most likely due to the fact that dispersion contributes less to the interaction. The TII structures, with a more significant contribution from dispersion, showed a slightly more marked basis set dependence than TI. The contribution of BSSE is still significant, however, and contributes 0.8–1.0 kcal mol−1, even at aug-cc-pVQZ. The BSSE is nearly constant across T-shaped structures, though, meaning that their relative energy gaps are much less basis set dependent.
The fact that TI and TII structures are nearly isoenergetic implies a lack of specificity among T-shaped structures. However, this entire class of structures possesses the aforementioned specificity, relative to PD. Structures with parallel phenyl rings exhibit noticeably stronger binding energies than those with perpendicular rings. Similar specificity has been observed in PD and T configurations of the naphthalene dimer,78 relative to benzene dimer. This specificity in the PDI dimer, however, can be achieved via ligands instead of additional aromatic rings.
Worth noting are the results of the semi-empirical SCS(MI) method,47 also shown in Table 1. These results confirm a standard conclusion that MP2 overestimates the strength of dispersion interactions. For example, our lowest-energy structure (RP-0) is over-bound by nearly 3.3 kcal mol−1. The qualitative trends presented throughout this discussion, however, are not changed by the across-the-board reduced binding of SCS(MI). The dispersion-bound complexes are still the most stable, and notable configurational specificity is still displayed. The complexes with significant dispersion contributions (S, PD, and RP-0) show the most significant reduction of the binding energy, and the PD class is reduced in energy below the SP-2hb structure. T-shaped structures also show reduced binding energies, owing to the fact that dispersion still contributes in this class of structures. We note that, since the structures presented herein contain a varying mixture of dispersion and electrostatics, a simple scaling of components of the correlation energy may not be appropriate for relative energy gaps. Nonetheless, the SCS(MI) trends are also qualitatively confirmed by the ΔCCSD(T) corrections, shown in the final column of Table 1. While the latter results show even greater reduction in binding energy, they should be tempered by the fact that the 6-31G* basis set has been shown to systematically over-emphasize this reduction.70 (CCSD(T) calculations with larger basis sets were cost-prohibitive.) Still, the relative energy ordering is essentially the same between SCS-MI and ΔCCSD(T) and, except for the SP-2hb structure, is also essentially the same as the MP2 results. Thus, we conclude that SCS(MI) provides a reasonable quantification of the degree to which the MP2 binding energies are in error.
Other tilted structures and higher-order saddle points almost certainly exist; however, such characterization of the entire potential energy surface is not the goal of the current work. Several reasonable structures—and the factors governing the magnitude and direction of their interaction—have been found and characterized. Further exploration of parts of the potential energy surface with direct relevance to PDI SAMs is the subject of the following section.
3.2 Potential energy curves
The configurations and degree of order in SAMs are dictated by several competing factors. Two of these factors are the distance-dependent magnitude of interactions among adsorbates and the directional dependence of these interactions. In order to quantify the range and direction in which these interactions are significant, relevant potential energy curves have been constructed. In each case, frozen aug-cc-pVDZ monomers have been utilized. While geometry relaxation effects are non-zero, they do not influence the qualitative behavior of these curves except in the high barrier regions, which do not significantly affect the physics of the problem; furthermore, a SAM configuration would lead to (quasi-) symmetric forces on each adsorbate, further justifying the use of such monomers.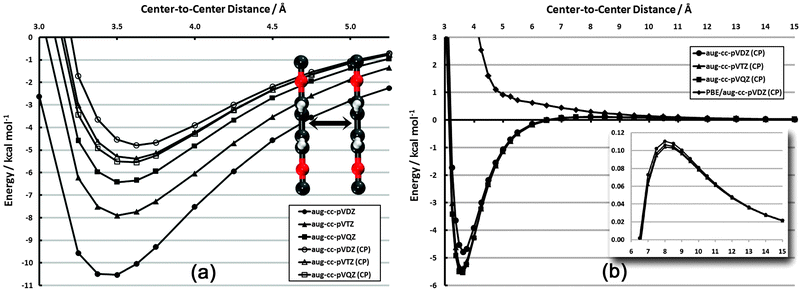 | ||
| Fig. 3 Frozen-monomer potential energy curve for the sandwich structure of the PDI dimer. (a) Basis set dependence in vdW well (CP = counterpoise correction75). (b) Full interaction curve for distances up to 15 Å. Inset: close-up of repulsive quadrupole–quadrupole region (note different scale). | ||
In Fig. 3(b), the competing influence of dispersion and electrostatics can clearly be seen. While the dispersion interaction (r−6) is favorable out to nearly 6.5 Å, the unfavorable quadrupole–quadrupole interaction (r−5) begins to dominate at longer distances. Still, the sum of the two interactions never reaches beyond +0.11 kcal mol−1. This electrostatic portion of the curve is also nearly basis-set-independent.
For comparison, the results for CP-corrected dual-basis PBE/aug-cc-pVDZ are also shown (on MP2 structures). This gradient-corrected functional, as mentioned above, does not properly account for dispersion interactions. Indeed, the attractive vdW well seen with MP2 is purely repulsive with PBE. The repulsive r−5 portion of the plot is also noticeably more repulsive with PBE. While PBE is expected to capture the electrostatic aspects properly, the erroneous dispersion behavior still contributes out to at least 10 Å and skews the nominally electrostatic properties.
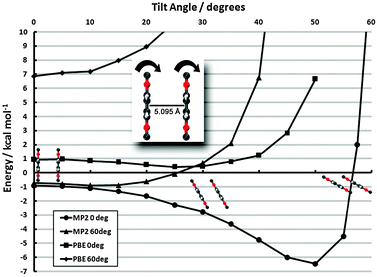
 monolayer unit cell on a Au(111) surface, using the lattice spacing of a0 = 4.16 Å reported in ref. 60. These parameters translate to a separation of
monolayer unit cell on a Au(111) surface, using the lattice spacing of a0 = 4.16 Å reported in ref. 60. These parameters translate to a separation of 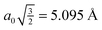 . Face-to-face (0° offset) and 60°-offset scans are shown in Fig. 4(a) and (b), respectively, which provide insight for potential monolayer configurations (see section 3.3) and the degree to which these configurations are free to rotate. The monomers are again fixed at the aug-cc-pVDZ geometry, and only CP-corrected aug-cc-pVDZ results are presented.
. Face-to-face (0° offset) and 60°-offset scans are shown in Fig. 4(a) and (b), respectively, which provide insight for potential monolayer configurations (see section 3.3) and the degree to which these configurations are free to rotate. The monomers are again fixed at the aug-cc-pVDZ geometry, and only CP-corrected aug-cc-pVDZ results are presented.
 | ||
| Fig. 4 Frozen-monomer potential energy curve for the rotation of one monomer along its isocyano axis. The intermonomer separation is fixed at 5.095 Å and offsets of 0° and 60° are shown. Results are presented for CP-corrected aug-cc-pVDZ, using (a) DB-RI-MP2 and DB-DFT (PBE functional) and (b) DB-RI-MP2. | ||
Focusing on the 0°-offset configuration first (Fig. 4(a)), a somewhat surprising result is found. The 180° structure (analogous to the S structure, above) is not the lowest energy point on the curve. Instead, the 90° point (analogous to TII-90) is 1.5 kcal mol−1 lower in energy. At this longer separation—1.6 Å beyond the optimal separation in S—the T-shaped structure is closer to its equilibrium geometry. Thus, for two monomers fixed at lattice positions on a surface, the T-shaped configuration is more favorable. These lattice binding constraints often influence which monolayer morphologies are available and preferred. Note, however, that the barrier to rotation in this configuration is small. For comparison, DFT (PBE) results are also shown in Fig. 4. The results are purely repulsive and show no conformational specificity. Thus, PBE predicts exactly the wrong qualitative behavior.
The 60°-offset scan displays significantly more angular dependence, owing to the closer approach of the monomers. The parallel structure is again not the minimum energy configuration; a spin angle of approximately 30° is 1.4 kcal mol−1 lower in energy. In this configuration, the rotating monomer’s π face is rotated toward the π face of the fixed monomer, forming a rotated analogue of the PD-0 structure. The presence of this minimum is again due to the beyond-equilibrium spacing of the two monomers and is not indicative of a lower-energy rotated PD-0 structure. Interestingly, the surface is very flat in the 10–80° range. Inside of this 80° point, however, the monomers quickly approach their vdW radii, and a large barrier connects back to the parallel structure. While the use of frozen monomers in this curve artificially inflates the barrier height, significant structural rearrangement would be required to avoid vdW impingement; thus, the qualitatively high barrier is reasonable. The presence of this barrier is significant. For monomers locked in a configuration commensurate with the underlying surface, this “spinning” motion among adsorbates strongly influences the available interactions. This barrier could never be traversed thermally (since the barrier is much larger than the Au-PDI binding energy of approx. 0.5 eV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60) and, thus, limits the rotational freedom of adsorbates. Of course, a full analysis of surface rotational freedom would include the potential for rotation of a PDI monomer on the metal surface, which is not included here. As a first approximation, however, the sum of the two would provide reasonable insight to this flexibility.
60) and, thus, limits the rotational freedom of adsorbates. Of course, a full analysis of surface rotational freedom would include the potential for rotation of a PDI monomer on the metal surface, which is not included here. As a first approximation, however, the sum of the two would provide reasonable insight to this flexibility.
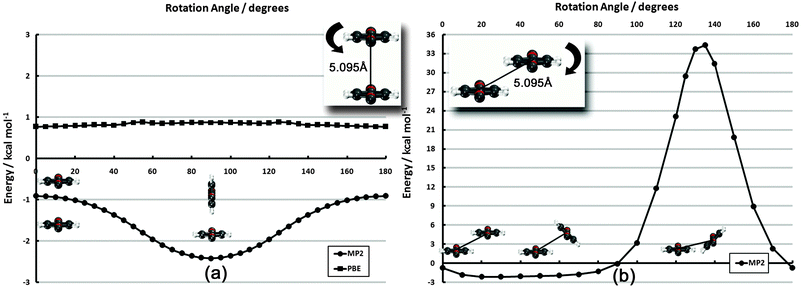
 | ||
| Fig. 5 Frozen-monomer potential energy curve for the parallel rotation of both monomers along their isocyano axes. The intermonomer separation is fixed at 5.095 Å. Results are presented for CP-corrected DB-RI-MP2/aug-cc-pVDZ. | ||
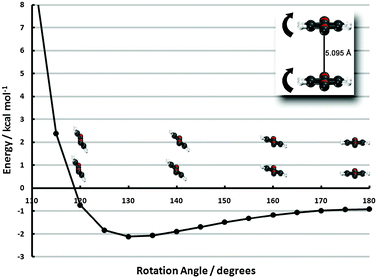
 | ||
| Fig. 6 Frozen-monomer potential energy curve for the out-of-plane tilt motion of both monomers. The center-to-center separation is fixed at 5.095 Å and offsets of 0° and 60° are shown (refer to insets of Fig. 4 for visual depictions of these offsets). Results are presented for CP-corrected aug-cc-pVDZ DB-RI-MP2 and DB-DFT (PBE functional). | ||
The 0°-offset configuration—beginning 1.6 Å beyond the minimum of the sandwich potential energy curve—shows a strong propensity to tilt. A roughly 50° degree tilt from the vertical leads to an interaction energy lowering from −0.9 to −6.5 kcal mol−1, due to more favorable electrostatics, akin to the PD-90C/PD-90N structures. Tilting beyond this point, however, quickly leads to structures inside the vdW radii and an enormous barrier. The 60°-offset displays a much shallower minimum since less tilting is required to approach vdW contact. In fact, the difference between the untilted structure and the minimum (20° tilt) is less than 0.2 kcal mol−1. While the pronounced minimum of the tilted 0°-offset configuration is promising for stabilizing the monolayer, the 60°-offset structure’s quick approach of vdW contact essentially rules out the possibility of attaining the former’s deep well in high-coverage surface configurations. Some intermediate between the two, however, would be a strong driving force for (tilted) ribbon structures. While PBE results have thus far been firmly established to be qualitatively incorrect, we note in passing that even PBE predicts a 0.5 kcal mol−1 preference to tilt in the 0° configuration, due to electrostatics.
3.3 Surface configuration models
One of the motivations for quantifying prototype systems, such as the PDI dimer, is the transfer of these fundamental quantities to larger chemical systems. The results of the previous sections allow for the assessment of adsorbate interactions in SAM configurations. In this section, reasonable models of SAM configurations are presented that account for neighboring interactions and provide an estimate of the cohesive energy of the monolayer. As mentioned previously, these models wholly ignore the presence of the metal. They essentially treat the monolayer as a two-dimensional molecular crystal, confined to surface lattice separations. While certainly an approximation, this treatment is reasonably justified. The study by Li60 indicates that the Au–CN bond is only 0.5 eV (11.5 kcal mol−1)—strong enough to bind a surface monolayer but weak enough to not significantly perturb the electronic structure of the remainder of the adsorbate molecule. In fact, density difference maps showed little, if any, change in electron density beyond the bound isocyano ligand. The electronic structure in the vicinity of the bound ligand does change, and this fact is further confirmed by the ≈70 cm−1 shift in the isocyano stretch frequency used to identify the binding moiety experimentally.16,81,85,86 The pendant substituent, however, shows no change in frequency, and frequencies associated with the phenyl ring atoms exhibited small frequency changes.86The change in the electronic structure of the bound CN group certainly will influence the dispersion and electrostatic interactions among adsorbates. As a first approximation, however, we ignore this induced change in binding. This approximation is analogous to the commonly used method82 in reflection–absorption infrared spectroscopy (RAIRS) for determining monolayer tilt angles (see ref. 16, for example). Using gas-phase adsorbate frequencies and the fact that the intensity of the observed signal can only be due to dynamic dipoles perpendicular to the surface, the average tilt angle of an isotropic monolayer may be estimated. Underlying this method, however, is the assumption that the properties of the adsorbate molecules do not appreciably change upon adsorption. As the adsorbate molecules get larger by adding bulkier substituents, more phenyl rings (section 3.4), and spacers between the rings, this approximation should improve.
The three configurations considered by Li et al.60 are analyzed here; Fig. 7 shows a reconstruction of these structures. The first is a full-coverage (Θ = 1) configuration, commensurate with the underlying Au(111) surface. The configuration chosen places next-nearest neighbors parallel (end-to-end) and has a unit cell of 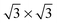 . It will hereafter be referred to as the Standard full-coverage configuration. A Herringbone
. It will hereafter be referred to as the Standard full-coverage configuration. A Herringbone 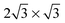 configuration was also considered in full coverage, in which neighboring rows adopt a non-parallel relative configuration and next-nearest neighbors are again aligned end-to-end. Note that the rotation angle in our Herringbone configuration is slightly different (60° vs. 40.9°) from that of ref. 60. The reasons for this more symmetric structure are discussed below. Finally, a low-coverage (Θ = ⅓) configuration was also tested, which is simply a
configuration was also considered in full coverage, in which neighboring rows adopt a non-parallel relative configuration and next-nearest neighbors are again aligned end-to-end. Note that the rotation angle in our Herringbone configuration is slightly different (60° vs. 40.9°) from that of ref. 60. The reasons for this more symmetric structure are discussed below. Finally, a low-coverage (Θ = ⅓) configuration was also tested, which is simply a 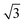 expansion of the Standard configuration.
expansion of the Standard configuration.
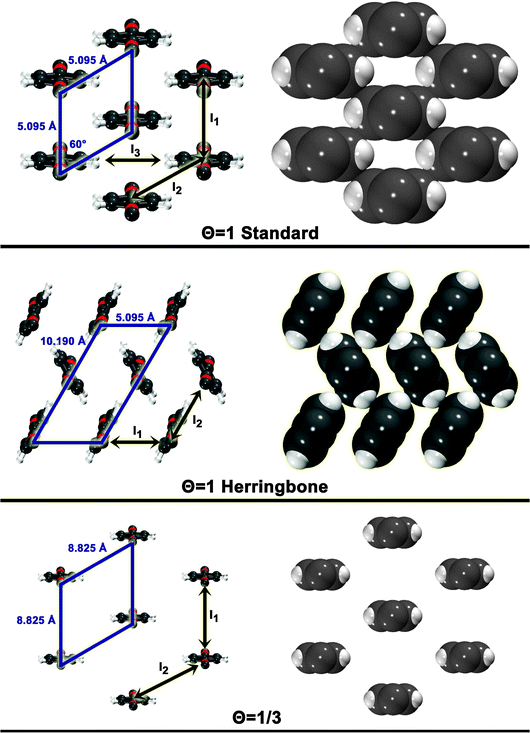 | ||
| Fig. 7 Surface configuration models. For each configuration, a skewed top view is shown on the left. A space-filling top view (based on atomic vdW radii) is depicted on the right. The unit cell is shown for each. Also shown are the dimer interactions contributing to each model (In). | ||
The simplest model for the adsorbate–adsorbate interaction in these configurations involves the sum of all nearest-neighbor interactions (properly accounting for double-counting). Such interactions are represented pictorially in Fig. 7 as In. For the standard configuration, one set of next-nearest neighbor interactions was also included; while the center-to-center distance between next-nearest neighbors is 8.825 Å in this configuration, the width of the adsorbate places the hydrogens, for example, only 4.495 Å apart. The results of these models and their component interactions are shown in Table 2. Frozen monomers with aug-cc-pVDZ structures are used. Results for CP-corrected, T → Q extrapolated MP2 and SCS(MI) MP2 are presented; an analysis of basis set effects for these models is given in the ESI.†
| Configuration | I 1 | I 2 | I 3 | Model | MP2 | SCS(MI) MP2 | PBEa |
|---|---|---|---|---|---|---|---|
| a The pair of PBE results for each configuration is shown as [this work]/[ref. 60]. | |||||||
| Θ = 1 Standard | −0.97 | −1.46 | +0.54 |
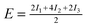
|
−3.35 | −0.90 | +8.01/+8.86 |
| Θ = 1 Herringbone | −1.59 | −1.93 | — |
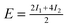
|
−5.45 | −3.27 | +5.65/+5.04 |
| Θ = ⅓ Standard | 0.10 | 0.21 | — |
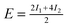
|
+0.52 | +0.46 | +1.17/+1.07 |
Both full-coverage (Θ = 1) configurations are found to be stably bound, in the absence of the metal, by −3.35 (Standard) and −5.45 (Herringbone) kcal mol−1 monomer−1. The low-coverage configuration is slightly unbound; the intermonomer spacing of this configuration places the adsorbates in the slightly repulsive quadrupole–quadrupole range discussed in section 3.2.1. Based on the adsorbates alone, the full-coverage Herringbone structure is predicted to be the most stable. If the interaction with the metal was constant across these structures, this ordering would apply. This assumption most likely is not the case, however, and a definitive assignment of the most stable structure would require an analysis of this property. Ref. 60 includes an estimate of the adsorbate–metal interaction; however, this estimate also includes the shift of adsorbate–adsorbate interactions due to the presence of the metal and does not incorporate geometry relaxation after including PBE-D. Thus, the Au-PDI interaction cannot be directly compared to these numbers.
The failure of DFT (PBE) for this interaction has already been firmly established and need not be discussed in detail for these models. However, the PBE results for our current pairwise model do allow for direct comparison to the results of Li, also reproduced in the last column of Table 2. The per-monomer interaction energies are in good agreement (within ≈10%) with the periodic, plane-wave calculations. Inclusion of the remaining next-nearest-neighbor interaction in the Standard full-coverage configuration further brings the model in agreement (8.71 vs. 8.86 kcal mol−1 monomer−1, see ESI†). These next-nearest-neighbor interactions were excluded from the MP2 models since they were found to be negligible (0.09 kcal mol−1) for the Standard configuration. Thus, the pairwise models—at least for PBE—are able to quantitatively reproduce cohesive energies of the infinite-slab models.
The remaining discrepancy between the models in the Standard configuration is due to the small effects of geometry relaxation and the plane-wave pseudopotential. The latter is the more significant contributor, as confirmed by plane-wave calculations performed for the current work. The pairwise model is in nearly perfect agreement—8.90 vs. 8.86 kcal mol−1 monomer−1—when the plane-wave protocol is utilized for both the pairwise and periodic calculations. These additional plane-wave PBE calculations (refer to ref. 60 for methodology details) were performed for this work on the MP2-optimized structures; detailed results may be found in Table S6 of the ESI.† This result is interesting in its own right, since three-body effects are wholly negligible. Note that the perturbative presence of the metal substrate cannot yet be discounted; the plane-wave results with which our models are compared also neglected the electronic (but not geometric) perturbation of the monomers during the interaction energy calculation.
The Herringbone configuration exhibits a slightly larger error. This result is due to the use of a different monolayer rotational configuration in our pairwise model from in ref. 60. Our 60° angle (relative to the horizontal in Fig. 7) was only 40.9° in the optimized structure of Li. The highly symmetric 60° structure was chosen as a more general prototype for a Herringbone structure. The 40.9° structure, on the other hand, was optimized with the PBE functional, which has already been established to incorrectly describe the interaction. A check of the two-body model for this work, similar to the one described above, at the 40.9° configuration confirms that two-body effects are sufficient when identical structures are compared. The model error, relative to periodic monolayer calculations, is only 0.15 kcal−1 monomer−1 (refer to ESI† for details). Consequently, the I2 interaction—dominant in the repulsive PBE calculation—is higher in energy at 60° and explains the overestimate. With MP2, however, this I2-type interaction makes the largest favorable contribution and thus leads to different structural behavior, justifying our use of a different structure. An optimization of the rotational angle within this two-body model has not been performed but would be an interesting extension of this methodology. The small but slightly repulsive interaction of the low-coverage configuration is also estimated well with these models.
Consistency within the DFT results does not, of course, guarantee that the MP2 two-body models are accurate. The additivity of dispersion interactions, correlated three-body effects, and the screening of such long-range effects cannot be assessed in this comparison. A final test (not shown in the tables) was performed by removing the central monomer of the heptamer depicted pictorially in Fig. 7 and calculating the MP2 cohesive energy. The results indicate that such effects are negligible; the resulting cohesive energy is within 0.2 kcal mol−1 monomer−1 of the pairwise models, implying that these simple models are, at the very least, consistent with cluster calculations.
The absence of three-body effects implies that DFT-D may be a viable tool in such calculations. A comparison with the results of ref. 60, however, signifies that this observation—at least for PBE-D—may not be the case. When the empirical dispersion contribution was added to the results of the periodic PBE calculations, the ordering of the configurations is swapped. Whereas MP2 predicts −3.35/−5.45/+0.52 kcal mol−1 monomer−1 (Standard/Herringbone/Low)—an order confirmed by SCS(MI) (−0.90/−3.27/+0.46)—PBE-D predicts +2.08/−0.46/+0.92. While no direct experimental data is available for comparison, the PBE-D results illogically imply that the next-nearest-neighbor interaction in the full-coverage Standard configuration is sufficient to swamp any stabilizing effect of I1 and I2. In fact, this I3 interaction (+0.67 kcal mol−1 with PBE) is insufficient to account for the repulsion exhibited by DFT-D, meaning that a net de-stabilizing force is provided by I1 and I2—a fact wholly inconsistent with the results of this work. Thus, the applicability of PBE-D in monolayer configurations and/or its performance for isocyano groups must be re-examined.§
With the results of section 3.2.4, estimating the cohesive adsorbate interactions in tilted configurations is also possible. The full-coverage configuration was tilted out-of-plane, and the model energies are shown in Fig. 8. These calculations do, in fact, indicate a propensity to tilt. The optimum tilt angle is ≈15°, where the cohesive energy is −2.5 kcal mol−1 monomer−1 (aug-cc-pVDZ). The propensity to tilt, however, is small. Only a 0.7 kcal mol−1 monomer−1 gap separates this minimum energy structure from the fully vertical structure, and a further 20° may be traversed before the monolayer adsorbate–adsorbate interaction is unbound. While the face-to-face tilt in section 3.2.4 indicates a strong driving force away from vertical, the agostic interaction (I2, shown pictorially in the space-filling models of Fig. 7) is dominant during a monolayer tilt. This lack of specificity in tilt angle and relatively flat potential energy surface may explain the presence of disordered configurations.81,87 Alternatively, the marked difference in the tilting propensity of face-to-face and agostic interactions may lead to relatively disordered structures which maximize the former.
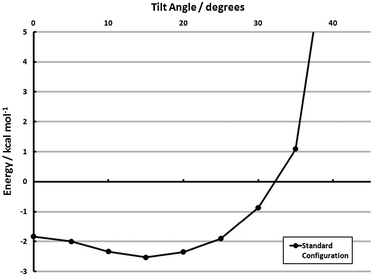 | ||
| Fig. 8 Effect of tilting from vertical for the surface configuration model (MP2/aug-cc-pVDZ) of Θ = 1 (Standard). See section 3.3 for explanation of models. | ||
The key quantities of interest, however, in determining the uniformity of a monolayer are (1) the cohesive energies presented in Table 2, (2) quantitative measures of the adsorbate’s ability to tilt/rotate, and (3) the barriers connecting the configurations in Table 2/Fig. 7. The first has already been presented, and the second is available. The barrier to out-of-plane tilt is given in ref. 60. A PDI-on-Au structure with a 41° tilt is only 0.9 kcal mol−1 higher in energy than the vertical configuration, and a 21°-tilted structure is isoenergetic with its vertical counterpart. Thus, the cohesive energy of the adsorbate–adsorbate interactions must be strong enough to offset the thermal anisotropy if an ordered monolayer is to be formed. Simply put, the per-monomer interaction energies depicted in Table 2—particularly those computed with the SCS(MI) model—are not strong enough to overcome these fluctuations. The Standard configuration, for example, when including this PDI–Au tilting specificity, is roughly isoenergetic at both vertical and tilted configurations (see Fig. 8). Thus, the main conclusion from these models is that, while certain monolayer structures are favored over others (a fact found only with electron correlation), the magnitude of the cohesive energy of these monolayers is insufficient to form an ordered array. This result is consistent with several experimental findings.81,87
3.4 Increasing dispersion
The RAIRS results of ref. 16, 81 and 87 imply that the degree of order in SAMs of organic isocyano complexes may be increased significantly by increasing the number of phenyl rings in the conjugated complex. The electron transport properties of these larger systems warrant further investigation, but from the standpoint of the monolayer alone, significant improvement in the uniformity of the monolayer may be achieved. The authors of ref. 81 considered the series consisting of PDI (CN–Ph–NC), BPDI (CN–Ph–Ph–NC), and TPDI (CN–Ph–Ph–Ph–NC). By BPDI, the gap between the two metal-bound isocyano vibrational peaks had sufficiently reached the baseline, indirectly indicating a larger degree of order. Slightly more resolution between the peaks was achieved with TPDI.The previous sections have indicated that several competing factors influence monolayer morphology, but an interesting question involves the quantitative degree to which additional phenyl rings influence the magnitude of the interaction. As a simple assessment of this question, frozen-monomer sandwich curves (analogous to those in section 3.2.1) were constructed for the PDI/BPDI/TPDI series, using CP-corrected aug-cc-pVDZ and planar, frozen monomers. (Gas-phase BDPI and TPDI, like biphenyl, are non-planar and adopt a twist between the phenyl rings. Indirect evidence exists that the planar configuration, however, is adopted in monolayers.88 The additivity results presented below should not strongly be affected in either case.) These results, in the vicinity of the vdW minimum, are shown in Fig. 9.
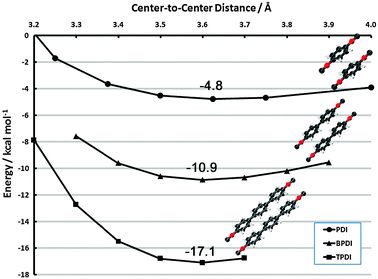 | ||
| Fig. 9 Face-to-face frozen monomer curves in the vicinity of the vdW minimum for PDI, BPDI and TPDI. Results are CP-corrected DB-RI-MP2/aug-cc-pVDZ. | ||
The additive nature of dispersion from the phenyl rings is clearly evident. In the vicinity of 3.6 Å for each complex, the minimum binding energies are −4.8, −10.9, and −17.1 kcal mol−1 for PDI, BPDI, and TPDI, respectively. (A full structural optimization of (BPDI)2, possible with dual-basis aug-cc-pVDZ, shows a minimum at 3.39 Å but is only 0.3 kcal mol−1 lower in energy than the frozen-monomer structure). Thus, each subsequent phenyl ring adds approximately 6 kcal mol−1 of stabilizing dispersion. This contribution is noticeably more than the interaction in benzene dimer, for example. We attribute this fact to two sources. First, the π system is delocalized over the entire phenyl ring system in these cases, whereas benzene dimer possesses terminal hydrogen atoms. Second, the face-to-face dispersion is further enhanced by face-to-neighboring-face interactions. The sandwich curves in section 3.2.1 indicate extremely long-range interactions, and the neighboring ring is well within this distance. This qualitative behavior has been observed previously in naphthalene dimer.78,89–91 The latter interaction could potentially be perturbed in non-planar BPDI/TPDI units (or, alternatively, drive them toward planarity in the dimer). Since we anticipate that this effect will be small, we reserve an investigation of its effect for future work.
Other potential energy curves (spin, tilt, etc.) were not computed for these larger complexes. This preliminary analysis, however, confirms that the magnitude of dispersion in BPDI and TPDI should be more than sufficient to lock the monolayers into stable configurations, as observed experimentally.81
4. Conclusions
A thorough investigation of the PDI dimer has been performed, utilizing recently developed dual-basis RI-MP2 methodology with very large basis sets. Several stable dimer configurations were found, all of which bind more strongly than the benzene dimer in similar configurations. The structures are dictated by a delicate balance of dispersion and electrostatics, and the strength of the resulting interactions is notably basis set dependent. Only one structure is bound with HF and DFT, indicating the strong contribution of dispersion and the need for correlated-electron methodologies. The most strongly bound structure is a rotated-parallel structure with favorable electrostatics and dispersion; this structure is bound nearly three times as strongly as the benzene dimer. The source of this pronounced binding is additional dispersion contributions from the delocalized π system on the isocyano ligands. The same dispersion contribution was seen in monosubstituted benzene dimers,8,9 but, to our knowledge, the much stronger effect of π–π interactions between substituents has not been explored. This structural motif is, therefore, likely in many para-disubstituted benzenes with polar substituents; the analogous structures for non-polar substituents, however, where competing electrostatic effects are weak, require further study. Unlike benzene dimer, the PDI dimer exhibits significant conformational specificity, particularly between parallel-displaced and T-shaped structures. This specificity is achieved through ligand substitution, whereas similar results in unsubstituted systems have required additional aromatic rings.The merit of exploring prototypical systems, however, is their transferability to more complex systems of interest. By computing potential energy curves in surface monolayer configurations, as well as pairwise interaction models, the cohesive energy among PDI adsorbates was estimated. Though bound, the strength of the interactions was found to be low. The geometric restriction to binding sites on the surface diminishes the interaction energy to well below the binding energies of the optimized dimer structures, even when PDI’s propensity toward a non-vertical tilt is taken into account. Such a result underscores the importance of calculations in monolayer configurations, as opposed to free-dimer optimizations. The magnitude of the interaction between adsorbates, however, was found to increase dramatically with additional phenyl rings in the adsorbate, implying the larger degree of monolayer order seen experimentally. These larger adsorbates are also predicted to tilt, consistent with experimental findings on similar systems.16
The models presented herein neglect the interaction with the metal surface but are reasonably justified based on upon previous DFT studies of the PDI–Au interaction. These models will not be transferable to small adsorbates when the metal’s perturbation of the electronic structure is significant, such as small alkane-thiols. For weakly-bound or large adsorbates, however, such as PDI or long alkane-thiols, these models appear reasonable. Simply put, DFT is currently the method of choice for describing the interaction of an adsorbate with a metal surface. MP2 performs poorly for these systems, where orbital spacings are extremely small.92 Conversely, correlated-electron theories are currently required for a description of the dispersion between adsorbates, a property predicted qualitatively wrong by many current DFT functionals (although recent progress37,93–97 in this area is quite promising). This work has focused wholly on the latter property. An accurate, computationally inexpensive method capturing both properties is still lacking, which is the motivation for a simple, modelistic treatment. Further refinement of the models to include conformational (tilt/twist) DFT calculations in surface configurations are suggested, in order to provide estimates of the configurational flexibility of the surface.
Acknowledgements
R.P.S. thanks Alex Sodt for Q-Chem-to-VMD conversion scripts. Funding for this work has been provided by the National Science Foundation under Grant No. CHE-0535710 (R.P.S., R.A.D., and M.H.-G.), as well as DOE/BES Grant DE-FG02-06ER46262 (Y.L. and G.G.). M.H.-G. is a part owner of Q-Chem, Inc.References
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2004, 108, 10200–10207 CrossRef CAS.
- M. O. Sinnokrot, E. F. Valeev and C. D. Sherrill, J. Am. Chem. Soc., 2002, 124, 10887–10893 CrossRef CAS.
- Y. C. Park and J. S. Lee, J. Phys. Chem. A, 2006, 110, 5091–5095 CrossRef.
- R. Podeszwa, R. Bukowski and K. Szalewicz, J. Phys. Chem. A, 2006, 110, 10345–10354 CrossRef CAS.
- J. G. Hill, J. A. Platts and H. J. Werner, Phys. Chem. Chem. Phys., 2006, 8, 4072–4078 RSC.
- R. A. DiStasio, G. von Helden, R. P. Steele and M. Head-Gordon, Chem. Phys. Lett., 2007, 437, 277–283 CrossRef.
- T. Janowski and P. Pulay, Chem. Phys. Lett., 2007, 447, 27–32 CrossRef CAS.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2003, 107, 8377–8379 CrossRef CAS.
- M. O. Sinnokrot and C. D. Sherrill, J. Am. Chem. Soc., 2004, 126, 7690–7697 CrossRef CAS.
- A. L. Ringer, M. O. Sinnokrot, R. P. Lively and C. D. Sherrill, Chem.–Eur. J., 2006, 12, 3821–3828 CrossRef CAS.
- T. Yokoyama, S. Yokoyama, T. Kamikado, Y. Okuno and S. Mashiko, Nature, 2001, 413, 619–621 CAS.
- I. Feinstein-Jaffe, F. Frolow, L. Wackerle, A. Goldman and A. Efraty, J. Chem. Soc., Dalton Trans., 1988, 469–476 RSC.
- M. J. Irwin, G. Jia, J. J. Vittal and R. J. Puddephatt, Organometallics, 1996, 15, 5321–5329 CrossRef CAS.
- J. Guo and A. Mayr, Inorg. Chim. Acta, 1997, 261, 141–146 CrossRef CAS.
- Y. Yamamotoa, H. Suzuki, N. Tajima and K. Tatsumi, Chem.–Eur. J., 2002, 8, 372–379 CrossRef.
- J. J. Stapleton, T. A. Daniel, S. Uppili, O. M. Cabarcos, J. Naciri, R. Shashidhar and D. L. Allara, Langmuir, 2005, 21, 11061–11070 CrossRef CAS.
- M. D. Porter, T. B. Bright, D. L. Allara and C. E. D. Chidsey, J. Am. Chem. Soc., 1987, 109(12), 3559–3568 CrossRef CAS.
- C. D. Bain, E. B. Troughton, Y. T. Tao, J. Evall, G. M. Whitesides and R. G. Nuzzo, J. Am. Chem. Soc., 1989, 111(1), 321–335 CrossRef CAS.
- S. Tsuzuki, K. Honda, T. Uchimaru and M. Mikami, J. Chem. Phys., 2006, 124(11), 114304 CrossRef.
- A. Goursot, T. Mineva, R. Kevorkyants and D. Talbi, J. Chem. Theory Comput., 2007, 3(3), 755–763 CrossRef CAS.
- J. Chen, W. Wang, J. Klemic, M. A. Reed, B. W. Axelrod, D. M. Kaschak, A. M. Rawlett, D. W. Price, S. M. Dirk, J. M. Tour, D. S. Grubisha and D. W. Bennett, Ann. N.Y. Acad. Sci., 2002, 960, 69–99 CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- S. Kristyàn and P. Pulay, Chem. Phys. Lett., 1994, 229, 175–180 CrossRef CAS.
- D. C. Langreth and J. P. Perdew, Phys. Rev. B: Condens. Matter, 1980, 21, 5469–5493 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter, 1986, 33, 8800–8802 CrossRef.
- J. P. Perdew, Phys. Rev. B: Condens. Matter, 1986, 33, 8822–8824 CrossRef.
- J. P. Perdew, Phys. Rev. B: Condens. Matter, 1986, 34, 7406 CrossRef.
- D. C. Langreth and M. J. Mehl, Phys. Rev. B: Condens. Matter, 1983, 28, 1809–1834 CrossRef CAS.
- D. C. Langreth and M. J. Mehl, Phys. Rev. B: Condens. Matter, 1984, 29, 2310 CrossRef.
- R. Ahlrichs, R. Penco and G. Scoles, Chem. Phys., 1977, 19, 119–130 CrossRef CAS.
- X. Wu, M. C. Vargas, S. Nayak, V. Lotrich and G. Scoles, J. Chem. Phys., 2001, 115(19), 8748–8757 CrossRef CAS.
- Q. Wu and W. Yang, J. Chem. Phys., 2002, 116(2), 515–524 CrossRef CAS.
- P. Jurecka, J. Cerný, P. Hobza and D. R. Salahub, J. Comput. Chem., 2007, 28(2), 555–569 CrossRef CAS.
- P. Hobza and C. Sandorfy, J. Am. Chem. Soc., 1987, 109, 1302–1307 CrossRef CAS.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 5287–5293 RSC.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639 CrossRef CAS.
- C. Møller and M. Plesset, Phys. Rev., 1934, 46, 618 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Ohm, M. Heiser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283 CrossRef CAS.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143 CrossRef CAS.
- M. Feyereisen, G. Fitzgerald and A. Komornicki, Chem. Phys. Lett., 1993, 208, 359 CrossRef CAS.
- Y. Jung, A. Sodt, P. M. W. Gill and M. Head-Gordon, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6692 CrossRef CAS.
- P. Hobza, H. L. Selzle and E. W. Schlag, Chem. Rev., 1994, 94, 1767–1785 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2003, 118(20), 9095–9102 CrossRef CAS.
- J. Antony and S. Grimme, J. Phys. Chem. A, 2007, 111(22), 4862–4868 CrossRef CAS.
- R. A. DiStasio, Jr and M. Head-Gordon, Mol. Phys., 2007, 105, 1073–1083 CrossRef CAS.
- T. Takatani and C. D. Sherrill, Phys. Chem. Chem. Phys., 2007, 9, 6106–6114 RSC.
- R. C. Lochan, Y. Shao and M. Head-Gordon, J. Chem. Theory Comput., 2007, 3, 988–1003 CrossRef CAS.
- Y. Jung, Y. Shao and M. Head-Gordon, J. Comput. Chem., 2007, 28, 1953–1964 CrossRef CAS.
- R. C. Lochan and M. Head-Gordon, J. Chem. Phys., 2007, 126, 164101 CrossRef.
- Y. M. Rhee and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 5314–5326 CrossRef CAS.
- W.-Z. Liang and M. Head-Gordon, J. Phys. Chem. A, 2004, 108(15), 3206–3210 CrossRef CAS.
- R. P. Steele, R. A. DiStasio, Jr, Y. Shao, J. Kong and M. Head-Gordon, J. Chem. Phys., 2006, 125(7), 074108 CrossRef.
- K. Wolinski and P. Pulay, J. Chem. Phys., 2003, 118(21), 9497–9503 CrossRef CAS.
- R. P. Steele, Y. Shao, R. A. DiStasio and M. Head-Gordon, J. Phys. Chem. A, 2006, 110(51), 13915–13922 CrossRef CAS.
- R. A. DiStasio, Jr, R. P. Steele and M. Head-Gordon, Mol. Phys., 2007, 105, 2731–2742 CrossRef.
- T. Nakajima and K. Hirao, J. Chem. Phys., 2006, 124(18), 184108 CrossRef.
- R. P. Steele and M. Head-Gordon, Mol. Phys., 2007, 105(19), 2455–2473 CrossRef CAS.
- Y. Li, D. Lu, S. A. Swanson, J. C. Scott and G. Galli, J. Phys. Chem. C, 2008, 112, 6413 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS.
- R. P. Steele, R. A. DiStasio, Jr and M. Head-Gordon, J. Chem. Theory Comput., 2009, 5, 1560–1572 CrossRef CAS.
- Y. Shao, L. Fusti-Molnar, Y. Jung, J. Kussmann, C. Oschsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O’Neill, R. A. DiStasio, Jr, R. C. Lochan, T. Want, G. J. O. Beran, N. A. Besley, J. M. Herbert, C. Y. Lin, T. V. Voorhis, S. H. Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. M. Rhee, J. Ritchie, E. Rosta, C. D. Sherrill, A. C. Simmonett, J. E. Subotnik, H. L. W. III, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer III, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 3172 RSC.
- P. Pulay, Chem. Phys. Lett., 1980, 73, 393 CrossRef CAS.
- P. Pulay, J. Comput. Chem., 1982, 3, 556 CrossRef CAS.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116(8), 3175–3183 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243 CrossRef CAS.
- S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Phys. Chem. A, 1999, 103, 8265–8271 CrossRef CAS.
- M. L. Leininger, I. M. B. Nielsen, M. E. Colvin and C. L. Janssen, J. Phys. Chem. A, 2002, 106, 3850–3854 CrossRef CAS.
- P. Jurecka and P. Hobza, Chem. Phys. Lett., 2002, 365, 89–94 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef.
- J. Stone, An Efficient Library for Parallel Ray Tracing and Animation Master’s thesis, Computer Science Department, University of Missouri-Rolla, 1998 Search PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, USA, 2001 Search PubMed.
- M. Colapietro, A. Domenicano, G. Portalone, I. Torrini, I. Hargittai and G. Schultz, J. Mol. Struct., 1984, 125, 19–32 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
- S. Tsuzuki, T. Uchimaru and M. Mikami, J. Phys. Chem. A, 2006, 110, 2027–2033 CrossRef CAS.
- R. A. DiStasio, Jr, R. P. Steele, Y. M. Rhee, Y. Shao and M. Head-Gordon, J. Comput. Chem., 2007, 28, 839 CrossRef.
- N. K. Lee, S. Park and S. K. Kim, J. Chem. Phys., 2002, 116(18), 7910–7917 CrossRef CAS.
- A. Heikkilä and J. Lundell, J. Phys. Chem. A, 2000, 104, 6637–6643 CrossRef.
- I. Alkorta, I. Rozas and J. Elguero, Theor. Chem. Acc., 1998, 99, 116–123 CrossRef CAS.
- S. A. Swanson, R. McClain, K. S. Lovejoy, N. B. Alamdari, J. S. Hamilton and J. C. Scott, Langmuir, 2005, 21, 5034–5039 CrossRef CAS.
- J. J. Stapleton, P. Harder, T. A. Daniel, M. D. Reinard, Y. X. Yao, D. W. Price, J. M. Tour and D. L. Allara, Langmuir, 2003, 19, 8245–8255 CrossRef CAS.
- E. Barrena, C. Ocal and M. Salmeron, J. Chem. Phys., 2001, 114(9), 4210–4214 CrossRef CAS.
- P. Ghorai and S. Glotzer, J. Phys. Chem. C, 2007, 111(43), 15857–15862 CrossRef CAS.
- J. I. Henderson, S. Feng, T. Bein and C. P. Kubiak, Langmuir, 2000, 16, 6183–6187 CrossRef CAS.
- S. M. Gruenbaum, M. H. Henney, S. Kumar and S. Zou, J. Phys. Chem. B, 2006, 110, 4782–4792 CrossRef CAS.
- S. Kim, K. Ihn, T. Kang, S. Hwang and S. Joo, Surf. Interface Anal., 2005, 37, 294–299 CrossRef CAS.
- A. N. Caruso, R. Rajesh, G. Gallup, J. Redepenning and P. A. Dowben, J. Phys. Chem. B, 2004, 108, 6910–6914 CrossRef CAS.
- S. Tsuzuki, K. Honda, T. Uchimaru and M. Mikami, J. Chem. Phys., 2004, 120(2), 647–659 CrossRef CAS.
- C. Gonzalez and E. C. Lim, Chem. Phys. Lett., 2000, 322, 382–388 CrossRef CAS.
- T. R. Walsh, Chem. Phys. Lett., 2002, 363, 45–51 CrossRef CAS.
- G. Frenking, I. Antes, M. Bŏhme, S. Dapprich, A. W. Ehlers, V. Jonas, A. Neuhaus, M. Otto, R. Stegmann, A. Veldkamp and S. F. Vyboischikov, Reviews in Computational Chemistry, VCH, New York, 1996, vol. 8 Search PubMed.
- T. Thonhauser, A. Puzder and D. C. Langreth, J. Chem. Phys., 2006, 124, 164106 CrossRef CAS.
- T. Thonhauser, V. R. Cooper, A. P. S. Li, P. Hyldgaard and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125112 CrossRef.
- A. Puzder, M. Dion and D. C. Langreth, J. Chem. Phys., 2006, 124, 164105 CrossRef.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Potential energy surfaces, PDI surface models and Cartesian coordinates. See DOI: 10.1039/b902194a |
| ‡ Current address: Department of Chemistry, Yale University, New Haven, CT 06520, USA |
| § Note that the work in ref. 60 utilized the DFT-D parameterization of ref. 98. A preliminary analysis indicates that the more recent parameterization of ref. 99 exhibits stronger binding energies for this system. |
| This journal is © the Owner Societies 2010 |
