Scoring the sum of correlated results in analytical proficiency testing

Abstract

In proficiency tests the participants' results are usually converted into scores. In some schemes the participants are required to report the sum of the concentrations of a number of analytes and this total also is converted into a score. In such instances the scoring procedure for the total should be mathematically consistent with that for the separate analytes. When these analytes are determined from a single test portion, however, the errors in the results from a participant are likely to be correlated because some stages of the analysis are common to all of the analytes. For a consistent outcome, the scoring method must take account of such correlation.

---

Scoring in proficiency tests

Proficiency testing comprises the regular distribution of typical test materials for blind analysis by the participants in the scheme, using their routine methods.¹ Its primary purpose is to enable participant laboratories to judge the success of their analytical systems in terms of fitness for purpose. Participation in an appropriate scheme is now mandatory for accreditation.

In a round of a proficiency test, most scheme providers convert a participant's analytical result x into a z-score given by z = (x − x_A)/σ_p, where the assigned value x_A is the provider's best estimate of the true value. The assigned value is usually taken as the consensus of all of the participants' results, often a robust mean. The standard deviation for proficiency σ_p in a round—informally called the ‘target value’—is preferably a prescribed uncertainty that characterises fitness for purpose in the appropriate analytical sector.¹ It is important to emphasise, for the purposes of the following discussion, that such a target value is not designed to characterise the participants' results but to specify in advance the required performance—it is independent of the participants' results. This σ_p value is predetermined by the scheme provider and available to the participants at the time of analysis.

Correlation in results

When a number of analytes are determined from a single test portion, many stages of the analytical method are common to all of the analytes. Variation in procedure at these stages will affect the results of all of the analytes similarly. In a proficiency test that circumstance gives rise to a correlation among the errors in participant's results for the analytes. This is not a problem per se because the i-thanalyte is scored separately according to its individual target value σ_p(i).

In some instances, however, legislation or custom requires laboratories to report the total concentration of a group of analytes, “total aflatoxins” for example, as well as the individual concentrations. For the purposes of proficiency testing the total concentration should then be scored as well. However, the target value for the total concentration should be mathematically consistent with the target values used for the individual analytes. Were that not the case, a participant could conceivably receive ‘satisfactory’ z-scores for all of the individual analytes but an ‘unsatisfactory’ z-score for the total concentration. (‘Satisfactory’ and ‘unsatisfactory’ are used non-pejoratively as informal labels for the conditions |z| < 2 and |z| > 3 respectively.)

A consistent target value for the total σ_p(T) must take account of the covariances² cov_p(i,j) between the analytesi and j, so that

Here, however, the covariances (like the individual σ_p(i)values) have a special prescriptive meaning so cannot be estimated directly from the participants' results. They have to be evaluated from the prescribed individual target values and the observed correlation coefficients r(i, j) between analytesi and j over all participants, via the identity cov_p(i, j) = r(i, j)σ_p(i)σ_p(j). Then the consistent target value for the total concentration is

where σ^T_p = [σσ_pp(1),σσ_pp(2),⋯,σ_p(n)] is the row vector of the n prescribed target values and R is the observed n × n correlation matrix.

In the absence of a knowledge of R, a possible ‘cautious’ approach would be to assume that the analytes are perfectly correlated, that is, with all r(i, j) = 1. Eqn (1) and (2) then reduce to σ^′_p(T) = ∑_iiiσσ_pp(ii). A contrasting expedient, here called ‘naive’, would be to ignore any covariance by assuming that all of the correlation coefficients are zero-valued. The target value for the total concentration is then given by . The discrepancy between these extremes can be substantial, approaching a factor of 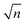when the σ_p values are comparable in magnitude. A poor choice between these extremes could therefore have a potentially serious effect on z-scores for the total concentration.

Example

The data were taken from a single round (identity not disclosed) of a FAPAS³ proficiency test. There were four analytes, aflatoxins B1, B2, G1 and G2, expressed as ppb mass fraction. There were 74 participant laboratories submitting a complete set of results. The four predetermined target values were respectively σ^T_p = [1.03 0.56 0.72 0.37]. The data showed a moderate amount of correlation, with the correlation matrix R as follows

	B1	B2	G1	G2
B1	1.00	0.67	0.38	0.30
B2	0.67	1.00	0.45	0.76
G1	0.38	0.45	1.00	0.18
G2	0.30	0.76	0.18	1.00

The three alternative target values for the total aflatoxins were calculated as:

• consistent σ_p(T) = 2.09;

• ‘cautious’ σ^′_p(T) = 2.68;

• ‘naive’ σ^″_p(T) = 1.42.

The corresponding z-scores for total aflatoxins are shown in Fig. 1. There are substantial differences among the three interpretations. The ‘naive’ method for calculating σ_p(T) identified 12 laboratories with |z| > 3 (i.e., requiring investigative and/or remedial action on the part of the participant) but the ‘cautious’ method identified only four. The consistent method necessarily gave an outcome between these extremes. (Note: in FAPAS the value of σ_p(T) used falls close to ‘cautious’ and thus avoids scores of unduly large magnitude.)

Fig. 1 z-Scores for total aflatoxins calculated by using different estimates of the target value. Each point shows the result from a single participant. Two extreme outliers are not shown.

Conclusions

Proficiency test providers should be aware of a potentially important inconsistency in the target value for the total concentration of a number of analytes if the participants' results are correlated and the covariances not accounted for. The same problem might affect individual participants wanting to construct an ‘overall’ score for a number of analytes.

In these contexts it is important also to be aware that the correlations among a particular suite of analytes may vary considerably from round to round. This is largely determined by the concentrations of the analytes: near detection limits substantial random contributions will almost eliminate any correlations that might predominate at higher concentrations. Because of this circumstance the use of a single ‘global’ estimate of R for successive rounds would probably be inappropriate.

References

1. M. Thompson, S. L. R. Ellison and R. Wood, The International Harmonised Protocol for the Proficiency Testing of Analytical Chemistry Laboratories, Pure Appl. Chem., 2006, 78, 145–196.
2. AMC Technical Briefs, 2008, vol. 30, ISSN 1757 5958, http://www.rsc.org/images/brief%2030_tcm18-119170.pdf.
3. FAPAS Secretariat, Central Science Laboratory, Food and Environment Research Agency, Sand Hutton, York YO41, 1LZ UK.

---