Random packing of model polymers: local structure, topological hindrance and universal scaling

Abstract

The random packing of rigid objects has not only engrossed mathematicians since biblical times but is receiving attention for numerous applications and processes involving microgels, granular media, colloids, glasses, liquids, synthetic polymers and biomolecules. While dense random assemblies of single hard spheres have been extensively investigated both experimentally and theoretically over the past 50 years, it was only recently that analogous problems for chains of hard spheres have been addressed. We highlight the relevance of these recent advances, and describe the most salient characteristics of the “maximally random jammed” state for hard sphere chains. Particular emphasis is placed on the scaling behavior of chain dimensions and topology with packing density. We also discuss the potentially far-reaching implications of an unexpected connection that has been found between entanglements (intermolecular constraints) and knots (of intramolecular origin) regarding their dependence on volume fraction.

---

Manuel Laso

Manuel Laso (MSc UPM 1983, PhD ETH Zürich 1986) has been a professor of Materials Science at the Universidad Politécnica de Madrid since 1995. He has been Privatdozent at ETH Zürich (1996–1999), visiting professor at the Isaac Newton Institute of the University of Cambridge (1996), at the Universität Erlangen-Nürnberg (2004), and is an elected Fellow of the Institute of Physics (2004). His research interests include statistical mechanics of chain molecules, and numerical methods in polymer physics and complex fluids.

Nikos Ch. Karayiannis

Nikos Ch. Karayiannis received his diploma (1997) and PhD (2002) in Chemical Engineering from the University of Patras (Greece). After an internship in BP-Amoco (2002, USA) he continued his research activities as a post-doctoral fellow in ICEHT–FORTH (2002–2005, Greece) and ISOM/ETSII (2006–2008, UPM, Spain). His research interests include simulation studies of synthetic and biological polymer systems through hierarchical modelling approaches.

Katerina Foteinopoulou

Katerina Foteinopoulou studied physics at the University of Patras, Greece (BSc 1997, MSc 1999). She received her PhD in 2005 from the same university in collaboration with ICEHT–FORTH. She is currently working as a postdoctoral researcher at the Universidad Politécnica de Madrid, Spain. Her main research interests include macroscopic simulations of complex flow problems and computational studies of the viscoelastic and rheological properties of polymers.

Marc L. Mansfield

Marc L. Mansfield received a BA in Physics from the University of Utah (1977) and a PhD in Chemistry from Dartmouth College (1980). He was an Assistant Professor of Engineering Materials at the University of Maryland from 1983 to 1985. From 1985 to 1999 he worked as an Associate Research Scientist at the Michigan Molecular Institute in Midland, Michigan. Since 1999 he has been a Professor in the Department of Chemistry and Chemical Biology, Stevens Institute of Technology, Hoboken, New Jersey, USA. His research interests include the theory and modelling of transport properties of macromolecules and nanoparticles and topological effects in macromolecular conformation and dynamics.

Martin Kröger

Martin Kröger studied mathematics and physics (1985–1991), and received a PhD in Theoretical Physics (1994) from the Technical University of Berlin (TUB). He was senior scientist at TUB (1995–2003) and ETH Zurich (1997–2005), and invited professor at the Universities of Metz (1995) and Strasbourg (1996). He is currently Professor for Computational Polymer Physics at the ETH Zurich (since 2006). His research focuses on coarse-grained models for complex liquids, stochastic differential equations, computational physics, applied mathematics, and statistical physics of anisotropic fluids.

---

1. Introduction

The random packing of objects has received a great deal of attention since early historical times. How spheres, whether oranges or molecules, stack up when poured randomly into a vessel is an intriguing problem with a wide range of practical applications. Scientists have long accepted the notion that, given enough stirring and shaking, a random assembly of particles always settles to a maximum density, a state somewhat loosely defined as random close packing (RCP). Bernal and Finney et al.^1,2 performed an outstanding series of classical experiments in the 1960s (see Fig. 1) that gave the initial impetus for an uninterrupted series of advances in the understanding of dense random packing, and in the analysis and characterization of the RCP state.

Fig. 1 Photograph of a ball-and-spoke model or irregular structure constructed by Bernal⁵¹ to be as “irregular as possible” using spokes of lengths 2.75 to 4.0 inches in proportions roughly the same as those observed in liquid distribution functions. Spokes of different length are distinguished by colors in the printed version of the original article. Our current article focuses on randomly packed chains of tangent hard spheres, which are unfortunately more difficult to visualize this way (see Fig. 2a), where two of the spokes per ball have been converted into bonds. Reprinted with permission from ref. 51. Copyright 1959 Macmillan Publishers Ltd.

Although the statement of the random close packing problem seems to be simplicity itself (loosely speaking: “put together an arbitrarily large number of identical spheres as compactly and as randomly as possible”), it is remarkable that even the definition of RCP was recently revised by Torquato et al.,³ and replaced by the more rigorous statistical–mechanical definition of the maximally random jammed (MRJ) state. According to Torquato et al.³ a particle is jammed in a structure when it cannot be moved if the positions of all other particles in the system are fixed. The opposite of a jammed particle (i.e. a freely roaming, caged particle) is denoted as a “rattler”.³ Consequently, an ideal (infinitely sized) random packing is considered as jammed if all of its hard spheres are jammed. In practice, computer-generated MRJ structures are of finite size and unavoidably contain a very small fraction of “rattlers”, their amount being protocol dependent.³

Given that more than four centuries passed between Kepler's conjecture about the densest regular packing (that of the face-centered cubic) and its mathematical proof by Hales,⁴ it is not surprising that the determination of the volume fraction φ occupied by the spheres at the MRJ state remains to this day refractory to analytical approaches. The missing proof notwithstanding, both experiments and computer simulations have converged on a widely accepted value of φ ≃ 0.64 for single spheres at the MRJ state,^2,3,5–8 while the densest possible ordered packing of monodisperse spheres has a volume fraction of . In spite of the dearth of analytical results, work on dense random assemblies has progressed significantly, and has also been extended to non-spherical objects,⁹ to frictionless particles,¹⁰ to mixtures of dissimilar spheres,¹¹ and to packing in higher dimensions.^5,12 This extensive body of knowledge has found widespread application in the physics of amorphous and granular materials, colloids, biology, perturbation theory in thermodynamics, and even in communication theory, among others.^1,3,13,14

Compared with random packing of single spheres, very little attention has been devoted to the investigation of dense assemblies of freely-jointed chains of tangent hard spheres, although they are considered as the second type of ideal amorphous solids,^15,16assemblies of hard spheres being the ideal amorphous solids of the first kind. In spite of chains of hard spheres being the simplest and most fundamental model system for synthetic and biological polymers, neither experiments nor simulations to determine their density and structure at their MRJ state had been forthcoming. This situation was due, on the one hand to the difficulty of constructing laboratory mechanical models, and on the other hand to the computational complexity of generating MRJ structures of chains of hard spheres. It was only very recently that the problem of determining the MRJ state of chain molecules could be solved through extensive Monte Carlo (MC) simulations.¹⁷ While very large (up to a million spheres) systems of dense random packing of single hard spheres can be generated almost routinely nowadays,¹⁸ the determination of the MRJ state for hard sphere chains requires the combined use of several advanced off-lattice MC algorithms¹⁹ in order to efficiently sample their configuration space (see Fig. 2a and 2b for representative configurations of hard sphere chain systems near the MRJ state).

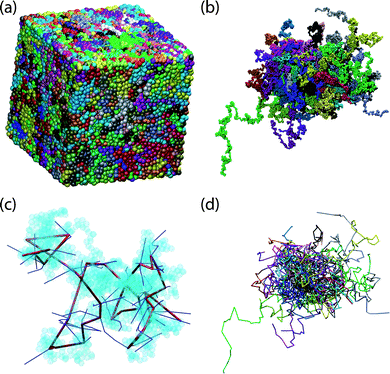Fig. 2 Clockwise starting from top left: representative configuration of a 54-chain, hard sphere system of molecular length N = 1000 in the vicinity of the MRJ state, with coordinates of sphere centers (a) wrapped, subject to three-dimensional periodic boundary conditions and (b) fully unwrapped in space. (c) An arbitrary selected single chain of high knotting complexity (10.153)⁴⁴ with constituent sites shown as transparent spheres. Also shown is the corresponding primitive path, and segments of other primitive paths with which it is entangled (see also Fig. 7). (d) The underlying primitive path network, after application of the Z1 topological algorithm (see also ref. 35 and Fig. 5), with entanglement coordinates unwrapped in space. Image created using the VMD software.⁵²

2. The maximally random jammed state of hard sphere chains

Thanks to the MC scheme described in detail in ref. 19, it has been possible to generate configurations and to accurately determine the local structure and dimensions of freely-jointed chains of tangent hard spheres in the entire range of volume fractions up to the MRJ state. The MC protocol is built around: (i) modified versions of chain connectivity altering moves²⁰ tailored to provide rapid long range equilibration even in the vicinity of the MRJ state and (ii) localized moves all executed in an adaptive¹⁹ configurational bias (CB)²¹ pattern, where the number of trial configurations strongly depends on packing density.¹⁹ The approach consists of two stages: first, starting from a very dilute system MC simulations are conducted with the aforementioned mix of moves and at regular intervals shrinkages of the simulation cell are attempted until the box reaches the desired volume.¹⁹ The amplitude of the attempted box reduction depends strongly on packing density. Finally, long trajectories of statistically uncorrelated representative multi-chain configurations are produced through extensive MC simulations (of the order of 10¹¹ steps) under constant volume.¹⁹

Since the computational efficiency of the MC algorithm in equilibrating the long range system characteristics is affected by neither the average molecular length N, nor the packing density φ,¹⁹ it was possible to simulate from relatively short oligomers (N = 12) all the way into the asymptotic, infinite chain regime (N = 1000). As a consequence, conclusive evidence has been collected about generic features such as the MRJ state,¹⁷ the universal scaling of chain dimensions^22,23 and underlying topology²³ with packing density, and the evolution of local ordering²⁴ with increasing packing density. To start with, it was found that hard sphere chains reach their MRJ state at the same volume fraction as the packings of single spheres do (within statistical uncertainty) φ^MRJ ≈ 0.638 ± 0.004, regardless of chain length.¹⁷ As shown in Fig. 3, in the vicinity of the MRJ φ^*,marg(N) ∝ φ^*,marg_∞(1 + O(N⁻¹)) state the pair radial distribution function g(r) of chain systems closely resembles that of single sphere ones, although the double tangency condition has a small but noticeable effect especially at distances close to the sphere diameter (r = 1). While it is trivial to prove that φ^MRJ for chains cannot be higher than for single spheres,† a rigorous proof of the equality φ^MRJ_{single spheres} = φ^MRJ_chains, although tantalizingly close,‡ is still missing. The MRJ state for chain molecules is characterized by the system becoming jammed, in the sense that the proportion of inner spheres§ that are able to perform an arbitrarily small “flip” move without either incurring overlaps with other spheres, or violating the connectivity of the chains, is very small (less than 1%). The inset of Fig. 3 shows vividly how the fraction of “flipper” spheres (i.e. spheres that are able to perform small displacements subject to the constraints discussed above) declines sharply as the MRJ state is approached, in a way similar to that of “rattlers”³ for single hard spheres. This precipitous drop is the hallmark, and the accepted “signature” of jamming. The question is thus settled that neither chain length nor the tangency/connectivity constraint, which were responsible in the past for the computational intractability, hinder the packing of chains with respect to single spheres. Fig. 2a gives an illustrative impression of the extreme packing conditions at the MRJ state, and highlights the difficulty of devising efficient configuration–sampling algorithms.

Fig. 3 Radial distribution function g(r), for hard sphere chains and single hard spheres in the vicinity of the MRJ state. Inset: percentage of “flipper” hard spheres as a function of packing density. For the definition of “flipper” spheres see definition in text.

Local ordering was investigated through the characteristic crystallographic element (CCE) norm, a descriptor which is sensitive both to radial and orientational deviations from perfect local order and remains strictly discriminating between different, competing crystal structures.^17,24 The order analysis based on the CCE norm revealed that, at the MRJ state, the portion of sites with either HCP-like (hexagonal close packed) or FCC-like (face-centered cubic) local environment is very small (less than 4% in total).^17,26 It was also found that the mean coordination number for hard sphere chain packing at the MRJ state equals 6 (2d, where d is the dimensionality of the simulated system)²⁶ as expected from the isostatic condition and in agreement with the simulations by Donev et al.^3a on monatomic hard sphere jammed analogs.

3. Universal scaling behavior of chain dimensions

Chain connectivity is the key distinguishing feature of model polymers with respect to single spheres. It endows dense systems of chains of hard spheres with a rich structure and physical behavior. In addition, thanks to the simplicity of their geometry and of the potential interactions, hard sphere chains display universal features with maximal clarity. In this respect, the MC numerical experiments reported in ref. 17, 22 and 23, have shown that hard sphere chains are the first polymer system for which the full range of universal static scaling laws^27,28 can be observed as packing density φ increases up to the MRJ state. The exploration of the entire volume fraction range 0 ≤ φ ≤ φ^MRJ has revealed that chain dimensions display four clearly distinct scaling behaviors with increasing φ. These four regimes, often described as “dilute”, “semi-dilute”, “marginal”, and “concentrated”, are characterized by a regime-specific power dependence of chain size on volume fraction as displayed in Fig. 4. Chain stiffness is quantified through the characteristic ratio defined as C_N = <R²>/(N − 1)l² where <R²> is the mean square end-to-end distance and l is the bond length, equal to the sphere diameter. The log–log plot of C_Nvs. φ in Fig. 4 allows the universal exponents to be read off directly. The values found in the four regimes (0.0 ± 0.1, −0.23 ± 0.003, −1.0 ± 0.1, and 0.0 ± 0.1 respectively)²³ fully confirm theoretical predictions and experimental findings of 0.0 (dilute),^27–29 −0.23 (semi-dilute),^27,28,30 −1.0 (marginal),²² and 0.0 (concentrated).^22,29,30 Furthermore, the established equality φ^MRJ_{single spheres} = φ^MRJ_chains for single spheres and for hard sphere chains at the MRJ state has also allowed a correspondence to be established between configurations of single spheres and configurations of chains.²² This correspondence can be exploited by means of graph theoretical methods to predict the crossover volume fractions between the high concentration regimes. Both the marginal to concentrated φ^*,conc, and semi-dilute to marginal φ^*,marg crossovers are predicted to be chain independent to leading order, with N⁻¹ corrections:²²

φ^*,conc(N) ∝ φ^*,conc_∞(1 + O(N⁻¹))

with:

φ^*,conc_∞ ≃ 0.59; φ^*,marg_∞ ≃ 0.32 (2)

in agreement with the values shown in Fig. 4. It is remarkable how faithfully the full range of expected behaviors is captured by this simplest possible molecular model. Although the first order behavior of φ^*,conc and φ^*,marg had been conjectured qualitatively,³⁰ it is the identification of the MRJ state for hard sphere chains that has made it possible to determine the exact forms of eqn (1) and (2) including prefactors and coefficients.

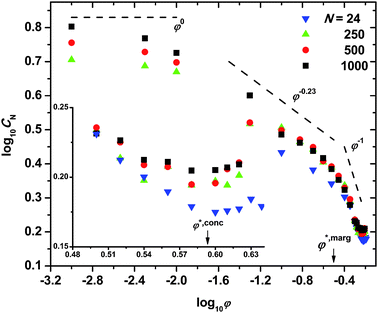Fig. 4 Double logarithmic plot of the characteristic ratio C_N, as a function of packing density, φ. Lines with characteristic slopes are drawn as a guide to the eye. Inset: logarithm of characteristic ratio versus (linear) volume fraction in the marginal and concentrated regimes. φ^*,marg and φ^*,conc mark the predicted²² crossovers for the transitions from semi-dilute to marginal, and from marginal to concentrated regimes, respectively.

4. Topological constraints: entanglements and knots

A great deal of the unique dynamical and rheological behavior of polymers stems from the uncrossability of chains,³¹ which has been traditionally analyzed in terms of “entanglements”, the heart of modern theories of polymer dynamics.^27,32,33 In parallel to the vast number of theoretical and experimental approaches, efficient computational algorithms have been recently developed by various groups in order to calculate the interchain topological constraints (entanglements) and the corresponding primitive paths.^34–38 The primitive path (PP) of a polymer chain immersed in a sea of obstacles (e.g. other chains) is defined as the shortest path connecting the ends of the chain that does not violate the topological constraints (uncrossability) imposed on it, and whose length strictly and continuously decreases during the minimization process. For a multi-chain system the primitive path is the shortest multiply disconnected path. Everaers and coworkers.³⁴ recently showed that the above definition of the primitive path agrees with the entanglement density that yields the experimentally observed value of the plateau modulus. It has also been established that all different topological algorithms based either on the original annealing process^34,36,37 or on the more recent (direct³⁵ or stochastic³⁸) geometric approaches provide very similar results for the underlying primitive path topology and entanglement statistics.

The extreme simplicity of hard sphere chains makes them an ideal statistical mechanics model on which to analyze universal entanglement behavior.²³ In particular, the analysis of primitive path networks as a representation of states of polymers from solutions to jammed amorphous solids is an area of great current relevance. In our work, primitive paths were extracted from the corresponding hard sphere chains by means of the state-of-the-art Z1 algorithm.³⁵ This algorithm solves the problem of the shortest multiple disconnected path by minimizing the Euclidean length, subject to constraints arising from the initial (parent) state. Alternative approaches for the determination of the primitive path had been explored in ref. 39. By transforming the Doi–Edwards³² physical concept of entanglements into a minimization problem, the Z1 algorithm provides an approximate but still accurate geometrical solution. The code uses kinks originally located at particle positions that tend to diminish during the length minimization process; it operates at an optimum “time step” and uses a self-adapting grid to speed up computations. Upon convergence of the minimization procedure (when the total contour length of the primitive paths does not decrease between successive iterations) the number of entanglements equals the number of interior kinks of the shortest path. The schematic representation of the algorithmic procedure implemented in the Z1 code is shown in Fig. 5. Fig. 2 further shows the transformation through the topological algorithm of the parent hard sphere chains (Fig. 2b) to the corresponding primitive paths (Fig. 2d).

Fig. 5 Schematic representation of the extraction of primitive paths from the parent atomistic chain as incorporated in the Z1 algorithm.³⁵ Top: original configurations where the primitive paths coincide with the atomistic chains as kinks are located in particle positions. Middle: iteration of the minimization procedure where the contour lengths of the primitive paths are reduced, and non-constraint kinks are removed from the system. Chain ends are held fixed through the iterative procedure. Bottom: final configurations after convergence where the total path reaches its shortest value. One entanglement (internal kink) is assigned to the primitive paths shown in black and green, while the one shown in blue possesses two entanglements.

The evolution of the entanglement density with the polymer volume fraction φ is of particular interest, since the complex, non-intuitive dependence of the number of entanglements on φ gives rise to the very different types of rheological behavior which have been observed experimentally as concentration increases up to the melt. Results of the topological analysis leading to the primitive paths for the asymptotically long (N = 1000) hard sphere multi-chain system up to the MRJ state are shown in Fig. 6. Four easily distinguishable scaling regimes, characterized by specific scaling exponents, can be observed for the dependence of the average number of entanglements per chain, more precisely, the number of segments of the primitive path 〈Z〉, on packing density.²³ The ranges of the scaling regimes along with the corresponding scaling exponents are:²³ (I) 0 ≤ φ ≤ φ^*,semi; 〈Z〉 ∼ φ^{0.0 ± 0.1}, (II) φ^*,semi ≤ φ ≤ 0.45; 〈Z〉 ∼ φ^{0.60 ± 0.15}, (III) 0.45 ≤ φ ≤ φ^*,conc; 〈Z〉 ∼ φ^{0.0 ± 0.1} and (IV) φ^*,conc ≤ φ ≤ φ^MRJ; 〈Z〉 ∼ φ^{4.0 ± 0.4}.

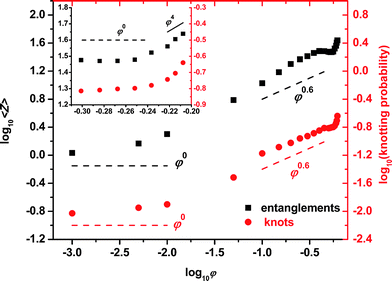Fig. 6 Double logarithmic plot of the (left axis) average number of segments of the primitive path 〈Z〉 and of the (right axis) fraction of knotted chains for the N = 1000 hard sphere chain system. Lines with characteristic slopes are drawn as guides to the eye. Inset: zoom into the marginal and concentrated regimes.

While entanglements have been at the root of modern theories of polymer dynamics since its inception,³² the interest in knots as an alternative analysis pathway of topological constraints is quite recent.^40–42 For example topological studies based on the concept of knots had so far been presented for single ring polymers (φ → 0), where it had been empirically observed that the probability of being unknotted depends on N as m^NN^a or alternatively e^−N/N₀ with m slightly less than unity, a close to zero, and N₀ a large number which depends on the sphere radius.⁴² In the present work, knots were identified by the technique proposed by Mansfield.⁴⁰ Since knot theory only defines knots in closed paths, to apply it on the topology of linear polymers each chain is converted into a closed polygon. While there exists numerous ways of connecting the two chain ends, it was found that the chain closure scheme has no effect on neither the ranges of the scaling regimes nor on the values of the corresponding exponents.²³ Therefore, individual chains were extracted from the configurations generated by the MC algorithm, converted into a closed polygon, and its knotting was determined using the technique described in ref. 40. This method is based on the concept of a knot group, which is simultaneously more discriminating and easier to calculate than the knot invariants that have been used in such studies in the past (Gauss winding number, or the Alexander, Jones, or HOMFLY polynomials).⁴³ Starting from an arbitrary projection of an embedded graph, this method generates a sequence of representations, any of which is a full and complete representation of the knot group. This sequence of representations is compared against the entries in a previously determined look-up table.⁴⁴ The matching entry identifies the knot as well as its complexity.⁴⁰

The results of such a knotting analysis for the same large set of configurations of the hard sphere, multi-chain system (N = 1000) up to the MRJ state are also included in Fig. 6 (right axis), allowing for a direct comparison with the corresponding scaling behavior of entanglements (left axis). The similarity, within the statistical uncertainty, of the scaling exponents for entanglements and knots is a most unexpected result for a very simple reason: entanglements are, by definition, a multi-chainconstruct, while knotting is primarily a single-chain phenomenon. Thus, knotting is a purely intramolecular characteristic, whereas entanglements constitute a purely intermolecular measure of topological hindrance. Furthermore, entanglements seem to be localized in space, whereas knotting is a global, “delocalized” property of a chain. Yet the evidence collected on the hard sphere chains strongly suggests that, in a very general sense, knots must be equivalent to entanglements. In other words, the multi-chain phenomenon of entanglement leaves an unequivocally recognizable imprint on the shape of individual chains: once the scale factor between knots and entanglements is found (roughly speaking, the vertical shift between the two sets of symbols in Fig. 6), it should be possible to determine the dependence of the number of entanglements on the volume fraction Σ^ent(φ) from the dependence of the number of knots on volume fraction Σ^knot(φ), by analyzing the knotting of single chains extracted from the multi-chain ensembles over the entire volume fraction range.

This remarkable finding may actually have a simple explanation. While the original concept of an entanglement is a dynamic one (as beautifully shown in the pioneering simulations of Kremer and Grest),⁴⁵ all current algorithms for determining entanglements are based on static, essentially geometric arguments. In very simplistic terms, topological algorithms detect entanglements by holding the ends of all chains fixed, and by simultaneously “tightening” the chains as if they were retractable rubber bands, until a minimum overall length, compatible with chain uncrossability, is reached. On the other hand, knotting algorithms start by connecting the ends of a given chain, and then determine the type of knot (e.g. based on knot group or knot invariants). Although the two types of analyses seem to be unrelated at first sight, the essential information both of them ultimately require is contained in the succession of over- and under-crossings of two-dimensional projections of the chains (or single chain in the case of the knotting analysis). Fig. 7, which is meant to be qualitatively suggestive only, illustrates how the difference in the sequence of crossings between the trefoil and the unknot configurations results in very different knotting, and also different entanglement characteristics. If we symbolically represent by ω^knot(φ,±,±,±,…) and ω^ent(φ,±,±,±,…) the functional dependence of knots and entanglements on volume fraction, and on the underlying distribution of sequences of crossings for a particular entangled chain molecular system, the scaling similarity of Fig. 6 implies that both must be directly related to a universal “topological constrain” function Ω(φ,±,±,±,…) by a simple proportionality: ω^knot ∝ ω^ent ∝ Ω(φ,±,±,±,…), so that their ratio ω^knot(φ,±,±,±,…) : ω^ent(φ,±,±,±,…) is a system/chemistry dependent constant. Thus, in an ensemble average sense, single, highly knotted chains can be considered proper class representatives of highly entangled, multi-chain systems. This similarity may lead to a refinement and revised evaluation of current methods of characterization of entanglements: once the entanglements of a particular system have been determined, additional information such as spacing between entanglements, reptation tube diameter, etc. is obtained in what can be called a “post-processing” analysis. A knotting analysis however yields basically “delocalized” information: the number and the complexity (type) of knots. No further information can be extracted. If, however, the basic information content of knots and entanglements is the same, as Fig. 6 strongly suggests, the natural question is then to what extent the “post-processing” step imposes a structure on the results which is not contained in the original system, but which stems from explicit or implicit assumptions (e.g. freezing of dynamic degrees of freedom, Gaussian behavior of primitive paths, type of distribution of entanglements along chains, etc.).

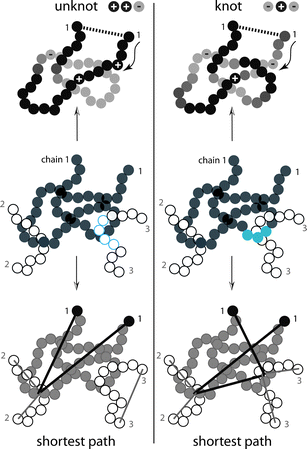Fig. 7 Schematic drawing highlighting the different configurational information giving rise to knotting (top) and entanglement (bottom). Shown in the middle of the two columns are two configurations of a single linear chain (no. 1) of tangent spheres together with two of the surrounding chains (no. 2 and 3), which differ in their topological constraints. The analysis of knots⁴⁰ operates on the conformation of the single chain. Over- and under-crossings as the chain is traversed starting at one of its two ends are marked by “+” and “−” signs, respectively. The analysis of the entanglement network operates on the configurational information of the whole system and yields the shortest multiply disconnected path.³⁵ During the minimization procedure the ends of the sub paths (so called primitive paths; shown are primitive paths for chains 1–3) remain fixed in space (see also Fig. 5). While for the analysis of knots the information of ‘above’ and ‘under’ within a single chain is of the utmost importance, and the information about surrounding chains irrelevant, for the analysis of the entanglement network exactly the opposite is true. Chain thickness is irrelevant for both methods.

5. Entanglement, knotting and aggregation in biophysics

In practice, the observation that both measures of topological constraints for chain systems scale with identical universal exponents may open up a new and potentially very powerful avenue for the understanding of complex biological problems which are out of computational reach nowadays. A prominent example is the long established correspondence between human neurodegenerative diseases and the genetic expansion of a chromosomal trinucleotide repeat sequence.⁴⁶ In Huntington's disease, pathogenesis is known to be caused by a polyglutamine sequence of more than 36 amino acids. Such expanded sequences lead to aggregation and to the ultimate appearance of protein inclusions in the affected neurons.⁴⁷ The nucleation event for aggregation involves folding within a single chain. A great effort is currently being devoted to the modelling of this single chain folding event for sequences of moderate length (up to approximately 50 residues). These investigations make use of advanced simulation methods, like steered molecular dynamics (MD), transition path sampling^48,49 replica exchange MD,⁵⁰ and of massive, large scale computational resources. Such detailed analyses at the level of a single chain⁴⁷ are at the current limit of feasibility, even for relatively small polypeptide sequences. A similarly detailed approach to the collective entanglement behavior of a multi-polypeptide system to form an aggregate is a rather hopeless undertaking, and will remain so for the foreseeable future. However, the universal character of the similarity between entanglement and knotting suggests that a great deal of information about the emergence and evolution of very large, computationally intractable, polypeptide aggregates, such as those responsible for Huntington's disease, could be rigorously gleaned from the analysis of single polypeptide chains.

6. Conclusions and potential applications

The recent determination and understanding of the hitherto unknown structure of the dense random packing of hard sphere chains up to their MRJ state has answered several long standing questions in the physics of polymers, complex fluids, statistical mechanics and thermodynamics. Furthermore, an analysis of chain topological hindrance has uncovered an unsuspected connection between entanglements and knots. This connection deserves urgent, deeper investigation, as it may open a new avenue for the analysis of the very complex collective behavior of multi-chain, biomolecular systems. In addition, current efforts focus on the extension of the simulation studies to dense model polymer systems of varied molecular architectures (branched, stars and rings) either in the bulk or at interfaces (nanofillers, confined geometries and solid surfaces) and on the effect of chain stiffness on the jamming transition and statistics. There is every reason to expect that the universal aspects displayed by the hard sphere chain model system will apply to chemically realistic chains, so that the physical insights afforded by this simplest model of chain molecular soft matter will have substantial practical applications.

Acknowledgements

We acknowledge financial support by the EC through Contract No. NMP3-CT-2005-016375 and generous allocation of computational resources by CeSViMa (UPM, Spain) and CSCS (Switzerland).

References

1. J. D. Bernal, Nature, 1960, 185, 68–70; G. D. Scott, K. R. Knight, J. D. Bernal and J. Mason, Nature, 1962, 194, 956.
2. J. D. Bernal and J. L. Finney, Discuss. Faraday Soc., 1967, 43, 62; J. L. Finney, Proc. R. Soc. London, Ser. A, 1970, 319, 479.
3. (a) S. Torquato, T. M. Truskett and P. G. Debenedetti, Phys. Rev. Lett., 2000, 84, 2064–2067; (b) A. Donev, S. Torquato and F. H. Stillinger, Phys. Rev. E, 2005, 71, 011105; (c) A. Donev, S. Torquato and F. H. Stillinger, J. Comput. Phys., 2005, 202, 737–764.
4. T. C. Hales, Ann. Math., 2005, 162, 1065–1185; T. C. Hales, Discrete Comput. Geom., 2006, 36, 5–20.
5. J. G. Berryman, Phys. Rev. A, 1983, 27, 1053–1061.
6. G. D. Scott and D. M. Kilgour, Br. J. Appl. Phys., 1969, 2, 863–866.
7. R. D. Kamien and A. J. Liu, Phys. Rev. Lett., 2007, 99, 155501.
8. A. V. Anikeenko, N. N. Medvedev and T. Aste, Phys. Rev. E, 2008, 77, 031101.
9. F. H. Stillinger, J. Comput. Phys., 1971, 7, 367–384; V. S. Kumar and V. Kumaran, J. Chem. Phys., 2005, 123, 074502; V. S. Kumar and V. Kumaran, J. Chem. Phys., 2006, 124, 204508.
10. C. S. O’Hern, S. A. Langer, A. J. Liu and S. R. Nagel, Phys. Rev. Lett., 2002, 88, 075507; C. S. O’Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. E, 2003, 68, 011306; N. Xu, J. Blawzdziewicz and C. S. O’Hern, Phys. Rev. E, 2005, 71, 061306.
11. S. Punnathanam and P. A. Monson, J. Chem. Phys., 2006, 125, 024508; R. Lenick, X. J. Li and Y. C. Chiew, Mol. Phys., 1995, 86, 1123–1135.
12. G. Parisi and F. Zamponi, J. Stat. Mech. – Theory Exp., 2006, P03017.
13. A. S. Keys, A. R. Abate, S. C. Glotzer and D. J. Durian, Nat. Phys., 2007, 3, 260–264.
14. C. Radin, J. Stat. Phys., 2008, 131, 567–573.
15. Z. H. Stachurski, Phys. Rev. Lett., 2003, 90, 155502.
16. I. H. Kim and Y. C. Bae, Fluid Phase Equilib., 2000, 167, 187–206.
17. N. C. Karayiannis and M. Laso, Phys. Rev. Lett., 2008, 100, 050602.
18. A. Donev, F. H. Stillinger and S. Torquato, Phys. Rev. Lett., 2005, 95, 090604.
19. N. C. Karayiannis and M. Laso, Macromolecules, 2008, 41, 1537–1551.
20. P. V. K. Pant and D. N. Theodorou, Macromolecules, 1995, 28, 7224–7234; N. C. Karayiannis, V. G. Mavrantzas and D. N. Theodorou, Phys. Rev. Lett., 2002, 88, 105503.
21. J. J. de Pablo, M. Laso and U. W. Suter, J. Chem. Phys., 1992, 96, 2395–2403; J. I. Siepmann and D. Frenkel, Mol. Phys., 1992, 75, 59–70.
22. M. Laso and N. C. Karayiannis, J. Chem. Phys., 2008, 128, 174901.
23. K. Foteinopoulou, N. C. Karayiannis, M. Laso, M. Kröger and M. L. Mansfield, Phys. Rev. Lett., 2008, 101, 265702.
24. N. C. Karayiannis, K. Foteinopoulou and M. Laso, J. Chem. Phys., 2009, 130, 074704.
25. J. Pach and P. K. Agarwal, Combinatorial Geometry, John Wiley, New York, 1995.
26. N. C. Karayiannis, K. Foteinopoulou and M. Laso, J. Chem. Phys., in press.
27. P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, 1980.
28. S. F. Edwards, Proc. Phys. Soc., 1966, 88, 265–280.
29. M. Daoud, J. P. Cotton, B. Farnoux, G. Jannink, G. Sarma, H. Benoit, R. Duplessix, C. Picot and P. G. de Gennes, Macromolecules, 1975, 8, 804–818; J. P. Cotton, M. Nierlich, F. Boué, M. Daoud, B. Farnoux, G. Jannink, R. Duplessix and C. Picot, J. Chem. Phys., 1976, 65, 1101–1108.
30. G. J. Fleer, M. A. Cohen Stuart, J. M. H. M. Scheutjens, T. Cosgrove and B. Vincent, Polymers at Interfaces, Chapman and Hall, London, 1993.
31. M. Kröger, Rheology, 1995, 5, 66–71; T. Aoyagi and M. Doi, Comput. Theor. Polym. Sci., 2000, 10, 317; M. Kröger and S. Hess, Phys. Rev. Lett., 2000, 85, 1128–1131.
32. M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, Oxford, 1988.
33. T. C. B. McLeish and R. G. Larson, J. Rheol., 1998, 42, 81–110; T. C. B. McLeish, Adv. Phys., 2002, 51, 1379–1527; A. E. Likhtman and T. C. B. McLeish, Macromolecules, 2002, 35, 6332–6343; R. S. Graham, A. E. Likhtman and T. C. B. McLeish, J. Rheol., 2003, 47, 1171–1200; G. Marrucci, Science, 2003, 301, 1681–1682; M. Kröger, Phys. Rep., 2004, 390, 453–551; T. C. B. McLeish, Phys. Today, 2008, 61, 40–45.
34. R. Everaers, S. K. Sukumaran, G. S. Grest, C. Svaneborg, A. Sivasubramanian and K. Kremer, Science, 2004, 303, 823–826; K. Kremer, S. K. Sukumaran, R. Everaers and G. S. Grest, Comput. Phys. Commun., 2005, 169, 75–81; S. K. Sukumaran, G. S. Grest, K. Kremer and R. Everaers, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 917–933; S. Leon, N. van der Vegt, L. Delle Site and K. Kremer, Macromolecules, 2005, 38, 8078–8092; N. Uchida, G. S. Grest and R. Everaers, J. Chem. Phys., 2008, 128, 044902.
35. M. Kröger, Comput. Phys. Commun., 2005, 168, 209–232; K. Foteinopoulou, N. C. Karayiannis, V. G. Mavrantzas and M. Kröger, Macromolecules, 2006, 39, 4207–4216; S. Shanbhag and M. Kröger, Macromolecules, 2007, 40, 2897–2903; K. Foteinopoulou, N. C. Karayiannis, M. Laso and M. Kröger, J. Phys. Chem. B, 2009, 113, 442–455.
36. S. Shanbhag and R. G. Larson, Phys. Rev. Lett., 2005, 94, 076001; Q. Zhou and R. G. Larson, Macromolecules, 2005, 38, 5761–5765; S. Shanbhag and R. G. Larson, Macromolecules, 2006, 39, 2413–2417.
37. R. S. Hoy and M. O. Robbins, Phys. Rev. E, 2005, 72, 061802; R. S. Hoy and M. O. Robbins, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 3487–3500; R. S. Hoy and G. S. Grest, Macromolecules, 2007, 40, 8389–8395.
38. C. Tzoumanekas and D. N. Theodorou, Macromolecules, 2006, 39, 4592–4604; C. Tzoumanekas and D. N. Theodorou, Curr. Opin. Solid State Mater. Sci., 2006, 10, 61–72; K. Kamio, K. Moorthi and D. N. Theodorou, Macromolecules, 2007, 40, 710–722; T. Spyriouni, C. Tzoumanekas, D. N. Theodorou, F. Müller-Plathe and G. Milano, Macromolecules, 2007, 40, 3876–3885.
39. M. Kröger and H. Voigt, Macromol. Theory Simul., 1994, 3, 639–647; M. Kröger, J. Ramirez and H. C. Öttinger, Polymer, 2002, 43, 477–487.
40. M. L. Mansfield, J. Chem. Phys., 2007, 127, 244901; M. L. Mansfield, J. Chem. Phys., 2007, 127, 244902.
41. M. Lang, W. Michalko and S. Kreitmeier, J. Comput. Phys., 2003, 185, 549–561; E. Rawdon, A. Dobay, J. C. Kern, K. C. Millet, M. Piatek, P. Plunkett and A. Stasiak, Macromolecules, 2008, 41, 4444–4451.
42. K. Koniaris and M. Muthukumar, Phys. Rev. Lett., 1991, 66, 2211–2214; A. Y. Grosberg, A. Feigel and Y. Rabin, Phys. Rev. E, 1996, 54, 6618–6622.
43. R. H. Crowell and R. H. Fox, Introduction to Knot Theory, Ginn & Co., Boston, MA, 1963; C. C. Adams, The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, W. H. Freeman & Co., NY, 1994; V. F. R. Jones, Bull. Amer. Math. Soc., 1985, 12, 103–111; M. D. Frank-Kamenetsskii and A. V. Vologodskii, Sov. Phys. Usp., 1981, 24, 679–695.
44. C. Livingston , J. C. Cha, Table of Knot Invariants (Indiana University: http://www.indiana.edu/%E2%88%BCknotinfo) accessed January 2009.
45. K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086.
46. C. J. Cummings and H. Y. Zoghbi, Hum. Mol. Genet., 2000, 9, 909–916.
47. P. J. Skinner, B. T. Koshy, C. J. Cummings, I. A. Klement, K. Helin, A. Servadio, H. Y. Zoghbi and H. T. Orr, Nature, 1997, 389, 971–974.
48. P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318.
49. M. Chopra, A. J. Reddy, N. L. Abbott and J. J. de Pablo, J. Chem. Phys., 2008, 129, 135102.
50. N. Rathore, M. Chopra and J. J. de Pablo, J. Chem. Phys., 2005, 122, 024111.
51. J. D. Bernal, Nature, 1959, 183, 141–147.
52. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.

---

Footnotes

† Assume that there exists a state/ensemble in which hard sphere chains strictly pack more densely than single spheres. Remove the bonds in all chains in each configuration of this ensemble. The result is an ensemble of hard spheres at the same density as the starting chain system, in contradiction with the hypothesis.

‡ It would suffice to prove that for a given MRJ structure of single hard spheres, it is always possible to link them into chains of the desired length so as to create an MRJ structure of hard sphere chains. Algorithms able to perform this task in most specific cases are known,²⁵ a proof that guarantees their success in all cases is however not known.

§ In a fashion analogous to the “jammed” state of inner spheres a chain end is “jammed” if it is not able to perform an arbitrarily small “reptation” or “rotation” move subject to holonomic constraints.

---