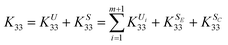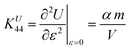DOI:
10.1039/B811677F
(Paper)
Soft Matter, 2009,
5, 173-181
Elastic properties of graft copolymers in the lamellar phase studied by self-consistent field theory
Received
14th July 2008
, Accepted 10th September 2008
First published on 23rd October 2008
Abstract
The linear elasticity of graft copolymer melts in the lamellar phase was examined by the self-consistent field theory solved in real space. The extensional and shear moduli, which are used to derive the Young's modulus, are found to be dependent on the architecture parameters of graft copolymers (the number of branches and the distribution of junction points). Compared with the shear modulus, the extensional modulus makes a greater contribution to the Young's modulus. The graft copolymers with the larger branch number exhibit the better mechanical properties. For the physical origin of the improvement of mechanical properties, the contribution of internal energy is the main drive, while the contribution of entropy to the moduli is negative or neglected. The distribution of junction points was also found to play a role in determining the elastic properties. These findings gained through the theoretical calculations may provide useful information for designing graft copolymers with enhanced properties.
Introduction
Block copolymers can spontaneously self-assemble into a variety of ordered microstructures. The elasticity of block copolymer microstructures is of great interest in the development of materials, such as thermoplastic elastomers and pressure-sensitive adhesives. Therefore, the development of theoretical methods for predicting the macroscopic mechanical properties of block copolymers from knowledge of the microscopic structure is crucial.1,2 The need for such predictions becomes increasingly important as new synthesis methods are now available that can produce many new exciting architectures.
The molecular architecture of polymers has been long recognized as an important factor for tailoring the materials’ properties. Changing the molecular architecture from simple linear diblock copolymers to graft copolymers exerts a marked effect on the mechanical properties of the copolymers, which has sparked considerable interest and is being extensively investigated.3–9 For example, Kennedy et al. demonstrated that the graft copolymer molecular architecture can be used for improving the mechanical properties of the thermoplastic elastomer (TPE).4,5 The graft copolymers comprising a rubbery backbone and glassy branches are much suitable for TPEs. Recently, Zhu et al. synthesized a series of graft copolymers with polyisoprene (PI) as backbone and polystyrene (PS) as branches, which offered new opportunities to study the effect of molecular architecture on the morphology and in turn on the mechanical properties.8,9 They found that the graft copolymer materials show significantly higher elongation than the commercial materials when comparable stress is achieved at a break. It was also found that the Young's modulus becomes larger with an increasing number of branches. Therefore, the concept of using graft copolymers as TPEs not only reveals a new type of materials with an exceptional property profile, but also indicates that the material properties can be tuned by varying the molecular architecture. However, the understanding of the better mechanical properties of the graft copolymers is still lacking. Inspired by these findings, we present a first theoretical investigation on the elastic properties of graft copolymers.
So far, a variety of theoretical tools have been used to predict the elastic properties of materials.10–14 Self-consistent field theory (SCFT) has been widely used to investigate the thermodynamics properties of polymer systems.15–20 One prominent characteristic of this theory is that it allows us to incorporate many specific features of polymer models, such as molecular architecture and composition gradient,21–23 stiffness of chain,24,25 and presence of nanoparticles.26–28 Recently, Tyler and Morse used the SCFT in reciprocal space to examine the linear elasticity of the body-centered cubic and gyroid phases of block copolymers.29 They found that the reduced elastic moduli are universal functions of interaction parameters, volume fraction, and block asymmetry. In addition, they compared the calculated elastic moduli with the existing experimental results. Subsequently, Thompson et al. presented a real-space SCFT method for calculating the elastic moduli of multiblock copolymers and block copolymer/nanoparticle composites30,31 They not only predicted the effects of the number of blocks of multiblock copolymers and adding nanoparticles into the copolymers on the elastic properties, but also explained the physical origins of the observed effects. Liang and co-workers used the same method to study the effects of polydispersity and architecture of triblock copolymers on the elastic properties.32,33 Maniadis et al. incorporated the elastic stress and strain fields into the SCFT.34 They showed that the local stress is reduced at interface, but slightly enhanced in the vicinity of the interface.
These SCFT results are all found to be in good qualitative agreement with the experimental findings, indicating that the approach based on SCFT is a powerful methodology to deduce the macroscopic properties of a material from the knowledge of microscopic structure. It should be pointed out that all these SCFT calculations were performed in melt state. SCFT has difficulty in predicting the elastic properties of a non-melt system due to its own shortcoming. However, the results obtained from melt state could be applicable to the situation in non-melt system.
In our previous study, we adopted the SCFT to investigate the morphology and phase behavior of graft copolymers.35,36 In the simplest diblock copolymer system, there are two thermodynamic variables which determine the phase behavior, which are the composition and the parameter χN (χ is the Flory–Huggins parameter and N is the polymerization degree). With respect to the graft copolymers, there exist another two architecture parameters affecting the self-assembly behavior of copolymers. The two parameters are the number of branches (m) and the distribution of junction points (τ). After incorporating these two parameters into the SCFT framework, we examined the phase behavior of graft copolymers. It was found that the morphology transition between the lamellar and cylindrical phases can be triggered by tailoring the m and τ parameters.35 In addition, the molecular architecture also has an important impact on the self-assembly behavior of graft copolymers in dilute solution.36
In present work, we elucidated the effect of architecture parameters on the elastic properties of graft copolymers in melt state. The extensional and shear moduli were calculated by SCFT methodology for the graft copolymers in lamellar phase. The physical origins of the architecture effects on the elastic moduli were also investigated. The moduli can be tailored by changing the architectural parameters of graft copolymers and the internal energy contribution plays a main role in determining the moduli. We expect that the present study may offer some useful information for designing graft copolymers with enhanced properties.
Theory
A schematic representation of the molecular architecture of the graft copolymer studied in the present work is shown in Fig. 1. m flexible homopolymer B grafts are spaced along the flexible homopolymerA backbone. The degrees of polymerization of the A backbone and per B graft are NA and NB, respectively. The statistical segment length of A- and B-type segments is b. The volume fraction of A-type segment in the system is denoted by fA, and that of B-type segment is fB = 1 − fA. In present model, the position of ith graft is given by τi = τ1 + (i − 1)(1 − 2τ1)/(m − 1). This means that the grafts are equally spaced along the backbone parametrized from 0 to 1.
 |
| | Fig. 1 The molecular architecture of the graft copolymer with m = 4. Flexible homopolymer B grafts are spaced along the flexible homopolymerA backbone. The ith graft is located at τi = τ1 + (i − 1)(1 − 2τ1)/3. | |
Next, we introduce the linear elasticity model for graft copolymers in the lamellar phase. The variation of the total free energy of a crystal for small deformations is37
where
Kijkl is a tensor of rank four, called the elastic modulus tensor (
i,
j,
k,
l = 1, 2 or 3), and
uij is the strain tensor. The elastic modulus tensor for a crystal in terms of the strain tensor is given by
| |  | (2) |
where
u = 0 denotes a strain tensor with zero components. The tensor
Kijkl can be unchanged when the dummy indices
i and
j, or
k and
l, and the pairs
ij and
kl are interchanged. The number of different components of a rank-four tensor is reduced to 21. If the crystal possesses symmetry, there exist relations between the various components of the tensor
Kijkl. For a tetragonal symmetry with a preferred
z axis,
Kijkl contains just six independent non-zero components. Under the transformation between
x and
y axis directions, the general expression for the elastic free energy in the tetragonal system is given by
37| | | Fel= ½Kxxxx(uxx2 + uyy2) + ½Kzzzzuzz2 + Kxxzz(uxxuzz + uyyuzz) + Kxxyyuxxuyy + 2Kxyxyuxy2 + 2Kyzyz(uxz2 + uyz2) | (3) |
Another notation used for
Kijkl is the Voigt notation
Kµν with
µ and
ν taking values from 1 to 6 in correspondence with
xx,
yy,
zz,
yz,
zx,
xy. The above equation can be rewritten as
| | | Fel = ½K11(uxx2 + uyy2) + ½K33uzz2 + K13(uxxuzz + uyyuzz) + K12uxxuyy + 2K66uxy2 + 2K44(uxz2 + uyz2) | (4) |
For the lamellar structure perpendicular to the
z axis, deformations along the
x or
y axis directions (parallel to the lamellar structure) have no effect on the free energy of the system. By extending/compressing along the
z axis (see
Fig. 2a), the
uxx and
uyy components should be zero. The
uzz component remains non-zero and it has a value of
ζ/
l, where
ζ is the absolute deformation, and
l is the length of material. The equation for the elastic free energy,
eqn (4), can be written as
Fel = ½
K33uzz2, where
uzz =
ζ/
l is the relative deformation. If the object undergoes a shear along a plane perpendicular to the
y axis (see
Fig. 2b), the modulus
K44 is obtained. The only non-zero strain tensor compound is
uyz =
ζ/2
l. Therefore, the elasticity free energy for a lamellar structure reduces to
30| | | Fel = ½[K33uzz2 + 4K44(uyz2 + uxz2)] | (5) |
 |
| | Fig. 2 A schematic of a material undergoing extension (a) and shearing (b). θ is the amount of shear. The amount of deformation is exaggerated. | |
The free energy per chain for graft copolymer melts in context of SCFT can be written as
| | 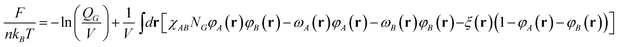 | (6) |
where
kB is Boltzmann's constant,
T is the temperature,
n is the number of
graft copolymers in system, and
V is the volume of system.
χAB and
NG(=
NA +
mNB) refer to the Flory–Huggins interaction parameter and the total number of segments in a
graft copolymer, respectively.
φA(
r) and
φB(
r) are respectively the local volume fractions of
A and
B segments, while the conjugated fields are
ωA(
r) and
ωB(
r). The incompressibility (
φA(
r) +
φB(
r) = 1) is introduced by a Lagrangian multiplier
ξ(
r).
QG is the single-chain partition function, which can be computed according to
QG = ∫
drqA(
r,1).
qA(
r,s) is the backbone propagator, providing the probability that the end of the section chain of length
sNA is constrained at
r. The backbone propagator is divided into
m + 1 segments,
| | | qA(r,s) = qA(j)(r,s)for τj≤s<τj+1 j = 0,1,⋯,mτ0 ≡ 0, τm+1 ≡ 1 | (7) |
where each segment satisfies the modified diffusion equation:
| |  | (8) |
and is subject to the following initial conditions:
| | qA(j)(r,τj) = qA(j−1)(r,τj)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qB(r,1) qB(r,1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j = 1,2,⋯,m qA(0) (r,0) = 1 j = 1,2,⋯,m qA(0) (r,0) = 1 | (9) |
Here,
qB(
r,
s) is a propagator for
B graft that satisfies the following modified diffusion equation:
| |  | (10) |
and is subject to the initial condition
qB(
r,0) = 1 for the free end of the graft at
s = 0. We also define a back propagator of the
jth
B chain,
qBj+ (
r,
s). It satisfies the same diffusion equation as
qB(
r,
s) and starts on the end of the
B chain tethered to the backbone. It is therefore subject to the initial condition
| |  | (11) |
In terms of these propagators, the densities are given by
| |  | (12) |
| |  | (13) |
where
φiA(
r) is the density of backbone blocks between
τi-1 and
τi. More details about the SCFT for
graft copolymers can be found in our previous studies.
35,36
The linear elastic moduli can be obtained by the SCFT energy of graft copolymer melts. We can numerically calculate the equilibrium free energy of graft copolymers using eqn (6). The system is slightly deformed from the equilibrium structures by varying the size or shape of the simulation box (Fig. 2). The free energy of the deformed lamellar structure is recalculated by self-consistent field theory. We adopt the real-space algorithm for SCFT introduced by Drolet and coworkers,20,38 which searches for the equilibrium or metastable states. The relation of free energy versus the relative deformation is constructed. The elastic moduli can be numerically evaluated by taking the second derivative of the SCFT energy with respect to the relative deformation.
To yield the extensional and shear moduli, we use two ways to deform the system: an extension/compression, which yields K33, and a simple shear, which yields K44. With respect to extension/compression, the free energy of the lamellar phase in the equilibrium box size is evaluated first. Then the box is extended/compressed by a small change in a direction perpendicular to the lamella (Fig. 2a). Correspondingly, the free energy of the deformed lamellar structure is recalculated each time. In our simulation for extension/compression, the free energy is calculated in a rectilinear grid of evaluation points. For the shearing (Fig. 2b), however, a nonorthogonal coordinate system is used to calculate the free energy. The coordinate transformation is performed: x′ = x, y′ = y/sinθ, z′ = z − ycotθ, where the symbol (′) denotes the nonorthogonal coordinate, and θ gives the amount of shear. As a result, all of the integrals must be subject to a factor of Jacobian determinant sinθ. For the free energy of SCFT, however, all the integrals are normalized by the volume of the system, which equals to Vsinθ in the deformation system. The only change in the numerical calculation is the nonorthogonal Laplacian operator in the diffusion equation. For the solution of the diffusion equation, we employ the Baker–Hausdorff operator splitting formula,39,40 which is based on the Fourier transformation between real space and reciprocal space. The Laplacian operator in reciprocal space can be written as
| |  | (14) |
where
k′ is the wave vector. The diffusion equation for a shear system can be calculated by performing a standard Fourier transformation, using the Laplacian operator for the shear system given by
eqn (14), and implementing a standard inverse Fourier transformation.
41
We can apply this method to compute the elastic moduli for lamella formed by the graft copolymers with different architectural parameters, such as the distribution of junction points and the number of branches. In order to understand the physical origin of the differences in the mechanical properties for the graft copolymers with various molecular architectures, the free energy of SCFT is separated into physically relevant contributions. Here, the free energy of graft copolymers (in units of kBT) can be decomposed as42
| |  | (15) |
Here,
U and
S are the internal energy and entropy, respectively.
Ui is the internal energy contributed from blocks between
τi−1 and
τi.
SE is the entropy of the end point of the backbone (
s = 1).
SC is the conformational entropy of a molecule. Using the standard Gaussian model and SCFT, the corresponding components of the free energy can be written as
| |  | (16) |
| |  | (17) |
| |  | (18) |
where
ρE(
r) =
VqA(
r,1)/
QG.
The values of elastic moduli K33 and K44 can be obtained by taking the second derivative of the SCFT energy with respect to the relative deformation ε. The calculation can be carried out as
| |  | (19) |
The modulus
K33 can be decomposed into the components
| | 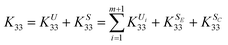 | (20) |
where the components
KU33,
KS33,
KUi33,
KSE33, and
KSC33 are identified with the derivative in
eqn (19). Similarly, the decomposition is suitable for
K44.
To compare with the existing experimental results, a standard definition of the Young's modulus, E, in terms of the extensional and shear moduli, is used and it is given by37
| |  | (21) |
SCFT calculation results
In the present work, we investigate the effect of molecular architecture on the elastic properties of graft copolymers in a lamellar phase. Two import parameters characterizing the molecular architecture of graft copolymers are included in the model: the number of branches (m) and the position of first junction point (τ1). The interaction strength of the average constituting single graft copolymerh = χABNG/m is taken to be a value of 20.0,43 sufficient to produce microphase separation in the bulk. We restrict attention to the graft copolymers with the backbone volume fraction fA at 0.45, where the lamellar structure is formed.
1. Effect of the branch number
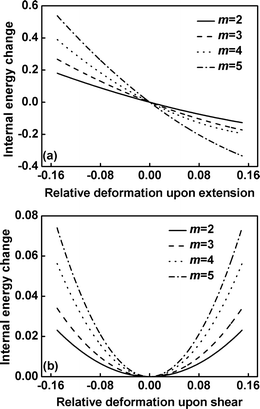
Fig. 3 shows the changes in free energy upon deformation for the graft copolymers with various branch numbers at τ1 = 0.10. The free energies of systems have been zeroed at the equilibrium state, which corresponds to the relative deformation ε = 0. To guarantee the validity of linear elastic theory in small deformation range, the elastic response is within 15% strain. Fig. 3(a) and (b) present the cases of the extension/compression and shear deformations, respectively. The change in free energy upon deformation becomes marked as the branch number increases. In comparison with the shear deformation, the variation in free energy upon extension/compression deformation is much larger. As shown in Fig. 3, the parabolic character of these curves indicates that the linear elastic theory can be applicable.30,37 The polynomials are used to fit these curves, and K33 and K44 can be obtained by taking the second derivative of the free energy change with respect to the relative deformation.
 |
| | Fig. 3 The change in free energy (in units of kBT) between the undeformed and deformed structures upon extension/compression (a) and shearing (b) for graft copolymers with various values of m at τ1 = 0.10. In part (a), the negative and positive values of deformation are compression and extension, respectively. | |
The elastic moduli K33 and K44 as a function of the number of branches for the graft copolymers with the position of first junction point τ1 = 0.10, 0.20, and 0.30 are shown in Fig. 4(a). Increasing the number of branches gives rise to the linear increase in extensional modulus (K33). The shear modulus K44 versus m has a raise over the range 2 ≤ m ≤ 5. It is also noted that the effect of τ1 on K33 and K44 becomes marked when m is greater. The shear modulus is smaller in comparison with the extensional modulus. Therefore, the Young's modulus E (calculated using eqn 21) mainly depends on the contribution of extensional modulus K33. A plot of E versus m for graft copolymers with τ1 = 0.10, 0.20, and 0.30 is shown in Fig. 4(b). The data is plotted on a semilog scale. As can be seen, the graft copolymers with larger m and smaller τ1 have larger Young's modulus.
 |
| | Fig. 4 The dimensionless elastic moduli K33, K44, and E as a function of the number of branches for graft copolymers with τ1 = 0.10, 0.20, and 0.30. | |
To understand the origin of the increase in the elastic moduli with increasing m, we decompose the K33 and K44 moduli into two parts according to eqn (16)–(18). One is the contribution from the internal energy (U), and the other arises from the entropy (-TS). For example, Fig. 5 shows the internal energy change contributions to the total free energy change for extension/compression and shear of the graft copolymers with various values of branch number at τ1 = 0.10. The contribution of internal energy change to the total free energy change of the graft copolymers with the larger branch number appears to be greater upon increasing the relative distortion. Unlike the total free energy, the curves of internal energy components upon extension deformation do not display the parabolic character but have the large first derivative (as shown in Fig. 5a). However, according to eqn 19, the curvature of the components can still be evaluated from the second derivative of the respective energy components with respect to the relative deformation ε.
 |
| | Fig. 5 The internal energy change (in units of kBT) versus the relative deformation for extension/compression (a) and shear (b) of graft copolymers with various values of branch number at τ1 = 0.10. | |
Taking the second derivative of internal energy and entropy changes with respect to the relative deformation, we obtain the moduli contributed from the internal energy and entropy for graft copolymers with various values of m, which are listed in Table 1. K33 is the total extensional modulus, and is the sum of KU33 and KS33, which are the moduli from the contributions of internal energy and entropy, respectively. K44 is the total shear modulus, and is the sum of KU44 and KS44, which are the moduli from contributions of internal energy and entropy, respectively. As can be seen, the internal energy contribution (KU33 and KU44) is mainly responsible for the total elastic moduli. The remarkable increase in moduli (KU33 and KU44) from the internal energy contributes mainly to the increase in the total moduli with increasing m. In contrast, the contribution of entropy (KS33and KS44) to the total elastic moduli is negative or negligible.
Table 1 Components of the dimensionless K33 and K44 moduli for graft copolymers with various values of branch number at τ1 = 0.10
| |
K
U
33
|
K
S
33
|
K
33
|
K
U
44
|
K
S
44
|
K
44
|
|
m = 2 |
2.357 |
0.0214 |
2.378 |
2.051 |
−1.959 |
0.0920 |
|
m = 3 |
4.217 |
−0.289 |
3.928 |
3.021 |
−2.819 |
0.202 |
|
m = 4 |
6.835 |
−0.831 |
6.004 |
4.099 |
−3.585 |
0.514 |
|
m = 5 |
9.070 |
−1.459 |
7.611 |
6.582 |
−4.326 |
2.255 |
We can further understand the elastic behavior by considering the features of graft copolymers. The width of lamellar interface remains practically unchanged when the deformations are small. Meanwhile, few A segments are migrated into the energetically unfavorable B region and vice versa. Thus, the absolute amount of energetically unfavorable AB contacts almost remains the same in the undeformed and deformed structures. The deformations paralleled to the lamellar structure do not change the periodicity of the structure and the free energy of the system. The lamellar structure can be considered as one-dimensional. As a result, the internal energy U upon extension/compression can be written as31
| |  | (22) |
where
α is a constant,
ε is the relative deformation, and
d* is the thickness of the equilibrium lamella. Taking the second derivative of internal energy with respect to the relative deformation, we obtain the value of
KU33, which is given by
| |  | (23) |
The equation indicates that the internal energy contribution to K33 is proportional to the number of branches, but inversely proportional to the domain spacing. As the number of branches increases, while the volume fraction of graft chains is kept the same, the length of single branch chain has a decrease. In addition, the length of backbone blocks between the neighbor junctions becomes shorter with increasing the branch number at fixed τ1. As a result, increasing the number of branches gives rise to the decrease in the lamellar thickness d*.35 By combing this analysis with eqn (23), it can be concluded that the modulus from the contribution of internal energy is greater for the graft copolymers with larger branch number.
Similarly, the internal energy upon shearing is31
| |  | (24) |
where
θ is a measure of the amount of shear and
ε = cot
θ characterizes the relative deformation. The modulus from contribution of internal energy can be obtained by taking the second derivative of free energy with respect to
ε and is given by
| | 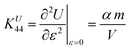 | (25) |
As the equilibrium volume
V is compressed upon increasing the
m, the internal energy contribution to the modulus becomes greater according to
eqn (25). However, the effect is depressed by the entropy contribution to the modulus, which becomes a larger negative value at larger
m (as shown in
Table 1). As a consequence, the contribution of shear modulus to Young's modulus is smaller than that of extensional modulus.
2. Effect of the junction point distribution
Dependence of the moduli of graft copolymers on the junction point distribution is further examined. Table 2 shows the elastic properties of graft copolymers with various values of τ1 at m = 3. The contribution of K33 to the Young's modulus is greater than that of K44. As τ1 value increases, for K33, K44, and E, there is a raise at the smaller τ1 region, a drop at the intermediate τ1 region, and a raise at the larger τ1 region.
Table 2 The dimensionless elastic moduli K33, K44, and E for graft copolymers with various values of τ1 at m = 3
| |
K
33
|
K
44
|
E
|
|
τ
1 = 0.02 |
3.704 |
0.0925 |
0.346 |
|
τ
1 = 0.05 |
3.831 |
0.149 |
0.379 |
|
τ
1 = 0.10 |
3.928 |
0.202 |
0.408 |
|
τ
1 = 0.15 |
3.755 |
0.188 |
0.388 |
|
τ
1 = 0.20 |
3.687 |
0.0700 |
0.336 |
|
τ
1 = 0.25 |
3.608 |
0.0767 |
0.332 |
|
τ
1 = 0.30 |
3.360 |
0.0850 |
0.315 |
|
τ
1 = 0.35 |
3.215 |
0.0890 |
0.304 |
|
τ
1 = 0.40 |
3.313 |
0.134 |
0.329 |
|
τ
1 = 0.42 |
3.362 |
0.156 |
0.342 |
To further understand the effect of the τ1 on the elastic properties, we decompose the moduli KU33 and KU44 into the contribution from the internal energy per block according to eqn (15), because the total moduli are mainly determined by the contribution of internal energy. Fig. 6 displays the contributions of internal energy change Ui from blocks between τi−1 and τi to the total free energy change as a function of the relative deformation upon the extension/compression and shear of the graft copolymers with m = 3 and τ1 = 0.15. The curves of U1 and U2 are similar to U4 and U3, respectively, indicating that the modulus KU133 (KU233) is almost identical to KU433 (KU333). It is ascribed to the fact that the architecture of graft copolymers is symmetric and the lengths of two free end blocks are equal. For the graft copolymers with the architecture parameters m = 3 and τ1 = 0.15, the lengths of free end blocks and the inner blocks are 0.15 and 0.35, respectively. The contributions of internal energy U2 and U3 to total free energy appear to be greater in comparison with those of U1 and U4.
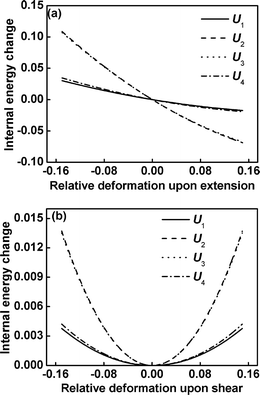 |
| | Fig. 6 The internal energy change Ui (in units of kBT) for blocks between τi−1 and τiversus the relative deformation for extension/compression (a) and shear (b) of graft copolymers at m = 3 and τ1 = 0.15. | |
The contribution of internal energy change U1 as a function of the relative deformation upon extensional/compression and shear of graft copolymers with various values of τ1 at m = 3 is illustrated in Fig. 7. For the graft copolymers with τ1 = 0.05, corresponding to the shorter free end blocks, the contribution of internal energy change U1 to the total free energy change is smaller. As the length of free end blocks gradually increases, the contribution of internal energy U1 to the total free energy becomes marked. In the case of τ1 = 0.40, corresponding to the longer free end blocks, the total free energy arises almost from the internal energy for the free end blocks.
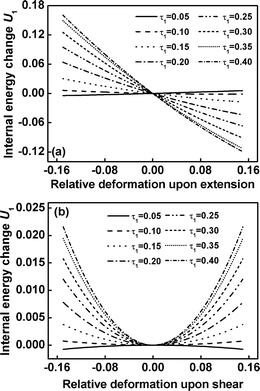 |
| | Fig. 7 The internal energy change U1 (in units of kBT) for block between τ0 and τ1 versus the relative deformation for the extension/compression (a) and shear (b) of graft copolymers with various values of τ1 at m= 3. | |
Table 3 shows the moduli from the individual contribution of the different blocks of backbone obtained by analyzing the internal energy Ui. The moduli contributed from entropy are also listed. In the table, KUi33 are the extensional moduli from the contribution of internal energy for blocks between τi−1 and τi. KUE33 and KUC33 are the extensional moduli from the contributions of the entropy of the backbone end point and conformation, respectively. KUi44 are the shear moduli from the contribution of internal energy for blocks between τi−1 and τi. KUE44 and KUC44 are the shear moduli from the contributions of entropy of backbone end point and conformation, respectively. When τ1 is smaller, corresponding to the longer inner “chain”, the total value of KU33 (KU44) arises mainly from the contributions from the inner blocks KU233 and KU333(KU244and KU344). With an increase in τ1, the length of free end blocks can be comparable with that of the inner blocks. The difference in moduli contributed from the free end blocks and inner blocks becomes small. When τ1 is larger, corresponds to the longer free end “chain”, the contribution of free end blocks to the total modulus becomes dominant and that of inner blocks becomes negative. Therefore, the moduli from the contributions of internal energy Ui depend on the length of blocks between τi−1 and τi. In other words, the modulus KU33 (KU44) from the contribution of total internal energy is associated with the total length of backbone. When the junctions are redistributed (τ1 is changed), the lengths of free end blocks and inner blocks change, but the total length of backbone is kept invariable. Thus, the moduli from the contribution of total internal energy do not have a significant change as τ1 varies from 0 to 0.50. Under this condition, the contribution of entropy to the total modulus plays a role in tuning the mechanical properties of graft copolymers. As shown in Table 3, the modulus from the contribution of entropy at smaller value of τ1 is smaller in comparison with those at intermediate or larger values of τ1(the entropy contribution is negative). This results in the larger value of Young's modulus when τ1 is smaller.
Table 3 Components of dimensionless K33 (a) and K44 (b) for graft copolymers with various values of τ1 at m = 3
| (a) |
K
U
1
33
|
K
U
2
33
|
K
U
3
33
|
K
U
4
33
|
K
S
E
33
|
K
S
C
33
|
K
33
|
|
τ
1 = 0.05 |
0.0391 |
1.914 |
1.907 |
0.0709 |
−0.0612 |
−0.0390 |
3.831 |
|
τ
1 = 0.10 |
0.212 |
1.848 |
1.833 |
0.324 |
−0.163 |
−0.126 |
3.928 |
|
τ
1 = 0.15 |
0.576 |
1.773 |
1.764 |
0.690 |
−0.309 |
−0.739 |
3.755 |
|
τ
1 = 0.20 |
0.896 |
1.492 |
1.498 |
0.898 |
−0.302 |
−0.795 |
3.687 |
|
τ
1 = 0.25 |
1.257 |
1.142 |
1.134 |
1.179 |
−0.278 |
−0.826 |
3.608 |
|
τ
1 = 0.30 |
1.514 |
0.689 |
0.683 |
1.540 |
−0.301 |
−0.765 |
3.360 |
|
τ
1 = 0.35 |
1.628 |
0.355 |
0.332 |
1.637 |
−0.346 |
−0.391 |
3.215 |
|
τ
1 = 0.40 |
1.866 |
−0.118 |
−0.0956 |
1.938 |
−0.348 |
0.0703 |
3.313 |
| (b) |
K
U
1
44
|
K
U
2
44
|
K
U
3
44
|
K
U
4
44
|
K
U
E
44
|
K
U
C
44
|
K
44
|
|
τ
1 = 0.05 |
−0.0668 |
1.495 |
1.442 |
−0.00916 |
−0.178 |
−2.534 |
0.149 |
|
τ
1 = 0.10 |
0.0663 |
1.441 |
1.408 |
0.106 |
−0.116 |
−2.703 |
0.202 |
|
τ
1 = 0.15 |
0.334 |
1.220 |
1.202 |
0.375 |
−0.230 |
−2.712 |
0.188 |
|
τ
1 = 0.20 |
0.716 |
0.884 |
0.879 |
0.710 |
−0.371 |
−2.748 |
0.0700 |
|
τ
1 = 0.25 |
1.070 |
0.512 |
0.518 |
1.098 |
−0.491 |
−2.630 |
0.0767 |
|
τ
1 = 0.30 |
1.400 |
0.170 |
0.180 |
1.450 |
−0.579 |
−2.536 |
0.0850 |
|
τ
1 = 0.35 |
1.731 |
−0.146 |
−0.122 |
1.739 |
−0.638 |
−2.475 |
0.0890 |
|
τ
1 = 0.40 |
1.914 |
−0.296 |
−0.284 |
1.921 |
−0.714 |
−2.407 |
0.134 |
Discussion
In our theoretical calculations, we found that the graft copolymers with the larger branch number have the better elastic properties (as shown in Fig. 4). Some experimental evidences are available in the literature, supporting such theoretical predications of the mechanical properties of graft copolymers. Peiffer and Rabeony investigated the structure-property relationships of graft copolymers based on the poly(ethyl acrylate) as backbone and polystyrene as grafts.6 They found that an increase in branch number leads to enhanced mechanical properties. Recently, Gido and co-workers synthesized a series of well-defined graft copolymers with various molecular architectures.7–9 They studied the effects of molecular architectures on the mechanical properties and morphologies of the graft copolymers. A linear increase in the elastic moduli with increasing branch number was found in their studies. In our theoretical predictions, the tensile modulus has an increase with increasing the number of branches (as shown in Fig. 4), which are qualitatively consistent with the findings of experiments. However, the dependence of the Young's modulus on the branch number is non-linear in our calculations. Such discrepancies between our results and experimental data can be attributed to the simple SCFT model, which has not considered the fluctuation effects, actual sizes of the monomers, and polydispersity etc.44–46 In addition, we should emphasize that the calculations were performed in the melt state under small deformation. As for the non-melt system, the elastic properties cannot be predicted directly by the method combined by SCFT and linear elasticity model. But extending the results obtained from the melt state to non-melt situation would be a fairly “hand-waving” argument.
In our previous study, we examined the fraction of bridged conformation (the neighbor junctions are anchored at different domains) and the number of bridged chains per unit area, which are supposed to be associated with the mechanical properties of graft copolymers,35 as functions of the number of branches and the distribution of junction points. The fraction of bridged conformation shows a tendency of decrease with increasing τ1 and m. The number of bridged chains per unit area increases with increasing m. However, according to the present study, the bridged and looped conformations are not the primary factor determining the elastic moduli of graft copolymers with smaller value of τ1, as the system is dependent upon the quasi-equilibrium melt distortions in the linear regime. Gido and co-workers have reached a similar conclusion through analyzing the phase behavior of the graft copolymers.47–50 They established a constituting block copolymer hypothesis to explain the phase behavior of graft copolymers. The constituting block copolymer is the single graft copolymer by snipping the midpoint of the looped and bridged “chain”. The phase behavior of graft copolymers has analogy to that of the constituting block copolymers. For graft copolymers, the bridged and looped backbone blocks are quite relaxed away from the interface. In addition, the looped and bridged conformations are not under tension upon small distortion. Therefore, the conformations have a weak influence on the elastic moduli at small deformations close to the equilibrium state. The internal energy contributes mainly to the elastic moduli. We should note that the bridged conformation could play a significant role in determining the mechanical properties at fracture when the bridged blocks must be pulled out of the microstructures.
The graft copolymers have two free end blocks. The connectivity between the chain conformation and the mechanical properties does not consider the contribution of free end “chain”.51 As τ1 approaches 0.5, the length of inner blocks becomes short and the fraction of bridged conformation has a sharp decrease.35 The contribution of free end blocks cannot be neglected. Under this condition, the models, which utilize the fraction of bridged conformation to predict the mechanical properties of copolymer melts, are not suited to represent the real situation.51 In our calculations, the moduli (KU133 and KU433) from the contributions of free end blocks are associated with their lengths (as shown in Table 3). The total moduli of graft copolymers with larger value of τ1 depend mainly on the free end blocks. This is consistent with the real situation.
As for the diblock copolymers, the mechanical properties cannot be tailored by other parameters, when the thermodynamics variables (χN and fA) are fixed.29 In comparison with the block copolymers, two parameters (m and τ1) have distinct impact on the mechanical properties of graft copolymers. As shown in the present work, an increase in the number of branches can result in an improvement of the elastic moduli for graft copolymer melts. Meanwhile, changing the distribution of junction points can also tune the mechanical properties of graft copolymers. The SCFT calculation results are qualitatively consistent with the findings of experiments and may provide useful information for designing the graft copolymers with enhanced properties. However, the approach combined with SCFT and linear elasticity theory does not yield the direct relation of the free energy in deformation system to the experimentally observed moduli due to the lack of fields describing the viscoelasticity of polymer fluids. Thus, there is certain room for further improvement of self-consistent field theory. For example, the elastic stress and strain fields, which can handle the entanglement phenomenon in fluids, might be incorporated into the theory framework.52 Under this condition, more information regarding the relation between the structure and property of the graft copolymers may be obtained through the SCFT calculations.
Conclusions
We adopted the real-space self-consistent field theory to calculate the linear elastic moduli of graft copolymer melts in the lamellar phase by quasi-statically deforming the structures. The extensional and shear moduli are examined as functions of the architecture parameters of graft copolymers (the number of branches and the distributions of junction points). The value of Young's modulus depends mainly on the extensional modulus, and the contribution from the shearing modulus to Young's modulus is small or negligible. Increasing the number of branches gives rise to the enhancement in the mechanical properties. The modulus can be decomposed into the contributions from the internal energy and entropy portions. The values of extensional and shear moduli depend mainly on the contribution of internal energy. The contribution of entropy to the elastic moduli is negative or negligible. Meanwhile, the moduli of graft copolymers are also dependent on the distribution of junction points. To understand the effect of junction distribution on the moduli, the internal energy is broken up into the energy from respective blocks of backbone. It was found that the moduli contributed from the internal energy of different blocks of the backbone are associated with their lengths.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (50673026, 20574018). Support from the Doctoral Foundation of the Education Ministry of China (Grant No. 20050251008) and Projects of the Shanghai Municipality (06SU07002, 0652nm021, 082231, and B502) are also appreciated.
References
-
M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford Science Publications, New York, 1986 Search PubMed.
- T. C. B. McLeish, Adv. Phys., 2002, 51, 1379 CrossRef CAS.
- D. Gersappe, D. Irvine, A. C. Balazs, Y. Liu, J. Sokolov, M. Rafailovich, S. Schwarz and D. G Peiffer, Science, 1994, 265, 1072 CrossRef CAS.
- J. P. Kennedy and J. M. Delvaux, Adv. Polym. Sci., 1981, 38, 141 CAS.
-
J. P. Kennedy, in Thermoplastic Elastomers, ed. N. R. Legge, G. Holden, R. Quirk and H. E. Schroeder, Hanser, Munich, 1996 Search PubMed.
- D. G. Peiffer and M. Rabeony, J. Appl. Polym. Sci., 1994, 51, 1283 CrossRef CAS.
- R. Weidisch, S. P. Gido, D. Uhrig, H. Iatrou, J. W. Mays and N. Hadjichristidis, Macromolecules, 2001, 34, 6333 CrossRef CAS.
- Y. Zhu, R. Weidisch, S. P. Gido, G. Velis and N. Hadjichristidis, Macromolecules, 2002, 35, 5903 CrossRef CAS.
- Y. Zhu, E. Burgaz, S. P. Gido, U. Staudinger, R. Weidisch, D. Uhrig and J. W. Mays, Macromolecules, 2006, 39, 4428 CrossRef CAS.
- Z. G. Wang, J. Chem. Phys., 1994, 100, 2298 CrossRef CAS.
- C. Yeung, A. C. Shi, J. Noolandi and R. C. Desai, Macromol. Theory Simul., 1996, 5, 291 CAS.
- I. W. Hamley, Phys. Rev. E, 1994, 50, 2872 Search PubMed.
- G. G. Pereira, J. Chem. Phys., 2002, 117, 1878 CrossRef CAS.
- G. A. Buxton and A. C. Balazs, J. Chem. Phys., 2002, 117, 7649 CrossRef CAS.
- E. Helfand, J. Chem. Phys., 1975, 62, 999 CrossRef CAS.
- K. M. Hong and J. Noolandi, Macromolecules, 1981, 14, 727 CrossRef CAS.
- M. W. Matsen, Soft Matter, 2006, 2, 1048 RSC.
- G. H. Fredrickson, Soft Matter, 2007, 3, 1329 RSC.
- M. W. Matsen and M. Schick, Phys. Rev. Lett., 1994, 72, 2660 CrossRef CAS.
- F. Drolet and G. H. Fredrickson, Phys. Rev. Lett., 1999, 83, 4317 CrossRef CAS.
- M. D. Lefebvre, M. Olvera de la Cruz and K. R. Shull, Macromolecules, 2004, 37, 1118 CrossRef CAS.
- X. Ye, T. Shi, Z. Lu, C. Zhang, Z. Sun and L. An, Macromolecules, 2005, 38, 8853 CrossRef CAS.
- G. M. Grason and R. D. Kamien, Phys. Rev. E, 2005, 71, 051801 CrossRef.
- M. W. Matsen and C. Barrett, J. Chem. Phys., 1998, 109, 4108 CrossRef CAS.
- V. Pryamitsyn and V. Ganesan, J. Chem. Phys., 2004, 120, 5824 CrossRef CAS.
- R. B. Thompson, V. V. Ginzburg, M. W. Matsen and A. C. Balazs, Science, 2001, 292, 2469 CrossRef CAS.
- J. Y. Lee, R. B. Thompson, D. Jasnow and A. C. Balazs, Phys. Rev. Lett., 2002, 89, 155503 CrossRef.
- L. Zhang, J. Lin and S. Lin, Macromolecules, 2007, 40, 5582 CrossRef CAS.
- C. A. Tyler and D. C. Morse, Macromolecules, 2003, 36, 3764 CrossRef CAS.
- R. B. Thompson, K. Ø. Rasmussen and T. Lookman, J. Chem. Phys., 2004, 120, 3990 CrossRef CAS.
- R. B. Thompson, K. Ø. Rasmussen and T. Lookman, Nano Lett., 2004, 4, 2455 CrossRef CAS.
- Y. Jiang, R. Huang and H. Liang, J. Chem. Phys., 2005, 123, 124906 CrossRef.
- R. Huang, Y. Jiang and H. Liang, ChemPhysChem, 2006, 7, 1950 CrossRef CAS.
- P. Maniadis, T. Lookman, E. M. Kober and K. Ø. Rasmussen, Phys. Rev. Lett., 2007, 99, 048302 CrossRef CAS.
- L. Zhang, J. Lin and S. Lin, J. Phys. Chem. B, 2007, 111, 351 CrossRef CAS.
- L. Zhang, J. Lin and S. Lin, J. Phys. Chem. B., 2007, 111, 9209 CrossRef CAS.
-
L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Butterworth-Heinemann, Oxford, 3rd edn, 1999 Search PubMed.
- G. H. Fredrickson, V. Ganesan and F. Drolet, Macromolecules, 2002, 35, 16 CrossRef CAS.
- G. Tzeremes, K. Ø. Rasmussen, T. Lookman and A. Saxena, Phys. Rev. E, 2002, 65 Search PubMed 041806.
- K. Ø. Rasmussen and G. Kalosakas, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 1777 CrossRef CAS.
-
M. Frigo and S. G. Johnson, The Fast Fourier Transform in the West 2.1.3, MIT, Cambridge, MA, 2000 (http://www.fftw.org) Search PubMed.
- M. W. Matsen and F. S. Bates, J. Chem. Phys., 1997, 106, 2436 CrossRef CAS.
- A. Shinozaki, D. Jasnow and A. C. Balazs, Macromolecules, 1994, 27, 2496 CrossRef CAS.
- S. T. Milner, Macromolecules, 1994, 27, 2333 CrossRef CAS.
- D. M. Patel and G. H. Fredrickson, Phys. Rev. E, 2003, 65, 051802 CrossRef.
- S. Qi, A. K. Chakraborty, H. Wang, A. A. Lefebvre, N. P. Balsara, E. I. Shakhnovich, M. Xenidou and N. Hadjichristidis, Phys. Rev. Lett., 1999, 82, 2896 CrossRef CAS.
- S. P. Gido, C. Lee, D. J. Pochan, S. Pispas, J. W. Mays and N. Hadjichristidis, Macromolecules, 1996, 29, 7022 CrossRef CAS.
- M. Xenidou, F. L. Beyer, N. Hadjichristidis, S. P. Gido and N. B. Tan, Macromolecules, 1998, 31, 7659 CrossRef CAS.
- C. Lee, S. P. Gido, Y. Poulos, N. Hadjichristidis, N. B. Tan, S. F. Trevino and J. W. Mays, Polymer, 1998, 39, 4631 CrossRef CAS.
- F. L. Beyer, S. P. Gido, C. Buschl, H. Iatrou, D. Uhrig, J. W. Mays, M. Y. Chang, B. A. Garetz, N. P. Balsara, N. B. Tan and N. Hadjichristidis, Macromolecules, 2000, 33, 2039 CrossRef CAS.
- K. Ch. Daoulas, D. N. Theodorou, A. Roos and C. Creton, Macromolecules, 2004, 37, 5093 CrossRef CAS.
- G. H. Fredrickson, J. Chem. Phys., 2002, 117, 6810 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2009 |
Click here to see how this site uses Cookies. View our privacy policy here. 


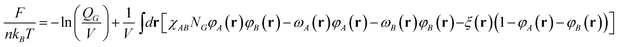

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qB(r,1)
qB(r,1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j = 1,2,⋯,m qA(0) (r,0) = 1
j = 1,2,⋯,m qA(0) (r,0) = 1