From genes to cells to tissues—modelling the haematopoietic system

Abstract

Haematopoiesis (or blood formation) in general and haematopoietic stem cells more specifically represent some of the best studied mammalian developmental systems. Sophisticated purification protocols coupled with powerful biological assays permit functional analysis of highly purified cell populations both in vitro and in vivo. However, despite several decades of intensive research, the sheer complexity of the haematopoietic system means that many important questions remain unanswered or even unanswerable with current experimental tools. Scientists have therefore increasingly turned to modelling to tackle complexity at multiple levels ranging from networks of genes to the behaviour of cells and tissues. Early modelling attempts of gene regulatory networks have focused on core regulatory circuits but have more recently been extended to genome -wide datasets such as expression profiling and ChIP-sequencing data. Modelling of haematopoietic cells and tissues has provided insight into the importance of phenotypic heterogeneity for the differentiation of normal progenitor cells as well as a greater understanding of treatment response for particular pathologies such as chronic myeloid leukaemia. Here we will review recent progress in attempts to reconstruct segments of the haematopoietic system. A variety of modelling strategies will be covered from small-scale, protein–DNA or protein–protein interactions to large scale reconstructions. Also discussed will be examples of how stochastic modelling may be applied to multi cell systems such as those seen in normal and malignant haematopoiesis.

---

Samuel Foster

Samuel Foster is a Medical Research Council funded PhD student in the Göttgens laboratory in the Department of Haematology, within the Cambridge Institute for Medical Research. His project involves investigating genome-wide transcriptional regulation within blood stem cells, as well as in depth analysis of individual candidate regulatory regions. Using in silico, in vitro and in vivo techniques, he hopes to identify novel underlying patterns within the transcriptional networks that control blood stem cells.

S. Helen Oram

S. Helen Oram is a Kay Kendall Clinical Research Fellow in the Department of Haematology at the University of Cambridge. She has an interest in the mechanisms and effects of aberrations in transcriptional control of key haematopoietic regulators in T-acute lymphoblastic leukaemia. She has completed clinical training in haematology at University College Hospital London where her primary interest was haemato-oncology.

Nicola Wilson

Nicola Wilson is a post-doctoral research associate in the Göttgens laboratory of the Department of Haematology within the Cambridge Institute for Medical Research. She undertook a PhD at the University of Leeds, looking at the transcriptional regulation of genes critical within haematopoietic lineage choice. Her current research interests are focused around understanding the transcriptional networks controlling blood stem cells with a particular interest in the identification of combinatorial regulatory codes.

Berthold Göttgens

Berthold Göttgens is Reader of Molecular Haematology at the University of Cambridge. His laboratory is based in the Cambridge Institute of Medical Research and forms part of a wider consortium of groups studying normal blood stem cells and leukaemia. The particular focus of the Göttgens group is the integration of experimental and computational approaches for further understanding of the transcriptional control of blood stem cells.

---

Introduction

Haematopoiesis represents one of the best studied mammalian developmental systems and studies of blood cells have been instrumental for advances in multiple areas of biomedical research. For example, haematopoietic stem cells (HSCs) are the best-understood adult stem cells and many of the paradigms for the wider field of stem cell biology have been derived from the study of HSCs.¹ Similarly, early paradigmatic gene loci for studying mammalian gene regulation have been the α- and β-globin gene loci which produce the protein chains required for oxygen transport by red blood cells.² Moreover, many seminal advances in our understanding of the molecular mechanisms of disease have also been achieved in the study of haematopoietic pathologies, such as the role of chromosome translocations in the development of cancer first recognised as the so-called Philadelphia chromosome arising from the 9:22 translocation found in chronic myeloid leukaemia.³ The principal reasons for the sustained high impact of haematopoiesis research lies in the fact that blood cells are easily accessible compared to other tissues and powerful assays to determine the biological functions of diverse blood cell types have been developed including those involving transplantation. Research over the last 50 years has therefore provided a roadmap of blood cell differentiation with unrivalled precision (see Fig. 1) compared to other organ systems. To date more than 50 different cell types are described, all of them functionally defined with advanced purification protocols involving sophisticated technologies such as immunomagnetic selection and fluorescence activated cell sorting.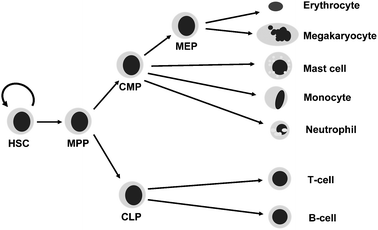

Fig. 1 Simplified haematopoietic tree. The haematopoietic stem cell is able to self-renew and give rise to multipotent progenitor cells, which in turn give rise to more restricted progenitors and ultimately the terminally differentiated cells of both the myeloid and lymphoid lineages. The true haematopoietic tree as it is currently understood contains over 50 different cell types. HSC = haematopoietic stem cell, MPP = multi-potent progenitor, CLP = common lymphoid progenitor, CMP = common myeloid progenitor, MEP = megakaryocyte-erythroid progenitor.

Given its status as a model system for mammalian development and because of the biomedical impact of haematological disease, increasing effort has been placed on developing models that describe various aspects of the haematopoietic system. The underlying events of the haematopoietic system can be modelled at multiple levels. Analysis can involve study of the intricate workings of core regulatory circuits, through investigation on an -omic and cellular level, up to examination of processes on a tissue-wide dimension. Work undertaken on all these levels has provided a greater understanding of the haematopoietic system, with each casting light on a fragment of the complex regulatory processes that underpin the haematopoietic hierarchy. Here we provide an overview of recent efforts to construct network models at various levels based on specific experimental, as well as theoretical examples, thus outlining how modelling the haematopoietic system is providing new insights that are relevant to both fundamental and translational biomedical research.

Core regulatory circuits

Underpinning the molecular control of haematopoiesis are core circuits of regulatory networks that, when unified, define the gene regulatory state of a particular cell. Whilst studying entire gene regulatory networks is often not practical, tackling individual sub-networks can provide a means to uncover fundamental principles such as the way in which key regulators are connected with each other. Research into these core regulatory circuits often follows a pattern referred to as a “bottom-up” approach.⁴ The process usually starts with a single protein–protein or protein–DNA interaction. The network is then constructed piece by piece fanning outwards from the original focal point. Prime examples of this, in the study of the haematopoietic system, are the regulatory interactions between the transcription factors Gata-1 and PU.1,^5–8 a triad of transcription factors composed of Scl/Tal1, Gata-2 and Fli1⁹ and the relationship between Gata-1 and the erythropoietin receptor (EpoR).^10–12 The two former interactions have been reviewed elsewhere^4,13,14 and we therefore focus our discussions here on the latter.

Both Gata-1 and EpoR are critical for erythropoiesis, i.e. the formation of red blood cells.^15–18 Palani and Sarkar describe the process of creating a mathematical model of the EpoR/Gata-1 core network, crucial to erythropoietic commitment, using an array of biochemical and kinetic data.¹⁹ The model is built upon the previously described relationship between EpoR and Gata-1.^10–12 Of the 44 parameters used in the model, the vast majority were obtained directly from the literature, others were refined from values in the literature or estimated using Gata-1 DNA binding time-course activity assays.¹⁹ The resulting mathematical model presents a bidirectional link between the lineage-specific receptor, EpoR, and the transcription factor Gata-1. The study is careful to make clear that whilst providing an insight into the relationship and mechanics of a small set of crucial erythropoietic molecular effectors, it only covers a small fraction of the full network controlling the process of erythropoiesis. Nevertheless, several aspects of the resulting model are worthy of note. The network described can exhibit ultrasensitivity and bistability between the two molecular effectors. This is a consequence of the links made between the regulation of EpoR transcription by Gata-1 and the activation of Gata-1 by the EpoR–PI3K/AKT cascade. This positive feedback loop provides a level of autoregulation that can be fine tuned due to the separation of the activation and synthesis of Gata-1. The model also appears to provide a meaningful link between an extrinsic and an intrinsic regulatory signal in the regulation of cell maturation as well as survival. The construction of this model is a clear example of how a core regulatory network can be modelled from previously described molecular relationships using, in this case, biochemical data.

Modelling from genome -wide expression datasets

Genome -wide modelling of transcriptional regulatory networks has been very successful to date in the study of bacteria and yeast. Recent advances in high-throughput technologies and computational analysis have allowed researchers to start applying this scale of modelling to higher eukaryotic systems, such as haematopoiesis. In particular the ability to study entire genomes/transcriptomes/proteomes means that network reconstruction is no longer restricted to “bottom-up” approaches focusing on core-regulatory circuits but can now be applied on a genome -wide level (“top-down”).

The creation of such large amounts of data has driven a demand for statistical and computational methods that can handle the required analysis. One such algorithm is the ARCANE algorithm which uses an information-theoretic method to analyse microarray expression profiles and identify gene product interactions.²⁰ This method differs from other existing computational methods that also use gene expression data to infer biochemical interactions, by having a low polynomial computational complexity, using the full range of data and not making assumptions about underlying networks.²⁰ This, it is suggested, ensures that ARCANE can identify interactions more accurately and more quickly than its rivals. ARCANE has been used to reconstruct a system-wide transcriptional network for human B cells²¹ from 336 B cell expression profiles, representing normal B cells, B cells transformed to represent B cell tumours and B cells that were experimentally manipulated to be similar to those seen in the lymph node germinal centre. With the resulting network containing ∼129 000 interactions, the number of interactions modelled was clearly at genome scale, which would not be achievable through methods used to study core-regulatory networks. The resulting network described how a small number of highly connected genes interact with most of the genes in the cell. Of interest, the proto-oncogene MYC emerged as one of the largest cellular hubs and was subjected to further in-depth investigation, which showed that >90% of inferred interactions corresponded to interactions seen in in vivo experiments.²¹ Whilst the authors acknowledge that work remains to be done to remove several limitations with the inferred network, the network does provide an example as to the possibilities now open for the construction of genome -wide networks.

Another recent study employing inference of regulatory interactions from genome -wide expression data was centred on an investigation of Toll-like receptor (TLR)-activated macrophages.²² By clustering gene expression data using a k-means algorithm, the authors were able to identify three distinct “waves” of transcription after stimulation by the TLR4 agonist bacterial lipopolysaccharide (LPS). Using the hypothesis that genes clustered through similar expression profiles might share similar cis-regulatory elements, cis-regulatory analysis was performed using the bioinformatic tool MotifMogul.²² The gene cluster with peak expression 1 h after LPS stimulation was predicted to have an over-representation of ATF/CREB binding sites. The only ATF/CREB family member up-regulated by LPS stimulation was ATF3. This observation served as a starting point to study the transcriptional network surrounding ATF3. Using protein–protein interaction maps, a link was made to two other proteins that were previously identified to be involved in TLR signalling, namely NF-κB and AP1,²² thus revealing potential combinatorial regulation downstream of ATF3. A common theme shared between this investigation and the MYC sub-network study is the use of large genome -wide datasets to reconstruct and visualise regulatory networks. However, both studies also agree that in silico inference alone is not yet sufficiently reliable to obviate the need for experimental validation when reconstructing complex networks from genome -wide data.

Reconstructing networks from ChIP-Seq analysis

The primary control of gene expression is exerted by combinatorial interactions of transcription factors with cis-regulatory elements, which together form the building blocks of transcriptional regulatory networks. Regulatory network reconstruction therefore requires the identification of the cis-regulatory elements (enhancers, promoters) and the upstream transcription factors which bind them. Traditional approaches for the identification of regulatory elements are laborious and low-throughput and have recently been superseded by genome -wide analysis taking advantage of 2nd generation sequencing technology, so-called ChIP-Seq (chromatin immunoprecipitation combined with Illumina 1G sequencing). This technique provides a novel method for the identification of genome -wide transcription factor target genes and its early successes have been focused on generating genome -wide maps of binding events for transcription factors involved in mediating pluripotency of embryonic stem cells.^23,24

As the technology is rapidly adopted by other fields, genome -wide catalogues of the binding sites for key haematopoietic transcription factors are generated. One such factor is encoded by the Scl (Tal-1) gene which encodes a basic helix-loop-helix (bHLH) transcription factor required for the specification of HSCs and the differentiation of the erythroid and megakaryocytic lineages.^25–27 Within the blood system, Scl is thought to be a key component of the regulatory networks controlling the specification and subsequent differentiation of HSCs.^9,14 Important upstream transcriptional inputs of murine Scl and its paralogue Lyl1 are Ets and Gata factors, as well as Scl itself.^28–34 Only a handful of direct downstream targets of Scl had been described, including Gata-1,³⁵Runx1,³⁶c-kit³⁷ and α-globin.³⁸ To fully understand the function of Scl within haematopoiesis it is particularly important to gain information on downstream targets at early developmental time points where Scl function is critical. A recent ChIP-Seq screen for Scl targets took advantage of the early progenitor cell line HPC-7 as a model system for blood stem/progenitor cells.³⁹ Stringent filtering of the ChIP-Seq data resulted in the identification of 228 high confidence binding events many of which occurred within or next to genes known to be important within transcription and signalling. To assess the in vivo functionality of regions bound by Scl, comprehensive in vivo validation was performed using F0 transgenic mouse embryos which validated 16 transcription factor genes as bona fide targets of Scl. Moreover, bioinformatic analysis highlighted that the consensus binding sites for several transcription factors were over-represented amongst the Scl-bound regions and subsequent analysis for one of these factors (Gata-2) demonstrated that 15/16 regions bound by Scl were also bound by Gata-2 (see Fig. 2). ChIP-Seq analysis followed by in vivo validation therefore provided a rapid means of clarifying the transcriptional hierarchies of several known haematopoietic regulators (Cbfa2t3h, Cebpe, Nfe2, Zfpm1, Erg, Mafk, Gfi1b, and Myb) as well as providing links to previously unsuspected novel candidate regulators.⁴⁰ Finally, data mining of protein–protein interactions curated from the literature showed extensive protein–protein interactions within this network many of which involved Scl and Gata-2 (see Fig. 2). This observation not only is suggestive of multiple feedback loops at the level of protein complexes but is also highly reminiscent of the embryonic stem cell pluripotency network.

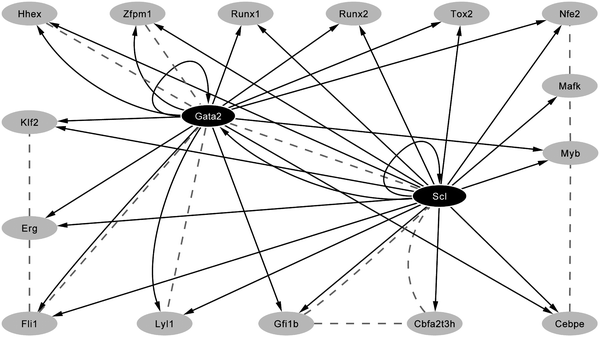Fig. 2 Scl- and Gata2-centric transcriptional network. In vivo validated core network. Each solid line indicates a binding event observed in a ChIP-Seq experiment which has then been functionally validated in transgenic assays, whereas the dashed lines represent protein–protein interactions curated from the literature.⁴⁰

Modelling behaviour of individual cells

Whilst studying regulatory networks by performing biochemical or genomic assays on bulk populations of cells is informative, important information on individual cell variability will be missed. To truly understand the control of cellular behaviour, it is therefore necessary to understand networks at a cellular level. A recent study using the multipotent mouse haematopoietic progenitor cell line EML investigated phenotypic heterogeneity at the cellular and molecular level by correlating phenotype to expression of the cell surface marker stem cell antigen 1 (Sca-1) as well as to the concentrations of key transcription factors. The authors demonstrated that outlying populations selected for either high or low Sca-1 expression levels reconstitute the parental distribution over time when cultured under self-renewing conditions.⁴¹ The Sca-1 outlier populations shared clonality with the entire starting population but varied through distinct transcriptomes. Using flow cytometry three populations of EML cells were isolated, as distinguished by either lowest, middle or highest 15% of Sca-1 expression. Modelling the causes for the distinct subpopulations observed within the clonal parental population led to the conclusion that the pattern was not due to transcriptional noise around a single attractor state. Instead, the cause of the expressional variation within the parental population of cells is probably the result of a system that contains numerous stable states each linked through processes involving stochastic, non-deterministic transitions.

The study illustrated that analysis using whole-population expression averaging may not fully take into account the potential biological roles of outlying subpopulations. This issue was investigated further by analysing whether the heterogeneity of Sca-1 expression observed in the clonal population of EML cells bore any correlation with variable differentiation potential. The fastest rate of erythropoiesis was observed in the Sca-1^low population, with the Sca-1^high population showing the slowest rate. This rate variance reduced as the subpopulations reverted back to the parental expression pattern when placed into culture under self-renewing conditions. Of note, it required almost an additional 2 weeks of culture, after Sca-1 expression appeared consistent between the subpopulations, until the erythropoietic differentiation potential was equal among cultures derived from the 3 subpopulations.

Intrigued by this variation in lineage choice between the Sca-1^low, Sca-1^mid, Sca-1^high populations, the authors set out to link this variability to protein levels known to affect erythroid lineage differentiation. Cross-antagonism between the Gata-1 and PU.1 transcription factors was known to affect erythroid lineage choice. Interestingly, Sca-1^high cells exhibited lowest Gata-1 expression and had higher PU.1 levels. Using granulocyte-macrophage colony-stimulating factor and interleukin-3, it was observed that, for the Sca-1 subpopulations, erythropoietic differentiation rates negatively correlated with myeloid differentiation rates. This showed that, at least on a small scale, heterogeneity within a clonal population can provide various cellular states each with distinct biological functions. The question remained whether this was small in scale, involving only Gata-1 and PU.1, or whether it was in fact a genome -wide pattern. Importantly, expression profiling of the three Sca-1 subpopulations revealed that the effect is genome -wide. Using significance analysis of microarrays (SAM), more than 3900 genes were highlighted as differentially expressed between the Sca-1^low and Sca-1^high populations. A further expression profile was taken from a population of cells 7 days after treatment with erythropoietin (Epo). This revealed that of the three Sca-1 subpopulations the Sca-1^low population was most similar to the fully differentiated Epo treated cells. However, the ability of all three subpopulations, including Sca-1^low, to revert back to parental Sca-1 expression, shows that these subpopulations are not pre-committed to any particular lineage choice. Following this work, what may previously have been dismissed as random fluctuations in gene expression causing short-lived cellular phenotypes or cellular gene expression noise,^42–47 can now be seen as a cellular-wide network, with each phenotypic subpopulation having its own biological function and potential.

Modelling of cell populations/tissues

There are a number of challenges that are faced when attempting to explain the behaviour of cells within tissues and populations of cells. These include the need to account for the macro effect of individual random events, that the subject of study may be inaccessible or unquantifiable and that there may be a desire to predict the future trajectory of a dynamic state. Importantly, by using validated mathematical models, it may be possible to tackle the inherent unpredictability of complex biological systems. The basis of stochastic modelling is to define the behaviour of each element in a system, based on its current state, and the state of the environment. This behaviour is formulated as stochastic differential equations, which describe the random behaviour of these elements, and essentially assign probability distributions to their states. They are defined behavioural assumptions based on educated guesses or real-world observations. From the stochastic differential equations, simulations may be run in order to determine the macro behaviour of the system over time. By comparing the output of the simulation with real-life observations, one can support or refute the model. The simulation may also give clues as to the limitations of the model or to areas that are less predictive and so point towards initial assumptions/equations that need to be adjusted to give better model performance. Stochastic modelling has been used to address a variety of questions in the field of haematopoiesis, such as (i) the behaviour of HSCs in the niche and in transplantation assays, (ii) the emergence of dominant clones in normal and malignant haematopoiesis, (iii) responses to treatment and the emergence of resistance to therapy in haematopoietic malignancies and (iv) determining optimal conditions for effective gene therapy.

Throughout the lifespan of the organism, haematopoietic tissue must produce a continuous supply of the correct number of differentiated, fully functional blood cells of each of the various types seen in adult blood. The mature cells are fully specified and, as such, are generally incapable of self-renewal or de-differentiation and re-differentiation into an alternative cell type. The source of all these various cells is the HSC. However, as the definition of an HSC is a functional one (they must be able to proliferate, differentiate, self-renew, and be able to reconstitute the blood system after marrow ablation), it is only possible to assign these characteristics to any one cell of interest after subjecting it to the appropriate biological assay during which the attributes and qualities of that cell will inevitably be altered. Another obstacle is that the total number of HSCs predicted in an organism is low, of the order of 100–200 HSCs per kg⁴⁸ meaning that an adult male human may have only 10 000 HSCs to sustain haematopoiesis throughout life. Attempting to locate and identify them is, therefore, a challenge in itself as is amassing a meaningful enough number of cells on which to perform multiple replicated assays. The heterogeneous nature of cell surface markers and of functional properties of stem cells adds further to the complexity of the situation.

By turning to stochastic calculus, one might attempt to generate a model that takes account of observations made of the output of the haematopoietic system, the maturing haematopoietic cells, and of observations made of the effect of the microenvironment on stem cells to predict the early, currently unobservable, behaviour of these cells. The inter-relationship between the current state and current behaviour of the stem cells, as described by a system of partial differential equations, is sufficiently complex such that they cannot be easily analytically solved and thus the behaviour of the system must be observed instead through simulation where random behaviour of the stem cells defined by the partial differential equations is simulated in discrete time space.

There has been interest in the application of stochastic calculus to HSC behaviour for many decades.^49,50 Much of the recent work in this field has been published by Roeder and colleagues who, in 2002,⁵¹ proposed a model whereby it was assumed that cells could inhabit and change state between two growth environments, one which promoted a quiescent state and the other that promoted a proliferating state (see Fig. 3). It was assumed that each state had a definably, but random, affinity to remain in the non-proliferating compartment or the cycling status. It was noted that cells in the non-proliferating compartment were likely to be attached to and receiving signals from stroma, whereas the cells in the proliferating compartment were likely to have detached. A number of assumptions were then overlaid on the model based on the propensity of any one cell to attach or detach from stroma in any given unit of time. Probability distributions for cycling times and attachment affinity were based on published data and in vitro observations. The resultant model was shown to accurately represent the contribution of donor stem cells to mature blood formation in chimeric animals following haematopoietic stem cell transplantation,⁵² the emergence of a dominant clone^53–56 as well as the variability noted in engraftment potential and replating ability of stem cells dependant on variations in the microenvironment.⁵⁷

Fig. 3 Representation of the Roeder/Glauche model.^51,67 The model shown above is based on the assumption that the development of haematopoietic stem cells depends upon microenvironmental signals. Accordingly, two different growth environments, one promoting ongoing ‘stemness’ and another promoting division and differentiation are proposed. The variable likelihood of the cells transiting from one environment to the other is modelled as a stochastic process, with transition probabilities dependant on the individual cellular affinity for its current environment and on the effect of attractors drawing cells towards the other state.

In order to test the ability of the model to accurately represent the variable clonogenic and repopulation potential of HSCs after bone marrow transplantation, Roeder et al.⁵² have shown that their model correctly demonstrated the clonal competitiveness and unstable chimerism seen in recipients after chimera formation and may also predict the effects of cytokine-induced disturbance of HSC contributor proportions in stable chimeras. This work has subsequently been extended^48,58–61 in an attempt to estimate the degree of clonal heterogeneity seen after transplant, to predict competitive differences between HSCs and to predict the end clonal composition of the recipient and was shown to closely follow experimental data.^58–61

An extension of the Roeder model is to consider that there may be more than one attractor drawing the stem cell away from the quiescent/self-renewing compartment. The Kirkland model⁶² uses a branching Markov process which models a population of stem cells proceeding randomly in a fashion entirely independent of its condition in the past. It takes account of the prospect that, following division, some of the progeny of a stem cell may acquire new and different properties which may also be modelled independently of each other and of the parent cell’s behaviour. The model has been validated by analysing the output of the stem cell compartment and accurately predicted fluctuations in contributions to that output by progressively changing dominant clones.

Modelling haematopoietic pathologies

The Roeder model can accurately model the experimental observation that dominant clones may emerge and disappear without significant negative effect in normal haematopoiesis^51,53 and, although a different mathematical approach has been employed, the Kirkland model⁶² also shows a progressive loss of diversity towards oligoclonality which closely models experimental data.^50,60 Stochastic modelling has also been applied to the challenge of deciphering the effects of malignant transformation of a single HSC such that it was rendered able to survive in the absence of the usual required microenvironment. By modelling the effect of 1 neoplastic HSC in a population of 10 000 HSCs a vast array of possible outcomes may be seen, from swift dominance of haematopoiesis by the neoplastic clone to prompt exhaustion and extinguishment of the neoplastic HSCs and their progeny.⁶³ Surprisingly, this second scenario was by far the most common outcome of simulation with 25% and 9% of malignant clones in mice and in cats, respectively, disappearing within the first week. Mean times to clonal dominance were also estimated and all results correlated with experimental data.^{48,60,64–66}

Chronic myeloid leukaemia (CML) and its specific therapy using the bcr-abl targeted tyrosine kinase inhibitorimatinib has emerged as the paradigm of molecularly targeted cancer therapy. Stochastic modelling has been applied with good effect to aspects of the disease as diverse as accurate modelling of the progressive dominance of the malignant clone,^54–56 changes in bcr-abl transcript levels,^54–56,67 the effects of commencing and terminating imatinib treatment^55,56 and the emergence of resistance to therapy.⁶⁸ Of principal interest is that both the Roeder⁵⁴ and the Michor⁶⁸ models accurately represent one of the most significant challenges in CML therapy, the persistence of low-level residual disease despite therapy.

In addition to exploring the utility of modelling in the context of haematological malignancies, similar approaches have been applied to the field of gene therapy. There are a great number of challenges in the path of a safe and effective gene therapy program involving the haematopoietic system; how to identify and acquire adequate numbers of HSCs, how to efficiently deliver the DNA to the HSC to be certain of adequate expression in the recipient, how many HSCs must be transplanted to be assured of adequate engraftment to alleviate clinical symptoms. Abkowitz et al.⁵⁸ utilised a computer simulated stochastic model in the late 1990s to predict the outcome of altering these variables. Modelling exercises such as these provided vital information as to the eventual impact of vector choice, HSC number transduced and transplanted at a time where the technical capability to perform the experiments in vivo was still in development, and their predicted outcomes have since been supported by experimental data.^{58,61,63,69,70}

Concluding remarks

The reconstruction of networks underpinning the haematopoietic system has provided important insights as to how key haematopoietic regulators interact and control important differentiation decisions. Studies of core regulatory circuits will continue to illuminate detailed molecular control mechanisms but will increasingly be complemented with genome -scale models inferred from genome -wide expression profiling as well as protein–DNA and protein–protein interaction datasets. However, the need for biological validation of computationally inferred regulatory relationships is likely to remain essential in the foreseeable future, suggesting an urgent need for the development of new experimental strategies that provide the level of through-put required for the validation of genome -scale inferred networks. Modelling haematopoiesis at the level of cell populations and whole tissues has already yielded valuable new insights into the dynamics of controlling self-renewal and differentiation of normal stem and progenitor cells and it is likely that lessons learnt from modelling the blood system will increasingly be applied to other stem cell systems including embryonic stem cells. As illustrated in its application to CML and gene therapy, modelling has also furthered our understanding of haematopoietic pathology with potentially important implications for the development of more effective treatment protocols. These early successes suggest that modelling will continue to make important contributions to research into the causes and potential treatments of haematological malignancies and may therefore establish a computational framework relevant to the wider field of cancer research. Moreover, the blood system seems ideal to attempt a synthesis of current modelling efforts which are largely restricted to generating models specifically at the molecular, cellular or tissue level. While the generation of an overarching computational view of the haematopoietic system will require significant innovation not least in terms of integrating diverse datasets, it would have the potential not only to serve as a paradigm for other mammalian tissues but may also have direct clinical relevance. Integrated modelling approaches may for example lead to the development of protocols for detection of cancers at an earlier stage and thus initiate treatment at a lower disease burden or predict the likelihood of resistance to or escape from therapy so that treatment plans might be adjusted to compensate on a ‘bespoke’ basis. Taken together therefore, application of stringent mathematical modelling to the wealth of information being supplied by the ever-expanding fields of genomics as well as developmental and cell biology will not only provide new methodologies to predict how genes, cells and tissues function in normal biology, but may also lead to the development of new treatment regimes with substantial therapeutic benefits.

Acknowledgements

Work in the authors’ laboratory is funded by the Leukaemia Research Fund, Medical Research Council, Cancer Research UK and the Kay Kendall Leukaemia Fund. Interpretation of mathematical methods was assisted by discussions with Mr Anthony Lawson.

References

1. S. H. Orkin and L. I. Zon, Cell, 2008, 132, 631–644.
2. P. Fraser and F. Grosveld, Curr. Opin. Cell Biol., 1998, 10, 361–365.
3. R. Kurzrock, H. M. Kantarjian, B. J. Druker and T. M., Ann. Intern. Med., 2003, 138, 819–830.
4. J. E. Pimanda and B. Gottgens, Int. J. Dev. Biol. , in press.
5. N. Rekhtman, F. Radparvar, T. Evans and A. I. Skoultchi, Genes Dev., 1999, 13, 1398–1411.
6. T. Yamada, F. Kihara-Negishi, H. Yamamoto, M. Yamamoto, Y. Hashimoto and T. Oikawa, Exp. Cell Res., 1998, 186–194.
7. P. Zhang, G. Behre, J. Pan, A. Iwama, N. Wara-Aswapati, H. S. Radomska, P. E. Auron, D. G. Tenen and Z. Sun, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 8705–8710.
8. P. Zhang, X. Zhang, A. Iwama, C. Yu, K. A. Smith, B. U. Mueller, S. Narravula, B. E. Torbett, S. H. Orkin and D. G. Tenen, Blood, 2000, 96, 2641–2648.
9. J. E. Pimanda, K. Ottersbach, K. Knezevic, S. Kinston, W. Y. Chan, N. K. Wilson, J. R. Landry, A. D. Wood, A. Kolb-Kokocinski, A. R. Green, D. Tannahill, G. Lacaud, V. Kouskoff and B. Gottgens, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17692–17697.
10. T. Chiba, Y. Ikawa and K. Todokoro, Nucleic Acids Res., 1991, 19, 3843–3848.
11. S. Kuramochi, Y. Ikawa and K. Todokoro, J. Mol. Biol., 1990, 216, 567–575.
12. L. I. Zon, H. Youssoufian, C. Mather, H. F. Lodish and S. H. Orkin, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 10638–10641.
13. S. Soneji, S. Huang, M. Loose, I. J. Donaldson, R. Patient, B. Gottgens, T. Enver and G. May, Ann. N. Y. Acad. Sci., 2007, 1106, 30–40.
14. D. Miranda-Saavedra and B. Gottgens, Curr. Opin. Genet. Dev., 2008, 18, 530–535.
15. S. Ghaffari, C. Kitidis, M. D. Fleming, H. Neubauer, K. Pfeffer and H. F. Lodish, Blood, 2001, 98, 2948–2957.
16. H. Wu, X. Liu, R. Jaenisch and H. F. Lodish, Cell, 1995, 83, 59–67.
17. T. Evans and G. Felsenfeld, Cell, 1989, 58, 877–885.
18. D. I. Martin and S. H. Orkin, Genes Dev., 1990, 4, 1886–1898.
19. S. Palani and C. A. Sarkar, Biophys. J., 2008, 95, 1575–1589.
20. A. A. Margolin, K. Wang, W. K. Lim, M. Kustagi, I. Nemenman and A. Califano, Nat. Protoc., 2006, 1, 662–671.
21. K. Basso, A. A. Margolin, G. Stolovitzky, U. Klein, R. Dalla-Favera and A. Califano, Nat. Genet., 2005, 37, 382–390.
22. M. Gilchrist, V. Thorsson, B. Li, A. G. Rust, M. Korb, J. C. Roach, K. Kennedy, T. Hai, H. Bolouri and A. Aderem, Nature, 2006, 441, 173–178.
23. J. Kim, J. Chu, X. Shen, J. Wang and S. H. Orkin, Cell, 2008, 132, 1049–1061.
24. J. Wang, S. Rao, J. Chu, X. Shen, D. N. Levasseur, T. W. Theunissen and S. H. Orkin, Nature, 2006, 444, 364–368.
25. M. A. Hall, D. J. Curtis, D. Metcalf, A. G. Elefanty, K. Sourris, L. Robb, J. R. Gothert, S. M. Jane and C. G. Begley, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 992–997.
26. L. Robb, I. Lyons, R. Li, L. Hartley, F. Kontgen, R. P. Harvey, D. Metcalf and C. G. Begley, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 7075–7079.
27. R. A. Shivdasani, E. L. Mayer and S. H. Orkin, Nature, 1995, 373, 432–434.
28. W. Y. Chan, G. A. Follows, G. Lacaud, J. E. Pimanda, J. R. Landry, S. Kinston, K. Knezevic, S. Piltz, I. J. Donaldson, L. Gambardella, F. Sablitzky, A. R. Green, V. Kouskoff and B. Gottgens, Blood, 2007, 109, 1908–1916.
29. M. A. Chapman, F. J. Charchar, S. Kinston, C. P. Bird, D. Grafham, J. Rogers, F. Grutzner, J. A. Graves, A. R. Green and B. Gottgens, Genomics, 2003, 81, 249–259.
30. B. Gottgens, C. Broccardo, M. J. Sanchez, S. Deveaux, G. Murphy, J. R. Gothert, E. Kotsopoulou, S. Kinston, L. Delaney, S. Piltz, L. M. Barton, K. Knezevic, W. N. Erber, C. G. Begley, J. Frampton and A. R. Green, Mol. Cell Biol., 2004, 24, 1870–1883.
31. B. Gottgens, A. Nastos, S. Kinston, S. Piltz, E. C. Delabesse, M. Stanley, M. J. Sanchez, A. Ciau-Uitz, R. Patient and A. R. Green, EMBO J., 2002, 21, 3039–3050.
32. S. Ogilvy, R. Ferreira, S. G. Piltz, J. M. Bowen, B. Gottgens and A. R. Green, Mol. Cell. Biol., 2007, 27, 7206–7219.
33. E. Delabesse, S. Ogilvy, M. A. Chapman, S. G. Piltz, B. Gottgens and A. R. Green, Mol. Cell. Biol., 2005, 25, 5215–5225.
34. L. Silberstein, M. J. Sánchez, M. Socolovsky, Y. Liu, G. Hoffman, S. Kinston, S. Piltz, M. Bowen, L. Gambardella, A. R. Green and B. Göttgens, Stem. Cells, 2005, 23, 1378–1388.
35. P. Vyas, M. A. McDevitt, A. B. Cantor, S. G. Katz, Y. Fujiwara and S. H. Orkin, Development, 1999, 126, 2799–2811.
36. J. R. Landry, S. Kinston, K. Knezevic, M. F. de Bruijn, N. Wilson, W. T. Nottingham, M. Peitz, F. Edenhofer, J. E. Pimanda, K. Ottersbach and B. Gottgens, Blood, 2008, 111, 3005–3014.
37. E. Lecuyer, S. Herblot, M. Saint-Denis, R. Martin, C. G. Begley, C. Porcher, S. H. Orkin and T. Hoang, Blood, 2002, 100, 2430–2440.
38. E. Anguita, J. Hughes, C. Heyworth, G. A. Blobel, W. G. Wood and D. R. Higgs, EMBO J., 2004, 23, 2841–2852.
39. O. P. Pinto do, A. Kolterud and L. Carlsson, EMBO J., 1998, 17, 5744–5756.
40. N. K. Wilson, D. Miranda-Saavedra, S. J. Kinston, N. Bonadies, S. D. Foster, F. Calero-Nieto, M. A. Dawson, I. J. Donaldson, S. Dumon, J. Frampton, R. Janky, X. H. Sun, S. A. Teichmann, A. J. Bannister and B. Gottgens, Blood, 2009, 113, 5456–5465.
41. H. H. Chang, M. Hemberg, M. Barahona, D. E. Ingber and S. Huang, Nature, 2008, 453, 544–547.
42. W. J. Blake, K. A. M., C. R. Cantor and J. J. Collins, Nature, 2003, 422, 633–637.
43. M. B. Elowitz, A. J. Levine, E. D. Siggia and P. S. Swain, Science, 2002, 297, 1183–1186.
44. M. Kaern, T. C. Elston, W. J. Blake and J. J. Collins, Nat. Rev. Genet., 2005, 6, 451–464.
45. J. M. Pedraza and A. van Oudenaarden, Science, 2005, 307, 1965–1969.
46. J. M. Raser and E. K. O’Shea, Science, 2004, 304, 1811–1814.
47. N. Rosenfeld, J. W. Young, U. Alon, P. S. Swain and M. B. Elowitz, Science, 2005, 307, 1962–1965.
48. J. L. Abkowitz, S. N. Catlin, M. T. McCallie and P. Guttorp, Blood, 2002, 100, 2665–2667.
49. A. P. Korn, R. M. Henkelman, F. P. Ottensmeyer and J. E. Till, Exp. Hematol., 1973, 1, 362–375.
50. J. E. Till, E. A. McCulloch and L. Siminovitch, Proc. Natl. Acad. Sci. U. S. A., 1964, 51, 29–36.
51. I. Roeder and M. Loeffler, Exp. Hematol., 2002, 30, 853–861.
52. I. Roeder, L. M. Kamminga, K. Braesel, B. Dontje, G. de Haan and M. Loeffler, Blood, 2005, 105, 609–616.
53. I. Roeder, K. Braesel, R. Lorenz and M. Loeffler, J. Biomed. Biotechnol., 2007, 2007, 84656.
54. I. Roeder and I. Glauche, J. Mol. Med., 2008, 86, 17–27.
55. I. Roeder, M. Herberg and M. Horn, Bull. Math. Biol., 2009, 71, 602–626.
56. I. Roeder, M. Horn, I. Glauche, A. Hochhaus, M. C. Mueller and M. Loeffler, Nat. Med., 2006, 12, 1181–1184.
57. I. Roeder, K. Horn, H. B. Sieburg, R. Cho, C. Muller-Sieburg and M. Loeffler, Blood, 2008, 112, 4874–4883.
58. J. L. Abkowitz, D. Golinelli and P. Guttorp, Mol. Ther., 2004, 9, 566–576.
59. J. L. Abkowitz, D. Golinelli, D. E. Harrison and P. Guttorp, Blood, 2000, 96, 3399–3405.
60. F. Bozorgmehr, S. Laufs, S. E. Sellers, I. Roeder, W. J. Zeller, C. E. Dunbar and S. Fruehauf, Stem Cells, 2007, 25, 2610–2618.
61. N. C. Josephson, K. M. Sabo and J. L. Abkowitz, Mol. Ther., 2000, 2, 56–62.
62. M. A. Kirkland, Exp. Hematol., 2004, 32, 511–519.
63. S. N. Catlin, P. Guttorp and J. L. Abkowitz, Blood, 2005, 106, 2688–2692.
64. J. L. Abkowitz and J. W. Adamson, Prog. Clin. Biol. Res., 1984, 71–80.
65. J. L. Abkowitz, P. J. Fialkow, D. J. Niebrugge, W. H. Raskind and J. W. Adamson, J. Clin. Invest., 1984, 73, 258–261.
66. J. L. Abkowitz, R. M. Ott, R. D. Holly and J. W. Adamson, Blood, 1988, 71, 1687–1692.
67. I. Glauche, M. Cross, M. Loeffler and I. Roeder, Stem Cells, 2007, 25, 1791–1799.
68. L. H. Abbot and F. Michor, Br. J. Cancer, 2006, 95, 1136–1141.
69. J. L. Abkowitz, M. L. Linenberger, M. A. Newton, G. H. Shelton, R. L. Ott and G. P., Proc. Natl. Acad. Sci. U. S. A., 1990, 87, 9062–9066.
70. B. Fehse and I. Roeder, Gene. Ther., 2008, 15, 143–153.

---

Footnote

† This article is part of a Molecular BioSystems themed issue on Computational and Systems Biology.

---