DOI:
10.1039/B823062E
(Paper)
Lab Chip, 2009,
9, 1874-1881
Microfluidics for cryopreservation†
Received
24th December 2008
, Accepted 12th March 2009
First published on 31st March 2009
Abstract
Minimizing cell damage throughout the cryopreservation process is critical to enhance the overall outcome. Osmotic shock sustained during the loading and unloading of cryoprotectants (CPAs) is a major source of cell damage during the cryopreservation process. We introduce a microfluidic approach to minimize osmotic shock to cells during cryopreservation. This approach allows us to control the loading and unloading of CPAs in microfluidic channels using diffusion and laminar flow. We provide a theoretical explanation of how the microfluidic approach minimizes osmotic shock in comparison to conventional cryopreservation protocols viacell membrane transport modeling. Finally, we show that biological experiments are consistent with the proposed mathematical model. The results indicate that our novel microfluidic-based approach improves post-thaw cell survivability by up to 25% on average over conventional cryopreservation protocols. The method developed in this study provides a platform to cryopreserve cells with higher viability, functionality, and minimal inter-technician variability. This method introduces microfluidic technologies to the field of biopreservation, opening the door to future advancements at the interface of these fields.
Introduction
Over the past decade, microfluidic systems have led to significant breakthroughs in a variety of biological applications such as point-of-care diagnostics, bioterrorism detection, and drug discovery through an interdisciplinary approach.1–7 In particular, microfluidic technology represents a new tool to manipulate biological samples such as blood, living cells, DNA, proteins, and small molecules by exploiting the dynamic properties of microscale transport phenomena.8–14 Microfluidic technologies can impact the field of biopreservation as well.13,15–18 For instance, microfluidic channels have recently been used to isolate healthy sperm cells.17 Also, innovative approaches were introduced to biopreserve oocytes in quartz capillary channels18 and to eject cell-encapsulating cryoprotectant (CPA) droplets directly into liquid nitrogen for cryopreservation.13 Several advances in biopreservation such as the use of electron microscopy grids, cryoloops, and nylon loops enable the cryopreservation of germ cells in particular at increasing heat transfer rates.16,19,20
Around the world, trillions of cells are biopreserved each day for manifold applications in medicine and biology including the production of antibodies and proteins as well as the preservation of blood cells, germ cells, and tissues.21,22 In cryopreservation, cells or tissues are cooled down to subzero temperatures in an effort to discontinue biological activity. This is followed by the subsequent warming up to physiological temperatures. The cryopreservation process is likely to cause cell damage during typical biopreservation protocols by means of: (i) osmotic shock; (ii) dehydration; and (iii) extracellular or intracellular ice crystal formation. Among these challenges, osmotic shock is observed during two distinct phases: before freezing and after thawing. A cell that has been exposed to repeated osmotic shock is less likely to survive in the severe process of freezing and thawing. Here, we introduce a new microfluidic technique to improve the overall cryopreservation outcome by minimizing osmotic shock.
CPAs are loaded before freezing and unloaded after thawing to minimize damage due to extracellular or intracellular ice formation. In standard cryopreservation protocols,15,23,24cells undergo a series of harmful anisotonic conditions during the loading and unloading of CPAs. While this initial cell injury may not be severe enough to lead to apoptosis pathways or cell lysis, it may still have a negative influence on cell recovery and survival during the biopreservation process.25 It is critical to understand the effect that osmotic shock has on the cell post-thaw viability during the loading and unloading of CPAs.
In the field of cryopreservation, most studies focus on “chill injury” caused by ice crystal formation in the intracellular and extracellular regions. Here, we develop a new approach to the sample preparation steps, which can impact the overall outcome of cryopreservation. During the loading and unloading steps, CPAs and water flow across the cell membrane depending on the CPA osmolarity imbalance between the intracellular and extracellular domains. This leads directly to osmotic shock.26,27 In the case of CPA loading process, in which CPA concentrations around cells increases suddenly, water is drawn out of cells and CPAs permeate into them. This impedes the normal transport mechanism of cell substrates and cofactors, which can induce metabolic shock. As for the CPA unloading phase, a sudden decrease in CPA concentrations in the extracellular region causes water to flow into cells and CPAs to flow out, which may result in swelling and initiate cell apoptosis or bursting as a result of mechanical trauma.28 These transport phenomena related to the biophysical features of cells are critical to successful cryopreservation. Some studies on the CPA transport behavior using microfluidic channels have been reported in the literature.29,30 For example, Fleming et al. extracted dimethyl sulfoxide (DMSO) from cells using diffusion phenomena in the microfluidic channel.29 More comprehensive understanding of these transport phenomena across the cell membrane is needed in order to develop an optimized protocol. Also, the correlation between osmotic shock due to sudden mass transport and the cryopreservation outcome must be described.
In the current study, we introduce microfluidics to the field of biopreservation to actively control the CPA concentration during loading/unloading steps of biopreservation. To understand the relationship between osmotic shock and cell membrane transport quantitatively, we carried out numerical simulations at two different scales: one at microscale for cell membrane transport and the other at macroscale for microfluidic channels. This new approach minimizes osmotic shock during sample preparation and enhances post-thaw cell viability compared to the standard biopreservation methods employed by other biomedical laboratories.
Materials and methods
Fabrication of a microfluidic device
To fabricate the microfludic channel in poly(dimethylsiloxane) (PDMS, Dow-Corning), soft lithography was employed in this study. After applying an adhesion promoter (MicroPrime MS8011, Shin-Etsu), photoresist (SU-8 2000, MicroChem) was spin-coated on a Si wafer uniformly. Then, the wafer was soft-baked and a pattern for microfluidic channels was developed on the wafer by exposing it to ultraviolet light. Poly(dimethylsiloxane) and curing agent (Dow Corning Sylgard 184 Silicone Elastomer Kit) were mixed at a ratio of 10 : 1 and poured over the wafer mold. After degassing, the PDMS was cured at 80 °C in an oven for 2 hours. The cured PDMS was peeled off the replica mold and bonded to a micro-glass slide (Corning) by treating with oxygen plasma (Harrick Plasma). Plastic PE tubes were connected to the device and syringe pumps (World Precision Instruments) were utilized to inject CPAs and cell suspension into the microfluidic channel.
Cell preparation and cryopreservation
HepG2 (hepatocellular carcinoma human liver) cells were purchased from ATCC (Manassas) and cultured in DMEM supplemented with 10% FBS in a 5% CO2 humidified incubator at 37 °C. HepG2 cells were passaged at approximately 80% confluence 3–4 times. We carried out live/dead tests of cells three times to obtain the corresponding cell viabilities. First, after trypsinizing cells, initial cell viability was measured by incubating them with a live/dead dye kit (0.5 µl of calcein AM and 1.5 µl of ethidium homodimer-1, Molecular Probes) in 1 ml of PBS for 10 min. In parallel, cells are resuspended in PBS and the cell density was kept at 1 × 106cells ml−1. For preparation of CPAs, 10% trehalose dehydrate (v/v) and 4% BSA were dissolved in PBS and 1,2-propanediol was added to the CPA solution corresponding to its molarity. The cell solution was sterilized and put into a syringe, which was loaded to the syringe pump. Under microscope visualization, HepG2 cell suspension was injected into the microfluidic device. When cells were passed through the channel, the second live/dead test was performed. The remaining cells were placed in a cryotube and stored in a freezer (−80 °C) for one day without using a special freezing container. The following day, the cells were thawed in a warm water bath (37 °C) and flowed into the microfluidic channel to unload CPAs. The third live/dead test was conducted to characterize the post-thaw viability of the cells. Also, the culture of post-thaw cells was observed to proliferate for 7 days. To check the functionality of the HepG2 cells, the metabolic activity of the post-thaw cells was detected using a metabolic assay kit (Vybrant cell Metabolic Assay Kit, V-23110, Invitrogen).
Theory
Microscale modeling of mass transport across cell membrane
A number of fundamental studies on the mass transport across cell membranes by diffusion have been carried out in the area of cellular biophysics in the past several decades. There are several models: a one-parameter model considering only solute permeabilities, a classic two-parameter model factoring in both water and solute permeabilities, and a three-parameter model, in which the interaction between solute and solvent is taken into account in terms of irreversible thermodynamics besides water and solute permeabilities.31–33 The three-parameter model has been widely accepted as the one that most closely simulates mass transport through the cell membrane. Assuming a permeable CPA to diffuse into and out of cells, water channels (aquaporins) and low molecular weight CPA channels may interact through cotransportation. In the three-parameter model (Kedem–Katchalsky model), the water and solute transport across a membrane is mathematically coupled by using the reflection coefficient. Depending on the reflection coefficient, water and CPA are transported through a common channel. This mathematical modeling can provide insight into fluid fluxes, volume changes, and CPA molarity of cells due to osmotic pressure. In the current study, when cells are immersed in the CPAs, the evolution of the osmotic mass transport is analyzed. Firstly, the water flux across the cell membrane is expressed as follows:34,35| |  | (2) |
| |  | (3) |
In which Lp is the membrane hydraulic conductivity, σs the membrane reflection coefficient of CPAs, R the universal gas constant, T the temperature, c the concentration of CPAs, A the cell surface area, E the cellular elastic modulus and Vw the water volume of cells. In addition, the superscripts i and e mean the intracellular and extracellular regions, respectively. Secondly, the CPA transport is modeled by the following equations:
| | | Jc = (1 − σ)cupJw + ωRTΔc | (4) |
| | 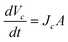 | (5) |
where
ω is the membrane permeability of CPAs and
cup is the upstream concentration of CPAs according to the water flux direction. The 4th order Runge–Kutta method is implemented to calculate
eqn (1)–(5) using C++ programming language. The parameters used in this study are listed in Table S1 in the ESI.
†
Macroscale modeling of microfluidic flow
We designed and fabricated a microfluidic device with a three input channel, which has dimensions 100 µm high, 100 µm wide, and 1.5 m long. The microfluidic channel offers seamless change in the concentration of CPAs along the channel by means of diffusion of CPAs. Since the channel is very narrow and long, the numerical calculation for the channel requires significant computing power, such as a 64-bit operating system. In this study, we performed finite element simulation. The flow behavior in the microfluidic channel is modeled using the steady state Navier–Stokes equations as follows:| | | ρu·∇u = ∇·η(∇u + (∇u)T) − ∇P | (6) |
where ρ and η represent the fluid density and viscosity, which are assumed to be linear functions of CPA concentration (rule of mixture). In addition, u denotes the velocity vector and P is the fluid pressure. Mass transport for a single species was taken into account assuming that CPAs interact only with water molecules and physical properties count only on the CPA concentration. The transport phenomenon of CPAs is governed by the following convection and diffusion equation at steady state:in which c is the concentration of CPAs and D indicates the diffusion coefficient of CPAs.
As a boundary condition, an average velocity was imposed at the inlet, which develops laminar flow in the microfluidic channel. At the outlet, the pressure was set to zero (atmospheric pressure). Also, no-slip condition (u = 0) was applied to all other boundaries. For mass balance, the concentration boundary condition was given to the inlets. In addition, the convective flux condition was imposed at the outlet, which means that mass diffusion in the normal direction to the outlet surface is negligible.
Results and discussion
Biopreservation comprises three main phases: (i) CPA loading; (ii) freezing, frozen storage, and thawing; and (iii) CPA unloading. We introduced a microfluidic device (Fig. 1A) to aid cryopreservation (Fig. 1B) that provides for the first time the ability to increase and decrease CPA concentrations in a controlled, progressive manner. To achieve this, the microfluidic channel has two inputs: one for cells and another for CPAs. As can be seen in Fig. 1A, the cells are injected in the middle of the channel. CPAs are simultaneously flowed into the microfluidic channel from the two sides. As the cells move down along the channel, the CPAs diffuse toward the center because of the difference in the CPA concentration ( ). As a result, cells that travel along the microfluidic channel experience changes in CPA concentrations progressively, thus minimizing osmotic shock. By regulating the flow rates of CPAs and cells suspended in PBS, we can actively control the concentration of CPAs. Since diffusion is not as fast as mass convection, long and narrow channel dimensions are required to achieve complete diffusion in the channel. The microfluidic approach can satisfy these requirements. After the freezing and thawing steps, we used the same microfluidic concept to unload CPAs from the thawed cells (Fig. 1C). In this case, we introduced the PBS solution from the two side channels, and the thawed cells are again injected in the middle. The CPA concentration of the thawed cells is reduced gradually along the channel through diffusion, thus addressing osmotic shock during CPA unloading phase.
). As a result, cells that travel along the microfluidic channel experience changes in CPA concentrations progressively, thus minimizing osmotic shock. By regulating the flow rates of CPAs and cells suspended in PBS, we can actively control the concentration of CPAs. Since diffusion is not as fast as mass convection, long and narrow channel dimensions are required to achieve complete diffusion in the channel. The microfluidic approach can satisfy these requirements. After the freezing and thawing steps, we used the same microfluidic concept to unload CPAs from the thawed cells (Fig. 1C). In this case, we introduced the PBS solution from the two side channels, and the thawed cells are again injected in the middle. The CPA concentration of the thawed cells is reduced gradually along the channel through diffusion, thus addressing osmotic shock during CPA unloading phase.
 |
| | Fig. 1 Schematic depiction of cell cryopreservation as introduced in this study. The microfluidic approach consists of three steps: (A) CPA loading; (B) freezing and thawing; and (C) CPA unloading. The microfluidic device was employed in an effort to progressively change the concentration of cyroprotectants prior to freezing and following thawing. In the CPA loading step (A), cells travel along the microfluidic channel, thereby experiencing a gradual change in CPA concentration. This can minimize osmotic shock to the cell. In the cell freezing and thawing steps (B), we followed a standard cryopreservation protocol. To unload the CPA from cells after thawing, they were infused into the microfluidic channel with a PBS buffer injecting through the two side channels at the same time (C). | |
Characterization of osmotic shock at microscale
Cell membranes have various transport pathways for substrates, fluids, ions, and gases relying on different physicochemical or biological mechanisms to help control the osmotic balance of animal cells.36,37Cell transport machinery associated with cryopreservation involves water and permeable solutes.38,39 In cryobiology, transport channel behavior is determined by CPA concentration and the rate of change during CPA loading/unloading. In particular, it is important to understand how the rate of CPA addition and removal affects osmotic shock to cells and resulting cell viability. Generally, one-step loading/unloading is employed in most conventional cryopreservation protocols whereas stepwise loading/unloading is used for germ cells.24Fig. 2A schematically represents three different loading/unloading profiles used in this study. While these three profiles have different rates of increasing or decreasing CPA concentrations, the final concentrations are the same (Fig. 2A). Our microfluidic approach using diffusion phenomena yields concave and convex CPA concentration profiles along the channel during loading and unloading steps, respectively. To examine the effect of the different profiles on water and CPA transport, and to develop a better microfluidic approach with minimal osmotic shock, we used the three-parameter model proposed by Kedem and Katchalsky (KK model).40 The KK model was derived based on irreversible thermodynamics and consists of three parameters: hydraulic conductivity, reflection coefficient, and solute permeability. To eliminate the influence of the model parameters (Table S1†), we defined characteristic parameters through dimensional analysis to non-dimensionalize the model system. It is known that water flux controlling cellular volume is dependent on the presence of water channels (aquaporins) on cell membranes and that it plays a key role in determining the severity of osmotic shock.34,35 We also confirmed this in our simulation results (Figs. 2B–E). In these plots, the maximum and minimum values play an important role, since they dictate the level of osmotic shock to the cell. We will first describe the loading steps (Figs. 2B and 2C) and then the unloading steps (Figs. 2D and 2E).
 |
| | Fig. 2 Effect of different CPA loading/unloading profiles on mass transport across cell membranes. (A) Schematic diagram of three different profiles considered in this study: one-step, stepwise, and microfluidic CPA loading/unloading. These different CPA loading/unloading scenarios lead to distinct mass transport profiles across cell membranes ((B)–(E)), which consequently results in different cell viabilities during cryopreservation. To understand the mass transport more comprehensively, we defined characteristic parameters and then non-dimensionalized physical quantities obtained through numerical modeling: initial water volume in the cell, V0, final CPA concentration, C0, characteristic time,  , and initial water flux, , and initial water flux,  , and initial CPA flux, , and initial CPA flux, 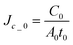 . (B) Dimensionless water fluxes across cell membrane during the CPA loading step. It was identified that the CPA loading/unloading profiles yield strikingly distinct water fluxes. The volume change of water drawn out of the cell is presented in the smaller diagram. (C) Dimensionless CPA fluxes through cell membrane are presented. Similarly to the water flux (B), the one-step loading was found to have the largest flux. In the smaller diagram, the change in CPA concentration was elucidated with respect to dimensionless time. (D) Dimensionless water fluxes across cell membrane during the CPA unloading step are shown. The mass transport during the CPA unloading step is different from that in the CPA loading step. The volume change of water penetrating into a cell was demonstrated in the smaller figure. (E) Dimensionless CPA fluxes across cell membrane during the CPA unloading step. The smaller figure presents the change in the CPA concentration in a cell over time. Overall, these changes in water and CPA fluxes across cell membrane (B)–(D) demonstrate how the microfluidic CPA loading/unloading approach can minimize the osmotic shock compared to the standard cryopreservation methods, one-step and stepwise loading/unloading cases. . (B) Dimensionless water fluxes across cell membrane during the CPA loading step. It was identified that the CPA loading/unloading profiles yield strikingly distinct water fluxes. The volume change of water drawn out of the cell is presented in the smaller diagram. (C) Dimensionless CPA fluxes through cell membrane are presented. Similarly to the water flux (B), the one-step loading was found to have the largest flux. In the smaller diagram, the change in CPA concentration was elucidated with respect to dimensionless time. (D) Dimensionless water fluxes across cell membrane during the CPA unloading step are shown. The mass transport during the CPA unloading step is different from that in the CPA loading step. The volume change of water penetrating into a cell was demonstrated in the smaller figure. (E) Dimensionless CPA fluxes across cell membrane during the CPA unloading step. The smaller figure presents the change in the CPA concentration in a cell over time. Overall, these changes in water and CPA fluxes across cell membrane (B)–(D) demonstrate how the microfluidic CPA loading/unloading approach can minimize the osmotic shock compared to the standard cryopreservation methods, one-step and stepwise loading/unloading cases. | |
In Fig. 2B, water flux through the cell membrane is modeled for the three loading protocols: one-step, stepwise, and microfluidic. The microfluidic approach starts with low absolute water flux that increases over time and finally reaches zero with osmotic balance. Please note that osmotic shock is determined by water flux, but not CPA flux, because the rate of water flux is much higher than that of the CPA.41 The standard one-step loading procedure causes the cell to experience high absolute flux immediately. Then, this flux decreases over time until it reaches a balance. The stepwise loading process lies in between the microfluidic and one-step approaches. Thus, we observe a secondary sharp absolute increase in flux due to the secondary loading step. These sharp increases in flux and peak values attained during CPA loading determine the impact of osmotic shock on the cells. The volume of water transported away from the cell is shown with the smaller diagram of Fig. 2B. Rapid water escape is observed for the one-step loading protocol, indicating the high levels of osmotic shock with this protocol. In addition to water flux, we investigated CPA flux through cell membranes as depicted in Fig. 2C. Similar to the case of water flux, the one-step protocol causes immediate high absolute CPA flux and then converges to a balance. This flux has a complex shape due to the co-transport phenomenon with water. CPA concentration in the cell is shown with the smaller diagram of Fig. 2C. The rapid CPA increase in the cell during the one-step approach is indicative of major osmotic shock. As seen from the same figure, this impact is decreased significantly by the microfluidic approach.
Microfluidic CPA unloading has the smallest dimensionless water flux, which implies a minimum osmotic shock (Fig. 2D). The CPA unloading stage takes more time than the CPA loading stage because of the decreased cell surface area and also has different profiles from the CPA loading stage (Figs. 2D and 2E). In the CPA unloading step, water flows into cells and CPAs move out of cells. The microfluidic loading case has the lowest water flux and CPA flux (Figs. 2D and 2E). On the other hand, the co-transport of water and CPA through a common channel results in a positive flux during stepwise and progressive loading/unloading cases unlike the one-step loading/unloading based on the three-parameter model. Overall, the quantitative model indicates that the microfluidic aproach to control CPA loading/unloading minimizes the osmotic shock to cells.
Characterization of microfluidic channel at macroscale
Based on modeling of mass transport through a cell membrane, we calculated appropriate microfluidic channel dimensions (100 µm × 100 µm × 1.5 m) as shown in Fig. 3A. To experimentally control diffusion in our fabricated device, we injected different colored liquids into the microfluidic channels and observed their behavior. Fig. 3B presents the channel inlets, through which yellow and green colored liquids were infused. To visualize and quantify the diffusion of CPAs in the channel, CPAs were dyed with a green fluorescent stain (Figs. 3C–H). Fluorescent images were taken along the channel (Figs. 3F–H). Laminar flow in the channel and CPA diffusion towards the center were verified and compared to the theoretical model. By changing injection flow rates at the inlets, we can control the diffusion pattern along the microfluidic channels. Fluorescence intensity was measured along the channel and analyzed based on the Lambert–Beer law.42 The fluorescent intensity was non-dimensionalized using the maximum intensity. The experimental results were in good agreement with the predicted computational results (Figs. 3I and J), indicating that we can predict and control the CPA loading/unloading profiles through the microfluidic approach.
 |
| | Fig. 3 (A) Photograph of the microfluidic device created in this study. The device possesses a long microfluidic channel with three inputs and one outlet, which offers a long distance to develop a complete diffusion along the channel. The yellow and green colored fluids were infused into the microfluidic channel to show the inlet. (B) Magnified image around the outlet of the channel is shown. To observe the CPA diffusion behavior experimentally, a fluorescent stain (FITC) was injected along with CPAs ((C)–(E)). Using the fluorescent intensity, the normalized 3D intensity images were prepared ((F)–(H)). As the CPAs flow along the channel, it was identified that the CPAs diffuse into the center of the channel until concentration equilibrium ((F)–(H)). The intensity was measured on an area of 100 µm × 100 µm and the intensity was normalized by using the maximum intensity. (I) Normalized CPA concentration variation along the microfluidic channel in the CPA loading step is shown. The flow rates of the CPA and cell suspension were kept at 20 µl/min each. Three independent experiments were conducted. The experimental and numerical results were in agreement. The concentration increased progressively through diffusion as we expected. (J) Normalized CPA concentration during unloading step is shown. The applied flow rates for the PBS and cell suspension were 20 µl/min and 2 µl/min, respectively. The concentration obtained experimentally as well as numerically decreased gradually. | |
Microfluidic cryopreservation: Viability and functionality
To investigate the enhancement achieved by the microfluidic approach, we prepared two sample groups. The first sample group encompasses samples prepared using the standard one-step or stepwise (1.5 M to 3 M) loading/unloading protocols illustrated in Fig. 2A. This acts as the control group (M indicates the molarity of 1,2-propanediol used in this study). For the second sample group, we progressively controlled the CPA concentration via the proposed microfluidic approach. Both sample groups go through the exact same freezing/thawing process, but different CPA loading/unloading steps. We followed a standard cryopreservation protocol,43,44 except for the fact that we did not employ a special freezing container that can offer more than 80% viability after thawing. This allows us to more clearly observe the osmotic shock effect.45,46 The special container would likely have increased the viability of the HepG2 cells used in this study. However, osmotic shock still affects the cell regardless of which freezing container is used. In particular, the osmotic effect can lead to more adverse influence in the case of sensitive cells such as oocytes and embryonic stem cells, which are the cell types that this protocol has been designed to work with. Fig. 4A shows viability studies at 2M CPA concentration. We observe that the microfluidic approach results in higher viability outcomes than the one-step protocol. The initial flask and pre-freeze viabilities are similar for both cases. However, the effect of osmotic shock is more pronounced for the one-step protocol, where the final viability outcome decreases by ∼15% (see Table S2). Fig. 4B demonstrates even more striking results at 3M, where we expect the effect to be more pronounced due to larger osmotic shock level. The one-step loading procedure gives lower viability percentages both pre-freezing and post-thawing when compared to the stepwise and microfluidic approaches (Fig. 4B). These viability results agree with the osmotic shock modeling results, where the highest osmotic shock is observed for the one-step case and the lowest osmotic shock is observed in the microfluidic approach. These results indicate that the reduction of osmotic shock to cells through the microfluidic approach can enhance the cell viability. The microfluidic approach results in ∼25% higher viability than the one-step approach, and ∼10% higher viability than the stepwise approach. To investigate the functionality of the cells after the thawing phase, we performed long-term culture of these cells for 7 days (Fig. 4C). Further, we performed a resazurin metabolic assay to determine functionality (Fig. 4D). Since healthy cells reduce non-fluorescent resazurin into red-fluorescent resorufin, the metabolic activity of the post-thaw cells can be observed.
 |
| | Fig. 4 (A) Viabilities measured through conventional one-step and microfluidic approaches in the case of 2M CPA concentration. In each sample, three different viabilities were measured: initial state, before freezing and after thawing. Data are mean ± SD (n = 3) obtained from three independent experiments. Statistical difference (P < 0.05) between the viabilities before freezing are denoted with an asterisk (*). # represents a statistical difference (P < 0.01) between the viabilities after thawing. (B) Viabilities obtained in the case of 3M CPA concentration are shown. An experiment to change the CPA concentration stepwise (1.5 M through 3 M) was added. Here, *, P < 0.05; **, P < 0.01; #, P < 0.01. (C) Bright field image taken after long-term culture (day 7). (D) Resorufin fluorescent image indicates the functionality of the thawed cells. Resazurin, a non-toxic and stable reagent that allows long-term monitoring of proliferating cells, which is reduced to resorufin. | |
Conclusions
Minimizing cell damage throughout the cryopreservation process can enhance overall outcomes. Osmotic shock impacts the cryopreservation of cells during the loading and unloading of CPAs. We propose a microfluidic approach to minimize the osmotic shock during the CPA loading phase before freezing and the CPA unloading phase after thawing. Also, we provide a theoretical explanation of how the microfluidic approach achieves this goal in comparison to conventional cryopreservation protocols using cell transport modeling. Finally, we show that biological experiments support the expected model and microfluidics improves the overall cryopreservation outcome over the standard protocols. This proposed method introduces microfluidic technologies to the field of cell biopreservation, opening up a new path for future advancements.
Acknowledgements
We are thankful to Drs. Du Yanan, Ali Khademhosseini, and Edward Haeggstrom for scientific discussions and technical support. We also thank Jacky Lau for contributing to this study as an undergraduate researcher. This work was supported by the National Institutes of Health Grant R21 EB007707. This work was performed fully at BAMM Labs (Bio-acoustic MEMS in medicine laboratories), Brigham and Women's Hospital, Harvard Medical School.
References
- M. A. Burns, B. N. Johnson, S. N. Brahmasandra, K. Handique, J. R. Webster, M. Krishnan, T. S. Sammarco, P. M. Man, D. Jones, D. Heldsinger, C. H. Mastrangelo and D. T. Burke, Science, 1998, 282, 484–487 CrossRef CAS.
- J. W. Hong and S. R. Quake, Nat. Biotechnol., 2003, 21, 1179–1183 CrossRef CAS.
- T. Okamoto, T. Suzuki and N. Yamamoto, Nat. Biotechnol., 2000, 18, 438–441 CrossRef CAS.
- A. Khademhosseini, J. Yeh, G. Eng, J. Karp, H. Kaji, J. Borenstein, O. C. Farokhzad and R. Langer, Lab Chip, 2005, 5, 1380–1386 RSC.
- U. Demirci, Journal Of Microelectromechanical Systems, 2006, 15, 957–966 CrossRef.
- X. Cheng, Y. S. Liu, D. Irimia, U. Demirci, L. Yang, L. Zamir, W. R. Rodriguez, M. Toner and R. Bashir, Lab Chip, 2007, 7, 746–755 RSC.
- X. Cheng, D. Irimia, M. Dixon, K. Sekine, U. Demirci, L. Zamir, R. G. Tompkins, W. Rodriguez and M. Toner, Lab Chip, 2007, 7, 170–178 RSC.
- N. M. Milovic, J. R. Behr, M. Godin, C. S. Hou, K. R. Payer, A. Chandrasekaran, P. R. Russo, R. Sasisekharan and S. R. Manalis, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13374–13379 CrossRef CAS.
- J. Fritz, M. K. Baller, H. P. Lang, H. Rothuizen, P. Vettiger, E. Meyer, H. Guntherodt, C. Gerber and J. K. Gimzewski, Science, 2000, 288, 316–318 CrossRef CAS.
- T. P. Burg, M. Godin, S. M. Knudsen, W. Shen, G. Carlson, J. S. Foster, K. Babcock and S. R. Manalis, Nature, 2007, 446, 1066–1069 CrossRef CAS.
- X. Zhu, K. L. Mills, P. R. Peters, J. H. Bahng, E. H. Liu, J. Shim, K. Naruse, M. E. Csete, M. D. Thouless and S. Takayama, Nat. Mater., 2005, 4, 403–406 CrossRef CAS.
- U. Demirci and G. Montesano, Lab Chip, 2007, 7, 1428–1433 RSC.
- U. Demirci and G. Montesano, Lab Chip, 2007, 7, 1139–1145 RSC.
- Y. Ling, J. Rubin, Y. Deng, C. Huang, U. Demirci, J. M. Karp and A. Khademhosseini, Lab Chip, 2007, 7, 756–762 RSC.
- P. Hyttel, G. Vajta and H. Callesen, Mol. Reprod. Dev., 2000, 56, 80–88 CrossRef CAS.
- M. Lane, B. D. Bavister, E. A. Lyons and K. T. Forest, Nat. Biotechnol., 1999, 17, 1234–1236 CrossRef CAS.
- B. S. Cho, T. G. Schuster, X. Zhu, D. Chang, G. D. Smith and S. Takayama, Anal. Chem., 2003, 75, 1671–1675 CrossRef CAS.
- A. Arav, S. Yavin, Y. Zeron, D. Natan, I. Dekel and H. Gacitua, Mol. Cell Endocrinol., 2002, 187, 77–81 CrossRef CAS.
- A. Martino, N. Songsasen and S. P. Leibo, Biol. Reprod., 1996, 54, 1059–1069 Search PubMed.
- M. Lane and D. K. Gardner, Mol. Reprod. Dev., 2001, 58, 342–347 CrossRef CAS.
- L. Rienzi, F. Martinez, F. Ubaldi, M. G. Minasi, M. Iacobelli, J. Tesarik and E. Greco, Hum. Reprod., 2004, 19, 655–659 CrossRef CAS.
- M. Fishaut, N. Murphy, R. Yanagihara and K. McIntosh, J. Clin. Microbiol., 1980, 11, 687–690 CAS.
- P. Mazur, K. W. Cole, J. W. Hall, P. D. Schreuders and A. P. Mahowald, Science, 1992, 258, 1932–1935 CrossRef CAS.
- N. Ogonuki, K. Mochida, H. Miki, K. Inoue, M. Fray, T. Iwaki, K. Moriwaki, Y. Obata, K. Morozumi, R. Yanagimachi and A. Ogura, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13098–13103 CrossRef CAS.
- S. J. Paynter, A. Cooper, L. Gregory, B. J. Fuller and R. W. Shaw, Hum. Reprod., 1999, 14, 2338–2342 CrossRef CAS.
- B. Litkouhi, D. Marlow, J. J. McGrath and B. Fuller, Cryobiology, 1997, 34, 23–35 CrossRef CAS.
- J. A. Gilmore, L. E. McGann, J. Liu, D. Y. Gao, A. T. Peter, F. W. Kleinhans and J. K. Critser, Biol. Reprod., 1995, 53, 985–995 Search PubMed.
- E. Klipp, B. Nordlander, R. Kruger, P. Gennemark and S. Hohmann, Nat. Biotechnol., 2005, 23, 975–982 CrossRef CAS.
- K. K. Fleming, E. K. Longmire and A. Hubel, J. Biomech. Eng., 2007, 129, 703–711 CrossRef CAS.
- H. Chen, H. Shen, S. Heimfeld, K. K. Tran, J. Reem, A. Folch and D. Gao, International Journal of Heat and Mass Transfer, 2008, 51, 5687–5694 CrossRef CAS.
- G. A. Ateshian, M. Likhitpanichkul and C. T. Hung, J. Biomech., 2006, 39, 464–475.
- F. W. Kleinhans, Cryobiology, 1998, 37, 271–289 CrossRef CAS.
- E. J. Woods, J. Liu, J. A. Gilmore, T. J. Reid, D. Y. Gao and J. K. Critser, Cryobiology, 1999, 38, 200–208 CrossRef CAS.
- Z. F. Cui, R. C. Dykhuizen, R. M. Nerem and A. Sembanis, Biotechnol. Prog., 2002, 18, 354–361 CrossRef CAS.
- L. Y. Li, Computational Materials Science, 2006, 35, 75–83 CrossRef CAS.
- M. Denda, J. Hosoi and Y. Asida, Biochem. Biophys. Res. Commun., 2000, 272, 134–137 CrossRef CAS.
- J. A. Hernandez and E. Cristina, Am. J. Physiol., 1998, 275, C1067–1080 CAS.
- L. Y. Li, B. J. Tighe and J. W. Ruberti, Biomech. Model Mechanobiol., 2004, 3, 114–123 CrossRef CAS.
- H. H. Chen, J. J. Purtteman, S. Heimfeld, A. Folch and D. Gao, Cryobiology, 2007, 55, 200–209 CrossRef CAS.
- O. Kedem and A. Katchalsky, Biochim. Biophys. Acta, 1958, 27, 229–246 CAS.
-
D. T. Haynie, Biological
Thermodynamics, Cambridge University Press, Cambridge, 2001 Search PubMed.
- J. Bursch, R. Johs and P. Heintzen, Fortschr. Geb. Rontgenstr. Nuklearmed., 1970, 112, 259–266 Search PubMed.
- T. B. Darr and A. Hubel, Cryobiology, 2001, 42, 11–20 CrossRef CAS.
- Y. Miyamoto, S. Suzuki, K. Nomura and S. Enosawa, Cell Transplant, 2006, 15, 911–919 CrossRef.
- L. Sui, R. Nomura, Y. Dong, F. Yamaguchi, K. Izumori and M. Tokuda, Cryobiology, 2007, 55, 87–92 CrossRef CAS.
- Y. Hirano, Y. Nishimiya, S. Matsumoto, M. Matsushita, S. Todo, A. Miura, Y. Komatsu and S. Tsuda, Cryobiology, 2008, 57, 46–51 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting information and supplementary tables. See DOI: 10.1039/b823062e |
|
| This journal is © The Royal Society of Chemistry 2009 |
Click here to see how this site uses Cookies. View our privacy policy here. 

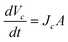
 ). As a result, cells that travel along the microfluidic channel experience changes in CPA concentrations progressively, thus minimizing osmotic shock. By regulating the flow rates of CPAs and cells suspended in PBS, we can actively control the concentration of CPAs. Since diffusion is not as fast as mass convection, long and narrow channel dimensions are required to achieve complete diffusion in the channel. The microfluidic approach can satisfy these requirements. After the freezing and thawing steps, we used the same microfluidic concept to unload CPAs from the thawed cells (Fig. 1C). In this case, we introduced the PBS solution from the two side channels, and the thawed cells are again injected in the middle. The CPA concentration of the thawed cells is reduced gradually along the channel through diffusion, thus addressing osmotic shock during CPA unloading phase.
). As a result, cells that travel along the microfluidic channel experience changes in CPA concentrations progressively, thus minimizing osmotic shock. By regulating the flow rates of CPAs and cells suspended in PBS, we can actively control the concentration of CPAs. Since diffusion is not as fast as mass convection, long and narrow channel dimensions are required to achieve complete diffusion in the channel. The microfluidic approach can satisfy these requirements. After the freezing and thawing steps, we used the same microfluidic concept to unload CPAs from the thawed cells (Fig. 1C). In this case, we introduced the PBS solution from the two side channels, and the thawed cells are again injected in the middle. The CPA concentration of the thawed cells is reduced gradually along the channel through diffusion, thus addressing osmotic shock during CPA unloading phase.


 , and initial water flux,
, and initial water flux,  , and initial CPA flux,
, and initial CPA flux, 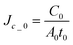 . (B) Dimensionless water fluxes across cell membrane during the CPA loading step. It was identified that the CPA loading/unloading profiles yield strikingly distinct water fluxes. The volume change of water drawn out of the cell is presented in the smaller diagram. (C) Dimensionless CPA fluxes through cell membrane are presented. Similarly to the water flux (B), the one-step loading was found to have the largest flux. In the smaller diagram, the change in CPA concentration was elucidated with respect to dimensionless time. (D) Dimensionless water fluxes across cell membrane during the CPA unloading step are shown. The mass transport during the CPA unloading step is different from that in the CPA loading step. The volume change of water penetrating into a cell was demonstrated in the smaller figure. (E) Dimensionless CPA fluxes across cell membrane during the CPA unloading step. The smaller figure presents the change in the CPA concentration in a cell over time. Overall, these changes in water and CPA fluxes across cell membrane (B)–(D) demonstrate how the microfluidic CPA loading/unloading approach can minimize the osmotic shock compared to the standard cryopreservation methods, one-step and stepwise loading/unloading cases.
. (B) Dimensionless water fluxes across cell membrane during the CPA loading step. It was identified that the CPA loading/unloading profiles yield strikingly distinct water fluxes. The volume change of water drawn out of the cell is presented in the smaller diagram. (C) Dimensionless CPA fluxes through cell membrane are presented. Similarly to the water flux (B), the one-step loading was found to have the largest flux. In the smaller diagram, the change in CPA concentration was elucidated with respect to dimensionless time. (D) Dimensionless water fluxes across cell membrane during the CPA unloading step are shown. The mass transport during the CPA unloading step is different from that in the CPA loading step. The volume change of water penetrating into a cell was demonstrated in the smaller figure. (E) Dimensionless CPA fluxes across cell membrane during the CPA unloading step. The smaller figure presents the change in the CPA concentration in a cell over time. Overall, these changes in water and CPA fluxes across cell membrane (B)–(D) demonstrate how the microfluidic CPA loading/unloading approach can minimize the osmotic shock compared to the standard cryopreservation methods, one-step and stepwise loading/unloading cases.

