Modelling and optimization of micro optofluidic lenses
Chaolong
Song
,
Nam-Trung
Nguyen
*,
Say-Hwa
Tan
and
Anand Krishna
Asundi
School of Mechanical and Aerospace Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798. E-mail: mntnguyen@ntu.edu.sg
First published on 19th February 2009
Abstract
This paper reports the modelling and experimental results of a liquid-core liquid-cladding optofluidic lens. The lens is based on three laminar streams in a circular chamber. The stream lines and the curvature of the interface can be predicted accurately using the theory of two-dimensional dipole flow in a circularly bounded domain. The model establishes basic relations between the flow rate ratio of the core/cladding streams and the radius of curvature and consequently the focal length of the lens. Compared to a rectangular chamber, this new circular design allows the formation of a liquid-core liquid-cladding lens with perfect curvatures. The circular design allows tuning a perfect curvature ranging from the chamber radius itself to infinity. The test device with a circular lens chamber with 1 mm diameter and 50 µm height was fabricated in PDMS. The lens shape as well as the stream lines were characterized using fluorescent dye and tracing particles. Experimental results agree well with the analytical results predicted by the model.
Introduction
Micro lenses with tuneable focal length can find a wide range of applications in lab-on-a-chip (LOC) systems. The integration of micro lenses into microfluidic system can improve the portability and make the system cost-efficient. Camou et al. used photolithography to fabricate PDMS 2D optical lenses,1 which were demonstrated to improve the performance of fluorescent spectroscopy detection. Wenger et al. explored the combination of a latex microsphere with low numerical aperture (NA) lens to enable the detection of single molecules.2 However their solid-based optical lenses are not tuneable. The focal length is fixed after the fabrication of lens, and the smoothness of interface of the lens depends on the fabrication process. Liquid interfaces are atomically smooth and their curvature is maintained by the interfacial tension. The refractive indices of most liquids are in the range of 1.3 to 1.6, which is comparable to glass and most polymeric materials. The smooth curved interfaces and the high refractive index make liquids ideal materials for designing lenses.Liquid lenses with tuneable focal length have been reported in the past. The radius of curvature was controlled by pressure-driven deflection of a thin elastomeric membrane3,4 or by electrowetting.5,6 These lenses require an actuator for tuning the focal length. Thus, they are expensive to fabricate and not compatible to most passive microfluidic systems. Recently, micro optofluidics has been emerging as an active research field, where liquid flows in microchannels are used to realize optical components. The small size of microchannels leads to a small Reynolds number and a stable laminar flow. The smooth and relatively stable interfaces between different liquids are ideal for designing different optical components, such as waveguides, lenses and mirrors.7 The simplest application of laminar liquid streams with mismatched refractive indices are liquid-core liquid-cladding waveguides.8 Hydrodynamic control of the liquid streams can be used to define the optical path. In the past, we have demonstrated the on-chip generation of a dye laser as well as the splitting and switching capability of the optical signal in a micro optofluidic device.9 The curved interface between two immiscible liquids can be achieved with the contact angle at the liquid/liquid/solid interface5,6 or with the Dean flow in a curved channel.10 In the latter case, a small radius of curvature and a short focal length can be achieved. Recently, Tang et al. reported a dynamically reconfigurable liquid-core liquid-cladding lens using the curved interfaces in a rectangular chamber.11 This paper reported experimental results of the micro optofluidic lens formed by hydrodynamic spreading of a core stream, which has a higher refractive index than that of the side stream. The curvature of the lens is tuned by the flow rate ratios of the three streams. The current design, with a rectangular chamber, suffers from the problem of distortion of the lens shape due to recirculation flow at high flow rates. To the best of our knowledge, there are no theoretical works describing the interaction between the fluidic and the optical aspects of this lens type.
In this paper, we propose a new design with a circular chamber to realize a perfect lens curvature. The paper focuses on the fluidic aspect of the lens design. First, a model for the interface shape is established based on the theory of two-dimensional dipole flow in a circularly bounded domain. Next, the paper derives the basic relations between the flow rate ratio of the core/cladding streams and the radius of curvature, and consequently the focal length of the lens. Although traditional precision engineering can fabricate optical lenses with a pre-defined curvature of interface by using grinding and polishing, this is a mechanical-contact method, thus the optical smoothness is limited. Our model provides a method to configure optofluidic lenses with a mathematically pre-defined curvature, whose interface is automatically smooth. Experiments were carried out to verify the theory. The shape of the micro optofluidic lens was visualized using fluorescent dye and fluorescent particles.
Model of liquid-core liquid-cladding lens in a circular chamber
Dipole flow model for lens shape
Fig. 1 depicts the basic concept of a liquid-core liquid-cladding optofluidic lens in a circular chamber. Our design is based on liquid flow at low Reynolds numbers, and thus promises to form laminar streams in the lens chamber. The core stream sandwiched by two cladding streams enters the circular chamber and then expands to develop the lens-shape. Manipulating the flow rates of the three streams allows tuning of the curvature of the interface of the lens, and consequently changes the focal length. In our design, the width of the channel is much smaller than the dimension of the chamber, so the entrance and exit of the circular chamber act approximately as a source and sink, respectively. Therefore, the flow field in the circular chamber can be approximately described by a source-sink pair model bounded in a circular domain. Based on this model, we calculate the curvature of the interface between core and cladding streams, and consequently the focal length of the fluidic lens. | ||
| Fig. 1 The concept of the micro optofluidic lens with a circular lens chamber. The shapes and dimensions of the lens are tuneable by the flow rates of core and cladding streams: (a) double-convex lens; (b) plano-convex lens; (c) convergent-meniscus lens. | ||
Koplik et al.12 discussed the trajectories of tracer particles in a two-dimensional dipole flow field in a circularly bounded domain. In this source-sink pair model, a source of strength Q is placed at (−a, 0) in the Cartesian coordinates, and a corresponding sink of strength −Q is located at (a, 0). The flow field is determined by two parameters: the distance 2a between the source and sink, and their strength Q. This field can be described by the complex potential:
 | (1) |
In the case of the lenses depicted in Fig. 1, the source and sink can be assumed to be located at the circumference of the circular domain (a = R). The complex potential can be written as:
 | (2) |
The corresponding streamlines are shown in Fig. 2. For the mathematical simplicity, only the positive half of the y-axis (y > 0) is taken into consideration. In this region, the stream function can be simplified into:
 | (3) |
 | ||
| Fig. 2 Streamlines of source-sink pair in a circularly bounded domain with source and sink located at the circumference. | ||
The streamlines are a cluster of curves ψ = Ci(i = 1,2,3…). Thus, the coordinates (x, y) at each streamline should satisfy the equation:
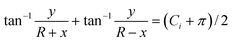 | (4) |
For each specific Ci, eqn (4) defines a curve representing a streamline. The two terms at the left hand side of the eqn (4) are the angles α and β depicted in Fig. 3(a). Since the sum of the angles α and β is a constant for each specific streamline, thus the angle ∠MPN = π − (α + β) is also a constant. According to the law of sines, the point P is located at a circle with a radius equal to r = R/sin(α + β). Therefore, the track of point P satisfying eqn (4) should be an arc of radius R/sin(α + β). Thus, each streamline in Fig. 2 is an arc with a radius r:
 | (5) |
 | ||
| Fig. 3 (a) The coordinate of point P satisfies the eqn (4) and the trajectory of point P is an arc with a radius r = R/sin(α + β); (b) interface positions of a lens. | ||
Because of symmetry, the streamlines in the other semi-plane (y < 0) should also comply with the conclusion above. For streams with different viscosities, the interface position at x = 0 can be derived based on the theory of hydrodynamic focusing reported previously.9 With a given interface position, the radius of curvature can be determined using eqn (5). A liquid interface with a well-defined radius of curvature and a mismatch in refractive indices can serve as an optofluidic lens. According to the above model, the curvature of the interface is tuneable by controlling the flow rate ratio of the streams. Next, the relationship between the flow rate ratio and the curvature of the interface is derived. For simplicity, the following are derived for core liquids and cladding liquids with the same viscosity.
According to the theory of potential flow, the first derivative of the complex potential with respect to z represents the velocity field ![[V with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0056_20d1.gif) = (u,v). The real and imaginary parts of this first derivative represent the velocity components in x-axis and y-axis, respectively. Differentiating W in eqn (2) with respect to z results in the velocity components:
= (u,v). The real and imaginary parts of this first derivative represent the velocity components in x-axis and y-axis, respectively. Differentiating W in eqn (2) with respect to z results in the velocity components:
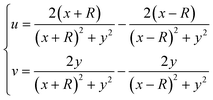 | (6) |
At the centre cross-section of the chamber (x = 0) the velocity components are.
 | (7) |
The curvatures of the two interfaces determine the positions of A2 and B2 (Fig. 3(b)), and therefore decide the flow rates for core and cladding flows:
 | (8) |
Simply by substituting x = 0 into eqn (5), the relationship between the radius of interface and the position of intersection between interface and y-axis is retrieved by solving the equation
| y2 − 2ry + R2 = 0 | (9) |
 | (10) |
This relationship of radius of interface versus position of intersection is illustrated in Fig. 4. As the position of the interface approaches the circumference of the chamber, the radius of interface approaches the radius of the chamber.
 | ||
| Fig. 4 Radius of interface versus the position of intersection between the corresponding interface and y-axis (both radius and position are normalized by the radius R of the circular chamber). | ||
Suppose the radii for  and
and  are r1and r2, respectively, according to eqn (10), the positions of intersections between these arcs and the y-axis are calculated as:
are r1and r2, respectively, according to eqn (10), the positions of intersections between these arcs and the y-axis are calculated as:
 | (11) |
Substituting (11) into (8) results in the fluxes of core and cladding flows, which correspond to the stream flow rates:
 | (12) |
Gaussian optics model
In the case of the optofluidic lens, two optically smooth interfaces are formed by three streams of flow, and each interface has a constant curvature of radius. This structure can be simply and sufficiently described by a combination of two surfaces which are rotationally symmetric about the optical axis, as illustrated in Fig. 5. In this situation, the principle planes located across the surface vertices and their positions lH and l′H are given as: | (13) |
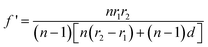 | (14) |
 | ||
| Fig. 5 A thick lens is constructed by a combination of two surfaces with given radii of curvature that are rotationally symmetrical about the optical axis. | ||
Combining (13) and (14), the positions of focal points with respect to front and rear surface vertices are, respectively:
 | (15) |
Taking the cladding as the reference, the relative refractive indices of core and cladding streams are n and 1, respectively.
Focal length is an important parameter to characterize a lens. At given refractive indices, the focal length is a function of the radii of the two interfaces. For mathematical simplicity, we confine the degrees of freedom to only one by assuming a case of symmetrical double-convex lens (Fig. 1 (a)) or fix one radius of interface at a infinitely large value, which is actually the case of a plano-convex lens, Fig. 1 (b). Then, we discuss the flow rate ratios between core and cladding streams under a given focal length.
In the case of a symmetrical double-convex lens (Fig. 1 (a)), the moduli of radii of two interfaces are both equal to r. The focal length is formulated as:
 | (16) |
Where r is the radius of the interface of the lens, n is the relative index of core stream, and d is the distance between the vertices of two interfaces. In the case of r ≫ d, the focal length in eqn (16) has an approximate expression:
 | (17) |
Under the assumption that the moduli of radii of two interfaces are equal, the flow rate ratio between cladding and core streams according to (12) is:
 | (18) |
Substituting relation (17) into (18), the relationship between the flow rate ratio and the focal length of the symmetrical double-convex optofluidic lens is:
 | (19) |
Fig. 6 (a) depicts the relation between focal length and flow rate as well as refractive index. The focal length is almost linearly proportional to the flow ratio. At the same refractive index, the higher the flow rate ratio between the cladding and the core, the longer the focal length. At the same flow rate ratio, the higher the refractive index, the shorter the focal length.
 | ||
| Fig. 6 Relationships between flow rate ratio and focal length (the dimension of focal length is normalized by the radius of circular chamber): (a) symmetrical double-convex lens, (b) plano-convex lens. | ||
In the case of a plano-convex lens, as depicted Fig. 1 (b), one radius of an interface is infinitely large r2 = ∞; while the other has a finite dimension r1 = r. Then the focal length can be simplified into:
 | (20) |
Under this assumption, the flow rate ratio between cladding B and core streams A is, as following eqn (12):
 | (21) |
It is obvious that the cladding flow from inlet C takes up half the space of the circular chamber, which means the flow rate of stream C is simply the sum of the flow rates of core stream A and cladding stream B. Fig. 6 (b) shows the relationship between focal length and flow rate ratio between cladding B and core A.
Experiments
The test devices were fabricated in polydimethylsiloxane (PDMS) using the soft lithography technique. The mask was printed on a transparency film with a resolution of 8000 dpi. The transparency mask was subsequently used for defining the negative mould of the lens in a 50 µm thick SU-8 layer. PDMS was mixed from the two components with a weight ratio of 10:1, and then poured into the SU-8 mould. PDMS was cured in vacuum oven at 60 °C and cooled at room temperature for 24 hours. The PDMS was then peeled off from the master mould, the 0.5 mm diameter access holes were punched. The moulded part was subsequently bonded to another flat PDMS part after treating both surfaces with oxygen plasma. Needles with an inner diameter of 0.33 mm and an outer diameter 0.64 mm were press fit into the access holes and worked as fluidic interconnections. With this technology, a circular lens chamber with a diameter of 1 mm and a height of 50 µm was realized. The width of the inlet and exit channels is 50 µm.In our experiment, the cladding liquid is de-ionized (DI) water mixed with w/w fluorescence dye (fluorescein disodium salt C20H10Na2O5, Acid Yellow 73 or C.I. 45350) and 3 µm red fluorescent particles (Duke Scientific Co.) were used to visualize the cladding liquid and its stream lines. The separated fluorescent bands of the fluorescent particles (540/610 nm) and of the dye (490/520 nm) allows easy imaging by switching the epi-fluorescent attachments on the microscope (Nikon EclipseTE 2000-S, Japan). DI water works as the core liquid. The liquids were kept in 5 ml glass syringes, which are driven by two syringe pumps (KDS230, KD Scientific Inc, USA) which allow any flow rate ratio needed. A sensitive CCD camera (HiSense MKII) attached to the microscope was used to capture the fluorescent images.
Results and discussions
First, flow visualization with fluorescent particles verified that the streamlines in the circular chamber have a perfect arc-shape, which is of great importance for designing the optofluidic lens. As mentioned above, red fluorescent particles are diluted in the two cladding flows that maintain the same flow rates as that of core flow. A sufficiently long exposure time of 85 ms was chosen, within which a particle can travel from the inlet to the outlet of the circular chamber. In this way, the particles will leave a streak line on the image, as illustrated in the inset of Fig. 7. Since the flow is laminar in our case, the streak lines of the particles correspond to the streamlines of the flow in the chamber. We extracted a group of positions for each of three paths showed in Fig. 7, and used an arc to fit each of them. The agreement between the extracted positions and fitting arcs confirms that the streamlines in the circular chamber have a perfect arc-shape, which can not be achieved with a rectangular chamber.11 | ||
| Fig. 7 The streamlines of the flow in the circular chamber are extracted by tracing of fluorescent particles. The asterisks in the figure represent the experimental results, the lines are the fittings arcs (all dimensions are normalized by the radius of the lens chamber). | ||
To verify the theory for predicting the relationship between the flow rate ratio and the curvature of the interface, blue light was used to excite the fluorescent dye dissolved in the cladding flows. The core flow with no fluorescent dye appears black on the image. The interface between the dark and bright region was extracted, its curvature was also evaluated under different flow rate ratios between core and cladding flows.
For the case of a symmetric lens, as illustrated in Fig. 8, the flow rate of core stream was fixed at 0.6 mL h−1, while the flow rates of two cladding streams vary equally from 0.1 mL h−1 to 1.2 mL h−1. The corresponding Reynolds number ranges from 0.44 to 1.67, and the Peclet number estimated for the fluorescent dye ranges from 444 to 1667. In this way, a symmetrical biconvex lens was achieved, and the curvature of interface is tuned by varying the flow rates of cladding streams. When the flow rate of cladding streams decreases, the interface of this fluidic lens approaches the wall of the chamber while still remaining as an arc-shape. In the case of the lens reported by Whitesides' group,11 the paraxial region of the lens was not bent with a perfect arc-shape, but was flat, especially when the interface approaches the wall of their rectangular chamber. Therefore, our circular design to form the fluidic lens is demonstrated here to have inherently robust wide-range tuneability. This advantage allows the realization a smaller radius of interface, and thus a shorter focal length, which shows a potential to increase the level of integration of a lab-on-a-chip optical component.
 | ||
| Fig. 8 Symmetrical case. The flow rates of two cladding streams are kept the same. The flow rate of the core stream is varied to achieve symmetrical biconvex lenses with different interface curvatures. The insets illustrate the fluorescence images of the lenses. The dimensions are normalized by the radius of circular chamber. The flow rate of core stream was kept at 0.6 mL h−1, and the flow rate of cladding stream varies from 0.1 mL h−1 to 1.2 mL h−1. The corresponding Reynolds number ranges from 0.44 to 1.67, and the Peclet number ranges from 444 to 1667. | ||
The relationship between the flow rate ratio and the curvature of the interface can be analytically described by using eqn (12):
 | (22) |
To test the fluidic lens in the case of an asymmetric lens, we fixed the flow rates of the core and the upper cladding streams equally at 0.6 mL h−1 (insets in Fig. 9), and varied the flow rate of the lower cladding stream in a range from 0.15 mL h−1 to 2.7 mL h−1. The corresponding Reynolds number ranges from 0.75 to 2.17, and the Peclet number ranges from 750 to 2167. A plano-convex lens is achieved when the flow rate of lower cladding stream is equal to the sum of the flow rates of the core and the upper cladding stream. When the flow rate ratio decreases, a biconvex lens is formed. If the flow rate ratio is larger than 2, a meniscus lens can be constructed. With this test, different kinds of lenses were demonstrated in our circular chamber design.
 | ||
| Fig. 9 Asymmetrical case. The flow rates of the upper cladding and core streams are kept the same, and the flow rate of the lower cladding stream is varied to achieve biconvex, plano-convex, and meniscus lenses. The insets illustrate the fluorescence images of the lenses. The dimensions are normalized by the radius of the circular chamber. The flow rates of the upper cladding and core streams are fixed equally at 0.6 mL h−1, and the flow rate of the lower cladding varies from 0.15 mL h−1 to 2.7 mL h−1. The corresponding Reynolds number ranges from 0.75 to 2.17, and the Peclet number ranges from 750 to 2167. | ||
The curvatures of lower and upper interfaces can also be mathematically defined by the flow rate ratio derived from eqn (12) assuming equal flow rates of the core stream and the upper stream:
 | (23) |
The device was also tested at higher flow rates, whose Reynolds numbers range from 2 to 9. When the Reynolds number is relatively small, the flow can be fully developed in the circular chamber and follows stream lines predicted with the dipole theory. However, with an increasing Reynolds number, the inertia causes flow separation at the entrance of the chamber. The flow passes through the chamber without following the streamlines as in the low flow rate case. This phenomenon causes the lens to be shifted along the flow direction and the shape of the lens is distorted (Fig. 10). Therefore, working on a low Reynolds number probably smaller than 2 is necessary for the lens to be well developed.
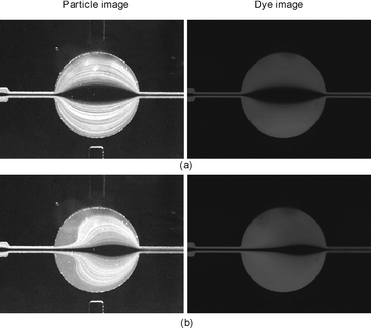 | ||
| Fig. 10 Effect of flow separation on lens shape: (a) low flow rate 3.6 mL h−1 (Re = 2) (b) high flow rate 16.2 mL h−1 (Re = 9). | ||
Conclusions
We reported the theoretical and experimental results of a micro optofluidic lens based on the liquid-core liquid-cladding concept. The lens chamber was designed as a circular shape to achieve a good curvature at the liquid interface. Experimental results validate the model describing the lens shape based on the two-dimensional dipole flow theory. The model predicts the relationships between the flow rate ratio between the core stream and the cladding stream and the radius of curvature, and consequently the focal length of the lens. The design with a circular lens chamber allows the realization of an optofluidic lens with a perfect arc shape. The test device was fabricated in PDMS. The lens chamber and the microchannels have a height of 50 µm. The streak lines of tracing fluorescent particles at low Reynolds numbers showed that the stream lines of the flow in the lens chamber follows a perfect arc. Experimental results of the interface curvatures agree well with the analytical results predicted by the model.References
- S. Camou, H. Fujita and T. Fujii, Lab Chip, 2003, 3, 40–45 RSC.
- J. Wenger, D. Gerard, H. Aouani and H. Rigneault, Anal. Chem., 2008, 80, 6800–6804 CrossRef CAS.
- M. Agarwal, R. A. Gunasekaran, P. Coane and K. Varahmyan, J. Micromech. Microeng., 2004, 14, 1665–1673 CrossRef.
- L. Pang, U. Levy, K. Campbell, A. Groisman and Y. Fainman, Optics Express, 2005, 13, 7928 CrossRef.
- S. Kuiper and B. H. W. Hendriks, Appl. Phys. Lett., 2004, 85, 1128–1130 CrossRef CAS.
- C. C. Cheng and J. A. Yeh, Optics Express, 2007, 15, 82140.
- D. Psaltis, S. R. Quake and C. Yang, Nature, 2006, 442, 381–386 CrossRef CAS.
- D. B. Wolfe, R. S. Conroy, P. Garstecki, B. T. Mayers, M. A. Fischbach, K. E. Paul, M. Prentiss and G. M. Whitesides, Proc. Natl Acad. Sci. U. S. A., 2005, 101, 12434–12438.
- N. T. Nguyen, T. F. Kong, J. H. Goh and C. L. N. Low, J. Micromech. Microeng., 2007, 17, 2169–2174 CrossRef.
- X. L. Mao, J. R. Waldeisen, B. K. Juluri and T. J. Huang, Lab Chip, 2007, 7, 1303–1308 RSC.
- S. K. Y. Tang, C. A. Stan and G. M. Whitesides, Lab Chip, 2008, 8, 395–401 RSC.
- J. Koplik, S. Redner and E. J. Hinch, Phys. Rev. E, 1994, 50, 4650–4671 Search PubMed.
| This journal is © The Royal Society of Chemistry 2009 |
