Structure and superconductivity of the intercalation compounds of TiNCl with pyridine and alkali metals as intercalants

Abstract

Highly crystalline TiNCl with the FeOCl structure was prepared by chemical vapor transport, and intercalated with pyridine (Py) and alkali metals (A = Li, Na, K, and Rb). The structure of each intercalation compound was determined by the Rietveld refinement. Pyridine molecules were taken up to a composition Py_0.25TiNCl, and arranged with the molecular plane perpendicular to the TiNCl layers. The pyridine intercalated compound showed superconductivity at a transition temperature (T_c) of 8.6 K. The alkali metal intercalated compounds A_xTiNCl also became superconductors with much higher T_cs of ∼16.3 K. Upon intercalation the TiNCl crystalline layers are mutually shifted in such a way that the primitive cell was changed into different kinds of polytypes with centered cells, depending on the dimensions of the intercalants between the layers. The ab initio electrical band calculation suggested that the pyridine and alkali metal intercalated compounds have different density of states (DOS) profiles, and should have different characters in superconductivity.

---

Introduction

There are two types of layer structured polymorphs of metal nitride halides, MNX (M=Ti, Zr, Hf; X=Cl, Br, I), α- and β-forms with the FeOCl and the SmSI structures, respectively.¹ All compositional combinations of the β-forms of MNX (M=Zr, Hf; X=Cl, Br, I) form intercalation compounds with alkali metals and become superconductors.² The Li intercalated β-ZrNCl (Li_xZrNCl) has a superconducting transition temperature (T_c) of 13–15 K.^3,4 The highest T_c has been recorded at 25.5 K for the Li and THF (tetrahydrofuran) cointercalated β-HfNCl, Li_0.48(THF)_yHfNCl.⁵ The β-form contains double honeycomb-like MN layers sandwiched by close-packed chlorine layers as shown in Fig. 1. β-MNX are semiconductors with band gaps larger than 3–4 eV.^6,7 The superconductivity is considered to occur in the electron-doped nitride layers. Characterization of the superconductivity has been carried out extensively, and revealed that this is a quasi two dimensional superconductor like high-T_c cuprates,⁸ but an electron-doped system; the electron density of states at the Fermi level N*(E_F) was found to be as small as ∼0.25 states eV⁻¹ spin f.u.⁹ However, the electron–phonon coupling constant λ in Li_xZrNCl was estimated to be less than 0.22,¹⁰ which was too small to reproduce the observed value of T_c. Moreover, remarkably large superconducting gap ratios 2Δ/k_BT_c = 5.0–5.6 and 4.6–5.2 were reported by break junction¹¹ and heat capacity measurements,¹⁰ respectively. At present, it is very difficult to interpret the above experimental results consistently by a conventional phonon-mediated BCS mechanism. A different mechanism such as a charge-fluctuation mechanism has now been suggested.^4,9

Fig. 1 Structure of β-MNX: views along the c-axis (a) and along the b-axis (b).

The α-type layered polymorph has an orthogonal MN layer network separated by halogen layers as shown in Fig. 2. It will be interesting to compare the superconductivity of the different types of networks if the α-type layered compounds also become superconductors. The structure of the α-form can be characterized as a lower density polymorph against the dense β-form.¹² The metal atoms in the β-form are 7-fold coordinated by 4 nitrogen and 3 halogen atoms, whereas in the α-form the metal atoms are only 6-fold coordinated by 4 nitrogen and 2 halogen atoms. As a matter of fact, some β-forms containing large halogen atoms (β-ZrNI, β-HfNBr and β-HfNI) are prepared by the high pressure transformation of the corresponding α-forms.¹²

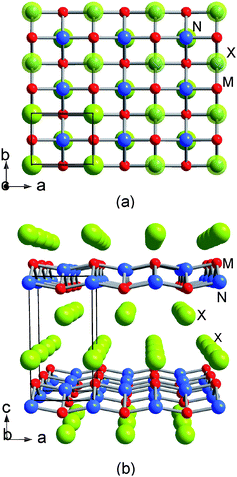Fig. 2 Structure of α-MNX: views along the c-axis (a) and along the b-axis (b).

The titanium compounds crystallize only in the α-type structure. It is well known that FeOCl is isotypic with TiNCl and forms an intercalation compound with pyridine¹³ whereby the electrical conductivity increases by about seven orders on intercalation. The remarkable enhancement of the conductivity is considered to be due the charge transfer from the organic Lewis base to the FeOCl layers. FeOCl also forms an intercalation compound with Li.^14,15 In our previous study, the intercalation compound of α-HfNBr with Li was examined.¹⁶α-HfNBr formed a Li intercalated compound by reaction with n-butyllithium, and the yellow color of the pristine crystals was changed to black. Despite the color change, the intercalated crystals were found to be a Mott-insulator, and showed the existence of localized electron spins. In the present study, some intercalation compounds of TiNCl have been prepared using pyridine and alkali metals, and new superconductors have been found as described below.

Experimental

Materials

TiNCl was prepared according to the method reported by Juza and Heners¹⁷ The method was slightly modified. Ammonia gas was passed over TiCl₄ in a vertical Pyrex glass reaction cell for about 3 h. The reactant was self-heated by the heat evolved by the intense exothermic reaction. The resulting black solid was continuously heated in the same reaction cell at 400 °C for 3 h under the ammonia gas stream. Ammonium chloride crystals were grown on the upper part of the reaction cell. TiNCl formed at the bottom of the glass cell and a small amount of ammonium chloride were vacuum sealed in a Pyrex glass tube and kept in a horizontal furnace with a temperature gradient of 400–440 °C for 3–7 days. The as-prepared product was purified by chemical vapor transport to the higher temperature zone as highly crystalline TiNCl.¹⁸ The lattice parameters and atomic coordinates determined by the Rietveld refinement are shown in Table 1 and 2, and are in good agreement with those reported by Juza and Heners.¹⁷Alkali metal azides (AN₃, A = Li, K, Rb) were prepared from NaN₃ (Sigma) by ion-exchange according to the method described elsewhere.^19–21 All the azides were purified by recrystallization from the respective ethanol solutions.

Table 1 Lattice parameters, selected bond distances, angles, and superconductivity of TiNCl intercalation and related compounds

	TiN	TiNCl	LixTiNCl	NaxTiNCl	KxTiNCl	RbxTiNCl	PyxTiNCl
a Basal spacing, d = c for the primitive cell, and d = c/2 for the centered cells. b A–Cl Distance in ACl with the rock (salt structure).
Space group	Fm-3m (no. 225)	Pmmn (no. 59)	Pmmn (no. 59)	Bmmb (no. 63)	Immm (no. 71)	Immm (no. 71)	Bmmb (no. 63)
Z	4	2	2	4	4	4	4
Lattice parameters/Å
a	4.244	3.9382(1)	4.0114(1)	4.0170(1)	4.0605(1)	4.0375(10)	3.9787(6)
b		3.2582(1)	3.2726(1)	3.2737(1)	3.2932(1)	3.2899(8)	3.283(4)
c		7.8001(1)	7.9211(2)	16.8835(6)	17.722(1)	18.398(7)	27.014(7)
d ^a		7.8006(1)	7.9210(1)	8.4418(3)	8.861(1)	9.200(4)	13.507(4)
Selected bond distances (Å) and angles (°)
Ti–N (i)	2.122	2.0077(8)	2.00098(4)	2.024(9)	2.0433(5)	2.0251(42)	2.0270(3)
Ti–N (ii)	2.122	2.0145(23)	1.9890(33)	1.9355(40)	1.9288(21)	2.054(32)	1.9833(2)
Ti–Cl		2.4299(12)	2.5361(14)	2.5332(26)	2.5699(16)	2.442(17)	2.4377(4)
Ti–Ti	3.001	3.0029(8)	2.8781(7)	2.8915(14)	2.8923(8)	2.9523(93)	2.985(3)
A–Cl A: alkali metal			2.536 (2.588)^b	2.597(1) (2.810)^b	3.197(1) (3.145)^b	3.345(1) (3.284)^b
N–Ti–N (α)	180	157.50(1)	172.73(1)	165.78(1)	167.02(13)	170.9(17)	157.89(1)
N–Ti–N, Ti–N–Ti (β)	90	107.93(1)	110.71(1)	115.49(1)	117.23(12)	106.4(14)	111.48(1)
Superconductivity
T c , K	5.6		16.5	16.3	16.3	16.3	8.6
Fraction (%)			0.5	13.3	31.0	4.3	18.8

---

Table 2 Atomic coordinates and occupancy parameters of TiNCl and the intercalation compounds

TiNCl
Atom (site)	x	y	z	Occ	B /Å^2
a Geomtry optimized data by CASTEP. b Refined without including pyridine molecules.
Ti (2b)	0	1/2	0.1011(1)	1	1
N (2a)	1/2	1/2	0.0509(5)	1	1
Cl (2a)	0	0	0.3322(2)	1	1
Rwp, Rexp (%)	1.73, 1.845

---

LixTiNCl
Atom (site)	x	y	z	Occ	B /Å^2
Ti (2b)	0	1/2	0.0794(1)	1	1
N (2a)	1/2	1/2	0.0633(7)	1	1
Cl (2a)	0	0	0.3240(2)	1	1
Li (2a)	1/2	1/2	0.3340^a	—	—
Rwp, Rexp (%)	2.02, 1.29

---

NaxTiNCl (Na0.22TiNCl0.98)
Atom (site)	x	y	z	Occ	B /Å^2
Ti (4c)	0	1/4	−0.2120(1)	1	1
N (4c)	0	-1/4	−0.2732(4)	1	1
Cl (4c)	0	-1/4	−0.0975(2)	0.978(5)	1
Na (4c)	1/2	1/4	0	0.215(5)	1
Rwp, Rexp (%)	2.35, 1.07

---

KxTiNCl (K0.22TiNCl0.90)
Atom (site)	x	y	z	Occ	B /Å^2
Ti (4j)	1/2	0	0.7151(1)	1	1
N (4i)	0	0	0.2718(2)	1	1
Cl (4i)	0	0	0.1038(1)	0.898(2)	1
K (2c)	0	0	1/2	0.442(2)	1
Rwp, Rexp (%)	1.09, 1.31

---

RbxTiNCl (Rb0.19TiNCl0.75)
Atom (site)	x	y	z	Occ	B /Å^2
Ti (4j)	1/2	0	0.7122(8)	1	1
N (4i)	0	0	0.2791(28)	1	1
Cl (4i)	0	0	0.1141(10)	0.75(4)	1
Rb (2c)	0	0	1/2	0.37(2)	1
Rwp, Rexp (%)	3.60, 1.32

---

PyxTiNCl ^b (Py0.25TiNCl)
Atom (site)	x	y	z	Occ	B /Å^2
Ti (4c)	0	1/4	−0.2221(4)	1	1
N (4c)	0	-1/4	−0.2635(17)	1	1
Cl (4c)	0	-1/4	−0.1554(5)	1	1
Rwp, Rexp (%)	4.06, 1.08

---

Intercalation

The intercalation of pyridine (Py) was carried out from the vapor phase using a home-made volumetric apparatus equipped with a pressure transducer (MKS BARATRON 390HA-01000). The vapor pressure change of pyridine was measured in a constant volume reactor at room temperature (25 °C). The reaction of the alkali metals was performed using the azides which were thermally decomposed into reactive alkali metals and nitrogen gas under vacuum. A mixture of TiNCl and the respective alkali metal azide was loaded in a hexagonal BN (h-BN) cell (8 mm in inner diameter, 10 mm in depth) with a h-BN cover, which was in turn placed in a Pyrex glass tube. The temperature of the mixture was slowly raised under vacuum to decompose the azide with a temperature range of 240–350 °C. The start of the decomposition was monitored as the pressure increased due to the evolution of nitrogen gas and the completion of the decomposition was decided to be when the vacuum returned to the starting value. After the decomposition, the glass tube was vacuum sealed with the h-BN cell, and annealed in a furnace at 300 °C for about one week. All the manipulation of the air-sensitive compounds was carried out in an Ar filled glove box (MBRAUN).

Analyses and characterization

The X-ray diffraction (XRD) patterns of TiNCl and the intercalated samples were measured using an imaging plate (IP) Guinier camera (Huber G670) with monochromated Cu Kα1 (λ = 1.540596 Å) and Mo Kα1 (λ = 0.709260 Å) radiation. The sample was sealed in a thin Pyrex glass capillary with a diameter of about 0.3 mm. The intercalated samples were very air-sensitive. The use of a glass capillary can protect the samples from being exposed to humid air, and can avoid the preferred orientation of the layered samples by rotating the capillary on the goniometer as well. The XRD powder patterns were analyzed by the Rietveld refinement program, TOPAS-Academic.²² The IP Guinier diffractometer can cover the diffraction 2θ range 4–100° with a step of 0.005°. The diffraction pattern in a range 4.5–90° for Cu Kα1 and 4–45° for Mo Kα1 radiation was used for the refinement by the full profile fit with a Pseudo Voigt type profile function. In most cases, the equivalent isotropic temperature factors (B, Ų) were assigned to a fixed value of 1.0. The background due to a glass capillary was refined by the TOPAS-Academic program rather than removing the blank. The calibration of the imaging plate was performed using LaB₆ powder as a standard. The magnetic susceptibility measurement was carried out using a SQUID magnetometer (Quantum Design MPMS-5) under a magnetic field of 20 Oe in zero field cooled (ZFC) and field cooled (FC) processes. The electrical resistivity was measured on a pellet sample. The powder samples were pre-compressed into pellets with a diameter of 7 mm with a thickness of ∼0.4 mm, and were then re-compressed under hydrostatic pressure conditions up to 1.2 kbar in an evacuated nylon bag. The resistivity was measured using a cryostat down to 6 K by a conventional 4-probe method. The sample pellet with silver electrodes was evacuated and sealed with He gas in a small cell, using an indium metal gasket, which was then taken out from the glove box to measure the electrical resistivity. Geometry optimization calculations of the pyridine intercalated TiNCl were performed using the quantum mechanical program DMol3 Solid,^23–25 provided with the Materials Studio suite by Accelrys. The electrical band structure was calculated using the program CASTEP^26,27 with the GGA-PBE (generalized gradient approximation, Perdew–Burke–Ernzerhof) functional and ultrasoft potentials at the default fine setting.

Results and discussion

1. Pyridine intercalation

The amount of pyridine uptake by TiNCl was measured in a vapor pressure of 20 Torr (i.e., a relative vapor pressure of ∼0.8) at 25 °C. The uptake amount was estimated from the pressure decrease and shown in Fig. 3 as a function of the square root of reaction time. The uptake amount increased linearly with the square root of time in the early stage of the reaction and finally reached a value of 0.25 mol/mol. This finding suggests that the Py uptake proceeded via a diffusion mechanism. After the reaction, the sample was sealed in a thin Pyrex glass tube in an Ar glove box, and the XRD pattern was measured by the IP Guinier camera. The basal spacing (d) of TiNCl increased from 7.80 to 13.51 Å, and the XRD pattern can be indexed with an orthorhombic unit cell of a = 3.9787(6), b = 3.283(4), and c = 27.014(7) Å. The lattice parameters of the ab plane are essentially unchanged by the intercalation. The c parameter is twice as large as the basal spacing, and the systematic extinction observed in the XRD pattern (h + l = 2n + 1) suggests that the primitive cell of the pristine TiNCl (space groupPmmn) is changed into a centered cell with the space group Bmmb. This change indicated that the TiNCl crystalline layers are mutually shifted parallel to the plane along the a-axis by a/2 to have the different polytype. The increase of the basal spacing (Δd = 13.51–7.80 = 5.71 Å) suggests that Py molecules are oriented with the molecular plane almost perpendicular to the TiNCl layers in the interlayer space.

Fig. 3 Pyridine uptake by TiNCl as a function of the square root of time.

The Rietveld analysis was performed using the above orthorhombic unit cell without including pyridine. The result is shown in Fig. 4; the lattice parameters, selected bond distances and angles of the TiNCl layers are compared with the other intercalation compounds in Table 1 and 2. It is certainly difficult to refine the orientation of pyridine molecules, however, the organic molecules with weaker X-ray scattering power are presumably uniformly distributed between the layers. The intensities of the X-ray reflections should mainly reflect the host TiNCl structure and symmetry. The atomic coordinates could also be tentatively refined as shown in the tables. The XRD data clearly demonstrates that the two-dimensional layer structure of TiNCl is maintained by the intercalation of Py molecules, with only the stacking sequence of the layers being changed to shift to a different polytype from Pmmn to Bmmb. The arrangement of Py molecules between the layers will be discussed later in more detail in relation to the geometry optimization of the structure.

Fig. 4 Rietveld analysis of the X-ray diffraction pattern of Py_0.25TiNCl. Open circles show the observed data points and the solid line represents the calculated diffraction pattern. The expanded scale pattern is shown in the upper frame.

2. Alkali metal intercalation

Alkali metals were intercalated by the reaction of TiNCl with alkali azides. The azides began to decompose in a temperature range 250–330 °C and the resulting alkali metals reacted with TiNCl. A typical reaction condition consisted of the following: a molar mixing ratio of AN₃/TiNCl = 1/2. After the completion of the decomposition, the sample was annealed at 300 °C for 7 days. The resulting compounds were taken out in an Ar glove box, and sealed in a thin Pyrex glass capillary to measure the XRD pattern with the Guinier camera. The lattice types were estimated from the systematic extinction of the reflections, and the lattice parameters and atomic coordinates were refined by the Rietveld method. Fig. 5 displays the local arrangement of the TiNCl layer around the Ti atom. The bond distances and angles marked in this figure are compared in Table 1 for various intercalated compounds.

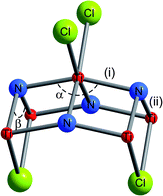Fig. 5 Local coordination surrounding the Ti atom in the TiNCl layer. The bond distances and bond angles marked are given in Table 1 for various TiNCl intercalation compounds.

Fig. 6 shows the XRD pattern of the TiNCl after the reaction with KN₃ followed by annealing. The space group (S. G.) of the reaction product was Immm with a systematic extinction (h + k + l = 2n + 1) of the X-ray reflection peaks, suggesting that the TiNCl layers are shifted (a + b)/2 in the ab plane. The pattern showed the formation of KCl, implying that some of Cl ions were withdrawn from the interlayer space by K to form KCl on the surface of the crystal. The Rietveld refinement was made on the two coexisting phases, and the occupation parameters of the Cl and K sites were also refined. The composition of the product was estimated to be K_0.22TiNCl_0.90 from the refined site occupation parameters. The shift of the layers can provide interstices for K ions to be coordinated by 8 chlorine atoms from two adjacent TiNCl layers as shown in Fig. 7. The atomic distance K–Cl is estimated to be 3.197(1) Å from the refined coordinates, in accordance with the value 3.145 Å for KCl with the rock salt structure. The other alkali metal intercalated compounds were also analyzed in a similar manner and the results are summarized in Table 1 and 2 together with the Py intercalated compound and TiNCl.

Fig. 6 Rietveld analysis of the X-ray diffraction pattern of K_xTiNCl. Open circles show the observed data points and the solid line represents the calculated diffraction pattern. The expanded scale pattern is shown in the upper frame. The top and bottom tip marks are calculated 2θ angles for the Bragg peaks of K_xTiNCl and KCl, respectively.

Fig. 7 Schematic structural illustration of the TiNCl polytypes with intercalated cations between the layers.

In the case of the reaction with LiN₃, the formation of LiCl was not detected. The c-axis parameter slightly increased from 7.8006(1) to 7.9210(1) Å, and the a-axis parameter also increased from 3.9382(1) to 4.0114(1) Å. Although the reaction did not bring about a change in polytype, with the unit cell remaining the same as the primitive cell, apparently Li intercalation still occurred in TiNCl. The small change in the c-axis parameter can be interpreted in terms of the size of the Li ions. The small Li ion can fit in the space between two adjacent layers, formed by four Cl atoms and one Cl atom, as shown in Fig. 7. In the LiCl rock salt structure the Li–Cl distance is 2.588 Å, which corresponds to the shortest Li–Cl distance 2.536 Å in the Li intercalation compound. The atomic coordinates and the occupancy of the Li site cannot be determined by the XRD data. The coordinates were estimated by the geometry optimization as given in Table 2 by CASTEP. The electrochemical Li intercalation in TiNCl was studied by Kuhn et al.²⁸ They reported that around 0.5 mol of Li/TiNCl could be reversibly intercalated. Although no structural data was given, it is likely that a similar compound was obtained in the electrochemical process. The Li intercalation compound of FeOCl was first reported by Rouxel and Palvadeau.¹⁴ The Li ions were placed in the 5-fold coordination site in FeOCl as used in the TiNCl compound of this study.

Fig. 8 shows the XRD pattern of the Na intercalated compound. The systematic extinction observed in the XRD pattern (h + l = 2n + 1) of the Na intercalated compound suggested that it has a polytype with a Bmmb centered cell like the pyridine intercalated compound. This suggests that the TiNCl layers shift along the a-axis by a/2 as shown in Fig. 7. As can be seen from the XRD pattern, a small amount of NaCl formation was detected, and a part of TiNCl remained unreacted. The Rietveld refinement was made on the three coexisting phases system. The occupation parameters of the Cl and the Na sites were also refined. The refinement gives a good fit with the observed data. The shortest Na–Cl distance was calculated to be 2.597(1) Å, which is also in good agreement with the value of 2.81 Å of NaCl. The Na ions are 6-fold coordinated by Cl atoms. The composition of the compound was estimated to be Na_0.22TiNCl_0.98 from the refined site occupation parameters (Table 2).

Fig. 8 Rietveld refinement of the X-ray diffraction pattern of Na_xTiNCl. Open circles show the observed data points and the solid line represents the calculated diffraction pattern. The expanded scale pattern is shown in the upper frame. The top, middle, and bottom tip marks are calculated 2θ angles for the Bragg peaks of Na_xTiNCl, TiNCl, and NaCl, respectively.

The Rb intercalated compound has a polytype with the space groupImmm like the K intercalated compound. It appears that alkali metal atoms with large ionic radii like K and Rb have a tendency to have a body centered cell with large interstices with 8–fold coordination between the layers, as shown in Fig. 7. The Rietveld refinement was made on the three phase coexisting system like the Na intercalated case. The composition was estimated to be Rb_0.19TiNCl_0.75 from the refined site occupation parameters given in Table 2.

3. Superconductivity

The magnetic susceptibility of the product was measured as a function of temperature by SQUID magnetometer under a magnetic field of 20 Oe. The results on K_xTiNCl and Py_0.25TiNCl are shown as typical results in Fig. 9 and 10, respectively. The Py intercalated TiNCl showed a steep decrease in susceptibility at 8.6 K and K_xTiNCl at 16.3 K which are significantly higher than the T_c = 5.6 K of TiN with the NaCl structure.²⁹ The superconducting volume fractions were estimated to be 11 and 31% respectively, from the theoretical value for perfect diamagnetism. The T_c and the superconducting fractions of the other samples are listed in Table 1. Although the superconducting fractions are not very high, such large diamagnetic values are explained only by superconductivity. As seen from the XRD patterns of Fig. 4, 6 and 8, the intercalated compounds were obtained as single phases with trace amounts of unreacted TiNCl and small amounts of the respective alkali metal chlorides such as NaCl and KCl. The superconducting fraction is not directly related to the chemical purity of the products. It is likely that the superconducting condition should be more sensitive to the defects, local composition, crystallinity, and so on. We have tried to prepare superconducting samples with much larger superconducting fractions by changing the preparation conditions such as the amount of alkali azides mixed, annealing temperatures and reaction times. The grain size of TiNCl was also varied to obtain higher superconducting fractions. However, we have not improved the fractions very much from the values shown in Table 1.

Fig. 9 Magnetic susceptibility of K_xTiNCl as a function of temperature.

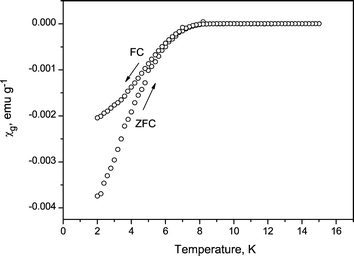Fig. 10 Magnetic susceptibility of Py_0.25TiNCl as a function of temperature.

The K and Py intercalated samples were compressed to discs as described in the Experimental, and the electrical resistivities were measured down to 6 K. The results are shown in Fig. 11 and 12 respectively. Both samples showed metallic behavior; the resistivities decreased with the decrease of temperature. The K_xTiNCl sample had a transition at ∼16 K, although zero resistivity was not attained down to 6 K. The transition temperature is in good agreement with the T_c observed by the magnetic susceptibility measurement. It is reasonable to conclude, therefore, that the semiconducting TiNCl is changed into a metallic conductor with a superconducting transition at 16 K. Pyridine intercalated samples also showed metallic temperature dependence, and the resistivity also decreased with the decrease of temperature. However, unexpectedly, the resistivity began to increase from about 80 K, and did not show a superconducting transition corresponding to the susceptibility measurement. The reason is not clear. It is very likely that the electrode contact by silver paste on the sample pellet deteriorated during the measurement. The contact of the electrodes appears to be very important. The resistivity in a different sample showed a negative temperature dependence from room temperature.

Fig. 11 Electrical resistivity of K_xTiNCl as a function of temperature.

Fig. 12 Electrical resistivity of Py_0.25TiNCl as a function of temperature. The resistivity was expected to decrease along the dotted line down to a transition temperature.

4. Ab initio eletronic band structure calculation

The band structures of K_xTiNCl were calculated based on the XRD data shown in Table 1 and 2 by the ab initio quantum mechanical software package CASTEP; a 6 × 3 × 6 Monckhorst-Pack mesh was used for k-point sampling with the Brillouin zone of the orthorhombic unit cell. The composition K_0.5TiNCl was used, in which the K site is fully occupied. The band structure and the density of states (DOS) profile obtained are shown in Fig. 13. Similar band and DOS profiles were calculated on the K_0.5TiNCl (without including K atoms) and on the pristine TiNCl, and are shown in Fig. 14 and 15 for comparison. Woodward and Vogt³⁰ examined the electronic structure of TiNCl and some related MNX compounds at the extended Hückel level. They demonstrated that TiNCl had a direct transition type band structure at the G (Γ) point. Our calculation also supports their results, having the direct band gap at G and Z points. The band gap of the pristine TiNCl was calculated to be 0.63 eV, however, the ab initio calculation usually underestimates the gap value. The actual optical band gap can be estimated to be around 1.5–2.0 eV for TiNCl.

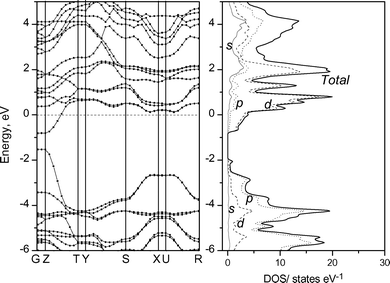Fig. 13 Band structure and DOS profile of K_0.5TiNCl.

Fig. 14 Band structure and DOS profile of K_0.5TiNCl without including K atoms.

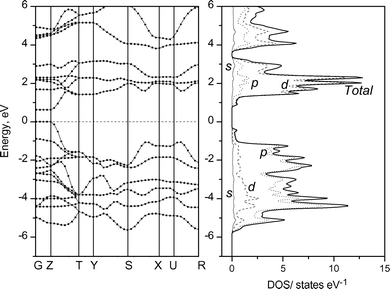Fig. 15 Band structure and DOS profile of the pristine TiNCl.

It is reasonable that the band structure for the pristine TiNCl, with the space groupPmmn, and that of (K_x)TiNCl (without including K atoms), with the space groupImmm, are very similar since the interaction between the layers is very weak, and thus the influence of the difference in polytype should be very small. The small difference in the details of the band shape between the two TiNCls can be mainly ascribed to the distortion of the layer structures associated with intercalation. The dispersion along or parallel to the c-axis, i.e., G–Z, T–Y, and X–U are very small, reflecting the weak interaction between the layers through chlorine atoms. Upon intercalation of K, the basic band structure is kept, and the doped electrons fill the conduction bands, which are mainly composed of Ti-3d orbitals. It is interesting to note that the Fermi level goes up to the flat bands in the S–X and U–R paths, which are coupled with a sharp dispersion band in the Z–T path. This is the so called “sharp and flat band” scenario for superconductivity proposed by Simon.³¹ From the chemistry view point the two band picture contains a broad band for itinerant electrons and a narrow band for locally paired electrons. When the flat band lies on the Fermi level, the maximum T_c values would be expected. The valence band is mainly composed of N-2p and Cl-3p orbitals. In the real compound, chlorine sites are partially removed, and have defects, which also act as electron donors. The superconductivity of the chlorine deintercalated compounds β-ZrNCl_1−x and β-HfNCl_1−x was discussed elsewhere.²¹ The real band structure should be modified but the basic features would not be changed. The flat band could be located exactly at the Fermi level by adjusting the doping level.

The crystal structure of Py_0.25TiNCl was estimated by geometry optimization by using a software package DMol3 Solid from Accelrys. A 2 × 2 × 1 supercell (a = 7.9516, b = 6.5588, c = 27.0024 Å) was constructed from 4 unit cells with the space group Bmmb (Table 1) and four pyridine molecules were placed in the supercell. The P1 symmetry supercell containing (C₅NH₅)₄(TiNCl)₁₆ was obtained, and geometrically optimized with a 3 × 4 × 3 Monkhorst–Pack k-point grid using LDA PWC (local density approximation, Perdew–Wang) functional. The geometry optimization convergence thresholds were set at the fine level. The optimized structure is shown in Fig. 16. The Py molecules are arranged with the molecular plane perpendicular to TiNCl layers, and the plane was slightly tilted against the bc-plane to attain a closed packing. As the initial condition, the nitrogen atoms of the pyridine rings were directed upward and downward alternately against the TiNCl layers. The atomic coordinates of the geometry optimized structure is given in the ESI‡. In Fig. 17 the XRD pattern for Py_0.25TiNCl, shown in Fig. 4, was compared with the simulated pattern obtained using the supercell and the geometry optimized atomic coordinates. Here only the background, the scale parameter and the peak profile were refined by the Rietveld program. Note that the fitting is slightly improved by adding pyridine molecules compared with the refinement made without Py molecules in Fig. 4.

Fig. 16 The arrangements of Py molecules in Py_0.25TiNCl obtained by geometrical optimization by DMol3 Solid. A 2 × 2 × 1 supercell is used; the views along the b-axis (top) and along the c-axis (bottom). Nitrogen atoms are orange-colored.

Fig. 17 Simulated XRD pattern of Py_0.25TiNCl using the atomic coordinates obtained by the geometry optimization (solid line). Open circles show the observed data (Fig. 4). The expanded scale pattern is shown in the upper frame. The tip marks are calculated 2θ angles for the Bragg peaks. The background and the pattern profile were refined by TOPAS-Academic to compare the calculated and observed patterns.

The band structure of Py intercalated TiNCl was calculated by CASTEP on the basis of the structure obtained by the geometry optimization with the 2 × 2 × 1 supercell and a composition (C₅NH₅)₄(TiNCl)₁₆. A 3 × 3 × 3 Monkhorst–Pack k-point mesh was used. The obtained DOS profile is shown in Fig. 18. The profile is very different from the one obtained for K_0.5TiNCl in Fig. 13. The DOS profile has new peaks in the band gap of TiNCl. The partial DOS (PDOS) of pyridine molecules are shown by shadowed bands. The new band in the band gap is attributed to the HOMO band of pyridine. The LUMO of pyridine is located about 4 eV above the HOMO level and is not shown in the figure. The Py intercalated compound is a superconductor and shows metallic behavior in the conductivity at room temperature. However, the calculated band structure has a gap between the Py HOMO band and the TiNCl conduction band. It is reasonable to estimate that the Fermi level should be located in the middle of the tail of the TiNCl conduction band by the charge transfer. The band structures of Py intercalated compound and alkali metal intercalated ones are very different. The mechanism of the superconductivity should also be very different as found in the remarkable difference of T_cs.

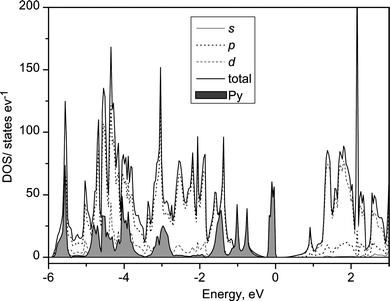Fig. 18 DOS profile of Py_0.25TiNCl based on the calculated structural model shown in Fig. 16. The shaded profile shows the PDOS of Py molecules.

Discussion

The crystallographic parameters of all the intercalation compounds of TiNCl prepared in this study are summarized in Table 1 and 2. Upon intercalation, the lattice parameters increased slightly in the ab plane; the c-axis parameter, or the basal spacing (d), increased reflecting the size of the intercalants. The stacking sequence of the layers is changed by the shift of the layers, depending on the size of the alkali metal ions. The size of the intercalated cation appears to control the shift of the layers as shown in Fig. 7. Larger cation sizes mean higher coordination numbers for cations by chlorine atoms. A polytype shift was also observed in the formation of β-type intercalation compounds. β-ZrNCl and β-HfNCl have the SmSI type layer stacking,³² which was changed into the YOF type layer stacking by the intercalation of Li and Na.^33,34 The two polytypes are composed of the same structural slabs [Cl-M-N-N-M-Cl] (M = Zr, Hf) stacked together by van der Waals forces, but the layer stacking sequence are different; the slabs repeat in two different sequences of ABC and ACB for the SmSI and the YOF types, respectively. We have also reported that the deintercalation of chlorine atoms from β-ZrNCl induced the polytype shift from SmSI to YOF.²¹

Upon intercalation, the bond angle N–Ti–N (α) increased from 157.5 to up to 170.9° and the Ti–Cl distance also tended to increase slightly, the two-dimensional structure being essentially unchanged. The increase of the ab lattice parameters and the bond distances can be explained in terms of the doping of electrons into the conduction bands, i.e., antibonding bands. It is interesting to note that the Ti–N bond distance of the pristine TiNCl, as well as the intercalation compounds, is shorter than that of TiN with the rock salt structure, implying there are stronger covalent bonds within the TiNCl layer. Note that when the N–Ti–N (α) angle value approaches 180°, the TiN layers of TiNCl can be seen as fragments of the rock salt TiN structure sliced along the plane, parallel to the (110) plane, although the N–Ti–N (β) angle is in a range 110–117°, which is larger than 90° of the sliced TiN. The TiN puckered layer of TiNCl has shorter Ti–N bond distances than the TiN of the rock salt structure, and accordingly the Ti–Ti distance was 2.88–2.95 Å within the layer and was shorter than 3.001 Å in TiN (Table 1).³⁵ The remarkably higher T_c of the electron-doped TiNCl compared with that of TiN must be relevant to the shorter Ti–N and Ti–Ti distances in the strong covalent network. It should also be noted that in the superconductivity of electron doped β-ZrNCl and β-HfNCl, the bond distances Zr–N and Hf–N of the pristine crystals are 2.130 and 2.114 Å respectively, which are shorter than the 2.289 and 2.263 Å of ZrN and HfN with the rock salt structure respectively.³⁶

In a previous study, Li intercalated compounds of α-HfNBr were prepared.¹⁶ Highly crystalline α-HfNBr can be prepared by chemical transport as a single phase without contamination of the β-type polymorph,³⁷ since β-HfNBr can only be prepared by high pressure and high temperature treatment.¹² The other α-forms such as α-ZrNCl and HfNCl are much more difficult to prepare as highly crystalline single phases. The Li intercalation was performed by using n-butyllithium solution in hexane. The resulting Li intercalated compound had a composition α-Li_0.56HfNBr with a primitive unit cell. A Li naphthalene solution in THF was also used as another lithiation reagent, which formed a cointercalated compound Li_x(THF)_yHfNBr with a body centered cell. Both intercalation compounds were found to be Mott-insulators with electrical resistivity larger than 2 × 10⁷ Ω cm. The magnetic susceptibility measurement of α-Li_0.56HfNBr demonstrated that the compound was paramagnetic with 0.2 unpaired electrons per formula unit, i.e., about 40% of the doped electrons are localized at the reduced Hf sites. The color of α-HfNBr changed from yellow to black upon Li intercalation due to the charge transfer.

In high-T_ccuprate superconductors, the antiferromagnetic coupling of Cu²⁺ (S = 1/2) is suppressed by carrier doping, and the system becomes a superconductor. In α-HfNBr the doped electrons are strongly trapped by Hf atoms; the temperature dependence of the paramagnetic susceptibility of α-Li_0.56HfNCl χ = C/(T−θ) + χ_o had a θ value as small as 0.04(2) K, implying that the coupling of Hf³⁺ moments are negligibly small. Contrarily, the doped electrons in β-HfNCl and β-HfNBr with the honeycomb network are delocalized and induce relatively high T_cs of 24–26 K as reported previously.² It was found that β-Li_xZrNCl, with a doping level as low as x = 0.06, showed superconductivity and the T_c decreased as the doping level increased.⁴ This unusual behavior of the T_c against the concentration of the carrier doping also suggests the unconventional superconductivity of layered nitride chlorides. In the case of the present study of α-TiNCl the electrons are delocalized over the two-dimensional structure and become superconducting. This is quite a contrast to the appearance of the localized electron spins in Li doped α-HfNBr with an isomorphous structure. A detailed theoretical study is needed to understand the mechanism of the different behaviors of the doped electrons in the same α-MNX layer structure but with different metal atoms. It is also important to compare the superconductivities in the different networks, β-type honeycomb and α-type orthogonal nitride layers to find a clue to understand the unconventional superconductivity.

Conclusions

The intercalation compounds of TiNCl with an organic Lewis base pyridine, and various alkali metals such as Li, Na, K, and Rb were prepared and found to become superconductors with T_cs of 6.8 and ∼16.3 K respectively. These are the first superconductors to be found in the α-type (the FeOCl structure) layer structured nitride halides. The basic two-dimensional structure of TiNCl is maintained upon intercalation, but the crystalline layers are shifted to form new polytypes with a different stacking sequence of the layers. The electrical band structure calculation demonstrated that the K doped TiNCl has “sharp and flat dispersion bands” at the Fermi level, which will be favorable for the high-T_c superconductivity. The superconductivity of the Py intercalated compound is caused by a charge transfer. The HOMO band of Py is located between the band gap of TiNCl. The Fermi level should be placed in the broad tail of the conduction band. More detailed theoretical studies are needed for further discussion on the superconducting mechanism. The pyridine intercalation compound can be classified into an organic–inorganic superconductor which will open a new research field of superconductors.

Acknowledgements

This study has been supported by a Grant-in-Aid for Scientific Research (Grants 19105006, 19051011 and 19014016) of the Ministry of Education, Culture, Sports, Science, and Technology of Japan.

References

1. S. Yamanaka, Annu. Rev. Mater. Sci., 2000, 30, 53.
2. S. Yamanaka, K. Hotehama, T. Koiwasaki, H. Kawaji, H. Fukuoka, S. Shamoto and T. Kajitani, Physica C, 2000, 341–348, 699.
3. S. Yamanaka, H. Kawaji, K. Hotehama and M. Ohashi, Adv. Mater., 1996, 8, 771.
4. Y. Taguchi, A. Kitora and Y. Iwasa, Phys. Rev. Lett., 2006, 97, 107001.
5. S. Yamanaka, K. Hotehama and H. Kawaji, Nature, 1998, 392, 580.
6. M. Ohashi, S. Yamanaka and M. Hattori, J. Ceram. Soc. Jpn. Int. Ed., 1989, 97, 1175.
7. C. Felser and R. Seshadri, J. Mater. Chem., 1999, 9, 459.
8. H. Tou, Y. Maniwa, T. Koiwasaki and S. Yamanaka, Phys. Rev. B, 2001, 63, 20508.
9. H. Tou, Y. Maniwa, T. Koiwasaki and S. Yamanaka, Phys. Rev. Lett., 2001, 86, 5775.
10. Y. Taguchi, M. Hisakabe and Y. Iwasa, Phys, Rev. Lett., 2005, 94, 217002.
11. T. Ekino, T. Takasaki, T. Muranaka, H. Fujii, J. Akimitsu and S. Yamanaka, Physica B, 2003, 328, 23.
12. S. Yamanaka, K. Itoh, H. Fukuoka and M. Yasukawa, Inorg. Chem., 2000, 39, 806.
13. F. Kanamaru, M. Shimada, M. Koizumi, M. Takano and M. Takada, J. Solid State Chem., 1973, 7, 297.
14. J. Rouxel and P. Palvadeau, Rev. Chim. Miner., 1982, 19, 317.
15. T. R. Halbert, in Intercalation Chemistry, ed. M. S. Whittingham and A. J. Jacobson, Academic Press, New York, 1982, Chap. 12.
16. S. Yamanaka, H. Okumura and L. Zhu, J. Phys. Chem. Solids, 2004, 65, 565.
17. R. Juza and J. Heners, Z. Anorg. Allg. Chem., 1964, 332, 159.
18. M. Ohashi, S. Yamanaka and M. Hattori, J. Solid State Chem., 1988, 77, 342.
19. M. Dion, Y. Piffard and M. Tournoux, J. Inorg. Nucl. Chem., 1978, 40, 917.
20. S. Andersson and A. D. Wedsley, Nature, 1960, 187, 499.
21. L. Zhu and S. Yamanaka, Chem. Mater., 2003, 15, 1897.
22. A. Coelho, TOPAS-Academic v. 4.1: General Profile and Structure Analysis Software for Powder Diffraction Data, Brisbane, 2007.
23. DMol 3 Solid is available from Accelrys, Sun Diego, CA.
24. B. Delley, J. Chem. Phys., 1990, 92, 508.
25. B. Delley, J. Chem. Phys., 2000, 113, 7756.
26. CASTEP is available from Accelrys, San Diego, CA, http://www.accelrys.com.
27. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristal., 2005, 220, 567.
28. A. Kuhn, H. Hoppe, J. Strähle and F. García-Alvarado, J. Electrochem. Soc., 2004, 151, A843.
29. H. O. Pierson, Handbook of Refractory Carbides and Nitrides, Noyes Publications, New Jersey, 1996, pp. 224.
30. P. M. Woodward and T. Vogt, J. Solid State Chem., 1998, 138, 207.
31. A. Simon, Angew. Chem., Int. Ed. Engl., 1997, 36, 1788.
32. X. Chen, T. Koiwasaki and S. Yamanaka, J. Solid State Chem., 2001, 159, 80.
33. S. Shamoto, K. Takeuchi, S. Yamanaka and T. Kajitani, Physica C, 2004, 402, 283.
34. X. Chen, L. Zhu and S. Yamanaka, J. Solid State Chem., 2002, 169, 149.
35. H. A. Wriedt and J. L. Murray, Bull. Alloy Phase Diagrams, 1987, 8, 378.
36. S. Yamanaka and H. Tou, Curr. Opin. Solid State Mater. Sci., 2001, 5, 545.
37. J. Oro-Sole, M. Vlassov, D. Beltran-Porter, M. T. Caldes, V. Primo and A. Fuertes, Solid State Sci., 2002, 4, 475.

---

Footnotes

† This paper is part of a Journal of Materials Chemistry theme issue on Layered Materials. Guest editors: Leonardo Marchese and Heloise O. Pastore.

‡ CCDC reference number 708195: the atomic coordinates of the geometry optimized structure of Py_0.25TiNCl. For crystallographic data in CIF or other electronic format see DOI: 10.1039/b819541b

---