Molecular models and simulations of layered materials†
Randall T.
Cygan
*a,
Jeffery A.
Greathouse
a,
Hendrik
Heinz
b and
Andrey G.
Kalinichev
c
aGeochemistry Department, Sandia National Laboratories, Albuquerque, New Mexico 871895-0754, USA. E-mail: rtcygan@sandia.gov; Tel: +1 505 844 7216
bDepartment of Polymer Engineering, University of Akron, Akron, Ohio 44325-0301, USA. E-mail: hendrik.heinz@uakron.edu; Tel: +1 330 972 7467
cDepartment of Chemistry, Michigan State University, East Lansing, Michigan 48824-1322, USA. E-mail: kalinich@chemistry.msu.edu; Tel: +1 517 355 9715
First published on 26th February 2009
Abstract
The micro- to nano-sized nature of layered materials, particularly characteristic of naturally occurring clay minerals, limits our ability to fully interrogate their atomic dispositions and crystal structures. The low symmetry, multicomponent compositions, defects, and disorder phenomena of clays and related phases necessitate the use of molecular models and modern simulation methods. Computational chemistry tools based on classical force fields and quantum-chemical methods of electronic structure calculations provide a practical approach to evaluate structure and dynamics of the materials on an atomic scale. Combined with classical energy minimization, molecular dynamics, and Monte Carlo techniques, quantum methods provide accurate models of layered materials such as clay minerals, layered double hydroxides, and clay–polymer nanocomposites.
 Randall T. Cygan | Randall T. Cygan was born in Oak Park, Illinois, USA in 1955. He received his Ph.D. degree in geochemistry and mineralogy in 1983 from the Pennsylvania State University. He is a Distinguished Member of Technical Staff in the Geochemistry Department of Sandia National Laboratories. His current research includes investigations of mineral dissolution, adsorption phenomena, and shock metamorphism using various spectroscopies and molecular simulation. |
 Jeffery A. Greathouse | Jeffery A. Greathouse was born in Washington, D.C. in 1970. He received his Ph.D. in 1996 in physical chemistry from the University of California at Davis, working with Dr Donald McQuarrie, followed by postdoctoral research with Dr Garrison Sposito at the University of California at Berkeley. He is a Senior Member of Technical Staff in the Geochemistry Department at Sandia National Laboratories, and his research involves molecular simulation of aqueous systems, mineral–water interfaces, and nanoporous materials. |
 Hendrik Heinz | Hendrik Heinz was born in Chemnitz, Germany in 1975. He received a M.S. in Chemistry (2000) and a Ph.D. in Materials Science (2003) from ETH Zurich. After postdoctoral work at the Air Force Research Laboratory, Wright-Patterson Air Force Base, he became an Assistant Professor at the University of Akron (2006). His current research focuses on inorganic–(bio)organic interfaces and computational tools for the development of biomimetic, energy conversion, and construction materials. |
 Andrey G. Kalinichev | Andrey G. Kalinichev studied thermophysics at the Odessa Technological Institute, Ukraine, and received his Ph.D. (1986) in chemical physics from the Russian Academy of Sciences, where he subsequently headed the Physical Research Laboratory at the Institute of Experimental Mineralogy in Chernogolovka. He is currently a Research Associate Professor of chemistry at Michigan State University. He was one of the first to employ classical molecular computer simulations in geochemistry, which remains the focus of his current research interests. |
Introduction
Layered materials not only have proven to be of technological importance in a variety of industrial and medical applications including catalysis, molecular separations, and drug delivery, but they are critical to a number of environmental issues involving the fate of contaminants and groundwater quality.1,2 Common layered materials of significance in materials applications include clay minerals and layered double hydroxide compounds. In general, clay minerals are comprised of multiple layers of hydroxylated and coordinated tetrahedral and octahedral sheets.3 Smectite clays, such as the common mineral montmorillonite, are characterized by substitution of lower-valency metal cations (Mg2+ for Al3+ or Al3+ for Si4+) within the sheets to create a net negative charge that is compensated by interlayer cations that are typically solvated by water molecules. The extent of such structural substitutions (as defined in layer charge) combined with relative humidity control the swelling ability of smectite minerals. Mica, or, more specifically, muscovite (ideally KAl2Si3AlO10(OH)2) is a highly-charged layered material and is incapable of swelling. In contrast to cationic clays, layered double hydroxides (LDHs) have related structures whose hydroxide layers have net positive charge and the interlayers are comprised of hydrated anions.1 The most common phase among naturally occurring LDHs is hydrotalcite (Mg6Al2(OH)16CO3·4H2O) where the Al3+ substitutes for Mg2+ in a brucite (Mg(OH)2) layer with CO32− and water in the interlayer.The layered structure of clay minerals and LDHs is responsible for many unique chemical and physical properties of these materials. Of most technological significance is the ability of many of these layered materials to intercalate neutral molecules or charged chemical species into their interlayers. From the intercalation of inorganic metal cations to large organic polymers, from the sequestering of metal pollutants and radionuclide contaminants to biomolecules for drug delivery, layered materials present a versatile class of phases for a wide set of applications. However, to fully understand the complex structure of these materials and the critical mechanisms of intercalation it has become necessary to use modern molecular simulation methods, especially because many of the layered materials are restricted to nano-sized morphologies and are less suitable for conventional experimental analysis.
This Application article provides a general review of clay minerals and LDHs from the perspective of molecular simulation. Computational chemistry methods including classical force field and electronic structure techniques are summarized, and numerous applications of the simulation methods to layered materials are reviewed. Nanocomposite materials based on clay–polymer structures are presented along with examples of large-scale molecular simulations involving inorganic–organic interactions. Finally, the structure and dynamics of LDH materials are reviewed with a discussion of their vibrational behavior as obtained through molecular simulation.
Classical force field methods and layered materials
Classical methods in computational chemistry usually take the form of molecular dynamics (MD) or Monte Carlo (MC) simulation, with the aim of sampling phase space of the system once it has reached thermodynamic equilibrium. The simulations are normally performed under conditions analogous to equilibrium statistical mechanical ensembles, so one or more state variables remain fixed during the simulation. Popular ensemble choices include microcanonical (NVE), canonical (NVT), isothermal–isobaric (NPT), and grand canonical (µVT), where the variables N, V, E, T, P, and µ represent number of particles, volume, total energy, temperature, pressure, and chemical potential, respectively. Classical methods include electronic effects only indirectly through approximate interatomic and oligo-body interaction energy terms (force field), so classical simulations do not require enormous amounts of CPU resources. Parallelized MD codes scale nearly linearly with system size and can accommodate very large (>106 atoms) systems.4,5 Approximations made on clay–clay interactions can be grouped into three categories, as described below.For simulations of layered clay minerals, a preliminary issue is whether to treat the mineral lattice as a rigid framework, or to allow flexibility of bonds, angles, and dihedrals within the clay. The rigid framework approach has the advantage of lower computational cost and is easier to parameterize, since only nonbonded interactions between the clay and interlayer species are included. However, such simplified models are inherently limited by the immobility of the lattice atoms, which precludes complete exchange of energy and momentum among the interacting atoms of the mineral substrate and the interlayer or surface molecules. Therefore, the atomistic description of the structural and dynamic behavior of surface and interlayer species can become distorted in such models. The magnitude of this distortion and whether it can be safely neglected ultimately depends on the characteristic time scales of the different types of relevant atomic motion and the degree of mechanical coupling between them in the simulated systems. For hydrated phases, such as clay minerals and LDHs, the time scales of vibrational and librational motions for surface OH groups are comparable to those of similar motions of interlayer water molecules and hydrated ions in the aqueous phase. Therefore, accurate representation of the dynamics of such processes as adsorption, surface hydration and complexation, and hydrogen bonding can be inherently limited if the atoms of the mineral substrate are “frozen” in a rigid lattice. Surface diffusion rates of ions and water molecules can also be overestimated. However, many structural and thermodynamic (swelling) properties of layered materials can be successfully studied within the rigid framework approach. Skipper et al.6 employed the rigid framework approach in the first MC simulations of hydrated smectites. They were also the first to parameterize silicate O atoms with interatomic energy terms consistent with water O atoms. In this case, the MCY (Matsuoka, Clementi, and Yoshimine) water model7 was used. This idea gains merit when one considers that silicate O atoms can occupy first-shell coordination positions around adsorbed cations. Borrowing on the ideas of inner- and outer-sphere coordination complexes, Sposito termed this an inner-sphere surface complex.2 Thus, a consistent description of intermolecular interactions among mineral lattice atoms, surface and interlayer molecules, and bulk aqueous phase is essential for realistic molecular modeling of hydration phenomena in such systems. The adaptation of water O parameters for molecular simulations of hydrated clays was later extended to include such water models as TIP4P (transferable intermolecular potential four point)8 and SPC/E (simple point charge extended).9 The general structure and performance of these and other frequently used molecular models of H2O in reproducing many important properties of water in a wide variety of physical and chemical environments are discussed and compared in detail in several recent reviews.10–14
The prototype clay system in these early studies was montmorillonite, and the interlayer region consisted of hydrated alkali metal cations. The interlayer structure is usually obtained from one-dimensional atomic density profiles, cation and water radial distribution functions, and water orientation profiles.15 Since then, the range of clay systems has been extended to beidellite,16 hectorite,16,17 and mica.18 Interlayer divalent cations have also been simulated, including the alkaline earth metals and polyatomics such as UO22+.19 The interlayer structures of organics such as methane20 and methanol21 have been studied for oil and gas applications. Density profiles of interlayer water from MC and MD simulations have confirmed the layering of distinct water layers in the clay galleries, in agreement with isotopically labeled neutron diffraction experiments.22 The diffusion of interlayer cations and water has also received much attention and has been recently reviewed.23
In addition to interlayer structure and dynamics, an underlying motivation for simulations of hydrated clays is to better understand the phenomenon of intracrystalline swelling. The basal d-spacing of natural clays such as Na-montmorillonite increases in stepwise fashion with increasing relative humidity, corresponding to an integral number of water layers (up to three) between adjacent clay layers. A comparison of d-spacing values from simulation with the corresponding X-ray diffraction values is a stringent validation of the short-range parameters in a particular force field. Initially, NPT simulations were used to understand the hysteresis effect in clay swelling,8 but subsequent µVT simulations (Fig. 1) have revealed free energy minima as the clay swells.24,25 The link between free energy minima and clay hydration was later confirmed by NPT simulations, showing a relationship between clay swelling behavior and interlayer cation radius.26
 | ||
| Fig. 1 Grand canonical MC results (µVT ensemble) for clay swelling free energy, ΔG, plotted as a function of clay layer spacing, sz, for Na-montmorillonite at 298 K.25 The results are shown for increasing values of the relative water chemical potential, µ − µo. Stable swelling states are found for the one-layer hydrate (12.4 Å) and two-layer hydrate (15.3 Å) as the water chemical potential (relative humidity) is increased. Reprinted with permission. Copyright 2006, American Chemical Society. | ||
The increase in inexpensive computing power has led to a second generation of force fields for simulating clays, so that flexibility within the clay lattice can now be considered. The structure and dynamics of interlayer species is more accurately simulated when momentum transfer between those molecules and the clay lattice is included. Additionally, model clay systems may be expanded to include hydroxylated surfaces, which cannot be accurately modeled using a rigid lattice. Flexible force fields usually require many more potential energy terms (bond stretch, angle bend, and dihedral) that present added difficulty in parameter development. Parameters for these two- and three-body terms are typically derived by fitting to ab initio calculations, or by comparisons with vibrational spectra. These force fields can be conveniently divided into two groups: those that include two- and three-body interactions (angle bend, dihedral), and those that only include two-body interactions (bond stretch or van der Waals).
Teppen and coworkers27 were the first to derive bonded force field parameters specifically for layered clay minerals. Their bond stretch and three-body parameters for silicate interactions were adapted from the general parameters of Hill and Sauer,28 which are included in an all-purpose force field (cff91).29 Heinz and coworkers30 also developed a force field based on cff91, but they applied a novel technique to derive atomic charges based on atomization enthalpies, ionization potentials, and comparison to experimentally available electron deformation densities.31 In conjunction with a novel approach to assign van der Waals parameters, this has led to the reproduction of surface and interface energies in quantitative agreement with experiment, reducing earlier deviations of several 100% to less than 10%.32,33 Starting from scratch, Bougeard et al.34 developed bonded parameters specifically for a 1:1 clay (kaolinite), based on ab initio calculations of representative cluster models. They have since extended their force field to include 2:1 clays as well.35 Finally, we note the existence of one flexible force field that adds the feature of atomic polarizability for layer O atoms.36 All atoms are assigned their formal charges, and a core-shell model is used for oxygen polarizability. The core-shell model has been widely used for bulk oxide minerals and their surfaces.37 While useful for energy minimization calculations, MD simulations require a very short timestep to compensate for the small mass of the shell term.
Several research groups have employed a computationally simpler approach to flexible force fields without adding three-body interactions. The entire clay lattice is modeled as a collection of independent atoms governed only by quasi-ionic interatomic interactions. These approaches differ in the type of pairwise interactions beyond the usual electrostatic term. In one case, a two-body Morse function is used.38 The limitation in this case is the lack of mid-range van der Waals interactions between lattice atoms. The force field of Sato et al.39 also uses a two-body Morse function for pairwise interactions, but pairwise van der Waals interactions are included. This force field was used to examine trends in clay bending constant under uniaxial stress up to 0.7 GPa. Such simulations are impossible if the clay is treated as a rigid lattice. A recently introduced but widely used force field (CLAYFF) simplifies the two-body interactions even further by including only electrostatic and van der Waals terms between pairs of clay atoms.40 A bond-stretch term is still required for layer hydroxyl groups. By extending the system size to nearly 10 million atoms, Coveney and colleagues41–44 used CLAYFF in MD simulations to show thermal sheet fluctuations on the micrometer length scale. These results can be used to calculate elastic constants, which are difficult to obtain experimentally due to the small size of clay crystals, and impossible to obtain with a rigid clay lattice.
At one time, treating the clay as a rigid lattice was the only practical method of completing simulations of clays and clay interfaces in a timely manner. And the inclusion of volume changes during MC simulations allowed structural quantities like the basal d-spacing to be obtained from MC simulation and compared with experiment. However, modern MC codes contain algorithms for intramolecular (and lattice flexibility) moves, so the flexible force fields discussed above can be used in MC simulation. We conclude that the minimal increase in computation time needed to include clay flexibility makes the rigid lattice approach all but impractical.
For even larger system sizes, an entire clay unit cell may be treated as a united atom, enabling the simulation of macroscopic properties such as exfoliation. The united atom approach is routinely used on polymer systems, in a bead-spring format. By extension, a clay sheet can be represented by a bead-spring plane model45 as discussed below. The obvious limitation is the lack of molecular detail within the clay lattice, or at edges and surfaces, but the large systems sizes and long time scales required to calculate some macroscopic properties are impractical using an all-atom approach. MC or MD simulations using coarse-grained models are therefore at least 103 times faster, and benefit from tuning to interfacial and mechanical properties of experimental systems and all-atom molecular models. For example, Pandey and coworkers used the bead-spring plane model to examine exfoliation tendencies of clay platelets as a function of temperature and solvent properties.46
With a flexible framework, it is possible to investigate vibrational motion. Vibrational analysis can be accomplished through normal mode analysis of a geometry-optimized structure, or auto-correlation analysis from MD simulation. In the simplest approach, an atomic velocity auto-correlation function can be converted via Fourier transform to a power spectrum (see later section), which is not subject to quantum selection rules and best compared with vibrational data from inelastic neutron scattering experiments. Simulated infrared and Raman spectra are obtained from Fourier transform of dipole moment and polarizability tensor auto-correlation functions, respectively.34
Electronic structure methods and layered materials
Recent years have seen a significant increase in the use of electronic structure calculations in the evaluation of layered materials, especially in applications relating to the structure of complex clay minerals and a few layered double hydroxide phases. These efforts have developed from the earlier classical simulations as computational resources have improved in speed and storage, and have become more accessible to the computational chemist. Rather than rely on the simple balls and springs model associated with classical simulations, electronic structure methods examine the distribution of electrons using wavefunctions and molecular orbitals obtained through approximate solutions to the Schrödinger equation. Hartree–Fock and density functional theory (DFT) methods47–49 are the common ab initio approaches used to derive energy-minimized structures and to evaluate electron density, electrostatic potentials, thermodynamics, spectroscopic data, reaction mechanisms, and other properties. In contrast to standard Hartree–Fock methods that emphasize the wavefunction, DFT relies on the density of electrons and includes electron correlation by correcting for the local distortion of an orbital in the vicinity of another electron. DFT uses efficient numerical methods and a local density approximation (LDA) or more sophisticated generalized gradient approximation (GGA) to account for electron correlation. Also, plane-wave pseudopotential DFT methods50,51 are often used in simulations of layered materials by implementing a plane-wave expansion that accounts for the valence electrons of the atoms. Despite the availability of sophisticated quantum chemistry software and massively parallel supercomputers, electronic structure calculations are typically limited to hundreds of atoms in contrast to the millions often examined using classical methods.Early applications of electronic structure methods examined relatively simple cluster models—on the order of tens of atoms—designed to represent the critical local binding environments associated with bridging oxygens (Si–O–Si(Al)) common to many layered aluminosilicate materials.52–55 Most of these studies relied on a standard Hartree–Fock approach or, in some cases, a perturbed Hartree–Fock method to correct for electron correlation. These methods eventually evolved with advances in theory and the availability of new software that allowed the energy determination and geometry optimization of periodic structures.
Clay minerals occur in nature having a wide range of compositional and structural variation; however, most molecular simulation studies have examined idealized representative structures derived from a conventional classification scheme. Dioctahedral clay minerals are characterized by two trivalent atoms, typically Al3+, and a vacancy among the three sites that form the basic structure of the octahedral sheet while a trioctahedral clay is characterized by three divalent atoms, often Mg2+ and Fe2+. The 2:1 and 1:1 nomenclature signifies the ratio of tetrahedral to octahedral sheets that combine to form the composite layers characteristic of a clay mineral. Substitution of metals having a dissimilar valency among the octahedral and tetrahedral sites generates a net negatively charged layer common to expandable smectite phases, and which can accommodate compensating interlayer cations, water molecules, and the intercalation of organic ions or molecules.
Bulk structure determinations have been obtained for relatively simple endmember clay minerals using periodic DFT methods and often including full relaxation of all atomic positions and cell parameters.56–60 Kaolinite (1:1 dioctahedral),57,59,61 dickite (1:1 dioctahedral),56,57,62pyrophyllite (2:1 dioctahedral),58,60,63–66 talc (2:1 trioctahedral),64,67 and several smectites (2:1 dioctahedral)60,68–71 have been investigated by several research groups in this manner, often using multiple DFT and optimization methods. There have been few published studies involving electronic structure calculations of layered double hydroxide materials (see final section). These investigations used DFT methods and examined the enhanced catalytic ability of intercalated compounds.72
A comparison of optimized talc (Mg3Si4O10(OH)2) and pyrophyllite (Al2Si4O10(OH)2) structures as derived by a periodic plane-wave pseudopotential DFT method64 is provided in Fig. 2. The endmember 2:1 clay phases are uncharged having no cation substitutions and, consequently, no charge-compensating interlayer species. Layer–layer interactions occur primarily through van der Waals forces. Hydroxyl groups associated with the octahedral sheet are disposed differently in the two structures due to the existence of vacancies in the dioctahedral pyrophyllite. The highest occupied molecular orbitals (HOMO) are superimposed onto the optimized structures and indicate the most likely regions of the layered material for reactivity and selectivity, especially as key orbitals relate to adsorption and surface reactions.73
 | ||
| Fig. 2 Fully-optimized structures of 2 × 1 × 2 supercells of talc and pyrophyllite clay minerals obtained with a periodic plane-wave pseudopotential DFT code. Orthographic view is along the (100) crystallographic direction. The constant pressure optimization allows all cell lengths, cell angles, and atomic positions to be relaxed without any symmetry constraints.64 The trioctahedral talc exhibits hydroxyl groups that are configured normal to the clay layer while the dioctahedral pyrophyllite has the hydroxyls situated sub-parallel to the layer in response to the presence of octahedral vacancies. The highest occupied molecular orbitals (HOMO), highlighted in blue and gold, are associated primarily with the hydroxyl oxygens in both structures, although those for pyrophyllite exhibits some minor component in the interlayer. The HOMO calculations were calculated for the optimized structure using an all-electron DFT at the generalized gradient approximation.74 | ||
Several simulation studies have used DFT methods to investigate the relative stabilities of various cation substitutions and their distributions in the clay sheets55,60,71 and the significance of hydroxyl orientation and behavior in the clay structure, including vibrational spectra.56,57,64,68,75 Electronic structure calculations of the adsorption of organic molecules to clay surfaces,62,76–79 especially for those molecules that pose a public threat as environmental contaminants, have provided critical structural and thermodynamic details not easily obtained through experimental methods.
In contrast to classical models, quantum methods also allow the direct simulation of chemical reactions in which electrons and atoms are rearranged in decomposition, condensation, proton transfer, oxidation–reduction, or other reactive processes. Recent investigations by Sainz-Díaz and colleagues,65,80–82 for example, have examined dehydroxylation mechanisms in dioctahedral phases. Additionally, MD methods can be combined with electronic structure calculations to circumvent the use of empirical force fields. Ab initio MD83 and Car–Parrinello84 deterministic methods have been used to examine layered materials and obtain atomic trajectories, although such simulations are limited to relatively small system sizes (tens to hundreds of atoms) and short simulation times (tens of ps). Noteworthy studies include the MD simulation of proton transfer and water behavior on the edge of pyrophyllite,63,85 dehydroxylation reactions of pyrophyllite,80,81vibrational spectra of clays,56,57,64 and adsorption phenomena involving clay surfaces.86–90
Inorganic–organic and nanocomposite phases
Layered silicates are widely used as thixotropic agents in drilling fluids,91 additives in paints and cosmetics,92 fillers in layered silicate/polymer nanocomposites, well defined substrates for the measurement of surface forces, and for the patterning of surfactants, polymers, and proteins on the nanoscale.93 Interfaces of layered silicates with water and organic matter, including structural, thermal, mechanical, optical, and electrical properties, are therefore of great interest and molecular simulations have contributed to the understanding of many observations,94–102 in a quantitative way.30–33,45,46,103–109 This includes structural features such as gallery spacings in 0.5% to 5% agreement with X-ray patterns30,32,104,107,109 and computed surface and interface energies in 1% to 10% agreement with measured surface tensions and cleavage energies.32,33 A critical role can also be attributed to the valence electron density at the defect sites and the distribution of charge defects in the mineral which have been included in the models according to an extended Born cycle31 and solid-state NMR data.104 As a result, data from differential scanning calorimetry (DSC),30,32,104,105,107IR spectra,30,32,104,105,107NMR spectra,30,32,104,105,107 NEXAFS,30,104,105AFM,30,104 dielectric behavior,96 and approximate mechanical properties108 have been consistently explained on the basis of simulations and contribute to the understanding of conformations of adsorbed molecules on clay mineral surfaces, the dynamics of self-assembled monolayers, thermal transitions, and other interfacial processes. We consider two examples in the following discussion.In polymer/layered silicate nanocomposites, a major challenge is the exfoliation of the nanometer-thick aluminosilicate layers in a given polymer matrix.91 The process is thermodynamically spontaneous when the polymer and filler components react with each other, which corresponds to a negative interface tension. More typically, however, small positive interface tensions between non-reactive miscible components can also lead to exfoliation when assisted by mechanical agitation or extrusion in the molten state. To better understand the properties of the interfacial region between layered silicate, surfactant, and polymer matrix, the separation of the clay mineral layers has been simulated using all-atom models (Fig. 3),32,33 and the interaction between polymer chains and layered silicate surfaces has been simulated using coarse-grain models.45,46 Chemically specific conclusions, however, are mostly drawn from all-atom MD simulation.
 | ||
| Fig. 3 Cleavage of montmorillonite layers by stepwise separation in MD simulation.33 The energy and representative structures are shown for (a,b) potassium montmorillonite and for (c,d) octadecylammonium-modified montmorillonite (CEC = 91 mequiv/100g). Reprinted with permission. Copyright 2006, American Institute of Physics. | ||
In natural alkali-montmorillonite (Fig. 3a,b) the redistribution of interlayer cations upon separation leads to a large cleavage energy in excess of 100 mJ/m2. The predominant contribution is Coulomb energy which drops rapidly within 0.8 nm separation, and a smaller contribution is van der Waals energy which becomes negligible beyond 2 nm separation. The large overall cleavage energy cannot be recovered during the formation of an interface with relatively non-polar polymers such as polyethylene, polystyrene, or nylon-6 which exhibit surface tensions in the 30–50 mJ/m2 range. Therefore, natural alkali-montmorillonite does not exfoliate in this environment. In organically modified montmorillonite (Fig. 3c,d) the cleavage energy is significantly reduced because the cationic ammonium head groups are separated by the alkyl backbone, and the interlayer thickness is greater than 0.8 nm (Fig. 3d). Therefore, the cleavage energy comprises almost no Coulomb contribution and consists of a small van der Waals contribution. The range of surface tensions of common polymers is sufficient to form such an interface.33 Therefore, organic surface modification of montmorillonites increases the likelihood of exfoliation of high aspect ratio aluminosilicate layers in polymer matrices. The molecular interpretation on the basis of the simulation is supported by various experimental observations, such as cleavage energies and surface tensions.33 Measured cleavage energies for mica were 375 mJ/m2 versus 383 mJ/m2 in the simulation (not shown) and for montmorillonite 50–200 mJ/m2 (cation exchange capacity of 40–150 mequiv/100g) versus 133 mJ/m2 in the simulation (CEC = 91 mequiv/100g). The surface tension of C18-montmorillonite was analyzed as 1, 40, 41 mJ/m2 (Coulomb, van der Waals, total)91 by contact angle measurements and computed as −1, 39, 38 mJ/m2 in the simulation (including an entropy correction of −2 mJ/m2 to the cleavage energy in Fig. 3c).33 Minor long range forces (less than 1 mJ/m2) with more than 3 nm separation appear to be associated with minor Coulomb forces due to small lateral displacements of the cationic head groups.
The extended two-dimensional structure of layered silicates can also be exploited for the design of light-driven nanoscale actuators on the basis of azobenzene (Fig. 4).106 The cis-transisomerization of azobenzene and its derivatives occurs quantitatively even in sterically constrained geometries, as supported by MD simulation, UV/Vis, and X-ray data.98,106 Therefore, a bistable mechanical response perpendicular to the stacking direction of the silicate layers can be achieved upon laser pumping at the photostationary states. An upright orientation and conformational rigidity of the intercalated azo dye are critical to achieve a significant difference in interlayer density and concomitant switching of the gallery spacing d (Fig. 4). Significant actuation above 10% appears to be further assisted by the presence of co-intercalates which can reversibly exit from or enter into the gallery to compensate, and possibly overcompensate, associated changes in interlayer density. In contrast, no uniform changes in gallery height upon cis-transisomerization were observed in the presence of flexible alkyl spacers in the surfactants at low cation exchange capacity, as supported by simulation results and X-ray measurements.106
 | ||
| Fig. 4 Snapshots of montmorillonite (CEC = 143 mequiv/100g) modified with phenylazophenylammonium ions in near-upright orientation on the surface. The basal plane spacing changes by 2.17 Å (11%) on photoisomerization. The average tilt angle of the connectors between the ammonium N atoms and the phenyl 4′-C atoms of the surfactants relative to the surface normal increases from 27° to 58° upon trans → cis conversion. The cis-configured surfactant assumes a higher interlayer density.106 | ||
These examples illustrate the utility of modeling and simulation to understand the subtle interplay of factors which determine the properties of interfaces in layered materials. Specifically related to nanocomposites, the following factors can be addressed in simulations: (1) cation exchange capacity of the mineral, (2) head group of the surfactant (e.g. primary ammonium versus quaternary ammonium), (3) chemistry and length of the surfactant modifiers, (4) chemistry of the polymer main chains and the polymer side chains, (5) degree of polymerization, (6) molecular weight distribution, and (7) processing conditions of the polymer/clay nanocomposite. Furthermore, organically decorated surfaces of clay minerals are not always composed of homogeneous layers of surfactants or surfactant/cation mixtures. They can consist of spatially separate regions of homogeneous surfactant layers and of non-exchanged alkali ions as identified by AFM95 and by MD simulation104 at high CEC. In both cases, however, there are regions composed of homogeneous surfactant layers which display average segmental tilt angles and thermal phase transitions according to their packing density (defined as the cross-sectional area of the surfactant chains in relation to the available surface area).105 Reversible order–disorder transitions of the tethered surfactant backbones upon heating are typically observed at intermediate packing density (0.2 to 0.75) while lower or higher packing densities result in excessively low or high degrees of order which prevent thermal transitions.105 Gallery spacing, interlayer density, percentage of gauche conformations, and lateral diffusion constants (which can sometimes lead to a second thermal phase transition)30,104 have been computed for various ammonium surfactants in very good agreement with X-ray, IR, NMR, and DSC data.107 The quantitative analysis of cleavage energies and interfacial tensions with common polymers may lead to suggestions for enhancing exfoliation in nanocomposites.
Layered double hydroxides and vibrational spectroscopy
Layered double hydroxides, also known as anionic clays, are unusual clay-like materials having positively charged layers and, consequently, large ion exchange capacities for inorganic or organic anions. Their lamellar structures are based on brucite-like Mg(OH)2 layers,1,110,111 which can be chemically “variable” by allowing for partial substitution of the divalent metal ions by trivalent metal ions leading to the permanent positive layer charge. The general chemical formula for many LDHs may be written as| (MII(1−y)MIIIy(OH)2)y+(y/m)Am−·xH2O | (1) |
 | ||
| Fig. 5 Crystal structure of Mg2Al-Cl layered double hydroxide, (Mg2Al(OH)6)Cl·2H2O (Cl-hydrotalcite). Green balls = Cl−, red sticks = O of water or OH, white sticks = H of water or OH, dark gray octahedra = Al of hydroxide layer, blue octahedra = Mg of hydroxide layer. | ||
This important class of clay-like materials can be easily synthesized with a wide range of main layer cations and interlayer inorganic and/or organic anions and finds a variety of applications as catalysts,117,118 carriers for drugs,119,120 media for molecular separation, environmental remediation, and many other technological purposes.1,110,111,121,122
The positive layer charge of LDHs provides important contrast with the negative layer charges typical of aluminosilicate clays and offers an excellent opportunity to investigate fundamental structural and dynamical properties of anionic interlayer and surface species, thus making these materials also important as good models for understanding aqueous solutions confined in nano-pores.123–135
Intercalation of large organic anions into LDH structures can be difficult, but recent experimental studies have shown that enhanced swelling leading to exfoliation (delamination) of the LDH layers can be achieved in solution if the LDH is loaded with suitable organic intercalates.117 Such exfoliation offers a gentle way of opening the interlayer space to allow insertion of large organic or bio-molecules. Recent experimental and computational MD modeling studies of the structure and swelling behavior of LDHs intercalated by citrate,128,130glutamate,132 and several smaller carboxylic acids129 are consistent with these observations and suggest that the interaction energies of such species with the LDH structure are weaker than those of small inorganic anions such as Cl−, CO32−, or SO42−,113 allowing for larger expansions and potentially delamination in water.
Understanding of the chemical behavior and transport properties of the interlayers and surfaces of LDHs and other layered structure materials requires knowledge of the molecular scale structural environments of the interlayer and surface species and their dynamical behavior on many length and time scales.
Vibrational spectroscopy (Raman and infrared) makes a considerable contribution to this effort, but interpretation of the spectral features related to interlayer and surface environments is often difficult due to compositional complexity, structural disorder, and the wide range of complicated, typically low-frequency motions that contribute to the observed spectra. While the mid- and high-frequency spectra of hydrous oxides and hydroxides are dominated by relatively easily interpretable metal–oxygen (M–O) and O–H stretching modes and M–O–M and H–O–H bending modes, the vibrational modes related to interlayer and surface species are mostly intermolecular. They often involve complex interactions among water molecules, interlayer or surface ions, and the substrate oxide or hydroxide layer. Because the significance of LDHs and other clay-like materials is mostly related to their reaction and anion exchange properties, understanding the structure and dynamical behavior of their interlayer and surface species is crucial to advancing their technological applications. These issues can be most effectively addressed by a combination of spectroscopic and computational approaches.
In recent years, MD computer simulations of these materials have been rapidly developing and proving to be an especially effective tool in unraveling the complicated interplay of structural, energetic, and dynamic properties of LDHs.40,42–44,72,114,125–129,131,133–136
The FIR spectra of LDHs and similar hydrous layered phases reflect both the low-frequency lattice vibrations associated with torsional motions of the hydroxide layer and intermolecular vibrations resulting from the complex combination of relatively weak hydrogen bonding interactions within the anion–water interlayers and between these interlayers and main hydroxide layers.127,133 The intermolecular modes involve the relative motions of interlayer species as a whole and may be either translational or librational (rotational) in origin. The frequencies of translational vibrations depend upon the total molecular mass, whereas the rotational vibrations are functions of molecular moments of inertia and are expected to have higher intensity in the spectra.137
Connection between observed and MD-simulated vibrational spectra can be made by calculating either the power spectra of atomic motions averaged across the entire MD trajectory or the frequencies of the normal modes of vibration for one or more individual representative snapshots of a simulation. The complex motions of hydrous interlayers and mineral surfaces are more accurately represented in the calculated power spectra, while the normal mode analysis can be useful principally as an effective tool to visualize specific types of motion, but without providing statistically meaningful quantitative information. The normal mode analysis technique relies on the search of the nearest local minimum of the total potential energy for the investigated structure.138
In addition to the limitations imposed by the harmonic approximation of the potential energy minimum typically utilized in this technique, the series of computed energy-minimized (i.e., effectively “frozen” at 0 K) atomic configurations used in the normal mode analysis does not fully represent the phase space of a dynamic system at a finite temperature. Thus, the normal mode calculations generally yield frequencies and intensities that are somewhat different than those obtained from the power spectra. In contrast, the power spectra calculated from the MD-simulated atomic trajectories contain the entire distribution of the power of all atomic motions in the system throughout the simulation as a function of frequency and with certain restrictions can be compared to the observed vibrational spectra.
The power spectra are usually obtained as Fourier transformations of the so-called velocity auto-correlation function (VACF), which is calculated directly from the MD-generated dynamic trajectories of the atoms in the simulated system:139,140
| C(t) = 〈v(0)·v(t)〉 = ∫v(0)·v(t)dΓ | (2) |
Qualitatively, the VACF indicates how fast the system or its individual atoms “forget” the velocities they had at a particular moment in time, indicated here as t = 0. Fourier transformation of C(t) gives the spectral density of atomic motions, also called the power spectrum or the vibrational density of states:
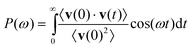 | (3) |
A great advantage of this approach is that it allows one to calculate not only the total vibrational spectrumvia VACF of all moving atoms in the system, but also components of the spectra reflecting specifically certain motions of individual atom types (e.g., Mg and O of OH), or certain specific directions of atomic motion. Thus it is possible to calculate the individual components of the VACF tensor for a given atom type, and analyze the anisotropy of the motion. For layered materials, the analysis of the three principal anisotropic contributions, XX, YY, and ZZ, provides very detailed quantitative insight into x-, y-, (parallel to the layering) and z- (perpendicular to the layering) projections of the velocity vectors and therefore the atomic motions along different crystallographic directions, greatly enhancing vibrational band assignment and spectral interpretation.127,133,136
In comparing computed power spectra and experimentally observed vibrational spectra, it is important to keep in mind that the two are not physically the same, with the result that the calculated and experimental band intensities cannot be directly compared. The experimental IR band intensities are related to the Fourier transform of the time correlation function for the total electric dipole moment of the simulated system, while the experimental Raman intensities are related to the Fourier transform of the time correlation function for quantum polarizability of the system.140 In contrast, the total computed power spectrum simply includes contributions from all atomic motions recorded in the VACF. However, since in the MD simulations each moving atom bears a partial charge, all atomic motions contribute to the fluctuations in the electric dipole moment of the system. Thus, the number of bands and their positions in the observed and computed spectra are strongly related, although the relative band intensities cannot be quantitatively compared using the methods described. Nevertheless, Fig. 6 clearly demonstrates the degree of agreement achievable between calculated and experimental FIR spectra, independently measured using two different instruments.127 Thus, MD modeling proves to be highly effective in quantitative investigations of the structure and dynamics of water and ions in the mineral interlayers by directly probing the intermolecular and H-bonding interactions and providing significant support with band assignments to the complicated patterns of atomic motions present in such complex systems as interlayers of LDHs, clays, nano-pores of zeolites, and other heterogeneous fluid media dominated primarily by hydrogen bonding. Additionally, simulated spectra can aid in the interpretation of overlapping bands observed in experimental spectra.
![Comparison of calculated power spectrum for [LiAl2(OH)6]Cl·H2O (black line) with observed FIR spectra. The red and blue lines represent two datasets collected using two different spectrometers.127](/image/article/2009/JM/b819076c/b819076c-f6.gif) | ||
| Fig. 6 Comparison of calculated power spectrum for [LiAl2(OH)6]Cl·H2O (black line) with observed FIR spectra. The red and blue lines represent two datasets collected using two different spectrometers.127 | ||
Conclusions
Molecular simulations provide a critical tool in the modern day analysis of structure, thermodynamics, kinetics, transport, reaction mechanisms, spectroscopy, and other key processes associated with layered materials. Considerable insight into the fundamental physics and chemistry of these materials is provided by the combined use of state-of-the-art methods of computational chemistry and advanced supercomputing resources. In combination with modern analytical tools—especially those utilizing advanced synchrotron-based diffraction, microscopy, and spectroscopy methods—molecular simulations provide a research opportunity to advance our knowledge of these complex materials. In this fashion, we have demonstrated that researchers can overcome the limitations imposed by the nano-sized state of synthetic LDHs or natural clay minerals and by the lack of suitably-sized crystals required for single crystal refinements.Several results highlight the significant contributions of molecular simulation in our understanding of structure, dynamics, and energetics of layered materials: (1) the phenomenon of crystalline swelling is now well understood, thermodynamically stable layer hydrates have been identified; (2) cell parameters, and surface and interface energies of clay minerals can be computed in quantitative agreement with experiment; (3) self assembly and dynamics of surfactants on clay mineral surfaces can be accurately simulated, in very good agreement with a variety of experimental data (X-ray diffraction, surface and interface energies, charge defect distribution, DSC, IR spectra, NMR spectra, NEXAFS spectra, AFM, and dielectric and mechanical properties).
A major research need lies in our ability to validate the molecular models with experiment, and achieve an accuracy that is competitive with the best experimental technique. The success of molecular-based simulations relies not just on whether the models are correct but if they are relevant to the application. Useful simulations provide answers to existing questions, or suggest new questions to be addressed in the laboratory. In particular, the simulation of complex interfaces with long chain polymers is now feasible but as yet computational power is limited. Additionally, there remain issues regarding the implementation of a biomolecular force field, the convention of combination rules, and the scaling of certain nonbonded interactions.
The limited availability of 104 (or more) processors through supercomputers or grid computing allows only a few computational chemists access to the power needed to perform large-scale classical MD simulations, for example, on a million-atom system for a million time steps. Expectations are for petascale computational platforms to become available in the next few years allowing more researchers the opportunity to regularly perform such calculations on their own institutional supercomputer, through national supercomputer centers, or through a national or international grid network. Also, it is expected that ab initio MD simulations will become more commonplace and that the accuracy of DFT methods will improve through the development of new functionals, especially those that can suitably treat the hydroxyl and water interactions associated with layered materials. Challenges will remain in extending the ab initio MD simulations to include larger-sized systems (thousands of atoms) and for longer simulation times (hundreds of ps) that are more appropriate for attaining equilibrated structures, thermodynamics, and dynamic properties. The complex structure and composition of layered materials—especially with the diversity of interlayer chemistry—and the technological importance of nanocomposite materials will continue to challenge chemists.
Acknowledgements
We are grateful for support from the U.S. Department of Energy, Office of Basic Energy Sciences, Geosciences Research received through the Sandia contract and university grants DE-FG02-00ER-15028 and DE-FG02-08ER-15929. We also appreciate support from the Air Force Research Laboratory, Wright-Patterson Air Force Base, the University of Akron, the Ohio Supercomputing Center, and ETH Zurich. Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin company, for the U.S. Department of Energy under Contract No. DEAC04-94AL85000.References
-
P. S. Braterman, Z. P. Xu and F. Yarberry, in Handbook of Layered Materials, eds. S. M. Auerbach, K. A. Carrado and P. K. Dutta, Marcel Dekker, 2004, pp. 373–474 Search PubMed
.
-
G. Sposito, The Surface Chemistry of Soils, Oxford University Press, New York, 1984 Search PubMed
.
-
R. E. Grim, Clay Mineralogy, second edn., McGraw-Hill, New York, 1968 Search PubMed
.
- S. Plimpton, Journal of Computational Physics, 1995, 117, 1–19 CrossRef CAS
.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918 RSC
.
- N. T. Skipper, K. Refson and J. D. C. McConnell, J. Chem. Phys., 1991, 94, 7434–7445 CrossRef CAS
.
- O. Matsuoka, E. Clementi and M. Yoshimine, J. Chem. Phys., 1976, 64, 1351–1361 CrossRef CAS
.
- E. S. Boek, P. V. Coveney and N. T. Skipper, J. Am. Chem. Soc., 1995, 117, 12608–12617 CrossRef CAS
.
- D. E. Smith, Langmuir, 1998, 14, 5959–5967 CrossRef CAS
.
-
A. G. Kalinichev, in Molecular Modeling Theory: Applications in the Geosciences, eds. R. T. Cygan and J. D. Kubicki, Geochemical Society and Mineralogical Society of America, Washington D.C., 2001, pp. 83–129 Search PubMed
.
- D. van der Spoel, P. J. van Maaren and H. J. C. Berendsen, J. Chem. Phys., 1998, 108, 10220–10230 CrossRef CAS
.
- J. L. Finney, Philosophical Transactions of the Royal Society B: Biological Sciences, 2004, 359, 1145–1165 Search PubMed
.
- B. Guillot, J. Mol. Liq., 2002, 101, 219–260 CrossRef CAS
.
- W. L. Jorgensen and J. Tirado-Rives, Proceedings of the National Academy of Sciences of the United States of America, 2005, 102, 6665–6670 CrossRef CAS
.
- N. T. Skipper, G. Sposito and F.-R. C. Chang, Clays Clay Miner., 1995, 43, 294–303 CAS
.
- J. A. Greathouse and G. Sposito, J. Phys. Chem. B, 1998, 102, 2406–2414 CrossRef CAS
.
- C. J. Hartzell, R. T. Cygan and K. L. Nagy, J. Phys. Chem. A, 1998, 102, 6722–6729 CrossRef CAS
.
- S. H. Park and G. Sposito, Phys. Rev. Lett., 2002, 89 Search PubMed
085501.
- O. F. Zaidan, J. A. Greathouse and R. T. Pabalan, Clays Clay Miner., 2003, 51, 372–381 CrossRef CAS
.
- S.-H. Park and G. Sposito, J. Phys. Chem. B, 2003, 107, 2271–2290
.
- N. T. Skipper, P. A. Lock, J. O. Titiloye, J. Swenson, Z. A. Mirza, W. S. Howells and F. Fernandez-Alonso, Chem. Geol., 2006, 230, 182–196 CrossRef CAS
.
- D. H. Powell, H. E. Fischer and N. T. Skipper, J. Phys. Chem. B, 1998, 102, 10899–10905 CrossRef CAS
.
- B. Rotenberg, V. Marry, J. F. Dufreche, N. Malikova, E. Giffaut and P. Turq, C.R. Chimie, 2007, 10, 1108–1116 Search PubMed
.
- T. J. Tambach, E. J. M. Hensen and B. Smit, J. Phys. Chem. B, 2004, 108, 7586–7596 CrossRef CAS
.
- D. E. Smith, Y. Wang, A. Chaturvedi and H. D. Whitley, J. Phys. Chem. B, 2006, 110, 20046–20054 CrossRef CAS
.
- D. A. Young and D. E. Smith, J. Phys. Chem. B, 2000, 104, 9163–9170 CrossRef CAS
.
- B. J. Teppen, K. R. Rasmussen, P. M. Bertsch, D. M. Miller and L. Schafer, J. Phys. Chem. B, 1997, 101, 1579–1587 CrossRef CAS
.
- J.-R. Hill and J. Sauer, J. Phys. Chem., 1995, 99, 9536–9550 CrossRef CAS
.
- J. R. Maple, M. J. Hwang, T. P. Stockfisch, U. Dinur, M. Waldman, C. S. Ewig and A. T. Hagler, J. Comput. Chem., 1994, 15, 162–182 CrossRef CAS
.
- H. Heinz, H. J. Castelijns and U. W. Suter, J. Am. Chem. Soc., 2003, 125, 9500–9510 CrossRef CAS
.
- H. Heinz and U. W. Suter, J. Phys. Chem. B, 2004, 108, 18341–18352 CrossRef CAS
.
- H. Heinz, H. Koerner, K. L. Anderson, R. A. Vaia and B. L. Farmer, Chem. Mater., 2005, 17, 5658–5669 CrossRef CAS
.
- H. Heinz, R. A. Vaia and B. L. Farmer, J. Chem. Phys., 2006, 124, 224713 CrossRef
.
- D. Bougeard, K. S. Smirnov and E. Geidel, J. Phys. Chem. B, 2000, 104, 9210–9217 CrossRef CAS
.
- M. Arab, D. Bougeard and K. S. Smirnov, Phys. Chem. Chem. Phys., 2002, 4, 1957–1963 RSC
.
- C. I. Sainz-Díaz, A. Hernández-Laguna and M. T. Dove, Phys. Chem. Miner., 2001, 28, 130–141 CrossRef CAS
.
-
S. C. Parker, N. H. de Leeuw, E. Bourova and D. J. Cooke, in Molecular Modeling Theory: Applications in the Geosciences, eds. R. T. Cygan and J. D. Kubicki, Geochemical Society and Mineralogical Society of America, Washington D.C., 2001, pp. 63–82 Search PubMed
.
- S. Hwang, M. Blanco, E. Demiralp, T. Cagin and W. A. Goddard, J. Phys. Chem. B, 2001, 105, 4122–4127 CrossRef CAS
.
- H. Sato, A. Yamagishi and K. Kawamura, J. Phys. Chem. B, 2001, 105, 7990–7997 CrossRef CAS
.
- R. T. Cygan, J.-J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266 CrossRef CAS
.
- J. L. Suter, P. V. Coveney, H. C. Greenwell and M. A. Thyveetil, J. Phys. Chem. C, 2007, 111, 8248–8259 CrossRef CAS
.
- M. A. Thyveetil, P. V. Coveney, H. C. Greenwell and J. L. Suter, J. Am. Chem. Soc., 2008, 130, 4742–4756 CrossRef CAS
.
- M. A. Thyveetil, P. V. Coveney, J. L. Suter and H. C. Greenwell, Chem. Mater., 2007, 19, 5510–5523 CrossRef CAS
.
- M.-A. Thyveetil, P. V. Coveney, H. C. Greenwell and J. L. Suter, J. Am. Chem. Soc., 2008, 130, 12485–12495 CrossRef CAS
.
- R. B. Pandey, K. L. Anderson, H. Heinz and B. L. Farmer, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 1041–1046 CrossRef CAS
.
- R. B. Pandey, K. L. Anderson and B. L. Farmer, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 3580–3589 CrossRef CAS
.
-
R. T. Cygan and J. D. Kubicki, Molecular Modeling Theory: Applications in the Geosciences, Geochemical Society and Mineralogical Society of America, Washington D.C., 2001 Search PubMed
.
-
W. J. Hehre, L. Radom, P.v.R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, John Wiley and Sons, New York, 1986 Search PubMed
.
- R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746 CrossRef CAS
.
- V. Milman, B. Winkler, J. A. White, C. J. Pickard, M. C. Payne, E. V. Akhmatskaya and R. H. Nobes, Int. J. Quantum Chem, 2000, 77, 895–910 CrossRef CAS
.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS
.
- G. V. Gibbs, M. M. Hamil, S. J. Louisnathan, L. S. Bartell and H. Yow, Am. Mineral., 1972, 57, 1578–1613 CAS
.
- J. A. Tossell and G. V. Gibbs, Acta Crystallographica, Section A: Foundations of Crystallography, 1978, 34, 463–472 Search PubMed
.
- B. J. Teppen, C.-H. Yu, S. Q. Newton, D. M. Miller and L. Schäfer, J. Mol. Struct., 1998, 445, 65–88 CrossRef CAS
.
- V. Timón, G. I. Sainz-Díaz, V. Botella and A. Hernández-Laguna, Am. Mineral., 2003, 88, 1788–1795 CAS
.
- L. Benco, D. Tunega, J. Hafner and H. Lischka, Chem. Phys. Lett., 2001, 333, 479–484 CrossRef CAS
.
- L. Benco, D. Tunega, J. Hafner and H. Lischka, Am. Mineral., 2001, 86, 1057–1065 CAS
.
- C. H. Bridgeman, A. D. Buckingham and N. T. Skipper, Mol. Phys., 1996, 89, 879–888 CrossRef CAS
.
- J. D. Hobbs, R. T. Cygan, K. L. Nagy, P. A. Schultz and M. P. Sears, Am. Mineral., 1997, 82, 657–662 CAS
.
- C. I. Sainz-Díaz, V. Timón, V. Botella, E. Artacho and A. Hernández-Laguna, Am. Mineral., 2002, 87, 958–965 CAS
.
- D. Tunega, G. Haberhauer, M. H. Gerzabek and H. Lischka, Langmuir, 2002, 18, 139–147 CrossRef CAS
.
- A. Michalkova, D. Tunega and L. T. Nagy, THEOCHEM, 2002, 581, 37–49 CrossRef CAS
.
- S. V. Churakov, J. Phys. Chem. B, 2006, 110, 4135–4146 CrossRef CAS
.
- J. P. Larentzos, J. A. Greathouse and R. T. Cygan, J. Phys. Chem. C, 2007, 111, 12752–12759 CrossRef CAS
.
- C. I. Sainz-Díaz, E. Escamilla-Roa and A. Hernández-Laguna, Am. Mineral., 2004, 89, 1092–1100 CAS
.
- B. R. Bickmore, K. M. Rosso, K. L. Nagy, R. T. Cygan and C. J. Tadanier, Clays Clay Miner., 2003, 51, 359–371 CrossRef CAS
.
- E. Scholtzova, D. Tunega and L. T. Nagy, THEOCHEM, 2003, 620, 1–8 CrossRef CAS
.
- V. Botella, V. Timón, E. Escamilla-Roa, A. Hernández-Languna and C. I. Sainz-Díaz, Phys. Chem. Miner., 2004, 31, 475–486 CrossRef CAS
.
- A. Hernández-Laguna, E. Escamilla-Roa, V. Timón, M. T. Dove and C. I. Sainz-Díaz, Phys. Chem. Miner., 2006, 33, 655–666 CrossRef CAS
.
- C. I. Sainz-Díaz, E. Escamilla-Roa and A. Hernández-Laguna, Am. Mineral., 2005, 90, 1827–1834 CrossRef CAS
.
- D. Tunega, B. A. Goodman, G. Haberhauer, T. G. Reichenauer, M. H. Gerzabek and H. Lischka, Clays Clay Miner., 2007, 55, 220–232 CrossRef CAS
.
- H. C. Greenwell, W. Jones, P. V. Coveney and S. Stackhouse, J. Mater. Chem., 2006, 16, 708–723 RSC
.
-
R. B. Woodward and R. Hoffmann, The Conservation of Orbital Symmetry, Verlag Chemie GmbH, Weinheim, 1970 Search PubMed
.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS
.
- M. Mookherjee and L. Stixrude, Am. Mineral., 2006, 91, 127–134 CrossRef CAS
.
- A. J. A. Aquino, D. Tunega, G. Haberhauer, M. H. Gerzabek and H. Lischka, J. Comput. Chem., 2003, 24, 1853–1863 CrossRef CAS
.
- A. Michalkova, L. D. Johnson, L. Gorb, O. A. Zhikol, O. V. Shishkin and J. Leszczynski, Int. J. Quantum Chem, 2005, 105, 325–340 CrossRef CAS
.
- A. Michalkova and D. Tunega, J. Phys. Chem. C, 2007, 111, 11259–11266 CrossRef CAS
.
- N. U. Zhanpeisov, J. W. Adams, S. L. Larson, C. A. Weiss, B. Z. Zhanpeisova, D. Leszczynska and J. Leszczynski, Struct. Chem., 1999, 10, 285–294 CrossRef CAS
.
- E. Molina-Montes, D. Donadio, A. Hernández-Laguna and C. I. Sainz-Díaz, J. Phys. Chem. A, 2008, 112, 6373–6383 CrossRef CAS
.
- E. Molina-Montes, D. Donadio, A. Hernández-Laguna, C. I. Sainz-Díaz and M. Parrinello, J. Phys. Chem. B, 2008, 112, 7051–7060 CrossRef CAS
.
- E. Molina-Montes, V. Timón, A. Hernández-laguna and C. I. Sainz-Díaz, Geochim. Cosmochim. Acta, 2008, 72, 3929–3938 CrossRef CAS
.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186 CrossRef CAS
.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS
.
- S. V. Churakov, Geochim. Cosmochim. Acta, 2007, 71, 1130–1144 CrossRef CAS
.
- D. Tunega, L. Benco, G. Haberhauer, M. H. Gerzabek and H. Lischka, J. Phys. Chem. B, 2002, 106, 11515–11525 CrossRef CAS
.
- D. Tunega, M. H. Gerzabek, G. Haberhauer and H. Lischka, Eur. J. Soil Sci, 2007, 58, 680–691 CrossRef CAS
.
- D. Tunega, M. H. Gerzabek and H. Lischka, J. Phys. Chem. B, 2004, 108, 5930–5936 CrossRef CAS
.
- D. Tunega, G. Haberkauer, M. H. Gerzabek and H. Lischka, Soil Sci., 2004, 169, 44–54 CrossRef CAS
.
- B. J. Teppen, C. H. Yu, S. Q. Newton, D. M. Miller and L. Schäfer, J. Phys. Chem. A, 2002, 106, 5498–5503 CrossRef CAS
.
-
T. J. Pinnavaia and G. W. Beall, eds., Polymer-Clay Nanocomposites, Wiley, New York, 2000 Search PubMed
.
- H. H. Murray, Appl. Clay Sci., 2000, 17, 207–221 CrossRef CAS
.
- Y. Lvov, K. Ariga, I. Ichinose and T. Kunitake, J. Am. Chem. Soc., 1995, 117, 6117–6123 CrossRef CAS
.
-
R. F. Giese and C. J. van Oss, Colloid and Surface Properties of Clays and Related Minerals, Dekker, New York, 2002 Search PubMed
.
- W. A. Hayes and D. K. Schwartz, Langmuir, 1998, 14, 5913–5917 CrossRef CAS
.
- J. D. Jacobs, H. Koerner, H. Heinz, B. L. Farmer, P. Mirau, P. H. Garrett and R. A. Vaia, J. Phys. Chem. B, 2006, 110, 20143–20157 CrossRef CAS
.
- G. Lagaly and A. Weiss, Koll. Z.Z. Polym., 1970, 237, 364–368 CrossRef CAS
.
- T. Okada, Y. Watanabe and M. Ogawa, J. Mater. Chem., 2005, 15, 987–992 RSC
.
- M. A. Osman, M. Ploetze and P. Skrabal, J. Phys. Chem. B, 2004, 108, 2580–2588 CrossRef CAS
.
- M. A. Osman, G. Seyfang and U. W. Suter, J. Phys. Chem. B, 2000, 104, 4433–4439 CrossRef
.
- R. A. Vaia, R. K. Teukolsky and E. P. Giannelis, Chem. Mater., 1994, 6, 1017–1022 CrossRef CAS
.
- A. Weiss, A. Mehler and U. Hofmann, Z. Naturforsch., B: Chem. Sci., 1956, 11, 431–434
.
- E. Hackett, E. Manias and E. P. Giannelis, J. Chem. Phys., 1998, 108, 7410–7415 CrossRef CAS
.
- H. Heinz and U. W. Suter, Angew. Chem. Int. Ed., 2004, 43, 2239–2243 CrossRef CAS
.
- H. Heinz, R. A. Vaia and B. L. Farmer, Langmuir, 2008, 24, 3727–3733 CrossRef CAS
.
- H. Heinz, R. A. Vaia, H. Koerner and B. L. Farmer, Chem. Mater., 2008, 20, 6444–6456 CrossRef CAS
.
- H. Heinz, R. A. Vaia, R. Krishnamoorti and B. L. Farmer, Chem. Mater., 2007, 19, 59–68 CrossRef CAS
.
- O. L. Manevitch and G. C. Rutledge, J. Phys. Chem. B, 2004, 108, 1428–1435 CrossRef CAS
.
- Q. H. Zeng, A. B. Yu, G. Q. Lu and R. K. Standish, Chem. Mater., 2003, 15, 4732–4738 CrossRef CAS
.
-
D. G. Evans and R. C. T. Slade, in Layered Double Hydroxides, eds. X. Duan and D. G. Evans, Springer, Berlin, 2006, vol. 119, pp. 1–87 Search PubMed
.
-
V. Rives, Ed., Layered Double Hydroxides: Present and Future, Nova Publishers, 2001 Search PubMed
.
- A. V. Besserguenev, A. M. Fogg, R. J. Francis, S. J. Price, D. Ohare, V. P. Isupov and B. P. Tolochko, Chem. Mater., 1997, 9, 241–247 CrossRef CAS
.
- X. Q. Hou, D. L. Bish, S. L. Wang, C. T. Johnston and R. J. Kirkpatrick, Am. Mineral., 2003, 88, 167–179 CAS
.
- X. Q. Hou, A. G. Kalinichev and R. J. Kirkpatrick, Chem. Mater., 2002, 14, 2078–2085 CrossRef CAS
.
- T. Hibino and M. Kobayashi, J. Mater. Chem., 2005, 15, 653–656 RSC
.
- A. I. Khan and D. O'Hare, J. Mater. Chem., 2002, 12, 3191–3198 RSC
.
- S. P. Newman and W. Jones, New J. Chem., 1998, 22, 105–115 RSC
.
- D. Tichit and B. Coq, Cattech, 2003, 7, 206–217 CrossRef CAS
.
- J.-H. Choy, S.-Y. Kwak, Y.-J. Jeong and J.-S. Park, Angew. Chem., 2000, 39, 4041–4045 CrossRef
.
- W. M. Kriven, S. Y. Kwak, M. A. Wallig and J. H. Choy, Mater. Res. Soc. Bull., 2004, 29, 33–37 Search PubMed
.
- F. Basile, M. Campanati, E. Serwicka and A. Vaccari, Appl. Clay Sci., 2001, 18, 1–2 CrossRef CAS
.
- G. R. Williams and D. O'Hare, J. Mater. Chem., 2006, 16, 3065–3074 RSC
.
- W. Kagunya, P. K. Dutta and Z. Lei, Physica B, 1997, 234–236, 910–913 CrossRef CAS
.
- W. W. Kagunya, J. Phys. Chem., 1996, 100, 327–330 CrossRef CAS
.
- A. G. Kalinichev and R. J. Kirkpatrick, Chem. Mater., 2002, 14, 3539–3549 CrossRef CAS
.
- A. G. Kalinichev, R. J. Kirkpatrick and R. T. Cygan, Am. Mineral., 2000, 85, 1046–1052 CAS
.
-
R. J. Kirkpatrick, A. G. Kalinichev, J. Wang, X. Hou and J. E. Amonette, in The Application of Vibrational Spectroscopy to Clay Minerals and Layered Double Hydroxides, ed. J. T. Kloprogge, Clay Mineral Society, Aurora, Colorado, 2005, vol. 13, pp. 239–285 Search PubMed
.
- P. P. Kumar, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. B, 2006, 110, 3841–3844 CrossRef CAS
.
- P. P. Kumar, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. C, 2007, 111, 13517–13523 CrossRef CAS
.
- Q. Li and R. J. Kirkpatrick, Am. Mineral., 2007, 92, 397–402 CrossRef CAS
.
- S. P. Newman, T. Di Cristina, P. V. Coveney and W. Jones, Langmuir, 2002, 18, 2933–2939 CrossRef CAS
.
- M. X. Reinholdt and R. J. Kirkpatrick, Chem. Mater., 2006, 18, 2567–2576 CrossRef CAS
.
- J. W. Wang, A. G. Kalinichev, J. E. Amonette and R. J. Kirkpatrick, Am. Mineral., 2003, 88, 398–409 CAS
.
- J. W. Wang, A. G. Kalinichev and R. J. Kirkpatrick, Geochim. Cosmochim. Acta, 2006, 70, 562–582 CrossRef CAS
.
- J. W. Wang, A. G. Kalinichev, R. J. Kirkpatrick and X. Q. Hou, Chem. Mater., 2001, 13, 145–150 CrossRef CAS
.
- P. S. Braterman and R. T. Cygan, Am. Mineral., 2006, 91, 1188–1196 CrossRef CAS
.
-
A. Finch, P. N. Gates, K. Radcliffe, F. N. Dickson and F. F. Bentley, in Chemical Applications of Far Infrared Spectroscopy, Academic Press, London, 1970, pp. 1–23 Search PubMed
.
-
J. D. Kubicki, in Molecular Modeling Theory: Applications in the Geosciences, eds. R. T. Cygan and J. D. Kubicki, Geochemical Society and Mineralogical Society of America, Washington D.C., 2001, pp. 459–483 Search PubMed
.
- D. Kleinhesselink and M. Wolfsberg, Surf. Sci., 1992, 262, 189–207 CrossRef CAS
.
-
D. A. McQuarrie, Statistical Mechanics, Harper & Row, New York, 1976 Search PubMed
.
Footnote |
| † This paper is part of a Journal of Materials Chemistry theme issue on Layered Materials. Guest editors: Leonardo Marchese and Heloise O. Pastore. |
| This journal is © The Royal Society of Chemistry 2009 |
