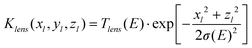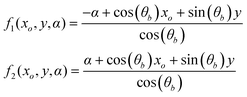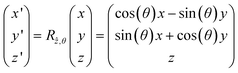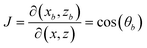Quantitative analysis in confocal micro-PIXE—general concept and layered materials
Received
30th September 2008
, Accepted 11th February 2009
First published on 6th March 2009
Abstract
In a typical micro-PIXE set-up the insertion of an X-ray optic such as a polycapillary half lens, in front of the X-ray detector in combination with the focused charged particle micro-beam creates a confocal geometry and thus a probing-volume. By moving the sample across the probing-volume, spatially resolved characteristic X-ray intensities are detected. The aim of this work is to present a theoretical model that describes the micro-PIXE intensities in confocal geometry in the case of either layered-structured materials or materials composed of major–minor elements exhibiting concentration gradients within depth. The influence of various experimental parameters such as the beam energy, spatial resolution of the X-ray lens, micro-beam dimensions, irradiation and detection angles, as well as the structure (thickness, composition) of the individual layers that compose the analyzed sample, is investigated by means of simulations of the PIXE yield at various positions of the analyzed sample within the probing volume. The advantages and limitations of the micro-PIXE analysis in confocal geometry are presented through examples and discussed, in particular with respect to the differential PIXE analysis.
Introduction
Particle and X-ray induced fluorescence radiation techniques have been developed over the last forty years to provide quantitative analysis of homogeneous materials within almost the whole periodic table and with sensitivity even down to the ppb or ppt region. Lateral spatial resolution has been also attained at the micrometer regime, however, to reach similar in-depth or 3D elemental specific resolution is still an open problem to be tackled by the scientific community. In the case of Particle Induced X-ray Emission (PIXE), several important attempts have been reported in the literature aiming to provide analytical methodologies for depth resolved analysis. All the efforts, up to now, utilize PIXE analysis at variable incident energy or projectile impact angle. A strong dependence of the X-ray ionization cross section with respect to the proton energy and thus with the depth at which the X-ray production takes place has triggered and motivated the development of the so-called differential PIXE analysis since 1995. Various analytical strategies have been developed so far by different groups, whereas the most examined materials are paint layers and plating of archaeological metallic objects. Neelemeijer et al.1,2 using GUPIX and thick target analysis identified the sequence of paint layers composed by characteristic elements through the systematic increase/decrease of their integral intensities for increasing proton energy. This approach results in a rough semi-quantitative characterization of material composed of up to three different layers. PIXE analysis at variable impact angle (0–70°) and fixed detection angle has been utilized by Weber et al.3 This way the effective thickness of layers crossed by the incident beam changes and results in evolution of characteristic X-ray intensities. Again, this methodology is suitable for identifying elements in different layers but cannot reveal their detailed depth profile. For the particular case of gold jewellery items, Demortier et al.4 have proposed an analytical procedure based on the CuKα/AuLβ intensity ratio at different proton energies, in order to identify the presence and then to characterize the composition of a surface layer enriched in gold (with a layer thickness extended up to about 10 µm). The observed PIXE yield at specific proton energy represents an integral quantity to which an elemental concentration profile within the whole range of protons in the sample contributes. Since the weight of contribution depends on the emitter depth, it is necessary to formulate a deconvolution algorithm. Brissaud and his collaborators5,7 have developed an algorithm to determine mean elemental concentration profiles (in arbitrary units) in layered structured painting materials. The same group has argued that the analysis of an abrupt change of the slope of the PIXE yield versus projectile energy provides an elegant opportunity to identify the location of an element and thus the sequence of layers in a startified material. The most laborious and universal solution of the deconvolution problem has been developed by Smit et al.8 The method is based on a virtual sample slicing and χ2-minimization of the differences between the measured and calculated X-ray yields. The algorithm has been extensively applied in the quantitative determination of in-depth elemental profiles in plated metallic objects and paint materials.9,10
The development of polycapillary X-rays lenses during the last decade opened a new era in the field of X-ray microscopic analysis. Among the first applications of X-ray lenses in the field of X-ray fluorescence analysis was the formation of X-ray micro-beams with diameters of the order of a few micrometers. Later, the polycapillary X-rays lenses were introduced also in the detection channel to form a confocal geometry. Laboratory or synchrotron induced 3D-XRF spectroscopy provides nowadays an advanced characterization of materials with depth resolving capability together with probing of the elemental composition of individual structures.11–16 A quantitative model proposed by Malzer and Kanngießer17 that was recently experimentally validated18 provides a necessary frame for interpretation of the confocal micro-XRF data (intensity profiles) and the determination of elemental in-depth concentrations in stratified materials. Very recently, the concept of the confocal set-up was transferred successfully to the field of the micro-PIXE technique by implementing a polycapillary half lens in front of the X-ray detector and taking advantage of an excellent spatial resolution of an ion micro-beam. The first applications using a proton microbeam in vacuum19 and under atmospheric pressure20 have clearly demonstrated the potential of the technique in the analysis of stratified materials to resolve elemental in-depth profiles. The particular advantage of an ion microbeam for fast lateral scanning has driven 3D elemental investigations. Žitnik et al.21 have presented 3D element selective imaging of aerosol micro particles captured in thick quartz filters with a micron spatial resolution aiming finally to deduce in-depth concentration profiles for the strong emitters of the sample (Fe, Ca and S).
In the present paper, a theoretical model for quantitative analysis in confocal micro-PIXE geometry is developed and presented. The proposed quantification approach uses an analytical description for the energy dependent spatial response function of the X-ray lens at the focal region. By incorporating an analytical description of the micro-beam profile, the probing-volume is analytically described through the sensitivity function expressed in spatial coordinates in an analogous manner to the one for 3D micro-XRF in confocal geometry.17 The proton induced X-ray intensity is calculated by virtually slicing of the sample and taking into account the well known processes (ionization, energy loss of protons and self-attenuation of characteristic X-rays) involved in the production of PIXE yield by a layer of infinitesimal thickness. The integral of such infinitesimal PIXE yields weighted by the sensitivity function in the fixed detector set-up results in the total PIXE intensity that depends on the sample position and on the lateral position of the micro-beam. Extensive simulations were performed for different types of materials to illustrate the inherent features of the confocal micro-PIXE approach and to examine the depth sensitivity of the method with respect to various experimental parameters and in comparison to differential PIXE analysis.
Description of the confocal micro-PIXE set-up geometry
The confocal micro-PIXE set-up geometry is defined by means of: a) the micro-beam space/flux distribution around its focal plane and b) of the X-ray lens acceptance function (spatial resolution) laterally at its focal plane but also along the optical axis. In this section, the two set-up components will be described analytically, at first separately in their own coordination system and next in a common ‘main’ coordination system. In addition, the concept of the confocal alignment will be formulated.
A typical micro-PIXE setup utilizes a pair of perpendicular slits to define the cross section of the beam. It is therefore plausible to describe suitably the beam cross section with a rectangle and assume a homogeneous flux density distribution. The rectangular shape can be expressed mathematically in terms of two Heaviside functions, one for the horizontal and another one for the vertical coordinate, respectively. As it has been shown,19 the cross section of the micro-beam does not change noticeably along its propagation direction for about 200–300 µm from the focal plane. Therefore, within this region, we can describe the spatial distribution of the micro-beam with unity intensity as follows:
| |  | (1) |
This equation holds for a beam of a width of 2
α in the horizontal direction and a height of 2
β, while
xb,
yb and
zb are the Cartesian coordinates as represented in
Fig. 1.
 |
| | Fig. 1 Graphical representation of a typical confocal micro-PIXE geometry. A rectangular ion microbeam (yellow) irradiates a sample which is observed though the sensitive detection-volume of a polycapillary lens (the red surface represents an isosurface of the lens acceptance for a given X-ray energy). | |
In the case of the focusing X-ray optics devices, several authors have investigated the flux density distribution of X-ray beams formed by polycapillary lenses.22–25 The spatial distribution of the focused X-ray micro-beams has been examined experimentally by means of either knife edge or wire scan methods and it has been found to be represented by a Gaussian function. Therefore, it has been suggested17 that a two-dimensional Gaussian bell function is the best candidate for the description of the profile of a focused X-ray micro-beam. Wolff et al.26 have recently provided a thorough experimental investigation of the energy dependence of the polycapillary half-lens spot size, when it is utilized either in the focusing or collecting mode, namely when the incoming or outgoing X-ray beam is parallel, respectively. In both cases, the spatial distribution of the focused beam or of its acceptance function can be described by a Gaussian-like function, however in the later (collecting) mode, much larger spot sizes are produced and the differences increase as the energy of the transmitted X-rays is decreased. The effect can be interpreted in terms of a divergence effect that is stronger for lower X-ray energies emitted isotropically and captured by the half lens in the collecting mode, comparing with a parallel beam (synchrotron radiation with small angular divergence) entering inside the lens, well aligned with the parallel capillaries.26 Thus, we will finally adopt that in our case (collecting mode) the spatial resolution of the lens exhibits the same shape like the flux density distribution of a focused X-ray micro-beam. If we denote by yl the direction of the capillary axis and by xl, zl the axes in the plane perpendicular to the lens axis (Fig. 2), the acceptance function Klens of the polycapillary X-ray lens can be written as follows:
| | 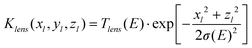 | (2) |
where
Tlens represents the X-ray lens transmission efficiency. The characteristic width
σ as well as
Tlens depend on the energy of the
photons that propagate through the lens. On the other hand, the width
σ could be considered independent of the coordinate
yl in the range of 100–150 µm, which is the length much larger than the diameter of a typical ion micro-beam.
 |
| | Fig. 2 Geometrical parameters of the confocal micro-PIXE geometry. | |
At this point we should introduce formally the concept of the confocal alignment. Let's assume for the moment that the origins of the ‘lens’ and ‘beam’ coordination systems are located at the exit of the X-ray lens and at the end of the last quadruple magnet, respectively. Therefore, the lens and the beam coordinates of the center of symmetry of each focal region will be described at each coordination system as P1: (0, f2, 0) and P2: (0, F, 0), where f2 and F are the focal distances for the X-ray lens and the ion micro-beam, respectively. The experimental procedure for producing a confocal set-up aims to bring together the two centers of symmetry (points P1 and P2), whereas alignment is attained by making coplanar the planes (xb, yb) and (xl, yl). If these requirements are fulfilled, the intersection of the X-ray lens and micro-beam focal regions creates the so-called probing volume, whereas its center of symmetry determines actually the confocal point of the set-up.
The functions Kbeam and Klens have been already defined analytically in their own coordination system. However, for developing a quantitative model it is required to express both in a common ‘main’ coordination system associated with the sample. The two axes of the ‘main’ coordination, x and z are in the plane parallel to the sample surface and z is parallel to zb and zl for an aligned set-up. The ‘main’ system is placed with its origin into the confocal point of the set-up. The y axis is then normal to the sample surface and its orientation with respect to the beam and polycapillary (or detector) axis is described by the angles θb and θl, respectively. These two angles can assume a negative or a positive sign depending on the geometry of the experimental set-up (the orientation of coordinate axes). When the origin of all three coordination systems coincide, all the z-axes coincide and the functions Kbeam(xb, yb, zb) and Klens(xl, yl, zl) can be expressed in the main coordination system after rotation around the common z-axis for an angle θb and θl, respectively:
Thus, the lens acceptance function can be expressed as follows:
| |  | (3) |
In ion micro-beam focusing devices (nuclear microprobes), it is possible to move in a reproducible way and with sub-micrometer accuracy the micro-beam in the plane perpendicular to its propagation axis. This experimental possibility adds considerable flexibility, precision and speed towards 3D elemental profile investigations in a confocal geometrical set-up. Therefore, it would be convenient to consider a more general case with the ion micro-beam focal point P2 shifted relative to the position of P1 (see Fig. 1). In this case, if the point P1 is given by (x1, y, z1) ‘main’ coordinates, the point P2 will be (x1 + xo, y, z1 + zo), with the (xo, 0, zo) vector defining the externally applied translation of the center of the beam. In order to transform now an arbitrary set of beam coordinates (xb, yb, zb) into the corresponding one of the ‘main’ system (x, y, z) we must apply, prior to the aforementioned rotation a translationx → x + xo and z → z + zo. Thus, the spatial distribution of the ion micro-beam flux will be expressed in the ‘main’ spatial coordinates as follows:
| | | Kbeam(xb, yb, zb)dxbdzb ≡ Kbeam(x − xo, y, z − zo)cos(θb)dxdz | (4a) |
where,
| |  | (4b) |
The factor cos(θb) is due to the Jacobian of transformation dxbdzb → J·dxdz where:
Analytical description of the probing micro-volume: The confocal micro-PIXE sensitivity function
The fundamental difference regarding the implementation of the confocal PIXE technique in comparison to the conventional PIXE analysis is that the sample is moving through the focal region of the set-up and individual PIXE spectra are recorded at each position. Let's consider now the PIXE yield produced by a sample of infinitesimal thickness dy, as it is moved through the probing volume at different positions y (Fig. 2). In principle, when the layer dy is positioned in such a way that it crosses the set-up confocal point, the detected PIXE intensity should be maximum; on the contrary, when the layer dy is getting away from the set-up focus, the detected PIXE intensity is decreased. It is therefore plausible to consider that in the confocal geometry, the infinitesimal PIXE yield of layer dy is modulated by a kind of a weight function whose value depends on y, the position of the sample with respect to the confocal point. Recent experimental results of confocal PIXE measurements have shown that the shape of this function resembles quite accurately a Gaussian function.19,20 However, it is important to provide a theoretical explanation for this dependence by means of a mathematical model that describes the variation of the PIXE intensities when a sample of infinitesimal thickness is moving across the confocal probing volume. The variation of PIXE intensity as a function of position y of the thin layer dy relatively to the set-up focus at a given lateral position of the micro-beam will be expressed in terms of the sensitivity function K(y) of the confocal PIXE set-up, which is obtained by the convolution of the micro-beam profile Kbeam and of the X-ray lens acceptance function Klens, as follows:| |  | (5) |
The bounds of the integral in eq. (5) are limited by Heaviside functions in the expression for Kbeam, thus eq. (5) can be written finally as follows:
| |  | (6a) |
where:
| | 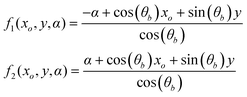 | (6b) |
| |  | (6c) |
After some calculus applied on eq. (6a), while for simplicity substituing xo = zo = 0 without loss of generality, the confocal micro-PIXE depth sensitivity function is expressed by the following analytical formula:
| | | K(y) = K(0, y, 0) = const·[erf(ky + λ) − erf(ky − λ)] | (7a) |
with:
| |  | (7b) |
and
| |  | (7c) |
It is evident from eq. (7a) that the shape of the sensitivity profile K(y) is determined by the difference of two error functions. This result seems to contradict the experimental findings that suggest a Gaussian profile. It is therefore necessary to investigate further eq. (7a) and to show that indeed a Gaussian function is a good approximation under the experimental conditions of the previous confocal PIXE experiments.19,20 In a formal way, we would like to determine the parameters C and s that may approximate the following equality:
| |  | (8) |
It is important to note that the λ parameter represents the ratio of the “effective” width of the micro-beam α/cos(θb) that the polycapillary optic observes on the sample with respect to its effective width σ/cos(θl). To proceed we expand the two parts of eq. (8) around y = 0:
| |  | (9a) |
| |  | (9b) |
If the higher order terms can be neglected, the equality of the zero and first order coefficients yields an analytical expression for the corresponding factor C and the Gaussian width s, as follows:
| |  | (10b) |
The validity of the aforementioned approach can be examined numerically by calculating the percentage difference between the exact expression (K-function, eq. (7)) and the corresponding one for the approximated expression (Gaussian function expressed by the second half of eq. (8) in combination with eq. (10)) for a wide range of parameter λ by means of the following expression:
| |  | (11) |
The results are presented in Fig. 3 for the k parameter equal to 0.1 µm−1 and for a wide range of λ values. It can be observed that for λ values up to 0.5 for example, there is no significant difference by implementing the Gaussian function to represent the depth sensitivity of the confocal micro-PIXE set-up. At the edges of the gaussian profile, however, the difference may raise up to 10% (positions ∼ −25, +25 µm). This fact does not imply serious problems for an accurate description of an experimental profile, since the PIXE intensity at these positions has been already decreased to less than 0.1% of the maximum (centroid) intensity. In conclusion, the small (y/s)2 approximation is practically valid for the current performances of polycapillary X-ray lenses (FWHM ≥ 15–20 µm for energies around 8 keV) and for typical ion micro-beam sizes (under atmospheric pressure a typical micro-beam size is in the region of 15–20 µm while in vacuum the size of the beam is a few micrometers or less).
 |
| | Fig. 3 The difference between the exact sensitivity K function (eq. 6) and the Gaussian approximation (eq. 8) with respect to the λ value for various positions y from the confocal point of the set-up. The parameter k is 0.1 µm−1, which is a typical value in a confocal experiment. The red line corresponds to λ = 0.5. | |
When an ion micro-beam width is small, so that α ≪ σ, and λ → 0, the width of the sensitivity function is given by the limiting case of eq. (10b):
| |  | (12) |
The aforementioned relationship actually expresses the width of the set-up sensitivity function by means of the projected standard deviation of the polycapillary acceptance Gaussian function on the direction of the sample's normal.
PIXE yield in confocal geometry
The conventional PIXE yield production for a thick homogeneous target irradiated by charged particles of initial kinetic energy E0 is expressed as an integral of the infinitesimal PIXE production yield y∞Z,Xj(E) per proton energy loss dE:27| |  | (13a) |
where| |  | (13b) |
and:| |  | (13c) |
| |  | (13d) |
In the above formulas, Z is the atomic number of the analyte, Xj the detected characteristic X-ray line, Np is the number of the incident charged particles with kinetic energy E0, ΔΩd the solid angle subtended by the detector, Nav the Avogadro's number, AWZ the atomic weight of the analyte and CZ its corresponding concentration inside the homogeneous target, σZXj the characteristic X-ray production cross section as a function of the incident particle energy E, S is the stopping power for the charged particles at energy E, µ(EZXj) the mass attenuation coefficient for the characteristic X-ray energy inside the analyzed target, while the θl and θb angles have been defined previously.
In order to introduce the confocal PIXE production yield, it would be necessary to express first the infinitesimal PIXE yield (eq. (13)) in terms of the depth parameter y′ = −y (Fig. 4a) and generalizing its application for a depth-inhomogeneous sample of thickness d described by a depth variable density ρ(y′) and analyte concentration CZ(y′):
| |  | (14a) |
where
y′:[0, min(
d,
R·cos
θb)].
 |
| | Fig. 4 Conventional PIXE (a) and confocal micro-PIXE (b) geometrical parameters in the analysis of a thick target. | |
In the above relationship, R denotes the range of the protons in the sample matrix, whereas y′ denotes the depth inside the sample where the charged particles have kinetic energy equal to E. This depth can be determined through the following expression:
| |  | (14b) |
In the confocal geometry the proton induced characteristic X-ray intensities that are emitted from a layer of infinitesimal thickness dy′ placed at sample depth y′ are modulated by the sensitivity function K(y), where y denotes the given distance for the layer dy′ with respect to the confocal point. In the more general case (see Fig. 4b), a infinitesimal layer dy is at coordinate y and the sample surface is positioned at y0 with respect to the confocal set-up focus-point. When y0 = 0 the sample surface is located exactly at the confocal point, whereas the positive or negative values of the parameter y0 refer to the case where the confocal point is within or outside the sample, respectively.
Next, by introducing the confocal PIXE sensitivity function KZXj(y), the PIXE yield dY∞Z,Xj(y0, y) produced by an infinitesimaly thin slice dy is given in confocal geometry by the following expression:
| |  | (15a) |
where,
| |  | (15b) |
In the above relationship, ΔΩl denotes the solid angle subtended by the active surface of the front side of the polycapillary X-ray lens. Integrating the formula (15a) along the whole sample thickness (or over the protons range, if this is smaller), the total confocal PIXE yield is deduced as a function of its (surface) position y0 inside the confocal micro volume, as follows:
| |  | (15c) |
Description of the ‘CPIXE1D’ simulation code
A platform-independent simulation code ‘CPIXE1D’, has been written in C++ with the aim to simulate the confocal PIXE yield. In this way the dependency of the PIXE yield in confocal geometry can be investigated from the various points of view: the geometrical set-up parameters, the instrumental parameters and the sample structural and compositional parameters. This is important to reveal the significance and effect on the detected PIXE intensities as the probing volume is moving within the sample. Of particular interest is to examine how and to which extent the shape of the intensity profile, the position and intensity of the maximum or several maxima provide semi-quantitative information regarding the composition, structure or in-depth elemental in-homogeneities of the sample. The code simulates PIXE intensities (eq. (15)) for any given elemental composition of a multi-layered sample, whereas the in-depth concentration gradients are described by means of a large number of layers with gradual increase/decrease of a particular elemental concentration. Besides the description of the structure of the sample (number of layers and respective thickness and elemental composition for each layer), the code input includes geometrical characteristics of the setup (X-ray detection and ion-beam impinging angles), physical parameters such as the ion beam type and its initial kinetic energy together with the set-up instrumental parameters such as the cross section of the ion micro-beam, the FWHM of the lens acceptance function, the lens transmission and detector intrinsic efficiency versus the characteristic X-ray energy. Furthermore, since an ion micro-probe allows fast deflection of the beam with micrometer precision, the code simulates PIXE yield versus depth for both scanning modes that can be in principle experimentally implemented: in the first the sample is moved through the confocal probe volume with a micrometer step, while in the second mode the microbeam is moved to change the lateral beam coordinates whereas the sample remains at the fixed position. The equivalency of the two scanning modes for layered materials is illustrated in Fig. 5. For example, if the changes of s and α, β are neglected a beam deflection to the xo coordinate corresponds to a sample translationy equal to:| |  | (16) |
 |
| | Fig. 5 Schematic diagram indicating the equivalence of beam and sample scanning modes in a confocal micro-PIXE analysis of layered materials (eq. 16). | |
In the thick target, the integral of the yield expression (eq. (15b)) is calculated numerically, so that the sample is divided in small slices according to the user-defined step. For the efficient optimization of the code, the steps are preferably defined in ion-beam energy loss units (keV). The code translates internally the energy step to length units (eq. (14b)) according to the local elemental composition and density of the sample under investigation although the ab-initio length definition of the integration step is an option. The differential X-ray yield of each slice, as well as its depth position, is calculated and stored. Then, all differential yields are convoluted with the corresponding value of the confocal sensitivity for every position y of the sample's surface with respect to the confocal point. Finally, all the convoluted differential yields are summed producing thus the total confocal PIXE yield versus the experimental sample position y. The database for the ionization cross sections has been adopted from the ECPSSR parametrization28,29 whereas the stopping power for the charged energetic particles in matter is calculated with Ziegler's parameterization.30 Furthermore, for the X-ray emission lines, fluorescence yields, relative intensities and mass attenuation coefficients the Elam database is used.31
Results
Simulations of confocal PIXE intensities are presented for both (sample or beam) scanning modes and for the three typical sample structures: 1) A pure monoelement (Ni) layer of variable thickness, 2) a two-layer structured sample with silicon oxide as a matrix and various Fe concentrations among the two layers and 3) a pictorial layered sample structure, composed by three different paint layers of inorganic pigments mixed with an organic binder. The simulations were done for a 3 MeV proton beam with a confocal geometry defined by θb = 0 and θl = 45° as the ion-beam and the detection angle, respectively. In the sample scanning mode the movement is implemented along the beam axis. The FWHM of the lens acceptance function was arbitrary set equal to ∼18 µm for Ni-Kα, whereas for the lower or higher characteristic X-ray energies a E−1 scaling was adopted. The simulations were performed for a proton micro-beam with a small cross section (2α = 1 µm), but the influence of a finite size micro-beam with comparable or even greater size than the lens FWHM, i.e. with 2α = 20 µm or 2α = 100 µm respectively, was also examined to estimate depth sensitivity of the technique.
In Fig. 6, the PIXE intensity profiles for a Ni foil of variable thickness are presented for a proton micro-beam width of 1 µm. The Gaussian like shape of the Ni intensity profiles can be described quite satisfactory by three experimental parameters; the height and the position of the maximum of the distribution together with the associated FWHM (considering a Gaussian function as a reasonably accurate fitting function). It is obvious that by increasing the foil thickness, the intensity at each position increases and the width of the distribution becomes slightly broader, whereas the position of the maximum of the distribution drifts to more positive y values (Table 1). It is characteristic, that by increasing the thickness of Ni foil, the yield at each target position and in particular at its maximum, follows the respective increase of the conventional PIXE yield (K = 1, y0 = 0 and ΔΩd = ΔΩl in eq. (15)) versus thickness (last column of Table 1).
Table 1 Parameters of the simulated Ni profiles (Fig. 6) deduced by means of the Gaussian fits. The values in the last column are normalized conventional PIXE yields (K = 1, y0 = 0 and ΔΩd = ΔΩl in eq. (15))
|
Ni µm |
Max.Height a.u. |
Max. Posit. mm |
FWHM µm |
PIXE Yield a.u. |
| 1 |
1.0 |
0.33 |
25.2 |
1.0 |
| 7 |
5.9 |
2.95 |
25.7 |
5.1 |
| 20 |
8.6 |
5.86 |
27.7 |
8.0 |
| 100 |
8.7 |
6.18 |
28.2 |
8.3 |
 |
| | Fig. 6 Simulation of confocal micro-PIXE intensity profiles for various thicknesses of pure Ni foils (E0 = 3 MeV, θb = 0°, θl = 45°, 2α = 1 µm, FWHMNiKα ∼ 18 µm). | |
The second example refers to a composite sample structure which consists of two layers with similar matrix composition (SiO2), the first one including 1% of Fe, while for the second layer three different Fe concentrations (1%, 2% and 10%) were introduced. In Fig. 7, the respective Fe intensity profiles versus sample position are plotted assuming different sizes for the proton micro-beam, namely 1, 20 and 100 µm, respectively. The higher in-depth concentration of Fe produces an intense asymmetric profile for positive y positions of the sample (i.e. as the set-up focus moves within the sample volume), that becomes more pronounced as the Fe concentration is increased in the second layer. However, for the largest proton microbeam size (2α = 100 µm), the intensity distribution appears with a rather smooth behavior, whereas the relative increase of Fe from 1 to 2% produces almost a negligible change in the shape and a rather small increase in Fe intensity, with respect to the profiles obtained with a proton micro-beam of much smaller size. These results provide a first insight into the dynamics of the confocal PIXE intensity profiles. Attempting a qualitative interpretation, the general trend of the intensity profiles discriminates clearly not only the homogenous case against the case with in depth Fe enrichment, but provides also extra information; the increased Fe concentration in the second layer is clearly associated with a second local maximum of the distribution versus sample position with an intensity quite sensitive to the actual Fe concentration. Considering a slightly different case, namely assuming Fe concentration equal to 1% only in the first 10 µm of a silicon oxide matrix (Fig. 8), the strong differentiation with the homogeneous case (with a constant 1% Fe concentration in the sample) is also evident regarding all the features of the simulated intensity profiles, such as the maximum position, the width at half maximum, the degree of asymmetry for positive y positions, etc.
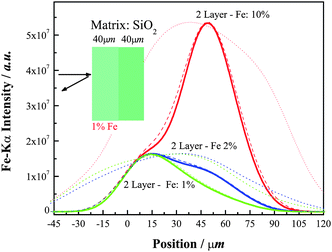 |
| | Fig. 7 Simulation of confocal micro-PIXE Fe-Kα depth profiles for a two-layered quartz matrix having 1% of Fe concentration in the first layer (40 µm) and various Fe concentrations (1, 2 and 10%) in the second layer. Calculations were done for three different widths of the microbeam: 1 µm (continuous line), 20 µm (dashed) and 100 µm (dotted), (E0 = 3 MeV, θb = 0°, θl = 45°, FWHMFeKα ∼ 20 µm). | |
 |
| | Fig. 8 Simulation of confocal micro-PIXE Fe-Kα depth profiles from a quartz sample of 10 µm thickness and of infinite thickness, respectively, (E0 = 3 MeV, θb = 0°, θl = 45°, 2α = 1 µm, FWHMFeKα ∼ 20 µm). | |
The sample and beam scanning modes were both selected to examine a three-layer pictorial sample structure. The proton-microbeam size was set equal to 1 µm. The first layer (d1 = 20 µm) is composed of 5% of azurite, the second (d2 = 30 µm) of 5% lead-tin yellow pigment, whereas the third layers consists of a 100% calcium carbonate substrate (d3 = 100 µm). The pigments of the first two layers have been diluted in an organic binder. The results are presented in Fig. 9a–f. From the positions of the maxima of the respective intensity profiles we can conclude in a rather straightforward manner the number of layers and the elemental composition of each layer, namely that a Cu based pigment composes the first layer, Pb coexists with Sn in the second layer, whereas the two first layers are placed on a Ca based substratum. The maxima of the intensity profiles of Pb-Mα, Sn-Lα and Pb-Lα characteristic X-rays differ for a few micrometers, mainly due to the higher self-absorption within the sample of the less energetic X-rays that shifts to the left the maximum of the corresponding profiles. Furthermore, the difference among Cu-Kα and Pb-Lα maxima (23.1 µm) provides a first good estimate for the quantity (d1 + d2)/2. Furthermore, if an experimental method is available for an accurate estimation of the confocal point and consequentially the y position of the sample, for example by using as reference the maximum of the intensity profile by an infinitely thin, single-element, surface layer, intentionally added onto the sample surface, a rather good estimate of the first layer thickness may result giving subsequently also the second layer thickness. These estimates are more reliable as the layer thicknesses become smaller, in the range of 10 µm or less. It is obvious that the confocal micro-PIXE technique shows one of its unique advantages for layered samples composed of different elements per layer.
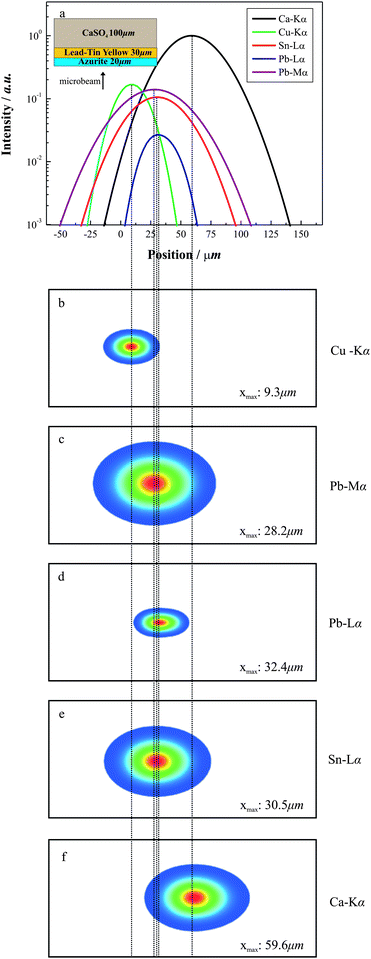 |
| | Fig. 9 Simulated confocal micro-PIXE data (intensity profiles and raster (2D) mappings) from the analysis of a multilayered paint sample, (E0 = 3 MeV, θb = 0°, θl = 45°, 2α = 1 µm). | |
Discussion—depth sensitivity of the confocal micro-PIXE
The simulations presented in the previous paragraph were performed for a constant impact proton energy and geometry, namely, beam, detector and sample orientations. The variation of these experimental parameters (differential confocal micro-PIXE) or at least their careful optimization for a specific application can certainly provide improved analytical information. For example, the optimum position of the detector with respect to the incident particle beam is the perpendicular direction in order to minimize the dimensions of the probing micro-volume. Further on, in a layered structured material, we can effectively increase the inter-layer thickness by tilting the sample towards the beam, i.e.θb → −90°. In order to examine the effect of the geometry, let's consider two quartz layers of 10 µm thickness each, containing 1% and 2% of Fe concentration, respectively. In Fig. 10 various Fe intensity profiles are presented for different set-up geometries. In the optimum case, the two branches that appear in the Fe intensity profile indicate in a rather straightforward manner the presence of two individual layers, the second one with an enhanced Fe concentration.
 |
| | Fig. 10 Simulated confocal micro-PIXE Fe-Kα depth profiles from a two layered quartz structure (10 µm each layer), using various geometrical arrangements (sample orientation with respect to the beam and lens axis direction, respectively, θb/θl) for the confocal setup (E0 = 3 MeV, 2α = 1 µm, FWHMFeKα ∼ 20 µm). | |
Simplifying the principal concept of the confocal micro-PIXE, we can summarize that it provides differential PIXE intensities as the probing micro-volume moves, either in the sample or the beam scanning mode, from outside the sample towards its depth. At each sample or beam position, the Gaussian like spatial response function of the probing micro-volume (for small beam sizes with respect to the lens focus), gives different weight to the conventional infinitesimal PIXE yield versus depth. A lot of similarities with the differential PIXE technique become apparent; in this method too, by varying the impact particle energy the probing depth is increased and the infinitesimal PIXE intensities versus depth are assigned with different weights for different impact proton energies and finally, the measured PIXE differential yield is obtained by integration of infinitesimal PIXE intensities. Although a global comparison between the two experimental techniques is outside the scope of the present work, it is useful to attempt a first comparative examination of their respective depth sensitivity. Therefore, we have determined the depth from which 90% of the measured PIXE yield originates with respect to the sample position (confocal set-up) or with respect to the proton impact energy (differential PIXE). The sample structure was taken the same as the one considered in the previous paragraph, i.e. a silicon oxide matrix that contains 1% of Fe concentration in the first layer (40 µm) and 2% in the second layer of the same thickness (Fig. 11a) or vice-versa (Fig.11b). In both figures, the sample position is indicated on the lower horizontal axis, whereas the proton impact energy is indicated on the upper horizontal axis. From these results it follows: a) the confocal micro-PIXE effectively probes deeper depths and b) in the confocal micro-PIXE technique the probing depth varies much sharper by changing the sample position than in the differential PIXE by changing the proton impact energy, since the gradient of the confocal micro-PIXE curve is much steeper, in particular at larger depths. Again, this comparison shows part of the inherent potential of the two techniques, since it neglects, in quantitative terms, the weight that each infinitesimal layer contributes to the measured PIXE yield. Therefore, let's consider within a quartz matrix that contains 1% of Fe concentration, a lamina of 3 µm thickness with increased Fe concentration (3%), placed at depth of 5 µm and 30 µm, respectively. In Figs. 12a and 12b the relative contribution of Fe Kα radiation with respect to the total PIXE Fe yield is indicated versus the sample position and versus the ion impact energy. Two different geometries were adopted in the case of the confocal micro-PIXE simulations. It is obvious and very characteristic that the Fe ‘anomaly’ in the case of the confocal micro-PIXE affects the measured Fe yield with higher sensitivity. More specifically, the partial contribution from the 3 µm lamina with 3% Fe concentration provides more enhanced but also localized contribution (with respect to the sample position) to the total Fe yield, whereas the optimum geometry in the confocal micro-PIXE set-up further improves the sensitivity.
 |
| | Fig. 11 Comparison for the in-depth probing sensitivity between confocal micro-PIXE and differential PIXE by means of the depth up to which 90% of the observed Fe-Kα PIXE yield originates. (Sample: two layers quartz matrix with 1 or 2% of Fe in the first or second layer −40 µm, E0 = 3 MeV, θb = 0°, θl = 45°, 2α = 1 µm, FWHMFeKα ∼ 20 µm). | |
 |
| | Fig. 12 Comparison of the in-depth probing sensitivity for the confocal micro-PIXE and the differential PIXE technique by estimation of the contribution of a local Fe inhomogeneity (3% in a lamina of thickness 3 µm) to the total Fe yield. (Sample: quartz matrix with 1% Fe concentration, E0 = 3 MeV, 2α = 1 µm, FWHMFeKα ∼ 20 µm, θb/θl = 0° /45° and θb/θl = −45° /45°). | |
The present model has been applied for the real stratified materials19,20 in order to produce theoretical intensity profiles that fit the experimental one. This way it was possible to suggest a local Fe inhomogeneity in a glazed ancient ceramic sample,19 or to describe the in-depth concentration profile of elements associated with corrosion products developed artificially onto the surface of a copper alloy.20 The next step is to proceed and develop a reconstruction algorithm that it based on a χ2 minimization procedure between the model and experimental confocal micro-PIXE data.
A model for a confocal micro-PIXE analysis aiming to reconstruct 3D element-specific local distributions has been very recently proposed by Žitnik et al.21,32 To achieve this, both scanning modes should be experimentally combined, whereas the sample is divided in microscopic cubic cells. The formulation offers in quantitative terms the contribution of each cubic cell to the element specific intensity recorded per pixel from sequential 2D-images produced at each sample position by the microbeam scanning mode. The authors have applied this formalism in the case of PM10 aerosol particles immersed into a very low density matrix (quartz filter) and determined positions and relative concentrations of dust particles.32
Conclusions
We have developed a quantitative model that describes confocal micro-PIXE data for stratified materials. The model incorporates the effect of the finite ion micro-beam dimensions and the restricted spatial resolution of an X-ray lens to generate the sensitivity function of the confocal set-up probing micro-volume in a closed form. The Gaussian-like dependence of the sensitivity function has been validated for the case that the proton micro-beam size is much smaller than the lateral size of the lens field of view in the focal point. The model is applicable for both scanning modes that may be implemented in the analysis of a stratified material, namely either the sample movement or the beam lateral scanning. Among the experimental parameters, the angles that the beam direction forms with the sample surface and the detector, respectively, are critical and may improve considerably the sensitivity of the confocal micro-PIXE technique. For various cases of stratified materials, the simulated intensity profiles and 2D elemental maps have demonstrated that even the raw confocal micro-PIXE data include unique analytical information that may provide first clues for the structure of the analyzed sample. In comparison with differential PIXE, in principle, the confocal micro-PIXE technique seems to exhibit an enhanced sensitivity in respect to the spatial resolution that should be proved in practice by the analysis of the same real sample by both techniques in the future.
References
- C. Neelemeijer, W. Wagner and H. P. Schramm, Nucl. Instr. and Meth. B, 1996, 118, 338 CrossRef CAS.
- C. Neelemeijer and M. Mäder, Nucl. Instr. and Meth. B, 2002, 189, 293 CrossRef.
- G. Weber, J. M. Delbrouck, D. Strivay, F. Kerff and L. Martinot, Nucl. Instr. and Meth. B, 1998, 139, 196 CrossRef CAS.
- G. Demortier and J. L. Ruvalcaba-Sil, Nucl. Instr. and Meth. B, 1996, 118, 352 CrossRef CAS.
- P. Midy and I. Brissaud, Nucl. Instr. and Meth. B, 1995, 103, 489 CrossRef CAS.
- I. Brissaud, G. Lagarde and P. Midy, Nucl. Instr. and Meth. B, 1996, 117, 179 CrossRef CAS.
- G. Lagarde, P. Midy and I. Brissaud, Nucl. Instr. and Meth. B, 1997, 132, 521 CrossRef CAS.
- Ž. Šmit and M. Holc, Nucl. Instr. and Meth. B, 2004, 219–220, 524 CAS.
- Ž. Šmit, J. Istenič and T. Knific, Nucl. Instr. and Meth. B, 2008, 266, 2329 CrossRef CAS.
- Ž. Šmit, M. Uršič, P. Pelicon, T. Trček-Pečak, B. Šeme, A. Smrekar, I. Langus, I. Nemec and K. Kavkler, Nucl. Instr. and Meth. B, 2008, 266, 2047 CrossRef CAS.
- B. Kanngießer, W. Malzer and I. Reiche, Nucl. Instr. and Meth. B, 2003, 211–212, 259 CrossRef.
- B. Kanngießer, W. Malzer, A. Fuentes Rodriguez and I. Reiche, Spectrochim Acta B, 2005, 60, 41 CrossRef.
- B. Kanngießer, I. Mantouvalou, W. Malzer, T. Wolff and O. Hahn, J. Anal. At. Spectrom., 2008, 23, 814 RSC.
- A. R. Woll, J. Mass, C. Bisulca, R. Huang, D. H. Bilderback, S. Gruner and N. Gao, Appl Phys A, 2006, 83(2), 235 CrossRef CAS.
- K. Janssens, K. Proost and G. Falkenberg, Spectrochim Acta B, 2004, 59, 1637 CrossRef.
- B. M. Patterson and G. J. Havrilla, American Laboratory, 2006, 38(8), 15 Search PubMed.
- W. Malzer and B. Kanngießer, Spectrochim Acta B, 2005, B60(9–10), 1334 CrossRef.
- I. Mantouvalou, W. Malzer, I. Schaumann, L. Lühl, R. Dargel, C. Vogt and B. Kanngießer, Anal. Chem., 2008, 80, 819, DOI:10.1021/ac701774d.
- A. G. Karydas, D. Sokaras, Ch. Zarkadas, N. Grlj, P. Pelicon, M. Žitnik, R. Schütz, W. Malzer and B. Kanngießer, J. Anal. At. Spectrom., 2007, 22, 1260 RSC.
- B. Kanngießer, A. G. Karydas, R. Schütz, D. Sokaras, I. Reiche, S. Röhrs, L. Pichon and J. Salomon, Nucl. Instr. and Meth. B, 2007, 264, 383 CrossRef.
- M. Žitnik, P. Pelicon, N. Grlj, A. G. Karydas, D. Sokaras, R. Schütz and B. Kanngießer, Appl. Phys. Lett., 2008, 93, 094104, DOI:10.1063/1.2976163.
- K. Proost, L. Vincze, K. Janssens, N. Gao, E. Bulska, M. Schreiner and G. Falkenberg, X-Ray Spectrom., 2003, 32, 215 CrossRef CAS.
- J. Gormley, T. Jach, E. Steel and Q.-F. Xiao, Adv. X-Ray Anal., 1997, 41, 239.
- N. Gao and I. Ponomarev, X-Ray Spectrom., 2003, 32, 186 CrossRef CAS.
- M. Haschke and M. Haller, X-Ray Spectrom., 2003, 32, 239 CrossRef CAS.
- T. Wolff, I. Mantouvalou, W. Malzer, J. Nissen, D. Berger, I. Zizak, D. Sokaras, A. G. Karydas, N. Grlj, P. Pelicon, R. Schütz, M. Žitnik and B. Kanngießer, J Anal. At. Spectrom., 2009 10.1039/b817828c.
- J. L. Campbell and J. A. Cookson, Nucl. Instr. and Meth. B, 1984, 3, 185 CrossRef.
- Z. Liu and S. J. Cipolla, Comp. Phys. Comm., 1996, 97, 315 Search PubMed.
- S. J. Cipolla, Comp. Phys. Comm., 2007, 176, 157 Search PubMed.
-
J. F. Ziegler, J. P. Biersack and U. Littmark, The stopping and range of ions in solids, The Stopping and Ranges of Ions in MatterVol. 1, Pergamon Press, New York, 1985 Search PubMed.
- W. T. Elam, B. D. Ravel and J. R. Sieber, Radiat. Phys. Chem., 2002, 63, 121 CrossRef CAS.
-
M. Žitnik, P. Pelicon, N. Grlj, A. G. Karydas, D. Sokaras, R. Schütz, and B. Kanngießer, submitted.
|
| This journal is © The Royal Society of Chemistry 2009 |
Click here to see how this site uses Cookies. View our privacy policy here.