The green solvent ethyl lactate: an experimental and theoretical characterization

Abstract

Ethyl lactate is a green, and economically viable, alternative to traditional solvents whose extensive use and scale-up to industrial level requires a deep and accurate knowledge of its properties in wide pressure–temperature ranges. In this work, the pressure–volume–temperature and pressure–viscosity–temperature behaviors are reported together with several derived properties of remarkable importance for process design purposes. The structure of the liquid is analyzed at the microscopic level using the Density Functional Theory and from classical molecular dynamics simulations. It is shown the competing effect of intra and intermolecular hydrogen bonding mainly through preferred positions. The predictive ability of the forcefield used for molecular dynamics simulations is studied, showing good results for most of the considered properties. Monte Carlo/Gibbs ensemble simulations were carried out to predict the phase equilibria of the fluid, considering the absence of experimental data.

---

Introduction

The problem of solvents is ubiquitous to most of the chemical and related industries,¹ because they are present not only for production and purification purposes but they appear also in the final products, thus they affect the whole product cycle. The world demand of solvents is forecasted to increase in the next years,^2,3 and although the use of compounds with strong effects on the environment will decrease,² as a consequence of international regulations, the industrial needs will lead to an increased demand of new fluids. The use of solvents is at a multi-ton scale, the world demand is approaching 20 million metric tons per year.³ Together with the volatile character and very poor environmental and toxicological profiles of the most commonly used compounds, there is a need for alternative solvents that may replace the present ones.^1,4–6 Several approaches within the green chemistry framework have been proposed in the last few years;¹ supercritical fluids and ionic liquids being the most promising and extended ones among academia, if specialized literature is analyzed.^7,8 In spite of the promising characteristics of these alternative fluids, their extension to large scale industrial applications is very scarce nowadays, especially for ionic liquids.⁹ Moreover, the technological and economical viability of these alternative solvents is still under study and thus their extension to large-scale industrial processes would not be straightforward and it would require several years together with systematic and costly studies. Hence, other alternative organic solvents, with characteristics more similar to the traditional ones, may be considered and studied if their properties are adequate both from technological and environmental viewpoints. The industrial replacement of traditional solvents for these alternative organic solvents may be faster considering that the technologies required for their use are similar to the present ones and thus the economical costs of the replacement would be lower than for the other alternatives. Moreover, the industry probably would be less reluctant to get involved in the transition toward these solvents because of their similarities to the present ones.

Among these alternative organic solvents with adequate properties, ethyl lactate (EL) is one of the most promising ones.¹⁰EL is the main member of the lactate esters family. It has very favourable toxicological properties,¹¹ it does not show any potential health risks, it is not teratogenic, and it readily undergoes metabolic hydrolysis because of estearase enzymatic activity to ethyl alcohol and lactic acid, this last compound being a natural metabolite in humans. Moreover, the low toxicity of EL may be inferred from its FDA (USA Food and Drug Administration) approved use in food products. The ecotoxicity of EL is very low,¹² and thus its environmental profile is very adequate considering that it is completely biodegradable in a very short time. In case of vapors release, EL is a non-ozone depleting fluid. From an economical viewpoint, the replacement of traditional solvents by EL is clearly favoured considering that the recently developed technologies^13–16 allow its production from carbohydrate feedstocks at very low and competitive prices. Moreover, the use of carbohydrates as a starting point in its production leads to a renewable product, and thus sustainable, not rising from petrochemical sources. The reduced energy use in its production decreases its costs but also the effect on the environment. Moreover, the production of EL from carbohydrate feedstocks is not a competition to food because low-cost agricultural waste may be considered as a source of carbohydrates. Although the open literature on uses of EL, pure or mixed, is not very extensive, reported results show that it may be applied successfully for different processes as its used as a cleaning solvent,¹⁷ for the manufacturing of magnetic¹⁸ and electronic devices,¹⁹ or for applications ranging from the pharmaceutical²⁰ to the paint industries.²¹

The replacement of any solvent by a new one requires a deep and accurate knowledge of the properties for the selected candidate in wide pressure/temperature ranges to carry out cost-effective and reliable process design for the application required,²² thus allowing to keep the production targets. A detailed analysis of the literature shows that thermophysical data for EL are almost absent, only some properties at conditions close to the ambient ones may be found.^23–26 This absence of reliable information hinders any development of processes for EL, and thus the main objective of this work is to provide these values. The measurement of properties as a function of pressure and temperature is very time consuming and economically costly,²⁷ thus the studied properties have to be selected according to their importance, both from practical and basic science purposes. In this work, the results of pressure–volume–temperature (PVT) and pressure–dynamic viscosity–temperature (PηT) studies on EL are reported. PVT measurements were carried out considering they provide most of the thermodynamic information for the studied fluid, and the values of density and derived coefficients such as isothermal compressibility of thermal expansion coefficients are required for many industrial purposes. Moreover, the knowledge of the PηT behavior, and of its derived pressure and temperature coefficients, is of great importance for any fluid, considering how this property affects the heat or mass transfer processes or their use in the design of relevant operations such as fluids pumping or boilers.

Although the experimental measurement of physical properties is the most accurate and straightforward way of getting the required data, the theoretical prediction of these properties is also very important considering the cost of measurements and the impossibility of obtaining values for all the possible conditions. Thus, in this work a theoretical study is carried out with two main objectives: (i) to analyze the molecular level structure of EL studying its hydrogen-bonding ability and (ii) to develop predictive tools that allow to infer microscopic structure/macroscopic properties relationships. This theoretical study would provide valuable information on the way that EL molecules develop intermolecular interactions, their effect on the fluid structure, and thus a basis on which to analyze the effect of possible solute molecules on fluid EL properties and thus the solvent ability of EL. The theoretical study was carried out using three different approaches: (i) Density Functional Theory (DFT), to study the short range interactions and the energetics and structure of EL molecules, (ii) classical molecular dynamics simulations (MD), to study the long-range fluid structure and to provide a predictive tool for the EL macroscopic properties and (iii) Monte Carlo simulations, to predict phase equilibria.

As the S-enantiomer is the prevailing one, in this study, all the experimental and theoretical studies were performed only for this isomer.

Results and discussion

Density Functional Theory computations

The optimized structure of EL in the gas phase calculated at the B3LYP/6–311++g** theoretical level is reported in Fig. 1. The main feature that should control the EL liquid structure is its ability to develop intra (among the hydroxyl hydrogen and carbonyl and/or alkoxy oxygens) and intermolecular hydrogen bonding. The ability to develop intramolecular hydrogen bonding relies on the relative position of the hydroxyl hydrogen respective to the oxygens in the EL molecule. It has been previously reported for the smallest member of the lactate family, methyl lactate (ML),²⁸ that in the gas phase: (i) hydroxyl groups tends to eclipse carbonyl groups, and thus intramolecular interaction is preferentially developed with the carbonyl oxygen, and (ii) intramolecular hydrogen bonding among hydroxyl hydrogen and carbonyl oxygen is strong and the out-of-plane movement of the hydroxyl hydrogen, that weakens the interaction, evolves through a large torsional barrier. Nonetheless, this barrier decreases on going to solution because of the competing effect of possible intermolecular interactions. Results reported in Fig. 1 show the behavior for EL very close to that previously reported for ML, the distance and angle between the hydroxyl hydrogen and carbonyl oxygen allows the development of strong intramolecular hydrogen bonding. The electrostatic potential energy surface (ESP) shows regions of negative values for hydroxyl and carbonyl oxygens, whereas the alkoxy oxygen is clearly embedded within the positive, hydrophobic, region rising from the ethyl chain. Hence, the interaction among hydroxyl and carbonyl groups should be preferred than the possible one between hydroxyl and alkoxy groups; the increase of the alkyl chain length in comparison with ML²⁸ reinforces the preference for the first interaction position. The dipole moment calculated for EL is 10.5% larger than for ML,²⁸ this is in agreement with the effect rising from the larger alkyl chain.

Fig. 1 Optimized gas phase structure of the most stable, lower energy, conformer for EL monomer computed at the B3LYP/6–311++g** theoretical level. Atom color code: gray = carbon, white = hydrogen, and red = oxygen. Arrow shows calculated dipole moment whose value is also reported in the Figure. Dashed line shows intramolecular hydrogen bonding. Electrostatic potential mapped on an electronic density surface isovalue of 0.0005 au is reported together with the map color legend.

The infrared spectra was also computed for the optimized geometry reported in Fig. 1, the hydroxyl stretching band was obtained at 3550.8 cm⁻¹, this band is in good agreement with the experimental gas phase value reported in the literature for the monomer (3562 cm⁻¹).²⁹ The theoretical values obtained for EL are red-shifted by 3.3 cm⁻¹ in comparison with ML,²⁸ which is in agreement with the experimental 3.5 cm⁻¹ red-shifting.²⁹ This red-shifting correlates with the slight increase for O–H distance (0.0001 Å) on going from ML to EL, and thus it shows a slightly stronger intramolecular hydrogen bond for EL probably due to inductive effects²⁹ because of the larger alkyl chain. The comparison among theoretical and literature²⁹infrared spectra show that in the gas phase the monomer structure reported in Fig. 1 prevails over other possible isomers.²⁸ Although gas results provide valuable structural information on EL, it has been previously reported²⁸ the strong effect of surrounding media on lactate intramolecular hydrogen bonding. This effect was studied using the IEF-PCM approach in which the solvent media are treated as a continuum. Hence, in Fig. 2 we report the variation of the O–H stretching frequency for the EL monomer, as a function of the dielectric constant used to simulate the solvent. To allow a straightforward comparison, the structure reported in Fig. 1 was directly calculated for different values of the dielectric constant without optimization. The experimental value of dielectric constant for EL is 15.70 at 298.15 K,²³ thus it is a moderately polar solvent. The increasing dielectric constant leads to a red-shifting of the O–H stretching frequency in comparison with gas phase values. If we compare the gas value for EL and the value obtained when EL molecules are surrounded by a continuous media, which dielectric constant is that of EL, a 39.1 cm⁻¹ red-shifting is obtained, and thus intramolecular hydrogen bonding seems to be strengthened in going to solution. But this is a simplified view of the problem, because when the dielectric constant of the surrounding media increases, the hydroxyl hydrogen tends to move out of plane, and thus the development of intramolecular hydrogen bonding is hindered in spite of the red-shifting obtained. Moreover, this effect is reinforced if the molecules of the surrounding media are able to act as acceptor/donors of hydrogen bonding, although this effect can not be analyzed through the IEF-PCM approach because it considers a continuous surrounding media instead of a discrete molecular one. Thus, we have calculated the optimized structures of EL as a function of the dielectric constant of the surrounding media, the values of the dihedral angle that shows the position of the hydroxyl hydrogen regarding the carbonyl oxygen (8–7–6–9 in Fig. 1) are reported in Fig. 3. Results reported show that as the polarity of the surrounding media increases, the dihedral angle first increases sharply (up to ∼ε = 10) and then slowly, reaching an asymptotic value of 57.5°. This dihedral is 49.90° when ε = 15.7, and thus the position of the hydroxyl hydrogen in a fluid, which polarity mimics that of EL is clearly out of plane, hence intramolecular hydrogen bonding is remarkably weakened and hydroxyl hydrogens would be able to develop intermolecular hydrogen bonding with neighbour EL molecules. This is in agreement with the increasing O–H distance with increasing ε, Fig. 3, and with the large red-shifting obtained for its stretching frequency (258.1 cm⁻¹ on going from ε = 1 to ε = 79). Nonetheless, this interpretation has to be confirmed with the molecular dynamics results, in which EL molecules are treated explicitly instead of the continuum model used to describe the surrounding medium in IEF-PCM approach.

Fig. 2 O–H stretching IR vibrational frequency in EL monomer computed at the B3LYP/6–311++g** theoretical level using and IEF-PCM approach as a function of the dielectric constant, ε, of the solvent. Dielectric constant for EL obtained from ref. 23. Frequency scaled with a factor 0.96. Data calculated for the structure reported in Fig. 1 without optimization.

Fig. 3 (●) 8–7–6–9 dihedral angle, and (■) O7–H8 bond distance, in EL computed at the B3LYP/6–311++g** theoretical level using and IEF–PCM approach as a function of the dielectric constant, ε, of the solvent. Values obtained from structure optimization for each value of the dielectric constant. Atom numbering as in Fig. 1.

To analyze the characteristics of the intramolecular hydrogen bonding in EL monomer in more depth, we have carried out Atoms in Molecules (AIM)³⁰ and Natural Bond Orbital (NBO)³¹ studies; all the calculations were done for the monomer optimized structure in the gas phase, Fig. 1. Results of AIM calculations are summarized in Fig. S1 (ESI),† the first evidence of H-bonding according to the AIM formalism is the existence of a bond path between two atoms and the existence of a bond critical point, BCP, in the middle of the path.^32,33 The molecular graph reported in Fig. S1a (ESI)† keeps the Lewis bonding scheme in the molecule, intramolecular H-bonding between H8 and O10 positions is clearly inferred from this Figure. A second AIM criterion according to the AIM formalism to define an H-bond considers that electron density at BCP, ρ_BCP, and the laplacian of that electron density, ∇²ρ_BCP, must be within the 0.002–0.035 and 0.024–0.139 ranges, respectively, (both in atomic units);^32,33 this criterion is also fulfilled by the H8⋯O10 interaction. The values of ρ_BCP and ∇²ρ_BCP for the H8⋯O10 are large, and thus this is a strong H-bond (ρ_BCP and ∇²ρ_BCP are ∼70% of the top limit in the defined ranges). The ∇²ρ_BCP is reported in Fig. S1b (ESI)† close to the studied intramolecular H-bond, we should remember that ∇²ρ_BCP < 0 shows charge concentration, whereas ∇²ρ_BCP > 0 indicates charge depletion. The large charge depletion between H8 and O10 corresponds to the strong H-bond, however the charge concentration on H8 is not polarised toward O10.

NBO analysis provides valuable information on the energy of H-bonds. The interaction O7–H8⋯O10 should be determined by the hyperconjugation induced charge transfer between the O10 electron lonely pairs (donor) and the antibonding orbitals for the O7–H8 bond (acceptor), n_O→σ*_O–H. This hyperconjugation effect is analyzed in Fig. S2 (ESI),† the calculated second order perturbation energy, E(2), is surprisingly low for the charge transfer of both oxygen lone pairs. For the first lone pair, E(2) < 0.5 kcal mol⁻¹, the interaction between the orbital for this pair and that for σ*_O–H is clearly hindered both because of the shapes and phases reported in Fig. S2 (ESI);† moreover, the orbital for the lone pair has a 59/41% s/p relationship, whereas for σ*_O–H it is 80/20%. For the second lone pair, a larger value of E(2) is obtained, and although this value would contribute to stabilize the hydrogen bond, it is low considering the small value for the energy difference among the donor and the acceptor, Fig. S2 (ESI).† The orbital for the second oxygen lone pair is almost a pure p orbital, 0.1/99.9% s/p relationship, and thus its properties are very different to those for σ*_O–H, hence although hyperconjugation is produced for this H-bond, it is not as high as for other H-bonds. Moreover, the Fock matrix element between the donor and acceptor NBO orbitals, F_ij, is very low, Fig. S2 (ESI),† which is the main reason of the low E(2) values.

As both in gas and liquid phases EL would be composed not only by monomers but also by multimers, several association complexes formed by 2, 3 and 4 EL molecules are also analyzed and reported in Fig. 4. Several dimers may be considered for EL, with different topologies and thus with different H-bonding strengths. We report the two most stable calculated structures, Fig. 4: (i) symmetric dimers with two reciprocal O–H⋯C=O interactions leading to an 8-ring structure (2A) and (ii) dimers rising from the insertion of the O–H group of a molecule into the intramolecular H-bond of a second one leading to a disrupted 5-ring structure (2B). 2A dimer is slightly more stable than 2B, this is in agreement with literature results,²⁹ although the energy difference between both dimers reported here (0.37 kcal mol⁻¹) is lower than the one previously calculated (1.20 kcal mol⁻¹ at B3LYP/6–31g* or 2.39 kcal mol⁻¹ at MP2/6 + 31 + g* theoretical levels),²⁹ probably due to a larger basis set used in this work. In dimer 2A both H-bonds are totally symmetric and with the same length, whereas for 2B one of the H-bonds is larger, and thus weaker. The calculated IR spectra for both dimers is in good agreement with the experimental one, a value of 3483.6 cm⁻¹ is calculated for the asymmetric O–H stretching band, which experimental value is 3517 cm⁻¹.²⁹ For 2B, two peaks are calculated at 3433.9 and 3514.5 cm⁻¹, the assignment of experimental bands for this dimer is not totally resolved but several peaks in the 3500–3550 cm⁻¹ are obtained.²⁹

Fig. 4 Optimized gas phase structures of the most stable, lower energy, multimers of EL computed at the B3LYP/6–311++g** theoretical level. Atom color code: gray = carbon, white = hydrogen, and red = oxygen. ΔE = counterpoise corrected binding energies in kcal mol⁻¹. Distances in Å.

The AIM analysis of dimers is reported in Fig. 5 and Table 1, results support the existence of bond paths that define H-bonds for both dimers. For 2A, both H-bonds are totally equivalent as the values of ρ_BCP and ∇²ρ_BCP show, these values are large and point to strong H-bonding. BCPs for O5⋯H31 and O19⋯H13 interactions, Fig. 5, are well defined by the behavior of the Laplacian of electron density reported in Fig. 5, the contour plots for both H-bonds are equivalent, thus justifying their similarities. The study of 2B dimer shows that the two H-bonds involved are disimilar, the O24–H31⋯O3 interaction (hydroxyl–hydroxyl type) is clearly stronger than the O3–H13⋯O19 one (hydroxyl–carbonyl type), Table 1. ∇²ρ shows a stronger charge concentration in the region between donor and acceptor for the hydroxyl–hydroxyl interaction, which is also inferred from the larger ρ_BCP. NBO analysis for both dimers supports AIM conclusions, Table 2. For 2A dimer, the hyperconjugation induced charge transfer between acceptor and donor is equivalent for both H-bonds. Moreover, for each H-bond the calculated second order perturbation energy for each oxygen donor pair is almost equivalent, because although for the first pair the energy difference between donor and acceptor is larger, F_ij is also larger. For 2B dimer, E(2) values are clearly larger for the hydroxyl–hydroxyl interaction, being the E(2) associated with the second oxygen donor pair remarkably larger. This large E(2) value is the main cause of the stronger H-bond for the hydroxyl–hydroxyl interaction in 2B, and of the small energetic difference between 2A and 2B dimers, Fig. 4. The molecular origin of this large E(2) value is in the large F_ij, the symmetry of donor and acceptor orbitals allow an efficient charge transfer between them.

Table 1 AIM analysis of EL multimers computed in gas phase at the B3LYP/6–311++g** theoretical level. Electron density at BCP, ρ_BCP, Laplacian of electron density at BCP, ∇²ρ_BCP, for the H-bonds. Multimers as in Fig. 6 and 7

	H-bond	ρ BCP /a.u.	∇^2ρBCP/a.u.	H-bond	ρ BCP /a.u.	∇^2ρBCP/a.u.	H-bond	ρ BCP /a.u.	∇^2ρBCP/a.u.	H-bond	ρ BCP /a.u.	∇^2ρBCP/a.u.
2A	O5⋯H31	0.023	0.089	O19⋯H13	0.023	0.089	—	—	—	—	—	—
2B	O3⋯H31	0.027	0.096	O19⋯H13	0.018	0.067	—	—	—	—	—	—
3	O8⋯H27	0.023	0.077	O22⋯H45	0.029	0.091	O40⋯H9	0.025	0.082	—	—	—
4	O40⋯H9	0.022	0.076	O22⋯H45	0.025	0.089	O58⋯H27	0.024	0.078	O8⋯H63	0.023	0.078

---

Table 2 NBO analysis of EL multimers computed in the gas phase at the B3LYP/6–311++g** theoretical level. Second order perturbation energy, E(2), energy difference among the donor and the acceptor, ΔE, and Fock matrix element between the donor and acceptor, F_ij. Multimers as in Fig. 5. All hyperconjugation induced charge transfers are of n_O→σ*_O–H type, from the oxygen lone pairs (pair 1 or 2) to corresponding antibonding O–H orbital

	Donor	Donor pair	Acceptor	E(2)/kcal mol^−1	ΔE/a.u.	F ij /a.u.
2A	O5	Pair 1	H31–O24	3.74	1.16	0.059
		Pair 2		3.82	0.74	0.049
	O19	Pair 1	H13–O3	3.73	1.16	0.059
		Pair 2		3.81	0.74	0.049
2B	O3	Pair 1	H31–O24	2.10	0.98	0.041
		Pair 2		8.18	0.81	0.073
	O19	Pair 1	H13–O3	1.40	1.13	0.036
		Pair 2		1.86	0.70	0.033
3	O8	Pair 1	H27–O22	3.54	0.97	0.052
		Pair 2		6.23	0.80	0.064
	O22	Pair 1	H45–O40	1.79	0.96	0.037
		Pair 2		12.50	0.81	0.090
	O40	Pair 1	H9–O8	2.23	0.97	0.042
		Pair 2		8.83	0.81	0.076
4	O8	Pair 1	H63–O58	3.40	0.93	0.050
		Pair 2		5.98	0.77	0.061
	O40	Pair 1	H9–O8	1.72	0.92	0.036
		Pair 2		12.00	0.78	0.086
	O22	Pair 1	H45–O40	2.14	0.93	0.040
		Pair 2		8.48	0.78	0.073
	O58	Pair 1	H27–O22	3.40	0.93	0.051
		Pair 2		5.88	0.76	0.061

---

Fig. 5 AIM analysis for EL multimers. (a) Molecular graphs; small red dots represent bond critical points (BCP), small yellow dots represent ring critical points (RCP), pink lines represent bond paths, yellow lines represent ring paths, large dots represent attractors (atoms). (b) Contour plot for the Laplacian of electron density, ∇²ρ, in the vicinity of several hydrogen bonds; red dot represents BCP for hydrogen bonding, red dashed line represents bond path for hydrogen bonds, green curves represent positive isosurface values of ∇²ρ and black curves represent negative isosurface values of ∇²ρ.

Trimers and tetramers are reported in Fig. 4, large stabilization energies are obtained for both complexes. H-bonds are formed through hydroxyl/hydroxyl interactions leading to cyclic structures. The AIM analysis of the cyclic trimer shows that the three H-bonds are very similar from a topological viewpoint, Table 1, only the interaction for O22⋯H45 position shows a slightly stronger interaction. Nevertheless, the shapes of the contour plots for the Laplacian of electron density, Fig. 5, show almost equivalent charge depletions between donors and acceptors for the three H-bonding positions. NBO results reported in Table 2 for the trimer confirms the AIM results, the calculated second order perturbation energy for the O22⋯H45 interaction is stronger, although the energy difference between donor and acceptor is equivalent for the three H-bonds, the larger F_ij value for the O22⋯H45 position justifies this behavior because of the shapes and phases of the involved orbitals. Moreover, the interaction with the first lone pair of oxygens for the three H-bonds is clearly less efficient than with the second pair because of the larger energy difference between donor and acceptor and their lower orbital symmetry. Results for the cyclic tetramer are analogous to those for the trimer, AIM analysis shows symmetric charge depletions for all the H-bonds, and NBO results point to preferred interactions through the second oxygen lone pair for the four positions.

Thermophysical properties

The pressure/temperature effect on the main properties of EL (in the ranges of 278.15–358.15 K and 0.1–60 MPa, for density, or 1–70 MPa, for dynamic viscosity) are reported in Tables S1–S5 (ESI)† and Fig. 8–10. Fitting coefficients of density according to the TRIDEN equation³⁴ and of dynamic viscosity with a Tait-like equation are also reported.³⁵

Fig. 6 (●) Experimental density, ρ, and calculated isobaric thermal expansivity, α_P, isothermal compressibility, k_T, and internal pressure, P_i, as a function of pressure, P, for different temperatures. Lines: TRIDEN fitting function for density (parameters from Table S2, ESI)† and guide-lines for the remaining properties. Arrows indicate increasing temperature: 278.15 to 358.15 K in 10 K steps.

Fig. 7 Free volume, V_F, of liquid EL, estimated from the Sanchez-Lacombe equation of state with parameters from Table 2. (a) Panel shows isothermal results with the arrow indicating increasing temperatures (from bottom to top), (b) Panel shows isobaric results with the arrow indicating increasing pressures (from top to bottom) and (c) panel shows relationship between V_F and relaxation amplitude for multimeric associates obtained from DRS studies²³ at 0.1 MPa with the arrow indicating increasing temperatures (from right to left).

Fig. 8 (●) Experimental dynamic viscosity, η, as a function of pressure, P, and temperature, T, for EL. From top to bottom in (a) 278.15 to 358.15 K in 10 K steps and (b) 70, 60, 50, 40, 30, 20, 10 and 1 MPa. Lines: fitting function (parameters from Table S4, ESI).† Arrows indicate (a) increasing temperature and (b) increasing pressure.

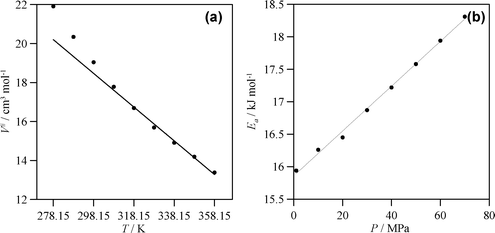Fig. 9 (a) Activation volume, V^#, and (b) Arrhenius activation energy, E_a, calculated from eqn (3) and Arrhenius equation for experimental viscosity data reported in Table S3 (ESI).† Lines: linear fits. In (a) linear fit for T > 298.15 K to show deviations at lower temperatures.

Fig. 10 Comparison between (●) experimental and (○) calculated density, ρ, and isobaric thermal expansivity, α_P, for EL at 0.1 MPa as a function of temperature. Simulated values, sim subindex, calculated from OPLS-AA molecular dynamics. Continuous lines showed for guiding purposes.

Literature density data for EL are very scarce,^24–26 and, to our knowledge, all the reported values have been measured only at atmospheric pressure, hence a full comparison with our data is not possible. Nevertheless, percentage deviations of our 0.1 MPa density data (close to atmospheric conditions) with literature data are very low, thus deviations of 0.03% with the data reported in ref. 25 at 298.15 K and 0.08, 0.12 and 0.11% with the data reported in ref. 24 at 298.15, 308.15 and 318 K, respectively, are obtained. Literature viscosity data are even scarcer, the extrapolation of our data to 0.1 MPa leads to a value 5% larger than the value reported in ref. 24 and 3% larger than the one reported in ref. 36, both at 298.15 K.

Density increases with pressure for isotherms and decreases with temperature for isobars, Fig. 6a, as we may expect. Density values are relatively large, thus pointing to an efficient packing, both by steric and intermolecular interaction effects. To obtain more information about the EL structure from PVT data, the Sanchez-Lacombe³⁷ equation of state, SL-EOS, was applied, with its parameters obtained from least-squares fitting of experimental density results, Table 3. SL-EOS has proved to be useful for the description of PVT behavior for many different fluids,^38–40 although it is a purely physical lattice-fluid model it allows valuable information on the efficiency of the molecular packing and on the available free volumes in the fluids to be inferred, this information being obtained from the fitted model parameters. Very low percentage deviations are obtained for EL, despite the simplicity of the model and considering that it is a three-parametric EOS, thus this simple EOS is able to represent accurately the behavior of this complex fluid over the wide pressure/temperature ranges studied. The molar hard-core volume is the main parameter obtained from the SL-EOS analysis; it may be interpreted as the total volume, without free space, of one mole of particles. Thus, the free volume, V_F, in liquid EL can be obtained from eqn (1):

V_F = V−υ*r (1)

Table 3 Parameters of Sanchez-Lacombe equation of state obtained by fitting to experimental PVT data for EL. T*, P*, ρ* reducing characteristic parameters, r segment number of one molecule, ε* segment interaction energy, υ* segment volume and %AAD percentage absolute average deviation of the fitting to experimental data

^a P*/MPa	^a r	^a ε*/J mol^−1	^b T*/K	^b ρ*/kg m^−3	^b υ*/cm^3 mol^−1	^bHard-core volume (υ*×r)/cm^3 mol^−1	%AAD
a Fitted parameters. b Calculated parameters.
549.2	13.0	4295.3	516.6	1160.4	7.82	101.7	0.09

---

Where V is the experimental molar volume, for each temperature and pressure, and υ*r is the hard-core volume from SL-EOS, Table 3. Free volume is a very important property for any solvent because it is strongly related with properties such as gas solubility or solute solvation. V_F reported in Fig. 7, shows moderate values increasing with temperature and decreasing with pressure. The available V_F can be related with three main factors: (i) esteric effects, that contribute to increase it, (ii) the extension of hydrogen bonding, that decrease V_F and (iii) the dynamics of these interactions. The shape of EL allows an efficient packing through intermolecular interactions, H-bonded complexes, Fig. 4, lead to low void spaces because of the preferred orientations of EL molecules. The extension of hydrogen bonding interactions should determine the efficiency of the packing. Although any EL molecule can develop H-bonds through three different positions (carbonyl oxygen, alkoxy oxygen and hydroxyl group), and thus a hydrogen bonding dynamic network with high cooperativity of remarkable cohesive nature may be obtained, previously reported dielectric relaxation spectroscopy, DRS, results have discarded the existence of associates larger than tetramers,²³ which is in agreement with the moderate free volumes. In fact, there is a strong linear correlation among the intensity of the relaxation amplitude of the DRS peak assigned to multimers and the values of free volume, Fig. 7c, thus showing how the extension of multimers’ aggregation determines the values of free volume.

Isobaric thermal expansivity, α_P, and isothermal compressibility, k_T, are also reported in Fig. 6; both properties show the regular behavior of most fluids: decreasing with increasing pressure along isotherms and increase with increasing temperature along isobars. k_T is related with the extension of the H-bonding, compounds with the ability of developing spatial networks would have lower compressibilities.⁴¹ Although for EL the possibility of developing H-bond networks is discarded, its compressibility is moderately low, thus pointing to efficient interactions among molecules.

Internal pressure, P_i, is reported in Fig. 6. This property contains very valuable information on the structure of the fluid because of its relationship with cohesive forces. Nonetheless, the differences between P_i and cohesive energy density, c, should be remarked, considering that both properties are equivalent only for non-associated fluids, whereas for associated ones, c > P_i.⁴²c is a measure of the total molecular cohesion, because it is the sum to all attractive intermolecular forces per unit volume that are broken when the fluid is vaporized to the ideal gas state. However, P_i is the change in internal energy per mole when the fluid undergoes a very small isothermal expansion, thus this expansion does not necessarily disrupt all the intermolecular forces, and P_i is mainly affected by weak intermolecular forces (dispersive, repulsive and weakly dipolar), which are strongly affected by the intermolecular distance. One of the main characteristics of any H-bond is that they restrict the motion of molecules into the packing of a liquid, and although H-bonds are distance dependent, they do not markedly affect the internal pressure of a fluid.^42,43 Thus, we have tried to relate the difference between c and P_i properties with the strength of intermolecular forces, the interaction energy assigned to specific intermolecular forces (strong dipole–dipole and hydrogen bonding), U_sp, could be defined as:^42,43

U_sp = cV_i−P_iV_i (2)

Where, V_i is the molar volume. To calculate c parameter we use the vaporization enthalpy obtained from the literature at 298.15 K (ΔH_vap = 52.5 kJ mol⁻¹),⁴⁴ thus, all the calculations were carried out at 298.15 K and 0.1 MPa. The experimental literature ΔH_vap data leads to a U_sp = 0.27 kcal mol⁻¹, this value is remarkably low if it is compared with the H-bond strengths reported in Fig. 4 for the main studied multimers. It is also too low considering the large dipole moment of EL reported in Fig. 1 that should also contribute to U_sp. Several reasons may be considered for this discrepancy. (i) P_i values are too high because the method proposed in this work for estimation of internal pressure is not accurate. To explore this possibility we have carried out the same analysis for methanol, for which U_sp has been determined from experimental P_i data,⁴³ thus using our previously reported P_i data⁴⁵ we obtain U_sp = 5.69 kcal mol⁻¹ which is just 0.76% larger than the value obtained from experimental P_i. Hence, the reported values for P_i obtained from PVT data are reliable. (ii) ΔH_vap data are too low, although there is a slight discrepancy among the data reported in the literature, all of them are in the 50–53 kJ mol⁻¹ range.^18,44,46 Nevertheless, ΔH_vap data are reported for mixtures of enantiomers⁴⁶ or it is not indicated which enantiomer has been studied.⁴⁴ Thus, we have calculated ΔH_vap using the Pitzer-Carruth-Kobayashi group contribution method,⁴⁷ leading to ΔH_vap = 57.1 kJ mol⁻¹, thus U_sp = 1.37 kcal mol⁻¹ is obtained, this value is still too low, in fact if we consider that P_i values are accurate, ΔH_vap should be ∼30% larger than the value reported in ref. 43. Hence, in our opinion, the trend to form cyclic aggregates through H-bonding in EL is at least partially affected by the very small isothermal expansion for which P_i is defined; at least 30% of P_i should be originated in H-bonds and strong dipolar interactions.

Dynamic viscosity data are plotted in Fig. 8 as a function of pressure and temperature, and pressure–viscosity, α_η, and temperature–viscosity, β_η, derived coefficients are reported in Table S5 (ESI).† Moderate viscosities are obtained in the whole pressure/temperature ranges studied, this is important for any heat or mass transfer operations in which this solvent could be applied because too high viscosity values would hinder its application. As a rule, the stronger the intermolecular forces the higher the viscosity, and thus these forces are obviously weakened upon temperature increases and reinforced with increasing pressure. Pressure effect on viscosity changes on going from low to high temperatures, whereas for T≤ 298.15 K the behavior is clearly non-linear, for T > 298.15 K an almost linear increase with pressure is obtained. The pressure effect on viscosity is frequently explained according to eqn (3):

η_isothermal = η_pexp(PV^#/RT) (3)

Where η_p is a pre-exponential factor and V^# is the activation volume. The fits to eqn (3) show very low deviations. V^# is calculated for all the studied isotherms and reported in Fig. 9a, a clearly non linear behavior is obtained showing remarkable larger values for the lower temperatures and then an almost linear variation. This behavior shows that viscosity is more pressure dependent at lower than higher temperatures because of the stronger intermolecular forces at the lower temperatures and considering the larger free volume available, which allows a better flow, at higher ones. This is supported by the α_η behavior reported in Table S5 (ESI),† whereas for 298.15 K, an increase of 70 MPa leads to a 5.5% increase in α_η, at 358.15 K it increases by 3.4%. The temperature behavior of viscosity reported in Fig. 8b is even more complex, with a remarkable viscosity increase for T < 298.15 K. Temperature effect on viscosity was tried to fit to an Arrhenius type behavior, at low temperatures there is a deviation from this behavior, in fact results are more accurately fitted to a Volger-Fulcher-Tamman (VFT) equation. Nevertheless, to obtain the values of the activation energy, E_a, Arrhenius fits were done for T > 298.15 K for each isobar, with results reported in Fig. 9b. E_a increases in an almost linear way for the pressure range studied, with values in good agreement with the H-bonding energies reported in Fig. 4 and with the previously reported DRS results.

Molecular dynamics simulations

Results obtained from these simulations infer more detailed information about molecular level structure in the studied fluid. We have considered OPLS-AA forcefield⁴⁸ for all the simulations, parameters used are reported in Tables S6–S10.† To validate the reported forcefield parameterization, and thus to assure the reliability of structural features inferred from the simulations, calculated properties were compared with experimental ones. In Fig. 10, density and isobaric thermal expansivity comparisons are reported. Simulated densities are always larger than experimental ones with deviations roughly 3–4% for the pressure/temperature ranges studied. The use of Merz-Singh-Kollman, MK, charges may lead to a larger coulombic energetic contribution that would be the origin of the larger densities. Predictions on isobaric thermal expansivity allow inferring if the simulations are able to capture the changes on density with temperature at constant pressure; this is of great importance because of the stronger temperature effect on intermolecular forces if compared with pressure effect. Predicted α_P values are always 10–20% lower than experimental ones, this is in agreement with stronger intermolecular forces in the model system, nevertheless, the temperature trend is properly captured by the simulations. Although these deviations may seem too large, they are in the common range of predicted properties, the degree of agreement over the studied pressure/temperature ranges is reasonable, considering the purely predictive character of the model and the complexity of the studied fluid, and should allow reliable insights into EL properties and structure. The calculated intermolecular interaction energy, E_int, is reported in Fig. 11, although the predicted E_int are larger than the ones inferred from the experimental vaporization enthalpy,⁴⁴ the values show strong intermolecular interactions that are weakened upon increasing temperature. E_int for EL is larger than the one previously reported for ML,²⁸ this behavior is in agreement with the increasing vaporization enthalpy upon alkyl chain length increase.⁴⁶

Fig. 11 Intermolecular interaction energy, E_int, for EL at 0.1 MPa as a function of temperature calculated from OPLS-AA molecular dynamics simulations.

Structural features are analyzed using radial distribution functions for selected pairs, RDFs, Fig. 14 and 15. A very important factor that should be analyzed in molecular dynamics simulations is the effect of the simulations’ length on the predictions, thus we have carried out simulations for longer times to study if the structural features are affected. In a previous work, we reported the long residence times of EL in H-bonded clusters through DRS results,²³ thus although self-diffusion coefficients for EL are not too low (as the molecular dynamics predicted values show), simulations should be extended to a time that assures reliable structural results. In Fig. 12 we report RDFs for the pair 8–10 (hydroxyl hydrogen-carbonyl oxygen) for different simulation times; this pair is the most important one to analyze intermolecular H-bonding as reported in Fig. 4. RDFs are not remarkably affected by a simulation time 4-times larger, peaks positions and intensities remain constant and thus simulations are reliable for the studied lengths.

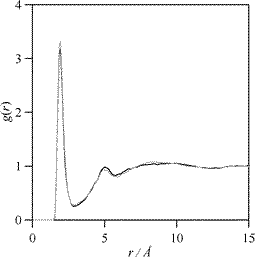Fig. 12 Site–site radial distribution function, g(r), for the 8–10 pair in EL calculated from OPLS-AA molecular dynamics simulations at 298 K and 0.1 MPa. Atom numbering as in Fig. 1. (black line) simulation time 500 ps, (gray line) simulation time 2 ns.

Fig. 13 Site–site radial distribution functions, g(r), for EL calculated from OPLS-AA molecular dynamics simulations at (black line) 278 K, 0.1 MPa and (gray line) 358 K, 0.1 MPa. Atom numbering as in Fig. 1.

Fig. 14 Intramolecular dihedral angle distribution function for EL calculated from OPLS-AA molecular dynamics simulations at 298 K and 0.1 MPa. Atom numbering as in Fig. 1.

Fig. 15 Mean square displacement, msd, and self-diffusion coefficient, D, for EL calculated from OPLS-AA molecular dynamics simulations as a function of temperature. In panel (a) 278–358 K in 10 K steps from bottom to top. In panel (b) symbols show calculated D values according to Einstein's relation from msd and line shows fit to Arrhenius’ equation.

Intermolecular H-bonding may be developed through three main positions: (i) OH⋯OC (positions 8–10, Fig. 1), (ii) OH⋯OH (positions 8–7, Fig.1) and (iii) OH⋯O_ALKOXY (position 8–11, Fig. 1). The energetic and structural analysis reported in previous sections have showed that interactions through 8–10 and 8–7 positions are formed, whereas 8–11 H-bonding should be discarded because of steric hindrance. For the most stable studied dimers, Fig. 4, 8–10 and 8–7 interactions are present (although 8–10 prevails over 8–7), whereas cyclic higher aggregates are produced by 8–7 interactions. Thus, the analysis of RDFs for these pairs would lead to information on the prevailing associates in the liquid phase. The analysis of results reported in Fig. 13, first discards the 8–11 H–bonding thus confirming gas phase DFT results. H-bonding through 8–10 and 8–7 positions are clearly inferred from the sharp and intense peaks obtained, RDFs show maxima at 1.95 Å for both positions but interaction through 8–10 is clearly stronger than through 8–7 (peak maximum is 48.8% larger), thus dimers would prevail over higher associates reported in Fig. 4 (specially 2A formed through 8–10 interactions) in spite of the large stabilization energies reported in Fig. 4. Nonetheless, 8–7 H-bonding is also present in liquid EL. RDFs for EL are larger than the ones previously reported for ML,²³ which is in agreement with stronger H-bonding. RDFs for 8–10 and 8–7 interaction show small weak features beyond the first sharp peak with maxima at 5.05 and 3.50 Å, respectively, thus pointing to at least a second solvation shell and a certain degree of cooperativity in the H-bonding. The temperature effect on 8–10 and 8–7 RDFs is very similar, first peak maxima decreases 33.2 and 35.8%, respectively, on going from 278 to 358 K, hence the strength of both interactions is almost the same, which is in agreement with the strength of dimers reported in Fig. 4. Pressure effect is not reported in Fig. 13 because it is almost negligible for both positions in the pressure range studied.

We have also analyzed in Fig. 13 the RDFs for the head (position 4, Fig. 1) and tail (position 15, Fig. 1) methyl groups. RDFs for tail–tail interactions (15–15) show two well defined solvation shells at 4.10 and 8.25 Å, whereas for head–head interactions (4–4) a weaker peak appears also at 4.10 Å and a second shell at 8.75 Å. The cross head–tail interaction shows two shells at 4.10 and 8.45 Å. Hence, we may infer the existence of a continuous apolar domain within liquid EL.

To study EL conformation in the liquid phase it is important to analyze the possibility of developing intramolecular hydrogen bonding competing with intermolecular interactions. We report in Fig. 14 the probability distribution function for two important dihedral angles that show the relative position of hydroxyl and carbonyl groups within EL molecules. The first dihedral, 7–6–9–10 (atom code Fig. 1), shows a well defined peak at 21°, thus showing that hydroxyl and carbonyl groups are slightly out of plane. Moreover, the 8–7–6–9 dihedral distribution shows a maximum at 73°, thus the development of intramolecular H-bonding between the hydroxyl hydrogen and the carbonyl oxygen is clearly hindered, the hydroxyl group is moved out of plane if compared with the obtained monomer in the gas phase, Fig. 1. These results are in good agreement with the monomer values reported in Fig. 3 as a function of the dielectric constant of the surrounding media, and more remarkably with the values of dihedrals for dimer 2A reported in Fig. 4 (25 and 66° for 7–6–9–10 and 8–7–6–9 dihedrals, respectively). Thus, intramolecular H-bonding in liquid EL almost vanishes to develop intermolecular interactions mainly through 2A cyclic dimers.

The dynamic behavior of EL was studied using the self-diffusion coefficient, D, calculated from the Einstein relation:

where the quantity in brackets is the mean square displacement, msd. In Fig. 15, the msd calculated from the molecular dynamics simulation is reported for the first 60 ps of simulation (after equilibration) as a function of temperature. A linear behavior is observed leading to the D coefficients from the slope of the linear fittings. To the best of our knowledge, there is no literature data for ELD coefficients, thus no comparison is possible between predicted and experimental data. Nonetheless, low diffusion coefficients are obtained, which is in agreement with the large intermolecular interaction energies reported in Fig. 11. The calculated coefficients approximately follow an Arrhenius behavior, Fig. 15b, from which the activation energy for diffusion may be calculated, the 34.1 kJ mol⁻¹ value shows a strongly interacting fluid with low molecular mobility.

Monte Carlo/Gibbs ensemble. Phase equilibria predictions

A detailed analysis of the literature shows the absence of phase equilibria studies for EL, only vapor pressure data may be found in ref. 44, in fact, not even any critical data is reported for this compound. This absence of data hinders the development of common predictive models used in the industry for the analysis and design of processes, such as equations of state, in which EL would be involved. Hence, we have carried out Monte Carlo/Gibbs ensemble⁴⁹ simulations to predict EL phase equilibria, in conjunction with the remaining properties reported in this work, to obtain a full picture of the behavior of this relevant fluid. The critical properties were calculated from the simulated data using the law of rectilinear diameters and a scaling law, assuming an Ising exponent β = 0.325. In Fig. 16, the vapor–liquid coexistence curve together with vapor pressure data are reported. A good agreement is obtained between experimental and calculated vapor pressure data, whereas the absence of saturation density data hinders any comparison. These phase equilibria data should be considered as an initial estimation until experimental data is available, nevertheless the quality of vapor pressure predictions points to accurate equilibria data from these Monte Carlo simulations.

Fig. 16 (a) Vapor–liquid coexistence curve and (b) vapor pressure for EL. (●) Calculated from Monte Carlo simulations with OPLS-AA forcefield and parameters reported in Tables S6–S10 (ESI),† (+) calculated critical point and (gray line) in panel (b), experimental values from ref. 44. Values within panel (a) show calculated critical point.

Conclusions

A wide scope study on EL structure and properties is reported using a combined experimental/theoretical approach. EL structure in the liquid phase is characterized by remarkable intermolecular associations through H-bonding, leading to mainly cyclic dimers although the presence of higher complexes such as cyclic trimers or tetramers is also important. Intermolecular interactions are developed through hydroxyl/carbonyl interactions, whereas the alkoxy position is sterically hindered to develop H-bonding. Alkylic groups tend to arrange in apolar domains across the fluid with tail/tail (terminal ethyl groups) arrangements. These complexes have remarkable association energies and their formation leads to a weakening of the intramolecular H-bonding through an out-of-plane movement of the hydroxyl group in EL. Calculated intermolecular interaction energies show a highly structured fluid, with low molecular mobility leading to low self-diffusion coefficients. Thermophysical properties reported show a dense fluid with moderate viscosity, which is a candidate suitable to be applied in different industrial fields.

Experimental

Materials

EL ((−)-Ethyl (S)-2-hydroxypropionate, CAS Number 687–47–8, 99.7% purity from gas chromatography, water content < 0.05% from Karl Fischer coulometric titration) was purchased from Fluka. It is a colorless and clear liquid that was degassed by ultrasound before any measurement and used without any additional purification.

PVT behavior

The apparatus used in the PVT measurements was previously described in detail.^45,50 The system is installed around a high-pressure vibrating tube densimeter. The cell temperature is controlled and measured to ±1×10⁻² K and the pressure was kept constant to ±5×10⁻³ MPa and measured to ±1×10⁻² MPa. The pressure transducer and thermometer were previously calibrated through well defined and traceable procedures. For proper apparatus calibration, a 14-parameter equation was used⁵⁰ with n-hexane (Fluka, 99.9%) and water (Millipore, resistivity 18.2 mΩ cm) as reference fluids.⁵¹ The effect of sample viscosity on density readings is below the accuracy limit of measurements (±1×10⁻⁴ g cm⁻³), thus raw data without viscosity corrections were used in this work.

Experimental density data were fitted to the 10-parameter TRIDEN equation developed by Ihmehls and Gmehling.³⁴ From the fitting equation the derived properties isobaric thermal expansivity, α_P, isothermal compressibility, k_T, and internal pressure, P_i, were calculated.⁵²

PηT behavior

Viscosity measurements were carried out using an electromagnetic viscometer VINCI Tech. EV1000.³⁵ Sample temperature is controlled and measured to ±1×10⁻² K and pressure to ±1×10⁻² MPa. Temperature and pressure sensors were previously calibrated through traceable procedures. Apparatus calibration was done using certified oils provided by the manufacturer. Viscosity accuracy was estimated to be ±1% in the full scale.

Experimental viscosity data were fitted for the whole pressure-temperature range to a 7-parameters Tait-like equation.^52,53 Pressure-viscosity, α_η, and temperature-viscosity, β_η, coefficients were calculated from fitting coefficients.

DFT calculations

DFT calculations were carried out with the Gaussian 03 package⁵⁴ according to Density Functional Theory (DFT), using the Becke gradient corrected exchange functional⁵⁵ and Lee-Yang-Parr correlation functional⁵⁶ with three parameters (B3LYP)⁵⁷ method. 6–311++g** basis set was used along this work. Calculations in solution were carried out using the self-consistent reaction field approach (SCRF) with the solvent treated as a continuum using the integral equation formalism of the PCM approach (IEF-PCM).⁵⁸ The cavity in which the solute is placed in the IEF-PCM approach was built using the united atom model in all the cases, a value of 1.2 was used to scale all the radii and 70 tesserae to divide the spherical surfaces. Atomic charges were calculated to fit the electrostatic potential⁵⁹ according to the Merz-Singh-Kollman (MK)⁶⁰ scheme. Interaction energies for complexes, ΔE, were calculated as the differences among the complex and sum of EL monomer energies at the same theoretical level, with basis set superposition error (BSSE) corrected through the counterpoise procedure.⁶¹

Molecular dynamics simulations

Classical molecular dynamics simulations were carried out using the TINKER molecular modelling package.⁶² All simulations were performed in the NPT ensemble; the Nosé-Hoover method⁶³ was used to control the temperature and pressure of the simulation system. The motion equations were solved using the Verlet Leapfrog integration algorithm.⁶⁴ The molecular geometries were restrained according to the shake algorithm.⁶⁵ Long-range electrostatic interactions were treated with the smooth particle mesh Ewald method.⁶⁶ The simulated systems consist of cubic boxes with 200 molecules to which periodic boundary conditions were applied in three directions. The simulations were performed using a cutoff L/2 Å radius for the non-bonded interactions, L being the box side. Initial boxes were generated using the PACKMOL program⁶⁷ that uses the BOX-QUACAN⁶⁸ local-minimization method to obtain adequate starting configurations. These boxes were minimized according to the MINIMIZE program in the TINKER package to a 0.01 kcal mol⁻¹Å⁻¹rms gradient, then several heating and quenching steps in the NVT ensemble up to 500 K were performed after which a 100 ps NVT equilibration molecular dynamics simulation was run at the set temperature; finally, from the output NVT simulation configuration, a run of 500 ps (time step 1 fs) in the NPT ensemble at the set temperature and pressure was run, from which the first 100 ps were used to ensure equilibration (checked through constant energy) and the remaining 400 ps for data collection. EL was described according to the so-called Optimized Potential for Liquid Simulations (all atom version) OPLS-AA.⁴⁸ MK charges obtained through B3LYP/6–311++g** calculations were used in the simulations.

Monte Carlo/Gibbs ensemble simulations

Coupled–decoupled⁶⁹ dual cutoff⁷⁰ configurational bias⁷¹ simulations using the MF-CPN strategy⁷² were performed using MCCCS Towhee code in the NVT-Gibbs ensemble.⁴⁹ Ewald sum method was used to handle the columbic interactions. Vapor–liquid coexistence calculations require a 2-box simulation, the probability of the molecule transfer move between both boxes was set to achieve one accepted movement every 5–10 cycles, where a cycle is N moves (with N being the number of molecules). The probability of the remaining moves was set to 0.002 for volume changes, to 0.01 for type 1 aggregation volume bias moves, and equally divided between translation, rotation and configurational bias regrowths. OPLS-AA forcefield was applied with the same parameters as for molecular dynamics simulations. Simulations were performed on 200 total EL molecules. Systems were equilibrated for 50 000 cycles (1 × 10⁷ Monte Carlo Steps) and the production runs of 40 000 cycles (8 × 10⁶ Monte Carlo Steps) were broken into 20 blocks for error estimation.

Acknowledgements

The financial support by Junta de Castilla y León, Project BU-020A/07, and Ministerio de Educación y Ciencia, Project CTQ2005–06611/PPQ, (Spain) is gratefully acknowledged.

References

1. J. M. DeSimone, Science, 2002, 297, 799.
2. R. Höfer and J. Bigorra, Green Chem., 2007, 9, 203.
3. World solvents. Industry study with forecast to 2007 & 2012 for 14 countries & six regions, The Freedonia Group, Cleveland, 2003.
4. R. A. Sheldon, Green Chem., 2005, 7, 267.
5. C. Capello, U. Fischer and K. Hungerbühler, Green Chem., 2007, 9, 927.
6. W. M. Nelson, Green solvents for chemistry: perspectives and practice, Oxford University Press, New York, 2003.
7. N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123.
8. J. M. DeSimone, W. Tumas, (Eds.), Green Chemistry using liquid and supercritical carbon dioxide, Oxford University Press, New York, 2003.
9. P. L. Short, Chem. Eng. News, 2006, 84, 15.
10. J. C. Warner, A. S. Cannon and K. M. Dye, Environ. Impact Assess. Rev., 2004, 24, 775.
11. J. J. Clary, V. J. Feron and J. A. van Velthuijsen, Regul Toxicol. Pharmacol., 1998, 27, 88.
12. C. T. Bowner and R. Hooftman, Chemosphere, 1998, 37, 1317.
13. N. Asthana, A. K. Kolah, D. R. Vu, C. T. Lira and D. Miller, Org. Process Res. Dev., 2005, 9, 599.
14. J. Gao, X. M. Zhao, L. Y. Zhou and Z. H. Huang, Chem. Eng. Res. Des., 2007, 85, 525.
15. D. J. Benedict, S. J. Parulekar and S. P. Tsai, Ind. Eng. Chem. Res., 2003, 42, 2282.
16. O. Sánchez, G. Vidriales, E. Morales and E. Ortiz, Chem. Eng. J., 2006, 117, 123.
17. K. Trychta, D. A. Sandberg and M. Henry, Pollution Prevention Rev., 2001, 44, 33.
18. S. M. Nikles, M. Piao, A. M. Lane and D. E. Nikles, Green Chem., 2001, 3, 109.
19. W. Den, F. Ko and T. Huang, IEEE T. Semicond. M., 2002, 15, 540.
20. F. Mottu, A. Laurent, D. A. Rufenach and E. Doelker, PDA J. Pharm. Sci. Technol, 2000, 54, 456.
21. D. L. White, J. A. Bardole, Paint and Finish Removers. In: Kirk-Othmer encyclopedia of chemical technology, John Wiley and Sons, New York, 2000.
22. R. Dohrn and O. Pfohl, Fluid Phase Equilibr., 2002, 194–197, 15.
23. S. Aparicio, S. Halajian, R. Alcalde, B. García and J. M. Leal, Chem. Phys. Lett., 2008, 454, 49.
24. J. Chen and H. Chu, J. Chem. Eng. Data, 2007, 52, 650.
25. J. M. Resa, J. M. Goenaga, A. I. Sanchez and M. Iglesias, J. Chem. Eng. Data, 2006, 51, 1294.
26. S. Peña, R. Murga, M. T. Sanz and S. Beltrán, Fluid Phase Equilibr, 2005, 230, 197.
27. J. D. Raal, A. Muhlbauer, Phase Equilibria: Measurement and Computation, CRC, Washington DC, 1997.
28. S. Aparicio, J. Phys. Chem. A, 2007, 111, 4671.
29. N. Borho and M. A. Suhm, Org. Biomol. Chem., 2003, 1, 4351.
30. R. F. W. Bader, Atoms in Molecules: a Quantum Theory, Oxford University Press, Oxford, 1990.
31. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
32. U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747.
33. P. L. A. Popelier, J. Phys. Chem., 1998, 102, 1873.
34. E. C. Ihmehls and J. Gmehling, Ind. Eng. Chem. Res., 2001, 40, 4470.
35. S. Aparicio, R. Alcalde, B. García, J. M. Leal, J. Phys,. Chem., Submitted.
36. J. A. Riddick, W. B. Bunger, T. K. Sakano, Organic Solvents: Physical Properties and Methods of Purification, Wiley–Interscience, New York, 1986.
37. I. C. Sanchez and R. H. Lacombe, Macromolecules, 1978, 11, 1145.
38. B. Coto, F. Mossner, C. Pando, R. G. Rubio and J. A. R. Renuncio, Fluid Phase Equilibr., 1997, 133, 89.
39. K. Gauter and R. A. Heidemann, Ind. Eng. Chem. Res., 2000, 39, 1115.
40. H. Machida, Y. Sato and R. L. Smith, Fluid Phase Equilibr., 2008, 264, 147.
41. M. Rodnikova and J. Barthel, J. Mol. Liq., 2007, 131–132, 121.
42. M. J. R. Dack, Chem. Soc. Rev., 1975, 4, 211.
43. E. V. Ivanov and V. K. Abrosimov, J. Struct. Chem., 2005, 46, 856.
44. M. Temprado and J. S. Chickos, Thermochim. Acta, 2005, 435, 49.
45. S. Aparicio, B. García, R. Alcalde, M. J. Dávila and J. M. Leal, J. Phys. Chem. B, 2006, 110, 6933.
46. J. S. Chickos and W. E. Acree Jr, J. Phys. Chem. Ref. Data, 2003, 32, 519.
47. G. F. Carruth and R. Kobayashi, Ind. Eng. Chem. Fundam., 1972, 11, 509.
48. W. L. Jorgensen, D. S. Maxwell and J. Tirado–Rives, J. Am. Chem. Soc., 1996, 118, 11225.
49. J. R. Errington and A. Z. Panagiotopoulos, J. Phys. Chem. B, 1998, 102, 7470.
50. B. García, S. Aparicio, R. Alcalde, M. J. Dávila and J. M. Leal, Ind. Eng. Chem. Res., 2004, 43, 3205.
51. E. W. Lemmon, M. O. McLinden, D. G. Friend, Thermophysical Properties of Fluid Systems. In: NIST Chemistry WebBook, NIST Standard Reference Database Number 69, Eds. P. J. Linstrom, and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, June 2005, (http://webbook.nist.gov).
52. M. J. Dávila, S. Aparicio, R. Alcalde, B. García and J. M. Leal, Green Chem., 2007, 9, 221.
53. M. J. P. Comuñas, A. Baylaucq, C. Boned and J. Fernández, Int. J. Thermophys., 2001, 22, 749.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, J. A. Pople, J. A. Gaussian, 03 (Revision C.02), Gaussian, Inc., Wallingford CT, 2004.
55. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
56. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
57. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
58. E. Cances and B. Mennucci, J. Math. Chem., 1998, 23, 309.
59. U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129.
60. B. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431.
61. S. Simon, M. Duran and J. J. Dannenberg, Chem. Phys., 1996, 105, 11024.
62. J. W. Ponder, J. W. TINKER, Software tool for molecular design. 4.2 ed, Washington University School of Medicine, 2004.
63. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695.
64. M. P. Allen, D. J. Tildesley, Computer Simulation of LiquidsClarendon Press: Oxford, UK, 1989.
65. J. P. Rickaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327.
66. U. L. Essmann, M. L. Perera, T. Berkowitz, H. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577.
67. J. M. Martínez and L. Martínez, J. Comput. Chem., 2003, 24, 819.
68. A. Friedlander, J. M. Martínez and S. A. Santos, Appl. Math. Opt., 1994, 30, 235.
69. M. G. Martin and J. I. Siepmann, J. Phys. Chem. B, 1999, 103, 4508.
70. T. J. H. Vlugt, M. G. Martin, B. Smit, J. I. Siepmann and R. Krishna, Mol. Phys., 1998, 94, 727.
71. J. I. Siepmann and D. Frenkel, Mol. Phys., 1992, 75, 59.
72. M. G. Martin and A. L. Frischknecht, Mol. Phys., 2006, 104, 2439.

---

Footnote

† Electronic supplementary information (ESI) available: AIM analysis for EL monomer (Fig. S1), NBO analysis for EL monomer (Fig. S2), experimental density and derived properties (Table S1), fitting parameters of TRIDEN correlation of density (Table S2), dynamic viscosity (Table S3), fitting parameters for correlation of viscosity (Table S4), viscosity–derived coefficients (Table S5), MK Atomic charges (Table S6), forcefield parameters (Tables S7–S10). See DOI: 10.1039/b811909k

---