Product vibrational distributions in polyatomic species based on quasiclassical trajectory calculations
Received
30th June 2009
, Accepted 28th August 2009
First published on 19th September 2009
Abstract
By including anharmonicity and Coriolis coupling terms, we have improved our earlier quasi-classical method for vibrational mode analysis in polyatomic species, which was based on a harmonic approach. Because accurate methods have been developed only for diatomic and triatomic systems, the new algorithm was tested against accurate methods for diatomic molecules, and against the semiclassical fast Fourier transform (FFT) method for triatomic species, finding excellent agreement. The new algorithm is designed to be used with dynamics studies based on quasi-classical trajectory (QCT) calculations, and it is general for any polyatomic species.
I. Introduction
The knowledge of the reactant and product vibrational distributions is of great importance in the dynamics study of reactive systems. Issues as important as mode selectivity are closely related to this information. In the case of small molecules, typically diatomic or triatomic, accurate vibrational eigenvalues can be obtained quantum-mechanically. However, in the more general case of polyatomic systems where the dynamics studies are usually performed by computing classical or quasi-classical trajectories (QCT), the semiclassical methods represent an interesting alternative to the quantum methods.
In the simplest case of diatomic molecules, the vibrational quantum number, n, can be found by the Einstein-Brillouin-Keller (EBK) semiclassical quantization of the action integral,1
| | 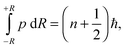 | (1) |
where
p is the linear momentum for the rotating oscillator and ±
R are the vibrational turning points.
In the case of triatomic or polyatomic molecules (N≥ 3), the calculation of vibrational action variables is quite challenging because of anharmonic and Coriolis coupling between the vibrational modes, and only methods for triatomic molecules have been developed and well tested. The calculation of “good” vibrational action variables has been widely studied, but in dynamics applications using quasi-classical trajectory calculations, only two methods have been well established: the fast Fourier transform (FFT) approach, and the adiabatic switching (AS) method. The first was developed by Schatz et al.,2,3 Binney and Spergel,4 and Martens and Ezra,5 and applied in QCT calculations by Schatz et al.6,7 Basically, the integrals which determine the good action variables are evaluated using Fourier series representations of the coordinates (qi) and momenta (pi),
| |  | (2) |
where
Mi is the number of turns that this trajectory takes around the phase-space
pi−
qi plane during one vibrational period. These integrals are well defined only if trajectories are quasiperiodic and, due to its easier implementation for problems with many degrees of freedom, the Sorbie-Handy approach is usually used.
8–10
An alternative for determining good action variables is the adiabatic switching (AS) method.11–15 In brief, a time-dependent Hamiltonian is chosen as:
where
Ho is a normal-mode Hamiltonian,
S(
t) is a switching function varying smoothly between 0 and 1, and Δ
H =
H−
Ho, where
H is the total Hamiltonian. In other words, the integration of a trajectory describing molecular vibrations begins by assuming a harmonic Hamiltonian (zero-order approach), adding smoothly the anharmonic corrections and the Coriolis coupling until the total Hamiltonian has been obtained.
Both methods, FFT and AS, are dependent on the choice of coordinate system, and are accurate in the absence of Fermi resonances.2,3,5 As mentioned above, these two methods have been widely used in triatomic systems. However, in the case of the AS approach, Bowman et al.14 developed the method for a tetratomic system, H2CO, while Castillo et al.16 recently used the AS approach in the polyatomic Cl + CH4hydrogen abstraction reaction, applying it only to the determination of the initial conditions of the QCT calculations. Therefore, the application of good action variables in polyatomic systems is a research field of great interest nowadays.
Our research group has developed a quasi-classical harmonic alternative to the aforementioned methods to obtain vibrational action variables in polyatomic systems, that will be referred to as the NMA (normal mode analysis) approach.17–26 Basically, as input we use the last geometry (coordinates and momenta) of the reactive trajectories. The projection of the displacement and momentum matrices onto the respective normal-mode space allows us to compute the kinetic and potential energies, and therefore the total vibrational energy, for each normal mode. Using the harmonic approach, we can obtain the vibrational action from this energy. (A detailed description and the incorporation of anharmonic effects, will be presented in Section II.B.) Note that the rotational motion is removed before the NMA, i.e., the vibrational and rotational motions are treated independently. In the case of diatomic molecules, we tested17 our quasi-classical harmonic NMA approach against more sophisticated methods, namely the EBK method, obtaining differences of 2%. We would like to stress first that the NMA approach has been devised and implemented exclusively to be used with dynamics studies based on QCT calculations, and second that the advantage of the NMA approach is that it can be applied as a “black box” method to diatomic, triatomic, or any polyatomic system with no user intervention.
In the present work, the objective is twofold. Firstly, we will analyze some improvements to the harmonic NMA approach, namely, the inclusion of anharmonicity and Coriolis terms. Secondly, since there are no general methods for polyatomic systems (more than three atoms), we will check the validity of the NMA approach by comparing it to the FFT method for triatomic species, and to the EBK method for diatomics, using QCT calculations. Thus, the paper is organized as follows: section II briefly outlines the harmonic and anharmonic NMA approach. Section III presents an analysis of the importance of anharmonicity in the NMA approach. The comparison of the NMA and FFT methods for triatomics and NMA and EBK for diatomics is presented in section IV. Finally, in section V conclusions are given.
II. Theoretical methods
A. Fast Fourier transform (FFT) approach
In QCT applications this approach can be used to obtain the initial conditions of the coordinates and momenta, and to determine the product vibrational actions from the coordinates and momenta at the end of each reactive collision. This approach has been widely developed by Schatz et al.2,3,6,7 for triatomic systems, and explores the relationship between good action variables and the Fourier representation of oscillator coordinates. A complete description of the method can be found in the original papers, and here we only present it briefly.
The EBK expression for the quantization of action variables is
| |  | (4) |
where for each
i vibrational mode,
ci specifies a closed path in phase space, and
ni represents the quantum number for each vibrational mode. Those authors evaluated these actions using the Sorbie-Handy approximation,
8–10| | 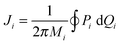 | (5) |
where the trajectories are quasiperiodic, and
Mi is the number of turns that this trajectory takes around the
pi−
qi plane during one period, which can be equated to
ω·
T/2
π, where
T is the time interval over which the coordinates and momenta have been determined by numerical integration, and
ϖ is the good frequency associated with the vibrational mode. The essence of the FFT approach is a Fourier series representation of the coordinates and momenta in
eqn (5),
| | 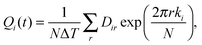 | (6) |
| |  | (7) |
where it is assumed that the coordinates and momenta are known at equally spaced time steps,
tk =
kΔ
T, with
k = −
N/2,… +
N/2, and
T =
NΔ
T, is the total time interval in the calculation.
Dir and
Fir are the Fourier coefficients obtained by fast Fourier transform methods,
| |  | (8) |
| | 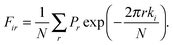 | (9) |
Bearing in mind that the coordinates and momenta are real functions, the evaluation of
eqn (5) leads to
| |  | (10) |
In the case of the determination of product vibrational actions, the inputs of the FFT approach are the final coordinates and momenta at the end of each reactive collision. The integration of
eqn (5) is followed over several vibrational periods (for instance 100), which permits one to obtain good action vibrational variables for the triatomic product. To the best of our knowledge, nowadays the implementation of this method is limited to triatomic systems. For these calculations, Schatz
7 developed the ACTION computer program, which will be used in the present paper for comparison.
B. Normal mode analysis (NMA) approach
For a reaction with two products, the energy of the products can be exactly partitioned into translational, rotational, and vibrational energy of the two co-products by analyzing the angular momenta and motion of the center of masses of the fragments. This allows one to exactly compute the vibrational energy, Evib, of each co-product. The issue is how to distribute this vibrational energy between the vibrational normal modes.
Assuming the validity of a harmonic independent normal mode treatment, the vibrational energy deposited on the ith normal mode, Eihar, can be computed as the sum of a kinetic, Eikin,har, and a potential energy, Eipot,har.
| | | Eihar = Eikin,har + Eipot,har. | (11) |
The kinetic energy can be computed using the vector of linear momenta in unscaled Cartesian coordinates projected onto the normal mode space. Thus, if
plγ is the
γ component (
γ =
x,
y,
z) of the momentum of the
l atom, and
cilγ is the
lγ component of the
ith normal mode eigenvector, one has
| | 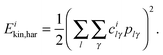 | (12) |
Note that the mass factor in the kinetic energy cancels out since we are using unscaled Cartesian momenta and mass-weighted normal mode eigenvectors.
In the harmonic approximation, the potential energy is computed as
| | | Eipot,har = ½(ωiΔi)2, | (13) |
with
ωi being the frequency of the
ith mode and Δ
i the displacement along the
ith normal mode. This displacement is obtained from the differences between the equilibrium unscaled Cartesian coordinates vector,
Xeq, and the unscaled Cartesian coordinates of the fragment at the final step of the reactive trajectory,
X, projected onto the normal mode space, so that
| | 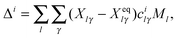 | (14) |
with
Ml being the mass of the
lth atom. This mass accounts for the transformation from mass-weighted to unscaled Cartesian coordinates and introduces the correct reduced mass of vibration in
eqn (13).
Eqns (11) through (14) allow one to compute the vibrational energy in each mode by using a purely harmonic independent normal mode approximation, which is the procedure we have used extensively in previous work.17–26
To improve this description, in the present work we will take into account anharmonicity and Coriolis coupling.
First we will focus on the anharmonic effects on the potential energy. To avoid using a complicated anharmonic analysis of the products, we will first compute a geometry, Xi,ex, in which all normal modes are at their equilibrium positions while mode i is excited to the same extent as in the X geometry, Δi,
| | | Xi,exlγ = Xeqlγ + cilγΔi. | (15) |
The energy to excite the molecule from its equilibrium geometry,
Xeq, to the
Xi,ex geometry,
Eiex, can be computed exactly by evaluation of the potential energy in both geometries,
| | | Eiex = V(Xi,ex) −V(Xeq), | (16) |
and one can assume that this excitation energy is the potential energy deposited in mode
i.
However, one can also assume that the potential energy for mode i is an energy, Eirel, that results from relaxing mode i in the X geometry,
| | | Eirel = V(X) −V(Xi,rel), | (17) |
with
Xi,rel being the geometry
X in which the
ith mode has been relaxed to its equilibrium position,
| | | Xi,rellγ = Xlγ−cilγΔi. | (18) |
Therefore, the difference between
Xi,ex and
Xi,rel is that in the first case the geometry is excited for the
ith mode and relaxed for the remaining modes, while in the second the geometry is excited for all the modes except the
ith. Therefore,
Eiex is the energy required to excite mode
i while all the remaining modes are in their equilibrium geometry, while
Eirel is the energy released when mode
i is relaxed to its equilibrium geometry while the remaining modes are kept at their conformation at
X. Therefore, the differences between
Eiex and
Eirel are due to coupling between modes, and it is trivial to show that in the case of a diatomic molecule with a single vibrational mode both energies are the same.
However, as we will see later, neither of the two approaches performs better than the harmonic approach, since none of them adequately deal with mode–mode coupling. Indeed, we found that a pragmatic approach which seems to work very well is simply to average both energies. Thus, the anharmonic contribution from the potential energy to the vibrational energy of mode i is computed as
| | | Eipot,anh = ½(Eiex + Eirel). | (19) |
We will further discuss this issue in Results section.
For the kinetic contribution, we found that the harmonic approach works very well (see Results section). However, it can also be improved by adding a term that includes the contribution to the Cartesian momenta due to Coriolis coupling. Thus, the kinetic energy is
| |  | (20) |
where
ζi,jlγ is the component
lγ of the Coriolis coupling vector between modes
i and
j,
and
Wγ is the component
γ of the angular velocity vector.
The anharmonic vibrational energy for mode i is thus obtained as
| | | Eianh = Eikin,anh + Eipot,anh. | (22) |
To check the validity of this approach one can to take into account that the total vibrational energy,
Evib, which is known exactly, has to fulfil the condition:
| |  | (23) |
where
Eivib can be either
Eihar or
Eianh depending on the level of approximation used. Note also that, if one defines a distortion energy
Edist, as the difference between the energies of the
X and
Xeq geometries,
| | | Edist = V(X) −V(Xeq), | (24) |
it is obvious that this energy is only due to the distortion caused by the vibrations, since the two products are sufficiently separated as to have no potential energy of interaction. Therefore,
| |  | (25) |
where
Eipot can be either
Eipot,har or
Eipot,anh. As a consequence,
| |  | (26) |
where
Eikin can be either
Eikin,har or
Eikin,anh. Both
Evib and
Edist can be computed exactly, so one can gauge the accuracy of computation of the kinetic energy per mode comparing
Evib and

(see
eqns (23) and (26)), while
eqn (25) allows one to measure the accuracy of the computation of the potential energy per mode. Note that
Evib is exactly known from the QCT analysis of the results, while
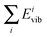
is computed from the present approach. If our approach is correct,
eqn (23) has to be fulfilled.
For the NMA approach we have written a program specifically designed for this purpose, which uses as input information the final coordinates and momenta at the end of each reactive collision. Note that for the QCT calculations we use the VENUS code27 which employs a space fixed frame. Therefore, a change to a body fixed frame is necessary before the projection onto the normal mode space. The energy in each normal mode was computed from this information, and assuming the harmonic approximation (even when the vibrational energy is computed using an anharmonic approach), the action variable, ni is calculated from the vibrational energy and harmonic vibrational frequency using the well-known expression
and rounded to the closest integer to obtain the vibrational quantum number of mode
i.
28
The main limitation of the NMA approach is the harmonic approximation used for the calculation of the action and integer quantum number, which is not valid for highly excited states. Moreover, the rotational and vibrational motions are treated independently and rotation–vibration coupling is neglected. Finally, this approximation could not be appropriate when the mixing between modes is important. However, in a previous work17 for diatomic products we compared the harmonic NMA approach with more sophisticated methods, namely the EBK method as implemented in VENUS96, obtaining differences of about 2%.
III. Harmonic versus anharmonic NMA: vibrational distribution of the tetratomic CHD2 product in the CH2D2 + F → CHD2 + FH reaction
The analysis of the vibrational population of the tetratomic CHD2 product of the CH2D2 + F → CHD2 + FH reaction on the 2006 surface19 was performed using the harmonic and anharmonic NMA approaches. 7637 trajectories were run, from which 1131 corresponded to the reaction under study. The collision energy was set to 2.30 kcal/mol and the impact parameter randomly chosen between 0 and 3.5 Å. Since we have no accurate values of the vibrational distribution of the CHD2 co-product, we will focus our study on analyzing the validity of the NMA approximation through the use of eqns (25) and (26) and on comparing the harmonic and anharmonic approaches. Note, however, that strictly speaking fulfilling these two equations does not guarantee that the distribution of the vibrational energy between the different vibrational modes is correct. Nevertheless, it is very likely that if eqns (25) and (26) are satisfied, then the NMA approach is reasonable, and one can expect that it will be able to predict the correct vibrational distribution in the products.
We will start by analyzing the calculation of the kinetic energy. Fig. 1 shows a plot of 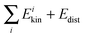 versus Evib (eqn (26)). Panel a shows the harmonic results while panel b includes Coriolis coupling in the kinetic energy. As one can see, the harmonic results are very close to the y = x line, meaning that the sum of the kinetic contributions to the energy is very close to its exact value. Thus, the mean unsigned difference between
versus Evib (eqn (26)). Panel a shows the harmonic results while panel b includes Coriolis coupling in the kinetic energy. As one can see, the harmonic results are very close to the y = x line, meaning that the sum of the kinetic contributions to the energy is very close to its exact value. Thus, the mean unsigned difference between  and Evib is only 0.39 kcal/mol. One can therefore assume that the kinetic contribution to the normal mode energy is satisfactorily calculated under the harmonic approach, and that the Coriolis coupling has a minor influence. However, some slight improvement is found, as seen in the somewhat minor scattering of the points around the y = x line seen in panel b, and in the mean unsigned difference between
and Evib is only 0.39 kcal/mol. One can therefore assume that the kinetic contribution to the normal mode energy is satisfactorily calculated under the harmonic approach, and that the Coriolis coupling has a minor influence. However, some slight improvement is found, as seen in the somewhat minor scattering of the points around the y = x line seen in panel b, and in the mean unsigned difference between  and Evib, which is 0.32 kcal/mol. Since including the Coriolis coupling has a negligible computational cost, it is advisable to take it into account.
and Evib, which is 0.32 kcal/mol. Since including the Coriolis coupling has a negligible computational cost, it is advisable to take it into account.
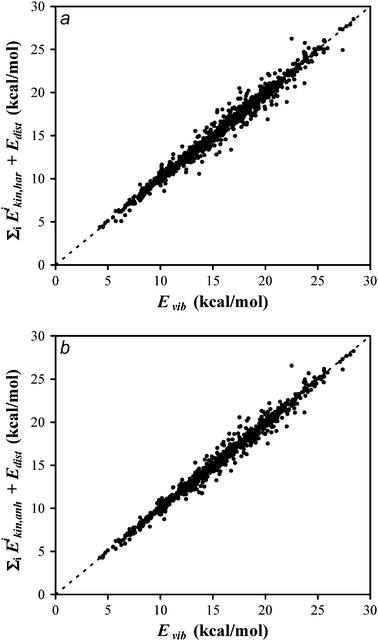 |
| | Fig. 1 Plot of the total vibrational energy computed using the harmonic (panel a) and anharmonic (panel b) approximations for the kinetic normal-mode energies and the distortion energy for the potential energy versus the exact total vibrational energy. Perfect agreement would be the y = x dashed line. | |
As for the potential energy, Fig. 2 shows plots of 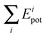 versus Edist. Panel a shows the harmonic results (eqn (13)), panel b the anharmonic results computed by relaxation of the ith mode (eqn (17)), panel c the anharmonic results computed by excitation of the ith mode (eqn (16)), and panel d the anharmonic results obtained by averaging the relaxation and excitation energies (eqn (19)). (The mean unsigned differences are 0.90, 1.18, 1.37, and 0.14 kcal/mol, for panels a through d.)
versus Edist. Panel a shows the harmonic results (eqn (13)), panel b the anharmonic results computed by relaxation of the ith mode (eqn (17)), panel c the anharmonic results computed by excitation of the ith mode (eqn (16)), and panel d the anharmonic results obtained by averaging the relaxation and excitation energies (eqn (19)). (The mean unsigned differences are 0.90, 1.18, 1.37, and 0.14 kcal/mol, for panels a through d.)
 |
| | Fig. 2 Plot of the distortion energy computed as the sum of the harmonic (panel a), relaxation (panel b), excitation (panel c), and anharmonic (panel d) normal-mode energies versus the exact distortion energy. Perfect agreement would be the y = x dashed line. | |
From panel a one can infer that anharmonicity has a significant role, since the deviation from the y = x line increases with energy, becoming quite significant at high energies. However, from an optimistic point of view one can see that the deviations are quite symmetrically scattered around the y = x line, so that some sort of error compensation can be expected.
Panels b and c show that normal-mode coupling is non-negligible, since both plots differ significantly. This could be a sign of an important coupling between modes. Moreover, neither of the two approaches is better than the harmonic approach, with the additional drawback that the aforementioned symmetry with respect to the y = x line is lost. Thus, it seems that the fully independent harmonic normal mode approach works very well because there is some cancellation between normal mode anharmonicity and mode–mode coupling.
The fact that the sum of the energies obtained by excitation shows positive deviations while the energies obtained by relaxation show negative deviations from the y = x line seems to indicate that changing mode i costs less when the other modes are not in their equilibrium position. In other words, it takes less energy to distort an already distorted geometry.
The true normal mode energy should lie somewhere between the Eirel and Eiex values, since the vibrational motion implies simultaneous changes for all the modes. Therefore, we estimated the anharmonic normal-mode energy as the average of the Eirel and Eiex values. Panel d shows that this approximation works very well, as is also reflected in the aforementioned very low mean unsigned difference between  and Edist (0.14 kcal/mol).
and Edist (0.14 kcal/mol).
Having computed the vibrational energy per mode, one can obtain the vibrational quantum number using eqn (27) and rounding to the nearest integer. The results are given in Table 1. Their most important feature is how similar they are, indicating that anharmonicity is not an important issue in the analysis of the normal mode population of the CHD2 product of the reaction, even when the population of excited levels is significant.
Table 1 Vibrational populations for the CHD2 product in the CH2D2 + F → CHD2 + FH reaction
| Frequency/cm−1 |
ν
|
Population (%) |
| Harmonic |
Anharmonic |
| 3141 |
0 |
96 |
98 |
| |
1 |
4 |
2 |
| 2362 |
0 |
93 |
94 |
| |
1 |
7 |
6 |
| 2228 |
0 |
90 |
92 |
| |
1 |
10 |
8 |
| 1268 |
0 |
76 |
77 |
| |
1 |
19 |
19 |
| |
2 |
4 |
4 |
| 1022 |
0 |
66 |
67 |
| |
1 |
24 |
23 |
| |
2 |
8 |
7 |
| 525 |
0 |
35 |
38 |
| |
1 |
28 |
24 |
| |
2 |
16 |
14 |
| |
3 |
10 |
11 |
IV. Performance of the NMA method: comparison with FFT and EBK methods
In the previous section, we analyzed the importance of anharmonicity, and Fig. 1 and 2 showed that the total vibrational energy is accurately computed using the NMA method. However, we have not yet checked the accuracy of the mode distribution of the vibrational energy. Since more accurate methods exist for diatomic and triatomic molecules, we will next use these as benchmarks.
Firstly, we computed the population of the vibrational states of the triatomic NH2 product in the NH3 + H → NH2 + H2 reaction using the FFT method. To perform the QCT calculations we employed an analytical potential energy surface developed in our group29 modified in order to avoid spurious wells near the ammonia inversion transition state.30 A total of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories were run, of which 878 were reactive. The rotational and collision energies were randomly sampled according to a Maxwell-Botzmann distribution of energies at 2000 K, and the NH3 molecule was at its vibrational ground state. The impact parameter was randomly chosen between 0 and 2.5 Å.
000 trajectories were run, of which 878 were reactive. The rotational and collision energies were randomly sampled according to a Maxwell-Botzmann distribution of energies at 2000 K, and the NH3 molecule was at its vibrational ground state. The impact parameter was randomly chosen between 0 and 2.5 Å.
The final geometries and momenta of the reactive trajectories were taken, and a NH2 simulation was performed with a time-step of 0.01 fs for 512 time steps for each point in the Fourier analysis, with a total of 1024 points. Once the “good action” values were determined, the quantum state was obtained by rounding it up to its nearest integer. The population of each vibrational state is shown in panel a of Fig. 3. Almost 50% of the amidogen product is found in its ground state, about 20% has one quantum of vibrational excitation in the bending mode, and the rest populates various of the lowest excited vibrational states.
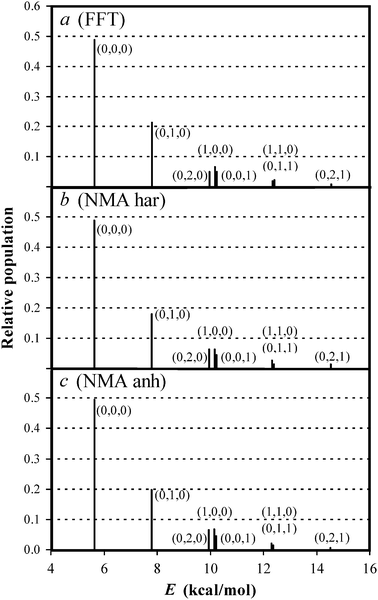 |
| | Fig. 3 Populations of the vibrational states of the NH2 product, in the NH3 + H → NH2 + H2 reaction, labeled (l, m, n), where l is the quantum number for the asymmetric stretching, m for the bending, and n for the symmetric stretching mode, as computed using the FTT (panel a), harmonic NMA (panel b) and anharmonic NMA (panel c) methods. | |
Panels b and c of Fig. 3 show the NMA results using the harmonic (b) and anharmonic (c) approximations. The agreement between the three panels in the figure is excellent, showing that anharmonicity is not important in this case, and also that the distribution of the vibrational energy among modes is correctly performed by the NMA method.
Next, we computed the population of the vibrational levels of the diatomic FH product in the CH2D2 + F → CHD2 + FH reaction using the EBK semiclassical approach and the NMA method (Table 2). Note that Coriolis coupling is not present, and that (since there is only one mode), Eipot,anh = Eiex = Eirel. However, anharmonicity plays a significant role. One reason is that vibrational excitation is more important, and higher excited states are more anharmonic. Another reason may be that, since there is a single mode, there is no coupling between modes to compensate for the anharmonicity of the FH stretching mode Thus, the harmonic distribution is flatter, reaching a higher vibrational excitation than the anharmonic and EBK results, and underestimating the population of the v = 2 state. Inclusion of anharmonicity improves the results significantly, although the v = 2 population is slightly overestimated (11%), and as a consequence the v = 3 population is underestimated. Note, however, that for highly excited states poorer behaviour is also expected with the anharmonic NMA approach, since one is using eqn (27) with a harmonic value for the vibrational frequency. Thus, if instead of eqn (27), one employs the expression for the energy levels for a Morse potential to obtain the quantum numbers
| |  | (28) |
then the resulting populations listed in the last column of
Table 2 are in almost perfect agreement with those from the EBK method. Note, however, that the FH molecule in the PES we are using is described as a Morse oscillator, and therefore the choice of the anharmonic model potential was obvious. However, choosing an anharmonic model potential for a normal mode in a polyatomic molecule is not straightforward, and in addition, there might be no analytical expression for the energy levels, which would complicate the evaluation of the quantum number. Thus, to make the method more flexible and automatic, we would rather recommend the use of
eqn (27) despite its limitations in the case of highly excited molecules.
Table 2 Vibrational population for the FH product in the CH2D2 + F → CHD2 + FH reaction
| Frequency/cm−1 |
ν
|
Population (%) |
|
EBK
|
Harmonic |
Anharmonic |
Anharmonic with Morse energy levels |
| 4115 |
0 |
0 |
1 |
1 |
1 |
| |
1 |
8 |
14 |
9 |
8 |
| |
2 |
58 |
41 |
69 |
56 |
| |
3 |
32 |
30 |
20 |
35 |
| |
4 |
1 |
11 |
0 |
1 |
| |
>4 |
0 |
3 |
0 |
0 |
As a final test, we computed the population of the vibrational levels of the diatomic H2 product in the NH3 + H → NH2 + H2, listed in Table 3. Since vibrational excitation is not very important, once again we obtained perfect agreement between the anharmonic NMA and EBK results. The harmonic results showed more vibrational excitation, although the differences were very small.
Table 3 Vibrational population for the H2 product in the NH3 + H → NH2 + H2 reaction
| Frequency/cm−1 |
ν
|
Population (%) |
|
EBK
|
Harmonic |
Anharmonic |
| 4406 |
0 |
73 |
70 |
73 |
| |
1 |
22 |
22 |
22 |
| |
2 |
4 |
5 |
4 |
| |
>2 |
1 |
4 |
1 |
V. Conclusions
The vibrational distribution in polyatomic systems is a challenging problem in dynamics calculations. While accurate methods for diatomic and triatomic species are available in the literature, there is little published work on polyatomic species. We have here improved our earlier quasi-classical harmonic normal-mode analysis (NMA) for polyatomic species by including anharmonicity and Coriolis coupling corrections. We checked its validity by comparing the vibrational distribution it yielded with other more accurate methods. For triatomic species, we analyzed the triatomic NH2 product in the hydrogen abstraction reaction of ammonia and hydrogen. For diatomic species, we analyzed the H2 product in that reaction, and the FH product in the CH2D2 + F → CHD2 + FH reaction. In both cases, diatomic and triatomic species, where only the comparison is possible, the agreement with the more accurate methods was excellent. Finally, we compared the harmonic and anharmonic approaches in the NMA method, analyzing the polyatomic CHD2 product in the last mentioned reaction. We found that the anharmonicity has little importance for this tetratomic free radical.
In spite of its quasi-classical nature, the main advantages of the new algorithm developed in this work are that it is general for any polyatomic species, independent of the coordinate system, it requires no fit to anharmonic models or any other kind of external intervention, and it can be used as a “black box” for any molecular system.
Acknowledgements
This work was partially supported by the Junta de Extremadura, Spain (Project No. PRI07A009).
References
- W. L. Hase, R. J. Duchovic, X. Hu, A. Komornicki, K. F. Lim, G. h. Lu, G. H. Peslherbe, K. N. Swamy, S. R. Van de Linde, A. Varandas, H. Wang and R. J. Wolf, Quantum Chemistry Program Exchange Bulletin, 1996, 16, 671 Search PubMed.
- C. W. Eaker and G. C. Schatz, J. Chem. Phys., 1984, 81, 2394 CrossRef CAS.
- C. W. Eaker, G. C. Schatz, N. DeLeon and E. J. Heller, J. Chem. Phys., 1984, 81, 5913 CrossRef.
- J. Binney and D. Spergel, Monthly Roy. Astron. Soc., 1964, 206, 159 Search PubMed.
- C. C. Martens and G. S. Ezra, J. Chem. Phys., 1985, 83, 2990 CrossRef CAS.
- R. J. Duchovic and G. C. Schatz, J. Chem. Phys., 1986, 84, 2239 CrossRef CAS.
- G. C. Schatz, Comput. Phys. Commun., 1988, 51, 135 CrossRef CAS.
- K. S. Sorbie, Mol. Phys., 1976, 32, 1577 CrossRef CAS.
- K. S. Sorbie and N. C. Handy, Mol. Phys., 1977, 33, 1319 CrossRef CAS.
- K. S. Sorbie and N. C. Handy, Mol. Phys., 1976, 32, 1327 CrossRef CAS.
- R. T. Skodje, F. Borondo and W. R. Reinhardt, J. Chem. Phys., 1985, 82, 4611 CrossRef CAS.
- B. R. Johnson, J. Chem. Phys., 1985, 83, 1204 CrossRef CAS.
- E. E. Aubanel and D. M. Wardlaw, J. Chem. Phys., 1988, 88, 495 CrossRef CAS.
- Q. Sun, J. M. Bowman and B. Gazdy, J. Chem. Phys., 1988, 89, 3124 CrossRef CAS.
- A. Jackle and H.-D. Meyer, J. Chem. Phys., 1995, 102, 5605 CrossRef.
- F. J. Castillo, F. J. Aoiz and L. Bañares, J. Chem. Phys., 2006, 125, 124316 CrossRef.
- C. Rangel, J. C. Corchado and J. Espinosa-Garcia, J. Phys. Chem. A, 2006, 110, 10375 CrossRef CAS.
- J. Sanson, J. C. Corchado, C. Rangel and J. Espinosa-Garcia, J. Phys. Chem. A, 2006, 110, 9568 CrossRef CAS.
- J. Espinosa-Garcia, J. L. Bravo and C. Rangel, J. Phys. Chem. A, 2007, 111, 2761 CrossRef CAS.
- J. Espinosa-Garcia, J. Phys. Chem. A, 2007, 111, 3497 CrossRef CAS.
- J. Espinosa-Garcia, J. Phys. Chem. A, 2007, 111, 5792 CrossRef CAS.
- J. Espinosa-Garcia, J. Phys. Chem. A, 2007, 111, 9654 CrossRef CAS.
- J. Espinosa-Garcia, Chem. Phys. Lett., 2008, 454, 158 CrossRef CAS.
- J. Espinosa-Garcia and J. L. Bravo, J. Phys. Chem. A, 2008, 112, 6059 CrossRef CAS.
- C. Rangel, J. C. Corchado and J. Espinosa-Garcia, Phys. Chem. Chem. Phys., 2008, 10, 6776 RSC.
- J. Espinosa-Garcia, J. Chem. Phys., 2009, 130, 054305 CrossRef.
-
W. L. Hase, R. J. Duchovic, X. Hu, A. Komornicki, K. F. Lim, D.-h. Lu, G. H. Peslherbe, K. N. Swamy, S. R. Van de Linde, A. Varandas, H. Wang, R. J. Wolf, VENUS96: A General Chemical Dynamics Computer Program, QCPE Bull. 1996, 16, p. 43.
- Although improved binning procedures have been suggested and used in previous work, we have selected this rounding procedure for its simplicity. Note that we are applying the same procedure throughout the paper, independent of the way we compute the action variable and, therefore, using a more sophisticated binning procedure will not alter the comparisons performed and the conclusions obtained.
- J. C. Corchado and J. Espinosa-Garcia, J. Chem. Phys., 1997, 106, 4013 CrossRef CAS.
- M. Yang and J. C. Corchado, J. Chem. Phys., 2007, 126, 214312 CrossRef.
|
| This journal is © the Owner Societies 2009 |
Click here to see how this site uses Cookies. View our privacy policy here. 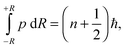


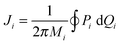
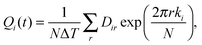


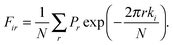

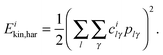
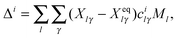




 (see eqns (23) and (26)), while eqn (25) allows one to measure the accuracy of the computation of the potential energy per mode. Note that Evib is exactly known from the QCT analysis of the results, while
(see eqns (23) and (26)), while eqn (25) allows one to measure the accuracy of the computation of the potential energy per mode. Note that Evib is exactly known from the QCT analysis of the results, while 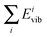 is computed from the present approach. If our approach is correct, eqn (23) has to be fulfilled.
is computed from the present approach. If our approach is correct, eqn (23) has to be fulfilled.
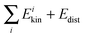 versus Evib (eqn (26)). Panel a shows the harmonic results while panel b includes Coriolis coupling in the kinetic energy. As one can see, the harmonic results are very close to the y = x line, meaning that the sum of the kinetic contributions to the energy is very close to its exact value. Thus, the mean unsigned difference between
versus Evib (eqn (26)). Panel a shows the harmonic results while panel b includes Coriolis coupling in the kinetic energy. As one can see, the harmonic results are very close to the y = x line, meaning that the sum of the kinetic contributions to the energy is very close to its exact value. Thus, the mean unsigned difference between  and Evib is only 0.39 kcal/mol. One can therefore assume that the kinetic contribution to the normal mode energy is satisfactorily calculated under the harmonic approach, and that the Coriolis coupling has a minor influence. However, some slight improvement is found, as seen in the somewhat minor scattering of the points around the y = x line seen in panel b, and in the mean unsigned difference between
and Evib is only 0.39 kcal/mol. One can therefore assume that the kinetic contribution to the normal mode energy is satisfactorily calculated under the harmonic approach, and that the Coriolis coupling has a minor influence. However, some slight improvement is found, as seen in the somewhat minor scattering of the points around the y = x line seen in panel b, and in the mean unsigned difference between  and Evib, which is 0.32 kcal/mol. Since including the Coriolis coupling has a negligible computational cost, it is advisable to take it into account.
and Evib, which is 0.32 kcal/mol. Since including the Coriolis coupling has a negligible computational cost, it is advisable to take it into account.
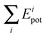 versus Edist. Panel a shows the harmonic results (eqn (13)), panel b the anharmonic results computed by relaxation of the ith mode (eqn (17)), panel c the anharmonic results computed by excitation of the ith mode (eqn (16)), and panel d the anharmonic results obtained by averaging the relaxation and excitation energies (eqn (19)). (The mean unsigned differences are 0.90, 1.18, 1.37, and 0.14 kcal/mol, for panels a through d.)
versus Edist. Panel a shows the harmonic results (eqn (13)), panel b the anharmonic results computed by relaxation of the ith mode (eqn (17)), panel c the anharmonic results computed by excitation of the ith mode (eqn (16)), and panel d the anharmonic results obtained by averaging the relaxation and excitation energies (eqn (19)). (The mean unsigned differences are 0.90, 1.18, 1.37, and 0.14 kcal/mol, for panels a through d.)
 and Edist (0.14 kcal/mol).
and Edist (0.14 kcal/mol).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories were run, of which 878 were reactive. The rotational and collision energies were randomly sampled according to a Maxwell-Botzmann distribution of energies at 2000 K, and the NH3 molecule was at its vibrational ground state. The impact parameter was randomly chosen between 0 and 2.5 Å.
000 trajectories were run, of which 878 were reactive. The rotational and collision energies were randomly sampled according to a Maxwell-Botzmann distribution of energies at 2000 K, and the NH3 molecule was at its vibrational ground state. The impact parameter was randomly chosen between 0 and 2.5 Å.

