Photoabsorption spectra from adiabatically exact time-dependent density-functional theory in real time
Mark
Thiele
and
Stephan
Kümmel
*
Physikalisches Institut, Universität Bayreuth, D-95440, Bayreuth, Germany. E-mail: stephan.kuemmel@uni-bayreuth.de
First published on 22nd April 2009
Abstract
Photoabsorption spectra for 2-electron singlet systems are obtained from the real-time propagation of the time-dependent Kohn–Sham equations in the adiabatically exact approximation. The latter is provided by the exact ground state exchange–correlation potential corresponding to the instantaneous density. The results are compared to exact data obtained from the solution of the interacting Schrödinger equation. We find that the adiabatically exact approximation provides very good results for transitions of genuinely single excitation character but yields incorrect results if double excitations contribute substantially. However, the extent of the error can vary: some double excitations are just shifted in energy whereas others are missed completely. These situations are analyzed with the help of transition densities.
I. Introduction
The importance of time-dependent linear response theory for the study of electronic matter can hardly be overestimated. From the calculation of dynamic polarizabilities, van der Waals coefficients and frequency-dependent dielectric constants to excitation spectra, linear response theory has a broad range of applications for atoms, molecules, clusters, and solid-state systems.1–6For the treatment of electrical response in the absence of magnetic fields time-dependent density-functional response theory is by now the most important method available. Its first application to the calculation of photoabsorption cross-sections of atoms7 even predates its formal foundation within the framework of time-dependent density functional theory (TDDFT).8TDDFT in the time-dependent Kohn–Sham (TDKS) framework maps the interacting many-electron problem onto a system of non-interacting particles which yield the same time-dependent density n(r,t). The evolution of the corresponding single-particle Schrödinger equations is governed by an effective potential incorporating all non-classical many-body effects into an exchange correlation (xc) contribution vxc(r,t). The xc potential is a well-defined but generally unknown functional of the time-dependent density that needs to be approximated in TDDFT applications.
A rigorous method to calculate excitation energies9–11 within linear response is based on the time-dependent exchange correlation kernel
 | (1.1) |
A second way of calculating excitation energies is provided by the propagation (real-time solution) of the TDKS equations. Here the photoabsorption spectrum is obtained from time-dependent dipole18–21 or higher order moments22 of an initially perturbed electronic configuration. Beside an accurate initial state this method requires an approximation of the exact time-dependent vxc. Once again, most available approximations are adiabatic, i.e., neglecting memory effects in vxc, so the problem with respect to states of multiple excitation character persists.
Consequently, the shortcomings of the adiabatic approximation to fxc or vxc that are responsible for the missing multiply excited states are attracting considerable attention.12,23 However, the issue is an involved one as basically all available approximations are not only adiabatic in time but also lack the correct spatially nonlocal dependency on the density. Thus, errors due to missing temporal nonlocality and incorrect spatial nonlocality are indistinguishably entangled in these approximations. In order to rigorously determine the consequences of the adiabatic approximation one needs to compare exact excitation energies to those obtained with the adiabatically exact fxc or vxc, i.e., functionals that are adiabatic in time but have the fully correct spatial dependency on the density.
A reliable scheme which allows to numerically construct the adiabatically exact (AE) approximation for vxc has recently been developed for the propagation approach.24 Its basic idea is to replace the time-dependent vxc by the exact ground-state xc-potential vxc,0 corresponding to the instantaneous density. In order to perform the desired comparison, one needs to resort to simple systems like the 2-electron singlet in one dimension, where both the exact and the adiabatically exact real-time propagations are possible.24–27 Previous studies of these model systems have concentrated on the regime of strong, nonperturbative, nonlinear excitations. In this article we will extend the developed methods to the real-time calculation of linear response photoabsorption spectra. The exact quantities as obtained from the propagation of the interacting time-dependent Schrödinger equation (TDSE) are compared to those stemming from the solution of the TDKS equations in the adiabatically exact approximation (AE-TDKSE).
This comparison reveals that some excitations are very accurately reproduced by the adiabatically exact approximation while others are found at wrong energies or are not present altogether. As we will see, the reproduced transitions can be related to single excitations and the failures to states having substantial double excitation character. We also demonstrate that transition densities can provide valuable additional and complementary information.
The article is organized as follows: in section two we introduce the governing equations of the studied systems and the boost-method used for the linear response calculations. Section three comprises our results including the spectra and transition densities before we provide a summary in section four.
II. Theoretical background
In the following section we introduce the governing equations of the 2-electron singlet system and the real-time formalism for linear response calculations. We will only consider the case of one spatial dimension, z.A Governing equations for the 2-electron singlet system
The one-dimensional (1D) 2-electron system is described by the Hamiltonian operator | (2.2) |
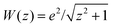 for Vee (always) and for the external potential whenever we consider the helium atom. This 1D model system has been found to reproduce the essential features of correlated electron dynamics.28–36
for Vee (always) and for the external potential whenever we consider the helium atom. This 1D model system has been found to reproduce the essential features of correlated electron dynamics.28–36
The eigenstates ψi(z1,z2) of (2.2) are the solutions of the interacting static Schrödinger equation (SE)
| H0ψi = Eiψi | (2.3) |
| ψi(z1,z2) = ±ψi(−z1,−z2) | (2.4) |
| ρif(z) = 2∫dz′ψi(z,z′)ψf(z,z′) | (2.5) |
Finally, as a closing remark on the static equations presented so far, we note that it is an important aspect of our work that in 1D it is possible to numerically invert the SE24 to find vext,0(z) for a given ground state density n0(z). This will also prove to be extremely useful in the (TD)DFT case which we discuss below.
The time-evolution of a general symmetric wave function ψ(z1,z2,t) follows from the solution of the time-dependent Schrödinger equation, iℏ∂tψ = Hψ, governed by
 | (2.6) |
| n(z,t) = 2∫|ψ(z,z′,t)|2dz′. | (2.7) |
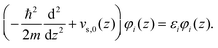 | (2.8) |
 | (2.9) |
For our studies, it is a most relevant feature of the KSE that it can be inverted to obtain the vs,0(z,t0) corresponding to a given density n0(z) = n(z,t0) at a fixed time t0 (i.e., interpreting n(z,t0) as a ground-state density). In this way the exact ground state xc potential can be obtained from
| vs,0(z,t0) = vext,0(z,t0) + vh(z,t0) + vxc,0(z,t0), | (2.10) |
v xc,0 is thus a spatially nonlocal functional of the corresponding ground state density. For the two-electron singlet system the exchange contribution to vxc is simply vx = −1/2vh so that in the following vhx = vh + vx = 1/2vh will often be separated from vc.
On the other hand, the exact time-dependent quantities are related to vext of eqn (2.6)via the usual expression
| vs(z,t) = vext(z,t) + vh(z,t) + vxc(z,t). | (2.11) |
As mentioned above these memory effects of vxc (or equivalently the frequency dependence of fxc) are crucial for TDDFT to reproduce the complete spectrum of excitations. Hence it is of considerable interest to study the specific situation when only the memory effects are missed by the employed approximation while the spatial dependence is taken into account exactly. This can be realized by the adiabatically exact approximation which is defined by treating the time-dependent density at a fixed time t = t0 as a ground state density, i.e., n(z,t0) = n0(z), and by replacing vxc(z,t0) by the exact vxc,0[n0(z′)](z) of ground state DFT. The latter quantity is generally unknown. However, it can be constructed numerically for 1D 2-electron singlet systems by using eqn (2.10).24 This substitution ensures that the full spatial nonlocality of vxc is treated exactly while memory effects are excluded. In this respect, the adiabatically exact approximation is fundamentally different from commonly used adiabatic approximations. It offers the chance to investigate exclusively the influence of memory effects on the excitation spectrum, allowing for unprejudiced insights into the nature of memory in vxc.
B Excitation energies from real-time TDDFT
In order to obtain photoabsorption spectra from propagating the TDSE or AE-TDKSE we need to apply a small initial perturbation to the system. For the dipole response this is done by boosting the correlated wave function according to | (2.12) |
| d(t) = ∫dzn(z,t)z. | (2.13) |
 | (2.14) |
| q(t) = ∫dzn(z,t)z2. | (2.15) |
The possibility to store the whole time-evolution of the density allows us to obtain the Fourier transform δn(z,ω) of the AE density fluctuation δn(z,t). The former evaluated at the excitation frequency ω0f is proportional to ρ0f,41, i.e.
| Im δn(z,ω0f) ∼ρ0f(z) | (2.16) |
C Relation to the Casida matrix approach
A more common way to obtain linear response excitation energies within TDDFT is via the frequency-dependent xc kernel. The Casida equation11 allows to derive the exact transition energies from (TD)DFT quantities. However, two density functionals are required as an input: first the ground state (DFT) vxc,0 is necessary to obtain the correct Kohn–Sham eigenvalues and eigenstates, secondly the frequency-dependent xc-kernel of TDDFT is needed to transform the KS eigenvalues into the exact excitation energies.Another issue relevant for the Casida formulation is the error introduced by the truncation of the underlying infinite-dimensional matrix equation. It is reasonable to assume that this approximation will only affect the high transition energies. Naturally, a related problem occurs in real-time propagation, where excitations above a certain energy will no longer be represented on the chosen discrete time coordinate grid.
Finally, the Casida formalism requires diagonalization of the truncated matrix system. Here some approaches rely on the so-called single pole approximation.9,23 Obviously, questions related to the diagonalization are completely circumvented in the real-time propagation.
III. Results and discussion
In the following we investigate the spectra of characteristic 1D 2-electron systems: the soft-core helium atom24,30,31,34 characterized by the ground state potential vext,0(z) = −2W(z), “Hooke’s atom” with vext,0(z) = (k/2)z2 (Hooke) and the “anharmonic Hooke’s atom” characterized by vext,0(z) = (k/2)(z2 +![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) z6) (A6-Hooke) with k = 0.1 a.u. and
z6) (A6-Hooke) with k = 0.1 a.u. and ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) = 0.01 a.u.27 (we use Hartree atomic units unless stated otherwise). The anharmonic term has been introduced to A6-Hooke to deliberately avoid the special properties of the harmonic system. The different systems are summarized in Table 1. The initial state for any time-dependent process is the ground state of the particular system. Quite generally, one should keep in mind that due to the finite numerical accuracy of the AE-TDKSE scheme, smaller spectral features should not be overinterpreted.
= 0.01 a.u.27 (we use Hartree atomic units unless stated otherwise). The anharmonic term has been introduced to A6-Hooke to deliberately avoid the special properties of the harmonic system. The different systems are summarized in Table 1. The initial state for any time-dependent process is the ground state of the particular system. Quite generally, one should keep in mind that due to the finite numerical accuracy of the AE-TDKSE scheme, smaller spectral features should not be overinterpreted.
A Helium
The soft-core helium system has the typical features of an atomic system in the sense of decreasing energy level spacings up to the first ionization threshold followed by a continuous spectrum.28,31,33 This is reflected in the dipole and quadrupole power spectra shown in Fig. 1 and 2. The numerical reliability of the AE-TDKSE propagation results is restricted to the energy range below ω≈ 0.7 a.u. In this regime, the inversion algorithms have converged sufficiently. The figures show that in the trust region the exact spectra are extremely well reproduced by the adiabatically exact ones. All transition peaks appear and are located almost at the exact energies. The latter were also calculated from the static SE (2.3) and agree with the values reported in Ref. 35. These findings imply that in this energy regime the xc kernel can only be weakly frequency dependent and the exact ground-state kernel is able to reproduce all transitions correctly. Thus, for the helium atom the AE approximation is extremely powerful not only for strong, non-perturbative fields,24 but also in the linear response regime.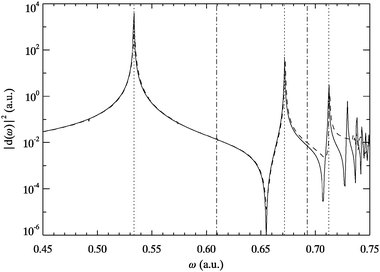 | ||
| Fig. 1 Dipole power spectrum for helium obtained from TDSE (solid line) and AE-TDKSE (dashed line). Vertical lines indicate the first five transition energies from the ground state to singlet states of odd (dotted) and even parity (dotted-dashed) as obtained from eqn (2.3). | ||
 | ||
| Fig. 2 Quadrupole power spectrum for helium obtained from TDSE (solid line) and AE-TDKSE (dashed line). Vertical lines indicate the first five transition energies from the ground state to singlet states of odd (dotted) and even parity (dotted-dashed) as obtained from eqn (2.3). | ||
In trying to understand the excellent performance of the AE approximation we now investigate the nature of the observed excitations. To this end we project the correlated final states ψf on symmetric KS product wave functions
 | (3.17) |
| ij | f | |||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | |
| 00 | 0.99 | |||||
| 01 | 0.92 | 0.02 | ||||
| 02 | 0.97 | |||||
| 03 | 0.03 | 0.90 | 0.03 | |||
| 04 | 0.93 | |||||
| 05 | 0.05 | 0.82 | ||||
| 06 | 0.04 | |||||
| 07 | 0.09 | |||||
| 09 | 0.01 | |||||
| 12 | 0.02 | |||||
The transition densities for helium are shown in Fig. 3. They can be interpreted as a momentary picture of the density redistribution during a transition: negative regions correspond to density removal while positive values signal density accumulation.42,43 As a consequence of symmetry, the transition density is always antisymmetric for dipole and symmetric for quadrupole excitations. For helium we find for the dipole transitions a purely left–right oscillation (sloshing mode) and for quadrupole transitions an inward–outward redistribution (breathing mode) of decreasing intensity for growing energy. These patterns provide a hydrodynamic interpretation of the electron motion during a transition.
 | ||
| Fig. 3 Exact transition densities ρ0n of helium excitations for n = 1 (solid), 2 (dotted), 3 (dashed) 4 (dotted-dashed) and 5 (triple-dotted-dashed). | ||
The discussion so far and the excellent performance of the AE approximation begs the natural question: Where are the double excitations that are expected to be missed by the adiabatically exact approximation? Unfortunately (for our analysis), for the 1D helium atom they only appear above the first ionization threshold.28,44 The lowest double excitations are in fact embedded in the one particle ionization continuum and thus have the character of autoionizing or Fano resonances.45,46 They can only be expected at energies around 1.3 a.u.28 which is far beyond the numerical accuracy of our AE-TDKSE scheme. Even if this regime could be reached, the peculiar degeneracy of a single and a double excitation which is characteristic of a Fano resonance would very likely complicate the analysis. Thus, we will now consider systems where the double excitations lie in the energy regime that can be resolved by the AE-TDKSE scheme.
To develop an intuition for what kind of systems one needs to study in order to find low-lying double-excitations, it is helpful to look at the problem from the KS perspective of independent particles. Due to the Coulombic asymptotics of the KS potential the single particle energy level spacing is quickly decreasing for growing energies (Rydberg series). This means that infinitely many single particle transitions are found at energies lower than one of the first double excitation. In order to circumvent this situation one needs a system with a more constant spacing of the energy levels. This requirement takes us to another typical 1D singlet system, namely Hooke’s atom. Here the intuitive argument based on the KS transitions implies that the excitation of two electrons to the first excited state (i.e., a double excitation) will be roughly in the energy range of the transition of one electron to the second excited state (one of the lower single excitations).36 As the energy spectrum of the harmonic external potential is completely discrete there is also no issue with Fano-type degeneracies.
B Hooke’s atom
The dipole response of Hooke’s atom is shown in Fig. 4. For this systems we found the AE-TDKSE results to be converged for ω < 1 a.u. Here the power spectrum is more irregular with respect to the order of positive and negative parity than for helium. Clearly the dominant transition for dipole excitations is at the harmonic frequency ω01 = (k/m)½, which is well reproduced by the AE-TDKSE results. This agreement is a consequence of the fact that to first order linear response the dipole boost resembles an applied time-dependent dipole field. Thus the response to the latter in Hooke’s atom is exactly reproduced by the adiabatically exact approximation due to the applicability of the harmonic potential theorem.27,47 The dominance of the harmonic frequency leads to suppression of higher dipole active transitions like f = 4,5 in agreement with almost vanishing oscillator strengths of these excitations.48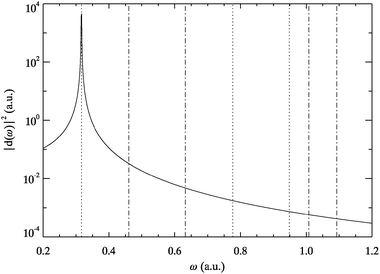 | ||
| Fig. 4 Dipole power spectrum for Hooke’s atom obtained from TDSE (solid line) and AE-TDKSE (dashed line directly on top). Vertical lines indicate transition energies of the ground state to singlet states of odd (dotted) and even parity (dotted-dashed). | ||
The quadrupole power spectrum (cf.eqn (2.14)) shown in Fig. 5 reveals that instead of the excitations f = 2,3 there is only one transition at ω≈ 0.5 a.u. in the AE approximation. Apparently we have finally encountered a situation where the adiabatically exact approximation does not yield the proper excitation frequency.
 | ||
| Fig. 5 Quadrupole power spectrum for Hooke’s atom obtained from TDSE (solid line) and AE-TDKSE (dashed line). Vertical lines indicate transition energies of the ground state to singlet states of odd (dotted) and even parity (dotted-dashed). | ||
Consequently, we investigate once more the single particle character of the relevant excitations. The projections of the final states on the Hooke KS basis are shown in Table 3. We find that, in contrast to the helium atom, even the lower states have nonvanishing double excitation contributions. The transition f = 1, though, is still predominantly of single excitation character in agreement with the ability of the AE-TDKSE to reproduce the corresponding peak in the spectrum. For f = 2, 3 there is already a strong contribution of the Φ11 product state which can explain the failure of the AE-TDKSE in this energy regime.
| ij | f | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 00 | 0.92 | 0.02 | 0.03 | ||||
| 01 | 0.81 | 0.10 | 0.05 | ||||
| 02 | 0.54 | 0.35 | |||||
| 03 | 0.03 | 0.72 | 0.18 | ||||
| 04 | 0.05 | 0.13 | |||||
| 05 | 0.05 | ||||||
| 11 | 0.07 | 0.43 | 0.40 | ||||
| 12 | 0.14 | 0.16 | 0.54 | ||||
| 13 | 0.02 | 0.49 | |||||
| 14 | 0.01 | 0.02 | |||||
| 22 | 0.14 | 0.36 | |||||
| 23 | 0.16 | ||||||
To obtain a better understanding of the relevant excitations we once more look at the transition densities. For the first six excitations they are shown in Fig. 6 and 7. We find sloshing (f = 1) and breathing (f = 2) type excitations as in the helium atom but also higher order transitions (f = 3–6) that no longer show a structure which can easily be related to one of these two types.
 | ||
| Fig. 6 Exact transition densities ρ0n of Hooke excitations for n = 1 (solid), 2 (dotted) and 3 (dashed). | ||
 | ||
| Fig. 7 Exact transition densities ρ0n of Hooke excitations for n = 4 (solid), 5 (dotted) and 6 (dashed). | ||
The transition densities can further be used to sort out which excitation is reproduced by the AE approximation and which is not. Based on the structure of the transition density, one can identify which exact transition belongs to which (shifted) AE peak. The adiabatically exact transition densities obtained from the Fourier transform of the time-dependent density (see above) provide some evidence that the peak at ω≈ 0.5 a.u. should correspond to the f = 2 excitation: as shown in Fig. 8 the structure of the first two transitions present in the AE spectrum closely resembles that of the exact excitations f = 1,2. This means that the second transition is properly reproduced by the AE-TDKSE with respect to its breathing-type character but it is shifted to the wrong energy. At the same time the f = 3 excitation is missed completely by the AE approximation. So despite the fact that in view of table 3 both the f = 2 and the f = 3 transitions could be termed “double excitations” the AE approximation treats them quite differently.
 | ||
| Fig. 8 Adiabatically exact transition densities of Hooke obtained from the Fourier transform of the time-dependent AE-TDKSE density (see text). The shown transition densities correspond to the adiabatically exact transitions found at ω≈ 0.32 (solid) and 0.50 a.u. (dotted), cf.Fig. 4 and 5. All curves were scaled so that the peak heights are roughly the same to allow for better comparison with the exact transition densities of Fig. 6. | ||
C Anharmonic Hooke’s atom
To obtain a more complex structure of the dipole response we finally turn to the anharmonic version of Hooke’s atom. The dipole power spectrum of A6-Hooke shown in Fig. 9 indicates that the first transition is well reproduced but the AE-TDKSE produces only one peak at ω≈ 1.3 a.u. instead of the f = 4 and f = 5 excitations. These energies are still well within the numerical validity regime of the AE-TDKSE which extends up to ω≈ 1.8 a.u. From the quadrupole power spectrum in Fig. 10 we can infer that the AE approximation produces a peak at ω≈ 0.77 a.u. instead of the f = 2 and 3 peaks. By varying the boost parameter we found the peaks at ω≈ 0.88 and 1.74 a.u. to be higher order effects that can be neglected in our discussion of the linear response regime. The excitations to f = 6,7 are not present in the AE spectrum. One may speculate that the AE-TDKSE scheme might still be approximately valid around ω≈ 2 a.u. and that thus the AE approximation reproduces only one peak (ω≈ 1.9 a.u.) in the range of the f = 6,7,8 quadrupole triple. This would correspond to the AE-TDKSE producing only one peak among the quadrupole double f = 2,3 and the dipole double f = 4,5 respectively. In any case we have encountered two more situations where peaks are shifted to wrong energies or missing completely from the AE spectrum. | ||
| Fig. 9 Dipole power spectrum for A6-Hooke obtained from TDSE (solid line) and AE-TDKSE (dashed line). Vertical lines indicate transition energies of the ground state to singlet states of odd (dotted) and even parity (dotted-dashed). | ||
 | ||
| Fig. 10 Quadrupole power spectrum for A6-Hooke obtained from TDSE (solid line) and AE-TDKSE (dashed line). Vertical lines indicate transition energies of the ground state to singlet states of odd (dotted) and even parity (dotted-dashed). | ||
The projections for A6-Hooke are shown in Table 4. Again, a strong double excitation character is present for f > 1. One may wonder whether this difficulty is generally just a consequence of the chosen basis set. To check this we also used the single particle states corresponding to the vext,0 of A6-Hooke as a basis (instead of the KS orbitals) and performed the overlap analysis once more. This leads to numbers quite similar to the ones reported in Table 4.
| ij | f | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 00 | 0.95 | 0.03 | 0.02 | |||||
| 01 | 0.91 | 0.07 | ||||||
| 02 | 0.31 | 0.63 | 0.03 | |||||
| 03 | 0.36 | 0.61 | ||||||
| 04 | 0.30 | |||||||
| 11 | 0.04 | 0.66 | 0.26 | 0.03 | ||||
| 12 | 0.08 | 0.56 | 0.31 | |||||
| 13 | 0.02 | 0.32 | 0.43 | |||||
| 14 | ||||||||
| 22 | 0.06 | 0.66 | 0.18 | |||||
| 23 | 0.05 | |||||||
| 33 | 0.02 | |||||||
Once more the success for the f = 1 transition seems to be a consequence of the predominant single excitation character of ψ1. The failure for f > 1 is again a consequence of considerable double excitation contribtion. It appears especially plausible that f = 6 is missing as ψ6 is exclusively of double excitation character.
The transition densities for A6-Hooke are shown in Fig. 11 to 12. Similar to Hooke’s atom we only find exclusive sloshing and breathing signatures for the lowest transitions. The higher excitations show a variety of patterns.
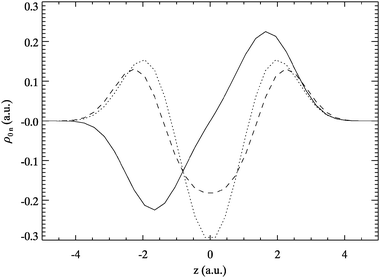 | ||
| Fig. 11 Exact transition densities ρ0n of A6-Hooke excitations for n = 1 (solid), 2 (dotted) and 3 (dashed). | ||
 | ||
| Fig. 12 Exact transition densities ρ0n of A6-Hooke excitations for n = 4 (solid), 5 (dotted), 6 (dashed) and 7 (dotted-dashed). | ||
For sorting out which AE excitation corresponds to which exact one the transition densities are again a helpful tool. Comparing the AE transition density at ω≈ 0.77 to the ones for f = 2 and 3 in Fig. 13 shows that the AE excitation rather resembles f = 2. This implies that the latter transition is shifted to the wrong excitation energy while f = 3 is completely absent. This is noteworthy because ψ3 has a smaller double excitation contribution than ψ2. A similar situation is found for f = 4,5 as shown in Fig. 14.
 | ||
| Fig. 13 AE transition density of A6-Hooke at ω≈ 0.77 a.u. (solid) and the exact ρ0f for f = 2 (dotted) and 3 (dotted-dashed). All curves were scaled to allow for better comparison. | ||
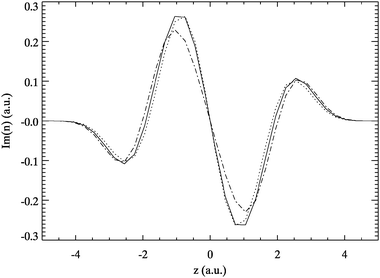 | ||
| Fig. 14 AE transition density of A6-Hooke at ω≈ 1.3 a.u. (solid) and the exact ρ0f for f = 4 (dotted) and 5 (dotted-dashed). All curves were scaled to allow for better comparison. | ||
IV. Summary and outlook
We have explored the performance of the adiabatically exact approximation—i.e., no temporal nonlocality but full spatial nonlocality—for the linear response of 2-electron systems. It is known that this approximation is not able to generally provide the exact excitation energies. This property follows from the Casida equation in a formal way but one is only beginning to understand its practical consequences for the adiabatically exact spectrum.12 In the present article we examine this relation more closely.So far, it has commonly been assumed that adiabatic approximations are missing the transitions of double excitation character, or at least shift them to wrong energies. On the other hand they are expected to work for single excitations. We found that this concept generally applies to the AE approximation, but that the situation is involved when double excitations are present.
For the lower discrete part of the spectrum of the helium atom the transitions are of genuinely single excitation character and hence the AE-TDKSE reproduces all peaks of the exact spectrum. It even locates them at the virtually exact energies. These findings imply that the xc kernel in this energy regime is well represented by its ω→ 0 limiting case, i.e., the ground state kernel. This situation is a consequence of the special nature of the system. Here double excitations are to be expected only above the first ionization threshold where they take the form of autoionizing resonances embedded in the one particle continuum.
The situation is different in the Hooke-type systems that we studied. Here large parts of the spectrum are incorrectly predicted by the AE approximation, i.e., peaks are shifted to wrong energies or missed completely. Already at the lower energies the double excitation character of a given transition is non-negligible. However, it is not straightforward to relate the failures for a specific transition to the corresponding magnitude of the double excitation contribution. Apparently it is not enough to consider the single particle character of an excitation to infer whether it will be missed or just shifted by the AE approximation.
We found transition densities to be a suitable tool to get deeper insight into the structure of specific excitations. Although they also do not provide a clear criterion to identify particularly nonadiabatic transitions, they allow for a better comparison of certain transitions and facilitate matching of exact transitions to peaks that are incorrectly shifted in the AE spectrum.
Finally, the transition densities provide a route to a more intuitive hydrodynamic view of electronic excitations. Such a hydrodynamical perspective may be a new way to obtain an understanding of nonadiabatic effects.27,49
Acknowledgement
We acknowledge financial support by the Deutsche Forschungsgemeinschaft.References
- J. F. Dobson and B. P. Dinte, Phys. Rev. Lett., 1996, 76, 1780 CrossRef CAS.
- G. F. Bertsch, J.-I. Iwata, A. Rubio and K. Yabana, Phys. Rev. B, 2000, 62, 7998 CrossRef CAS.
- I. V. Tokatly and O. Pankratov, Phys. Rev. Lett., 2001, 86, 2078 CrossRef CAS.
- G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601 CrossRef CAS.
- J. R. Chelikowsky, L. Kronik and I. Vasiliev, J. Phys.: Condens. Matter, 2003, 15, R1517 CrossRef CAS.
- D. Rappoport and F. Furche, J. Am. Chem. Soc., 2004, 126, 1277 CrossRef CAS.
- A. Zangwill and P. Soven, Phys. Rev. A, 1980, 21, 1561 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS.
- M. Petersilka, U. Gossmann and E. K. U. Gross, Phys. Rev. Lett., 1996, 76, 1212 CrossRef CAS.
- E. K. U. Gross, J. F. Dobson and M. Petersilka, in Density Functional Theory, ed. R. F. Nalewajski, Springer, Berlin, 1996, pp. 81–172 Search PubMed.
- M. E. Casida, in Recent Advances in Density Functional Methods, Part I, ed. D. P. Chong, World Scientific Publishing, Singapore, 1995, pp. 155–192 Search PubMed.
- N. T. Maitra, F. Zhang, R. J. Cave and K. Burke, J. Chem. Phys., 2004, 120, 5932 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 302, 375 CrossRef CAS.
- D. J. Tozer and N. C. Handy, Phys. Chem. Chem. Phys., 2000, 2, 2117 RSC.
- R. J. Cave, F. Zhang, N. T. Maitra and K. Burke, Chem. Phys. Lett., 2004, 389, 39 CrossRef CAS.
- J. Neugebauer, E. J. Baerends and M. Nooijen, J. Chem. Phys., 2004, 121, 6155 CrossRef CAS.
- K. J. H. Giesbertz, E. J. Baerends and O. V. Gritsenko, Phys. Rev. Lett., 2008, 101, 033004 CrossRef CAS.
- K. Yabana and G. F. Bertsch, Phys. Rev. B, 1996, 54, 4484 CrossRef CAS.
- U. Saalmann and R. Schmidt, Z. Phys. D, 1996, 38, 153 CrossRef CAS.
- F. Calvayrac, P. G. Reinhard and E. Suraud, Ann. Phys. (N.Y.), 1997, 255, 125 CrossRef CAS.
- M. Marques, A. Castro, G. Bertsch and A. Rubio, Comput. Phys. Commun., 2003, 151, 60 CrossRef CAS.
- M. Mundt and S. Kümmel, Phys. Rev. B, 2007, 76, 035413 CrossRef.
- H. Appel, E. K. U. Gross and K. Burke, Phys. Rev. Lett., 2003, 90, 043005 CrossRef CAS.
- M. Thiele, E. K. U. Gross and S. Kümmel, Phys. Rev. Lett., 2008, 100, 153004 CrossRef CAS.
- I. D’Amico and G. Vignale, Phys. Rev. B, 1999, 59, 7876 CrossRef CAS.
- P. Hessler, N. T. Maitra and K. Burke, J. Chem. Phys., 2002, 117, 72 CrossRef CAS.
- M. Thiele and S. Kümmel, Phys. Rev. A, 2009 Search PubMed , submitted.
- S. L. Haan, R. Grobe and J. H. Eberly, Phys. Rev. A, 1994, 50, 378 CrossRef CAS.
- D. G. Lappas, A. Sanpera, J. B. Watson, K. Burnett, P. L. Knight, R. Grobe and J. H. Eberly, J. Phys. B, 1996, 29, L619 CrossRef CAS.
- D. Bauer, Phys. Rev. A, 1997, 56, 3028 CrossRef CAS.
- S. L. Haan and R. Grobe, Laser Phys., 1998, 8, 885 CAS.
- D. G. Lappas and R. van Leeuwen, J. Phys. B, 1998, 31, L249 CrossRef CAS.
- W.-C. Liu, J. H. Eberly, S. L. Haan and R. Grobe, Phys. Rev. Lett., 1999, 83, 520 CrossRef CAS.
- M. Lein, E. K. U. Gross and V. Engel, Phys. Rev. Lett., 2000, 85, 4707 CrossRef CAS.
- R. Panfili and W.-C. Liu, Phys. Rev. A, 2003, 67, 043402 CrossRef.
- E. Orestes, K. Capelle, A. B. F. da Silva and C. A. Ullrich, J. Chem. Phys., 2007, 127, 124101 CrossRef CAS.
- A. S. de Wijn, S. Kümmel and M. Lein, J. Comput. Phys., 2007, 226, 89 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- Time-dependent Density Functional Theory, ed. M. Marques, C. Ullrich, F. Nogueira, A. Rubio, K. Burke and E. Gross, Springer, Berlin, 2006 Search PubMed.
- M. Mundt, S. Kümmel, R. van Leeuwen and P.-G. Reinhard, Phys. Rev. A, 2007, 75, 050501 CrossRef.
- R. A. Broglia, G. Coló, G. Onida and H. E. Roman, Solid State Physics of Finite Systems, Springer, Berlin, 2004 Search PubMed.
- S. Kümmel, K. Andrae and P.-G. Reinhard, Appl. Phys. B, 2001, 73, 293 CrossRef CAS.
- S. Tretiak and S. Mukamel, Chem. Rev., 2002, 102, 3171 CrossRef CAS.
- To the best of our knowledge this applies to all atomic systems.
- U. Fano, Phys. Rev., 1961, 124, 1866 CrossRef CAS.
- H. Friedrich, Theoretical Atomic Physics, Springer, Heidelberg, 2006 Search PubMed.
- J. F. Dobson, Phys. Rev. Lett., 1994, 73, 2244 CrossRef CAS.
- The oscillator strengths 2|〈ψ0|z|ψf〉|2ω0f can be computed directly from the exact eigenstates.
- C. A. Ullrich and K. Burke, J. Chem. Phys., 2004, 121, 28 CrossRef CAS.
| This journal is © the Owner Societies 2009 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)