An in situXAS investigation of the kinetics of the ammonolysis of Ga₂O₃ and the oxidation of GaN

Abstract

The ammonolysis of β-Ga₂O₃ to α-GaN and the oxidation of α-GaN to β-Ga₂O₃ have been studied by means of in situX-ray absorption spectroscopy (XAS), transmission electron microscopy (TEM) and scanning electron microscopy (SEM). In situ X-ray absorption measurements on polycrystalline powder particles on the gallium K-edge during both reactions give detailed information about the reaction kinetics. We were able to extract this kinetics by fitting linear combinations of β-Ga₂O₃ and α-GaN spectra only. The kinetics of the ammonolysis can be described well by an extended Johnson–Mehl–Avrami–Kolmogorow model, while the oxidation kinetics can be modelled by a shrinking core model. Investigations by means of TEM and SEM support the assumptions in both models. Our experimental results and the models are discussed in terms of the reaction energetics and the reaction mechanisms.

---

1. Introduction

Both the nitride and the oxide of the main group element gallium, GaN and Ga₂O₃, have important applications in commercial electronics. GaN exists in two modifications, the hexagonal wurzite modification (α-phase) and the metastable cubic zinc blende modification (β-phase).¹α-GaN is a direct semiconductor with a band gap of 3.45 eV² and serves as basic material for different optoelectronic devices, especially for light emitting diodes (LEDs) with blue and ultraviolet light emission.³ Other applications of α-GaN are heterostructure field effect transistors or Schottky rectifiers. A detailed overview of its electronic applications is given in ref. 4. Ga₂O₃ exists in several modifications. The most important and stable modification is β-Ga₂O₃, which crystallises in a monoclinic structure with the space groupC2/m.⁵β-Ga₂O₃ is a direct semiconductor with a band gap of 4.9 eV and is used as sensor material and in different high-temperature electronics applications.⁶

A common way of synthesising α-GaN is the ammonolysis of β-Ga₂O₃:

Ga₂O₃ + 2NH₃→ 2GaN + 3H₂O (1)

The reaction is accomplished by flowing ammonia over a β-Ga₂O₃ powder in a temperature range between 600 and 1100 °C.^3,7 For the conversion from the oxide to the nitride, reaction intermediates in the form of gallium oxynitrides were postulated.⁸ However, neither neutron scattering-, XRD- nor XAS-studies were able to confirm the presence of these intermediates.⁹ It is thus very likely that the ammonolysis proceeds directly from β-Ga₂O₃ to α-GaN.

The backward reaction from α-GaN to β-Ga₂O₃ can be performed by oxidation of α-GaN with oxygen gas:

2GaN + 3/2O₂→ Ga₂O₃ + N₂ (2)

In several studies the oxidation of α-GaN was analysed concerning its kinetics and growth mechanism. Wolter et al.^10,11 studied the wet and dry oxidation of α-GaN epilayers and powders. They found that during the oxidation of epilayers the newly formed β-Ga₂O₃ phase is formed by layer-growth on the α-GaN surface. The linear dependence of the oxide layer thickness on the reaction time was interpreted in terms of a rate law of 0th order with interface controlled growth. The β-Ga₂O₃ fraction during the oxidation of α-GaN powder particles grows linearly with time, too.¹⁰ However, no mechanistic explanation of this observation was given. Xu et al.¹² showed that there is a second reaction mechanism at temperatures above 1000 °C at the end of the reaction: While the beginning and the middle part of the reaction can be explained well by interface control (see Wolter), the end of the reaction is dominated by diffusion control.

Although the ammonolysis of β-Ga₂O₃ is of such enormous importance, systematic and quantitative studies of the reaction mechanism and the reaction kinetics have not yet been performed. It is therefore one aim of this work to investigate the kinetics of the ammonolysis of β-Ga₂O₃ powders under in situ conditions and to understand the underlying reaction mechanism. The kinetics of the oxidation of α-GaN-epilayers could be modelled by interfacial controlled layer growth.¹⁰ This model must be modified concerning its geometry when α-GaN powders are used as reactants. Therefore, another aim of our studies is to investigate the kinetics of the oxidation of α-GaN powders also under in situ conditions and to describe the kinetics quantitatively. In both cases, we use X-ray absorption spectroscopy (XAS) under in situ conditions, i.e. in the temperature range between 600–900 °C and in flowing, reactive gases (ammonia and oxygen, respectively).

The paper is organized as follows: in section 2, experimental details on the used β-Ga₂O₃ and α-GaN samples, the X-ray absorption experiments and the data handling are described. Section 3 contains the experimental results for the in situammonolysis of β-Ga₂O₃ and the in situoxidation of α-GaN, and in section 4, the experimental results on the kinetics are modelled and detailed reaction mechanisms are proposed for both the ammonolysis and the oxidation reaction.

2. Experimental

2.1 Samples

The starting materials are commercial, polycrystalline powders of α-GaN (Aldrich, >99.99%) and Ga₂O₃ (Alfa Aesar, >99.999%). Prior to use, the Ga₂O₃ powder was annealed for one day at 1400 °C in air to convert the commercial mixture of α- and β-Ga₂O₃ to the thermodynamically stable phase of β-Ga₂O₃. The ammonolysis of gallium oxide was also investigated on β-Ga₂O₃ powders that were obtained during the oxidation of GaN powders.

Prior to and after the reactions SEM-micrographs were recorded on a scanning electron microscope (LEO/Zeiss 1450VP) equipped with an EDX system (Oxford INCA). In addition, the samples were investigated by transmission electron microscopy (TEM) using a 200 kV FEI Tecnai F20 equipped with an energy filter (Gatan GIF 2000) and EDX (EDAX).

2.2 XAS experiments

The XAS experiments were performed at beamlines C and X at HASYLAB (Hamburg, Germany) in transmission geometry. Measurements have been done on the Ga K-edge (10 367 eV), using Si (111) double crystal monochromators and as ionisation chamber gases a N₂–Ar mixture (90 : 10) for I₀ and I₁ and pure Ar for I_ref (see Fig. 1). As energy reference a pellet of a cobalt gallium alloy (CoGa), diluted with BN was used.¹³ For filtering higher harmonics, the monochromator was de-tuned to 60% of the maximum intensity.

Fig. 1 Experimental setup for the in situXAS measurements.

The flow rates of the used gases (He, O₂ and NH₃) were controlled by three mass flow controllers (MFC, each with 100 mL min⁻¹). The gas-tight furnace consists of a 250 mm long corundum tube with an inner dimension of 14 mm. Water cooled flanges with Kapton windows allow the X-rays to pass the furnace. Heating is done by a platinum wire around the corundum tube, which allows operating up to temperatures of 1200 °C.¹⁴ An overview of the in situ setup is given in Fig. 1.

In each experiment, 5 mg of the respective starting material (Ga₂O₃ or GaN) were mixed with 40 mg BN powder and filled into the sample holder consisting of MACOR-ceramics. In front of and behind the sample, BN windows are used to hold the powder in place. Transport of the reactive gas to the powder particles is ensured by holes in the sample holder.

The ammonolysis of Ga₂O₃ according to eqn (1) was performed with pure ammonia gas at reaction temperatures of 660, 780, and 840 °C. The oxidation of GaN according to eqn (2) was done in pure oxygen atmosphere at reaction temperatures of 840 and 780 °C. In all experiments the flow rates of ammonia respectively oxygen were set to 30 mL min⁻¹, and the sample temperature was measured with a thermocouple in close vicinity of the sample.

The spectra on the Ga K-edge were measured over an energy range from 10 167–11 267 eV. Two different measurement modes were used. The quick scanning EXAFS mode (QEXAFS)¹⁵ was used to analyze the reaction kinetics in situ. Conventional step-scanning EXAFS was used to record structural changes. Here, the reaction was quenched after 5 min by changing the gas atmosphere to helium. After recording the spectrum, another 5 min reaction/XAS spectrum cycle was done, until 5 or more consecutive spectra showed no further changes.

2.3 XAS raw data handling

The analysis of the XAS raw data was done with the program Athena,¹⁶ according to the standard XAS procedures.¹⁷ Data smoothing was performed with a 3-point adjacent averaging cycle with three iterations. The energy scale was aligned to the inflection point of a CoGa spectrum with E₀(CoGa) = E₀(Ga) = 10 367 eV. Background removal was done with the AutoBK code¹⁸ with Rbgk = 1.0 Å. Fourier transformation of the k³-weighted EXAFS function χ(k) was done with a Kaiser-Bessel window function in a k-range from 2.6–12.5 Å⁻¹. For Ga₂O₃ and GaN, both measured at room temperature, the corresponding raw data, the k³-weighted χ(k), and the radial EXAFS distribution functions are shown in Fig. 2–4.

Fig. 2 Raw X-ray absorption spectrum of Ga₂O₃ (a) and GaN (b) measured at room temperature.

Fig. 3 k ³-weighted χ(k) of Ga₂O₃ (a) and GaN (b) extracted from the spectra shown in Fig. 2.

Fig. 4 Radial EXAFS distribution function of Ga₂O₃ (a) and GaN (b) (Fourier transformation of Fig. 3).

3. Results

3.1 In situ spectra during the ammonolysis of Ga₂O₃ and the oxidation of GaN

At all investigated temperatures, the recorded spectra during the ammonolysis of Ga₂O₃ and the oxidation of GaN show that the conversion to the product phase, GaN, respectively, Ga₂O₃ is complete. The last spectrum during the ammonolysis equals the GaN standard in Fig. 2b, and the last spectrum of the oxidation conforms to the Ga₂O₃ standard in Fig. 2a. The complete conversion is confirmed by X-ray diffraction of the product powders. As an example, Fig. 5 shows the energy calibrated and normalized spectra for both the ammonolysis reaction and the oxidation reaction at 780 °C. In both cases one can see a continuous development from the initial to the end condition. The resulting radial EXAFS distribution functions (RDF) are shown in Fig. 6 as a function of time.

Fig. 5 Changes in the near edge region of the spectra during the ammonolysis of Ga₂O₃ at 780 °C (a) and the oxidation of GaN at 780 °C (b). The insets show the respective complete spectra.

Fig. 6 Changes in the k³-weighted radial EXAFS distribution function during the ammonolysis of Ga₂O₃ at 780 °C (a) and during the oxidation of GaN at 780 °C (b).

During the ammonolysis of Ga₂O₃, the 1st coordination shell in the radial EXAFS distribution function shows only slight changes. In contrast the second peak in the RDF increases rapidly. That results from the nature of the second coordination shell around Ga atoms in GaN and Ga₂O₃. In the nitride, there is a clearly defined 2nd coordination shell with 12 gallium neighbours in a distance of 3.18 Å, whereas in the oxide the 2nd shell is very diffuse, with 20 gallium neighbours in a distance range from 3.04–3.44 Å. So, the partially destructive interference in k-space leads to a smaller amplitude in R-space. The opposite time-dependent behaviour is observed during the oxidation of GaN. Again, there is no remarkable change in the 1st coordination shell, but now the peak in the RDF which represents the second coordination shell decreases with increasing time rapidly because the second shell in the product Ga₂O₃ is less well defined than in the starting material GaN, as explained above.

Finally we note that the differences in the amplitudes of the RDFs of the in situspectra in Fig. 6 and the references shown in Fig. 4 are caused by the higher temperature during the in situ measurements, resulting in higher dynamic disorder (Debye–Waller factors) of the atoms.

3.2 Extraction of the reaction kinetics

To analyze the reaction kinetics depicted in Fig. 5 and 6 quantitatively the normalised, time-dependent in situspectra, μ(E,t), and the extracted time-dependent χ(k,t) are fitted according to eqn (3) and (4) with a linear combination of GaN and Ga₂O₃ reference spectra.

μ(E,t) = a_μ(t)·μ(E)_Ga2O3 + b_μ(t)·μ(E)_GaN (3)

χ(k,t) = a_χ(t)·χ(k)_Ga2O3 + b_χ(t)·χ(k)_GaN (4)

Here, μ(E)_i and χ(k)_i (i = Ga₃O₃, GaN) are the time-independent, normalized spectra (in E- and k-space) of Ga₂O₃ and GaN, while the weighting factors a_μ(t), b_μ(t), a_χ(t), and b_χ(t) are time-dependent and describe the reaction kinetics. We consider μ(E,t) and χ(k,t) separately for the following reason. For μ(E,t), the fitting range in energy space is from 20 eV before the edge to 50 eV behind the edge. This conforms to a fit of the XANES region, which is sensitive to changes in the electronic structure of the samples. For χ(k,t) the fits in the k-space are done in a fitting range from 2.5–9.0 Å⁻¹. This conforms to an EXAFS fit, which is sensitive to structural changes during the reaction.

Fig. 7a shows one particular in situspectrum (solid line) during the ammonolysis corresponding to t = 80 min in the time series in Fig. 5a. Also shown is the fitted spectrum (big dots) according to eqn (3). One can see a nearly perfect adaptation to the experimental curve. The contributions of the reference spectra of Ga₂O₃ (dotted dashed line) and GaN (dotted line) to the fit are also plotted. The remaining residual (dashed line) is very small (<2% of the measured spectrum) over the whole fitting range, and it shows no structure. This means, that the XANES-region reflecting the electronic structure at this particular time during the ammonolysis reaction can be described very well by a linear combination of GaN and Ga₂O₃spectra only.

Fig. 7 Results of linear combination fits in E-space (a) and in k-space (b). The in situspectrum (solid line) was taken during the ammonolysis of Ga₂O₃ at 780 °C after 80 min.

Fig. 7b shows the corresponding fitting result in k-space. Again, the fit (big dots) is in very good agreement with the experimental curve (solid line). Thus, the EXAFS-region reflecting the local structure around gallium atoms at this particular time during the ammonolysis reaction can also be described by a linear combination of GaN and Ga₂O₃spectra only (residual <8% of the measured spectrum). In order to further elucidate the presence of reaction intermediates or other spectral compounds not explained by the reference spectra, the residual in Fig. 7b was Fourier transformed, just like a regular χ(k) function. However, no noticeable EXAFS RDF-like features were detected in the residual. In addition, neither a systematic time dependence of the residuals nor a correlation between residuals at consecutive time steps was found which clearly indicates that the residuals are only due to noise.

Similar results are obtained for all spectra that were taken during the ammonolyis of Ga₂O₃ and during the oxidation of GaN. At all points in time, both the electronic structure (XANES) as well as the local structure around Ga atoms (EXAFS) is in excellent agreement with the respective linear combination of the references according to eqn (3) and (4). This leads to the conclusion that no other phases than GaN and Ga₂O₃ are present during both the ammonolysis and the oxidation reactions (within our detection limit for a new phase being in the percent range). A further analysis of the occurring phases using detailed X-ray and neutron diffraction is beyond the scope of this paper and will be published in an up coming paper.⁹

Another important point comes out by normalizing the sum of the weighting factors a_μ(t) and b_μ(t), respectively, a_χ(t) and b_χ(t) to one and comparing the remaining independent factors b^norm_μ(t) (from the fits in E-space) and b^norm_χ(t) (from the fits in k-space). We find that during the ammonolysis and the oxidation, at all reaction temperatures and over the whole reaction time, b^norm_μ(t) is equal to the corresponding b^norm_χ(t) (as an example, see Fig. 8). This means that the changes in the electronic structure (XANES-region) and in the short range order around Ga (EXAFS-region) proceed with the same rate. Thus, hereafter we will use only a(t) (=a^norm_μ(t) = a^norm_χ(t)) and b(t) (=b^norm_μ(t) = b^norm_χ(t)).

Fig. 8 Comparison of the weighting factors b^norm_μ(t) and b^norm_χ(t) during the ammonolysis of Ga₂O₃ at 780 °C.

The weighting factors a(t) and b(t) correlate linearly with the number of gallium atoms in a structurally equivalent environment and thereby with the phase fractions of GaN and Ga₂O₃. In Fig. 9a, the phase fraction of the product GaN during the ammonolysis of Ga₂O₃ is plotted vs. the reaction time, and in Fig. 9b, the phase fraction of the remaining GaN during its oxidation to Ga₂O₃ is plotted. Both curves for the ammonolysis and the oxidation show a completely different behaviour. During the ammonolysis of Ga₂O₃, there is an incubation time at the beginning of the reaction, where the phase fraction of GaN does not change. After this incubation time the reaction rate increases rapidly, reaches a maximum (inflection point of the graph), and then becomes smaller again. In contrast, the reaction rate during the oxidation of GaN has its maximum at the beginning of the reaction and then decreases continuously.

Fig. 9 Phase fraction of the product GaN during the ammonolysis of Ga₂O₃ for three different temperatures (a) and phase fraction of GaN during its oxidation to Ga₂O₃ for two reaction temperatures (b).

In the following section, the experimental reaction kinetics for both the ammonolysis of Ga₂O₃ and the oxidation of GaN will be modelled. For this, microscopic models will be proposed and adequate equations for the reaction kinetics will be derived. Finally, these equations will be fitted to the experimental data to obtain kinetic parameters.

4. Modelling of the reaction kinetics and discussion

4.1 Kinetics of the ammonolysis of Ga₂O₃

The shape of the kinetic graphs of the ammonolysis (Fig. 9a) is similar to the shape of the well-known Johnson–Mehl–Avrami–Kolmogorow kinetics that is used to describe crystallization processes, other phase transitions and also solid state reactions with a reaction front.^19–21 The quantitative description of the phase fraction x of the newly formed phase as a function of time t is given by the Johnson–Mehl–Avrami–Kolmogorow equation (JMAK equation):

x = 1 − exp(−(k·t)ⁿ) (5)

The parameter k is the rate constant of the reaction, and n is the Avrami exponent, which can take integer or half integer values smaller or equal to 4. The value of the Avrami exponent is a sign of the nature of the reaction mechanism and the reaction kinetics.²²

Looking exactly to the graphs in Fig. 9a reveals that the conversion from Ga₂O₃ to GaN does not start at the reaction time t = 0 min. There is an incubation time t₀ at the beginning of the reaction after which the amount of GaN starts to increase. The Johnson–Mehl–Avrami–Kolmogorow model, on the other hand, includes only the mechanistic steps of nucleation and growth of the nuclei. Any step before nucleation (e.g. bulk or grain boundary diffusion) is not considered in the JMAKeqn (5). On this account an incubation time t₀ is introduced:

x = 1 − exp(−(k·(t−t₀))ⁿ) (6)

The incubation time is not a fit parameter, but is estimated from the graphs in Fig. 9a as the time until which there is no noticeable increase of the phase fraction of GaN. Using eqn (6) the experimental curves in Fig. 9a can be fitted with k and n as fitting parameters. Typical fits are shown in Fig. 10. In all cases a good fit adaptation is achieved. All estimated incubation times t₀ and all fitting results for k and n are shown in Table 1.

Fig. 10 Phase fraction of GaN during the ammonolysis of Ga₂O₃ at 660 °C (a), 780 °C (b) and 840 °C (c) (dots) and fits with the extended JMAKeqn (6) (lines). The incubation times t₀ were estimated as described in the text.

Table 1 Estimated incubation times t₀ for the ammonolysis of Ga₂O₃ and fit parameters k and n obtained from the fits using the extended JMAKeqn (6).

T/°C	t 0 /min	k/min^−1	n	Reactant^a
a Com = commercial Ga2O3; Syn = Ga2O3 synthesized by oxidation of GaN.
660	0	0.0041 ± 0.0002	3.08 ± 0.07	Com
780	7	0.0122 ± 0.0003	2.99 ± 0.05	Com
780	4	0.0115 ± 0.0002	3.34 ± 0.11	Com
780	0	0.0101 ± 0.0001	3.09 ± 0.09	Com
780	0	0.0119 ± 0.0006	2.81 ± 0.09	Syn
840	11	0.1028 ± 0.0007	3.07 ± 0.12	Com
840	11	0.0701 ± 0.0005	3.44 ± 0.15	Com
840	9	0.0719 ± 0.0007	2.90 ± 0.12	Syn

---

Linearization of the JMAK equation by plotting ln(t−t₀) against ln(−ln(1 −x))—so called Sharp–Hancock plot²³—shows whether the reaction proceeds by a single reaction mechanism over the whole reaction time. The fact that the slopes in the Sharp–Hancock plots (Fig. 11) are constant during the whole reaction is an indicator that there is no change in the reaction mechanism and the rate determining step during the whole reaction time. In addition, the slopes—reflecting the Avrami exponents n—are approximately identical at the three investigated temperatures, indicating that the reaction mechanism does not change with temperature.

Fig. 11 Sharp–Hancock plot of the phase fraction x of GaN during the ammonolysis of Ga₂O₃ at different temperatures. Here, n is the slope of the curve, which reflects the Avrami exponent.

The obtained Avrami exponents in Table 1 and in Fig. 11 scatter around n = 3. This Avrami exponent reflects the following reaction mechanism.²² Fast nucleation at the beginning of the reaction and subsequent three-dimensional growth of nuclei with a constant growth rate. During the latter part of the reaction the formation of the new phase at the interface between the matrix and the nucleus is rate determining. Thus, our experimental data show that the ammonolysis of Ga₂O₃ starts with a fast nucleation of GaN nuclei and then the reaction is determined by further growth of GaN at the interface between Ga₂O₃ and GaN.

To verify the existence of GaN nuclei in the bulk or at the surface of Ga₂O₃ grains, Ga₂O₃-powder that was ammonolysed for 60 min at 780 °C (ca. 20% conversion, see Fig. 9a) was ground and analysed by TEM. The distribution of oxygen and nitrogen within individual particles was analysed by means of energy-filtering TEM (EFTEM)²⁴ using the oxygen and nitrogen K-edges (see Fig. 12).

Fig. 12 A conventional TEM bright field image of a ground Ga₂O₃ particle after partial ammonolysis (left). The corresponding EFTEM element distribution maps for nitrogen (middle) and oxygen (right), respectively.

A typical ground powder particle of relatively uniform thickness is shown in the TEM bright field image in Fig. 12 (left). The signal in the EFTEM element distribution map in Fig. 12 (middle) proves the non-homogeneous distribution of nitrogen within the investigated grain and indicates a small GaN nucleus of about 40 nm diameter at the lower left side of the particle (area of high signal). The corresponding oxygen distribution map in Fig. 12 (right) shows that the remaining part of the particle virtually consists only of Ga₂O₃.

Another interesting point comes out by examining SEM micrographs of the Ga₂O₃ reactant and the GaN product. Fig. 13 shows that the reactant particles have block shaped geometry. During the ammonolysis reaction these block-shaped grains are totally destroyed. The GaN product has a foam-like shape and one cannot identify individual grains. A possible explanation is that the formation of the inner GaN phase produces stress in the Ga₂O₃ bulk, because of the different molar volumes of Ga₂O₃ and GaN. After a certain reaction time the increasing stress results in destruction of the original grains.

Fig. 13 SEM-micrographs of the Ga₂O₃ reactant (a) and the GaN product (b).

Finally, we consider the rate constant k (Table 1). As expected the rate constant increases with increasing temperature, but there is no well defined Arrhenius behaviour. This may be due to the fact that at higher temperatures more ammonia is decomposed to hydrogen and nitrogen than at lower temperatures. Hence, the partial pressure of ammonia, which is the driving force for the ammonolysis, is not the same at the different temperatures.

4.2 Kinetics of the oxidation of GaN

The kinetic graphs of the oxidation of GaN in Fig. 9b show a completely different behaviour compared to the ammonolysis in Fig. 9a. There is no incubation phase, i.e. the conversion of GaN to Ga₂O₃ starts immediately, with the maximum reaction rate at the beginning of the reaction.

In the following section the layer growth model of the oxidation of GaN epilayers found by Wolter¹⁰ will be carried over to oxidation of GaN powder particles. With the assumption that the reaction kinetics proceeds by an interface controlled rate determining step, it is of huge importance to know the geometry of the powder particles. For this, SEM images were recorded. Fig. 14 shows that both the particles of the GaN reactant and the Ga₂O₃ product have blocked shaped geometry. Subsequently, this block shaped geometry of the particles will be approximated by a cylindrical model.

Fig. 14 SEM-micrographs of the GaN reactant (a) and the Ga₂O₃ product (b).

For further modelling, the block lengths and radii of about 100 particles were determined from the SEM-images. The values of the radius- and block length-distributions were fitted with a log-normal-function,²⁵ yielding an average block length of 2.96 ± 0.04 μm and an average particle radius of 0.256 ± 0.004 μm for the GaN reactant. For the Ga₂O₃ product the average block length is 3.32 ± 0.03 μm and the average particle radius is 0.287 ± 0.003 μm. In combination with the pictures in Fig. 14 these numbers show that the particle morphology and particle dimensions are well retained during the oxidation of GaN to Ga₂O₃.

This observation can be explained by a shrinking core model (Fig. 15) as reaction model, in which nitrogen will be substituted by oxygen and the structure changes from the wurtzite structure of α-GaN to the monoclinic structure of β-Ga₂O₃. Oxidation of the initial GaN cylinder particle starts at the surface. During growth of this Ga₂O₃ layer, the inner GaN cylinder shrinks.

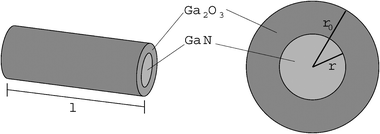Fig. 15 Cylindrical shrinking core model for the oxidation of a GaN grain to Ga₂O₃.

This model assumes that transport of oxygen and nitrogen is not rate determining, instead the proper reaction at the interface between the GaN and the Ga₂O₃ phase is the rate determining step. Under this assumption, the reaction rate is proportional to the area A of the interface between the inner and outer cylinder, dn_GaN/dt = −k·A, where k is the reaction rate constant per unit area. Because the cylinder has a high aspect ratio, we can neglect the top and bottom caps of the cylinder, resulting in A≈ 2πrl, and we can assume that the length l remains approximately constant. With these assumptions, the change of the amount of GaN, n_GaN, with time is given by:

Integration of this equation leads to:

r = r₀−kV^m_GaNt (8)

where r₀ is the initial radius of the GaN particles as determined in the analysis of the SEM-images and V^m_GaN is the molar volume of GaN (V^m_GaN = 1.37 × 10⁻⁵ m³ mol⁻¹).²⁶ As the radius r of the inner GaN cylinder scales linearly with time t, the total amount of GaN scales quadratically with time, n_GaN∝r². Finally, the phase fraction of GaN as a function of time is given by: With this equation the time-phase fraction graphs (Fig. 9b) can be fitted.

Fig. 16 shows that over the whole reaction time very good adaptations of the experimental data are achieved. The fitting results for the rate constant are k = (1.51 ± 0.1) × 10⁻⁴ mol m⁻² min⁻¹ at 780 °C and k = (4.07 ± 0.38) × 10⁻⁴ mol m⁻² min⁻¹ at 840 °C.

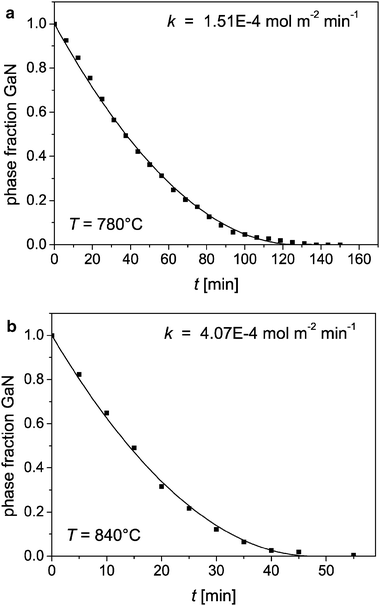Fig. 16 Phase fraction of GaN during its oxidation (dots) and fit with eqn (9) (lines) at 780 °C (a) and 840 °C (b).

The good fitting results confirm the derived model, which assumes that the reaction rate depends only on the area of the interface where the rate determining step takes place. The reaction is then independent of the reactant concentrations and so of 0th order. These results confirm the results of Wolter et al.¹⁰ for the oxidation of epilayers. The different shape of the time-phase fraction-diagrams is due to the different geometries of the GaN samples that were oxidised: While the samples in this work are powders with cylindrical geometry, where the interface area becomes smaller during the reaction, Wolter et al. investigated the oxidation of thin film samples, where the interface area is constant during oxidation. Wolter et al. studied also the oxidation of powders and reported a linear kinetics as well. From their experimental data it is, however, not cognizable whether the reaction was observed until complete oxidation. Probably, their linear kinetics corresponds only to the early stages of the reaction where the kinetics is indeed linear (see eqn (9) and Fig. 16).

4.3 Comparison of the ammonolyis of Ga₂O₃ and the oxidation of GaN

Finally, we will compare the ammonolysis of Ga₂O₃ and the oxidation of GaN concerning the thermodynamic driving forces for both reactions, the experimental results on the reaction kinetics and morphology, and the derived reaction mechanisms.

For the ammonolysis reaction (eqn (1)) the change in the standard Gibbs energy—calculated from literature values of the standard formation Gibbs energies of all reactants²⁷—is slightly positive at all investigated temperatures, e.g.Δ_RG⁰_m(1) = +80 kJ mol⁻¹ at 1000 K. Only due to the experimental conditions during the ammonolysis (p_NH3≈ 1 bar, p_H2O≪ 1 bar), the actual driving force Δ_RG_m(1) = Δ_RG⁰_m(1) + RT ln((p_H2O/p⁰)³/p_NH3/p⁰)²) becomes negative. Assuming p_H2O≈ 10 mbar we can estimate a typical value Δ_RG_m(1) ≈−35 kJ mol⁻¹ at 1000 K. The kinetics of the ammonolysis of Ga₂O₃ is characterized by an initial incubation time followed by a kinetics that can be described well by a Johnson–Mehl–Avrami–Kolmogorow model. The incubation time may reflect the fact that at first nitrogen must diffuse into the Ga₂O₃ grains (via bulk-, grain boundary- or crack-diffusion). Only subsequently, nucleation and growth of GaN nuclei can start which is described well by the JMAK model. In addition, the transport of ammonia through the powder bed of the reactor may contribute to the incubation time, making the interpretation of its actual value rather difficult. In contrast, the obtained Avrami exponents render possible a clear conclusion on the underlying mechanism. The Sharp–Hancock plots show unambiguously that the reaction mechanism does not change during the complete reaction from Ga₂O₃ to GaN nor does it change with temperature. All measured Avrami exponents n scatter around the value n = 3. This value conforms to a reaction mechanism with closed nucleation and 3D nucleus growth where the rate determining step is the formation of GaN at the interface between the GaN-nuclei and the Ga₂O₃-phase.

For the oxidation reaction (eqn (2)) the change in the standard Gibbs energy is Δ_RG⁰_m(2) = −782 kJ mol⁻¹ at 1000 K.²⁷ Assuming p_O2≈ 1 bar and p_N2≈ 10 mbar, the actual driving force during the oxidation is estimated as Δ_RG_m(2) ≈−820 kJ mol⁻¹, which is very large compared to the driving force for the ammonolysis reaction (eqn (1)). The oxidation of GaN can be modelled with a shrinking core model, where the formation of the Ga₂O₃ phase starts on the surface of the GaN grains without incubation time. During the reaction, the morphology of the grains does not change. Again the rate determining step of the reaction is the formation of the newly formed phase (here Ga₂O₃) at the interface between GaN and Ga₂O₃.

This means that for the ammonolysis and the oxidation reaction as well the rate determining step is the proper reaction at the interface between the old and the new phase. Hence, the difference in the observed morphologies—growth of nuclei during the ammonolysis and layer growth during the oxidation—must be due to the very first reaction steps that take place prior to growth, i.e. prior to transport of the reactants towards the existing interface. As shown above, the driving force for the ammonolysis of Ga₂O₃ is relatively small, Δ_RG_m(1) ≈− 35 kJ mol⁻¹, while the driving force during the oxidation of GaN is about twenty times larger, Δ_RG_m(2) = −820 kJ mol⁻¹. These values suggest that during the ammonolysis of Ga₂O₃ only a few, relatively large nuclei of GaN are formed, while during the oxidation of GaN many, relatively small nuclei of Ga₂O₃ are formed. A more quantitative analysis is possible within homogeneous nucleation theory²⁸ from which it is known that a nucleus of a new phase can only grow further if a critical radius r* = 2σ/Δg_V is exceeded. Here Δg_V is the Gibbs energy change per unit volume for the phase transition, and σ is the interface energy of the interface between the nucleus and the matrix. The nucleation rate is proportional to the number of critical nuclei N* ∼ exp(−ΔG*/k_BT) where ΔG* ∼σ³/(Δg_V)² is the Gibbs energy of formation of a nucleus of critical size. It is interesting to note that the interface energy σ is identical for both reactions under consideration. During the ammonolysis reaction (eqn (1)) a GaN nucleus grows within a Ga₂O₃ matrix and during the oxidation reaction (eqn (2)) a Ga₂O₃nucleus grows within a GaN matrix, leading in both cases to an interface Ga₂O₃/GaN. Thus, we can easily calculate the ratio of the critical radii for both reactions, r*_GaN/r*_Ga2O3 = Δg_V,Ga2O3/Δg_V,GaN, and the ratio of the critical Gibbs formation energies, ΔG*_GaN/ΔG*_Ga2O3 = (Δg_V,Ga2O3/Δg_V,GaN)². Converting the above molar Gibbs energies to Gibbs energies per volume we obtain r*_GaN/r*_Ga2O3≈ 20 and ΔG*_GaN/ΔG*_Ga2O3≈ 400. These results show that during the ammonolysis the nucleation rate is relatively low and only a few, relatively large nuclei of GaN are formed which grow independently and destroy the original morphology of the Ga₂O₃ grains. In contrast, the nucleation rate is much higher during the oxidation of GaN, and many, relatively small nuclei are formed. In the very early stages of the oxidation reaction these nuclei form preferentially on the surface of the GaN grains, and—once they have grown together—a dense oxide layer develops, thereby preserving the morphology of the GaN grains. The experimentally observed kinetics shows that during further growth diffusion through the layer is still faster than the reaction at the interface leading to the kinetics of 0th order in eqn (9).

5. Conclusions

In the present work the kinetics of the ammonolysis of β-Ga₂O₃ powders and the oxidation of α-GaN powders was investigated by in situX-ray absorption spectroscopy (XAS) performed on the Ga K-absorption edge. The time-resolved spectra could be described very well by a linear combination of the absorption spectra of Ga₂O₃ and GaN only. No evidence for the formation of additional phases was found. Independent fitting of the XANES- and the EXAFS-region gave identical results proving that the changes in the electronic structure and the short range order around Ga atoms during the ammonolysis of Ga₂O₂ and the oxidation of GaN proceed with the same speed.

The kinetics of the ammonolysis of Ga₂O₃ can be described very well by a Johnson–Mehl–Avrami–Kolmogorow model with an Avrami-exponent of ∼3 indicating a reaction mechanism with closed nucleation and 3D nucleus growth. The rate determining step of the reaction is the formation of the newly formed GaN phase at the interface between the GaN nuclei and the Ga₂O₃ matrix. These kinetic results are supported by SEM micrographs which show a severe change of the morphology of the reactants and by TEM micrographs which directly image isolated GaN nuclei during the ammonolysis. The oxidation kinetics of GaN can be modelled by a shrinking core model with cylindrical powder particles whose morphology does not change during the reaction. Again the rate determining step is the interfacial formation of the newly formed gallium oxide product phase.

The above results are supported by considering the chemical driving forces ΔG for both reactions which are extremely different, ΔG(oxidation) ∼25·ΔG(ammonolysis). As a consequence, the ammonolysis reaction is characterized by a small nucleation rate resulting in a few, relatively large nuclei—as observed experimentally. In contrast, the oxidation reaction is characterized by a high nucleation rate resulting in many, relatively small nuclei which—after coalescence—form a closed oxide layer—as found experimentally.

Acknowledgements

Financial support by the German Research Foundation (DFG Priority Program 1136) is gratefully acknowledged. The authors want to express their thanks to R. Zaunbrecher for making the SEM measurements, F. Dorn for recording the TEM micrographs, B. Huppertz and W. Axer for technical support and Dr E. Welter, Dr K. Rickers, Dr A. Webb and Dr D. Zajac (all HASYLAB@DESY) for support during the beam times.

References

1. O. Ambacher, J. Phys. D: Appl. Phys., 1998, 31, 2653.
2. C. M. Balkas and R. F. Davis, J. Am. Ceram. Soc., 1996, 79, 2309.
3. B. Schwenzer, J. Hu, R. Seshadri, S. Keller, S. P. Den Baars and U. K. Mishra, Chem. Mater., 2004, 16, 5088.
4. S. J. Pearton and F. Ren, Adv. Mater., 2000, 12, 1571.
5. M. Zinkevich and F. Aldinger, J. Am. Ceram. Soc., 2004, 87, 683.
6. S. Cho, J. Lee, I. Park and S. Kim, Mat. Lett., 2002, 57, 1004.
7. Y. J. Park, C. S. Oh, T. H. Yeom and Y. M. Yu, J. Cryst. Growth, 2004, 264, 1.
8. W. S. Jung, Mater. Lett., 2002, 57, 110.
9. D. Röhrens, J. Brendt, D. Samuelis and M. Martin, to be published.
10. S. D. Wolter, S. E. Mohney, H. Venugopalan, A. E. Wickenden and D. D. Koleske, J. Electrochem. Soc., 1998, 145, 629.
11. E. D. Readinger, S. D. Wolter, D. L. Waltemyer, J. M. Delucca, S. E. Mohney, B. I. Prenitzer, L. A. Giannuzzi and R. J. Molnar, J. Electr. Mater., 1999, 28, 257.
12. X. F. Xu, R. Zhang, P. Chen, Y. G. Zhu, Z. Z. Chen, S. Y. Xie, W. P. Li and Y. D. Zheng, Solid-State and Integrated-Circuit Technology, 2001, 2, 1205.
13. U. Koops, D. Hesse and M. Martin, J. Mater. Res., 2002, 17, 2489.
14. N. Hilbrandt and M. Martin, J. Synchr. Rad., 1999, 6, 489.
15. R. Frahm, Rev. Sci. Instrum., 1989, 60, 2515.
16. B. Ravel, Athena User’s Guide 1.0, 2007.
17. D. C. Koningsberger and R. Prins, X-Ray Absorption: Principles, Applications, Techniques of EXAFS, SEXAFS and XANES, Wiley-Interscience, New York, 1988.
18. M. Newville, P. Livins, Y. Yacoby, J. J. Rehr and E. A. Stern, Phys. Rev. B, 1993, 47, 14126.
19. M. Avrami, J. Chem. Phys., 1939, 7, 1103.
20. M. Avrami, J. Chem. Phys., 1940, 8, 212.
21. M. Avrami, J. Chem. Phys., 1941, 9, 177.
22. J. Burke, The Kinetics of Phase Transformations in Metals, Pergamon Press, 1965.
23. F. J. Humphreys and M. Hatherly, Recrystallisation and Related Annealing Phenomena, Elsevier, 2004.
24. C. Deininger, R. F. Egerton, F. Hofer, B. Jouffrey, D. Krahl, R. D. Leapman, J. Mayer, L. Reimer, H. Rose, P. Schattschneider, J. C. H. Spence and P. W. Hawkes, Energy-Filtering Transmission Electron Microscopy, ed. L. Reimer, Springer-Verlag, Berlin Heidelberg, 1995.
25. A. Jillavenkatesa, L.-S. H. Lum and S. Dapkunas, Particle Size Characterization, Report SP 960-1, National Institute of Standards and Technology.
26. Gmelin Handbook of Inorganic Chemistry, Volume C2, Ga–Compounds with Nitrogen, Springer-Verlag, Berlin, 1996.
27. I. Barin, Thermochemical Data of Pure Substances, VCH Publishers, Inc., Weinheimm, 1995.
28. R. Becker and W. Döhring, Annu. Phys., 1935, 24, 719.

---

Footnote

† Present address: Max Planck Institute for Solid State Research, Heisenbergstraße 1, 70569 Stuttgart, Germany

---