Correlating phase behaviour and diffusion in mesopores: perspectives revealed by pulsed field gradient NMR
Rustem
Valiullin
*a,
Jörg
Kärger
a and
Roger
Gläser
b
aFakultät für Physik und Geowissenschaften, Universität Leipzig, Linnéstr. 5, D-04103, Leipzig, Germany. E-mail: valiullin@uni-leipzig.de
bInstitut für Technische Chemie, Universität Leipzig, Linnéstr. 3, D-04103, Leipzig, Germany
First published on 16th March 2009
Abstract
Porous solids represent an important class of materials widely used in different applications in the field of chemical engineering. In particular, mesoporous hosts attract special attention due to their fascinating match of transport, geometrical and chemical properties. Not only a very high specific surface area, accessible for adsorption and heterogeneous catalysis, but also their efficient transport properties are the key factors determining optimal use of these materials. Therefore, a fundamental understanding of the correlations between the phase state of confined fluids, their transport properties and the geometrical features of confinement are of particular importance. Among the different analytical techniques, nuclear magnetic resonance (NMR) is especially suited to cover various crucial aspects of the highlighted issues. In this work, we provide a short overview of recent advances related to the interrelations of phase behaviour and diffusion in mesoporous materials studied using various NMR techniques.
 Rustem Valiullin Rustem Valiullin | Rustem Valiullin got his PhD degree from Kazan State University (Kazan, Russia) in 1997 and continued to work there as a Research Scientist. After two years postdoctoral work in the Royal Institute of Technology (Stockholm, Sweden), in 2003 he moved to the University of Leipzig, Germany as a fellow of the A. von Humboldt Foundation. Currently he is a Heisenberg fellow of the German Science Foundation at the Department of Interface Physics of Leipzig University. |
 Jörg Kärger Jörg Kärger | Jörg Kärger got his PhD in Physics in 1970 at Leipzig University, followed by the habilitation in 1978. As a member of Leipzig University since this time, research stays took him to Prague, Moscow, Fredericton and Paris. In 1994, he became Professor of Experimental Physics and head of the Department of Interface Physics. His research is dedicated to diffusion phenomena quite in general. |
 Roger Gläser Roger Gläser | Roger Gläser has studied chemistry at the University of Stuttgart, Germany and got there his PhD degree from the Institute of Chemical Technology in 1997. After that he worked at the Georgia Institute of Technology, Atlanta, USA. In 1999 he returned to the Institute of Chemical Technology, Stuttgart where he completed his habilitation in 2007. Presently, he is a Professor of Chemical Technology at the University of Leipzig and is head of the Institutes of Chemical Technology and Non-Classical Chemistry. |
I. Introduction
Since the discovery of the M41S-family of molecular sieves by the researchers of Mobil Oil Corp.,1,2 a plethora of ordered mesoporous materials with different compositions and surface properties was found including, for instance, the materials of the SBA-, HMS-, MSU-, TUD-, or CMK-type,3–8 periodic mesoporous organosilicates (PMOs),9 mesocellular silica foams (MCFs)10–12 or metal–organic frameworks (MOFs).13–15 The continuing interest in these materials, especially in view of applications in sorptive separations and heterogeneous catalysis, relies, inter alia, on their high specific surface areas and their large pore diameters with respect to the conventionally applied zeolites and related microporous materials. As a consequence, sorptives and reactants with considerably larger molecular dimensions have access to the inner surface area of these molecular sieves.16Moreover, a more rapid mass transfer into and egress of mesoporous materials offers obvious potential over their microporous counterparts.17,18 Mesopores have often been invoked to serve as “transport pores” for higher molecular reactants and, thus, enable and accelerate their transport to the active sites of solid catalysts.19 Prominent examples are the alkylation of benzene with propene to cumene over dealuminated mordenite-type zeolites20 or fluid catalytic cracking (FCC) of long-chain hydrocarbons over acidic faujasite-type zeolites.21 While in the sooner case, the mesopores are introduced into the catalyst by dealumination of the zeolite crystals, a mesoporous matrix around the zeolite crystallites provides access to the active surface sites in the latter. It was recently shown by pulsed field gradient (PFG) NMR that a transport optimization of FCC catalysts can be achieved by selecting a matrix for the active zeolite crystals with the appropriate mesopore size.22 The introduction of mesopores into the acidic faujasite catalyst by steam dealumination, however, does not have a pronounced effect on the hydrocarbon diffusivities within the micropores of the zeolite.23 Besides catalysis, mesoporous materials are attractive for the adsorptive uptake of substances with larger molecules such as enzymes for biocatalysis24 or pharmaceuticals for controlled drug release.25,26 Other potential application areas for mesoporous molecular sieves include nanofluidics, photonics, and optical switches.27–29
In addition to the apparent advantages regarding mass transfer, mesoporous materials exhibit most interesting properties with respect to the thermodynamic equilibria of the adsorbed phases. In addition to the dense “phase” adsorbed on the pore walls, there are solid, liquid, gaseous or supercritical phases within the pores with equilibrium and transition conditions significantly differing from those in the bulk.30,31 This difference is a result of the confinement of the phases within the mesopores. In contrast, micropores are, for most substances, too small for another phase but a dense adsorbed phase to exist and in macropores the influence of the walls on the phase behaviour within the pores is almost negligible. Apparently, the conditions for phase transitions are especially well-defined for ordered mesoporous materials, i.e., for materials with a narrow pore size distribution as typical for molecular sieves.
The deviation of the conditions for phase equilibria or transitions under confinement, in particular by mesopores, from those of the bulk is a general phenomenon and not limited to particular phases. For instance, both the liquid/gas and the solid/liquid coexistence curves and, consequently, the critical and the triple point are shifted towards lower temperatures and pressures compared to the bulk. Moreover, a rich set of experimental data is available to date revealing, with a sufficiently high accuracy, proportionality of these shifts to the reciprocal mesopore size. Thus, the dependence of the solid/liquid phase transition (melting point) on the mesopore diameter is routinely used nowadays for the determination of the mesopore diameter by thermoporometry.32–34 The same principle is exploited also in gas adsorption porometry.35 It is worth noting that a better understanding of these phenomena may be of indispensable practical relevance in most diverse fields, ranging from material science to biophysics.36–38
From the known phenomenon of sorption hysteresis, however, it is evident that the phase behaviour within mesoporous materials can be rather complex and that it depends on the way it is approached.39 Although these basic features have been reported long ago,40,41 a complete understanding of the phenomenon is still lacking. Beside fundamental interest, the practical importance of the problem is determined by the fact that the measurement of gas adsorption is widely used as a classical characterization technique35 and, in turn, is of enormous importance in the development of novel porous materials.42,43
While a wealth of studies is devoted to the nature and the thermodynamic equilibrium of phases within mesoporous solids, much less investigations were carried out to describe and understand the transport properties of mesopore-confined phases. It is obvious, of course, that the presence of different phase states or distributions will strongly affect the corresponding transport properties within the mesopores. This perspective focuses on diffusion within mesoporous materials in view of the behaviour of liquid and gas phases coexisting inside the mesopores. With respect to the theme of this special issue, the scope of this article is, thus, the treatment of the phases as “molecular assemblies”, rather than the behaviour of isolated molecular species in confined spaces of porous solids. The most important industrial applications of mesoporous materials, especially in sorption and heterogeneous catalysis, involve gas and/or liquid phases, not only in the bulk surrounding of the materials, but also within the mesopore space (vide supra). Other phase equilibria inside mesoporous solids such as those of solid/gas or solid/liquid systems will, thus, not be treated here.
Based on our previous experience, it is another goal of this article to highlight how transport measurements, especially by pulsed field gradient (PFG) NMR, can be used to infer on the phase behaviour within mesoporous solids. The information obtained from transport measurements is shown to be complementary to that typically extracted from sorption equilibrium data such as isotherms or isochores, i.e., from the loading of the sorptives as a function of the physical properties of the fluid phase outside the porous solid.
The present article is subdivided into five major sections. First, we describe the specific phase behaviour in mesopores and its partly significant differences from that in bulk phases. As mentioned above, this contribution will be restricted to the liquid/gas-coexistence and the related phenomena near the critical point. After a brief outline of how PFG NMR can be applied to measure different transport-related properties within porous solids (for more detailed description of this methods the readers may refer to ref. 44–49), two following sections will be focused towards the transport processes occurring in porous solids on the different porosity scales (micro- and macroporosity). Finally, we will summarize the current knowledge on the relation of transport properties and phase behaviour in mesoporous solids at conditions for which a transition of the pore-confined phases to the supercritical state occurs. We will give selected examples where this transition and the presence of a supercritical phase in the mesopores were utilized for applications in materials preparation, sorption, and heterogeneous catalysis. From the current knowledge, we will derive potential perspectives as to where and how the specific liquid/gas-phase behaviour and its effects on transport properties in mesoporous materials may be utilized in the future and outline the open scientific questions and challenges.
II. Fluid phase equilibria in mesopores
It is well known that the phase coexistence of fluids in porous solids is altered as compared to the bulk fluids. This is demonstrated by the sorption isotherms, a typical example of which is shown in Fig. 1. The shape of an isotherm reflects the interactions of the adsorbed molecules with the internal surface of the porous material as well as the effect of confinement on properties of the adsorbed fluid. At sufficiently low external gas pressures P the latter unequivocally determines the equilibrium between molecular ensembles adsorbed on the pore walls and the surrounding gas phase. This means that the sorption process, i.e., adding or releasing of molecules to or from the adsorbed (multi-)layers, is continued until the chemical potential equilibrates over the whole system. Notably, there are no imposed barriers of either type to prevent the equilibration under these conditions. At intermediate pressures, a sudden change of the amount adsorbed is observed, which is attributed to evaporation or capillary-condensation transitions. Importantly, both transitions occur at pressures well below the saturated vapour pressure Ps, manifesting the confinement effect upon the phase state. In addition, an important feature of mesoporous materials is the occurrence of hysteresis, where for a range of bulk gas pressures the sequence of states encountered on desorption does not coincide with that encountered on adsorption.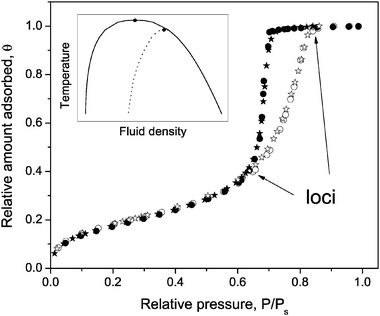 | ||
| Fig. 1 Relative adsorption (open symbols) and desorption (full symbols) isotherms of nitrogen in channels of porous silicon (dp≃ 6 nm), open at both ends (stars) and one end (circles), measured at 77 K. The inset shows a schematic phase diagram for a bulk liquid (solid line) and for a liquid confined within pores (dotted line). | ||
The pioneering theories of adsorption and hysteresis in pores are usually classified as capillary condensation theories.39 They are typically constructed around the idea of a shifted capillary condensation and evaporation transitions due to curved menisci, i.e., by considering equilibrium between the condensed phase with a curved meniscus in the pores and its vapour just above it. As a result, this situation may often be described by the famous Kelvin equation for the transition pressure Ptr, ln(Ptr/Ps) ∝ (1/r1 + 1/r2), where r1 and r2 are the principal meniscus radii. As an example, an open-ended cylindrical capillary with a radius r yields an instructive idea of the hysteresis development through a difference in geometry of the liquid menisci on desorption (spherical concave, 1/r1 + 1/r2 = 2/r) and adsorption (cylindrical concave, 1/r1 + 1/r2 = 1/r).50 Morphological details of the porous medium were also considered within this approach: In the so-called ink-bottle geometry, adsorption hysteresis was linked with a peculiar construction of the pore space.51,52 It was argued, for example, that narrow interconnections between large pores could delay the evaporation of liquids from them. This is the so-called pore-blocking effect, which was later widely used to describe the hysteresis phenomenon in random porous materials.53
Later on, density functional theories (DFT) and lattice gas models capturing microscopic features of the adsorption phenomena have been developed.30,54 Applying DFT to uniform pores, with increasing external vapour pressure the molecular ensemble in pores is found to remain in a gas-like state beyond the point of the true thermodynamical transition, i.e., the system persists in a local minimum of free energy. This is continued until the barrier separating the local and the global energy minima becomes small enough. The same is true for the desorption process concerning a liquid-like state. Importantly, microscopic theories thus point out the metastable character of the transitions. To extend these theories to real porous materials, i.e., to allow the simultaneous coexistence of gas-like regions and regions with a capillary-condensed phase, one has to artificially incorporate effects of the geometrical heterogeneity of pore structure.55,56
A more detailed analysis of realistic molecular ensembles under confinement using statistical thermodynamics has become possible due to the rapid progress of computer technologies. Exploiting quite different approaches, many details of phase equilibria in various model systems have been elucidated and rationalized.30,57–61 In particular, the results obtained using non-local DFT pointed out that in sufficiently big pores condensation occurs at the vapour-like spinodal, while desorption takes place at the equilibrium.57 The same conclusion has been drawn using molecular dynamics simulations of the molecular behaviour in one- and both-ends open pores.62 Moreover, this approach allowed the authors to address also the phenomenon of pore blocking, which is widely accepted to contribute to the development of hysteresis.53,63 Thus, using an ink-bottle pore as confining geometry, it was found that liquid can evaporate from a large cavity even if the neck of the ink bottle remains filled with the capillary-condensed phase.62 On the other hand, other studies confirmed the relevance of the pore-blocking mechanism,64 emphasizing the importance of the details of the pore structure and the involved interactions.
Progress in fabrication of nanoporous materials with well-defined structural properties made it possible to validate all these theoretical predictions by experimental means. Thus, using ordered mesoporous silica materials composed of spherical cage-like pores connected with each other by cylindrical pores and using different adsorptives, different regimes of desorption, namely controlled by pore-blocking or cavitation, have been identified.65,66 In particular, cavitation-controlled evaporation in ink-bottle pores with the neck size smaller than a certain critical value has become evident. In pores with larger necks, evaporation was found to be percolation-controlled. Remarkably, the results obtained with seemingly simpler pore geometry revealed less consistency with the theoretical expectations. Thus, on the basis of recent experimental studies using MCM-41 silica material with well-defined open-ended cylindrical pores, it was concluded that capillary condensation rather than evaporation takes place near a thermodynamical equilibrium transition.67,68 Note that this conclusion apparently contradicts the Cohan’s picture and poses important questions still to be answered. On the other hand, adsorption studies using porous alumina with well-defined cylindrical pores of diameters from 10–60 nm identified the desorption transition as the equilibrium one.69
It has to be noted that, although such materials as MCM-41 or SBA-15 are generally considered to be ideally organized, their real pore structure is subject to indispensable defects which appear, e.g., in PFG NMR studies70–74 and may affect the phase behaviour of the fluids therein. As a most demonstrative example, one may refer to mesoporous silicon. A number of adsorption studies using this material with channel-like, parallel pores have revealed very striking, sometime counterintuitive results.75–78 Thus, this material exhibits similar behaviour, irrespective of whether both or only one end is open. It has already been suggested earlier that these effects may be caused by surface roughness inherent to this material.77 Recent experiments79 and theoretical considerations using mean-field theory of a lattice gas80 confirmed the effects of a “quenched disorder” as the directing feature of adsorption hysteresis in pores of mesoporous silicon. Importantly, the disorder is thus found to be much more pronounced than expected based on the sole atomistic roughness. Thus, the linear (one-dimensional) pores in this material appear to exhibit all effects typically associated with materials with three-dimensional random pore networks. It is interesting to note that similar behaviour (e.g., irrelevance of closing of one of the channel ends) has recently also been obtained for self-ordered porous alumina, a material which is believed to be subject to less disorder effects.81 The origin of such a behaviour has still to be clarified.
For disordered mesoporous materials, the central questions about the interrelation between hysteresis and phase transitions has been recently addressed in a work based on mean field theory and Monte Carlo simulations for a lattice gas model.82,83 The calculations indicated that the hysteresis could be understood in terms of the effects of the spatial disorder upon the density distribution in the material. In particular, it was anticipated that hysteresis is associated with the appearance of a very large number of metastable states, represented by minima in the local free energy corresponding to different spatial distributions of the adsorbed fluid within the void space of the porous material. In this respect these systems resemble the hysteresis encountered in disordered magnetic systems.84 The major message of these studies was that slow dynamics associated with a rugged free energy landscape may greatly affect the phase equilibrium and prevent the system from equilibration.
The phenomena discussed above refer to temperatures below the bulk critical temperatures Tc. Plotting the average densities of the fluid at the loci of the hysteretic isotherm as a function of temperature, one may compile a hysteresis phase diagram, as shown by the inset in Fig. 1. Notably, these loci correspond (i) to coexisting multi-layered molecules on the surface and in the gaseous phase in the pore interior and (ii) to pores completely filled by the capillary condensate. The thus obtained hysteresis phase diagram is very much similar to the normal one of the bulk, but typically reveals a pore size-dependent temperature shift of the upper closure point.85–87
For the confined fluids, this point at the temperature Tch, called hysteresis critical point and corresponding to vanishing hysteresis, had earlier been considered as a counterpart of its bulk value Tc. This, however, has to be treated with caution. Indeed, in addition to the hysteresis critical temperature, one may as well define the pore critical point at Tcp.54 The latter is defined as the temperature where a jump in the adsorption isotherm caused by capillary condensation just disappears. The first observations, suggesting a differentiation between these two temperatures, Tch and Tcp, have again been made for MCM-41-type material. Pore uniformity allowed to measure the isotherms free of the disturbing effects of a pore size distribution, which, otherwise, would smear out the local condensation events over a certain pressure range. The obtained results unequivocally pointed out that Tch < Tcp < Tc.88 A simple explanation of the obtained relation Tch < Tcp could be provided by recalling the metastable character of the condensation and evaporation transitions in the hysteresis regime. With increasing temperature, the local free energy minima may become sufficiently small to be bypassed by the thermal fluctuations.30 Thus, the hysteresis loops would collapse at lower temperatures compared to Tcp.
III. Pulsed field gradient NMR
Nuclear magnetic resonance provides direct access to the key data of fluid behaviour in the porous space of interest: it is able to simultaneously record the number of molecules and their dynamical properties. Thus, measuring the NMR signal intensity in a sample of a porous solid as a function of the external gas pressure, one may compile the respective adsorption isotherm, as an indicator of the phase state in the pores. On the other hand, a number of other quantities may simultaneously be measured in the same sample under the same conditions. One of them, which will be in the focus of this review, is molecular translational mobility. Therefore, NMR may serve as a self-consistent experimental tool allowing to correlate phase state of a fluid in pores and its transport properties. The way in which this becomes possible may be rationalized using the classical interpretation of nuclear magnetism.44–46,89Under the influence of a magnetic field of intensity B0, each nucleus (i.e., the nuclear “spin”) performs a precessional motion about the direction of B0 with the angular frequency ω0 = γB0, where γ is the nuclear gyromagnetic ratio. By the application of a radio-frequency field of the same frequency ω0 over a well-defined short interval of time, the net magnetization in the sample can be turned from the direction of the magnetic field (the equilibrium position) into the plane perpendicular to it. The net magnetization rotating in this plane induces a voltage in the receiver coil surrounding the sample under consideration. The thus measured voltage is monitored as the NMR signal. Obviously, the intensity of this signal is proportional to the number of respective nuclei and hence to the number of molecules in the sample (one should, however, take account of nuclear magnetic relaxation effects, which for fluids in pores may be significant and may lead to relaxation weighting of the measured signal). The different Larmor frequencies of different nuclei (e.g., 1H, 13C or 2H) provide an additional option to separately track different species.
For rationalizing the way in which the translational mobility of the fluid molecules may be quantified, we consider the influence of field inhomogeneities on the Larmor frequencies ω0 of the nuclear spin system under study. Applying a magnetic field linearly increasing in the z direction, B = B0 + gz, ω0 = γB0 + γgz becomes a function of the z coordinate. With this inhomogeneous field held for a time δ, each spin will acquire a phase ϕ = γB0δ + γ∫δ0g(τ)z(τ) dτ. This procedure is sometime called “position-dependent phase encoding”. In the basic version of pulsed field gradient (PFG) NMR the sample is subjected to two pulses of “field gradients” of constant amplitude g and of duration δ with separation td. With two such pulses of opposite gradient directions, to the end of the second pulse re-phasing may not be complete and the phase difference Δϕ is given by:
 | (3.1) |
| S(q,td) = ∫P(z,td)eiqzdz, | (3.2) |
For unrestricted, normal diffusion, the propagator results as the solution of Fick’s second law with the initial concentration given by Dirac’s δ-function:
 | (3.3) |
| S(q,td) = exp(−q2Dtd). | (3.4) |
Deviations of S(q,td) from the exponential shape of eqn (3.4) may also result from a distribution of molecular mobilities along the sample. An important example, in the context of the present review, is a sample composed of a powder of small porous particles. For such materials, two molecular ensembles characterized by different diffusivities may easily be distinguished, namely those in the inner pore space and those between the porous particles. Very generally, the spin-echo diffusion attenuation for such two-phase systems (here, by “phase” we refer to transport characteristics of the diffusing species rather than to the physical state) may be written as:95,100
| S(q,td) = ∫Ψ(τa,τb)exp{−q2(Daτa + Dbτb)}dΩ. | (3.5) |
It is instructive to consider two limiting cases of slow and fast molecular exchange between the phases. In the first case, all individual molecular trajectories are confined to either of the phases, i.e. there exist only two possible time pairs Ω1 = {τa = td,τb = 0} and Ω2 = {τa = 0,τb = td}. The relative fractions of such trajectories, or corresponding values of Ψ(τa,τb), ultimately coincide with the fractions pa and pb (pa + pb = 1) of molecules in the two phases a and b, respectively. Therefore, the respective diffusion attenuation function is given by the sum of two exponents:
| S(q,td) = paexp{−q2Datd} + pbexp{−q2Dbtd}. | (3.6) |
| S(q,td) = exp{−q2td(paDa + pbDb)}. | (3.7) |
 | (3.8) |
The function ψ(τ) describes, in particular, how fast a molecular ensemble, initially residing in a particle, exchanges its molecules with the surrounding. Thus, for a spherical particle of radius R and an intra-particle diffusivity D, for diffusion-limited exchange (i.e., with no surface barriers, hindering the molecules to leave the particle at the interface with the surrounding phase) ψ(τ) is given by ref. 110
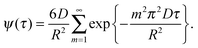 | (3.9) |
 | (3.10) |
To conclude this section, in recent years NMR progressed to provide a wealth of approaches to analyze different aspects of molecular dynamics in porous materials with inhomogeneities in the porous structure on very different length scales,112–114 including its possibility to quantify molecular diffusivities in mesopores under different external conditions. The simultaneously measured NMR signal intensity provides the option to correlate the transport properties with the phase state in the pores. Moreover, by stepwise changing the external conditions, e.g., the vapour pressure, one may create a gradient of the chemical potential between the gas phase and the confined fluid allowing to follow its equilibration by means of NMR. In this way, the results of macroscopic and microscopic techniques may be compared to reveal information on the fluid behaviour, which so far, was inaccessible.115,116 Altogether, a set of NMR approaches allow to address various aspects of molecular dynamics in mesoporous adsorbents of different pore architecture and macro-organization.
IV. Microscopic diffusivity in monoliths
In what follows, we are going to address different aspects of molecular dynamics in mesoporous materials. Referring, e.g., to heterogeneous catalysis involving porous catalysts, the whole molecular trajectories consist of diffusion paths within the porous particles intermitted by those in the free space between the particles (see Fig. 2). We will proceed by first considering the transport mechanisms within mesopores. Depending on various conditions, primarily those determined by the phase state of a fluid, these include surface diffusion, diffusion of molecules in multilayers, Knudsen diffusion and diffusion in the capillary-condensed phase. In disordered materials, e.g., random porous glasses, different molecular phases may coexist with each other in vastly different configurations, yielding, in their combination, very complex behaviours. The latter is evident even from a quick review of the literature data on diffusion in mesopores, reporting a wide spectrum of behaviour depending on pore size, adsorbate and surface properties, temperature, etc. refs. 117–124. Let us now start by considering some of these transport modes separately.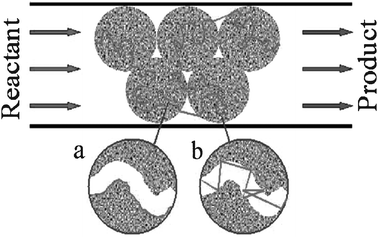 | ||
| Fig. 2 Schematic representation of the transport paths during the process of conversion of a reactant to a value-added product by heterogeneous catalysis in a mesoporous solid. (a) and (b) show the two limiting cases of intra-particle transport along the mesopores, namely surface diffusion and Knudsen diffusion, respectively. | ||
A Surface diffusion
Among the different mechanisms of molecular transport, surface diffusion plays a significant role, sometime being the dominating mechanism of the mass transfer through porous solids. Quite generally, it may be associated with a thermally-activated hopping motion of the guest molecules along the surfaces (see, e.g., the reviews125–127). For experimental studies of surface diffusion, two different approaches are commonly used. One of them is based on the creation of a gradient of the chemical potential (e.g. via pressure or concentration gradients) and measuring the resulting fluxes. In this way, the so-called coefficient of transport diffusion is measured. It contains information about both single-molecule and cooperative modes of the molecular transport. Another approach is designed to operate under equilibrium conditions by, e.g., “labelling” a molecule and following its trajectory.128–131 Such direct visualizations of the molecular trajectories on surfaces have illuminated many novel phenomena, like molecular clustering or mobility enhancement due to a specific molecule-substrate interaction. The analysis of the thus obtained single trajectories yields the so-called tracer diffusivity. Notably, exactly this quantity is as well probed by PFG NMR. The huge surface area of mesoporous adsorbents makes NMR applicable to probe surface diffusivity at sub-monolayer surface coverage.132 Importantly, this latter technique provides an ensemble-averaged quantity.The required surface coverage c (also referred to here as concentration) may conveniently be prepared by tuning the external gas pressure in contact with the mesoporous material. Such a setup can easily be implemented to the in situ operation in an NMR spectrometer,124 so that the adsorption (free induction decay (FID) signal intensity which is proportional to the number of spins in the sample) and diffusion (PFG NMR) could simultaneously be probed. Fig. 3 illustrates this possibility by showing the diffusivity of acetone in mesoporous silicon. The material was prepared by electrochemical etching of a (100)-oriented silicon wafer with a resistivity of 10 Ωcm using a current density of 30 mA cm2 in an electrolyte containing 50% aqueous solution of HF and C2H5OH in a volume ratio of 2 : 1. In this way, a foam-like structure with an average pore diameter of about 4 nm is formed.133 First, the adsorption isotherm has been compiled by measuring the FID signal intensity S as a function of the gas pressure. By using the BET equation,134 the amount adsorbed corresponding to one monolayer surface coverage was estimated and used for transformation to the surface concentrations c. The surface diffusivities Ds, measured in parallel, are, thereafter, plotted via c. Note that the originally obtained diffusivity data have been corrected (although the correction was minor) for the diffusion through the gaseous phase in the pore interior. This procedure will be explained in more detail in the following section.
 | ||
| Fig. 3 Surface diffusivity of acetone in porous silicon as a function of the surface coverage. The solid line is the function D*0c1/m−1 with D*0 = 16 × 10−10 m2 s−1 and m = 0.26. The inset shows the surface coverage c as a function of the relative pressure z with the solid line being the best fit of eqn (4.14) to the data. | ||
The most important message of Fig. 3 is that the diffusivity increases with increasing surface coverage. This is in contrast to what one expects for hard-core particles on homogeneous surfaces, where an increase of the number of particles leads to a decrease of the space available for diffusion. Due to this so-called site-blocking effect the surface diffusivity would rather decrease with increasing c. Remarkably, heterogeneity of the surface, e.g., site or saddle-energy disorder, inverts this trend. In a most simple way, this may be understood by considering the effect of site-energy disorder given by a distribution fs(E) of site energies E. Due to the activated character of the jump process, this leads to a corresponding distribution of the jump rates, with the latter being W(E) ∝ exp{−E/RT}.
With such a condition, the solution of the diffusion problem for a single particle is obtained in the frame of the so-called random trap model, resulting in a diffusivity a2〈1/W〉−1. Here, the brackets denote averaging over all surface sites and a is the inter-site distance.135,136 It is worth noting that the solution does exist only, if there exists a finite average residence time 〈1/W〉 and if the model implies that there is no correlation between neighbour site energies, i.e., if a random energy topography is assumed. The particle ensembles may be treated similarly. However, the probabilities of site occupancy, p(E), have to be properly accounted for:
| Ds = ∫fs(E)p(E)W−1(E)dE. | (4.11) |
To illuminate the basic predictions of eqn (4.11), it is more convenient to use it in a modified form:137,138
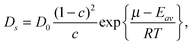 | (4.12) |
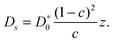 | (4.13) |
 | (4.14) |
 | ||
| Fig. 4 Surface diffusivity as a function of surface coverage calculated using eqn (4.13) assuming a generalized Freundlich isotherm (eqn (4.14)). Different curves refer to different surface heterogeneities represented by the parameter m. | ||
Let us now analyze the experimental data shown in Fig. 3 in this way. The inset shows the low-pressure part of the adsorption isotherm for acetone in porous silicon. It may be fitted using eqn (4.14) with m = 0.26. Remarkably, the diffusivity data at low surface coverage nicely follow the pattern D*0c1/m−1 (low-c limit of eqn (4.13)), with m = 0.26 obtained from the isotherm. Note that this functional dependence is expected to hold for c < 0.2, while in our case the range is extended up to c≈ 0.8. However, we consider this to occur accidentally. More detailed understanding and description of the surface diffusivities at intermediate and high coverage requires a proper account of, e.g., particle distribution over the surfaces.
In this subsection we did consider transport along the surfaces only. If, however, the molecules posses sufficient kinetic energy to overcome the energetic barrier to get away from the surface, they may perform movements along the gas phase in the pore interior. Before discussing the combined effects of different transport modes, we would like to address some aspects of pure diffusion in the gaseous phase under confinement.
B Diffusion in the gas phase
The coefficient of gas diffusion Dgas in random pore networks is generally represented as the diffusivity in a well-defined reference system (denoted in what follows by the subscript 0), divided by a tortuosity factor τ.140,141 For the two extreme cases, namely dominating molecule-molecule collisions (bulk diffusion, subscript b) and dominating molecule-wall collisions (Knudsen diffusion, subscript K), one thus may note | (4.15) |
| DK = ⅓ūd. | (4.16) |
| Db = ⅓ūλ. | (4.17) |
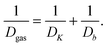 | (4.18) |
 | (4.19) |
Most importantly, in this way for the first time direct experimental evidence was provided141 that, on following the conception provided by eqn (4.15) to (4.18), the limiting cases of bulk diffusion and Knudsen diffusion have to be described by notably different tortuosity factors. In particular, in the Knudsen regime molecular propagation is found to be impeded by tortuosity effects much more intensely than under the conditions of bulk diffusion. Following refs. 147–149, this finding may be referred to an enhanced anti-correlation of subsequent molecular displacements during Knudsen diffusion in random pore networks. This means that during Knudsen diffusion-in addition to the same tortuosity-related enhancement of the diffusion path lengths as during bulk diffusion-there is an enhanced probability of backward-directed molecular displacements after collision with the pore wall. The findings of the PFG NMR diffusion measurements were nicely reproduced in mesoscopic kinetic Monte Carlo simulations with beds of zeolite NaX.150
Anti-correlation of molecular displacements after wall encounters is expected to intensify with increasing wall roughness. Both kinetic Monte Carlo simulations151–156 and analytical considerations151 confirm this assumption. Moreover, the kinetic Monte Carlo simulations154–156 revealed coinciding effects on the transport diffusivity and on the self-diffusivity, i.e. on the molecular propagation rates under both non-equilibrium and equilibrium conditions.157,158 Since, quite generally, for non-interacting diffusing particles transport diffusion and self-diffusion have to coincide and since during Knudsen diffusion, by its very nature, any interaction of the diffusants is excluded, this is exactly the behaviour to be expected.
C The effective diffusivity
With the two mechanisms of molecular transport in mesopores discussed, the overall one may be defined by both of them weighted appropriately. Before we will correlate these weights with the details of the phase equilibrium, let us consider two limiting situations: (i) at relatively low vapour pressures, before the onset of capillary condensation and (ii) at higher pressures, when the capillary-condensed bridges (small domains of the liquid extended over the whole pore cross-section) are formed. In the former case (i), the molecular displacements in both of the phases, the liquid one adsorbed on the pore walls and in the gaseous one in the pore interior, may proceed in parallel to each other. Thus, the problem becomes similar to that of a parallel connection of the resistivities. Therefore, the solution for the effective diffusivity Deff is given by ref. 159 and 160| Deff = pgasDgas + pliqDliq, | (4.20) |
In contrast, in the latter situation (ii) the propagation through a medium composed of two regions may require alternation between two regions. In the limiting case this is similar to the problem of sequential connection of resistivities. A corresponding general solution for the effective diffusivity Deff, is ref. 160
 | (4.21) |
The phase state is reflected by the adsorption isotherm θ(z), where θ is the amount adsorbed (also referred to as the pore filling factor) at the relative pressure z = P/Ps (with Ps denoting the saturation pressure). One may start to relate pgas and pliq to the given phase state with the set of equations:
| Ngas + Nliq = N, | (4.22) |
| Vgas + Vliq = V, | (4.23) |
 | (4.24) |
 | (4.25) |
It is clear that eqn (4.20) well holds for mesoporous materials with relatively big pore sizes and in the regimes where there are mono- and/or multi-layered molecules on the pore walls. To demonstrate the behaviour of Deff under these conditions, we have prepared mesoporous silicon samples with an average pore diameter of 10 nm. The recipe for their fabrication was similar to that given in section IVA, with the only differences in the doping level of the silicon wafer (resistivity of 10 mΩ cm) and the anodization current density (80 mA cm2). The acetone diffusivities measured in this material are shown in Fig. 5 as a function of the amount adsorbed θ.163 To do this, first the diffusivities had been measured as a function of the gas pressure and, using the simultaneously measured adsorption isotherm (not shown), the diffusivities were re-plotted versus θ. It is important to note that the isotherm reveals the onset of capillary-condensation being located at z≈ 0.7, corresponding to θ≈ 0.6. Thus, up to θ≈ 0.6, the multi-layered molecules on the pore walls coexist with the gaseous phase in the pore interior (parallel configuration), so that the use of eqn (4.20) is justified.
 | ||
| Fig. 5 Effective diffusivities for acetone in mesoporous silicon with an average pore diameter of about 10 nm as a function of the amount adsorbed. A monolayer is found at θ≈ 0.2. The dotted and dashed lines show the contributions by diffusion in the gaseous phase and in the phase adsorbed on the pore walls calculated viaeqn (4.20) and (4.24), respectively, with the solid line as their sum. | ||
One immediate consequence of eqn (4.24) is that pgas passes a maximum upon variation of θ. This is due to two competing effects, namely the increase of the gas density (controlled by z) and the decrease of the relative fraction of molecules in the gaseous phase (given by (1 −θ)/θ) with increasing P. Indeed, at low pore loadings (θ≲ 0.2), because of the adsorbate-surface interaction, the external pressure P must be appreciably decreased in order to release molecules from the surface. Thus, the term z in eqn (4.24) determines the behaviour of pgas at low loadings. With increasing θ, the situation is reversed, and the contribution of the gas phase to overall diffusion becomes dominating. Finally, however, with θ→ 1 and thus pgas→ 0 (eqn (4.24)), the gas phase contribution vanishes. Hence, irrespective of the fact that, with θ→ 0, the term (1 −θ)/θ goes to infinity, ρgas faster approaches zero, so that pgas becomes negligibly small.
Let us quantify these statements. As shown by the dotted line in Fig. 5, at intermediate loadings (θ from about 0.2 to 0.6) the magnitude of the term pgasDgas in eqn (4.20), where Dgas is given by eqn (4.19), is calculated to be comparable to the diffusivity at full saturation. With the adsorbed phase, the situation is less obvious, since we do not have an equivalent model for molecular diffusion in multi-layers. As a first approximation, however, we assume that the diffusivity does not appreciably change with the pore loading and that it is equal to the diffusivity at full pore loading. At sub-monolayer coverage the diffusivity behaves as shown in Fig. 3. Thus, the calculated overall dependence of the diffusivity in the adsorbed (liquid) phase on pore loading (pgasDK + (1 −pgas)Ds) results as that shown by the solid line in Fig. 5. It appears that it satisfactorily describes the experimental finding, except for a small difference in the region of the multi-layer adsorption. This reflects an underestimation of the diffusivity within the layer. With only these data, however, we do not yet feel ourselves totally confident that the diffusivity of the multi-layered molecules exceeds that of the capillary-condensed molecules, though they would clearly support such a conclusion.
The situation changes upon forming regions filled by the capillary-condensed liquid since, thus, the gaseous phase domains become spatially isolated (combination of parallel and sequential connections). Under such conditions, according to eqn (4.21), the overall diffusivity is predominantly controlled by the phase with the slowest diffusion. A nice exemplification of such a behaviour is provided by the diffusion behaviour in MAST activated carbon sample (MAST Carbon Ltd., Guildford, U.K.).164,165 Its structure is schematically shown in the inset of Fig. 6. The material used in this work was composed of 1 mm-big particles with a highly-networked internal pore structure. In addition to the micropores, there are incorporated isolated spherical holes with diameters of about 30 nm. The pore volumes of the micro- and mesopores are roughly identical.
 | ||
| Fig. 6 Effective diffusivity for cyclohexane in a MAST carbon sample as a function of the external gas density measured at 298 K. The dotted line shows the dependence expected by the use of eqn (4.20) with all known parameters. Use of the same parameters, but the sum of eqn (4.20) and (4.21) with the weights 0.4 and 0.6, instead of eqn (4.20) yields the solid line. The inset demonstrates a schematic structure of an individual MAST carbon bed. | ||
Fig. 6 shows the diffusivity of cyclohexane in this sample as a function of the external gas pressure P. In the figure the latter is presented by the gas density ρgas calculated viaeqn (4.25). The diffusivity increases with increasing gas pressure up to about ρgas = 0.25 kg m−3. This region corresponds to the mesopores filled by the gaseous phase. Further increase of ρgas is accompanied by the onset of capillary condensation in the mesopores, which nicely correlates with the deviation of the measured diffusivities from the dependence as expected viaeqn (4.20) for dominating gas phase diffusion (dotted line in Fig. 6). Now, due to a specific arrangement of the volumes occupied by the two phases, the transport should be described by a combination of eqn (4.20) and (4.21),160 namely by the appropriately weighted sum of these two equations rather than by eqn (4.20) alone. A correspondingly designed dependency is shown by the solid line and yields satisfactory agreement with the experimental data.
V. Macroscopic transport
Typically, the majority of porous materials are available as powders, i.e., they are composed of solid particles with an internal pore structure. Moreover, the pore structure itself may have different levels of organization, i.e., different types of porosities and length-scales. Thus, the overall molecular transport ultimately involves molecular exchange between regions with different mobilities. The state of the fluid and, hence, its transport properties in these various regions depend in a complex way on the external conditions. The objective of this section is to demonstrate how the NMR technique may be used to address such problems. Among different examples, a particularly interesting one will be to demonstrate how NMR allows a self-consistent comparative analysis of the data on molecular transport provided by macroscopic and microscopic measurements.A Molecular exchange between porous monoliths and their surroundings
We start our consideration with the probably most simple example—a mesoporous monolith in contact with the surrounding gas phase under equilibrium conditions. Here, one may clearly distinguish between two molecular ensembles with different transport properties, viz. molecules within the mesopores and in the surrounding phase. Thus, as discussed in section III, by recording their diffusivities one is able to attribute the molecules to either of these ensembles, and, moreover, one may monitor the exchange process between these two ensembles. Exchange times become directly accessible if they are within the time-scale of PFG NMR (1 ÷ 103 ms). For sufficiently long observation times, i.e., for molecular displacements notably exceeding the typical pore size as the general case with mesopores, diffusion within the monoliths is characterized by a single, effective diffusivity Deff (one has to be, however, aware of situations where it may not hold100). Under such circumstances, the most efficient method to quantify the exchange process is to follow the time-dependent fraction of molecules having the diffusivity Deff.We illustrate this approach by considering a model sample with pre-defined structural characteristics. The experimental results may thus be easily compared with the theoretical predictions. The sample consists of mesoporous silicon chips prepared by electro-chemical etching of silicon crystals.133 The parameters of the etching procedure and the initial silicon properties were chosen to yield pores with a diameter of about 6 nm.166 After formation of a thin porous layer, they were removed from the substrate. Thus, the thus formed pores have immediate contact to the surroundings at both ends of the layer, rendering essentially one-dimensional uptake and release processes. Five different films with different thicknesses L of 10, 20, 29, 41 and 52 μm were prepared and mixed with the respective masses mi = 29, 45, 50, 40 and 15 mg. The thus composed sample, consisting of porous films of different thicknesses, was, thereafter, outgassed in an NMR glass tube and brought into contact with a vapour of cyclohexane at 60 mbar. After equilibration the tube was sealed.
Fig. 7 demonstrates the normalized spin-echo diffusion attenuations for this model sample obtained using the 13-interval pulse sequence167 at different observation times td from 5 to 300 ms. First of all, we note a multi-exponential decay and a significant influence of the diffusion time. With increasing td, there is a tendency to converge to a single-exponential shape shown in the figure by the dotted line. This is a clear indication of the exchange process between regions with different molecular diffusivities in the system under study, namely within the pores and through the surrounding free space, respectively.
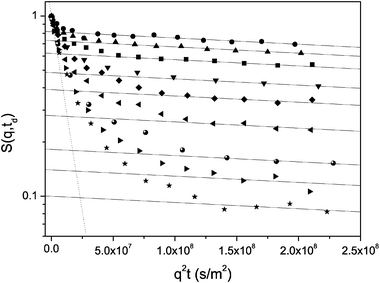 | ||
| Fig. 7 Normalized spin-echo diffusion attenuations for cyclohexane in porous silicon powder composed of small chips with different thicknesses. Different symbols refer to different diffusion times td from 5–300 ms (from top to bottom). The solid lines are shown as examples of the fit of the function psl exp{−q2Dsltd} to the data in the high-q region. The dotted line shows the exponential function to which the data converge upon increasing td. | ||
Let us now analyze the behaviour of the molecular ensemble characterized by the slowest diffusivity Dsl following the recipe described in section III. For the attenuation obtained with the shortest td = 5 ms, for which the effect of the exchange is minimal, Dsl and its respective fraction psl(td) in the spectrum of the diffusivities is easily found by fitting eqn (3.4) to the data in the high-q region. This is shown in the figure by the solid line. Thereafter, by fixing Dsl, the same procedure may be applied to the attenuation curves with larger diffusion times. The thus obtained dependence psl(td) is shown in Fig. 8.
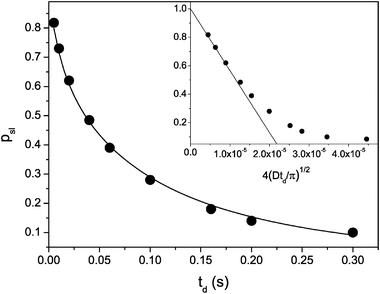 | ||
| Fig. 8 p sl obtained from the data in shown Fig. 7. The solid line shows eqn (5.26) with all relevant parameters, which are known independently. The inset demonstrates the same data, but plotted versus t1/2d. Here, the solid line shows the fit of eqn (5.28) to the data at short times. | ||
Obviously, the diffusivity Dsl, leading to the decrease of the number of molecules which have not left the pore segments during td, has to be associated with the diffusivity of cyclohexane in the porous silicon. Because all geometrical characteristics of the porous silicon in the sample under study are known, we may try to model the time dependence of psl(td) using eqn (3.8). Because the lengths Li are different for the channels of different porous silicon plates, one has to sum over all i, yielding:
 | (5.26) |
 | (5.27) |
In reality, the distribution of particle sizes is often not know. In this respect, it is instructive to analyze the short-time behavior psl(td). Applying Poisson’s summation formula to eqn (5.27) one may show that in this limit psl(td) is given by:
 | (5.28) |
B Surface barriers
Most techniques for studying mass transfer in porous media are based on following the rate of molecular uptake or release by the individual particles. They are referred to as macroscopic or mesoscopic techniques of observation,168–170 depending on whether the whole bed of nanoporous particles or an individual particle is in the focus of observation. A model-free discrimination between internal and external transport resistances, i.e., an unambiguous separation between the influences of intraparticle diffusion and of surface barriers, however, necessitates the measurement over path lengths notably below the particle sizes which is provided by the microscopic techniques only.As explained in the preceding section, PFG NMR is able to determine the relative amount of molecules (psl(td)/psl(0) in eqn (3.8) and (5.26)), which have not yet left the particles which they accommodated at time td = 0. Under the conditions of gas phase adsorption, the signal of the gas phase is negligibly small so that in this case psl(0) = 1 and there is no need for normalization by dividing psl(td) by psl(0). For variable td, this information is exactly that of a tracer exchange curve γ(td), with γ(td)(≡ 1 −psl(td)/psl(0)) denoting the relative amount of (labelled) molecules which, after time td, have left a particular porous particle, being replaced by other (unlabelled) ones from the surroundings and/or other particles. This special ability of PFG NMR is exploited by the so-called NMR tracer desorption technique, to which we have referred to already in section III.
The experimentally accessible tracer exchange curve γ(td) may most conveniently be correlated with the governing transport mechanisms via the method of moments.96,171,172 Thus, e.g., the “first” moment
| ∫∞0(1 −γ(t))dt≡∫∞0psl(t)/psl(0)dt = ∫∞0tψ(t)dt = tav | (5.29) |
 | (5.30) |
Thus, with the value of D directly determined by PFG NMR with sufficiently short observation times (diffusion path length during observation time much shorter than the particle size), the value of tav following viaeqn (5.29) from the “NMR tracer desorption curve” and the particle radius R accessible by microscopic inspection, the surface permeability follows directly from eqn (5.30). This option has been widely exploited for the exploration of the conditions under which either the production of zeolitic host systems174,175 or their technological use for mass separation and chemical conversion175–177 give rise to the formation of surface barriers.
The accuracy of this way of analysis is limited by the fact that the uncertainty of tav as resulting viaeqn (5.29) is typically of the order of a factor of 2. Hence, reliable data for the surface permeability are accessible only, if the second term in the right-hand side of eqn (5.30) notably exceeds the first one. The inclusion of the information provided by an analysis of the time dependence of the PFG NMR signal attenuation for large gradient intensities (see Fig. 7) has recently been shown to notably enhance this accuracy.178,179 It should be mentioned that also the thus attainable accuracies are still inferior to those reachable by the application of interference microscopy.180,181 Being able to directly monitor transient concentration profiles, this technique is essentially totally unaffected by the rate of intra-crystalline diffusion and allows the determination of surface permeabilities with unprecedented accuracy. As a big disadvantage, however, the measurements can only be performed with single crystallites with dimensions (favourably some tens of micrometers) which must notably exceed the minimum sizes still accessible by PFG NMR studies.
C Overall transport in powders and agglomerates
Many porous materials are available in the form of macroscopically big particles with a complex internal porous structure. Such structures may result from, for example, different levels of agglomeration leading to very different types of porosities in the sample. Depending on the external parameters, such as pressure or temperature, the local phase state in different regions may be quite different. In this section we are going to address how transport properties are correlated with the external conditions in materials with a hierarchy of typical length scales.As a representative example, we consider a commercially available MCM-41 material.1,2Fig. 9 shows the internal texture of an individual particle, where one may identify typical building blocks of sufficiently different dimensions. According to the literature data,182,183 the basic building units are individual, mesoporous quasi-crystallites with MCM-41 structure, i.e., traversed by cylindrical channels with a diameter of a few nanometres. These channels are hexagonally arranged resulting in an internal porosity of about 40%. As a next level of organization, the crystallites form clusters or grains with a dimension of a few hundred nanometres. Finally, the grains agglomerate to particles with a broad distribution of sizes from tens to hundreds of micrometers.
 | ||
| Fig. 9 Scanning electron micrograph of the internal texture of an MCM-41 particle comprising the individual MCM-41 crystallites and the secondary macroporous space. | ||
The diffusion attenuation functions for cyclohexane measured in the sample under study have been found to be slightly non-exponential and to depend on the observation time td which was varied from 3 to 300 ms. Such a behaviour is an indication of a macroscopic heterogeneity with the time-dependence being the consequence of the molecular exchange between different regions in the sample. In what follows, we are going to analyze the effective diffusivities Deff deduced from the attenuations in the low-q limit. The thus obtained values of Deff represent the ensemble-average over the sample and are shown in Fig. 10 as a function of the external gas pressure. With a value of 10−7 m2/s using the Einstein relation 〈r2〉 = 6Defftd, the extension of the regions with a uniform diffusivity may be estimated to be  . The latter appears to be of the order of the particle sizes. Therefore, the heterogeneity may be associated with the textural differences in the different particles.
. The latter appears to be of the order of the particle sizes. Therefore, the heterogeneity may be associated with the textural differences in the different particles.
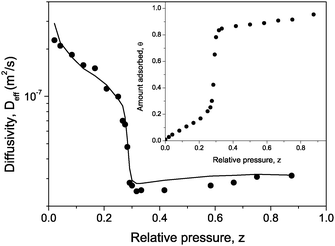 | ||
| Fig. 10 The effective diffusivity Deff for cyclohexane in MCM-41 agglomerates as a function of the relative vapor pressure z measured on the desorption branch. The solid line shows the best fit of eqn (5.31) to the experimental data. The inset shows the desorption isotherm normalized to the volume of the mesopores. | ||
To understand the pressure dependence of the diffusivity one may perform an analysis similar to that given in section IVC. In this case, also equilibrium between the mesopores in crystallites and the macropores formed between the grains and the particles has to be taken into account.184 In this way, one finally gets
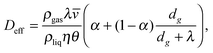 | (5.31) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) denote the mean free path and mean molecular velocity in the gas phase, η is the ratio of the meso- and macropore volumes, dg is the effective inter-grain distance, and α is the ratio of the intra-particle macropore volume to the total macropore volume, respectively. The best fit of eqn (5.31) to the experimental data is attained with α = 0.16 and dg = 0.61 μm (all other parameters are known) and is shown in Fig. 10.
denote the mean free path and mean molecular velocity in the gas phase, η is the ratio of the meso- and macropore volumes, dg is the effective inter-grain distance, and α is the ratio of the intra-particle macropore volume to the total macropore volume, respectively. The best fit of eqn (5.31) to the experimental data is attained with α = 0.16 and dg = 0.61 μm (all other parameters are known) and is shown in Fig. 10.
A more detailed analysis of eqn (5.31) suggests that the obtained dependency of Deff on the gas pressure is predominantly controlled by the equilibrium conditions between the gaseous and adsorbed phases in the mesopores. Thus, the slight decrease of Deff observed for decreasing pressures from z = 1 till the onset of the evaporation transition in mesopores may be referred to the decrease in the gas density ρgas in the macropores. At z≈ 0.3, the evaporation of the liquid out of the mesopores leads to a sudden increase of the relative fraction of the molecules in the macropores. In the low-pressure region the equilibrium is determined by the interaction of the liquid with the walls of the mesopore. Thus, the equilibrium conditions reasonably well explain the obtained results. Quantitative agreement between theory and experiment is clearly obtained only, if the characteristic geometrical features of macroporous space are taken into account. These are predominantly reflected by the diffusivity of the gas phase in the macropores. In the present case, it has been simply accounted for by summing up the transport resistivities due to intermolecular collisions and collisions with the grain walls.
Being able to record the rate of molecular displacements over different length scales, PFG NMR is able to assess the limiting processes of mass transfer in agglomerated catalyst particles formed by nanoporous crystals dispersed in a (macroporous) binder. As a prominent example, in Fluid Catalytic Cracking (FCC)21,185 catalyst particles with radii Rp of typically about 30 μm are applied which contain small zeolite crystals of type NaY with radii Rc of about 0.5 μm. In such materials it is not obvious whether overall exchange with the surrounding atmosphere is controlled by mass transfer through the binder or by mass exchange between each individual zeolite crystal and the surrounding binder. In fact, following an old tradition in overestimating the transport resistance of the genuine zeolite pore network,169 reactant and product transport within the zeolites is generally considered to be the rate-limiting process of overall mass transfer.186 However, recent detailed PFG NMR22,23,187 studies revealed exactly the opposite. In fact, by choosing the observation time td of the PFG NMR experiment in such a way that the experimentally covered molecular displacements are either much larger or much smaller than the zeolite crystallites, one is able to directly measure the diffusivities for molecular transport both within the individual zeolite crystals (Dc) and through the whole catalyst particle (Dp). With these diffusivities and the corresponding radii, eqn (3.10) allows a straightforward estimate of the respective time constants of molecular exchange. As a result, molecular mean life times within the individual zeolite crystals turned out to be much smaller than the mean life times within the catalyst particles, indicating that molecular transport through the particle rather than through the zeolitic component is the rate-controlling process in the overall mass transfer.22,23,187 During technical application, inter-crystalline exchange may clearly become impeded by the formation of surface resistance. In this case, replacing eqn (3.10) by eqn (5.30), one also has to take account of surface resistance (i.e., a finite value of the surface permeability γ).188
VI. Phase state and transport
A Dynamics in disordered pores under sub-critical conditions
So far, we have clearly demonstrated that the diffusion behaviour of guest molecules in mesoporous solids is strongly coupled to their phase state in the pores. The latter can be associated with a certain point on the sorption isotherm. As a very essential property of these materials, however, one has to be aware of the development of hysteresis. Thus, under identical external conditions, the phase state becomes dependent on the way how these conditions have been attained, i.e., on the “history”. It, thus, becomes quite interesting to compare the intrinsic diffusivities in the hysteresis region.This type of experiments can be easily carried out by performing PFG NMR diffusion measurements using NMR samples with a porous material connected to a reservoir with the vapour of a liquid under study. Thus, either by decreasing or increasing the vapour pressure in the reservoir, the effective diffusivities can be measured along with the sorption isotherm.124Fig. 11 shows one of the typical examples, demonstrating a well-pronounced hysteresis loop when the diffusivity is plotted versus the external gas pressure.132 It should be noted that such an approach has earlier been used to demonstrate that nuclear magnetic relaxation properties of adsorbed fluids may also differ for adsorption and desorption.189 We could show that this type of diffusion hysteresis is not limited to systems exhibiting adsorption hysteresis,190 but also holds for other types of hysteretic behaviour, for example freezing/melting hysteresis.191
 | ||
| Fig. 11 The effective diffusivity Deff (circles) for cyclohexane and its relative amount adsorbed (triangles) in Vycor porous glass (dp = 6 nm) measured on the adsorption (open symbols) and desorption (filled symbols) branches as a function of the relative gas pressure. | ||
Recalling the discussion of section IVC, the development of hysteresis in diffusivity-pressure coordinates might appear to be natural. Indeed, the external gas pressure defines the amount adsorbed θ, which is, in turn, different on adsorption and desorption as given by the sorption isotherms. Thus, one may simply attribute the difference in the diffusivities Deff to the difference in θ. Deff may clearly also be plotted directly as a function of the pore loading θ. Remarkably, upon such a transformation, hysteresis is still preserved as shown in Fig. 12.74 Moreover, for one and the same loading, the diffusivities are also found to differ for the various “scanning isotherms”,39i.e., for isotherm branches which result from incomplete cycles of adsorption and desorption. The thus obtained diffusivities lie inbetween the two main loops and it becomes obvious that, by a corresponding “tuning” of the history of pressure variation, in this way one may obtain a whole “spectrum” of arbitrary diffusivities.
 | ||
| Fig. 12 The effective diffusivity Deff for cyclohexane in Vycor porous glass (dp = 6 nm) of Fig. 11 as a function of the amount adsorbed θ. The filled rectangles show Deff measured during various “scanning isotherms”. | ||
As to the most important feature of the results in Fig. 12 we refer to the existence of several different diffusivities at one and the same pore loading θ. In ref. 74, two mechanisms which may contribute to the observed behaviour, have been discussed. The first one refers to the fact that, on desorption, the liquid in the regions with the capillary-condensed phase occurs in a somewhat stretched, lower-density state. This stretching effect means that, for one and the same θ, the liquid phase occupies a notably larger part of the pore space during desorption than during adsorption. The second mechanism is related to the differences in the microscopic distribution of the liquid phase within the porous solid.192–194 In our case, the PFG NMR data indicate that, on the micrometer length scale, such a distribution is homogeneous. The origin of different distributions on adsorption and desorption is, thus, attributed to an interplay between cavitation and pore-blocking effects, leading to the formation of more extended mesoscale regions of the capillary-condensed and gaseous phase during adsorption.74
The multiplicity of the diffusivities in Fig. 12 may thus be related to differences in the (history-dependent) density distribution over the pore space. This conception is in good agreement with the idea of a dynamically prohibited equilibration in random systems.82,83 Notably, being separated by large barriers in the system’s free energy, these out-of-equilibrium states, associated with different fluid distributions, are found to remain stable over very long intervals of time. Quite importantly, the non-invasive and non-perturbative access to the intrinsic molecular diffusivities in the pores using PFG NMR technique allows to provide further experimental evidence of such a scenario.
In this respect, it is interesting to note that while there is a great deal of experimental data for adsorption isotherms including hysteresis, much less attention has been given to the dynamics of systems exhibiting sorption hysteresis. Notably, there were a few experimental reports indicating that equilibration kinetics may slow down in the hysteresis region.195–198 An analytical description of the observed behaviour was undertaken by involving a priori assumptions on diffusion-controlled sorption. Thus, all features of the experiments, in particular a slowing down of uptake in the hysteresis region, have been attributed to a corresponding change of the diffusivity.
To address this issue in more detail, a comparative study of sorption kinetics and genuine diffusivities in one and the same material under almost the same external conditions have recently been performed using NMR.115,116 The experimental procedure included a small stepwise change of the external gas pressure. Thereafter, the resulting density relaxation, i.e., sorption kinetics, has been followed. After giving a sufficiently long time for the equilibration, the effective diffusivity Deff has been measured using PFG NMR. With the thus determined value of Deff and the geometry of the used mesoporous material (rod-shaped Vycor porous glass), the sorption kinetics under the condition of diffusion control can be easily predicted. Thus, with θ0 and θeq as the amounts adsorbed before the pressure steps and after equilibration, the uptake by a cylinder of radius a is given by ref. 110
 | (6.32) |
Fig. 13 shows the experimental data for the adsorption kinetics of cyclohexane into Vycor porous glass with a pore diameter of about 6 nm in two regions of the adsorption isotherm, namely out of and in the hysteresis region. In addition, it shows the predictions of eqn (6.32). Note that (i) Deff has been measured independently (see Fig. 11) and (ii) eqn (6.32) does not have any fitting parameters. Beyond the hysteresis region, the experimental data are found to be nicely reproduced. This confirms that under this condition mass transfer is in fact limited by diffusion. Remarkably, however, in the hysteresis region the model predicts much faster equilibration. This discrepancy between the observed time dependence of uptake and the prediction on the basis of the measured diffusivities unequivocally points out that only the early-stage uptake is controlled by diffusion.115 At later stages, however, the system equilibration is governed by extremely slow relaxation due to the thermally activated process of the liquid redistribution within the porous material. This process is reminiscent of a very slow process of phase separation of critical binary mixtures in porous media and successfully treated in the frame of random-field Ising systems.199,200
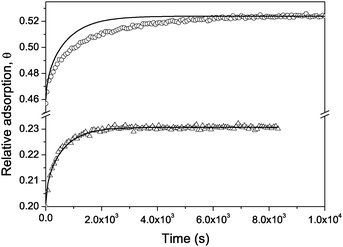 | ||
| Fig. 13 The adsorption kinetics for cyclohexane in Vycor porous glass (dp = 6 nm) out of (triangles) and within (circles) the adsorption hysteresis region following a small (5 mbar) pressure step. The solid lines show theoretical predictions using eqn (6.32) with all known parameters. | ||
B Cavitation-governed diffusivity enhancement
The experiments described in the preceding section have been performed under isothermal conditions. However, one may also affect and change the phase state of a liquid in pores using further experimental schemes, e.g. by varying the temperature and keeping the system volume constant. This experimental procedure is easily achieved by using sealed NMR samples containing a porous material and some volume available for the vapour above it. The impact of the external parameters on the molecular diffusivities under these conditions may most illustratively be demonstrated by a comparative study of two different samples. In one of them, in the whole temperature range probed in the experiments, the liquid under study should always completely cover the porous particles. That means that the mesopores will always be filled by the capillary-condensed phase. This sample will provide a reference diffusivity of the liquid in pores as a function of temperature. The second sample has to be prepared in such a way that only at the lowest temperature the mesopores are completely filled by the liquid. Thus, by changing the temperature, one may affect the equilibrium between the vapor phase above the porous material and the adsorbed phase.The results of such comparative experiments are shown in Fig. 14. The figure displays the diffusivities of n-pentane within the pore system of Vycor porous glass as a function of inverse temperature as obtained by PFG NMR method.201 In the over saturated sample, molecular diffusion is found to follow an Arrhenius dependence with an activation energy for diffusion typical of the bulk liquid.
 | ||
| Fig. 14 The effective intra-pore diffusivity for n-pentane in Vycor porous glass (dp = 6 nm) for samples with (filled circles) and without (filled triangles) excess liquid phase as a function of inverse temperature. | ||
In the other sample, however, starting from about 300 K, the diffusivities deviate from those in the reference sample. Let us consider what could be the impact of the temperature on the phase state within the mesopores. Recall, first, that this sample contains an amount of guest molecules ensuring complete filling of the mesopores only at the lowest temperature. Therefore, with increasing temperature, there is a competing process between either maintaining the vapour pressure in the gas phase surrounding the porous particles saturated or maintaining the liquid phase in the mesopores intact. At lower temperatures, up to about 300 K, under saturation (P/Ps) is found to be relatively small. This is provided by the evaporation of the liquid from the pores. At temperatures above 300 K, however, the latter process cannot compensate any more the strong decrease of the relative pressure P/Ps due to the dramatically increasing value of Ps. Thus, P/Ps becomes sufficient to trigger cavitation in the sufficiently large pores of the Vycor glass.
The enhancement of molecular propagation in the sample containing no excess liquid, thus, originates from the contribution of fast molecular diffusion in such cavitated regions of the porous structure. Molecular transport therein is considered to follow Knudsen diffusion, the simplest model one would imply under the given conditions. Exactly such a change of the phase state of the liquid in the pores, resulting in the formation of internal gas-filled regions with the establishment of extremely fast diffusion paths therein, leads to the increase in the slope of the Arrhenius plot of the diffusivity seen in Fig. 14.
C Dynamics in pores near the critical point
For two controlled pore glasses (CPGs) with different mean pore diameters in the mesoporous range (d = 6 or 15 nm), the diffusivities in the bulk and within mesopore space were measure by PFG NMR. Starting from a liquid phase around and inside the porous materials, the diffusivities for both pore glasses follow the Arrhenius dependence on increasing temperature. At a distinct temperature below the bulk critical temperature, however, upon a small temperature increase the diffusivities in both materials increase significantly. As an example, Fig. 15b shows such a diffusivity jump for a Vycor porous glass with dp = 6 nm. This jump in diffusivity is an indication of a phase transition from the liquid to a supercritical fluid within the pores of the material. The occurrence of the liquid/supercritical-phase transition is corroborated by the fact that the meniscus of the liquid phase above the pore glasses in the NMR tube rises strongly when reaching this temperature, as one may see in Fig. 15a. Upon reaching supercritical conditions, the density of the pore-confined phase decreases rapidly. A corresponding part of the liquid is, thus, expelled from the pores, eventually leading to the rising liquid meniscus.
 | ||
| Fig. 15 Temperature dependence of (a) the meniscus level in an NMR glass tube containing Vycor porous glass (dp = 6 nm) and cyclohexane in excess and of (b) the cyclohexane diffusivity in the bulk liquid phase (triangles) and in the Vycor porous glass particles. The solid lines show the model-based calculations.205 The vertical dashed and dotted lines indicate the positions of Tc and Tcp, respectively. | ||
Expectedly, the increase of the diffusivities in the CPGs is related to their pore diameter: the jump is more pronounced and its temperature, i.e., Tcp, is closer to that of the bulk critical temperature Tc for the material with the larger pores. The diffusivity change can, thus, be directly assigned to the shift of the phase transition caused by confinement of the phases in the mesopores. Notably, the temperature shift ΔT = Tc−Tcp is linearly correlated to the reciprocal pore diameter as earlier mentioned in other studies.30,85 Above the pore critical point, the diffusivity on the mesopores of the CPGs remains essentially constant at the value given by the mean free path in the mesopore according to the Knudsen diffusion limit.143 Evidently, we find this value to be higher for the material with the larger mean mesopore diameter.205
It is worth mentioning that the experimental diffusivity data in Fig. 15 can be quantitatively described by a simple analytical model based on gas-kinetic arguments.205,206 Here, the effective diffusivities in the pores are calculated by a weighted superposition of the diffusivities in the adsorbed phase (assumed to have a liquid density) and in the fluid phase in the interior of the pore space. The full lines in Fig. 15 denote the results of these calculations. Obviously, the experimentally observed data are well described by this simple model.
Materials preparation. While a supercritical phase itself is an attractive medium to produce nanomaterials,207 in the mesopores of a solid host it may be used to introduce guests into the pores or to chemically modify the walls within the pores of a mesoporous material. Due to the high diffusivity in the supercritical state, these processes can be achieved in significantly shorter times and with a better controllable loading than with conventional liquids. If the bulk phase surrounding the solid is also in the supercritical state, the virtually negligible surface tension of supercritical fluids may lead to a further acceleration. Two examples will illustrate these advantages.
Holmes et al.208 have demonstrated that nanostructured metals and semi-conductors within ordered mesoporous materials may be prepared with the aid of supercritical fluids. For instance, nanowires of Silicon or Germanium can be generated within MCM-41-type molecular sieves by a controlled decomposition of metal organic precursors in supercritical n-hexane. As opposed to conventional gas-phase procedures such as chemical vapour deposition (CVD), a complete filling of the internal pore volume can be achieved. Moreover, the metal deposition is completed within 15–30 min, whereas durations up to days are needed for the same deposition efficiency in liquid solvents. The resulting silicon-containing composite materials show a UV-photoluminescence with an emission maximum depending on the pore diameter of the mesoporous host. They are, thus, attractive as sensors or for other optical applications.
The reactive deposition of metals from supercritical fluid solutions (Supercritical Fluid Deposition, SFD) is particularly attractive for the preparation of solid catalysts.209 For this procedure, a metal organic complex is dissolved, for instance, in supercritical carbon dioxide in the presence of a solid support material. Through addition of hydrogen to the supercritical complex solution, the metal is directly deposited onto the support. Thus, both the solubilizing power of supercritical fluids for high-boiling compounds and the miscibility with gases like hydrogen are utilized in this application. First results for the deposition of platinum by reduction of the precursor complex cyclooctadienyldimethylplatinum(II) in supercritical carbon dioxide indicate that the SFD can be achieved in mesoporous materials such as MCM-41 (d = 2.3 nm), but not in microporous zeolites like silicalite-1 or beta.210
Sorption. Similar to the application for materials preparation described above, the sorption of functional compounds into mesoporous materials may benefit from the presence of a supercritical pore phase. Only very few investigations on the adsorption of substances from supercritical solutions onto mesoporous molecular sieves are reported in the literature so far. However, an application of sorption on a large-pore zeolite-type molecular sieve VPI-5 from supercritical solution may serve as an example. This molecular sieve was loaded within a short time with benzoic acid, salicylic and acetyl salicylic acid.211 The resulting composite materials are of potential interest for the controlled release of pharmaceutically active compounds.
Heterogeneous catalysis. The ample opportunities arising from the application of SCFs in heterogeneous catalysis were already referred to above.203 It should be emphasized here again that several studies in the literature invoke the improved transfer from a bulk supercritical phase to the catalysts surface or within the pores of a catalyst for the rationalization of high reaction rates under SCF conditions. So far, however, higher diffusivities in mesoporous materials achieved by “pressure-tuning” of the bulk phase have been measured indirectly only, e.g., by inference from density measurements via vibrational spectroscopy.204 Another, most interesting way to experimentally determine the effective diffusivity is from catalytic conversions under conditions for which the diffusion inside the mesopores of a catalyst is the rate-limiting step. Such a study was systematically conducted by Arunajatesan et al.212 for the double-bond isomerization of 1-hexene over a commercially available catalyst consisting of 0.6 wt% Pt on mesoporous γ-Al2O3 (average pore diameter d = 5 nm) close to critical point of the reactant (Tc = 231 °C, Pc = 31.7 bar). Varying the reaction temperature and pressure over a wide range of conditions, the effective diffusivities were calculated as a function of reduced density applying the Thiele concept to the mesopore diffusion-limited conversion rates at steady state.
Remarkably, the effective diffusivity in the mesopores of the 0.6 Pt/γ-Al2O3-catalyst can be tuned close to the critical point by two orders of magnitude. This range of diffusivities is clearly broader than that observed in by PFG NMR over the CPG with a similar pore diameter (vide supra). Note, however, that the corresponding experiments were not performed for systematically varied density, but just by heating a pure liquid hydrocarbon in the presence of the mesoporous solid enclosed in an NMR tube. Most interestingly and in perfect agreement with the findings from PFG NMR measurements on the CPGs, the maximum diffusivity in the mesoporous catalyst is observed for a reduced density slightly below that of the bulk phase. This, again, indicates that particularly high diffusivities can be achieved when the pore-confined phases reach the supercritical state. It is quite challenging to see whether this transport optimization via control of the phases inside the pore space can also be fruitfully exploited for other heterogeneously catalyzed conversions over (especially ordered) mesoporous materials.
VII. Conclusions and perspectives
Pulsed field gradient NMR has been established as a powerful tool to explore mass transfer in porous media. It allows the direct monitoring of the various constituents of overall mass transfer and the quantification of the relevant parameters, including the diffusivities of the guest molecules in different sample regions as well as their permeability through internal transport barriers and at the interface between the pore space and the surrounding atmosphere. Most importantly, this information is provided non-invasively, without any interference with the intrinsic processes of the sample under study. NMR spectroscopy has thus proven to be particularly qualified to explore the influences of the different phase states of the guest molecules on overall transport, opening novel routes for the transport-optimized design and performance of porous materials.Particular concern deserve those cases where, initiated by very small changes in temperature or pressure, phase transitions may lead to dramatic changes in the transport properties. This is especially evident for hierarchically structured pore systems. In this way, by transferring the fluid in the mesopores from sub- to supercritical state, the accessibility of the micropores in hierarchically organized porous materials, and hence, e.g., the effectiveness factor of heterogeneously catalyzed chemical reactions, may be dramatically enhanced. A specially interesting route for process design is offered by the experimentally demonstrated fact that a fluid in pores may already transit to the supercritical phase, while the surrounding, excess fluid is still in the liquid state. Thus, properly designed mesoporous materials can be used to spatially localize regions (possibly hierarchically organized), where by only a tiny change of the external parameters the fluid can be turned into a supercritical one, with all unique properties inherent to it, and vice versa. The design of processes based on such phenomena is notably facilitated by the fact that, irrespective of huge changes in the guest propagation rates within the mesopores, diffusion in the microporous space, i.e. in the region of relevance for the elementary processes of molecular separation and/or conversion, remains essentially unaffected.
Challenges of future research, which most notably will benefit from the potentials of PFG NMR, include (i) the establishment of a comprehensive view on diffusion in mesopores over the whole range of loadings and phases, including the supercritical state, (ii) experiments where transitions into the supercritical state are initiated by changing either temperature or pressure (rather than by coupled changes of both of them as so far generally considered) and (iii) the consideration of all these phenomena for multicomponent guest phases. A close correlation with the ample potentials of research in this field is a prime prerequisite of the success of these efforts. In fact, also in this respect, namely in its ability to be performed under the conditions of conventional sorption experiments, PFG NMR has proven to offer ideal conditions. Consequently, a deeper understanding of the correlation between phase behaviour and transport properties may lead to promising options in the future use of mesoporous materials in a very diverse range of applications including sorption, catalysis, sensors, life sciences, biochemistry and bio-systems.
Acknowledgements
The work has been done in the frame of the DFG Research Unit 877 and the International Research Training Group "Diffusion in porous materials", jointly supported by the Science Foundations of Germany (DFG, GRK 1056) and the Netherlands (NWO).References
- J. S. Beck, J. C. Vartuli, W. J. Roth, M. E. Leonowicz, C. T. Kresge, K. D. Schmitt, C. T. W. Chu, D. H. Olson, E. W. Sheppard, S. B. Mccullen, J. B. Higgins and J. L. Schlenker, J. Am. Chem. Soc., 1992, 114, 10834–10843 CrossRef CAS.
- C. T. Kresge, M. E. Leonowicz, W. J. Roth, J. C. Vartuli and J. S. Beck, Nature, 1992, 359, 710–712 CrossRef CAS.
- P. T. Tanev and T. J. Pinnavaia, Science, 1995, 267, 865–867 CrossRef CAS.
- S. A. Bagshaw, E. Prouzet and T. J. Pinnavaia, Science, 1995, 269, 1242–1244 CrossRef.
- R. Ryoo, S. H. Joo and S. Jun, J. Phys. Chem. B, 1999, 103, 7743–7746 CrossRef CAS.
- U. Ciesla and F. Schüth, Microporous Mesoporous Mater., 1999, 27, 131–149 CrossRef.
- G. J. D. Soler-Illia, C. Sanchez, B. Lebeau and J. Patarin, Chem. Rev., 2002, 102, 4093–4138 CrossRef.
- F. Schüth, Angew. Chem., Int. Ed., 2003, 42, 3604–3622 CrossRef.
- F. Hoffmann, M. Cornelius, J. Morell and M. Fröba, Angew. Chem., Int. Ed., 2006, 45, 3216–3251 CrossRef.
- P. Schmidt-Winkel, W. W. Lukens, D. Y. Zhao, P. D. Yang, B. F. Chmelka and G. D. Stucky, J. Am. Chem. Soc., 1999, 121, 254–255 CrossRef CAS.
- J. S. Lettow, Y. J. Han, P. Schmidt-Winkel, P. D. Yang, D. Y. Zhao, G. D. Stucky and J. Y. Ying, Langmuir, 2000, 16, 8291–8295 CrossRef CAS.
- D. T. On and S. Kaliaguine, J. Am. Chem. Soc., 2003, 125, 618–619 CrossRef.
- S. Kaskel, in Handbook of Porous Solids, ed. F. Schüth, K. S. W. Sing and J. Weitkamp, Wiley-VCH, 2002, vol. 2, p. 1190 Search PubMed.
- C. Janiak, Dalton Trans., 2003, 2781–2804 RSC.
- S. Kitagawa, R. Kitaura and S. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375 CrossRef CAS.
- A. Taguchi and F. Schüth, Microporous Mesoporous Mater., 2005, 77, 1–45 CrossRef CAS.
- M.-O. Coppens, J. Sun and T. Maschmeyer, Catal. Today, 2001, 69, 331–335 CrossRef CAS.
- C. H. Christensen, K. Johannsen, E. Toernqvist, I. Schmidt and H. Topsoe, Catal. Today, 2007, 128, 117–122 CrossRef CAS.
- D. R. Rolison, Science, 2003, 299, 1698–1701 CrossRef CAS.
- J. S. Beck and W. O. Haag, in Handbook of Heterogeneous Catalysis, ed. G. Ertl, H. Knötzinger and J. Weitkamp, Wiley-VCH, Weinheim, 1997, vol. 5, pp. 2123–2136 Search PubMed.
- R. von Ballmoos, D. H. Harris and J. S. Magee, in Handbook of Heterogeneous Catalysis, ed. G. Ertl, H. Knötzinger and J. Weitkamp, Wiley-VCH, Weinheim, 1997, vol. 4, pp. 1955–1986 Search PubMed.
- P. Kortunov, S. Vasenkov, J. Kärger, M. F. Elia, M. Perez, M. Stöcker, G. K. Papadopoulos, D. Theodorou, B. Drescher, G. McElhiney, B. Bernauer, V. Krystl, M. Kocirik, A. Zikanova, H. Jirglova, C. Berger, R. Gläser, J. Weitkamp and E. W. Hansen, Chem. Mater., 2005, 17, 2466–2474 CrossRef CAS.
- P. Kortunov, S. Vasenkov, J. Kärger, R. Valiullin, P. Gottschalk, M. F. Elia, M. Perez, M. Stöcker, B. Drescher, G. McElhiney, C. Berger, R. Gläser and J. Weitkamp, J. Am. Chem. Soc., 2005, 127, 13055–13059 CrossRef CAS.
- M. Hartmann, Chem. Mater., 2005, 17, 4577–4593 CrossRef CAS.
- W. Xia and J. Chang, J. Controlled Release, 2006, 110, 522–530 CrossRef CAS.
- M. Vallet-Regi, M. Colilla and I. Izquierdo-Barba, J. Biomed. Nanotechnol., 2008, 4, 1–15 Search PubMed.
- D. Kovalev and M. Fujii, Adv. Mater., 2005, 17, 2531–2544 CrossRef CAS.
- A. Holtzel and U. Tallarek, J. Sep. Sci., 2007, 30, 1398–1419 CrossRef.
- P. Barthelemy, M. Ghulinyan, Z. Gaburro, C. Toninelli, L. Pavesi and D. S. Wiersma, Nature Photonics, 2007, 1, 172–175 CrossRef CAS.
- L. D. Gelb, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, Rep. Prog. Phys., 1999, 62, 1573–1659 CrossRef CAS.
- K. Knorr, P. Huber and D. Wallacher, Z. Phys. Chem., 2008, 222, 257–285 CrossRef CAS.
- M. Brun, A. Lallemand, J. F. Quinson and C. Eyraud, Thermochim. Acta, 1977, 21, 59–88 CrossRef CAS.
- C. L. Jackson and G. B. McKenna, J. Chem. Phys., 1990, 93, 9002–9011 CrossRef CAS.
- J. Mitchell, J. B. W. Webber and J. Strange, Phys. Rep., 2008, 461, 1–36 CrossRef CAS.
- K. S. W. Sing, F. Rouquerol and J. Rouquerol, Adsorption by Powders and Solids, Academic Press, London, 1999 Search PubMed.
- L. Bocquet, E. Charlaix, S. Ciliberto and J. Crassous, Nature, 1998, 396, 735–737 CrossRef CAS.
- O. Beckstein and M. S. P. Sansom, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 7063–7068 CrossRef.
- M. Nosonovsky and B. Bhushan, Phys. Chem. Chem. Phys., 2008, 10, 2137–2144 RSC.
- D. H. Everett, in The Solid-Gas Interface, ed. E. Alison Flood, Marcel Dekker, Inc., New York, 1967, pp. 1055–1113 Search PubMed.
- J. M. van Bemmelen, Z. Anorg. Allg. Chem., 1897, 13, 233–356 Search PubMed.
- R. Zsigmondy, Z. Anorg. Allg. Chem., 1911, 71, 356–377 Search PubMed.
- T. J. Barton, L. M. Bull, W. G. Klemperer, D. A. Loy, B. McEnaney, M. Misono, P. A. Monson, G. Pez, G. W. Scherer, J. C. Vartuli and O. M. Yaghi, Chem. Mater., 1999, 11, 2633–2656 CrossRef CAS.
- Handbook of Porous Solids, ed. F. Schüth, K. S. W. Sing and J. Weitkamp, Wiley-VCH, 2002 Search PubMed.
- J. Kärger, H. Pfeifer and W. Heink, Adv. Magn. Reson., 1988, 12, 2–89 Search PubMed.
- P. T. Callaghan, Principles of Nuclear Magnetic Resonance Microscopy, Clarendon Press, Oxford, 1991 Search PubMed.
- R. Kimmich, NMR: Tomography, Diffusometry, Relaxometry, Springer-Verlag, Berlin Heidelberg, 1997 Search PubMed.
- W. S. Price, Concepts Magn. Reson., 1997, 9, 299–336 Search PubMed.
- W. S. Price, Concepts Magn. Reson., 1998, 10, 197–237 Search PubMed.
- G. H. Sørland and D. Aksnes, Magn. Reson. Chem., 2002, 40, S139–S146 CrossRef CAS.
- L. H. Cohan, J. Am. Chem. Soc., 1938, 60, 433–435 CrossRef CAS.
- E. O. Kraemer, in Treatise on Physical Chemistry, ed. H. S. Taylor, Van Nostrand, New York, 1931 Search PubMed.
- J. W. McBain, J. Am. Chem. Soc., 1935, 57, 699 CrossRef.
- G. Mason, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1988, 415, 453–486 Search PubMed.
- R. Evans, J. Phys.: Condens. Matter, 1990, 2, 8989–9007 CrossRef.
- G. Mason, J. Colloid Interface Sci., 1982, 88, 36–46 CrossRef CAS.
- P. C. Ball and R. Evans, Langmuir, 1989, 5, 714–723 CrossRef CAS.
- A. V. Neimark, P. I. Ravikovitch and A. Vishnyakov, Phys. Rev. E, 2000, 62, R1493–R1496 Search PubMed.
- F. Restagno, L. Bocquet and T. Biben, Phys. Rev. Lett., 2000, 84, 2433–2436 CrossRef CAS.
- A. V. Neimark, P. I. Ravikovitch and A. Vishnyakov, Phys. Rev. E, 2002, 65, 031505 CrossRef.
- P. A. Monson, Adsorption, 2005, 11, 29–35 CrossRef.
- I. Brovchenko and A. Oleinikova, in Handbook of Theoretical and Computational Nanotechnology, ed. M. Rieth and W. Schommers, American Scientific Publishers, 2005 Search PubMed.
- L. Sarkisov and P. A. Monson, Langmuir, 2001, 17, 7600–7604 CrossRef CAS.
- N. A. Seaton, Chem. Eng. Sci., 1991, 46, 1895–1909 CrossRef CAS.
- B. Coasne and R. J. M. Pellenq, J. Chem. Phys., 2004, 121, 3767–3774 CrossRef CAS.
- P. van der Voort, P. Ravikovitch, K. De jong, M. Benjelloun, E. Van Bavel, A. Janssen, A. Neimark, B. Weckhuysen and E. Vansant, J. Phys. Chem. B, 2002, 106, 5873–5877 CrossRef CAS.
- M. Thommes, B. Smarsly, M. Groenewolt, P. Ravikovitch and A. Neimark, Langmuir, 2006, 22, 756–764 CrossRef CAS.
- K. Morishige and Y. Nakamura, Langmuir, 2004, 20, 4503–4506 CrossRef CAS.
- E. A. Ustinov, Langmuir, 2008, 24, 6668–6675 CrossRef CAS.
- F. Casanova, C. E. Chiang, C.-P. Li, I. V. Roshchin, A. M. Ruminski, M. J. Sailor and I. K. Schuller, Nanotechnology, 2008, 315709 CrossRef.
- F. Stallmach, J. Kärger, C. Krause, M. Jeschke and U. Oberhagemann, J. Am. Chem. Soc., 2000, 122, 9237–9242 CrossRef CAS.
- F. Stallmach, A. Graser, J. Kärger, C. Krause, M. Jeschke, U. Oberhagemann and S. Spange, Microporous Mesoporous Mater., 2001, 44, 745–753 CrossRef.
- L. Gjerdåker, D. W. Aksnes, G. H. Sørland and M. Stöcker, Microporous Mesoporous Mater., 2001, 42, 89–96 CrossRef CAS.
- D. W. Aksnes, K. Førland and M. Stöcker, Microporous Mesoporous Mater., 2005, 77, 79–87 CrossRef CAS.
- S. Naumov, R. Valiullin, J. Kärger, R. Pitchumani and M.-O. Coppens, Microporous Mesoporous Mater., 2008, 110, 37–40 CrossRef CAS.
- B. Coasne, A. Grosman, N. Dupont-Pavlovsky, C. Ortega and M. Simon, Phys. Chem. Chem. Phys., 2001, 3, 1196–1200 RSC.
- B. Coasne, A. Grosman, C. Ortega and M. Simon, Phys. Rev. Lett., 2002, 88, 256102 CrossRef CAS.
- D. Wallacher, N. Kunzner, D. Kovalev, N. Knorr and K. Knorr, Phys. Rev. Lett., 2004, 92, 195704 CrossRef CAS.
- A. Grosman and C. Ortega, Langmuir, 2008, 24, 3977–3986 CrossRef CAS.
- S. Naumov, A. Khokhlov, R. Valiullin, J. Kärger and P. A. Monson, Phys. Rev. E, 2008, 78, 060601–4 CrossRef.
- P. A. Monson, J. Chem. Phys., 2008, 128, 084701 CrossRef.
- L. Bruschi, G. Fois, G. Mistura, K. Sklarek, R. Hillebrand, M. Steinhart and U. Gösele, Langmuir, 2008, 24, 10936–10941 CrossRef CAS.
- E. Kierlik, P. A. Monson, M. L. Rosinberg, L. Sarkisov and G. Tarjus, Phys. Rev. Lett., 2001, 87, 055701 CrossRef CAS.
- H. J. Woo and P. A. Monson, Phys. Rev. E, 2003, 67, 041207 CrossRef.
- J. P. Sethna, K. Dahmen, S. Kartha, J. A. Krumhansl, B. W. Roberts and J. D. Shore, Phys. Rev. Lett., 1993, 70, 3347–3350 CrossRef.
- C. G. V. Burgess, D. H. Everett and S. Nuttall, Pure Appl. Chem., 1989, 61, 1845–1852 CAS.
- M. Thommes and G. H. Findenegg, Langmuir, 1994, 10, 4270–4277 CrossRef.
- W. D. Machin, Langmuir, 1999, 15, 169–173 CrossRef CAS.
- K. Morishige and M. Shikimi, J. Chem. Phys., 1998, 108, 7821–7824 CrossRef CAS.
- M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, Wiley & Sons, Chichester, 2001 Search PubMed.
- P. Galvosas, F. Stallmach, G. Seiffert, J. Kärger, U. Kaess and G. Majer, J. Magn. Reson., 2001, 151, 260–268 CrossRef CAS.
- E. O. Stejskal and J. E. Tanner, J. Chem. Phys., 1965, 42, 288–292 CrossRef CAS.
- J. E. Tanner, J. Chem. Phys., 1970, 52, 2523–2526 CrossRef CAS.
- J. Kärger and W. Heink, J. Magn. Reson., 1983, 51, 1–7.
- F. Stallmach and P. Galvosas, Spin Echo NMR Diffusion Studies, Annual Reports on NMR Spectroscopy 61, ed. G. Webb, Academic Press, 2007, pp. 52–131 Search PubMed.
- A. I. Maklakov, V. D. Skirda and N. F. Fatkullin, in Encyclopedia of Fluid Mechanics, ed. N. M. Chremisinoff, Gulf-Publishing Co., Houston, 1990, vol. 9 Search PubMed.
- J. Kärger and D. Ruthven, Diffusion in Zeolites and Other Microporous Solids, Wiley & Sons, New York, 1992 Search PubMed.
- R. W. Mair, G. P. Wong, D. Hoffmann, M. D. Hürlimann, S. Patz, L. M. Schwartz and R. L. Walsworth, Phys. Rev. Lett., 1999, 83, 3324–3327 CrossRef CAS.
- D. ben Avraham and S. Havlin, Diffusion and Reactions in Fractals and Disordered Systems, Cambridge University Press, Cambridge, 2000 Search PubMed.
- J. Kärger and F. Stallmach, in Diffusion in Condensed Matter, ed. P. Heitjans and J. Kärger, Springer, Heidelberg, 2005 Search PubMed.
- R. Valiullin, V. D. Skirda, S. Stapf and R. Kimmich, Phys. Rev. E, 1997, 55, 2664–2671 Search PubMed.
- J. Kärger, Annalen der Physik, 1969, 24, 1 CrossRef.
- Y. Q. Song, L. Venkataramanan, M. D. Hürlimann, M. Flaum, P. Frulla and C. Straley, J. Magn. Reson., 2002, 154, 261–268 CrossRef CAS.
- P. T. Callaghan, S. Godefroy and B. N. Ryland, Magn. Reson. Imaging, 2003, 21, 243–248 CrossRef CAS.
- P. T. Callaghan and I. Furo, J. Chem. Phys., 2004, 120, 4032–4038 CrossRef CAS.
- J. Kärger, AICHE J., 1982, 28, 417–423 CrossRef.
- J. Kärger, W. Heink, H. Pfeifer, M. Rauscher and J. Hoffmann, Zeolites, 1982, 2, 275–278.
- D. Ruthven, Principles of Adsorption and Adsorption Processes, Wiley, New York, 1984 Search PubMed.
- C. Rödenbeck, J. Kärger and K. Hahn, Ber. Bunsen-Ges., 1998, 102, 929–944.
- C. Rödenbeck, J. Kärger, H. Schmidt, T. Rother and M. Rödenbeck, Phys. Rev. E, 1999, 60, 2737–2740 Search PubMed.
- H. S. Carslaw and J. C. Jaeger, Conduction of Heat in Solids, Clarendon Press, Oxford, 1946 Search PubMed.
- A. Yekta, J. Duhamel and M. A. Winnik, J. Chem. Phys., 1992, 97, 1554–1561 CrossRef CAS.
- J. Kärger, F. Stallmach, R. Valiullin and S. Vasenkov, in NMR Imaging in Chemical Engineering, ed. S. Stapf and S. Han, Wiley-VCH, Weinheim, 2005, p. 622 Search PubMed.
- R. Valiullin and M. Dvoyashkin, Adsorption, 2007, 13, 239–245 CrossRef CAS.
- Y.-Q. Song, H. Cho, T. Hopper, A. E. Pomerantz and P. Z. Sun, J. Chem. Phys., 2008, 128, 052212 CrossRef.
- R. Valiullin, S. Naumov, P. Galvosas, J. Kärger, H. J. Woo, F. Porcheron and P. A. Monson, Nature, 2006, 443, 965–968 CrossRef CAS.
- R. Valiullin, S. Naumov, P. Galvosas, J. Kärger and P. A. Monson, Magn. Reson. Imaging, 2007, 25, 481–484 CrossRef CAS.
- F. D’Orazio, S. Bhattacharja, W. P. Halperin and R. Gerhardt, Phys. Rev. Lett., 1989, 63, 43–46 CrossRef CAS.
- N. K. Dvoyashkin, V. D. Skirda, A. I. Maklakov, M. Belousova and R. Valiullin, Appl. Magn. Reson., 1991, 2, 83–91 CrossRef CAS.
- K. P. Tzevelekos, E. S. Kikkinides, A. K. Stubos, M. E. Kainourgiakis and N. K. Kanellopoulos, Adv. Colloid Interface Sci., 1998, 76–77, 373–388 CrossRef CAS.
- F. Courivaud, E. W. Hansen, S. Kolboe, A. Karlsson and M. Stocker, Microporous Mesoporous Mater., 2000, 37, 223–232 CrossRef CAS.
- D. W. Aksnes, L. Gjerdåker, L. Kimtys and K. Forland, Phys. Chem. Chem. Phys., 2003, 5, 2680–2685 RSC.
- I. Ardelean, C. Mattea, G. Farrher, S. Wonorahardjo and R. Kimmich, J. Chem. Phys., 2003, 119, 10358–10362 CrossRef CAS.
- C. Mattea, R. Kimmich, I. Ardelean, S. Wonorahardjo and G. Farrher, J. Chem. Phys., 2004, 121, 10648–10656 CrossRef CAS.
- R. Valiullin, P. Kortunov, J. Kärger and V. Timoshenko, J. Chem. Phys., 2004, 120, 11804–11814 CrossRef CAS.
- R. Gomer, Rep. Prog. Phys., 1990, 53, 917–1002 CrossRef CAS.
- J. V. Barth, Surf. Sci. Rep., 2000, 40, 75–149 CrossRef CAS.
- T. Ala-Nissila, R. Ferrando and S. C. Ying, Adv. Phys., 2002, 51, 949–1078 CrossRef CAS.
- B. G. Briner, M. Doering, H. P. Rust and A. M. Bradshaw, Science, 1997, 278, 257–260 CrossRef CAS.
- T. Mitsui, M. K. Rose, E. Fomin, D. F. Ogletree and M. Salmeron, Science, 2002, 297, 1850–1852 CrossRef CAS.
- G. Antczak and G. Ehrlich, Phys. Rev. Lett., 2004, 92, 166105 CrossRef.
- A. Zurner, J. Kirstein, M. Doblinger, C. Bräuchle and T. Bein, Nature, 2007, 450, 705–708 CrossRef CAS.
- R. Valiullin, P. Kortunov, J. Kärger and V. Timoshenko, J. Phys. Chem. B, 2005, 109, 5746–5752 CrossRef CAS.
- V. Lehmann, R. Stengl and A. Luigart, Mater. Sci. Eng. B, 2000, 69, 11–22 CrossRef.
- W. Rudzinski and D. Everett, Adsorption of Gases on Heterogeneous Surfaces, Academic Press, New York, 1992 Search PubMed.
- J. W. Haus and K. W. Kehr, Phys. Rep., 1987, 150, 263–406 CrossRef CAS.
- J. P. Bouchaud and A. Georges, Phys. Rep., 1990, 195, 127–293 CrossRef.
- R. Kirchheim, Defect Diffus. Forum, 1997, 143, 911–925 Search PubMed.
- L. M. Cameron and C. A. Sholl, J. Phys.: Condes. Matter., 1999, 11, 4491–4497 CrossRef CAS.
- R. Sips, J. Chem. Phys., 1950, 18, 1024–1026 CAS.
- P. Levitz, J. Phys. Chem., 1993, 97, 3813–3818 CrossRef CAS.
- S. Vasenkov, O. Geir and J. Kärger, Eur. Phys. J. E, 2003, 12, 35–38 CrossRef CAS.
- M. Knudsen, Annalen der Physik, 1909, 28, 75 CrossRef CAS.
- W. G. Pollard and R. D. Present, Phys. Rev., 1948, 73, 762–774 CrossRef CAS.
- J. Kärger and P. Volkmer, J. Chem. Soc., Faraday Trans. I, 1980, 76, 1562–1568 RSC.
- J. Kärger, M. Kocirik and A. Zikanova, J. Colloid Interface Sci., 1981, 84, 240–249 CrossRef.
- F. Rittig, C. G. Coe and J. M. Zielinski, J. Phys. Chem. B, 2003, 107, 4560–4566 CrossRef CAS.
- B. V. Derjaguin, Dokl. Acad. Sci. URSS, 1946, 7, 623 Search PubMed.
- V. N. Burganos, J. Chem. Phys., 1998, 109, 6772–6779 CrossRef CAS.
- J. M. Zalc, S. C. Reyes and E. Iglesia, Chem. Eng. Sci., 2004, 59, 2947–2960 CrossRef CAS.
- G. Papadopoulos, D. N. Theodorou, S. Vasenkov and J. Kärger, J. Chem. Phys., 2007, 126, 094702 CrossRef.
- K. Malek and M. O. Coppens, Phys. Rev. Lett., 2001, 8712, 125505 CrossRef.
- K. Malek and M. O. Coppens, Colloid Surf. A: Physicochem. Eng. Asp., 2002, 206, 335–348 CrossRef CAS.
- K. Malek and M. O. Coppens, J. Chem. Phys., 2003, 119, 2801–2811 CrossRef CAS.
- S. Russ, S. Zschiegner, A. Bunde and J. Kärger, Phys. Rev. E, 2005, 72, 030101 CrossRef.
- S. Zschiegner, S. Russ, A. Bunde and J. Kärger, EPL, 2007, 78 Search PubMed.
- S. Zschiegner, S. Russ, R. Valiullin, M. O. Coppens, A. J. Dammers, A. Bunde and J. Kärger, Eur. Phys. J.-Spec. Top., 2008, 161, 109–120 Search PubMed.
- A. Bunde, J. Kärger, S. Russ and S. Zschiegner, in Diffusion Fundamentals, ed. J. Kärger, F. Grinberg and P. Heitjans, Leipziger Universitätsverlag, Leipzig, 2005 Search PubMed.
- J. Kärger, Leipzig, Einstein, Diffusion, Leipziger Universitätsverlag, Leipzig, 2007 Search PubMed.
- J. Kärger, Adv. Colloid Interface Sci., 1985, 23, 129–148 CrossRef.
- A. Herrmann, L. Schimmele, J. Mossinger, M. Hirscher and H. Kronmuller, Appl. Phys. A, 2001, 72, 197–208 CrossRef CAS.
- J. Kärger, H. Pfeifer, E. Riedel and H. Winkler, J. Colloid Interface Sci., 1973, 44, 187–188 CrossRef.
- S. Vasenkov and J. Kärger, Magn. Reson. Imaging, 2005, 23, 139–145 CrossRef.
- R. Valiullin, P. Kortunov, J. Kärger and V. Timoshenko, Magn. Reson. Imaging, 2005, 23, 209–213 CrossRef CAS.
- S. R. Tennison, Appl. Catal. A: Gen., 1998, 173, 289–311 CrossRef CAS.
- M. Melillo, V. M. Gun’ko, S. R. Tennison, L. I. Mikhalovska, G. J. Phillips, J. G. Davies, A. W. Lyoyd, O. P. Kozynchenko, D. J. Malik, M. Streat and S. V. Mikhalovsky, Langmuir, 2004, 20, 2837–2851 CrossRef CAS.
- A. Khokhlov, R. Valiullin, J. Kärger, F. Steinbach and A. Feldhoff, New J. Phys., 2007, 9, 272 CrossRef.
- R. M. Cotts, M. J. R. Hoch, T. Sun and J. T. Markert, J. Magn. Reson., 1989, 83, 252–266 CAS.
- J. Kärger and D. Freude, Chem. Eng. Technol., 2002, 25, 769–778 CrossRef CAS.
- J. Kärger, Adsorption, 2003, 9, 29–35 CrossRef.
- J. Kärger, in Handbook of Heterogeneous Catalysis, ed. G. Ertl, H. Knötzinger, F. Schüth and J. Weitkamp, Wiley-VCH, Weinheim, 2008, vol. 3, pp. 1714–1727 Search PubMed.
- R. Barrer, Zeolites and Clay Minerals as Sorbents and Molecular Sieves, Academic Press, London, 1978 Search PubMed.
- M. Kocirik and A. Zikanova, Ind. Eng. Chem. Fund., 1975, 13, 347–350.
- J. Crank, The Mathematics of Diffusion, Clarendon Press, Oxford, 1975 Search PubMed.
- J. Kärger, M. Bülow, B. Millward and J. Thomas, Zeolites, 1986, 6, 146–150 CrossRef.
- J. Kärger, H. Pfeifer, R. Richter, H. Fürtig, W. Roscher and R. Seidel, AICHE J., 1988, 34, 1185–1189 CrossRef.
- J. Kärger, H. Pfeifer, J. Caro, M. Bülow, H. Schlodder, R. Mostowicz and J. Völter, Appl. Catal., 1987, 29, 21–30 Search PubMed.
- J. Völter, J. Caro, M. Bülow, B. Fahlke, J. Kärger and M. Hunger, Appl. Catal., 1988, 42, 15–27 Search PubMed.
- M. Krutyeva, S. Vasenkov, X. Yang, J. Caro and J. Kärger, Microporous Mesoporous Mater., 2007, 104, 89–96 CrossRef CAS.
- M. Krutyeva, X. Yang, S. Vasenkov and J. Kärger, J. Magn. Reson., 2007, 185, 300–307 CrossRef CAS.
- J. Kärger, P. Kortunov, S. Vasenkov, L. Heinke, D. R. Shah, R. A. Rakoczy, Y. Traa and J. Weitkamp, Angew. Chem., Int. Ed., 2006, 45, 7846–7849 CrossRef.
- L. Heinke, P. Kortunov, D. Tzoulaki and J. Kärger, Phys. Rev. Lett., 2007, 99, 228301 CrossRef CAS.
- C. G. Sonwane and S. K. Bhatia, Langmuir, 1999, 15, 2809–2816 CrossRef CAS.
- P. Selvam, S. K. Bhatia and C. G. Sonwane, Ind. Eng. Chem. Res., 2001, 40, 3237–3261 CrossRef CAS.
- R. Valiullin, M. Dvoyashkin, P. Kortunov, C. Krause and J. Kärger, J. Chem. Phys., 2007, 126, 054705 CrossRef.
- J. Weitkamp and L. Puppe, Catalysis and Zeolites, Springer, Berlin Heidelberg, 1999 Search PubMed.
- A. M. Avila, C. M. Bidabehere and U. Sedran, Chem. Eng. J., 2007, 132, 67–75 CrossRef CAS.
- J. Kärger and S. Vasenkov, Microporous Mesoporous Mater., 2005, 85, 195–206 CrossRef.
- J. Kärger, Chem. Eng. J., 2009, 145, 522–524 CrossRef.
- P. Porion, A. M. Faugere, P. Levitz, H. Van Damme, A. Raoof, J. P. Guilbaud and F. Chevoir, Magn. Reson. Imaging, 1998, 16, 679–682 CrossRef CAS.
- S. Naumov, R. Valiullin, P. Galvosas, J. Kärger and P. A. Monson, Eur. Phys. J. Special Topics, 2007, 141, 107–112 Search PubMed.
- M. Dvoyashkin, A. Khokhlov, R. Valiullin and J. Kärger, J. Chem. Phys., 2008, 129, 154702 CrossRef.
- J. H. Page, J. Liu, B. Abeles, H. W. Deckman and D. A. Weitz, Phys. Rev. Lett., 1993, 71, 1216–1219 CrossRef CAS.
- E. Hoinkis and B. Rohl-Kuhn, J. Colloid Interface Sci., 2006, 296, 256–262 CrossRef CAS.
- L. Xu, S. Davies, A. B. Schofield and D. A. Weitz, Phys. Rev. Lett., 2008, 101, 094502 CrossRef.
- P. Rajniak, M. Soos and R. Yang, AICHE J., 1999, 45, 735–750 CrossRef CAS.
- F. Stepanek, M. Kubicek, M. Marek, M. Soos, P. Rajniak and R. T. Yang, Chem. Eng. Sci., 2000, 55, 431–440 CrossRef CAS.
- J. W. Lee, W. G. Shim and H. Moon, Microporous Mesoporous Mater., 2004, 73, 109–119 CrossRef CAS.
- M. Soos, P. Rajniak and F. Stepanek, Colloid Surf. A: Physicochem. Eng. Asp., 2007, 300, 191–203 CrossRef CAS.
- D. S. Fisher, Phys. Rev. Lett., 1986, 56, 416–419 CrossRef CAS.
- D. A. Huse, Phys. Rev. B, 1987, 36, 5383–5387 CrossRef.
- M. Dvoyashkin, R. Valiullin and J. Kärger, Phys. Rev. E, 2007, 75, 041202 CrossRef.
- Chemical Synthesis Using Supercritical Fluids, ed. P. G. Jessop and W. Leitner, Wiley-VCH, Weinheim, 1997 Search PubMed.
- R. Gläser, in Handbook of Heterogeneous Catalysis, ed. G. Ertl, H. Knötzinger, F. Schüth and J. Weitkamp, Wiley-VCH, Weinheim, 2008, vol. 4, pp. 1987–2007 Search PubMed.
- M. S. Schneider, J. D. Grunwaldt and A. Baiker, Langmuir, 2004, 20, 2890–2899 CrossRef CAS.
- M. Dvoyashkin, R. Valiullin, J. Kärger, W.-D. Einicke and R. Gläser, J. Am. Chem. Soc., 2007, 129, 10344–10345 CrossRef CAS.
- M. Dvoyashkin, R. Valiullin and J. Kärger, Adsorption, 2007, 13, 197–200 CrossRef CAS.
- E. Reverchon and R. Adami, J. Supercrit. Fluid, 2006, 37, 1–22 CrossRef CAS.
- J. D. Holmes, D. M. Lyons and K. J. Ziegler, Chem.–Eur. J., 2003, 9, 2144–2150 CrossRef CAS.
- J. J. Watkins, J. M. Blackburn and T. J. McCarthy, Chem. Mater., 1999, 11, 213–215 CrossRef CAS.
- R. Gläser, M. Schmidt, S. Dapurkar, M. Türk and G. Upper, in Proceedings of 10th European Meeting on Supercritical Fluids, ed. M. Perrut, Lorraine, 2005 Search PubMed.
- C. Domingo, J. Garcia-Carmona, J. Llibre and R. Rodriguez-Clemente, Adv. Mater., 1998, 10, 672–676 CrossRef.
- V. Arunajatesan, K. A. Wilson and B. Subramaniam, Ind. Eng. Chem. Res., 2003, 42, 2639–2643 CrossRef CAS.
| This journal is © the Owner Societies 2009 |
