An NMR crystallographic approach for the determination of the hydrogen substructure of nitrogen bonded protons

Abstract

We present an approach for determining the positions of the hydrogen atoms in NH_x groups of crystalline materials. It is based on a combination of quantum-chemical DFT calculations and quantitative solid-state NMR measurements of N–H and H–H distances. The former provide the alignment of the NH_x groups within the crystal structure whereas the latter define their internal geometry. For the model system melem (C₆N₇(NH₂)₃) the N–H and H–H distances were determined to 1.055(7) Å using a Lee–Goldburg CP experiment and to 1.79(2) Å based on homonuclear double-quantum excitation with a R14⁶₂ sequence, respectively. The thus-obtained positions of the hydrogen atoms were verified by analysing ¹H–¹³C solid-state NMR cross-polarization build-up curves. The calculated polarization transfer rates depend on both the hetero- and the homonuclear second moments M^HC₂ and M^HH₂. Thus this experiment is highly sensitive to the positions of the hydrogen atoms within a given crystal structure. The agreement between calculated and experimentally observed transfer rate constants turned out to be poor if the calculations were based on single crystal diffraction data only. While the use of quantum chemical relaxed structure models improve the situation significantly, a satisfactory agreement could only be reached with the incorporation of the NMR distances into the optimized structure.

Our results prove that the combination of DFT structure optimizations with quantitative solid-state NMR experiments is a powerful and very accurate tool for the determination of the hydrogen substructure for a known structure model of heavy atoms only. Since the localization of the hydrogen atoms is often not possible based on X-ray diffraction data, the presented approach appears to be very promising for future applications.

---

1. Introduction

Hydrogen bonding plays a fundamental role in nearly all fields of chemistry.^1–12 The high interest in this versatile intermolecular interaction stems from its great impact on structural, and thus on many physical and chemical, properties. These include elementary properties like melting and boiling as well as specific effects like their significance for the secondary structure of proteins and for self-assembly in supramolecular chemistry.^{5–8,13–16} Therefore, investigations about hydrogen bonds, and especially their geometry, are undertaken in order to gain a profound understanding of the properties of the material of interest.^17–20

In the solid state crystal structures are often considerably dominated by the driving force of building a maximum of hydrogen bonds.^10,12,21,22 The structural properties of such materials are routinely examined with X-ray diffraction techniques. However, one of the drawbacks of these methods is that localizing hydrogen atoms viaX-ray diffraction is usually not possible.^18,23 As an alternative, neutron diffraction might be used which is significantly more useful in the localization of hydrogen atoms. This method is however not easily accessible and requires the deuteration of the materials.²⁴ Therefore in most cases hydrogen atoms are calculated with standard distances into a refined structure of heteroatoms and are left unrefined.¹ The position of a hydrogen atom, however, can be distinctly influenced by hydrogen bonding. It is determined by an interplay of the steric environment of the heteroatom and the intermolecular driving force for the formation of hydrogen bonds. This has an impact not only on the X–H distances but also on the angles and torsion angles of the hydrogen bond system.^1,25–29

Various approaches have therefore been developed for the localization of hydrogen atoms in hydrogen bonds.^4,18,30–36 In this regard, solid-state NMR appears very promising as it is a local method which is independent of the degree of crystallinity and, in contrast to X-ray diffraction, is very sensitive to protons due to their high gyromagnetic ratio and their natural abundance of nearly 100%.^37,38 Two main approaches can be found in the literature. On the one hand, X–H distances are determined from measurements of the X–H dipolar couplings using symmetry- or REDOR-based pulse sequences.^39–42 On the other hand X–H distances are correlated with the ¹H isotropic shift via comparison with similar compounds (which are often not available) or via quantum mechanical chemical shift calculations.^43,44

In the more special case with X being nitrogen, additionally, the ¹⁵N chemical shift interaction as well as dipolar couplings between ¹⁵N and ²H has been exploited.^45,46 Although the analysis of the ¹⁵N chemical shift benefits from a larger shift range and more strongly pronounced anisotropic properties still such data provide only relative information which can only be interpreted based on comparative results.⁴⁵ The derivation of NH distances based on ¹⁵N–²H dipolar coupling constants provides an alternative approach which as for neutron diffraction requires chemical deuteration. Furthermore, due to an non-negligible isotope effect⁴⁵ the ¹⁵ND distances obtained cannot be carried forward directly to the protonated systems. All these studies mentioned above mostly confine to the determination of X–H/D distances only and neglect angles and torsion angles.

In this article we present an approach for a more-accurate determination of the complete hydrogen substructure of NH_x (x = 1, 2) groups. This approach includes the measurement of N–H distances via the N–H dipolar coupling as presented e.g. in ref. 39–42. Additionally, we determine the H–N–H angle of NH₂groupsvia the H–H dipolar coupling. For the determination of the torsion angles of the NH_x groups relative to the heteroatoms the crystal structure is optimized under periodic boundary conditions with DFT methods. This allows determination of the substructure of the hydrogen atoms completely independent of diffraction techniques.

In order to probe the accuracy of the thus obtained data we employed quantitative ¹H–¹³C cross polarization experiments. These are very sensitive to accurate positions of the hydrogen atoms due to their dependency on the heteronuclear second moment of ¹³C and ¹H. They enable a comparison of the quality of the positions of the hydrogen atoms from single crystal data, from theoretical calculations and from NMR experiments.

For the demonstration of the efficiency of our approach we chose melem (C₆N₇(NH₂)₃) as a model system due to our interest in the structure determination of carbon nitride materials.^47–49 These materials, which are built of alternating carbon and nitrogen, suffer from poor crystallinity and as a result many crystal structures could not (or could only very recently) be solved.^49,50–52 Thus, the development of alternative approaches to diffraction techniques is of special interest for this class of materials. The crystal structure of melem was solved from powder X-ray diffraction data in 2003.⁵² It could be confirmed and further refined in 2006 by X-ray single crystal analysis.⁵³ Nevertheless, the three NH₂groups exhibit an unreasonable broad range of N–H distances between 0.87 to 1.01 Å. Thus, the exact hydrogen bond system of melem could so far not be described. In the following we will report our experiments for the determination of the N–H distances and the H–N–H angles from NMR experiments as well as the ab initio optimization of the crystal structure. After an evaluation of all these results with the cross polarization experiment we will finally discuss the hydrogen bond system of melem.

2. Experimental

2.1 Synthesis

For the NMR experiments a melem sample synthezised according to ref. 52 was used. The sample was enriched in ¹⁵N to about 25%.

2.2 Solid-state NMR spectroscopy

Solid-state NMR experiments were recorded on a commercial Avance II spectrometer (Bruker) operating at a proton frequency of 300 MHz. Samples were contained in 4 mm ZrO₂ rotors for the ¹⁵N and ¹³C measurements and in 2.5 mm ZrO₂ rotors for the ¹H experiments. Both were mounted in standard triple resonance MAS probes (Bruker). ¹³C and ¹H shifts are reported with respect to TMS, ¹⁵N shifts were referenced to nitromethane. Data collection of the ¹⁵N and ¹³C experiments was performed under broadband proton decoupling using a SPINAL-64 sequence with a nutation frequency of about 70 kHz.⁵⁴

The LG-CP experiments were implemented as described in ref. 55 and 56. The spinning frequency was set to 12 kHz. The LG decoupling conditions were determined employing the ¹³C signals of adamantane. Using a fixed decoupling frequency of 60 kHz the LG offset was optimized to give a splitting of 75 Hz for the triplet of the CH₂group.^57,58 For the optimization of the LG-CP Hartmann–Hahn conditions it has to be noted that the effective ¹H rf field (ν_eff) differs from the employed ¹H nutation frequency (ν(¹H)) of 60 kHz due to the LG offset .⁵⁹ The ¹⁵N nutation frequency was adjusted in order to match the Hartmann–Hahn condition of order ±1 (ν(¹⁵N) = ν_eff(¹H) ±1·ν_rot). The ¹⁵N excitation frequency was set to the middle of the two NH₂ signals. Under these conditions a build-up curve of 36 1D experiments with 96 transients each was recorded. The LG-CP time τ_CP was thereby increased in steps of 20 μs up to a maximum of 700 μs.

The R14⁶₂ double-quantum experiments were set-up with an excitation–reconversion–π/2–acquisition scheme. The phase cycling of the corresponding coherence pathway (0 →±2 → 0 →−1) was done using a four-step phase cycle for the receiver phase (0°, 90°, 180°, 270°) and an additional CYCLOPS for the π/2 read-out pulse which resulted in a 16-fold phase cycle. Therefore, in all, R14⁶₂ experiments 16 repetitions for each 1D experiment were performed. A repetition time of 10 s was used. After the reconversion time a short dephasing time of 100 μs was implemented before the π/2 read-out pulse.

Two variations for the R block of the R14⁶₂ sequence were implemented.^60–63 We used a simple π pulse at a spinning frequency (ν_rot) of 30 kHz. In contrast, at ν_rot = 15 kHz, the composite pulse 90_Φ°–270_−Φ° was used in order to achieve a better chemical shift compensation. Simulations revealed that this is necessary for this lower spinning frequency. For both variations the phase Φ of the R blocks was optimized.⁶⁴ Starting from the theoretical value of 77.14° an intensity maximum was found at 77.09° for a spinning frequency of 30 kHz and at 76.54° for 15 kHz. For the measurement of the build-up curves the excitation time was increased by one RR′ block for each experiment, so the timestep accounted to 9.52 μs (ν_rot = 30 kHz) and to 19.05 μs (ν_rot = 15 kHz). For the symmetric build-up curves the reconversion time was synchronously increased with the excitation time (τ_exc = τ_rec) while for the constant-time curves the reconversion time was decreased starting from τ_total with equal timesteps as the excitations time increases thus that τ_exc + τ_rec = τ_total. A total of 32 1D-experiments was measured for the symmetric build-up curves. For the extraction of H–H distances constant-time build-up curves with 17 (τ_total = 152.4 μs, ν_rot = 30 kHz) and 9 (τ_total = 152.4 μs, u_rot = 15 kHz) 1D-experiments were measured.

For the cross-polarization (CP) experiments a standard CP sequence without ramp or other modifications was employed. The spinning frequency was set to 4 kHz. The optimization of the Hartmann–Hahn match was performed using melem itself. Special attention was paid to ensure a Hartmann–Hahn condition of n = ±1. For the build-up curves 22 1D-CP experiments were measured increasing the CP contact time from 0.1 to 20 ms. Per experiment 512 transients were recorded using a repetition time of 10 s.

In advance of the measurement of the CP build-up curves we checked the dephasing behavior of the magnetization of ¹H and ¹³C during the spin-locks. Therefore we employed the pulse sequences presented in ref. 65. These revealed no significant dephasing in the relevant timescale of 20 ms (T_1ρ was estimated to some hundred milliseconds for both ¹H and ¹³C). According to ref. 65, T_1ρ could thus be neglected (compare to eqn (2) and (4) in Section 4).

2.3 Solid-state NMR simulations

Simulations for the LG-CP and the R14⁶₂ experiments were performed with the simulation package SIMPSON.⁶⁶ The spin systems, including Euler angles, were extracted from the PBC-optimized structure of melem (see Computational methods) using the program library Gau2Sim which was recently developed in our group.⁶⁷ For the fits of the simulated curves to the experimental data, least-square fits were performed using the fit routines of MATLAB⁶⁸ in a self-developed script which internally calls the program SIMPSON.

For the simulations of the LG-CP pulse sequence a spin system of a NH₂group including CSA and dipole tensors was extracted. CSA parameters were found to have only a minor influence on the build-up curves and were therefore omitted. However, for a correct simulation of the LG-CP conditions the proton isotropic chemical shift was set to the required LG offset. For the simulation of a 6-spin system the parameters of three additional hydrogen atoms with a maximum N–H distance of 3 Å were determined. It was proven that the corresponding 6-spin systems of the other two NH₂groups of melem result in almost identical build-up curves. The extraction of the N–H distances was performed with the 3-spin system (isolated NH₂group), thereby the optimal N–H distance was determined with MATLAB as described above under variation of the N–H distance and an overall scaling factor.

For the simulations of the R14⁶₂ data again one NH₂group was selected and the corresponding ¹H¹H dipole tensors were determined. For the extraction of the H–H distance for each of the four experiments (symmetric and CT curves both with ν_rot = 30 and 15 kHz) the following procedure was used: we performed simulations for the H–H distances from 1.70 to 1.87 Å using a spin-pair system. These were fitted to the experimental data using a scaling factor. For symmetric curves an additional exponential decay was used as fitting parameter to model the dephasing behaviour. For each theoretical distance from 1.70 to 1.87 Å the normalized root-mean-square deviation (rms) was calculated according to

where sim_i are the simulated and exp_i the experimental data points. The H–H distance of melem was then determined from the minimum of the rms values.

For the examination of the influence of remote hydrogen atoms, the distances and tensors for all three crystallographically independent NH₂groups including the protons within a maximum distance of 4 Å were determined. These overall up to 6 protons per NH₂group were employed in an individual simulation for each group. Finally the three build-up curves were added up as the experimental proton signals of the three NH₂groups cannot be resolved.

For the calculation of the 2nd moments (M₂) according to eqn (5) a MATLAB script was developed. For both the heteronuclear M^HC₂ and the homonuclear M^HH₂, atoms within a sphere with a radius of 30 Å around each crystallographic independent atom were included. For the final M^HC₂, the M^HC₂ of the carbon atoms underlying the same signal were summed up. As there was no differentiation between the hydrogen atoms in the calculations the M^HH₂ of all six hydrogen atoms were added for the final homonuclear M^HH₂.

2.4 Computational methods

The optimization of the crystal structure of melem was performed under periodic boundary conditions. Therefore we employed the CASTEP code as implemented in the program package MS modeling 4.0.^69–71 The crystal structure from the single crystal analysis was taken as a starting model and the fractional coordinates were relaxed within the space groupP2₁/c. The cell constants were kept fixed as they could be determined from the diffraction data. For the optimization we used the PBE functional, ultrasoft pseudopotentials, plane waves with an energy cutoff of 340 eV and a k-point sampling over 3 × 2 × 2 points.

3. Results and discussion

3.1 The N–H distance

For the determination of the N–H dipolar coupling of the NH₂groups in melem we employed the Lee–Goldburg cross polarization (LG-CP) pulse sequence.^55,56 In that sequence, after an initial ¹H π/2-pulse, the homonuclear ¹H dipolar coupling is suppressed with Lee–Goldburg (LG) decoupling.⁵⁹ Simultaneously, a ¹⁵N rf field is irradiated under Hartmann–Hahn conditions relative to the LG decoupling which induces a cross polarization (CP) transfer from ¹H to ¹⁵N. Due to the suppression of the homonuclear ¹H coupling, the LG-CP build-up curves reveal oscillations for short ¹H–¹⁵N internuclear distances which encode the corresponding dipolar coupling.

Fig. 1(a) shows a ¹⁵N CP-MAS spectrum and a melem molecule. As there is one complete molecule in the asymmetric unit of the crystal structure all signals must stem from the same molecule. The signals at −197 to −205 ppm can be assigned to the six outer tertiary nitrogen atoms (N_tert) of the ring system while the signal at −234 ppm belongs to the central atom (N_c).⁵² The resonances of the three NH₂groups per molecule can be found at −267 and −281 ppm whereby the latter one stands for two crystallographically inequivalent NH₂groups.

Fig. 1 (a) ¹⁵N CP-MAS spectrum of melem, with signal assignment from ref. 52, and molecular formula of melem. The asterisk marks an impurity; (b) comparison of the simulated LG-CP build-up curves for an isolated NH₂group (black) and for a NH₂group with three additional protons (gray); (c) experimental LG-CP build-up curves of melem (◇) with best fit (solid-line) for the signals at −281 and −267 ppm as well as their sum intensity.

In advance of the measurements of the LG-CP build-up curves, we performed simulations in order to examine the influence of remote hydrogen atoms. Fig. 1(b) shows a comparison of simulated build-up curves for an isolated NH₂group of melem and for the same NH₂group including all adjacent hydrogen atoms with a maximal N–H distance of 3 Å. These simulations reveal that the dipolar coupling to these remote hydrogen atoms has an impact only on the long-term behavior of the build-up curve. Thus, its first oscillation is characteristic for the N–H coupling within the NH₂groups, irrespective of further remote hydrogen atoms and can be employed for a reliable determination of the N–H distance.

The experimental LG-CP build-up curves of melem for the two NH₂ signals as well as their sum are depicted in Fig. 1(c). For the extraction of the distances, only the first oscillation (τ_CP up to 320 μs) and a small spinsystem of an isolated NH₂group was used. The best results of the refinement are shown in Fig. 1(c). For the signals at −281 and −267 ppm, distances of 1.059(7) Å and 1.050(6) Å were determined from the LG-CP build-up curves, respectively. Thus, they differ less than 0.01 Å. As the standard errors are in the same range, one can assume that the N–H distances in all three NH₂groups are almost identical. In the following investigations we therefore utilized the distance of 1.055(7) Å corresponding to the fit to the sum-intensity of the NH₂groups.

3.2 The H–H distance

The symmetry-based pulse sequence R14⁶₂ (in the following: R14) was selected for the determination of H–H distances within the NH₂groups of melem.^60,61 With this pulse sequence even large dipole couplings in the range of 20 kHz can be measured as the minimum timestep consists of two R blocks only (RR′)† which enables the detection of fast oscillations.^72,73

The R14 experiments were performed employing two different spinning frequencies (ν_rot) of 30 kHz and 15 kHz, for which the R block was implemented as a single π pulse and a composite pulse, respectively (see Section 2). Additionally, we measured both a symmetric and a constant-time build-up curve for each spinning frequency.

The ¹H spectrum of melem reveals a broad and uncharacteristic signal at about 8–9 ppm with a full-width-at-half-maximum of about 10 ppm, even at a spinning frequency of 30 kHz. An additional small and narrow signal at 4.4 ppm can be assigned to an impurity of surface water. The extremely large width of the main signal is to be accounted to the strong ¹H homonuclear dipolar coupling within the NH₂groups and inhibits a further analysis of the isotropic chemical shift. Furthermore, it impedes a discrimination of the ¹H signals of the three distinguishable NH₂groups for which we will determine an averaged H–H distance in the following.

An experimental symmetric build-up curve of the ¹H signal of the NH₂groups of melem with a spinning frequency of 30 kHz is depicted in Fig. 2(a). It shows a fast increase of intensity with a first pronounced maximum at τ_exc = 60 μs while the other oscillations are strongly damped. In analogy to the LG-CP experiment we first had to investigate the influence of remote hydrogen atoms on the simulated build-up curves before we could perform a reliable extraction of H–H distances. Therefore, we constructed spin systems with two (H–H pair of the NH₂group only) to six (up to four additional hydrogen atoms within a maximum distance of 4 Å) hydrogen atoms and simulated the corresponding symmetric build-up curves (see Fig. 2(a)). These reveal that a stepwise addition of further protons causes an increasing damping of the oscillations for excitation times more than 75 μs. Thus, the 6-spin system reproduces the experimental data more accurately than the spin-pair system.

Fig. 2 Experimental ¹H R14⁶₂ build-up curves of melem (◇) with simulated curves (solid lines) using spin systems of two to six spins and a spinning frequency of 30 kHz: (a) symmetric curves; (b) constant-time curves with τ_total = 152 μs; (c) constant-time curves with τ_total = 175 μs.

For the extraction of the distance, however, it would be of major interest to be able to work within the spin-pair approximation as the calculations for the larger systems are extremely time-consuming. This can be achieved due to the fact that the position of the first maximum is obviously independent of the regarded spin system and is dominated by the strongest dipole coupling. Thus, a fit of the simulated data to the first oscillation of the experimental curve will give reasonable results even if the weaker couplings are neglected.

For the constant-time (CT) procedure similar considerations have to be taken into account in advance of the experiment, as here each data point of the build-up curve implies a constant total mixing time τ_total. So τ_total should be set short enough to avoid the influence of remote spins but long enough to guarantee zero-crossings in the build-up curves which enable the extraction of distances. The latter condition is met with total mixing times which are longer than twice the excitation time of the first maximum in the symmetric build-up curve.

Fig. 2(b) depicts an experimental CT curve with a τ_total of about 150 μs which corresponds in a symmetric build-up curve to a data point with an excitation time of about 75 μs. As expected from the results above the simulated CT curves for the two- to six-spin systems show only minor differences and reproduce the experimental data well. In contrast, the simulated CT curves for a τ_total of 175 μs vary distinctly depending on the number of employed spins (see Fig. 2(c)). As only the simulations with five and more spins can reproduce the experimental data for that τ_total an extraction of distances with a two-spin system is not possible. Thus, in the following only CT curves with τ_total≈ 150 μs were employed.

For the final extraction of the H–H distance we performed spin-pair simulations for the relevant range of distances between 1.70 and 1.87 Å and fitted each simulation to the experimental data. Fig. 3(a) shows the dependency of the normalized rms deviation between simulation and experiment on the distance d for all four set-ups (symmetric and CT excitation curves both with ν_rot = 30 and 15 kHz). It becomes clear that the rms deviations for CT curves are distinctly more sensitive to the distance than for symmetric build-up curves. For the former a change in the distance of 0.02 Å already increases the rms deviation of about 2% while for the latter it causes an increase of only 0.2%.

Fig. 3 (a) Dependency of the rms deviation between experiment and simulation on the H–H distance d for the symmetric and the CT procedure, both with spinning frequencies of 30 and 15 kHz; (b–e) experimental (◇) and best fitting simulated R14⁶₂ build-up curves for (b) symmetric curve with ν_rot = 30 kHz, (c) symmetric curve with ν_rot = 15 kHz, (d) CT curve with ν_rot = 30 kHz and (e) CT curve with ν_rot = 15 kHz (both τ_total = 152 μs).

The positions of the minima in the rms curves represent the optimal distances. Fig. 3(b)–(e) shows all four experimental symmetric and CT build-up curves with these best fits. The optimal distances are summarized in Table 1 along with the rms deviations of the corresponding minimum. The latter lie in the range between 0.6 and 1.8% and thus do not differ markedly. Thus, all four build-up curves can be fitted with a similar quality. Since contradicting observations regarding an under- or overestimation of distances from symmetry-based pulse sequences are reported^64,74,75 no definite declaration can be made to which of the four data sets inhibits the smallest error. In the following we will, for that reason, employ the mean value of the four distances which accounts to 1.79(2) Å. In combination with the N–H distance of 1.055(7) Å we thus could determine the H–N–H angle of the NH₂groups of melem to 117(1)°.

Table 1 H–H distances d in a NH₂group of melem determined with the R14⁶₂pulse sequence using the symmetric and the constant-time procedure as well as spinning frequencies of 30 and 15 kHz and the corresponding rms calculated as defined in section 3

	30 kHz		15 kHz
	d/Å	rms (%)	d/Å	rms (%)
Symmetric	1.80(2)	0.9	1.80(2)	1.7
Constant time	1.75(1)	1.8	1.80(1)	0.6

---

3.3 Calculations

For a complete localization of the hydrogen atoms in a crystal structure not only are the N–H distances and the H–N–H angles of interest, but also the torsion about the NC bond, which describes the relative position of the hydrogen-bonded group in space. The torsion angles can distinctly differ from the geometry of the isolated molecule in order to build stronger hydrogen bonds. Therefore we performed an ab initio optimization of melem using density functional theory under periodic boundary conditions (PBC). As, in our case, the hydrogen atoms were already localized from the single crystal analysis, we could employ this structure as a starting point.

Fig. 4(a) compares the asymmetric unit of melem of the single crystal solution and of the PBC optimized structure. The ring system shows only minor differences as the positions of the heteroatoms changed by at most 0.08 Å during the optimization. In contrast, the position of the hydrogen atoms shifted up to 0.2 Å. This results in mean N–H distances of 1.03 Å in comparison to values of 0.87 to 1.01 Å in the single crystal structure. The H–N–H angles decrease from about 124° to about 121°.

Fig. 4 (a) Comparison of the asymmetric unit of melem of the single crystal solution (gray) and the PBC-optimized structure (black); (b) deviation from planarity in the PBC optimized structure of melem shown as an example for atom N10 (for atom numbering scheme and atom label code see Fig. 6).

The orientation of the NH₂groups in space also differ only marginally, so that obviously the torsion angles were already well-described from the single crystal analysis. They are in the range of 2 to 14°, relative to the ring system of the heteroatoms, and thus show partially distinct deviations from the planarity of the isolated molecule. These deviations are caused by the formation of hydrogen bonds as can be seen in Fig. 4(b).

It is interesting to note at this point that compared to the single crystal solution the distances and angles from the PBC optimized structure approach the values found with NMR experiments but do not match them. This is in agreement with the usual underestimation of dispersion forces and thus of hydrogen bonding in density functional theory.^32,76,77

3.4 Confirmation of the positions of the H atoms

In the preceding sections we described the successful determination of the positions of the hydrogen atoms in melem. However, by now we do not have any information about the quality of these data. In this section we will therefore present an independent verification of these positions using a quantitative ¹H–¹³C cross-polarization experiment.

Quantitative information from the cross polarization (CP) experiment can be obtained by measuring CP build-up curves. In principle, these build-up curves reveal an exponential transfer of polarization from ¹H to ¹³C:

I(t) = I₀{1 − exp[−k_CPt]} (2)

The corresponding transfer rate k_CP for each ¹³C-NMR signal is proportional to the heteronuclear second moment of ¹H and ¹³C (M^HC₂). M^HC₂ in turn is proportional to the sum of (r^HC)⁻⁶ which includes all H–C distances r_HC of carbon atoms belonging to this signal:^65,78–81Due to this dependency of the transfer rates k_CP on (r^HC)⁻⁶, minor changes in the position of both atoms have a great impact on the CP polarization transfer. If, like in our case, the positions of the carbon atoms in the crystal are well determined from diffraction data, the quantitative CP experiment thus enables a verification of the position of the hydrogen atoms.

The important point of this experiment is that C_CP must be equal for each NMR signal where C_CP is the constant of proportionality which we introduced in eqn (3).⁷⁸ It depends only on physical constants and on the experimental setup. Thus, in order to prove a given structure model the C_CP for each signal has to be determined from the experimentally accessible transfer rate kⁱ_CP and the corresponding second moments calculated from a given structure model. The structure model is then validated if the C_CP for all signals agree. This point will be employed in the following analysis.

Fig. 5(a) shows a ¹³C spectrum of melem. It reveals two signals at 156 and 165 ppm which can be assigned to the three CN₃ and to the three CN₂(NH₂) carbon atoms of the molecule, respectively.⁵² In Fig. 5(b) the CP build-up curves for both signals are depicted. As expected the magnetization of the CN₂(NH₂) signal increases distinctly faster than of the CN₃ signal due to the shorter H–C distances of the CN₂(NH₂) carbon atoms in the structure of melem.

Fig. 5 (a) ¹³C spectrum of melem; (b) experimental ¹H–¹³C CP build-up curves of melem (symbols) with fit (solid line) using a stretched-exponential function (eqn (4)); (c) logarithmic plot of the data points in (b) with linear fit of the initial gradient (solid line).

Both build-up curves were fitted with an exponential function according to eqn (2). However a reasonable fit could not be achieved using a monoexponential function, wherefore we had to employ a stretched exponential function for the fit depicted in Fig. 5(b)

I(t) = I₀{1 − exp[−(k_set)^b]} (4)

Here, the parameter b gives the deviation from monoexponentiality where a purely monoexponential function exhibits a b of 1. For the build-up curves of melem b-values of 0.81 (CN₂NH₂) and 0.93 (CN₃) were determined. This deviation can, on the one hand, be explained by a slight suppression of the dipole coupling through magic angle spinning. On the other hand, the intensity of both the CN₂NH₂ and the CN₃ signal is composed of the intensities of three crystallographically independent nuclei, namely the three CN₂NH₂ and the three CN₃ nuclei of the melem molecule which forms the asymmetric unit of the crystal. Thus, both build-up curves are the superposition of three monoexponential curves which in the sum may give rise to a deviation from monoexponentiality.

Assuming that the deviation from monoexponentiality is caused by local differences of the NH₂groups in the structure, their mean rate constant 〈k〉 can be determined from the initial regime of the build-up curves:⁸²

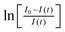For a convenient extraction of 〈k〉 we employed a normalized logarithmic plot of the stretched exponential functions (). It should exhibit a linear trend for t→ 0 with a slope equal to −〈k〉 and thus enables a direct determination of 〈k〉.⁸³

Fig. 5(c) shows the normalized logarithmic plot of the CP build-up curves of melem. Clearly in the initial regime a linear trend can be recognized which passes into a noisy curve when the build-up curve approaches its equilibrium intensity. The gradients determined from the fits depicted in Fig. 5(c) account to 〈k〉 = 2.32 × 10³ Hz for the CN₂NH₂ and to 〈k〉 = 0.49 × 10³ Hz for the CN₃ signal.

With this information we can now calculate the second moments from various structure models and determine the constants C_CP for both signals. As not the absolute C_CPs are of further interest but their equality we will discuss in the following the ratio R_CP with R_CP = C_CP(CN₃)/C_CP(CN₂NH₂) which must approach 1 for the correct structure model.

In Table 2 the sum of the second moments as expressed in eqn (5) are given for the single crystal solution as well as the PBC optimized structure. For the former the constants C_CP differ distinctly for the two NMR signals which results in a ratio R_CP of 1.52. Thus, as expected, in this structure the positions of the protons are not well determined. For the structure of the PBC-optimized cell the R_CP of 1.11 demonstrates that the optimization describes the positions of the protons distinctly better. However, the optimal value of 1 is obviously not reached.

Table 2 Calculated values for for both ¹³C signals of melem on the basis of various structure models as well as the corresponding constants C_CP and their ratio R_CP = C_CP(CN₃)/C_CP(CN₂NH₂)

Structure				C CP
		CN3	CN2NH2	CN3	CN2NH2	R CP
a SCS = structure from single crystal solution. b PBC-opt = PBC-optimized structure from last section.
Unaltered	SCS^a	100.93	730.99	14.48(9)	9.52(4)	1.52(1)
	PBC-opt^b	132.49	697.75	11.03(7)	9.97(4)	1.11(1)
d(N–H) = 1.055 Å	SCS^a	139.85	750.06	10.45(6)	9.27(4)	1.13(1)
	PBC-opt^b	139.90	699.68	10.44(6)	9.94(4)	1.05(1)
d(N–H) = 1.055 Å	SCS^a	131.53	638.94	11.11(7)	10.89(4)	1.02(1)
and ∠(H–N–H) = 116.9°	PBC-opt^b	135.26	642.32	10.80(7)	10.83(4)	1.00(1)

---

Subsequently the results from the NMR experiments, the N–H distance and the H–N–H angle, were incorporated into these two structures. The first step causes for both structures a decisive step toward a ratio R_CP of 1. However only with the inclusion of the H–N–H angle can an a R_CP of 1 be reached for both structure models.

Thus, the quantitative CP experiments proved that the results of our NMR experiments provide very accurate positions of the hydrogen atoms which cannot be achieved from X-ray diffraction data or PBC optimizations only. They furthermore showed that the torsion angles of melem were already well described from the single-crystal analysis. However, if the protons cannot be localized from X-ray diffraction data the orientation of the NH_x groups can be determined from calculations with equal quality.

3.5 The H bond system in melem

Fig. 6 shows the hydrogen bonding system of melem as given in the PBC-optimized structure with the incorporated NMR distances and angles. The general features of this system were already discussed in ref. 52 and 53. In short, five of the six hydrogen atoms of melem are involved in hydrogen bonding. The formation of a sixth hydrogen bond is sterically not possible.

Fig. 6 Hydrogen bonds in the crystal structure of melem as in the PBC-optimized structure with incorporated NMR distances.

The geometries, especially the N–H distances, of the three NH₂groups in the single crystal solution vary distinctly (see Table 3). As these differences are not correlated with the strength of the hydrogen bonds themselves (see Table 4) it has to be assumed that they stem from the low accuracy of the localization of hydrogen atoms with X-ray diffraction techniques. In contrast, the PBC-optimized structure shows only a tiny variation in the N–H distances (see Table 3). Thus, once more the assumption of approximately equal N–H distance (see LG-CP experiments) is corroborated. The difference in N–H distances between the PBC structure and the NMR data amounts to only 0.01 to 0.03 Å. However, larger differences are found for the H–N–H angles which are about 121° in the PBC structure, but only 117° from the NMR experiments. Thus the H–N–H angles diverge distinctly from the optimal angle of 120° for an sp²-hybridized group.

Table 3 Comparison of the geometric parameters (in Å and °, respectively) of the three NH₂groups of melem for the single crystal solution (SCS), the PBC-optimized structure (PBC-opt) and the PBC-optimized structure with incorporated NMR results (PBC-opt/NMR)

	H1–N8–H2			H3–N9–H4			H5–N10–H6
	d1	d2	∠	d1	d2	∠	d1	d2	∠
SCS	1.01	0.87	124.8	0.90	0.93	123.1	0.95	0.93	124.5
PBC-opt	1.03	1.02	120.2	1.02	1.03	120.4	1.04	1.04	121.6
PBC-opt/NMR	1.05	1.05	116.9	1.05	1.05	116.9	1.05	1.05	116.9

---

Table 4 Comparison of the distances (in Å) in the five hydrogen bonds of melem for the single crystal solution (SCS), the PBC-optimized structure (PBC-opt) and the PBC-optimized structure with incorporated NMR results (PBC-opt/NMR)

	H1⋯N	H2⋯N	H4⋯N	H5⋯N	H6⋯N
SCS	2.17	2.85	2.31	1.97	2.06
PBC-opt	2.16	2.73	2.16	1.81	1.91
PBC-opt/NMR	2.15	2.71	2.14	1.81	1.90

---

As can be seen from Table 4 all these modifications in the geometry of the NH₂groups result in hydrogen bonds with distinctly shorter H⋯N distances than from the single-crystal analysis. They are decreased by up to 0.16 Å resulting in two hydrogen bonds in the crystal structure of melem with a H⋯N distance of less than 2 Å. Thus, the hydrogen bond system in melem is definitely stronger than previously assumed.

4. Conclusion

We have presented an approach for the determination and the subsequent verification of the hydrogen substructure of NH_x groups in crystalline materials. We chose melem as a model system which belongs to the class of carbon nitride materials. These materials usually suffer from poor crystallinity and as a result their hydrogen atoms mostly cannot be localized.

We could successfully determine the averaged geometry of the three NH₂groups of melem. We measured the mean N–H and H–H distances using the Lee–Goldburg cross-polarization and the symmetry-based R14⁶₂pulse sequence, respectively. Here a N–H distance of 1.055 Å and an H–H distance of 1.79 Å was found, which corresponds to a H–N–H angle of 116.9°. Furthermore we employed an ab initio optimization under periodic boundary conditions for the determination of the relative orientation of the NH₂groups and the planar molecule.

These results were then evaluated with a quantitative ¹H–¹³C cross-polarization experiment which is very sensitive to the position of the hydrogen atoms. Here the ratio R_CP of the constants of proportionality for each signal (see eqn (3) and (5)) forms a measure for the quality of the proposed structure model which accounts to 1 for a correct structure. It was shown that the unmodified ab initio optimized structure with R_CP = 1.11 does not reach this optimum. However, if both the N–H distance and the H–N–H angle are incorporated into this structure the R_CP value of 1.0 proves that then the hydrogen atoms are localized very accurately. This demonstrates that the quantitative CP experiment is capable of detecting alterations of 0.02 Å as they arise in the N–H distance between the ab initio optimized structure and the NMR data.

It has to be noted that the effect of atomic level mobility was neglected in the presented work which can reduce the dipolar coupling and thus cause an underestimation of the distances. However, due to the long ¹H spin–lattice relaxation time of about 10 s and the large ¹H linewidth a significant reduction of the dipole coupling is unlikely and can be omitted.

In summary we could show that our approach provides accurate positions for hydrogen atoms. It presents a good alternative to a neutron diffraction experiment which is often not very readily available. Consequently it is very promising for future localizations of hydrogen atoms in NH_x groups when these cannot be determined from X-ray diffraction data.

Acknowledgements

We would like to thank Prof. Dr Bettina Lotsch and Prof. Dr Wolfgang Schnick, LMU München, Germany, for providing the ¹⁵N-enriched melem sample. Furthermore, we gratefully acknowledge financial support that was granted from the Deutsche Forschungsgemeinschaft (DFG) (project SE-1417/2-1).

References

1. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
2. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, Oxford, 1999.
3. G. A. Jeffrey and W. Saenger, Hydrogen Bonding in Biological Structures, Springer-Verlag, Berlin, 1991.
4. M. J. Calhorda, Chem. Commun., 2000, 801–809.
5. D. W. Bolen and G. D. Rose, Annu. Rev. Biochem., 2008, 77, 339–362.
6. D. F. Stickle, L. G. Presta, K. A. Dill and G. D. Rose, J. Mol. Biol., 1992, 226, 1143–1159.
7. A. J. Wilson, Soft Matter, 2007, 3, 409–425.
8. Hydrogen Bonded Polymers, vol. 207 of Adv. Polym. Sci., ed. W. Binder, Springer-Verlag, Berlin, 2007.
9. G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 8342–8356.
10. C. B. Aakeröy and K. R. Seddon, Chem. Soc. Rev., 1993, 22, 397–407.
11. L. J. Prins, D. N. Reinhoudt and P. Timmerman, Angew. Chem., Int. Ed., 2001, 40, 2382–2426.
12. G. R. Desiraju, Chem. Commun., 2005, 2995–3001.
13. J. D. van Beek, L. Beaulieu, H. Schäfer, M. Dumura, T. Asakura and B.H. Meier, Nature, 2000, 405, 1077–1079.
14. K. Gkionis, J. A. Platts and J. G. Hill, Inorg. Chem., 2008, 47, 3893–3902.
15. I. Alkorta, J. Elguero and G. S. Denisov, Magn. Reson. Chem., 2008, 46, 599–624.
16. R. P. Sijbesma, F. H. Beijer, L. Brunsveld, B. J. B. Folmer, J. H. K. K. Hirschberg, R. F. M. Lange, J. K. L. Lowe and E. W. Meijer, Science, 1997, 178, 1601–1604.
17. P. Gilli, V. Bertolasi, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 1994, 116, 909–915.
18. H. D. Lutz, J. Mol. Struct. (THEOCHEM), 2003, 646, 227–236.
19. G. Gilli and P. Gilli, J. Mol. Struct. (THEOCHEM), 2000, 552, 1–15.
20. V. Rajnikant, J. Dinesh and C. Bhavnaish, J. Chem. Crystallogr., 2008, 38, 211–230.
21. V. Rajnikant, J. Dinesh and C. Bhavnaish, J. Chem. Crystallogr., 2008, 38, 567–576.
22. A. Nangia, Acc. Chem. Res., 2008, 41, 595–604.
23. S. J. Grabowski and T. M. Krygowski, Tetrahedron, 1998, 54, 5683–5694.
24. J. A. Alonso, M. J. Martinez-Lope, A. Aguadero and L. Daza, Prog. Solid State Chem., 2007, 36, 134–150.
25. P. L. A. Popelier and R. F. W. Bader, Chem. Phys. Lett., 1992, 189, 542–548.
26. T. Steiner and W. Saenger, Acta Crystallogr., Sect. B, 1994, 50, 348–357.
27. T. Steiner, J. Phys. Chem. A, 2000, 104, 433–435.
28. T. Steiner, I. Majerz and C. C. Wilson, Angew. Chem., Int. Ed., 2001, 40, 2651–2654.
29. P. Chakrabarti and R. Bhattacharyya, Prog. Biophys. Mol. Biol., 2007, 95, 83–137.
30. L. Benco, D. Tunega, J. Hafner and H. Lischka, J. Phys. Chem. B, 2001, 105, 10812–10817.
31. J. Sehnert, K. Bärwinkel and J. Senker, J. Mol. Struct. (THEOCHEM), 2007, 824, 58–70.
32. P. G. Karamertzanis, G. M. Day, G. W. A. Welch, J. Kendrick, F. J. J. Leusen, M. A. Neumann and S. L. Price, J. Chem. Phys., 2008, 128, 244708.
33. S. P. Brown, M. Pérez-Torralba, D. Sanz, R. M. Claramunt and L. Emsley, Chem. Commun., 2002, 1852–1853.
34. J. M. Vadnerkooi, J. L. Dashnau and B. Zelent, Biochim. Biophys. Acta 980, 2005, 1749, 214–233.
35. M. Rosenberg, A. Loewenschuss and Y. Marcus, Phys. Chem. Chem. Phys., 2000, 2, 2699–2702.
36. N. S. Myshakina, Z. Ahmed and S. A. Asher, J. Phys. Chem. B, 2008, 112, 11873–11877.
37. R. K. Harris, J. Pharm. Pharmacol., 2007, 59, 225–239.
38. A. E. Aliev and K. D. M. Harris, Struct. Bonding, 2004, 108, 1–53.
39. G. R. Goward, I. Schnell, S. P. Brown, H. W. Spiess, H.-D. Kim and H. Ishida, Magn. Reson. Chem., 2001, 39, 5–17.
40. M. Schulz-Dobrick, T. Metzroth, H. W. Spiess, J. Gauss and I. Schnell, ChemPhysChem, 2005, 6, 315–327.
41. X. Zhao, J. L. Sudmeier, W. W. Bachovchin and M. H. Levitt, J. Am. Chem. Soc., 2001, 123, 11097–11098.
42. X. Zhao, W. Hoffbauer, J. Schmedt auf der Günne and M. H. Levitt, Solid State Nucl. Magn. Reson., 2004, 26, 57–64.
43. R. K. Harris, P. Y. Ghi, R. B. Hammond, C.-Y. Ma and K. J. Roberts, Chem. Commun., 2003, 2834–2835.
44. A.-C. Uldry, J. M. Griffin, J. R. Yates, M. Perez-Torralba, M. D. S. Maria, A. L. Webber, M. L. L. Beaumont, A. Samoson, R. M. Claramunt, C. J. Pickard and S. P. Brown, J. Am. Chem. Soc., 2008, 130, 945–954.
45. P. Lorente, I. G. Shenderovich, N. S. Golubev, G. S. Denisov, G. Buntkowsky and H.-H. Limbach, Magn. Reson. Chem., 2001, 39, 18–29.
46. I. Sack, A. Goldbourt, S. Vega and G. Buntkowsky, J. Magn. Reson., 1999, 138, 54–65.
47. N. E. A. El-Gamel, L. Seyfarth, J. Wagler, H. Ehrenberg, M. Schwarz, J. Senker and E. Kroke, Chem.–Eur. J., 2007, 13, 1158–1173.
48. B. V. Lotsch, M. Döblinger, J. Sehnert, L. Seyfarth, J. Senker, O. Oeckler and W. Schnick, Chem.–Eur. J., 2007, 13, 4969–4980.
49. L. Seyfarth, J. Sehnert, N. E. A. El-Gamel, W. Milius, E. Kroke, J. Breu and J. Senker, J. Mol. Struct. (THEOCHEM), 2008, 889, 217–228.
50. R. S. Hosmane, M. A. Rossman and N. J. Leonard, J. Am. Chem. Soc., 1982, 104, 5497–5499.
51. E. Kroke, M. Schwarz, E. Horvath-Bordon, P. Kroll, B. Noll and A. D. Norman, New J. Chem., 2002, 26, 508–512.
52. B. Jürgens, E. Irran, J. Senker, P. Kroll, H. Müller and W. Schnick, J. Am. Chem. Soc., 2003, 125, 10288–10300.
53. A. Sattler and W. Schnick, Z. Anorg. Allg. Chem., 2006, 632, 238–242.
54. B. M. Fung, A. K. Khitrin and K. Ermolaev, J. Magn. Reson., 2000, 142, 97–101.
55. B.-J. van Rossum, C. P. de Groot, V. Ladizhansky, S. Vega and H. J. M. de Groot, J. Am. Chem. Soc., 2000, 122, 3465–3472.
56. J. Becker, A. Comotti, R. Simonutti, P. Sozzani and K. Saalwächter, J. Phys. Chem. B, 2005, 109, 23285–23294.
57. K. W. Zilm and D. M. Grant, J. Magn. Reson., 1982, 48, 524–526.
58. T. Terao, H. Muira and A. Saika, J. Magn. Reson., 1982, 49, 365–367.
59. M. Lee and W. I. Goldburg, Phys. Rev. A, 1965, 140, 1261–1271.
60. M. Carravetta, M. Edén, X. Zhao, A. Brinkmann and M. H. Levitt, Chem. Phys. Lett., 2000, 321, 205–215.
61. M. Carravetta, A. Danquigny, S. Mamone, F. Cuda, O. G. Johannessen, I. Heinmaa, K. Panesar, R. Stern, M. C. Grossel, A. J. Horsewill, A. Samoson, M. Murata, Y. Murata, K. Komatsu and M. H. Levitt, Phys. Chem. Chem. Phys., 2007, 9, 4879–4894.
62. M. H. Levitt, Encyclopedia of Nuclear Magnetic Resonance, vol. 9: Advances in NMR, ed. D. M. Grant and R. K. Harris, John Wiley & Sons Ltd, Chichester, 2002, pp. 165–196.
63. M. H. Levitt, J. Chem. Phys., 2008, 128, 052205.
64. M. Carravetta, M. Edén, O. G. Johannessen, H. Luthman, P. J. E. Verdegem, J. Lugtenburg, A. Sebald and M. H. Levitt, J. Am. Chem. Soc., 2001, 123, 10628–10638.
65. W. Kolodziejski and J. Klinowski, Chem. Rev., 2002, 102, 613–628.
66. M. Bak, J. T. Rasmussen and N. C. Nielsen, J. Magn. Reson., 2000, 147, 296–330.
67. J. Sehnert, The Ab initio Calculation of the Chemical Shift Tensor and its Application for the Structure Determination in Ordered and Disordered Phases by Means of Solid-State Nuclear Magnetic Resonance, PhD thesis, Universität Bayreuth, 2007.
68. The language of technical computing. MATLAB; Math Works Inc., 24 Prime Park Way, Natick, MA 01760-1500, Copyright 1984–2004.
69. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
70. C. J. Pickard and F. Mauri, Phys. Rev. B, 2001, 63, 245101.
71. Accelrys software inc. MS Modeling v4.0.0.0 Copyright 2005.
72. T. Karlsson, J. N. Popham, J. R. Long, N. Oyler and G. P. Drobny, J. Am. Chem. Soc., 2003, 125, 7394–7407.
73. P. E. Kristiansen, M. Carravetta, J. D. van Beek, W. C. Lai and M. H. Levitt, J. Chem. Phys., 2006, 124, 234510.
74. J. Schmedt auf der Günne, J. Magn. Reson., 2003, 165, 18–32.
75. P. E. Kristiansen, M. Carravetta, W. C. Lai and M. H. Levitt, Chem. Phys. Lett., 2004, 390, 1–7.
76. P. Hobza and J. Sponer, Chem. Rev., 1999, 99, 3247–3278.
77. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 2154101.
78. C. A. Fyfe, A. C. Diaz, H. Grondey, A. R. Lewis and H. Förster, J. Am. Chem. Soc., 2006, 128, 11860–11871.
79. C. A. Fyfe and D. H. Brouwer, J. Am. Chem. Soc., 2006, 128, 11860–11871.
80. J. H. van Vleck, Phys. Rev., 1948, 74, 1168–1183.
81. C. Gardiennet, F. Marica, C. A. Fyfe and P. Tekely, J. Chem. Phys., 2005, 122, 054705.
82. P. Robyr, M. Tomaselli, J. Straka, C. Grob-Pisano, U. W. Suter, B. H. Meier and R. R. Ernst, Mol. Phys., 1995, 84, 995–1020.
83. B. Geil and G. Hinze, Chem. Phys. Lett., 1993, 216, 51–55.

---

Footnote

† For an introduction to the theory of symmetry-based pulse sequences please refer to the literature, e.g.ref. 60, 62 and 63.

---