Vibrational exciton coupling as a probe for phase transitions and shape changes of fluoroform aerosol particles
Ómar F.
Sigurbjörnsson
,
George
Firanescu
and
Ruth
Signorell
*
Department of Chemistry, University of British Columbia, 2036 Main Mall, Vancouver, Canada BC V6T 1Z1. E-mail: signorell@chem.ubc.ca; Fax: +1 (1)604 822![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2847
2847
First published on 12th November 2008
Abstract
Phase transitions and shape changes of aerosol particles play a fundamental role in atmospheric as well as technical processes involving aerosols. For the example of fluoroform particles, we demonstrate how information about both processes can be extracted from time-dependent infrared spectra by comparison with vibrational exciton calculations. We find volume crystallization rate constants for fluoroform particles in the range of Jv = 108–1010 cm−3 s−1 at a temperature of T = 78 K. Furthermore, our investigation reveals that supercooled fluoroform droplets crystallize to the most stable monoclinic bulk crystal structure. Immediately after crystallization, the particles have a cube-like shape which evolves with increasing time to an elongated shape. The present results provide new data for a better understanding of the Rapid Expansion of Supercritical Solutions when fluoroform is used as a supercritical solvent under expansion conditions which lead to fluoroform aerosol formation.
1. Introduction
Phase transitions of aerosol particles and associated shape changes of the particles are issues as topical as they are controversial (see ref. 1–12 and references therein). The lively interest in this area encompasses aspects of both fundamental and applied science. The former range from confinement effects on ensemble properties and non-equilibrium phenomena, e.g. supercooling of droplets, to the microscopic mechanism of phase transitions, e.g. surface vs. volume freezing.1,6,8,13–18 The discussion has found a broad echo in the atmospheric sciences since the phase behavior of aerosols determines weather processes by affecting the energy balance of the atmosphere. On Earth, water and its ices are the obvious focus of interest, but recent high-profile space missions have found other simple molecules, such as ammonia, methane, or ethane, to play a similar role in the atmospheres of certain planets and moons of our solar system (see ref. 19 and references therein). Most notably, the ongoing Cassini–Huygens mission has found methane and ethane cloud and rain formation on Saturn’s moon Titan that mimic weather processes on Earth, albeit at much lower temperatures (see ref. 20 and references therein). On a more applied note, the phase behavior of aerosols is crucial for technical processes involving aerosol formation, such as the Rapid Expansion of Supercritical Solutions (RESS).21,22 This micronization technique exploits the formation of mixed solvent–solute aerosols to generate extremely fine powders of non-volatile solute substances. For example, if the solute is a drug this offers a promising way to improve the bioavailability of pharmaceutics.22The present contribution is devoted to fluoroform (CHF3) as a prototype for strongly interacting dipolar fluids and especially as an attractive supercritical solvent for the micronization of drugs in the RESS process. In the RESS process, fluoroform aerosols are likely to be formed during the expansion in the region before the Mach disc. However, it is not clear whether the solvent CHF3 forms supercooled liquid aerosol droplets, solid amorphous particles, or crystalline particles. The present study aims to improve our understanding of these processes by studying the phase behavior and associated shape changes of fluoroform aerosol particles. More generally, our study demonstrates how the combination of collisional cooling for aerosol formation, non-invasive rapid-scan infrared spectroscopy, and modelling of vibrational aerosol spectra on a molecular level allows us to study shape and phase changes of unsupported free aerosol particles. This latter fact in particular distinguishes our contribution from many other studies in this field, which still rely on supported particles. Although it is not often appreciated, for weakly bound sensitive molecular aggregates it is crucial that processes such as phase and shape changes are investigated under conditions unperturbed by supports or invasive probes because these tend to distort the results in an unpredictable fashion.
2. Experiment and calculations
2.1 Experiment
We provide here only a brief description of the experimental setup. Additional details can be found in ref. 23 and 24. Fluoroform aerosol particles were formed by bath gas cooling in our collisional cooling cell at a temperature of 78 K. Prior to particle generation the precooled cell was filled with He bath gas, which after some minutes thermally equilibrated with the cell (78 K). The particles were then formed by rapid injection of a CHF3/He gas mixture (300–105 ppm CHF3 in He) into the cold He bath gas. The sample gas was injected through a stainless steel tube (7 mm diameter). The pulse duration (<1 s) was controlled by a Burkert solenoid magnetic valve. This rapid cooling led to supersaturation of the fluoroform gas and thus to condensation to particles. This technique has considerable advantages over the more common laboratory generation of weakly bound molecular aggregates by supersonic expansions using nozzles of varying design (slit nozzles, Laval nozzles). Collisional cooling affords much longer observation times (minutes to hours compared with ms at best in supersonic expansions) and unlike supersonic expansions it allows measurements under thermal equilibrium over a wide range of temperatures (4–298 K) and for a wide range of particles sizes (less than 1 nm to hundreds of micrometers). In the present investigation, the mean particle sizes varied between 20 and 700 nm, which allowed us to perform size-dependent experiments. We did not, however, observe any unusual size-dependent effects. Thermal equilibrium between particles and surrounding gas phase and a well-defined temperature are crucial for the study of phase transitions.At a bath gas temperature of 78 K, CHF3 aggregates were formed close to the freezing point of bulk fluoroform (T = 118 K). As shown in section 3.1, at the very beginning CHF3 gas condensed to supercooled liquid aerosol droplets. The ensuing crystallization dynamics of these droplets and the shape change of the resulting solid particles were recorded in situ with a rapid-scan Fourier transform infrared spectrometer (Bruker IFS 66 v/S) as a function of time. The time resolution was 30 ms at a spectral resolution of 2 cm−1.
As explained in section 3, the crystallization of the supercooled liquid droplets and the shape change of solid particles happen simultaneously for purefluoroform particles. To separate the time-scale of the two processes, we mixed traces of water (0.1% to 6% of the fluoroform content) into the gaseous fluoroform samples in order to speed up crystallization. When these gas mixtures were introduced into the cold cell, water condensed first to tiny solid ice particles which served as condensation nuclei for the formation of supercooled liquid CHF3 droplets. Once the liquid droplets were formed, the tiny solid water cores acted as nuclei for the heterogeneous crystallization of fluoroform droplets, which proceeds much faster than the crystallizationvia homogeneous nucleation prevalent in pure CHF3 particles. This allowed us to separate the crystallization temporally from the subsequent slower shape change of the crystalline particles.
2.2 Calculations
The crystallization of supercooled liquid droplets to solid particles is accompanied by a change in the shape of the particles. The band structure of infrared bands with strong molecular transition dipoles (>0.1–0.2 D) is sensitive to the particle’s shape23,25–28 and can thus be used as a probe for the particles’ shape. The vibrational exciton model allows us to calculate and therefore predict infrared band structures of such bands for different particle shapes when transition dipole coupling is the dominant interaction. The shape and how it changes can then be determined from a comparison of the experimental infrared spectra with exciton calculations for different particle shapes. For the present contribution, the overall vibrational Hamiltonian includes resonant dipole–dipole and dipole-induced dipole terms (1st and 2nd term in Aij, respectively, see ref. 27–28 for further details): | (1) |
Ĥ0 is the Hamiltonian for uncoupled molecular oscillators. The sum in (eqn (1)) extends over pairs of molecules, μi is the dipole moment vector of molecule i and λij is a scaled projection matrix:
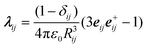 | (2) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) im, transition moments μim = 〈0|μi|im〉, and polarizability tensors αi. |im〉 is the mth eigenfunction of the ith molecular oscillator. Shifting the energy zero to the uncoupled ground state energy 〈0|Ĥ|0〉 further simplifies the Hamiltonian matrix elements:
im, transition moments μim = 〈0|μi|im〉, and polarizability tensors αi. |im〉 is the mth eigenfunction of the ith molecular oscillator. Shifting the energy zero to the uncoupled ground state energy 〈0|Ĥ|0〉 further simplifies the Hamiltonian matrix elements:| 〈km|Ĥ|ln〉 = δklδmnωkm + 2μ+kmAklμln | (3) |
The CHF3 aerosol particles consist of tens of thousands of molecules and therefore tens of thousands of oscillators so that the full diagonalization of the Hamiltonian is no longer viable. Instead we take a time-dependent approach to calculate absorption spectra directly from the dipole autocorrelation function. {EI} is the set of eigenvalues of Ĥ with corresponding eigenvectors |I〉 and transition moments MI = 〈0|μ|I〉 (overall dipole function  ). Then, the absorbance spectrum is proportional to
). Then, the absorbance spectrum is proportional to
 | (4) |
 | (5) |
To calculate C(t) we employ a second order time-propagation scheme.
 | (6) |
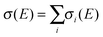 | (7) |
 | (8) |
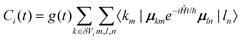 | (9) |
 | (10) |
3. Results and discussion
3.1 Spectral features of crystallization and shape change
Infrared spectroscopy is a particularly powerful method for investigating the crystallization behavior and shape changes of fluoroform aerosol particles. All mid-infrared bands (the CF3 deformation mode ν3, the CH bending vibration ν4, and the CF3 stretching modes ν5/ν2) show band structures that characteristically depend on the internal structure (phase). Under the present conditions, the phase is either a completely disordered state or the crystalline monoclinic phase also found in the bulk.33 However, only the ν5/ν2 band system around 1140 cm−1 is also sensitive to the particles’ shape and can thus provide information about shape changes. The band structures of the ν3 vibration around 696 cm−1 and the ν4 vibration around 1378 cm−1 are not influenced by the shape of the aerosol particles. The reason why the three band types behave so differently lies in their molecular transition dipoles. The strong transition dipole of the ν5 band (see Table 1 and ref. 30) leads to strong exciton coupling between all molecules within a certain aerosol particle. Since the ν2 band lies close to the ν5 band it is also involved in this coupling. As explained in ref. 27–29, this dipole coupling lifts the degeneracy of the uncoupled molecular eigenstates and leads to vibrational eigenfunctions that are delocalized over the whole aerosol particle. It is this delocalization which explains the shape sensitivity. The ν3 and ν4 vibrations, by contrast, have only small transition dipoles.30,32 Exciton coupling and shape effects are thus negligible for the band structures of these two bands.![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) , transition dipoles μ, and polarizabilities α. ε0 is the vacuum permittivity
, transition dipoles μ, and polarizabilities α. ε0 is the vacuum permittivity
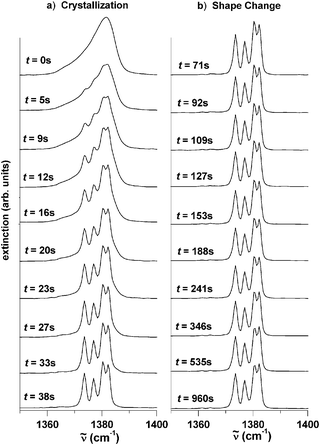
The different behavior of these mid-infrared bands allows us to distinguish between the crystallization process of aerosol particles and the shape changes of the crystalline particles once formed. Fig. 1–3 show both processes as a function of time in the region of the ν5/ν2 band, the ν4 band, and the ν3 band respectively. Panel a in each case illustrates the spectral evolution during the crystallization process followed in panel b by the spectral evolution caused by a subsequent change in the shape of the crystalline particles. All spectral changes happen continuously with increasing time after particle formation (t = 0 s). For clarity we only show snapshots of the particle spectra recorded at twenty different times, although in principle we can observe the whole crystallization process in great detail with a time resolution of ms. For the particular example shown in Fig. 1–3, the two processes—crystallization and shape change—are clearly separated in time. The shape change starts (t = 71 s) after crystallization is complete (t = 38 s). As explained in section 2.1 and further discussed below, this separation of time scales was achieved by the presence of traces of water-ice nuclei, which does not, however, affect the general conclusions.
 | ||
| Fig. 1 Time-dependent infrared spectrum of CHF3 aerosol in the region of the ν5/ν2 bands. (a) Temporal evolution during the crystallization of the particles in the presence of trace amounts of water ice nuclei. (b) Temporal evolution during the change of the particles’ shape from cube-like to elongated particles. t is the time after the particle formation (t = 0 s). | ||
 | ||
| Fig. 2 The same as in Fig. 1, but in the region of the ν4 band. | ||
 | ||
| Fig. 3 The same as in Fig. 1, but in the region of the ν3 band. | ||
We start with a discussion of the crystallization process (Fig. 1–3a). The spectrum measured directly after particle formation at time t = 0 s in Fig. 1–3a exhibits broad unstructured bands reflecting the high degree of disorder in the particles. These particles are either amorphous solid spheres or supercooled liquid droplets. Several considerations clearly point to the formation of supercooled liquid droplets. The first one is the fact that the temperature in the cooling cell is not too far from the melting point of fluoroform (118 K) and that fluoroform has a broad liquid range of 73 K. Secondly, throughout particle formation the actual CHF3 partial pressure in our cell lies 1–3 orders of magnitude above the extrapolated vapor pressure of liquid fluoroform at 78 K,34 which in turn probably lies much higher than the vapor pressure over the solid. The final argument comes from the comparison of the infrared spectrum calculated for an amorphous solid particle (not shown here) with the experimental spectrum in Fig. 1a for t = 0 s. The calculated spectrum of the ν5/ν2 band of the amorphous solid particle still shows some structure which does not agree with the completely structureless experimental spectrum. The arguments taken together clearly favor the formation of supercooled liquids.
During the crystallization process (t = 0–38 s) the absorption bands split into several sub-bands. After crystallization is complete (t = 38 s), the ν3 and ν4 bands show the same splitting pattern as found in the crystalline bulk.35 From these splitting patterns, we conclude that the particles have the same crystal structure as the crystalline bulk33 (monoclinic space groupP21/c with four molecules per unit cell). The behavior of the ν5/ν2 band system during the crystallization differs from what has just been described for the ν3 and ν4 bands. Its band structure is determined by strong transition dipole coupling between the molecules that make up the particle. Hence this band system is not only sensitive to tiny details in the internal structure of the particles, but also to the shape of the particles. As discussed in the next section, the analysis of this band allows us to determine the particle shape right after crystallization is complete.
Between t = 38 s (bottom trace of panel a in each Figure) and t = 65 s no further changes can be observed in the mid-infrared spectrum. After that time period, however, the ν5/ν2 band system (Fig. 1b) exhibits a second systematic change, whereas the ν4 band (Fig. 2b) and ν3 band (Fig. 3b) do not change any further. For the ν5/ν2 band, two side bands at about 1108 cm−1 and between 1145–1170 cm−1 grow with increasing time (see arrows in Fig. 1) relative to the central band region between 1125–1140 cm−1. The fact that only the ν5/ν2 band is sensitive to this second change clearly indicates that this change must influence the exciton coupling scheme within an aerosol particle. In principle this could happen by a change in the internal structure (phase change), a change in the particles’ size, or a change in the particles’ shape. The first two possibilities, however, can be ruled out. The stability of the ν3 and ν4 bands clearly speaks against a second phase change. The size of the particles cannot be the reason because the band structure is not sensitive to the particular size in the size range considered here (see explanations in ref. 27 and 36). The only possibility left is a change in the particles’ shape. The next section shows by comparison with exciton calculations that between t = 71 s and t = 960 s the particle ensemble transforms from one with mainly globular particles to an ensemble with an increasing contribution from elongated particles. The time scale for this shape change depends on the experimental conditions. We find that the shape change starts earlier and happens faster at low bath gas pressures (200 mbar) compared with high bath gas pressures (800 mbar). The same trend is also found for higher sample gas concentrations (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm) compared with low sample gas concentrations (600 ppm).
000 ppm) compared with low sample gas concentrations (600 ppm).
 | ||
| Fig. 4 Experimental infrared spectrum of pure fluoroform particles without ice nuclei. The spectrum was recorded 1165 s after particle formation. (a) Region of the ν4 band. (b) Region of the ν5/ν2 band. The long tails towards lower wavenumbers are due to elastic scattering of the light by the particles, which have in this case sizes in the upper nanometer range. | ||
For the particular example shown in Fig. 1–3, the crystallization process is temporally separated from the subsequent shape change of the crystalline particles. To achieve this separation of the two different processes, we had to speed up the crystallization process of fluoroform droplets and in addition, to delay the onset of the shape change as much as possible. This was achieved by altering the experimental conditions. The onset of the shape change was delayed by choosing a high bath gas pressure in the cooling cell (800 mbar). The crystallization process was accelerated by introducing a minor amount (up to 6% of the fluoroform content) of very small water ice nuclei, onto which fluoroform could condense. The heterogeneous crystallization that becomes possible through the presence of the water ice nuclei is much faster than the predominant homogeneous nucleation in the case of pure fluoroform droplets. Since the ice nuclei are tiny compared with the fluoroform particle as a whole they do not alter any of the spectroscopic features of pure fluoroform particles. In both cases, the features of crystallization and shape changes look exactly the same. The only difference is that for pure CHF3 particles crystallization and shape change overlap in time because crystallization happens much more slowly, as illustrated in Fig. 4. This spectrum was recorded 1165 s after particle formation. Traces a and b show the ν4 band and the ν5/ν2 band, respectively. The splitting pattern of the ν4 band is not yet completely resolved indicating that some particles of the ensemble are still liquid, in line with the broad features in the ν5/ν2 band system. At the same time the two side bands in that system (see arrows) indicate that some crystalline particles of the ensemble are already growing into elongated particles. At a comparable time (t = 960 s, Fig. 1) particles with ice nuclei are already completely crystalline and a large fraction of these crystalline particles already have an elongated shape. We note, however, that by deconvolution of the infrared spectra we can still distinguish between the two processes even in the case of pure fluoroform aerosol.
It is in principle possible to derive the kinetics of the crystallization process as well as the kinetics of the shape change of crystalline particles from time-dependent infrared spectra. We have already reported crystallization rate constants of pure fluoroform aerosol droplets in ref. 17. The emphasis of that contribution was to clarify whether it is possible to distinguish between surface nucleation and volume nucleation. We clearly demonstrated that this is not the case, both because of experimental uncertainties and because of approximations used in the derivation of the crystallization kinetics. For pure CHF3 droplets, we derived homogeneous crystallization rates of Jv = 108–1010 cm−3 s−1 if volume nucleation is assumed to dominate and Js = 103–105 cm−2 s−1 if surface nucleation is assumed to dominate. The presence of water ice nuclei leads to much faster heterogeneous crystallization rates that can be larger by orders of magnitude. Their exact value depends on the number and the size of the ice nuclei, which was varied for different experiments. For the change in the shape of the crystalline particles observed in Fig. 1b, we have not derived any rate constants. As discussed in the next section, we can only speculate about possible processes responsible for these shape changes. Without better knowledge of the processes involved and their mechanisms it is impossible to derive meaningful rate constants for the shape change.
3.2 Analysis of the particle shape by exciton calculations
Since the ν5/ν2 band system is dominated by exciton coupling it is sensitive to the shape of the aerosol particles. The comparison of exciton calculations for different particles’ shapes with the experimental infrared spectra thus allows us to find out more about the evolution of the particle shape as a function of time. There are two types of shape changes in Fig. 1–3. The first is associated with the crystallization of the supercooled liquid droplets (see traces a). The second shape change (traces b) has already been described in the previous section. It happens after crystallization is complete and thus corresponds to a shape change of crystalline fluoroform particles. We begin our discussion with the first type.At time t = 0 s, liquid supercooled droplets are formed with a spherical shape. Crystallization of these droplets is likely to alter this shape. Since individual particles of the ensemble crystallize instantaneously they will presumably retain a shape with very similar axis ratios directly after crystallization. Fig. 5 compares two exciton calculations (see section 2.2) for a crystalline spherical particle (trace a) and a crystalline particle with a cube-like shape (trace b) with the experimental spectrum directly after crystallization is complete (trace c, identical to the bottom trace of Fig. 1a). For the simulation in trace b, we used a monoclinic parallelepiped with equal side lengths to represent what we call a cube-like particle. Note that other cube-like shapes, such as perfect cubes or quasi-octahedra, show almost identical spectral features and are therefore not treated separately. The experimental spectrum consists of a broad band (70 cm−1) with a maximum of the extinction around 1130 cm−1 and pronounced secondary maxima. The exciton structure for a spherical particle (trace a) does not reproduce this band structure, which is a clear hint that after crystallization is complete the particles are no longer perfectly spherical. The experimental band structure is very well reproduced by exciton calculations of cube-like particles (trace b). The main features are clearly reflected in the calculated spectrum so that we conclude that during the crystallization process the shape changes from spherical droplets to cube-like crystalline particles. It is worth noting that we cannot expect perfect agreement of calculation and experiment in the finer details of the complex ν5/ν2 band system, above all because our calculations represent true predictions and not fits to the experimental spectra (none of the input parameters were fitted!). Their structure is determined by exciton coupling of the weak non-degenerate ν2 transition and the strong doubly-degenerate ν5 transition involving each of the thousands of molecules in an aerosol particle. The result is correspondingly sensitive to the exact values of the input parameters. In the exciton model described in section 2.2, all molecules in a unit cell are assigned the same transition dipole moment and the same transition frequency (see Table 1). For the monoclinic crystal structure this is an approximation, which we have to make because the values of these parameters for individual molecules in the unit cell are not known (typical differences in the transition wavenumbers are expected in the region of several cm−1). These are the reasons why details in the spectra cannot be reproduced perfectly by the present calculations. A more elaborate model, such as the Extended Exciton Model,29 might possibly afford better agreement as it treats intra- and intermolecular interactions in terms of appropriate force fields to account for structural changes and local molecular variations of transition frequencies and dipole moments. The development of a sufficiently accurate force field for crystalline CHF3 would be a major undertaking. Although interesting in its own right we do not expect that the results would affect our current conclusions.
 | ||
| Fig. 5 Infrared spectra in the region of the ν5/ν2 band. (a) Vibrational exciton calculation for a crystalline spherical particle. (b) Vibrational exciton calculation for a crystalline cube-like particle. (c) Experimental infrared spectrum of a crystalline cube-like particle (see t = 38 s in Fig. 1). | ||
Further analysis with our microscopic model allows us to get more insight into the molecular origin of the observed band structures in Fig. 5. From our quantum mechanical model, we can determine which region within an aerosol particle (molecules in the surface, or molecules in the core) contributes to a certain spectral feature. Such an analysis is depicted in Fig. 6 for a spherical crystalline particle on the left and a cube-like crystalline particle on the right. The upper panels show again the infrared spectra. The lower panels show the normalized excitation density (see eqn (10)) as a function of the distance from the particle’s center. Shell index 0 corresponds to the center of the particle and shell index 10 denotes the particle’s surface. Dark regions indicate strong vibrational excitation and light regions indicate weak vibrational excitations. The infrared spectrum of the crystalline sphere (left) is governed by three modes at 1130, 1150, and 1162 cm−1 that are completely delocalized over the particle. The band at 1130 cm−1 mainly arises from the ν2 transition while the other two bands derive their intensity from the doubly-degenerate ν5 transition. Note, however, that this gives only a general trend because both transitions are coupled since they are near resonant. More interesting is the excitation density of the cube-like particle on the right hand side in Fig. 6, because it allows us to understand the features of the experimental spectrum for t = 38 s (Fig. 1a and 5c). In the core of the particle (shell index 0 to about 6), the excitation density arises from several modes completely delocalized over the core. In this region, the density is a smooth function of the wavenumber contributing to a weak background in the infrared spectrum. The major structure in the infrared spectrum arises from the highly structured excitation density in the particle’s surface (shell index 7 to 10), which is a consequence of the cube-like shape, mainly it’s corners, which represent singularities in the surface curvature.
 | ||
| Fig. 6 Left panels: crystalline spherical particles. Right panels: crystalline cube-like particles. Upper panels: calculated infrared spectra in the region of the ν5/ν2 band. Lower panels: normalized excitation densities as defined in eqn (10). | ||
The characteristic of the second type of shape change is the growth of two side bands on both sides of the main peak with increasing time (see Fig. 1b). As we have reported for several other aerosol systems in previous publications,23–25,28,37 the evolution of side bands is indicative of the formation of elongated aerosol particles from initially mainly “globular” particles. The formation of elongated particles also shows the same qualitative dependence on the experimental conditions found in our previous studies: (i) elongated particles are formed quicker at lower bath gas pressures than at higher bath gas pressures; (ii) elongated particles are more easily formed at higher sample gas concentrations than at lower concentrations. As reported previously,23,24,28 the mechanism behind the growth process remains unclear. Both agglomeration and coagulation of cube-like particles as well as evaporation of small particles and recondensation onto larger particles are possible explanations. These similarities between the behavior of the fluoroform aerosols with previous observations are strong hints that we observe the same shape change here, i.e. the formation of elongated particles from initially mainly cube-like particles. Fig. 7 confirms this interpretation. It shows as a thick line in trace b the experimental spectrum recorded at t = 960 s (see Fig. 1), which exhibits pronounced side bands. For comparison, the thin dashed line shows again the spectrum of the cube-like particle recorded at t = 38 s. The pronounced side bands that appear at t = 960 s reflect the fact that the fraction of elongated particles in the ensemble has increased over time. This trend is reproduced by the simulated spectra in trace a. The thick line represents a linear combination of cube-like and elongated particles with axis ratios of 1:1:9, 1:9:1, and 9:1:1 (a:b:c axis, see ref. 33). Particles with all three different aspect ratios are equally included in the simulations because we do not know whether growth happens preferentially along one particular axis. The ratio of cube-like to elongated particles (the three different aspect ratios contribute equally) is 1:1. The thin dashed line shows again the exciton calculation for the pure cube-like particle from Fig. 5b. The general trends observed in the experimental spectra are clearly reproduced by these simulations. The characteristic side bands arise from elongated particles and are thus more pronounced for higher fractions of elongated particles in the ensemble. The simulations also reveal that the side band between 1140–1170 cm−1 is unique to the elongated particles with an axis ratio of 1:9:1, which stresses the importance of growth along the b axis. The other two types of elongated particles do not show this feature. Since they also do not exhibit any other characteristic features we cannot conclude from our simulations whether growth along the a and c axis is important in reality. From the above results, we conclude that cube-like crystalline particles formed directly after crystallization grow to elongated particles with increasing time. The simulations show that growth along the b axis is important for fluoroform particles. However, they do not provide information about the importance of growth along the a and c axis. We would like to mention at this point that the qualitative agreement between experiment and simulation could easily be improved by fitting a broader range of particle shapes (aspect ratios) and by adjusting the parameters in Table 1. With little more physical insight to be gained, however, we abstain from doing so.
 | ||
| Fig. 7 Infrared spectra of crystalline particles in the region of the ν5/ν2 band. (a) Vibrational exciton calculations. Thick line: a 1:1 mixture of cube-like and elongated particles. Thin dashed line: pure cube-like particles (see Fig. 5). (b) Experimental spectra. Thick line: a mixture of cube-like and elongated particles (estimated 1:1) after 960 s of particle growth. Thin dotted line: cube-like particles immediately after crystallization is complete (see Fig. 5). | ||
4. Summary
The understanding of aerosol spectra is still in its infancy. The major reason is the complexity of these systems with their many degrees of freedom. To go beyond a mere speculative interpretation of spectral features it is essential to analyze the experimental data with appropriate model calculations. The present study demonstrates how infrared spectra of molecularly-structured aerosol particles can be understood from molecular properties using the quantum mechanical vibrational exciton model. We have shown for the example of fluoroform aerosol that the combination of time-dependent infrared spectroscopy and quantitative modelling allows us to obtain a detailed understanding of dynamic processes such as crystallization and shape changes of aerosol particles.In addition to more fundamental spectroscopic aspects, the data found here for fluoroform aerosol, i.e.crystallization rate constants as well as infrared spectroscopic features of supercooled liquid droplets and crystalline particles of different shapes, are important for a better understanding of the Rapid Expansion of Supercritical Solutions. Because of its low critical data, fluoroform is an attractive supercritical solvent, e.g. for the micronization of drugs by RESS. During the expansion process, the solvent fluoroform can co-condense with the drug to form an aerosol. For this reason, the phase behavior of fluoroform aerosol particles can crucially influence the drug particle formation.
Acknowledgements
This project was financially supported by the Natural Sciences and Engineering Research Council of Canada, by the Canada Foundation for Innovation, and by the A.P. Sloan Foundation (R.S.). Allocation of cpu-time on WestGrid facilities is gratefully acknowledged.References
- J. F. Huang and L. S. Bartell, Kinetics of homogeneous nucleation in the freezing of large water clusters, J. Phys. Chem., 1995, 99, 3924–3931 CrossRef CAS.
- R. S. Disselkamp, S. E. Anthony, A. J. Prenni, T. B. Onasch and M. A. Tolbert, Crystallization kinetics of nitric acid dihydrate aerosols, J. Phys. Chem., 1996, 100, 9127–9137 CrossRef CAS.
- H. R. Pruppacher and J. D. Klett, Microphysics of clouds and precipitation, Kluwer Academic, Dordrecht, 1997 Search PubMed.
- A. J. Prenni, T. B. Onasch, R. T. Tisdale, R. L. Siefert and M. A. Tolbert, Composition dependent freezing nucleation rates for HNO3/H2O aerosols resembling gravity-wave-perturbed stratospheric particles, J. Geophys. Res., 1998, 103, 28439–28450 CrossRef CAS.
- D. Rosenfeld and W. L. Woodley, Deep convective clouds with sustained supercooled liquid water down to −37.5 °C, Nature, 2000, 405, 440–442 CrossRef CAS.
- D. Duft and T. Leisner, Laboratory evidence for volume-dominated nucleation of ice in supercooled water microdroplets, Atmos. Chem. Phys., 2004, 4, 1997–2000 CAS.
- G. P. Johari, Water’s size-dependent freezing to cubic ice, J. Chem. Phys., 2005, 122, 194504 CrossRef.
- D. A. Knopf, Do NAD and NAT form in liquid stratospheric aerosols by pseudoheterogeneous nucleation?, J. Phys. Chem. A, 2006, 110, 5745–5750 CrossRef CAS.
- R. Signorell and M. Jetzki, Phase behavior of methane haze, Phys. Rev. Lett., 2007, 98, 013401 CrossRef CAS.
- J. P. Reid, H. Meresman, L. Mitchem and R. Symes, Spectroscopic studies of the size and composition of single aerosol droplets, Int. Rev. Phys. Chem., 2007, 26, 139–192 CrossRef CAS.
- R. Wagner, S. Benz, O. Möhler, H. Saathoff, M. Schnaiter and T. Leisner, Influence of particle aspect ratio on the mid-infrared extinction spectra of wavelength-sized ice crystals, J. Phys. Chem. A, 2007, 111, 13003–13022 CrossRef CAS.
- Faraday Discussion 137: The Spectroscopy and Dynamics of Microparticles, Royal Society of Chemistry, Cambridge, 2008 Search PubMed.
- J. E. Kay, V. Tsemekhman, B. Larson, M. Baker and B. Swanson, Comment on evidence for surface-initiated homogeneous nucleation, Atmos. Chem. Phys., 2003, 3, 1439–1443 CAS.
- G. W. Turner and L. S. Bartell, On the probability of nucleation at the surface of freezing drops, J. Phys. Chem. A, 2005, 109, 6877–6879 CrossRef CAS.
- O. Stetzer, O. Möhler, R. Wagner, S. Benz, H. Saathoff, H. Bunz and O. Indris, Homogeneous nucleation rates of nitric acid dihydrate (NAD) at simulated stratospheric conditions—Part I: Experimental results, Atmos. Chem. Phys., 2006, 6, 3023–3033 CAS.
- P. W. Sutter and E. A. Sutter, Dispensing and surface-induced crystallization of zeptolitre liquid metal-alloy drops, Nature Materials, 2007, 6, 363–366 CrossRef CAS.
- Ó. Sigurbjörnsson and R. Signorell, Volume versus surface nucleation in freezing aerosols, Phys. Rev. E, 2008, 77, 051601 CrossRef.
- B. Zobrist, C. Marcolli, T. Peter and T. Koop, Heterogeneous ice nucleation in aqueous solutions: the role of water activity, J. Phys. Chem. A, 2008, 112, 3965–3975 CrossRef CAS.
- R. Courtin, Aerosols in the giant planets and Titan, Space Sci. Rev., 2005, 116, 185–199 CrossRef CAS.
- J. I. Lunine and S. K. Atreya, The methane cycle on Titan, Nature Geoscience, 2008, 1, 159–164 Search PubMed.
- J. W. Tom and P. G. Debenedetti, Particle formation with supercritical fluids—a review, J. Aerosol. Sci., 1991, 22, 555–584 CrossRef CAS.
- M. Türk, P. Hils, B. Helfgen, K. Schaber, H.-J. Martin and M. A. Wahl, Micronization of pharmaceutical substances by the Rapid Expansion of Supercritical Solutions (RESS): a promising method to improve bioavailability of poorly soluble pharmaceutical agents, J. Supercrit. Fluids, 2002, 22, 75–84 CrossRef CAS.
- R. Signorell, M. Jetzki, M. Kunzmann and R. Ueberschaer, Unraveling the origin of band shapes in infrared spectra of N2O–12CO2 and 12CO2–13CO2 ice particles, J. Phys. Chem. A, 2006, 110, 2890–2897 CrossRef CAS.
- G. Firanescu, D. Hermsdorf, R. Ueberschaer and R. Signorell, Large molecular aggregates: From atmospheric aerosols to drug nanoparticles, Phys. Chem. Chem. Phys., 2006, 8, 4149–4165 RSC.
- R. Signorell and M. K. Kunzmann, Isotope effects on vibrational excitons in carbon dioxide particles, Chem. Phys. Lett., 2003, 371, 260–266 CrossRef CAS.
- A. Bonnamy, M. Jetzki and R. Signorell, Optical properties of molecular ice particles from a microscopic model, Chem. Phys. Lett., 2003, 382, 547–552 CrossRef CAS.
- R. Signorell, Verification of the vibrational exciton approach for CO2 and N2O nanoparticles, J. Chem. Phys., 2003, 118, 2707–2715 CrossRef CAS.
- G. Firanescu, D. Luckhaus and R. Signorell, Phase, shape, and architecture of SF6 and SF6/CO2 aerosol particles: Infrared spectra and modeling of vibrational excitons, J. Chem. Phys., 2008, 128, 184301 CrossRef.
- G. Firanescu, D. Luckhaus and R. Signorell, Size effects in the infrared spectra of NH3 ice nanoparticles studied by a combined molecular dynamics and vibrational exciton approach, J. Chem. Phys., 2006, 125, 144501 CrossRef.
- S. M. Melikova, K. S. Rutkowski, P. Rodziewicz and A. Koll, Unusual spectroscopic properties of CHF3 dissolved in liquified Ar N2, CO, and CO2, Chem. Phys. Lett., 2002, 352, 301–310 CrossRef CAS.
- F. Baas and K. D. Van Den Hout, Measurements of depolarization ratios and polarizability anisotropies of gaseous molecules, Physica A, 1979, 95, 597–601 CrossRef.
- S. G. Ramesh and E. L. Sibert III, A study of the vibrations of fluoroform with a sixth order nine-dimensional potential: a combined perturbative-variational approach, Mol. Phys., 2005, 103, 149–162 CrossRef CAS.
- B. H. Torrie, O. S. Binbrek and B. M. Powel, Structure of solid fluoroform, Mol. Phys., 1996, 87, 1007–1013 CrossRef CAS.
- H. W. Xiang, Vapor pressures critical parameters, boiling points, and triple points of halomethane molecular substances, J. Phys. Chem. Ref. Data, 2002, 30, 1161–1197.
- B. Andrews, A. Anderson and B. Torrie, Raman and Infrared spectra of crystalline fluoroform, Chem. Phys. Lett., 1984, 105, 551–554 CrossRef CAS.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley-Interscience, New York, 1998 Search PubMed.
- M. Jetzki, A. Bonnamy and R. Signorell, Vibrational delocalization in ammonia aerosol particles, J. Chem. Phys., 2004, 120, 11775–11784 CrossRef CAS.
| This journal is © the Owner Societies 2009 |