Computational and FTIR spectroscopic studies on carbon monoxide and dinitrogen adsorption on a high-silica H-FER zeolite

Abstract

Adsorption (at a low temperature) of carbon monoxide and dinitrogen on a high-silica ferrierite-type zeolite (H-FER, Si : Al = 27.5 : 1) was investigated by means of variable temperature infrared spectroscopy and theoretical calculations at the periodic DFT level. This combined experimental and computational approach led to detailed characterization of several types of hydrogen-bonded OH⋯CO and OH⋯N₂ complexes, formed by interaction between the adsorbed molecules and the Brønsted acid OH groups of the zeolite. CO or N₂, forming linear complexes with OH groups pointing towards a sufficiently ample void space, show the largest adsorption enthalpy which was found to be in the (approximate) range of −25 to −29 kJ mol⁻¹ for CO and −15 to −19 kJ mol⁻¹ for N₂. Less stable OH⋯CO or OH⋯N₂ complexes can be formed when either the Brønsted acid OH group is involved in intra-zeolite hydrogen bonding or when the free space available is too small to allow formation of linear complexes without previous re-location of the proton of the OH group involved. The details of experimental IR spectra in the O–H, C–O, and N–N stretching regions could be interpreted on the basis of good agreement between experimental and calculated results.

---

1. Introduction

Zeolites containing Brønsted acid Si(OH)Al groups (protonic zeolites) find extensive usage as catalysts for a wide range of technological processes. Suffice it to say that, in the petrochemical industry, catalysis by protonic zeolites encompasses such transformations as alkane hydrocracking and skeletal isomerization, alkene and alkyne polymerization, alkylation and dehydro-aromatization,^1–7 which frequently involve hydrogen bonding followed by proton transfer.^6–9 Studies on zeolite Brønsted acidity, for which IR spectroscopy of adsorbed probe molecules is often used, should help to understand performance. Among such probe molecules, both CO and dinitrogen are frequently used.^10–15 When adsorbed (at a low temperature) on protonic zeolites, those molecules are well known to form hydrogen-bonded complexes with Brønsted acid Si(OH)Al groups; and formation of such complexes can be monitored by analysing ensuing changes in either the O–H stretching region, or in the corresponding C–O or N–N stretching bands.^11,16,17

However, besides spectroscopic features, the interaction energy involved in the hydrogen-bonding process and the detailed geometry of the complexes formed are also important aspects to analyse in order to improve understanding at the atomic level; which would also be desirable when considering that detailed studies on hydrogen bonding are relevant to several other fields, including theoretical chemistry, molecular recognition and association,¹⁸ and hydrogen exchange processes,^19–21 to name only a few examples.

The Brønsted acid sites in H-zeolites and the complexes formed with various small molecules were the subject of numerous theoretical investigations (e.g., ref. 22–28). Relevant reported results in relation to the present work would be referred to in the discussion.

Aiming at an increased understanding of hydrogen bonding in zeolites, we report on a combined computational and FTIR spectroscopic study on dinitrogen and carbon monoxide adsorption on protonic ferrierite (H-FER). Theoretical calculations, at the periodic DFT level, were used to (i) determine the location and stability of the zeolite Brønsted acid sites and (ii) calculate the binding energy of the hydrogen-bonded complexes as well as the vibrational frequency of the stretching mode of the adsorbed diatomic molecule. Variable temperature IR spectroscopy (VTIR)^29,30 was used to (i) obtain the spectroscopic features which characterize the gas adsorption process and (ii) derive the corresponding values of standard adsorption enthalpy and entropy. It is shown how the whole set of experimental and computational results can be used to obtain precise information on both, the gas–solid interaction mode and the energy balance involved in formation of the corresponding hydrogen-bonded complexes.

2. Materials and methods

2.1 Experimental details

A sample of ferrierite in the ammonium form (NH₄-FER) having a nominal Si : Al ratio of 27.5 : 1 was obtained from a commercial firm. Powder X-ray diffraction showed good crystallinity and confirmed the expected structure type; no additional diffraction peaks were observed. From this parent material, H-FER was obtained by in situ thermal treatment inside an IR cell, as described below. Total transformation of NH₄-FER into H-FER was checked by the absence (after the thermal treatment) of the IR absorption bands corresponding to the ammonium ion. For IR spectroscopy, a thin self-supported wafer of the zeolite sample was prepared and subjected to thermal activation (outgassing) in a dynamic vacuum (residual pressure smaller than 10⁻⁴ Torr) for 3 h at 700 K inside an IR cell, described elsewhere,^31,32 which allowed in situ sample activation, gas dosage and variable temperature IR spectroscopy to be carried out. After sample activation the cell was dosed with 0.2 Torr of helium (to facilitate thermal contact between the cell body and the sample wafer) and cooled with liquid nitrogen. After recording the background spectrum at liquid-nitrogen temperature the cell was dosed with either CO or nitrogen and closed, and a series of IR spectra was recorded upon gradual warming up of the IR cell. Simultaneously, temperature and gas equilibrium pressure inside the cell were registered. For that purpose, a platinum resistance thermometer (Tinsley) and a capacitance pressure gauge (MKS, Baratron) were used. Pressure correction (for helium) was determined from a calibration plot as described elsewhere.³² Precision of these measurements was better than ±10⁻² Torr for pressure and ±2 K for temperature. Transmission FTIR spectra were recorded, at 3 cm⁻¹ resolution, by using a Bruker IFS66 spectrometer. 64 scans were accumulated for each spectrum. In order to check reproducibility, and also for improving accuracy, two sets of variable temperature spectra were recorded for each sample.

2.2 Experimental determination of standard adsorption enthalpy and entropy

Series of IR spectra obtained over a temperature range while simultaneously recording IR absorbance, temperature and gas (CO or N₂) equilibrium pressure can be used to derive the standard adsorption enthalpy, ΔH⁰, and entropy, ΔS⁰, of the gas adsorption process by using the VTIR method explained in detail elsewhere.^29,30 To facilitate understanding of the results reported here, a summary of the method is given below.

Let eqn (1) represent the adsorption equilibrium of a molecule, M, at the adsorption centre, ZOH, representing a zeolite Brønsted acid site:

ZOH_(s) + M_(g)⇆ZOH–M_(ads) (1)

For any given temperature, T, the integrated intensity of a characteristic IR absorption band (from either the zeolite adsorbing centre or the adsorbed molecule) should be proportional to surface coverage, θ. Hence, this IR absorption band gives information on the activity (in the thermodynamic sense) of the adsorbed molecule and of the empty sites (1 −θ). Simultaneously, the equilibrium pressure, p, gives the activity of the gas phase. Therefore, the equilibrium constant, K, for the adsorption process (at that temperature) can be determined. Assuming Langmuir-type adsorption, K is given by eqn (2) below:

θ = K(T)p/[1 + K(T)p] (2)

The variation of K with temperature is related to standard adsorption enthalpy and entropy through the well-known van’t Hoff equation:

K(T) = exp(−ΔH⁰/RT)exp(ΔS⁰/R) (3)

Combination of eqns (2) and (3) leads to eqn (4) below:

ln{θ/[(1 −θ)p]} = (−ΔH⁰/RT) + (ΔS⁰/R) (4)

which can also be written as:

ln{A/[(A_M−A)p]} = (−ΔH⁰/RT) + (ΔS⁰/R) (5)

where A stands for the IR absorbance being actually measured and A_M is the maximum absorbance (corresponding to θ = 1). By determining θ (or relative absorbance) as a function of T and p for IR spectra obtained over a relatively large temperature range, eqn (4) or (5) gives direct access to the thermodynamic quantities ΔH⁰ and ΔS⁰ involved in the adsorption process under study.

2.3 Computational methods and models

2.3.1 H-FER. The ferrierite structure has an orthorhombic unit cell (T₃₆O₇₂, where T is either a Si or Al atom), space group Immm with four tetrahedral sites (T₁ : T₂ : T₃ : T₄ = 1 : 2 : 2 : 4) and eight framework oxygen atoms that are symmetrically independent.³³ The numbering scheme for T-positions and for framework oxygen atoms introduced by Vaughan is used;³³ note that this numbering scheme differs from that used in the Database of Zeolite Structures,³⁴ where T₁ and T₄ positions are switched. The structure of FER is depicted in Fig. 1, where the numbering scheme for framework atoms (tetrahedral sites) is also given for convenience. The main ten-member ring (10R) channel (M) along the [001] direction intersects with a perpendicular 8R channel (P) running along the [010] crystallographic direction. The 8-ring entrance window to the FER cage is formed on the intersection of M and P channels. More details about the FER structure can be found, e.g., in ref. 30.

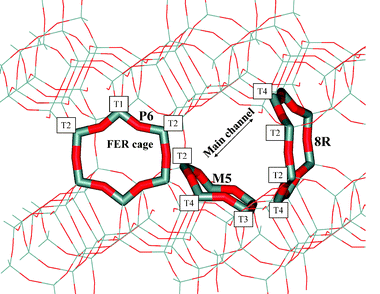Fig. 1 FER structure showing T-site numbering. The 8-member ring on the intersection of the main and perpendicular channel (8R), as well as the 5-member ring on the wall of the main channel (M5) and 6-member ring in the cage (P6), are depicted in a tube mode. Framework Si and O atoms are coloured in grey and red, respectively.

The unit cell (UC) of FER was optimized previously³⁵ for the all-silica form. Calculations at the periodic DFT level were performed with a double UC extended along the c direction (a = 19.147, b = 14.304 and c = 15.153 Å). Geometry optimisations were performed fixing the unit cell volume and shape and relaxing all atomic coordinates.

2.3.2 Computational methods. The interaction of CO and N₂ molecules with H-FER was modelled with periodic DFT calculations using the VASP program.^36,37 The projector augmented wave approximation (PAW)^38,39 and the plane wave basis set with a kinetic energy cut-off of 400 eV were used; Brillouin-zone sampling was restricted to the Γ-point. The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional^40,41 was employed. Zero-point energies (ZPE) of CO and N₂ adsorption complexes in H-FER were calculated within the harmonic approximation considering 12 degrees of freedom, while for the bare Brønsted protonic sites only 6 degrees of freedom were considered. Second derivatives were calculated numerically using two displacement steps in each direction with a step size of 0.005 Å. The sum of the electronic interaction energy, ΔE_el, and ZPE gives the internal energy change at 0 K that, at this temperature, is equal to the standard adsorption enthalpy ΔH⁰(0). Thermal corrections were calculated using the expression for ideal gas:

ΔH⁰(T) = ΔE_el + ΔZPVE − (7/2)RT (6)

The ω/r correlation method described below requires calculations with small cluster models at the coupled clusters level, including singles and doubles and perturbative triples (CCSD(T)), employing a large basis set; the valence-quadruple-ς quality basis set augmented with polarization functions (VQZP)⁴² was used. In addition, calculations on cluster models at the DFT level, employing PBE exchange–correlation functional and VQZP basis set were performed. Some geometry optimizations were performed with valence-triple-ς basis set with polarization functions (VTZP).⁴²

2.3.3 Calculation of CO and N₂ vibrational frequencies

The stretching frequencies of CO adsorbed on extra-framework metal cations (Cu⁺, Li⁺, Na⁺, and K⁺) in zeolites (FER and ZSM-5) have been reliably calculated using the ω/r correlation method.^35,43–46 In this contribution we explore the possibility of extending the ω/r correlation method for the description of the vibrational dynamics of CO adsorbed on Brønsted acid sites in H-FER, as well as the application of this method to N₂ vibrational dynamics. Within the concept of the ω/r correlation method, the C–O stretching frequency, ν_CO, is expressed as a function of CO bond length r_CO:

ν_CO[CCSD(T)] = a×r_CO[DFT] + b + Δν (7)

where anharmonicity, Δν = ν−ω, a and b were obtained from CCSD(T) and DFT calculations on a set of testing molecules. This set consisted of H₃O⁺CO, H₅O₂⁺CO (both restricted to C_2v symmetry) and FH·CO (C_∞v symmetry). The harmonic C–O stretching frequencies were calculated by numerical integration on a two-dimensional (considering C–O and H–C distances) 5 × 5 grid of points. The constant anharmonicity (−29 cm⁻¹) calculated previously⁴⁷ for free CO was assumed. A corresponding set of testing molecules was used for obtaining a and b parameters for the N–N stretching frequency. The anharmonicity Δν = −28 cm⁻¹ calculated at the CCSD(T)/VQZP level was used in all calculations on N₂ complexes. The resulting parameters are summarized in Table 1.

Table 1 Parameters of the ν/r (ω/r) correlations defined by eqns (7) and (8)

	Level of theory^a
System	Frequency	Geometry	a ^b	b
a Level of theory used for the frequency calculations and geometry optimization. CCSD(T) calculations were performed with VQZP basis set while PBE calculations were performed within the periodic model using energy cut off of 400 eV. b In Å^−1. c Defined by eqn (7). d Defined by eqn (8). e Correlation used for harmonic OH frequencies.
C–O^c	CCSD(T)	PBE	−8582.336	11975.4
N–N^c	CCSD(T)	PBE	−9400.100	12858.4
O–H^d	CCSD(T)	CCSD(T)	−14958.122	18080.4
	CCSD(T)	PBE	−13165.306	16522.1
	PBE (ωOH)^e	PBE	−14350.314	17707.3

---

The validity of eqn (7) was verified by calculations on the H₃Si-O(H)-AlH₃ model system (denoted 2-T cluster model) that is the simplest model of Brønsted acid site in zeolites. The geometries of 2-T·CO and 2-T·N₂ complexes were optimized at the PBE/VQZP level subjected to C_s symmetry constraints, and O–H⋯C–O (O–H⋯N–N) structures were constrained to be linear. The r_CO, r_OH, and r_HC (r_HN) distances and Al–O–H angle were re-optimized at the CCSD(T)/VQZP level and subsequently CO (N₂) frequencies were calculated numerically on the 5 × 5 grid of points. Calculated CCSD(T)/VQZP fundamental frequencies (2170 and 2339 cm⁻¹ for CO and N₂, respectively) were within 1 cm⁻¹ of those obtained from eqn (7). Therefore, the Δω correction term used previously in studies of CO on metal-exchanged zeolites^30,44,45 was set to zero.

2.3.4 Calculation of OH stretching frequencies. In order to compare calculated and experimental O–H stretching frequencies of the Brønsted acid sites the anharmonicity must be taken into account. Following the strategy of ref. 23 the O–H stretch can be considered as uncoupled from other vibrational degrees of freedom. Very small coupling between OH stretching and SiOH bending modes (2 cm⁻¹) was reported.⁴⁸ Only a small coupling between O–H stretching and bending modes was also found using a 3-D anharmonic description of Brønsted OH group in H-CHA.⁴⁹ A good correlation between the r_OH bond length and the O–H stretching frequency was pointed out previously.²⁷ However, it is now well recognized that OH stretching frequencies calculated at the DFT or MP2 level are typically overestimated and they need to be scaled.⁵⁰

Precise calculations of O–H stretching frequencies are extremely demanding on the accuracy of the method used for the description of the interatomic potential; even the CCSD(T) potential obtained at the complete basis set limit (CBS) often gives frequencies substantially deviating from those experimentally determined. For instance, for the OH group in gas phase HNO₃ the experimentally determined ω_OH and ν_OH frequency values are 3708 and 3552 cm⁻¹, respectively.⁵¹ Reported coupled-clusters type calculations, QCISD(T), employing the 6-311++G(2d,2p) basis set give an ω_OH value which is 100 cm⁻¹ overestimated.⁵² We have calculated ω_OH and ν_OH at the CCSD(T)/CBS level, and obtained the values 3765 and 3589 cm⁻¹, respectively; still about 50 cm⁻¹ overestimated.

It is, therefore, quite understandable that the stretching frequencies of Brønsted acid OH groups in zeolites were often calculated simply by rescaling harmonic frequencies obtained at the DFT level to match the experimental results. While such strategy works well for free Brønsted OH groups,²⁷ an unrealistically large shift in O–H stretching frequency upon the interaction with the CO molecule (almost twice as large as observed experimentally) was recently reported for H-MOR zeolite using PW91 or PBE exchange–correlation functionals; it has been concluded that the RPBE functional provided more reliable results.²⁴ Instead of using such a simple scaling we explored the possibility of using an ω/r correlation method in a similar way as described above for CO. The advantages of the ω/r correlation method over the simple scaling method include: (i) The ω/r correlation method does not mix errors due to the harmonic approximation and errors of the method used for the description of the electronic structure of the system, (ii) the ω/r method does not require the computationally demanding evaluation of the second derivatives, and (iii) the ω/r method has been shown to outperform the simple scaling method for CO in various environments.^46,53–55. However, it remains to be seen whether this strategy can be applied for OH stretching frequencies in zeolites. Therefore, OH frequencies were calculated for a set of testing molecules that includes the 2-T cluster models described above; calculations were performed for four different Si–O–Al angles (α = 106.5, 131.5, 146.5, and 156.5°). The minimum r_OH distance and Al–O–H angle were obtained for each value of α. Anharmonic OH stretching frequencies were obtained from numerical solution of the one-dimensional Schrödinger equation on a grid of 12 points in the range of −0.22 to +0.5 Å from equilibrium r_OH.

Following the strategy described in section 2.3.3 for CO and N₂, except that the anharmonicity of OH is not assumed to be constant, the O–H frequency can be calculated as:

ν_OH = a·r_OH + b + Δ_CC (8)

where Δ_CC is a correction due to the error of the CCSD(T) method set to −50 cm⁻¹ (see discussion of HNO₃ above); such Δ_CC happens to set the frequency of the Brønsted acid OH group pointing towards the void space of H-FER just on the value of the maximum of the band observed experimentally (see section 3.2.1). Based on the tests performed on the 2-T·CO cluster models it can be concluded that the ν_OH/r_OH correlation (employing CCSD(T) frequencies and DFT bond lengths) works well for free OH, and it is fair for the description of Brønsted OH groups involved in the formation of complexes with CO.

3. Results

3.1 Calculations

3.1.1 Structure and stability of Brønsted acid sites. Geometry, stability and O–H stretching frequencies were calculated for all possible Brønsted acid sites that may exist in the vicinity of each of the four distinguishable framework Al positions (Table 2); some of the Brønsted sites are depicted in Fig. 2. Note that the results presented here were obtained with a double UC (see section 2.3.1); calculations with a single UC unrealistically favour H-bonded adsorption complexes.

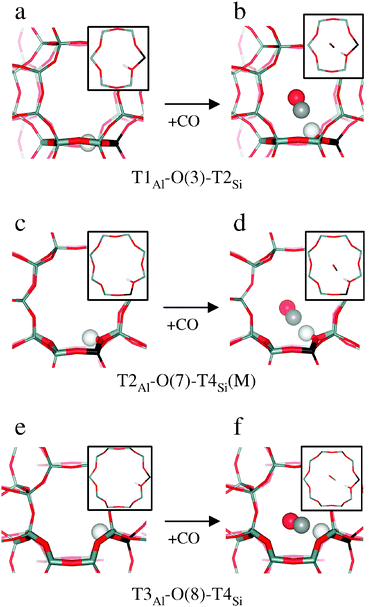Fig. 2 Formation of CO adsorption complexes (on the right) on various Brønsted acid sites (on the left). The Brønsted H atom is shown as a white ball, and the CO molecules are depicted as red (O) and grey (C) balls. Framework Al is shown in black.

Table 2 Relative stability of Brønsted acid sites in the vicinity of the four distinguishable framework Al positions

Al location	Oxygen position^a	H Location	ΔE^b kJ mol^−1	α/°	ν OH/cm^−1	ΔωOH(6D–1D)^c/ cm^−1
a Numbering scheme from ref. 33 adopted. The Brønsted acid sites located inside or slightly above a small ring are depicted in italic. b Relative energies of sites with respect to the energy of the most stable Brønsted proton site (T2Al–O(7)–T4Si). c Difference in harmonic OH frequencies calculated numerically from 6-D Hessian and those calculated using 1-D ωOH[PBE]/rOH[PBE] correlation.
T1	T1 Al –O(3)–T2Si	P6	1	137	3558	−12
	T1Al–O(4)–T3Si	P cage	8	138	3606	6
T2	T2Al–O(7)–T4Si	8R	0	134	3606	6
	T2 Al –O(3)–T1Si	P6	5	140	3587	−1
	T2Al–O(1)–T2Si	8R	17	149	3535	−2
	T2 Al –O(1)–T2Si	P6	27	154	3471	−22
T3	T3Al–O(8)–T4Si	M	2	133	3607	−1
	T3Al–O(4)–T1Si	P cage	10	136	3601	5
	T3Al–O(2)–T3Si	P cage	11	138	3598	−1
T4	T4Al–O(6)–T4Si	8R	4	137	3600	4
	T4Al–O(7)–T2Si	8R	6	139	3588	3
	T4Al–O(8)–T3Si	M	7	138	3615	6
	T4 Al –O(8)–T3Si	M5	10	137	3447	−65
	T4 Al –O(5)–T4Si	M5	17	150	3265	−155

---

Al in T1. The most stable Brønsted site in the vicinity of Al at T1 position is the site formed on O(3) framework oxygen atom (between T1 and T2 tetrahedral sites) located in the P6 ring separating two adjacent FER cages. At this T1_Al–O(3)–T2_Si site (Fig. 2a) the H atom is located inside the P6 ring in the proximity of two non-AlO₄ oxygen atoms (2.61 and 3.32 Å apart). As a result, the O–H stretching frequency (3558 cm⁻¹) is influenced by these close framework oxygen atoms (weak intra-zeolite hydrogen bond). The Brønsted acid site on the O(4) framework oxygen atom (T1_Al–O(4)–T3_Si) having the H atom pointing towards the void space of the FER cage is 7 kJ mol⁻¹ less stable than the T1_Al–O(3)–T2_Si site, and is characterized by a higher O–H stretching frequency (3606 cm⁻¹).

Al in T2. The most stable Brønsted acid site in the vicinity of Al at T2 position is the T2_Al–O(7)–T4_Si site (Fig. 2c) located in the 8R window at the channel intersection (ν_OH = 3606 cm⁻¹). The T2_Al–O(3)–T1_Si site located in the P6 ring is 5 kJ mol⁻¹ less stable and is characterized by a lower OH stretching frequency (3587 cm⁻¹). The other two Brønsted acid sites around Al in T2 are significantly less stable and, hence, are not likely to be populated.

Al in T3. The Brønsted acid site T3_Al–O(8)–T4_Si located in the main channel (Fig. 2e) is the most stable site for this framework Al position; it is characterized by ν_OH = 3607 cm⁻¹. The two other Brønsted acid sites in the vicinity of Al in T3 are located in the FER cage and they are 8 and 9 kJ mol⁻¹ less stable.

Al in T4. The most stable Brønsted acid site in the vicinity of Al at T4 position is the T4_Al–O(6)–T4_Si site located in the 8R window at the channel intersection and is characterized by ν_OH = 3600 cm⁻¹. The T4_Al–O(7)–T2_Si site, also located in the 8R window, is 2 kJ mol⁻¹ above the previous one and has an OH stretching frequency lower by 12 cm⁻¹. A rather low O–H stretching frequency (3447 cm⁻¹) was calculated for the T4_Al–O(8)–T3_Si Brønsted acid site that is located in the 5-member ring (M5) on the wall of the main channel. This low OH frequency is due to the formation of an intra-zeolite H-bond across the M5 ring (the distance between H and the closest non-AlO₄ oxygen atom is only 2.07 Å). Note however, that the structure corresponding to this local minimum is 3 kJ mol⁻¹ above that of another T4_Al–O(8)–T3_Si site where the Brønsted acid H atom is also bonded to the O(8) framework oxygen, but it points towards the void space available in the M channel.

In summary, when a Brønsted acid site is situated in the void space of the main or perpendicular channel (cage) or at the intersection of two channels (8R window) the OH vibrates towards the void space and shows a high frequency, in the range of 3588–3615 cm⁻¹. The difference between harmonic and anharmonic frequencies, Δν, is rather constant for these sites (about −160 cm⁻¹). Note also that the Al–O–Si angle (α) for these sites is in the narrow range 133–139°. The only exception is the T2_Al–O(1)–T2_Si site, that has α = 149° and ν_OH = 3535 cm⁻¹; this site, however, is relatively unstable and is not expected to be populated. For Brønsted acid sites located inside or slightly above a small ring (depicted in italic in Table 2), either P6 or M5 (T1_Al–O(3)–T2_Si or T4_Al–O(5)–T4_Si, respectively), the OH stretching dynamics is influenced by an intra-zeolite H-bond which results in ν_OH being lowered by as much as 300 cm⁻¹ with respect to that of the Brønsted acid sites (discussed above) that can vibrate into a void space. However, the Brønsted acid sites located in small rings are less stable than those pointing to a void space and, with the exception of the T1_Al–O(3)–T2_Si site, they are not expected to be observed in the experimental spectra. Thus, the difference between the O–H stretching frequency of the Brønsted acid sites in the free space (high-frequency band) and those in small rings (low-frequency band or tail) that can be observed experimentally is about 50 cm⁻¹.

The difference in harmonic OH frequencies calculated from 6-D Hessian (numerical 2nd derivatives) and those obtained from the 1-D ω[PBE]/r[PBE] correlation is presented in the last column of Table 2. The agreement between the two methods is excellent for Brønsted acid OH groups pointing towards the void space of the zeolite channels; however, such an agreement becomes less satisfactory when an intra-zeolite H-bond is formed between a Brønsted acid OH group and a framework oxygen atom, the observed discrepancy is likely due to the one-dimensional approximation assumed in the ω/r correlation method.

3.1.2 Periodic DFT investigation of the CO and N₂ adsorption complexes in H-FER. Table 3 reports the geometries, interaction energies, and vibrational frequencies (for both O–H stretching mode and C–O or N–N stretching mode of the adsorbed molecule) for complexes formed upon interaction of H-FER with CO (both C- and O-down) and N₂. The geometric parameters are defined in Fig. 3. Regardless of the position of the Brønsted acid H atom forming the adsorption complex, the interaction energies are reported with respect to the most stable Brønsted site in the vicinity of a particular framework Al atom. The CO adsorption complexes (interacting via C-end) will be discussed first; several of these complexes are depicted in Fig. 2.

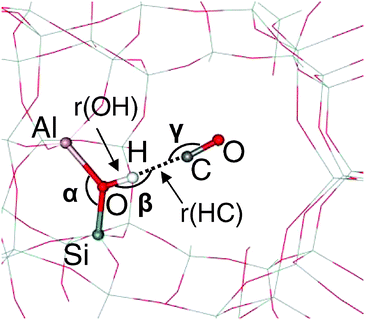Fig. 3 Definition of the geometric parameters (bond lengths and angles) for the OH⋯CO adsorption complex.

Table 3 Characteristics of CO and N₂ adsorption complexes formed in H-FER; structural parameters, stretching frequencies, and interaction energies are given in Å, cm⁻¹, and kJ mol⁻¹, respectively. The most stable CO adsorption complexes in the vicinity of each framework Al atom are depicted in bold.

Adsorbed Molecule	Al location	Adsorption complex^a	CO location	r(H⋯X)^b^,^c	β O–H⋯X^c	ν OH	ν CO ν NN	E def ^d	E el ^e	ΔH^0(200)^f
a Numbering scheme from ref. 33 adopted. b Distance between Brønsted acid hydrogen and adsorbed molecule. c X stands for the closer atom of diatomic molecule with respect to the Brønsted proton. d E def stands for deformation energy (see text). e Electronic interaction energies. f Adsorption enthalpies calculated for T = 200 K. g Interaction energy calculated with respect to most stable Brønsted acid proton site found in the vicinity of a particular framework Al atom.
CO	T1	T1Al–O(3)–T2Si	P cage	1.969	165	3314	2173	11.9	−13.3^g	−16.0
		T1Al–O(4)–T3Si	P cage	1.925	174	3304	2177	2.0	−19.0^g	−21.6
	T2	T2Al–O(7)–T4Si(P)	P cage	1.916	167	3293	2177	5.5	−21.1	−23.5
		T2Al–O(7)–T4Si(M)	M	2.002	159	3362	2174	3.3	−19.7	−22.0
	T3	T3Al–O(8)–T4Si	M	1.895	176	3287	2179	1.9	−26.8	−29.0
	T4	T4Al–O(6)–T4Si	P cage	1.891	176	3259	2175	2.9	−24.2	−26.3
		T4Al–O(7)–T2Si(P)	P cage	1.896	170	3251	2175	3.9	−21.0^g	−22.9
		T4Al–O(7)–T2Si(M)	M	1.937	160	3309	2177	5.2	−20.5^g	−21.6
		T4Al–O(8)–T3Si	M	1.940	174	3321	2178	3.4	−22.3^g	−24.5
OC	T1	T1Al–O(4)–T3Si	P cage	2.035	171	3539			−5.0	−8.8
	T2	T2Al–O(7)–T4Si	P cage	2.056	155	3551			−7.2	−10.9
	T3	T3Al–O(8)–T4Si	M	1.967	175	3536			−12.0	−15.2
	T4	T4Al–O(6)–T4Si	P cage	2.026	173	3532			−9.8	−13.3
N2	T1	T1Al–O(4)–T3Si	P cage	1.980	173	3473	2342	7.5	−9.2^g	−12.1
	T2	T2Al–O(7)–T4Si(P)	P cage	2.000	161	3483	2342	3.2	−11.1	−13.8
		T2Al–O(7)–T4Si(M)	M		151	3526	2339	1.1	−11.8	−14.9
	T3	T3Al–O(8)–T4Si	M	1.951	177	3469	2342	0.2	−16.7	−19.2
	T4	T4Al–O(6)–T4Si	P cage	1.969	175	3462	2342	0.9	−14.2	−16.8

---

The interaction of CO with Brønsted acid sites, which is driven by the electrostatic contribution,²³ is maximized when the adsorption complex has a (nearly) linear O–H⋯C–O arrangement. For all CO adsorption complexes found in H-FER, the H–C–O angle (Γ in Fig. 3) is nearly linear with a maximum deviation of 8° (not reported in Table 3). Also the angle O–H–C (β) is nearly linear, provided that the topology of the zeolite allows formation of such linear complex. In order to attain a linear O–H⋯C–O arrangement the O–H bond must point to the void space of the zeolite channel. While this is the case for some Brønsted acid sites (e.g., T3_Al–O(8)–T4_Si) the location of other Brønsted acid H atoms must change in order to form a stable complex with CO; this change is large in particular for those Brønsted acid sites involved in intra-zeolite H-bonding (e.g., T1_Al–O(3)–T2_Si and T4_Al–O(8)–T3_Si). To quantify the extent of the changes of Brønsted acid sites required to form an adsorption complex with CO, the deformation energy, E_def, was calculated as the difference in energy between H-FER at the geometry optimized without CO and that with CO (but after removing the contribution brought about by the CO molecule). E_def values for individual Brønsted acid sites are also reported in Table 3. Changes in geometry of the Brønsted acid site due to the formation of adsorption complexes with CO are also depicted in Fig. 2 for some selected sites.

The most stable CO adsorption complex is formed on the T3_Al–O(8)–T4_Si Brønsted acid site, where hydrogen is pointing towards the void space of the main channel and can interact with CO without the need to move much from its equilibrium position (E_def = 1.9 kJ mol⁻¹); this situation is depicted in Fig. 2e and f. The least stable adsorption complex (among those investigated here) is formed on the T1_Al–O(3)–T2_Si Brønsted acid site, where the hydrogen atom is originally involved in an intra-zeolite H-bond (Fig. 2a) and is significantly displaced in the CO adsorption complex (Fig. 2b); and that is reflected in a relatively high deformation energy (E_def = 11.9 kJ mol⁻¹). This deformation energy is higher than the energy difference between the T1_Al–O(3)–T2_Si and the T1_Al–O(4)–T3_Si Brønsted acid sites, thus, it is energetically favourable that the H atom moves from the T1_Al–O(3)–T2_Si site to the T1_Al–O(4)–T3_Si site when forming the adsorption complex with a CO molecule. When the Al atom is in the T2 framework position, the proton is located in the 8R window (T2_Al–O(7)–T4_Si site) and CO adsorption complexes can be formed where CO approaches the Brønsted acid site either from the P cage or from the M channel (these complexes are denoted T2_Al–O(7)–T4_Si(P) and T2_Al–O(7)–T4_Si(M), respectively); both of these complexes (reported in Table 3) have similar stability. Note, however, that the β angle is only 159° for the T2_Al–O(7)–T4_Si(M) complex formed with CO pointing to the main channel; this situation is depicted in Fig. 2d. Although E_def is relatively small for this site, the CO adsorption complex cannot adopt a linear O–H⋯C–O geometry due to the topology of the FER framework.

The C–O stretching frequencies calculated using the ν_CO/r_CO correlation are in the range of 2173–2179 cm⁻¹. Calculated vibrational frequencies of the O–H bond in the CO adsorption complexes are in the range of 3251–3362 cm⁻¹; they are significantly shifted to lower frequencies (about 300 cm⁻¹) with respect to those calculated for free OH. The O–H stretching frequencies calculated for the most stable CO adsorption complexes (depicted in bold in Table 3) are in the range of 3259–3304 cm⁻¹. The O–H stretching frequency is higher for complexes where CO cannot adopt a linear O–H⋯C–O geometry; in particular, ν_OH = 3362 cm⁻¹ for the T2_Al–O(7)–T4_Si(M) complex.

The interaction of H-FER with CO can also lead to the formation of O-down carbonyl complexes, but it is clear from Table 3 that the stability of O-down adsorption complexes is significantly lower than that of the corresponding C-down complexes (about 13–14 kJ mol⁻¹ lower, regardless of framework Al location). It is therefore expected that O-down adsorption complexes will either not form at all or be only a very minority species, hence they are not further discussed here.

The interaction of the N₂ molecule with H-FER was investigated only for the most stable Brønsted acid sites in the vicinity of each framework Al atom, except for Al in T1 where, on account of the large deformation energy reported for the T1_Al–O(3)–T2_Si site, the N₂ interaction with the T1_Al–O(4)–T3_Si Brønsted acid site was also considered. The relative stability of N₂ adsorption complexes closely follows the trends observed for CO complexes (discussed above); in general terms, the stability of the individual N₂ complexes is about 10 kJ mol⁻¹ smaller than the stability of the corresponding CO complexes. The only qualitative difference between the N₂ and CO complexes was found for those complexes formed on T2_Al–O(7)–T4_Si(P) and T2_Al–O(7)–T4_Si(M) sites, where in the case of N₂ complexes the former one is slightly less stable than the latter. Note however that, in analogy with CO, the T2_Al–O(7)–T4_Si(M)/N₂ complex is also characterized by a smaller O–H–N angle (β = 151°), and that is reflected in the higher ν_OH value calculated for this complex. With the exception of this complex, the O–H stretching frequencies calculated for the N₂ complexes are in the range of 3462–3483 cm⁻¹ which is about 140 cm⁻¹ shifted with respect to free OH.

3.2 Experimental results

3.2.1 Carbon monoxide adsorption. The blank IR spectrum, in the O–H stretching region, of the zeolite H-FER is shown in the inset of Fig. 4. The absorption band seen at 3747 cm⁻¹ corresponds to silanols, while that appearing at 3605 cm⁻¹ is the characteristic band of the zeolite Brønsted acid sites, as already reported by several authors.^56,57 It should be noted that this band is rather broad, and shows a tail on the low frequency side. Both of these features clearly point to some degree of heterogeneity of the acidic Si(OH)Al groups, in agreement with the computational results shown above. However, attempts at band resolution did not give quantitatively reliable results regarding CO adsorption enthalpy (because of inherent uncertainty about how the band should be decomposed). Therefore, we decided to use integrated intensity of the 3605 cm⁻¹ band as it appears in the spectra.

Fig. 4 Representative variable-temperature IR spectra (O–H stretching region) of CO adsorbed on H-FER. The spectra are shown in the difference mode (zeolite blank subtracted). Temperature (in K) and equilibrium pressure (Torr, in brackets) as follows: 1, 167 (0.57); 2, 178 (0.80); 3, 133 (0.94); 4, 191 (1.11); 5, 195 (1.19); 6, 202 (1.35); 7, 206 (1.44); 8, 215 (1.61); 9, 224 (1.75). Inset shows the blank zeolite spectrum in the O–H stretching region.

Upon interaction of the zeolite with adsorbed CO (in the low pressure range studied) the band due to silanols was not significantly altered, but the intensity of the band at 3605 cm⁻¹ was found to decrease to an extent which was a function of temperature. Simultaneously, a new (and much broader) band corresponding to hydrogen-bonded OH⋯CO species appeared, showing a maximum at 3308 cm⁻¹. This is shown in Fig. 4, which depicts some representative variable temperature spectra in the difference mode; i.e., after subtracting the blank zeolite spectrum. From two independent series of VTIR spectra covering the temperature range of 160–240 K, the van’t Hoff plot shown in Fig. 5a was obtained. Note that the integrated intensity of the 3605 cm⁻¹ band divided by its maximum value (i.e., the one corresponding to the zeolite blank spectrum) gives directly the fraction (1 −θ) of free OH sites, from which the corresponding θ value needed for using eqn (4) was obtained. From the linear plot in Fig. 5a, the value of ΔH⁰ = −28.6 kJ mol⁻¹ was derived for the standard enthalpy of H-bond formation (OH⋯CO complex) between CO and the Brønsted acid sites of H-FER. The corresponding standard entropy change was found to be ΔS⁰ = −147 J mol⁻¹ K⁻¹. The estimated limits of experimental error are ±1 kJ mol⁻¹ for enthalpy and ±10 J mol⁻¹ K⁻¹ for entropy.

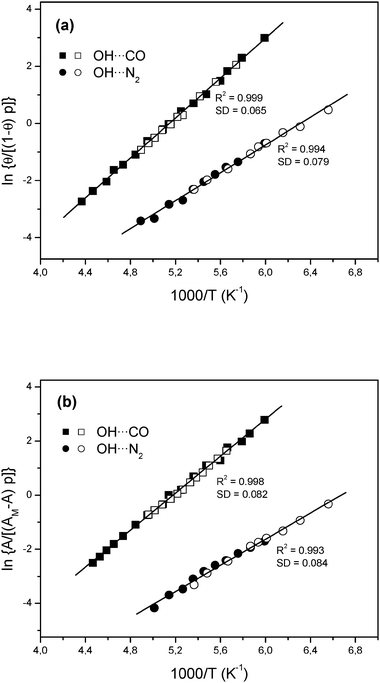Fig. 5 (a) Plot of the left-hand side of eqn (4) against reciprocal temperature for CO (squares) and N₂ (circles) adsorbed on H-FER; data obtained from the O–H stretching band at 3605 cm⁻¹. (b) Plot of the left-hand side of eqn (5) against the reciprocal temperature for CO (squares) and N₂ (circles) adsorbed on H-FER; data obtained from the C–O or N–N stretching bands at 2173 and 2331 cm⁻¹, respectively. The black and white symbols refer to two independent series of measurements for each case. R, linear regression coefficient; SD, standard deviation.

Representative VTIR spectra in the C–O stretching region are shown in Fig. 6. The band seen at 2173 cm⁻¹ corresponds to the CO stretching mode in OH⋯CO complexes. Note however, that at 77 K this band appears at a slightly higher frequency, 2175 cm⁻¹, as shown in the inset of Fig. 6. A small red-shift of the CO stretching band of adsorbed CO upon increasing the temperature (from 77 K upwards) was also frequently reported in the literature for other CO/zeolite systems.^11,58 The band seen (in Fig. 6) at 2137 cm⁻¹, which corresponds to weakly physisorbed (liquid-like) CO,^11,57 is of no concern here.

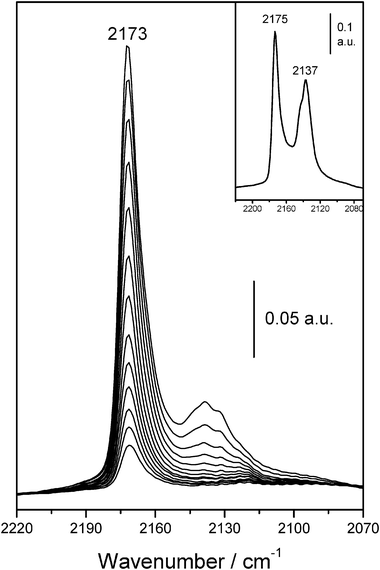Fig. 6 Representative IR spectra (C–O stretching region) of CO adsorbed on H-FER. From top to bottom, temperature goes from 169 to 229 K; and equilibrium pressure from 0.61 to 1.81 Torr. Inset shows the IR spectrum of CO adsorbed at 77 K.

It should also be noted that the formation of a small (temperature dependent) fraction of O-bonded OH⋯OC complexes is well documented in the literature for the case of CO adsorbed on the faujasite-type H–Y zeolite;⁵⁹ where the weak band corresponding to O-bonded species appeared at 2124 cm⁻¹, whilst the much stronger band corresponding to C-bonded OH⋯CO species was found at 2173 cm⁻¹. The very weak shoulder seen in the range of 2120–2124 cm⁻¹ in the spectra shown in Fig. 6 could have a contribution arising from OH⋯OC species (see section 3.1.2). But it should be noted that the ¹³CO counterpart (natural abundance about 1%) of the strong IR absorption band at 2173 cm⁻¹ should also show up at about 2124 cm⁻¹.

Two independent series of VTIR spectra in the C–O stretching region (band at 2173 cm⁻¹) were used to obtain the van’t Hoff plot depicted in Fig. 5b. From this linear plot, the corresponding values of standard adsorption enthalpy and entropy resulted in ΔH⁰ = −28.2 (±1) kJ mol⁻¹ and ΔS⁰ = −143 (±10) J mol⁻¹ K⁻¹. As expected, these values coincide (within experimental error) with those derived from the O–H stretching band; and this agreement between both sets of results gives further confidence. The average of both sets of results gives the final values of ΔH⁰ = −28.4(±1) kJ mol⁻¹ and ΔS⁰ = −145(±10) J mol⁻¹ K⁻¹ for the CO standard adsorption enthalpy and entropy, respectively.

3.2.2 Dinitrogen adsorption. Fig. 7 shows that, upon interaction of H-FER with adsorbed dinitrogen, the Brønsted acid Si(OH)Al band at 3605 cm⁻¹ is eroded to an extent which (for a fixed N₂ dose) increases when temperature is decreased. Simultaneously, a new (broader) band having a maximum at 3495 cm⁻¹ builds up; thus showing hydrogen bonding of N₂ with the zeolite Brønsted acid OH groups. In the N–N stretching region (see inset in Fig. 7) the characteristic IR absorption band of the hydrogen-bonded N₂ molecule appeared at 2331 cm⁻¹; the same wavenumber value was also reported by Bordiga et al.⁵⁷ for nitrogen adsorbed (at liquid nitrogen temperature) on H-FER.

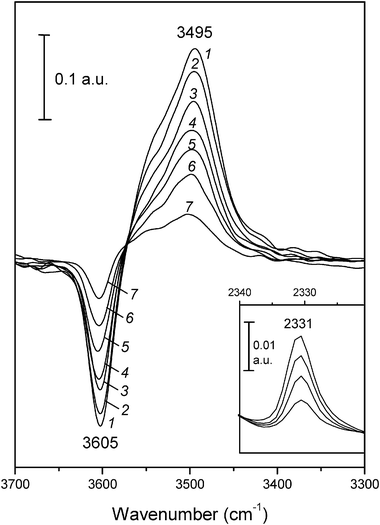Fig. 7 Difference variable-temperature IR spectra (zeolite blank subtracted) of N₂ adsorbed on H-FER. Temperature (in K) and equilibrium pressure (Torr, in brackets) as follows: 1, 152 (2.42); 2, 159 (2.85); 3, 166 (3.34); 4, 170 (3.56); 5, 176 (3.85); 6, 182 (4.10); 7, 194 (4.45). Inset shows some representative IR spectra in the N–N stretching region; from top to bottom, temperature goes from 153 to 183 K, and equilibrium pressure from 2.56 to 4.20 Torr.

Fig. 5a shows the linear plot of eqn (4) obtained from the whole set of data derived from two independent sets of measurements (covering the temperature range of 150–200 K) on the O–H stretching band at 3605 cm⁻¹. From the excellent linear fit obtained, the values of ΔH⁰ = −19.3 kJ mol⁻¹ and ΔS⁰ = −128 J mol⁻¹ K⁻¹ were derived for the standard adsorption enthalpy and entropy, respectively; i.e., for hydrogen bonding between N₂ and the H-FER Brønsted acid sites. Fig. 5b shows the corresponding linear plot of eqn (5), obtained from the temperature (and pressure) dependence of the integrated IR absorbance of the N–N stretching band at 2331 cm⁻¹. From this linear plot the values of ΔH⁰ = −18.9 kJ mol⁻¹ and ΔS⁰ = −134 J mol⁻¹ K⁻¹ were derived; as expected, they coincide (within experimental error) with those obtained from the O–H stretching band. The average of both sets of results gives the final values of ΔH⁰ = −19.1 kJ mol⁻¹ and ΔS⁰ = −131 J mol⁻¹ K⁻¹ for the nitrogen standard adsorption enthalpy and entropy, respectively. Estimated error limits are ±1 kJ mol⁻¹ for ΔH⁰, and ±10 J mol⁻¹ K⁻¹ for ΔS⁰.

4. Discussion

Fundamental frequency values calculated for the Brønsted acid OH groups in FER (Table 2) resulted in being in in the range of 3535–3615 cm⁻¹ for the OH groups pointing towards the free space (zeolite channels), while, due to intra-zeolite H-bonding, the OH groups pointing to the centre of a 6- or 5-member ring give lower frequency values (3265–3587 cm⁻¹). A similar lower frequency for the OH pointing to the centre of a 6R than that of the OH pointing towards the empty space (in the supercage) of zeolite H–Y was discussed in detail by Sauer et al.⁶⁰ Calculated frequencies for H–Y (3617 and 3574 cm⁻¹) were found to be in reasonable agreement with the corresponding experimental values⁶¹ (3623 and 3550 cm⁻¹).

Considering the relative stability of Brønsted acid sites, the experimentally observed band centred at 3605 cm⁻¹ (Fig. 4) should correspond to OH groups in the vicinity of Al in T2, T3 and T4, while the tail observed at the low frequency side should correspond to OH in the vicinity of Al in T1 position. Statistically, there is only 11% of T1 sites and hence the population of the low frequency OH is expected to be small. The experimentally observed OH band precisely shows a small tail at the low frequency side of the 3605 cm⁻¹ band which, according to the arguments above, should correspond to the Brønsted acid OH group in the vicinity of Al in T1. Note that this suggests some site-specificity of the Brønsted acid OH frequencies; for H-FER the low frequency tail corresponds to Al in T1.

Experimentally determined band maxima corresponding to the C–O and N–N stretching modes of adsorbed complexes were observed at 2175 and 2331 cm⁻¹ (spectra taken at 77 K), respectively. For CO, the corresponding frequencies calculated at the periodic DFT level using ν/r correlation (Table 3) agree very well with experimentally observed values. However, that agreement is not so good for the case of N₂, where calculated values of ν_NN deviate from the experimental ones by +11 cm⁻¹.

Regarding energy balance, the calculations give for the most stable OH⋯CO complexes (on T3_Al–O(8)–T4_Si and T4_Al–O(6)–T4_Si sites) ΔH⁰(200) values in the range of −26.3 to −29.0 kJ mol⁻¹. This is in excellent agreement with the experimentally determined value of −28.4 kJ mol⁻¹. However, it is worth noting that agreement between calculated and experimental values of ΔH⁰ is likely to involve some internal compensation of errors. Dispersion interactions are not taken into account in DFT calculations and, on the other hand, eqn (6) used for conversion of internal energy at 0 K into the corresponding enthalpy at 200 K is likely to overestimate the thermal correction. Thus, these two inherent inaccuracies of the calculation procedure are likely to (partially) cancel out each other.

The rather small interaction energy calculated for CO adsorption on the T1–O(4)–T3 Brønsted site (ΔH⁰ = −21.6 kJ mol⁻¹) is due to the fact that upon the interaction with CO the proton moves from the O(3) oxygen atom to the nearby O(4) oxygen atom, both of them interconnected by Al in T1 position. This movement of the proton accounts for the energy increase of 7 kJ mol⁻¹ (Table 3). Similarly, Suzuki et al.⁶² have recently reported that when ammonia is adsorbed on protonic chabazite, interaction with the OH group in the 6R is significantly weaker (by 20 to 30 kJ mol⁻¹) than interaction with OH groups in 8R, which point towards the open space.

For hydrogen-bonded OH⋯N₂ complexes, the calculated values of ΔH⁰(200) for the most stable complexes are in the range of −16.8 to −19.2 kJ mol⁻¹, to be compared with the experimentally determined value of −19.1 kJ mol⁻¹. Again, there is a good agreement between calculated and experimentally determined standard enthalpy of formation of the hydrogen-bonded OH⋯N₂ species; which is likely to be favoured to some extent (as in the case of OH⋯CO complexes) by internal compensation of errors.

Comparisons between ΔH⁰ values obtained for OH⋯CO and OH⋯N₂ complexes shows that the dinitrogen hydrogen-bonded complex is about 10 kJ mol⁻¹ less stable than the OH⋯CO complex. A similar stability difference was reported in the literature (regarding experimentally obtained data) for CO and N₂ adsorbed on some other protonic zeolites, as shown in Table 4. Also shown in this table is that the values of ΔH⁰ (for OH⋯CO and OH⋯N₂ complexes) correlate, as expected, with the corresponding red-shift of the Brønsted acid O–H stretching frequency upon hydrogen bonding.

Table 4 Relevant data for CO and N₂ hydrogen-bonded complexes in protonic zeolites

Zeolite	Si/Al Ratio	Δν(CO)^a	Δν(NN)^b	−ΔH^0(CO)^c	−ΔH^0(N2)^d	Ref.
a Red-shift (cm^−1) of the Brønsted-acid O–H stretching frequency upon hydrogen-bonding with CO. b Red-shift (cm^−1) of the Brønsted-acid O–H stretching frequency upon hydrogen-bonding with N2. c Standard enthalpy change (kJ mol^−1) in the formation of the OH⋯CO complex. d Standard enthalpy change (kJ mol^−1) in the formation of the OH⋯N2 complex. e Calculated values for most stable adsorption complexes (all other ΔH^0 values were experimentally determined).
H-FER	27.5	−297	−110	28.4	19.1	This work
				26–29^e	17–19^e	This work
H-ZSM-5	30	−303	−116	29.4	19.7	17
H-Y	5.6	−285	−98	25.6	15.7	17, 32

---

CO adsorption complexes in H-FER can be classified into three groups: (i) complexes formed on free OH groups (not involved in intra-zeolite H-bond) allowing a linear OH⋯CO arrangement to be adopted; these complexes involve the smallest deformation energy and, therefore, give the highest adsorption enthalpy (e.g., T3_Al–O(8)–T4_Si, Fig. 2e and f). (ii) Complexes on free OH groups which do not allow formation of a linear arrangement. In this case, either the H atom moves from its equilibrium position (which involves a deformation energy, e.g., T2_Al–O(7)–T4_Si(P)), or the CO adsorption complex deviates significantly from linearity (T2_Al–O(7)–T4_Si(M), Fig. 2c and d); in both cases the resulting adsorption enthalpy is smaller. (iii) Complexes on OH groups involved in intra-zeolite H-bonding; also in this case there is an energy penalty which results in an even smaller adsorption enthalpy. Either the H atom must be lifted above the plane of the ring (T1_Al–O(3)–T2_Si, Fig. 2a and b) or the H atom jumps to a different oxygen atom of the AlO₄ tetrahedron (e.g., from O(3) to O(4) when Al is in T1 position). A similar situation was found for N₂ complexes; the most stable complexes are formed on free OH groups allowing a linear OH⋯N₂ arrangement.

Upon formation of H-bonded CO or N₂ complexes, the O–H stretching band was experimentally found to red-shift by 297 and 110 cm⁻¹, respectively. The calculated values of this red-shift are about 300 cm⁻¹ for CO complexes and 140 cm⁻¹ for N₂ complexes. Although calculated and experimental values seem to be in close agreement, it should be noted that, to some extent, such an agreement is fortuitous; while the experimental shifts are measured between band maxima, the calculated values clearly depend on the specific Brønsted acid site being considered (Tables 2 and 3). For CO, considering only the most stable Brønsted acid sites and the most stable CO adsorption complexes formed in the vicinity of each framework Al, it is seen from Tables 2 and 3 that the calculated OH frequency shifts vary in the range of 254–341 cm⁻¹. It is therefore more meaningful to focus on the actual frequency of the red-shifted OH band than on the magnitude of the shift itself. It should also be remarked that the shoulder at the high-frequency side of the 3308 cm⁻¹ main band (Fig. 4) can be assigned to the non-linear OH⋯CO adsorption complexes (e.g., T2_Al–O(7)–T4_Si(M)); since the calculated frequencies for these complexes are significantly higher than those obtained for linear complexes (Table 3). Calculated O–H stretching frequencies for N₂ adsorption complexes cover a significantly smaller range (3462–3483 cm⁻¹) than in the case of CO complexes; with the exception of the non-linear N₂ adsorption complex formed at the T2_Al–O(7)–T4_Si(M) site that shows a frequency of 3526 cm⁻¹.

CO interaction with the protonic zeolites H-CHA and H-MOR was calculated, using a periodic DFT approach, by Ugliengo et al.²² and by Bucko et al.,²⁴ respectively. For H-CHA the value of interaction energy (at 0 K) ΔH⁰(0) = −16 kJ mol⁻¹ for the hydrogen-bonded OH⋯CO complex was reported. The geometry of this CO adsorption complex, which is located on a 8R in H-CHA, is very similar to that of the CO adsorption complexes formed on the 8R window in H-FER (T2_Al–O(7)–T4_Si and T4_Al–O(7)–T2_Si sites), for which ΔH⁰(0) is in the range from −16 to −18 kJ mol⁻¹ (Table 3, after subtracting the thermal correction energy, eqn (6)). For CO on H-MOR, Bucko et al.²⁴ reported E_el = −24.4 kJ mol⁻¹, obtained with the PW91 functional; this value falls within the range of E_el values reported in Table 3. On the contrary, a significantly lower value (E_el = −11.5 kJ mol⁻¹) was calculated by Bucko et al. using the RPBE functional.²⁴

5. Conclusions

Interaction of CO and N₂ with a high-silica H-FER zeolite was studied by a combined approach involving VTIR spectroscopy and calculations using a periodic DFT model, as well as cluster models and CCSD(T) level of theory. Based on the agreement obtained between experimental and calculated results, the following main conclusions were attained:

(i) The structure of the most stable Brønsted acid sites in the vicinity of each framework Al atom was obtained. In three out of four distinguishable Al positions, the Brønsted acid OH groups point towards a void space in the zeolite; these OH groups show the highest O–H stretching frequency. The smallest stretching frequency is shown by OH groups involved in intra-zeolite H-bonding.

(ii) Three types of adsorption complexes were identified for both CO and N₂, as follows: (a) adsorption complexes formed on free OH groups allowing a linear OH⋯CO or OH⋯N₂ arrangement to be attained; (b) complexes on free OH groups not allowing formation of a linear structure; (c) complexes on OH groups involved in intra-zeolite H-bonding. Complexes of type (a) are the most stable ones, while the complexes of type (c) are the least stable. The non-linear complexes of type (b) show the highest O–H stretching frequency.

(iii) The calculated and experimental adsorption enthalpy values are in good agreement; being up to −29 and −19 kJ mol⁻¹ for CO and N₂, respectively.

(iv) O-down CO adsorption complexes were not experimentally observed to form in any significant amount, in agreement with the calculated difference in stability of C- and O-down complexes (13–14 kJ mol⁻¹).

Acknowledgements

The Spanish MEC is gratefully acknowledged for supporting work done at the UIB (MAT2005-05350 and PCI2006-A7-0618). Work in IOCB was supported by grants of GACR (No. 203/06/0324), ME CR No. LC512, and project Z4 055 0506. Work at Charles University was supported by project MSM0021620857. We would also like to thank META Centre in Brno for continuous computational support.

References

1. Catalysis and Zeolites, ed. J. Weitkamp and L. Puppe, Springer Verlag, Berlin, 1999.
2. A. Corma, Chem. Rev., 1995, 95, 559.
3. T. L. M. Maesen, S. Calero, M. Schenk and B. Smit, J. Catal., 2004, 221, 241.
4. C. Lamberti, E. Groppo, G. Spoto, S. Bordiga and A. Zecchina, Adv. Catal., 2007, 51, 1.
5. G. Busca, Chem. Rev., 2007, 107, 5366.
6. S. Bordiga, G. Ricchiardi, G. Spoto, D. Scarano, L. Carnelli, A. Zecchina and C. O. Areán, J. Chem. Soc., Faraday Trans., 1993, 89, 1843.
7. Y. S. Jin, A. Aroux and J. C. Vedrine, Appl. Catal., 1988, 37, 1.
8. P. Ivanov and H. Papp, Appl. Surf. Sci., 2001, 179, 234.
9. G. Spoto, S. Bordiga, G. Ricchiardi, D. Scarano, A. Zecchina and E. Borello, J. Chem. Soc., Faraday Trans., 1994, 90, 2827.
10. A. Zecchina, S. Bordiga, G. Spoto, D. Scarano, G. Petrini, G. Leofanti, M. Padovan and C. O. Areán, J. Chem. Soc., Faraday Trans., 1992, 88, 2959.
11. A. Zecchina and C. O. Areán, Chem. Soc. Rev., 1996, 25, 187.
12. S. Bordiga, C. Lamberti, F. Geobaldo, A. Zecchina, G. T. Palomino and C. O. Areán, Langmuir, 1995, 11, 527.
13. M. A. Makarova, A. F. Ojo, K. Karim, M. Hunger and J. Dwyer, J. Phys. Chem., 1994, 98, 3619.
14. K. I. Hadjiivanov and G. N. Vayssilov, Adv. Catal., 2002, 47, 307.
15. A. Zecchina, G. Spoto and S. Bordiga, Phys. Chem. Chem. Phys., 2005, 7, 1627.
16. K. M. Neyman, P. Strodel, S. P. Ruzankin, N. Schlensog, H. Knözinger and N. Rösch, Catal. Lett., 1995, 31, 273.
17. C. O. Areán, J. Mol. Struct., 2008, 880, 31.
18. J. M. Lehn, Supramolecular Chemistry: Concepts and Perspectives, VCH, Weinheim, 1995.
19. Y. Marechal, in Proton Transfers in Hydrogen Bonded Systems, ed. Y. Marechal and T. Bountis, Plenum Press, New York, vol. B291, 1992.
20. Z. D. Nagel and J. P. Klinman, Chem. Rev., 2006, 106, 3095.
21. N. V. Belkova, E. S. Shubina and L. M. Epstein, Acc. Chem. Res., 2005, 38, 624.
22. P. Ugliengo, C. Busco, B. Civalleri and C. M. Zicovich-Wilson, Mol. Phys., 2005, 103, 2559.
23. I. N. Senchenya, E. Garrone and P. Ugliengo, J. Mol. Struct. (Theochem), 1996, 368, 93.
24. T. Bucko, J. Hafner and L. Benco, J. Phys. Chem. B, 2005, 109, 7345.
25. C. Tuma and J. Sauer, Phys. Chem. Chem. Phys., 2006, 8, 3955.
26. P. Ugliengo, B. Civalleri, C. M. Zicovich-Wilson and R. Dovesi, Chem. Phys. Lett., 2000, 318, 247.
27. M. Sierka and J. Sauer, J. Phys. Chem. B, 2001, 105, 1603.
28. A. Simperler, R. G. Bell, M. D. Foster, A. E. Gray, D. W. Lewis and M. W. Anderson, J. Phys. Chem. B, 2004, 108, 7152.
29. E. Garrone and C. O. Areán, Chem. Soc. Rev., 2005, 34, 846.
30. C. O. Areán, D. Nachtigallová, P. Nachtigall, E. Garrone and M. R. Delgado, Phys. Chem. Chem. Phys., 2007, 9, 1421.
31. A. A. Tsyganenko, P. Yu. Storozhev and C. O. Areán, Kinet. Catal., 2004, 45, 530.
32. C. O. Areán, O. V. Manoilova, A. A. Tsyganenko, G. T. Palomino, M. P. Mentruit, F. Geobaldo and E. Garrone, Eur. J. Inorg. Chem., 2001, 1739.
33. P. A. Vaughan, Acta Crystallogr., 1966, 21, 983.
34. http://www.iza-structure.org/databases/ .
35. O. Bludsky, M. Silhan, P. Nachtigall, T. Bucko, L. Benco and J. Hafner, J. Phys. Chem. B, 2005, 109, 9631.
36. G. Kresse and J. Hafner, Phys. Rev. B, 1993, 48, 13115.
37. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15.
38. P. E. Blochl, Phys. Rev. B, 1994, 50, 17953.
39. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
42. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
43. O. Bludsky, M. Silhan, D. Nachtigallova and P. Nachtigall, J. Phys. Chem. A, 2003, 107, 10381.
44. D. Nachtigallová, P. Nachtigall and O. Bludsky, Phys. Chem. Chem. Phys., 2004, 6, 5580.
45. E. Garrone, R. Bulanek, K. Frolich, C. O. Areán, M. R. Delgado, G. T. Palomino, D. Nachtigallová and P. Nachtigall, J. Phys. Chem. B, 2006, 110, 22542.
46. C. O. Areán, M. R. Delgado, K. Frolich, R. Bulanek, A. Pulido, G. F. Bibiloni and P. Nachtigall, J. Phys. Chem. C, 2008, 112, 4658.
47. O. Bludsky, M. Silhan and P. Nachtigall, J. Chem. Phys., 2002, 117, 9298.
48. H. Mix, J. Sauer, K. P. Schroder and A. Merkel, Collect. Czech. Chem. Commun., 1988, 53, 2191.
49. V. V. Mihaleva, R. A. van Santen and A. P. J. Jansen, J. Chem. Phys., 2004, 120, 9212.
50. G. Rauhut and P. Pulay, J. Phys. Chem., 1995, 99, 3093.
51. D. J. Donaldson, J. J. Orlando, S. Amann, G. S. Tyndall, R. J. Proos, B. R. Henry and V. Vaida, J. Phys. Chem. A, 1998, 102, 5171.
52. H. G. Kjaergaard, J. Phys. Chem. A, 2002, 106, 2979.
53. P. Nachtigall, M. R. Delgado, K. Frolich, R. Bulanek, G. T. Palomino, C. L. Bauca and C. O. Areán, Mircoporous Mesoporous Mater., 2007, 106, 162.
54. C. O. Areán, M. R. Delgado, C. L. Bauca, L. Vrbka and P. Nachtigall, Phys. Chem. Chem. Phys., 2007, 9, 4657.
55. P. Rejmak, M. Sierka and J. Sauer, Phys. Chem. Chem. Phys., 2007, 9, 5446.
56. V. L. Zholobenko, D. B. Lukyanov, J. Dwyer and W. J. Smith, J. Phys. Chem. B, 1998, 102, 2715.
57. S. Bordiga, G. T. Palomino, C. Pazè and A. Zecchina, Microporous Mesoporous Mater., 2000, 34, 67.
58. E. V. Kondratieva, O. V. Manoilova and A. A. Tsyganenko, Kinet. Catal., 2008, 49, 451.
59. C. O. Areán, A. A. Tsyganenko, O. V. Manoilova, G. T. Palomino, M. P. Mentruit and E. Garrone, Chem. Commun., 2001, 455.
60. J. Sauer, U. Eichler, U. Meier, A. Schafer, M. von Arnim and R. Ahlrichs, Chem. Phys. Lett., 1999, 308, 147.
61. M. W. Anderson and J. Klinowski, J. Chem. Soc., Faraday Trans. 1, 1986, 82, 3569.
62. K. Suzuki, G. Sastre, N. Katada and M. Niwa, Phys. Chem. Chem. Phys., 2007, 9, 5980.

---