Testing a modified model of the Poisson–Boltzmann theory that includes ion size effects through Monte Carlo simulations
Received
11th July 2008
, Accepted 15th October 2008
First published on 20th November 2008
Abstract
In this work we test the validity of a recent modified Poisson–Boltzmann (MPB) theory that includes ion size effects through a Langmuir-type correction. In particular, we will focus on an analytic charge–potential relationship accounting for such effects. Previous electric double layer (EDL) surveys have demonstrated that the inclusion of ions size in classical EDL theories, based on the Poisson–Boltzmann (PB) equation, can yield considerable improvements. In this sense, the theory we analyze assumes that, as a result of the excluded volume, the ion concentration close to the charged surface cannot exceed a fixed value determined by the close packing fraction. This leads to predictions of counterion concentrations (in this region) smaller than the corresponding PB values. In our opinion, it is worthwhile to test the validity of this novel theory. To this end, computer simulations appear as a useful tool for this kind of task. Our results prove that the above-mentioned analytical expression works fairly well for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes and large ions, and its predictions can be considerably improved with certain corrections in the estimation of some key parameters. However, it fails for multivalent electrolytes.
1 electrolytes and large ions, and its predictions can be considerably improved with certain corrections in the estimation of some key parameters. However, it fails for multivalent electrolytes.
1. Introduction
For many decades, the PB equation has been the cornerstone of the classical EDL theory. It has been extensively applied in colloid science, chemical physics as well as other research fields (e.g., semiconductor physics). Its conceptual and mathematical simplicity is responsible for the success of this classical approach. However, certain limitations of this mean field theory were obvious from the beginning. For instance, Stern was the first who noticed that the PB equation predicts unrealistic concentrations of counterions in the vicinity of the charged interface as a result of neglecting the ion dimensions. He tried to overcome this deficiency introducing the notion of the so-called Stern layer.1 However, the direct inclusion of ion size effects in the PB equation dates back to Bikerman, who added an excess term to the ideal chemical potential with this purpose.2 Since then, different corrections to the chemical potential have been proposed.3–9 Other authors have developed alternative approaches, such as lattice-based models,10–13 different modified PB equations14–17 or integral equation theories.18–20
Nowadays ion size effects are still a burning issue in colloid science. For instance, some researchers have recently studied their role in the ion layering at high salt concentrations,17 counterintuitive electrostatic phenomena (e.g. charge inversion20) and the competition of different ions in solutions with electrolyte mixtures.9 The deviations from the PB predictions of the charge–potential relationship have also been looked into in recent times.21–23 In particular, López-García et al. have analyzed a MPB equation that takes the finite ion size into account through a Langmuir-type correction.24 What is more, they have put forward an approximate analytical expression (including volume effects) for the charge–potential relationship. This could indeed be a valuable result since the surface charge density and the electric potential at the outer Helmholtz plane (OHP), usually known as diffuse potential, are key parameters in the description of the EDL. In any case, these authors claim that significant discrepancies with the classical predictions can appear even for typical sizes of hydrated ions (ranging mostly from 0.75 to 1 nm).25 In addition, López-García et al. have also extended their results to a nonequilibrium problem, calculating the effect of ion size on the electrophoretic mobility of a rigid spherical particle.26
In any case, one should keep in mind that the approach and the analytical expression proposed by López-García et al. were developed under certain assumptions. For instance, as a consequence of the excluded volume, the ion concentration in the vicinity of the charged surface cannot exceed a given value (determined by close packing). For that reason the Maxwell–Boltzmann distribution is modified introducing a Langmuir-type correction (as mentioned above). This is certainly an approximation whose validity could deserve further studies. In fact, it leads to predictions in disagreement with other approaches and simulations results. More specifically, monotonic ionic profiles with a saturation value next to the charged surface are reported from such approximation whereas other recent approaches predict non-monotonic profiles at high salt concentrations.17 This feature has also been corroborated by computer simulations.17,27 In addition, other theoretical and simulation results suggest that ion size effects go beyond expected (and intuitive) excluded volume effects. For instance, under certain conditions, the ion concentration in the proximity of the surface predicted by integral equation theories (accounting for ion size) is larger than that predicted by the PB scheme.20,27,28 Consequently, the reliability of the approach devised by the above-mentioned authors should be carefully examined. Computer simulations have become a useful tool for tasks like this in the last decades.
The aim of this work is therefore to test the validity of the analytical charge–potential relationship proposed by López-García et al. by means of Monte Carlo (MC) simulations. We will restrict ourselves to the case of a planar EDL. In our opinion, this is a good reference system because the solution of the PB equation is exact whereas for spherical particles only approximate solutions exist. Consequently, the discrepancies between simulation/MPB results and the classical PB theory can be unequivocally attributed to the inclusion of ion size effects. In addition, the solution for a planar EDL is widely known and even applied to spherical particles if the salt concentration is high enough. This is just when the ion volume effects are expected to be significant. The rest of the paper is organized as follows. First, some features of the so called charge–potential relationship are outlined and also some technical details about the MC simulations carried out in this work. Then, the computer simulation results are presented and compared to the theoretical predictions. Finally, some conclusions are highlighted.
2. Theory and simulations
In order to describe the spatial distribution of ionic species and the electrostatic potential distribution in the vicinity of a spherical macroion immersed in an infinite electrolyte solution, López-García et al. use a MPB approach that includes the volume excluded by the ions. To this end, the authors use a model developed in the 1990s by Adamczyk et al.29–31 which is in turn based on certain theories of the 1950s.32,33 The ionic concentrations and the electric potential profiles are obtained as functions of the parameter cmax, which stands for the maximum attainable concentration of the corresponding ions due to the volume occupied by each one of them (close packing). Considering the Langmuir-type correction for the excluded volume introduced by Adamczyk and Warszysnky,31 the local ion concentration can be expressed as| |  | (1) |
Here Zi and c∞i are the valence and the bulk concentration of the ionic species i, respectively, cmaxi is the maximum attainable concentration of the given ion type, and y and ξ are the dimensionless electric potential and the dimensionless spatial variable, respectively. The dimensionless electric potential is defined as:| | 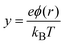 | (2) |
where e is the elementary charge, ϕ(r) is the electric potential, T is the absolute temperature and kB is the Boltzmann constant. The dimensionless spatial variable is ξ = κ(r−a), where a is the radius of the spherical macroion and κ the reciprocal Debye length,| |  | (3) |
Here, ε0 is the permittivity of the free space, εr is the relative permittivity of the solvent and NA is the Avogadro number. In this case, water at room temperature is assumed.
Substituting these dimensionless variables and local ion concentration in the PB equation for a charged spherical particle we obtain
| |  | (4) |
This is the MPB equation that describes the spatial variation of the electric potential for the EDL of a spherical charged particle, considering the finite size of ions.
To solve eqn (4), López-García et al. performed numerical calculations using the network simulation method, and obtained the electrostatic potential and the ion concentration profiles as a function of the distance from the surface of the macroion. These authors also propose approximate expressions (matching the numerical solution) for the charge–potential relationship. In particular, for large values of κa (planar EDL), such relationship turns out to be:
| |  | (5) |
where
σ0 is the surface charge density of the charged wall and
ψd is the diffuse potential. This is the equation that relates the dimensionless diffuse potential and the dimensionless surface charge density and takes ion size into account (for further details we refer the reader to the original paper
24).
The MC simulations carried out in this work are based on a primitive model (PM) of electrolyte, in which ions are considered as charged hard spheres and the solvent is modelled as a continuum with a uniform dielectric permittivity. We applied the Metropolis algorithm to a canonical ensemble for a collection of N ions confined in a rectangular prism (simulation cell) at constant temperature. The simulation cell has the dimensions W×W×L, where a charged plane wall is located at z = 0 and at z = L another impenetrable but uncharged plane wall is placed. Periodic boundary conditions were used in the lateral directions (x and y). The simulation cell contains the ionic electrolyte mixture corresponding to the bulk solution within a counterion excess neutralizing the surface charge of the charged wall to ensure the whole simulation cell is always neutral. The interaction energy between the mobile ions is given by
| |  | (6) |
where
d is the hydrated ion diameter (for all the ionic species), and
rij = |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij
ij| the distance between the ions
i and
j.
Eqn (6) accounts for the hard sphere nature of ions in the PM. The interaction energy of ion
i with the charged wall is
| |  | (7) |
zi is the
z-coordinate of particle
i. Due to the long range of the electrostatic interactions, the energy must be evaluated carefully. In these simulations, we have applied a procedure originally devised by Lekner and improved by Sperb later,
34,35 to which we will refer as the Lekner–Sperb method (
LSM). Lekner adapted the conventional Ewald summation for systems with two-dimensional periodicity as follows. A charge at
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
′ and its periodic replicas in
x and
y generate an interaction potential energy, per elementary charge, at
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
. This potential energy is given by
| | 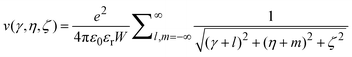 | (8) |
where the following rescaled coordinates have been used
| | | γ = |x−x′|/W, η = |y−y′|/W, ζ = |z−z′|/W. | (9) |
According to Lekner, this interaction potential energy can also be expressed as
| |  | (10) |
where
C is a constant depending on the reference state, and
s is the fast converging series
| |  | (11) |
At large arguments of
s this sum can be truncated due to the rapidly vanishing behaviour of the Bessel function,
K0. Nonetheless, for low values of

the function diverges, and a large number of terms could be required before its truncation. Sperb proposed a solution to this problem,
35 that we have applied together with the truncation criteria developed by Moreira and Netz.
36 Previous studies suggest that the LSM results are practically identical to those obtained with the so-called external potential method (which is not based on Ewald summations).
27 However, LSM simulations are more reliable at low salt concentrations and offers manageable expressions and well established truncation criteria. For these reasons, this method for evaluating energy was preferred.
Each simulation took between 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 180
000 and 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps per particle and the simulation systems were always thermalized before collecting data for averaging. The number of particles was maintained around 100 and for some representative systems it was doubled to check that the cell size was large enough and no important statistical deviations were induced. The acceptance ratio was kept between 0.3 and 0.5. The values of W, L and N vary according to the ion concentrations employed.
000 steps per particle and the simulation systems were always thermalized before collecting data for averaging. The number of particles was maintained around 100 and for some representative systems it was doubled to check that the cell size was large enough and no important statistical deviations were induced. The acceptance ratio was kept between 0.3 and 0.5. The values of W, L and N vary according to the ion concentrations employed.
The diffuse potential can be calculated from the simulated local ion concentrations as
| |  | (12) |
where
ρi(
z) is the local ion density, of the different ionic species (obtained from simulations), at a distance
z from the charged surface. Technically, the integral in
eqn (12) must be evaluated over a finite interval. For this reason, the upper limit is replaced by a cut-off distance,
Lc. This cut-off distance can be chosen to lie anyplace into the solution bulk, where the electroneutrality condition (

) must be satisfied. Nonetheless, it should be noticed that the computed fluctuations of

could be highly amplified due to the factor
d/2 −
z appearing in
eqn (12). To avoid this possible divergence on the
ψd calculation,
Lc must not be too large. In our simulations we employed values of
Lc around 0.5 L.
3. Results and discussion
Monovalent ions
First, the case of monovalent 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ions with the representative diameters 2, 1 and 0.75 nm will be analyzed. In Fig. 1 we show the dimensionless diffuse potential as function of the dimensionless surface charge density for ions of 2 nm, with cmax = 0.2 M (according to López-García et al.) and various salt concentrations (50, 25, 10 and 5 mM). In particular, the curves obtained from eqn (5), our computer simulation results and the PB prediction are plotted. A qualitative agreement between theory and simulation can be observed: each pair of curves (MPB and MC) corresponding to different salt concentrations exhibit a similar trend. However, there are certain quantitative deviations between them. Concerning general aspects, we should stress two features of the theory that are perfectly reproduced by the MC results. First, in a dimensionless charge–potential plot, there is a unique PB curve since the PB charge–potential relationship expressed in this manner does not depend on the salt concentration. However, the expression developed by López-García et al. predicts different curves for each salt concentration (through the ci∞/cmax ratio in eqn (5)), which is completely corroborated by our simulations. Second, the dimensionless diffuse potentials obtained from eqn (5) are larger than the PB values and the differences between them increase with the salt concentration and the dimensionless surface charge density. These features are entirely confirmed by the MC data. In any case, the large dimensionless diffuse potential values obtained at high surface charge densities deserve an additional comment. Given that counterions are strongly attracted to the charged surface, the space close to the macroion is expected to be replete of them. However, it should be kept in mind that the ionic diameter of 2 nm employed is rather large (and even unusual for certain monovalent ions, such as alkaline cations). Consequently, the space near the charged macroion is easily occupied by only a few counterions and turns into a practically inaccessible area to the other ions due to the hard core repulsion between them. Thus, counterions are unable to neutralize properly the surface charge of the macroion and extremely high values of the diffuse potential can be reported.
1 ions with the representative diameters 2, 1 and 0.75 nm will be analyzed. In Fig. 1 we show the dimensionless diffuse potential as function of the dimensionless surface charge density for ions of 2 nm, with cmax = 0.2 M (according to López-García et al.) and various salt concentrations (50, 25, 10 and 5 mM). In particular, the curves obtained from eqn (5), our computer simulation results and the PB prediction are plotted. A qualitative agreement between theory and simulation can be observed: each pair of curves (MPB and MC) corresponding to different salt concentrations exhibit a similar trend. However, there are certain quantitative deviations between them. Concerning general aspects, we should stress two features of the theory that are perfectly reproduced by the MC results. First, in a dimensionless charge–potential plot, there is a unique PB curve since the PB charge–potential relationship expressed in this manner does not depend on the salt concentration. However, the expression developed by López-García et al. predicts different curves for each salt concentration (through the ci∞/cmax ratio in eqn (5)), which is completely corroborated by our simulations. Second, the dimensionless diffuse potentials obtained from eqn (5) are larger than the PB values and the differences between them increase with the salt concentration and the dimensionless surface charge density. These features are entirely confirmed by the MC data. In any case, the large dimensionless diffuse potential values obtained at high surface charge densities deserve an additional comment. Given that counterions are strongly attracted to the charged surface, the space close to the macroion is expected to be replete of them. However, it should be kept in mind that the ionic diameter of 2 nm employed is rather large (and even unusual for certain monovalent ions, such as alkaline cations). Consequently, the space near the charged macroion is easily occupied by only a few counterions and turns into a practically inaccessible area to the other ions due to the hard core repulsion between them. Thus, counterions are unable to neutralize properly the surface charge of the macroion and extremely high values of the diffuse potential can be reported.
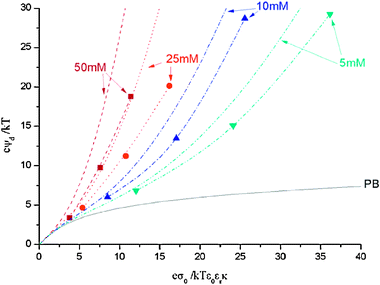 |
| | Fig. 1 Diffuse potential as function of surface charge obtained from simulations (symbols) and theoretical predictions (lines) for 2 nm ions at various salt concentrations: 50 mM (squares and dashed lines), 25 mM (circles and dot lines), 10 mM (up triangles and dash–dot lines), 5 mM (down triangles and dash–dot–dot lines). The lines accompanying the symbols obtained from simulations are just a guide for the eye. PB theory prediction is presented too (solid line). cmax is calculated for a SC arrangement. | |
In Fig. 2 we present the dimensionless diffuse potential as function of the dimensionless surface charge density, now for 1 nm ions with cmax = 1.5 M at different salt concentrations (100, 50, 25, 10 and 5 mM). A good qualitative agreement between theory and simulations is observed again. As in the case of larger ions (Fig. 1), the dimensionless diffuse potentials remain above the PB curve. However, the values of this property are not so large. In fact, for low salt concentrations and/or surface charge densities the MC potentials do not differ significantly from the PB results (in contrast with the large deviations reported for 2 nm). This feature is reasonable since the charged macroion surface charge is more easily neutralized by smaller ions.
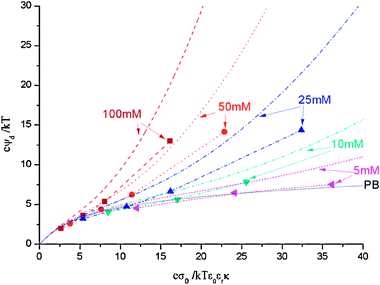 |
| | Fig. 2 Diffuse potential as function of surface charge obtained from simulations (symbols) and theoretical predictions (lines) for 1 nm ions at various salt concentrations: 100 mM (squares and dashed lines), 50 mM (circles and dot lines), 25 mM (up triangles and dash–dot lines), 10 mM (down triangles and dash–dot–dot lines), 5 mM (left triangles and short dashed lines). The lines accompanying the symbols obtained from simulations are just a guide for the eye. PB theory prediction is presented too (solid line). cmax is calculated for a SC arrangement. | |
In Fig. 3 the dimensionless diffuse potential as function of the dimensionless surface charge density is shown for 0.75 nm ions, with cmax = 4 M, at the same salt concentrations that in the case of 1 nm ions. As in the two cases analyzed before, predictions from eqn (5) and simulation results show similar trends and, to some extent, a good qualitative agreement is found once again. As expected, the theory accounting for ion size predicts results above the PB curve. However, under certain conditions (e.g., 5 mM), the simulated diffuse potentials are slightly smaller than their corresponding PB predictions.
 |
| | Fig. 3 Diffuse potential as function of surface charge obtained from simulations and theoretical predictions for 0.75 nm ions at various salt concentrations, cmax is calculated for a SC arrangement. Lines and symbols represent the same as in Fig. 2. | |
From the analysis of the three figures presented for monovalent ions, we can conclude that eqn (5) works reasonably well for large ions and/or high salt concentrations (at least, qualitatively speaking). For the smallest size studied here (0.75 nm), some discrepancies are reported. For instance, unlike the simulations, the theory never predicts dimensionless diffuse potentials under the PB values.
Improving the results for monovalent ions
As stated before, the ion size is included in the MPB theory through cmax (and assuming that cmax is the same for all ionic species, as the PM). The values of cmax corresponding to the effective ion diameters 2, 1 and 0.75 nm are 0.2, 1.5 and 4 M (in round numbers). These values (which were also used by López-García et al.24) can be calculated from| |  | (13) |
which involves the assumption of a simple cubic (SC) crystal (whose packing fraction is 52%). However, other lattices can also be assumed. For instance, we can consider the hexagonal close packed (HCP) structure, whose packing fraction is 74.05%. In such a case, the following approximate values for cmax are obtained: 0.28, 2.13 and 5.69 M (corresponding again to the effective ion diameters 2, 1 and 0.75 nm, respectively). In the light of this observation, the previous theoretical predictions were recalculated with the corresponding correction in cmax and compared again to the simulation data already presented.
In Fig. 4 we show the same simulation data as in Fig. 1 for 2 nm ions but now the theoretical curves are obtained from eqn (5) with cmax = 0.28 M (calculated for a HCP structure). As can be seen comparing with Fig. 1, the agreement between predictions and simulation data is much better. Thus the new assumption about the arrangement of ions can improve the results obtained from eqn (5) considerably.
 |
| | Fig. 4 Diffuse potential as function of surface charge obtained from simulations and theoretical predictions for 2 nm ions at various salt concentrations, cmax is calculated for a HCP arrangement. Lines and symbols represent the same as in Fig. 1. | |
Similarly, in Fig. 5 we present the simulation data for 1 nm ions again. The theoretical predictions have been calculated with the cmax for a HCP structure (2.13 M). As in the previous case, the agreement between theory and simulations improves.
 |
| | Fig. 5 Diffuse potential as function of surface charge obtained from simulations and theoretical predictions for 1 nm ions at various salt concentrations, cmax is calculated for a HCP arrangement. Lines and symbols represent the same as in Fig. 2. | |
In Fig. 6 we finally display simulation results and theoretical predictions for 0.75 nm ions considering the ions form a HCP structure (cmax = 5.69 M). Once more, the agreement between theory and simulations is enhanced. We can therefore conclude that the most reliable results are those obtained for the HCP structure. Consequently, we will only use the cmax values corresponding to a HCP structure hereafter.
 |
| | Fig. 6 Diffuse potential as function of surface charge obtained from simulations and theoretical predictions for 0.75 nm ions at various salt concentrations, cmax is calculated for a HCP arrangement. Lines and symbols represent the same as in Fig. 2. | |
Before ending the discussion of monovalent electrolytes, there is an aspect of eqn (5) that deserves an additional comment. As mentioned before, the dimensionless charge–potential relationships predicted from eqn (5) show very similar features: such curves are above the PB one and always bend upwards with increasing the surface charge density and/or the salt concentration. Our simulations confirm to a great extent such features. However, one should keep in mind that we are dealing with large ions. If smaller sizes are examined, the behaviour of the ψd−σ0 function becomes much richer. There are charge–potential relationships under and above the classical prediction, bending upwards and downwards. For instance, Bhuiyan et al. studied the charge–potential relationship by comparing a MPB equation with density functional theories (DFT) as well as MC simulations.22 In all cases shown therein, the diffuse potential bends downwards with increasing surface charge density. In relation to this, we would like to remark that these authors used an effective ion diameter of 0.3 nm in their calculations. Boda et al. analyzed the charge–potential for different ion diameters (0.2, 0.3 and 0.425 nm) by means of MC and DFT.21 Their results were similar to those obtained by Bhuiyan et al. On the other hand, González-Tovar et al. used the so-called hyper-netted-chain/mean-spherical approximation (HNC/MSA) and predicted both charge–potential relationships bending upwards and downwards.23 In this case, effective ion diameters between 0.425 nm and 0.9 nm were employed, reporting different behaviours in charge–potential curves depending on the ion size. In particular, they found functions that bend downwards for the smaller ion diameters, an inflexion curve for a diameter of 0.6 nm, and functions that bend upwards for larger ions. Finally, Quesada-Pérez et al. tested HNC/MSA through MC simulations and obtained the same inflexion in the potential curves for monovalent ions between 0.425 nm and 0.72 nm.27
Divalent counterions
Now the case of the asymmetric salt 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 will be analyzed. A previously published paper suggests that the electrokinetic behaviour of model colloids does not depend strongly on the coion valence.37 Consequently, the case of divalent coions will not be studied here. In Fig. 7 we present the dimensionless diffuse potential as function of the dimensionless surface charge density for 2 nm ions at different salt concentrations (50, 25, 10 and 5 mM). Unlike the case of 2 nm monovalent ions, the discrepancies between predictions and simulations are now outstanding. The predictions for the dimensionless diffuse potential show lower values and the qualitative differences between theory and simulations are now greater. In particular, the MC results for small surface charge densities are under the PB curve.
1 will be analyzed. A previously published paper suggests that the electrokinetic behaviour of model colloids does not depend strongly on the coion valence.37 Consequently, the case of divalent coions will not be studied here. In Fig. 7 we present the dimensionless diffuse potential as function of the dimensionless surface charge density for 2 nm ions at different salt concentrations (50, 25, 10 and 5 mM). Unlike the case of 2 nm monovalent ions, the discrepancies between predictions and simulations are now outstanding. The predictions for the dimensionless diffuse potential show lower values and the qualitative differences between theory and simulations are now greater. In particular, the MC results for small surface charge densities are under the PB curve.
 |
| | Fig. 7 Diffuse potential as function of surface charge obtained from simulations and theoretical predictions for 2 nm divalent ions at various salt concentrations, cmax is calculated for a HCP arrangement. Lines and symbols represent the same as in Fig. 1. | |
In Fig. 8 we show predictions from eqn (5) and simulation data for a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt made up of 1 nm ions at different concentrations (100, 50, 25, 10 and 5 mM). Compared to the case of 1 nm monovalent ions, the agreement between theory and simulations seems to have disappeared completely and MC data are all under the PB prediction, which should not occur according to eqn (5).
1 salt made up of 1 nm ions at different concentrations (100, 50, 25, 10 and 5 mM). Compared to the case of 1 nm monovalent ions, the agreement between theory and simulations seems to have disappeared completely and MC data are all under the PB prediction, which should not occur according to eqn (5).
 |
| | Fig. 8 Diffuse potential as function of surface charge obtained from simulations and theoretical predictions for 1 nm divalent ions at various salt concentrations, cmax is calculated for a HCP arrangement. Lines and symbols represent the same as in Fig. 2. | |
To end the analysis of divalent counterions, the results from simulations and predictions from eqn (5) for 0.75 nm divalent ions are displayed in Fig. 9 with the same salt concentrations as in Fig. 8. The theoretical dimensionless diffuse potentials are smaller than those obtained for monovalent 0.75 nm ions (Fig. 6) and for divalent 2 and 1 nm counterions (Fig. 7 and 8). However, simulation data remain under the PB curve (as expected). In general, for divalent counterions, the disagreement between theory and simulations is remarkable. As matters stand, we would like to point out a feasible cause for the failure of the theory for divalent counterions.
 |
| | Fig. 9 Diffuse potential as function of surface charge obtained from simulations and theoretical predictions for 0.75 nm divalent ions at various salt concentrations, cmax is calculated for a HCP arrangement. Lines and symbols represent the same as in Fig. 2. | |
A final consideration
In our opinion, ion size correlations can yield two types of very different (and even opposite) effects. The former occurs at extremely high electrolyte concentrations of large ions. Under such conditions, the excluded volume effect could be responsible for the saturation of the ionic profiles near the charge surface. This involves that the predictions of the counterion concentrations (in the vicinity of the surface) must be smaller than the corresponding PB values. We will refer to this situation, which is just one of the main assumptions of the theory analyzed here, as the saturation regime.
The other effect takes place if the saturation regime is not operative. More sophisticated approaches and simulations have proved that, in this other regime, the ion size correlations can lead to counterion concentrations larger than the PB values in the neighbourhood of the charged colloid, in contrast with saturation regime.20 The underlying physical mechanism of this somewhat paradoxical behaviour can be briefly elucidated as follows.28 Let us consider (as reference) a counterion in the proximity of the OHP (see Fig. 10). In a PB picture, other counterions can temporally interpose between the above-mentioned counterion and the colloid. Thus these other counterions screen the attraction experienced by the first one towards the charged surface. In considering the ionic size, however, the space between the charged surface and the first counterion cannot be occupied by others (due to their exclusion volumes). Consequently, the effective attraction between the counterion close to the OHP and the colloidal surface will be stronger than in the PB case (since the screening of other counterions between them will be avoided). The counterion concentration near the particle surface will therefore be larger than that predicted by a PB approach. Messina et al. have also analyzed the role of the excluded volume, but in terms of entropy.38
 |
| | Fig. 10 (a) Some counterions close to the OHP. Let us consider one of them as reference (for example, the one in the middle). (b) In a PB picture, the other counterions can temporally interpose between the reference ion and the charged surface. (c) In considering the ion size, the space between the charged surface and the reference counterion cannot be occupied by others. | |
In any case, our simulations (and previous studies) reveal that the success or failure of the theory analyzed here depends on whether the saturation regime appears or not. On the one hand, large monovalent counterions can reach the saturation regime easily. Thus, the counterion concentrations would be smaller than the PB predictions and the modified model of the PB theory would therefore work properly. On the other hand, the saturation regime would be unlikely for divalent (in general multivalent) counterions since: (i) strong electrostatic repulsions would prevent from high packing fractions; (ii) the number of counterions needed to neutralize the surface would be considerably smaller. As the situation would be far from the saturation regime, the number of ions in the vicinity of the charged colloid might be larger than the PB prediction, in contradiction with the modified model of the PB theory.
4. Conclusions
With the aim to test a modified PB theory that includes ion size effects through a Langmuir-type correction, we have performed MC simulations within a PM of electrolyte to generate numerically the dimensionless diffuse potential as a function of the dimensionless surface charge density, for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes. For 1
1 electrolytes. For 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salts, the theory is found to work appreciably well, particularly for high surface charge densities and/or large ionic sizes. Simulations confirm the existence of diffuse potentials considerably larger than the PB ones. In addition, this technique corroborates that the dimensionless charge–potential relationship does depend on the salt concentration (in contrast with the PB case). In any case, the predictions of the theory can be considerably improved assuming that counterions form a HCP structure instead a simple cubic one. On the other hand, for 2
1 salts, the theory is found to work appreciably well, particularly for high surface charge densities and/or large ionic sizes. Simulations confirm the existence of diffuse potentials considerably larger than the PB ones. In addition, this technique corroborates that the dimensionless charge–potential relationship does depend on the salt concentration (in contrast with the PB case). In any case, the predictions of the theory can be considerably improved assuming that counterions form a HCP structure instead a simple cubic one. On the other hand, for 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salts, the theory dramatically fails. The predictions of dimensionless diffuse potentials above the classic PB relationship are not corroborated by the MC charge–potential functions, which are mostly under such curve.
1 salts, the theory dramatically fails. The predictions of dimensionless diffuse potentials above the classic PB relationship are not corroborated by the MC charge–potential functions, which are mostly under such curve.
Acknowledgements
The authors are grateful to “Ministerio de Educación y Ciencia, Plan Nacional de Investigación, Desarrollo e Innovación Tecnológica (I+D+i)”, Project MAT2006-12918-C05-02, “Consejería de Innovación, Ciencia y Empresa de la Junta de Andalucía”, Projects P06-FQM-01869, P07-FQM-02496 and P07-FQM-02517, as well as the European Regional Development Fund (ERDF) for financial support. A.M.-M. also thanks the “Programa Ramón y Cajal, 2005, Ministerio de Educación y Ciencia-Fondo Social Europeo (RYC-2005-000829)”.
References
- O. Stern, Z. Elektrochem., 1924, 30, 508 CAS.
- J. J. Bikerman, Philos. Mag., 1942, 33, 384 CAS.
- M. J. Sparnaay, Trav. Chim. Pays-Bas, 1954, 77, 872 Search PubMed.
- N. F. Carnahan and K. E. Starling, J. Chem. Phys., 1969, 51, 635 CrossRef CAS.
- T. Boublik, J. Chem. Phys., 1970, 53, 471 CrossRef CAS.
- G. A. Mansoori, N. F. Carnahan, K. E. Starling and T. W. Leland, J. Chem. Phys., 1971, 54, 1523 CrossRef CAS.
- P. M. Biesheuvel and J. Lyklema, J. Phys.: Condens. Matter, 2005, 17, 6337 CrossRef CAS.
- P. M. Biesheuvel, F. A. M. Leermakers and M. A. Cohen Stuart, Phys. Rev. E, 2006, 73, 011802 CrossRef.
- P. M. Biesheuvel and M. van Soestbergen, J. Colloid Interface Sci., 2007, 316, 490 CrossRef CAS.
- I. Borukhov, D. Andelman and H. Orland, Phys. Rev. Lett., 1997, 79, 435 CrossRef CAS.
- V. Kralj-Iglic and A. Iglic, J. Phys. II, 1996, 6, 477 CrossRef CAS.
- K. Bohinc, V. Kralj-Iglic and A. Iglic, Electrochim. Acta, 2001, 46, 3033 CrossRef CAS.
- O. González-Amezcua and M. Hernández-Contreras, J. Chem. Phys., 2004, 121, 10742 CrossRef CAS.
- L. B. Bhuiyan, C. W. Outhwaite and S. Levine, Mol. Phys., 1981, 42, 105.
- S. Levine, C. W. Outhwaite and L. B. Bhuiyan, J. Electroanal. Chem., 1981, 123, 105 CrossRef CAS.
- S. Lamperski and C. W. Outhwaite, Langmuir, 2002, 18, 3423 CrossRef CAS.
- S. Lamperski and L. B. Bhuiyan, J. Electroanal. Chem., 2003, 540, 79 CrossRef CAS.
- S. L. Carnie, D. Y. C. Chan, D. J. Mitchell and B. W. Ninham, J. Chem. Phys., 1981, 74, 1472 CrossRef CAS.
- M. Lozada-Cassou, R. Saavedra-Barrera and D. Henderson, J. Chem. Phys., 1982, 77, 5150 CrossRef CAS.
- M. Quesada-Pérez, E. González-Tovar, A. Martín-Molina, M. Lozada-Cassou and R. Hidalgo-Álvarez, ChemPhysChem, 2003, 4, 234 CrossRef.
- D. Boda, D. Henderson, P. Plaschko and W. R. Fawcett, Mol. Simul., 2004, 30, 37 CrossRef.
- L. B. Bhuiyan and C. W. Outhwaite, Phys. Chem. Chem. Phys., 2004, 6, 3467 RSC.
- E. González-Tovar, F. Jiménez-Ángeles, R. Messina and M. Lozada-Cassou, J. Chem. Phys., 2004, 120, 9782 CrossRef CAS.
- J. J. López-García, M. J. Aranda-Rascón and J. Horno, J. Colloid Interface Sci., 2007, 316, 196 CrossRef CAS.
-
J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, London, 1992 Search PubMed.
- J. J. López-García, M. J. Aranda-Rascón and J. Horno, J. Colloid Interface Sci., 2008, 323, 146 CrossRef CAS.
- M. Quesada-Pérez, A. Martín-Molina and R. Hidalgo-Álvarez, J. Chem. Phys., 2004, 121, 8618 CrossRef CAS.
- M. Quesada-Pérez, E. González-Tovar, A. Martín-Molina, M. Lozada-Cassou and R. Hidalgo-Álvarez, Colloids Surf., A, 2005, 267, 24 CrossRef CAS.
- Z. Adamczyk, P. Belouschek and D. Lorenz, Ber. Bunsenges. Phys., 1990, 94, 1483 Search PubMed.
- Z. Adamczyk, P. Belouschek and D. Lorenz, Bull. Pol. Acc. Chem., 1991, 39, 424 Search PubMed.
- Z. Adamczyk and P. Warszysnky, Adv. Colloid Interface Sci., 1996, 63, 41 CrossRef CAS.
- H. Brodowsky and H. Strehlow, Z. Electrochem., 1950, 63, 262 Search PubMed.
- E. Wicke and M. Eigen, Z. Electrochem., 1952, 56, 551 Search PubMed.
- J. Lekner, Physica A, 1991, 176, 485 CrossRef.
- R. Sperb, Mol. Simul., 1998, 20, 179 CrossRef CAS.
- A. G. Moreira and R. R. Netz, Eur. Phys. J. E, 2002, 8, 33 CAS.
- A. Martín-Molina, M. Quesada-Pérez, F. Galisteo-González and R. Hidalgo-Álvarez, Colloids Surf., A, 2003, 222, 155 CrossRef CAS.
- R. Messina, E. González-Tovar, M. Lozada-Cassou and C. Holm, Europhys. Lett., 2002, 60, 383 CrossRef CAS.
|
| This journal is © the Owner Societies 2009 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes and large ions, and its predictions can be considerably improved with certain corrections in the estimation of some key parameters. However, it fails for multivalent electrolytes.
1 electrolytes and large ions, and its predictions can be considerably improved with certain corrections in the estimation of some key parameters. However, it fails for multivalent electrolytes.
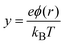




![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij| the distance between the ions i and j. Eqn (6) accounts for the hard sphere nature of ions in the PM. The interaction energy of ion i with the charged wall is
ij| the distance between the ions i and j. Eqn (6) accounts for the hard sphere nature of ions in the PM. The interaction energy of ion i with the charged wall is
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′ and its periodic replicas in x and y generate an interaction potential energy, per elementary charge, at
′ and its periodic replicas in x and y generate an interaction potential energy, per elementary charge, at ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) . This potential energy is given by
. This potential energy is given by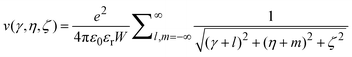


 the function diverges, and a large number of terms could be required before its truncation. Sperb proposed a solution to this problem,35 that we have applied together with the truncation criteria developed by Moreira and Netz.36 Previous studies suggest that the LSM results are practically identical to those obtained with the so-called external potential method (which is not based on Ewald summations).27 However, LSM simulations are more reliable at low salt concentrations and offers manageable expressions and well established truncation criteria. For these reasons, this method for evaluating energy was preferred.
the function diverges, and a large number of terms could be required before its truncation. Sperb proposed a solution to this problem,35 that we have applied together with the truncation criteria developed by Moreira and Netz.36 Previous studies suggest that the LSM results are practically identical to those obtained with the so-called external potential method (which is not based on Ewald summations).27 However, LSM simulations are more reliable at low salt concentrations and offers manageable expressions and well established truncation criteria. For these reasons, this method for evaluating energy was preferred.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 180
000 and 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps per particle and the simulation systems were always thermalized before collecting data for averaging. The number of particles was maintained around 100 and for some representative systems it was doubled to check that the cell size was large enough and no important statistical deviations were induced. The acceptance ratio was kept between 0.3 and 0.5. The values of W, L and N vary according to the ion concentrations employed.
000 steps per particle and the simulation systems were always thermalized before collecting data for averaging. The number of particles was maintained around 100 and for some representative systems it was doubled to check that the cell size was large enough and no important statistical deviations were induced. The acceptance ratio was kept between 0.3 and 0.5. The values of W, L and N vary according to the ion concentrations employed.
 ) must be satisfied. Nonetheless, it should be noticed that the computed fluctuations of
) must be satisfied. Nonetheless, it should be noticed that the computed fluctuations of  could be highly amplified due to the factor d/2 −z appearing in eqn (12). To avoid this possible divergence on the ψd calculation, Lc must not be too large. In our simulations we employed values of Lc around 0.5 L.
could be highly amplified due to the factor d/2 −z appearing in eqn (12). To avoid this possible divergence on the ψd calculation, Lc must not be too large. In our simulations we employed values of Lc around 0.5 L.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ions with the representative diameters 2, 1 and 0.75 nm will be analyzed. In Fig. 1 we show the dimensionless diffuse potential as function of the dimensionless surface charge density for ions of 2 nm, with cmax = 0.2 M (according to López-García et al.) and various salt concentrations (50, 25, 10 and 5 mM). In particular, the curves obtained from eqn (5), our computer simulation results and the PB prediction are plotted. A qualitative agreement between theory and simulation can be observed: each pair of curves (MPB and MC) corresponding to different salt concentrations exhibit a similar trend. However, there are certain quantitative deviations between them. Concerning general aspects, we should stress two features of the theory that are perfectly reproduced by the MC results. First, in a dimensionless charge–potential plot, there is a unique PB curve since the PB charge–potential relationship expressed in this manner does not depend on the salt concentration. However, the expression developed by López-García et al. predicts different curves for each salt concentration (through the ci∞/cmax ratio in eqn (5)), which is completely corroborated by our simulations. Second, the dimensionless diffuse potentials obtained from eqn (5) are larger than the PB values and the differences between them increase with the salt concentration and the dimensionless surface charge density. These features are entirely confirmed by the MC data. In any case, the large dimensionless diffuse potential values obtained at high surface charge densities deserve an additional comment. Given that counterions are strongly attracted to the charged surface, the space close to the macroion is expected to be replete of them. However, it should be kept in mind that the ionic diameter of 2 nm employed is rather large (and even unusual for certain monovalent ions, such as alkaline cations). Consequently, the space near the charged macroion is easily occupied by only a few counterions and turns into a practically inaccessible area to the other ions due to the hard core repulsion between them. Thus, counterions are unable to neutralize properly the surface charge of the macroion and extremely high values of the diffuse potential can be reported.
1 ions with the representative diameters 2, 1 and 0.75 nm will be analyzed. In Fig. 1 we show the dimensionless diffuse potential as function of the dimensionless surface charge density for ions of 2 nm, with cmax = 0.2 M (according to López-García et al.) and various salt concentrations (50, 25, 10 and 5 mM). In particular, the curves obtained from eqn (5), our computer simulation results and the PB prediction are plotted. A qualitative agreement between theory and simulation can be observed: each pair of curves (MPB and MC) corresponding to different salt concentrations exhibit a similar trend. However, there are certain quantitative deviations between them. Concerning general aspects, we should stress two features of the theory that are perfectly reproduced by the MC results. First, in a dimensionless charge–potential plot, there is a unique PB curve since the PB charge–potential relationship expressed in this manner does not depend on the salt concentration. However, the expression developed by López-García et al. predicts different curves for each salt concentration (through the ci∞/cmax ratio in eqn (5)), which is completely corroborated by our simulations. Second, the dimensionless diffuse potentials obtained from eqn (5) are larger than the PB values and the differences between them increase with the salt concentration and the dimensionless surface charge density. These features are entirely confirmed by the MC data. In any case, the large dimensionless diffuse potential values obtained at high surface charge densities deserve an additional comment. Given that counterions are strongly attracted to the charged surface, the space close to the macroion is expected to be replete of them. However, it should be kept in mind that the ionic diameter of 2 nm employed is rather large (and even unusual for certain monovalent ions, such as alkaline cations). Consequently, the space near the charged macroion is easily occupied by only a few counterions and turns into a practically inaccessible area to the other ions due to the hard core repulsion between them. Thus, counterions are unable to neutralize properly the surface charge of the macroion and extremely high values of the diffuse potential can be reported.







![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 will be analyzed. A previously published paper suggests that the electrokinetic behaviour of model colloids does not depend strongly on the coion valence.37 Consequently, the case of divalent coions will not be studied here. In Fig. 7 we present the dimensionless diffuse potential as function of the dimensionless surface charge density for 2 nm ions at different salt concentrations (50, 25, 10 and 5 mM). Unlike the case of 2 nm monovalent ions, the discrepancies between predictions and simulations are now outstanding. The predictions for the dimensionless diffuse potential show lower values and the qualitative differences between theory and simulations are now greater. In particular, the MC results for small surface charge densities are under the PB curve.
1 will be analyzed. A previously published paper suggests that the electrokinetic behaviour of model colloids does not depend strongly on the coion valence.37 Consequently, the case of divalent coions will not be studied here. In Fig. 7 we present the dimensionless diffuse potential as function of the dimensionless surface charge density for 2 nm ions at different salt concentrations (50, 25, 10 and 5 mM). Unlike the case of 2 nm monovalent ions, the discrepancies between predictions and simulations are now outstanding. The predictions for the dimensionless diffuse potential show lower values and the qualitative differences between theory and simulations are now greater. In particular, the MC results for small surface charge densities are under the PB curve.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salt made up of 1 nm ions at different concentrations (100, 50, 25, 10 and 5 mM). Compared to the case of 1 nm monovalent ions, the agreement between theory and simulations seems to have disappeared completely and MC data are all under the PB prediction, which should not occur according to eqn (5).
1 salt made up of 1 nm ions at different concentrations (100, 50, 25, 10 and 5 mM). Compared to the case of 1 nm monovalent ions, the agreement between theory and simulations seems to have disappeared completely and MC data are all under the PB prediction, which should not occur according to eqn (5).


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes. For 1
1 electrolytes. For 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salts, the theory is found to work appreciably well, particularly for high surface charge densities and/or large ionic sizes. Simulations confirm the existence of diffuse potentials considerably larger than the PB ones. In addition, this technique corroborates that the dimensionless charge–potential relationship does depend on the salt concentration (in contrast with the PB case). In any case, the predictions of the theory can be considerably improved assuming that counterions form a HCP structure instead a simple cubic one. On the other hand, for 2
1 salts, the theory is found to work appreciably well, particularly for high surface charge densities and/or large ionic sizes. Simulations confirm the existence of diffuse potentials considerably larger than the PB ones. In addition, this technique corroborates that the dimensionless charge–potential relationship does depend on the salt concentration (in contrast with the PB case). In any case, the predictions of the theory can be considerably improved assuming that counterions form a HCP structure instead a simple cubic one. On the other hand, for 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salts, the theory dramatically fails. The predictions of dimensionless diffuse potentials above the classic PB relationship are not corroborated by the MC charge–potential functions, which are mostly under such curve.
1 salts, the theory dramatically fails. The predictions of dimensionless diffuse potentials above the classic PB relationship are not corroborated by the MC charge–potential functions, which are mostly under such curve.
