A tutorial on multivariate calibration in atomic spectrometry techniques

Abstract

Coupling multivariate regression methods to atomic spectrometry is an emerging field from which important advantages can be obtained. These include lower workloads, increased laboratory turnarounds, economy, higher efficiency in method development, and relatively simple ways to take account of complex interferences. In this paper four typical regression methods (ordinary multiple linear regression, principal components regression, partial least squares and artificial neural networks) are presented in a practice-oriented way. The main emphasis is placed on explaining their advantages, drawbacks, how to solve the latter and how atomic spectrometry can benefit from multivariate regression. Finally, a retrospective review considering the last sixteen years is made to present practical applications on: flame-, hydride generation-, electrothermal-atomic absorption spectrometry; inductively coupled plasma spectrometry and laser-induced breakdown spectrometry.

---

1. Introduction

Measurement of trace metals has traditionally been performed by atomic spectrometric techniques, among which electrothermal atomic absorption spectrometry (ETAAS), inductively coupled plasma atomic emission spectrometry (ICP-AES) and inductively coupled plasma mass spectrometry (ICP-MS) stand out.¹ In particular, ETAAS shows good sensitivity, unrivalled specificity and broad applicability (providing an appropriate sample pre-treatment is performed). Nevertheless, this should not obscure the fact that there are still several issues that complicate its implementation, namely sample preparation, optimisation of the atomiser temperature, spectral and/or chemical interferences and calibration. The last item refers to how the standards are prepared and measured to fit the samples best and, hopefully, behave like them. Regarding ICP, its multi-elemental analysis capability is of great interest in many studies, and it is therefore used widely. However, matrix interferences still represent a severe problem for this technique, the high concentrations of easily ionisable elements being the main cause. Moreover, both ETAAS and ICP suffer important problems when solid samples are introduced directly into the atomisation systems (slurry-based techniques). In this case the slurry/sample preparation must be optimised carefully (e.g., including an exhaustive study on the operational conditions) to reduce matrix interferences and/or atomisation problems. Overall, conventional method development and optimisation are difficult, time-consuming, labour-intensive, costly and not totally efficient in all cases (despite many excellent results having been published).²

Nowadays chemometric methods offer efficient and powerful alternatives to complement/refine classical working procedures to either optimise a method or/and develop calibration models. This tutorial will focus only on the latter issue, as optimisation using experimental designs or evolutionary algorithms (simplex, evop, etc.) has become routine in many fields within analytical chemistry. On the contrary, despite the idea of combining multivariate regression and atomic absorption spectrometry not being new, and proving to yield cheap analytical methodologies, being environmentally friendly (because of a lower consumption of reagents, atomisers, modifiers, etc.), relatively fast and without trial and error assays, not many published papers can be found on this issue.

Calibration is defined as the operation that determines the functional relationship between measured values (e.g., signal intensities, absorbances (at particular signal positions), wavelengths) and analytical quantities characterizing types of analytes and their amount (content, concentration). Calibration includes the selection of the model, the estimation of the model parameters as well as their errors, and their validation.³

Several aspects must be underlined from the definition.

(i) Calibration is an empirical process and, accordingly, ad hoc.

(ii) Calibration leads to a functional relationship; this means that a given function (model) can be excellent for us and disastrous for other colleagues. Clearly, issues (i) and (ii) preclude the existence of universally good solutions. Further, as Mark pointed out in his practice-oriented book,⁴ calibrations do not exist by themselves: they are intimately intertwined with the nature of the samples and with the characteristics of the spectrophotometers that analysts use.

(iii) Selection of the proper function (model) is, often, a highly difficult matter. There are so many possible options that the analyst can feel overwhelmed and it might be tempting to just press a button in any software and forget the very basic principles underlying (correct application of) those models. Using Mark’s words again, such mystique related to the calibration process yielded SCSEAN (“super-calibrate-statistic-expeditions-algorithm-ad-nauseous”). This means that one should apply the simplest models possible (in mathematics, this is called parsimony) and only dig into more complex approaches when it is required by the problem at hand. According to Meloun et al.⁵ all regression diagnostics should examine the “regression triplet” (data, model, method) to assess the data quality for a proposed model, the model quality for a dataset and the fulfilment of the method assumptions.

(iv) Validation is a critical issue since it is the step of the model-development process that assesses model performance. First, and far from trivial, it has to be verified that the assumed model, often a straight line, is correct, i.e. that the experimental standards do define a true straight line. Some people would argue this is quite simple because “only” (?) the correlation coefficient and a scatter plot of the samples (e.g. absorbance versus concentration) are required. Nevertheless, remember that a high correlation coefficient does not necessarily imply that the points follow a straight line, and that many calibration plots seen these days are based on a scarce number of experimental points and, therefore, any decision is risky. Just consider how many “regression lines” have the form of a parabola on inspecting the residuals. Validating a proposed model is far from trivial and there is an overwhelming number of different statistics that may be applied in different situations; two excellent reviews covered some of them.^5,6

Then, once the chemist has evidence enough to support the straight line behaviour, the average error of the regression line has to be compared to his/her (client) needs. Is it low enough? Has it to be reduced? If it is fine, then he/she should test/validate the assumption. This means that he/she should analyse known samples (CRMs would be welcome) and test how good results are with that particular regression line (model). If they are fine, great!, then the model can be used routinely (provided it is tested periodically to verify that it remains valid).

If things are not simple when working with univariate data, they can be a nightmare in multivariate regression. It is worth noting that when a model/calibration (even the simplest one) has proved valid it is so only for the type of samples used for validation. In effect, any calibration is only acceptable as long as it is applied to samples for which it proved to yield good results.⁶ Some typical questions are: was the calibration set large enough to bracket future unknowns?; was its chemical variability large enough?; was variability at the validation set large enough to represent what can be obtained in routine samples?; will all samples be treated equally?; are the sample matrices always “similar”? All these have to be considered under the term validated calibration (validated model).

The aim of this paper is to present an introductory tutorial where the very basics of several well-known and broadly applied multivariate calibration methods are presented to atomic spectroscopists. They are explained sequentially in a practice-oriented way. Each new methodology is presented as a consequence of the shortcomings of the previous one. Mathematics have been kept to a minimum in order to simplify readability by unskilled (on chemometrics) analysts. Whenever possible, other tutorials or reviews are referred to in order to cope with more technical aspects and much emphasis is placed on explaining the advantages, requirements and limitations of the calibration methods studied hereinafter. Different from other tutorials on similar chemometric subjects, the present paper gives a review with practical applications where atomic spectrometry measurements (FAAS, ETAAS, ICP, etc.) were combined with multivariate calibration, restricted to the last sixteen years (1990–2006).

2. Classical calibration

Parsimony was introduced in the previous paragraphs as a positive issue. Is it worth, then, discussing other methods than the widely known adjustment to a straight line by the ordinary least squares (univariate) regression—OLSR—method? Well, it all depends on the problem at hand and whether it can be reasonably assumed that the basic principles of OLSR hold true. Their profound study is beyond the scope of this work and the reader is highly encouraged to review the references cited herein (and/or many other excellent publications). Critical issues to be addressed when constructing traditional OLSR calibration are whether errors on the independent variable (usually concentration, c, on the abscissa) can be discarded and if the dependent variable (usually absorbance, on the ordinate) is affected only by random errors (furthermore, they should be of the same order for any c), and also whether the experimental working range yields a straight-line behaviour. There are some other points to be considered as whether the wavelength is selective enough for the analyte. This means that there should exist a unique relation between the signal (peak height, peak area, etc.) and the concentration, without any other contribution other than a constant background. Note that unresolved peaks and interferences may bias the predictions.⁷

Many real situations do not lead to positive answers to all previous questions and, so, will present serious problems when classical calibration is performed. Just as an example, can errors on the concentrations be neglected when preparing ppb or ppt standards? Can concomitants be controlled/avoided? One solution (employed by different atomic spectroscopists, as will be presented later) consists in including known amounts of the interferents in the standards during their preparation and evaluating their participation in the signal being measured. This can be made by multiple ordinary linear least squares regression, MOLSR, which is the natural extension of OLSR and (typically) corresponds to the generalized Lambert–Beer–Bouguer’s law.

3. Multiple ordinary least squares regression

3.1. Generalization of the Beer’s law

As is well-know, generalizing the Lambert–Beer–Bouguer’s law implies that all species contributing to the total absorbance have to be known. Moreover, in order to solve the system of equations a wavelength uniquely characterizing each species should preferably be found. In many non-trivial real applications this requirement is not fulfilled and it limits the general applicability of this otherwise “simple” approach.

Interestingly, note that measuring a signal at different wavelengths is multivariate analysis (and the spectral data has to be represented by vectors, also termed first-order data⁷). In principle, as many instrumental wavelengths as interferents contributing to the measured signal are required, but since the interfering effects can be complex it may be advisable to measure absorbances at some additional wavelengths. This is called redundancy and, sometimes, it can be advantageous in order to evaluate interaction between interferents, significance of the coefficients, etc.

Multiple ordinary least squares regression (MOLSR) may be a good option in atomic spectrometry because quite often the samples undergo a previous treatment (acid digestion, ashing, etc.) which can somewhat “simplify” the final matrix. However, important drawbacks of this approach are identification of all concomitants in the unknown samples and/or their interactions, which might be almost impossible, and, of course, the increased experimental workload in order to quantify them (mainly on monoelemental techniques yielding transient signals, such as ETAAS).

Fortunately, these pitfalls can be overcome easily by generalizing the idea of “multiple wavelengths”. In most circumstances an atomic peak is registered and, indeed, such a peak is multivariate in nature (absorbance versus time) so it can be treated as any other typical molecular spectrum, where multivariate regression methods are applied frequently. Thus, it is the overall peak (its shape, height, total area, etc.) that becomes affected directly by concomitants and it should be possible to model it. The term “model” is used here in a loose sense but it immediately links the atomic peak with the initial definition of calibration. Recall that in univariate regression an empirical model relates a physical measurement (absorbance) to a cause (concentration). It follows that the whole atomic peak can be related to the concentration of the analyte and, maybe, of the concomitants. The only point here is to realize that there are no conceptual differences between the model given by c = 0.53 + 0.8 × A (λ) (a unique absorbance measured at a given λ) and the model given by c = 0.63 + 0.6 × A (t), where now the absorbance is measured at time t of the atomic peak (registered at a given λ).

The main advantage of the latter approach is that the use of the whole atomic peaks constitutes a straightforward way to implement multivariate regression and it generalizes the Lambert–Beer–Bouguer’s law in atomic spectrometry. According to Fig. 1 and using a classical formulation, we can write:

a(t₁) = c₁ × s₁(t₁) + c₂ × s₂(t₁) + … + c_k × s_n(t₁) a(t_j) = c₁ × s₁(t_j) + c₂ × s₂(t_j) + … + c_k × s_n(t_j)

To simplify understanding think of s₁(t₁) as the typical ε₁(λ₁) absorptivity term on the Lambert–Beer–Bouguer’s law. In order to reduce the number of indexes, we can use matrix notation and so:

a = c₁ × s₁+…+c_n·s_n = S·c, or a = S·c + e (1)

if a vector of random noise (random error, or e) is considered. Bold, lower case letters denote data vectors and bold, upper case letters denote data matrices.

Fig. 1 Decomposition of an atomic peak on its different components and related basic terms used throughout the text.

Since, in general, more than one standard is used to calibrate, eqn (1) becomes:

A = C × S + E (2)

where the matrix of absorbances (= A) has k rows (each row is an atomic peak for each k standard) and j columns (measuring times, j =1, 2,…, j) (i.e., A_(kxj)), the matrix of concentrations (= C) has k rows (= number of standards) and n columns (= absorbing species, i = 1, 2,…, n) (i.e., C_(kxn)), the matrix of the pure unit-concentration spectra or “regression coefficients” (= S) has n rows (= pure spectral atomic peak for each absorbing species, i = 1, 2,…, n) and j columns (= measuring times) (i.e., S_(nxj)) and, finally, E is a matrix containing experimental random errors, E_(kxj).

This formulation is usually termed the “classical” regression model⁸ because the absorbance is defined as a function of the pure spectra (unit concentrations) of the absorbing species and their concentrations, and therefore the concentrations of an analyte in several unknown samples are sought by measuring their corresponding atomic peaks. Therefore, once matrix S, containing the pure temporal profile for each absorbing species, unit concentration, was calculated in the calibration stage the concentrations on the unknowns are predicted using eqn (3).

C = S⁺ × a (3)

Here, a is the atomic peak registered for each unknown and S⁺ is the Moore–Penrose pseudo-inverse matrix (which is required because division is not defined for matrices; in its simplest form S⁺ = (S^T × S)^–1 × S^T) (the superscripts (^T) and (^–1) mean transpose of the matrix and inverse of the matrix, respectively).

3.2. Inverse regression

Despite the “classical” formulation seeming straightforward for most spectroscopists, it is not always the most appropriate one because, in general, the aim is to predict the concentration.⁶ Indeed, we all experienced the same question in current univariate regression; we fit something like A = a + b × C (a = intercept, b = slope) but, then, we want to predict the concentration, C, in an “inverse way”. This leads to severe statistical problems, not the lowest one being the fact that all equations to evaluate the standard error of the predicted values are only (good) approximations. Hence, there are several reasons why we recommend the so-called inverse methods in multivariate regression. These are as follows.

(i) Formulae get simplified and interpretations are simpler (not a trivial advantage in complex models).

(ii) Inverse models treat directly analyte concentrations as a function of spectral measurements^6,8 (not the opposite, as classical calibration does).

(iii) It was shown in several studies dealing with molecular spectroscopy (with a uniform distribution of the calibration standards representing well future unknowns) that prediction uncertainties were lower using the inverse approach (see, for example, Martens and Martens⁹ and Brereton⁶ for more discussions). Whether this can occur in atomic spectroscopy remains to be studied formally.

(iv) It has been proved that inverse models cope better with noise in the spectra so their predictions are better than those of “classical” models.⁸ The spectral variables now act as the “signals” from where the concentration is sought, hence random errors are permitted, as opposed to with classical calibration. Inverse regression is, accordingly, a way to comply with the critical requirement of the least squares criterion that there should not be errors (not even random) in the “independent” variables (whatever they are). This can be understood more easily if it is considered that nowadays, instruments are becoming so precise that random errors (uncertainty) on standards preparation might be of the same order as those from signal measurement. For instance, around 1% uncertainty can be expected in standards preparation (weighting and diluting) and around 5% in ETAAS measurement uncertainty of aqueous standards (around 1% for ICP techniques), so 1% is not negligible compared with 5%. Therefore, the “classical” calibration formulation (where error on the abscissa is not allowed) may not be correct because a more appropriate assumption would be that errors are present in the concentrations⁶ since they cannot be neglected. This has to be studied for each particular case. Unfortunately, the equations to evaluate the standard error of the predicted values are still (good) approximations.

(v) A major advantage of inverse methods is that concomitants do not participate explicitly in the equations (contrary to the “classical” applications of the Lambert–Beer–Bouguer’s law), which enables us to calibrate considering accurate concentrations only for the single analyte that we are interested at.⁸ Nevertheless, despite the fact that exact concentrations of the concomitants are not required it is necessary to vary them throughout the standards to increase the real variance modelled by the regression. The fact that only the concentrations of the analyte are needed may be quite surprising because c₁, c₂,…, c_k in the generalized Lambert–Beer–Bouguer’s law (eqn (1) and related explanations) are explicity considered on the equations. Fortunately, algebraic transformations can modify such a dependence to one based on the s_i(t_j) values (analogous to the ε values when working with the Beer’s law, see Mark⁴ for a simple understandable example), which are the regression coefficients.

Therefore, hereinafter, equations will refer to the inverse models (unless otherwise stated). As an example, the inverse calibration model for the example given in eqn (1) above is:

c = M × b + e (4)

where c and e are the analyte concentrations and random error vectors, respectively, of (k × 1) dimensions; M is the matrix of the measured spectra, with k rows (= samples) and j columns (= measuring times), and vector b (j × 1) contains the model regression coefficients. Prediction of new samples uses the same equation although with the corresponding measured spectral data and the (calibration-derived) b vector. Note that matrix M contains the overall atomic peaks for all calibration/standards/unknown samples and that no “distribution” among the different components that can contribute to each peak profile is required.

In addition to the five reasons above justifying preference of the “inverse” regression over the “classical” one (more technical details can be found elsewhere, e.g. see Olivieri et al.⁸ and Mark⁴ for a simple introduction) two practical motivations can be further underlined.

(i) Except for a theoretical perfect regression (i.e., only Gaussian random errors in the measured signal) the regressions “absorbance on concentration” and “concentration on absorbance” are not equivalent.¹⁰ In univariate regression this can be solved by weighting both the dependent and independent variables and performing iterative calculations¹¹ or applying bivariate least-squares regression.¹² In multivariate regression this problem has been addressed as well, although focused in principal components regression (a technique to be explained in Section 4.1).¹³ Inverse regression yields the solution in terms of the experimental atomic peak that we can register. See Brereton⁶ for a nice general-purpose example.

(ii) Spurious spectral effects not easy to (explicitly) account for, which may be present in the measurements, can be corrected for. In mathematical terms, it is said that the true signal and the noise are orthogonal and this would be implicit in the coefficients yielded by the models.⁸

3.3. Collinearity and overestimation

A critical issue regardless of the formulation considered (classical or inverse) is that there are severe restrictions to generalization of the MOLSR method. Going back to eqn (4), it is clear that the regression coefficients (b vector) have to be calculated on the calibration stage (as has always been the case even for OLS simplest applications). The solution is given by eqn (5):¹⁴

B = (M^T × M)^–1 × M^T × c (5)

Here new problems (the same as with eqn (3)) appear because since a matrix must be inverted, the algebraic requisite that its determinant has to be non zero must be verified. Put in other words, the matrix has to be non-singular. Singularity occurs whenever any independent variable (predictor is a preferred term: here any measuring time at which the atomic peak is recorded) is a perfect linear combination of other independent variables.¹⁴ From an intuitive point of view any spectroscopist knows the general appearance of an atomic peak because absorbance at instant t + 1 is clearly related to instant t, and so forth. This is called collinearity and yields singular data matrices. Situations where the matrix is not singular but is almost (a very low determinant) yield ill-conditioned matrices where too unstable estimates of the regression coefficients, which may be unreasonably large or have the wrong sign, are obtained. They are easy to detect because the associated variances are very large.^6,11 Recall here that such coefficients are purely mathematical, they may have no chemical meaning at all.^5,6,15

Recording the atomic peak using a large number of predictors, currently anything between 30 and 100 (even more), leads to a practical problem because in most cases many fewer standards are measured for calibration. In traditional terms, we would say that fewer equations are available than predictors and, so, fewer equations than unknown regression coefficients (think, for instance, of classical calibration using the generalized Lambert–Beer–Bouguer’s law). This is an overestimated regression model.⁵ In that case, M^T × M cannot be inverted and hence, even though the matrix was not singular, no unique solution would be obtained.¹⁴

To conclude, variables are collinear if there are high correlation or other near or exact linear relations among them.⁹ This problem cannot be solved even when the number of standards is increased and it is common to both “classical” and “inverse” formulations. It also leads to the pragmatic conclusion that MOLSR inverse models do not exhibit real advantages over classical models.⁶ Overestimation can be overcome by increasing the number of standards to, at least, the number of wavelengths or by selecting a very reduced set of uncorrelated predictors (“independent” variables) to perform MOLSR. Although the idea is simple, there is not a broadly accepted way to reach that set. In many commercial softwares backward and forward procedures, where the variables are being discarded or introduced successively, are available but they still have problems. See Caulcutt¹⁵ for more detailed explanations.

4. Regression methods based on data compression

It becomes apparent from the previous section that we would be interested in using as much information on the atomic peak as possible although without the problems caused by collinearity and/or the overdetermined system of equations.

There are several standard ways to handle both problems in the chemometrics field. All can be covered by the “data compression” heading. Two main approaches became popular:⁹ to use MOLSR on a set of a few carefully selected variables (pointed out above) and to regress the analyte concentrations onto a few linear combinations of the original predictors (those combinations are called components, factors or latent variables). In both cases the collinearity problem is solved and the final prediction equation is stable. In general, the second alternative is preferred. According to Martens and Martens⁹ the basic idea is that by using these new variables (linear combinations or factors) in the appropriate regression equations irrelevant and unstable information is avoided and only useful spectral information is employed. In addition, many times, a sound chemical interpretation is also possible with the aid of simple plots.

For the purpose of this tutorial only two classical, broadly applied methods will be discussed briefly: principal components regression and partial least squares regression. Both overcome multicollinearity problems by concentrating the atomic peak spectral information onto a reduced number of factors (this is termed rank reduction). The inverse formulation will be presented as it is typical of the chemometrics literature (the advantages reviewed in Section 3.2 become real).

4.1. Principal components regression

Principal components regression (PCR) is a popular, intuitive technique for developing regression models in systems where there is are a good deal of linear relationships (collinearity or covariance) in the predictors (independent variables). PCR works by, first, decomposing the set of predictors into its principal components (PCs), and then regressing the PC scores against the concentration of the analyte.¹⁶

Description of PCA (principal components analysis) is outside the scope of this paper. Here, only a recapitulation is given to simplify readability and interested readers are encouraged to either references 9,14 and 16 or some recent tutorials from Brereton,⁶ Geladi^17,18 or Woldet al.¹⁹ PCA is a mathematical process by which a data matrix is decomposed on a reduced set of two simpler and independent matrices. One contains information related to the samples (the scores matrix, T) whereas the other contains information related to the variables (the loadings matrix, P). Each row on T (i.e., t_i) and its corresponding column on P (i.e., p^T_i) constitute a principal component, PC. Hence, for a mean centred data matrix of atomic peaks, M = T × P^T + E, where the symbols M and E have the same meanings as in previous sections. Mean centring the data matrix is a common data pre-treatment which consists in subtracting the average value of a column from all values in that column. It is used to avoid the PCs being affected by the different metrics and/or ranges that can be associated to each variable (e.g., a variable whose absorbances range between 0.05–0.15 is not necessarily less important than another one varying from 0.50 to 0.60) and it has to be applied before proceeding with any multivariate technique.

Graphically, the PCs can be visualized as a new set of (convenient) new variables with several important properties: (i) they are orthogonal, i.e., the information explained by a PC is not present in the other PCs although this somewhat depends on the scaling being used;⁶ (ii) they are obtained successively so that the first PC explains most of the information, the second less (but more than the 3rd), and so forth; (iii) in general, a very reduced number of PCs (2, 3, 4,…) can explain almost all the information we had in the original set of atomic peaks. It derives from the latter property that random noise and unrelevant spectral artifacts are left out for the last PCs, which is highly advantageous.

PCA, and so PCR, yields two essential benefits: the number of variables is reduced dramatically (it can well happen that the initial set of 100 variables defining each atomic peak reduces to only 3 or 4 PCs) and they will be uncorrelated. Therefore, once the PCs are extracted the regression coefficients (b, see eqn (6)) can be calculated. Finally, the analyte concentration for an unknown sample can be predicted using eqn (7), where x is the (mean centred) atomic peak measured for the unknown.

B = P × (T^T × T)^–1 × T^T × c (6)

c_unknown = x × b (7)

How many PCs have to be considered is still a matter of discussion (see, for example, Martens and Martens,⁹ Massart et al.¹⁴ and Brereton⁶ for some options) but it is generally recommended to introduce some more PCs than those strictly required to describe M (the matrix of atomic peaks).

Unlike MOLSR, it is advantageous to use PCR when there are many fewer samples than variables in the regression problem. In the case where all PCs were retained in the model (which is very rarely the case), the predictions would be identical to those from MOLSR (at least in the case of more samples than variables). In some sense, it can be seen that the PCR model ‘converges’ to the MOLSR model as PCs are added¹⁶ (the more PCs, the less reduction in the number of variables and, so, the more similar the information used for both models).

Disappointingly, not all problems can be removed by applying PCR. The main issue is that although PCA do explain very well the spectral atomic peaks, it is not mandatory that the first PCs are useful to describe the concentration of the analyte. For instance, if we have a severe spectral artifact or an incomplete/interfered atomization on several samples, it may appear on the first PCs, but it will not be very useful to predict the analyte. What if a minor PC happens to be really important for predicting the concentration? In general, the first problem is not too risky as one will only have to increase the complexity of the model (i.e., add more PCs to the PCR model) to get good predictions, but the second problem is more complex because, in general, the latest PCs are discarded as they are supposed to contain only noise, hence the really useful information becomes lost unexpectedly.²⁰ A classical and reader-oriented paper from Sutter et al.²¹ deals with the selection of the proper number of components. More recently, Meloun et al.⁵ have reviewed the generalized principal component regression method that may be a potential solution to considering only relevant PCs for predicting the concentrations of analyte of interest. Further, Martínez et al.¹³ presented a PCR method where the uncertainties in the reference concentration and in molecular spectroscopic measurements were taken into account.

4.2. Partial least squares regression

In order to solve these last difficulties we have to recourse to a technique called partial least squares regression (PLSR). It was developed by Herman Wold during the 1960s and 1970s to address problems in econometric path-modelling^22–24 but became popular first in chemometrics. Two recent papers^25,26 review these early developments and provide a detailed chronological overview. Only about 15 years ago PLSR attracted statisticians’ attention^27,28 as it generalizes and combines features from PCR and MOLSR and proves particularly useful when a dependent variable (analyte concentration) has to be predicted from a (very) large set of (highly) correlated predictors.

The idea underlying PLSR is simple once PCR has been discussed, although the correct mathematical formulation is far more complicated. It turned out that PCR might either introduce “unuseful” components to evaluate the concentration of interest or let important ones out of the model. To avoid this, why not to calculate some new components (instead of the classical PCs) with the requisite that they are maximally correlated to the concentration of the analyte? In this way, we can simultaneously extract not only the most important information of the atomic peaks but the information which is really useful to get good predictions on the unknowns. This is done in an iterative process which has been described in detail many times (see, for example, McLennan and Kowalski,²⁹ Brereton⁶ or Woldet al.¹⁹ for a very simple approach, or any of the textbooks cited throughout this work). Here, it was decided not to develop a detailed formulation for the sake of simplicity, just to present the final equation for the regression coefficients (eqn (8)) and how to predict the analyte concentration on the unknown sample (eqn (9)).

B = W × (P^T × W)^–1 × (T^T × T)^–1 × T^T (8)

c_unknown = x × b (9)

where W is the so-called matrix of weights which, precisely, holds the relationship between the predictors (also termed “X-block”, mean centred atomic peaks) and the predictands (also termed “Y-block”, analyte concentration). Strictly speaking, matrices T and P are not the same as those shown for PCA and PCR although they can be thought of as PCA scores and loadings that have been adequately rotated to be more relevant for predicting c or Y-block.²⁹

One very important fact in PLS is that it supports errors both in the X- and Y-blocks.⁶ Besides, PLSR models lead to relatively simple graphs which may yield an enormous amount of visual information that, many times, can be interpreted chemically (this is not always fully exploited). Also, anomalous samples, curved distribution of samples, etc., can be visualized. Some examples are presented next.

A first critical step in any model development is to check for outlier samples since they can strongly bias the model. Many efforts should be devoted to assessing this issue. In general, a preliminary model is obtained and visual inspection of some typical plots and statistics diagnostics is carried out. A recent review details many statistics⁵ and they will not be repeated here (despite the fact that they were defined for MOLSR, they are of general applicability). Here, we present some useful and typical plots which can be obtained from most software packages. From the PLSR calculations, the “scores” (T matrix) contain the information about the samples, their similarities and how they distribute. It is straightforward, accordingly, to visualize if any of the samples separate. Fig. 2 reveals that samples #13 and #20 present a quite different behaviour in the factor 1–factor 2 (t1 versust2) and factor 1–factor 3 (t1 versust3) subspaces, respectively. This means that their most prominent spectral features do not agree totally with the other standards. In principle, samples #13 and #20 might be considered for elimination from the calibration set, and the model repeated.

Fig. 2 PLS scores plots to evaluate the presence of outlier samples in the X-block.

Fig. 3 represents how the scores (samples) relate to the concentration of the analyte. This is called a “tversusu” plot (scores of the X-block versus scores of the Y-block) and, for each factor, it represents how linear (in a straight line sense) such relation is. It allows us to determine whether the corresponding factor is modelling linear effects or whether a non-linear phenomenon is being included into the model. In the example, it can be seen that the two first factors hold good linearity and that all samples follow a similar pattern (otherwise, the sample(s) falling apart should be considered with some more detail to assess whether there were outliers). As expected, the first factor (by definition the most important one) shows the nicest “regression appearance”.

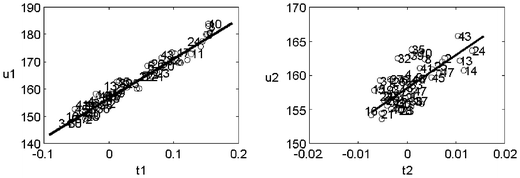Fig. 3 PLS “t versus u” plots to evaluate whether linear effects are being modelled by each factor.

Another very useful plot (not shown here because it is broadly used) is that involving plotting the actual (real) concentrations of the calibration (testing) set against those predicted for the same samples by the model under consideration. Departure from the “theoretical fit” (i.e., 45° line, slope = 1) points a probable biased regression. In addition, samples far from the regression line can be identified (they may be anomalous either in the X-block or in the actual concentration value). More examples and explanations can be found elsewhere.^6,18,19

Two diagnostic statistics are commonly plotted against each other to further evaluate the samples, i.e., the “leverage” and the “studentized residuals”. They are nicely defined elsewhere^5,29 and we will discuss only their typical plot (see Fig. 4). The studentized residuals are the scaled residuals (predicted concentration–actual concentration) so that they have unity variance. Following, a sample with a high studentized residual means that it has not properly been predicted by the model. The sample leverage is a measure of the influence that a sample has on the model. Samples that have unique values of the predictor variables tend to have high leverage on the model. Fig. 4 highlights three areas where the different behaviour of a sample can be attributed to a known reason (being an anomalous sample on the X- or Y-blocks). Influential samples like #10 have been modelled well. It behaves as an “influential” sample because, commonly, it corresponds to the lowest/highest concentration value of the training set. In the absence of other diagnostics pointing out an anomalous behaviour it should not be considered as an outlier.

Fig. 4 PLS plot of the sample studentized residuals versus sample leverage.

Fig. 5 can be used for the chemical interpretation of the PLSR model. The upper line (a) shows an atomic peak from an aqueous standard containing the analyte of interest and several potential concomitants, measured by ETAAS, and registered using 110 times. The arrows point out two smooth spectral “shoulders” (which suggest that other phenomena than the “pure” atomization peak are occurring). Lines (b) and (c) represent the PLSR “loadings” for factors 1 and 3, respectively (those corresponding to the 2nd factor could not be interpreted). Line (b) is, clearly, an “average” atomic peak and this is almost always observed.¹⁹ It represents the influence of the size of the overall measured peak on the concentration. Line (c) is more complex because it gives positive and relatively large loadings for those measuring times (predictors/independent variables) associated with the spectral shoulders. Hence, it seems that the 3rd factor is modelling any physical phenomena giving rise to those underlying, totally overlapped, peaks affecting the main atomization peak of the analyte. Finally, line (d) depicts which variables have the overall largest regression coefficients. They show that not only are the predictors defining the main peak useful to predict the analyte concentration, but the much smaller and almost hidden side-peaks. An acceptable interpretation of this fact may be that the frontal peak is related to easily volatilizable chemical species where the analyte is bounded. The last peak points towards more refractory species containing part of the analyte.

Fig. 5 Interpretation of the PLS model can be made comparing the original spectra (a), loadings of the first factors (b) and (c), and the regression coefficients (d).

For the sake of simplicity and brevity, selection of the proper number of PLS factors (components or latent variables) was deliberately omitted from the previous discussions. This critical issue still has not a universally-accepted way of being determined. Most reviews cited here explain several approaches, the most common one being cross-validation,^{6,17,19,20,29} whereby some samples are left out of the calibration set, the model obtained and the left-out samples predicted. The process is repeated a number of times considering different subsets of samples until all of them have been left-out. The number of factors is that yielding the lowest errors on the predictions. Several diagnostic plots can be obtained and all of them should be studied in much detail. Unfortunately this approach—despite it is being broadly applied—is not perfect and may lead to a wrong number of components and some other ways should be studied, mainly when experimental designs cannot be deployed because of the types of samples being studied. Just as an example, classical cross-validation was compared with several recent approaches in molecular spectrometry.³⁰

To summarise, PLSR is a method for constructing predictive models when the underlying factors are many and highly collinear. It is worth noting that the emphasis is on predicting the concentrations and not necessarily on understanding the underlying relationship between the variables, despite the fact that many times this is also possible. A final important advantage is that PLSR is capable of yielding good predictive models even when the underlying system is not linear, which can be frequent in spectroscopic measurements. This fact gives rise to another important point since the good properties of PLSR models can reduce the amount of work to be carried out in the laboratory. These issues will be considered further in the next sections where different published papers are reviewed.

5. Artificial neural networks

Artificial neural networks, ANN, constitute a new paradigm where natural computations instead of formal closed mathematical equations are used to develop predictive models. They are steadily being applied to solve complex problems, not easily handled by any of the previous methodologies, and this is why they are introduced here with some detail. ANN were originally introduced as a way to formulate highly simplified models of brain functioning. Accordingly, it is instructive to consider the broad analogies between ANN and biological neural cells to understand how they work.

ANN is a relatively loose term referring to computation models which have some kind of “distributed architecture”. This means that instead of a unique equation or systems of equations the ANN consist of highly interconnected “processing nodes” (in general termed neurons, analogous to biological neurons) to which multiple connections are linked (analogous to biological dentrites and axons).³¹Fig. 6 shows a typical ANN scheme where a set of neurons receive the chemical signals from the external world (input layer) and transfer them either to a final set of neurons (output layer) or to one or several intermediate layers which process the signals (hidden layers) and, finally, transfer their final result to the output layer. All layers and neurons are fully interconnected by the so-called weights (dentrites in real cells), which constitute the mathematical model itself.

Fig. 6 Scheme of (a) an artificial neuron compared with a biological neuron and of (b) an ANN.

The graphical arrangement of processing nodes and connections is termed the “architecture” of the ANN and it has to be optimised for each problem at hand, which is not trivial. As a general rule, the input layer is easily set by the chemist since as many neurons as predictor spectral variables are fixed. The output layer is also fixed in advance since, currently, a node is considered for regression problems. The connections or dentrites not only conduct the “signals” (numerical values) they receive from one/several neuron/s towards other neuron/s but distribute them by the weights. All these weights are optimised when the overall ANN is optimising itself.

What surprises in the ANN is that the neurons perform very simple calculations (in some cases they only fix a value, either 0 or 1). As for the brain, the complex regression model is composed of all weights and simple processing units which “organize themselves” to get good results. Each neuron decides first if the input signal (numerical value) is high enough to activate it and, if positive, transforms such an input to another numerical value (e.g., using the slope of a linear function) and, finally, transfers the new result to another neuron.

In simple terms each node i uses a transfer function f_i of the form (a profound discussion is beyond the scope of this paper, and the readers are encouraged to review one of the most famous books on ANN in chemometrics³²):

where y_i is the output of node i, x_j is the jth input to the node, and w_ij is the connection weight between nodes i and j. θ_i is the threshold (or bias) of the node: sometimes this is the activation value (i.e., a numerical sum below this value will cause the neuron not to perform a calculation and it remains inactive). Usually, f_i is non-linear, such as a heaviside, sigmoid, or Gaussian function but it can also be an straight line or a yes/no dichotomic value.^32,33

There are numerous types of ANN to address many types of chemical problems, such as pattern recognition, sample classification, multivariate regression, etc.^34–37 In any case, the general (important) rule is that three sample sets are required to properly develop an ANN: a calibration set, an external testing (validation) set and the set of true unknowns. The first set is obviously used to optimise (calibrate, train or learn) the architecture of the net: the number of hidden layers/nodes and the numerical values of the weights. The testing set (new, different samples with known values for the property of interest) is needed to verify that the ANN did not memorize the calibration samples. This is called over-fitting or over-training and, unfortunately, occurs quite easily. Over-training leads to a final model which is so focused on the calibration samples—it yields almost perfect predictions for them—that new samples are predicted wrongly. Therefore a compromise has to be reached between training and prediction (which should be potentiated). The testing set is constituted by new samples, uncorrelated to the previous ones, representing current samples to be measured but whose concentrations are already known. This set should never be used to optimise the ANN, just to test (verify or validate) it. Only after the external validation set has been satisfactorily predicted can the ANN be used to predict unknown samples. Of course, great care is required to get good calibration and testing and validation samples (absence of anomalous samples, bracketing of the working range, representativeness, etc.), but this is the case for any regression model.

The most common way to train the ANN is “backpropagation” (BPN). This is an algorithm conceived by Rumelhart et al.³⁸ to inform the net how wrong its predictions are after a model was developed using the calibration data. Most likely, the ANN will not predict properly after only considering the calibration data for the first time. Therefore, backpropagation causes the ANN model to be reviewed automatically and the weights updated to get a lower overall final prediction error. The algorithm entails: running the training set through the ANN; calculating the error incurred by the difference in actual and target network outputs; propagating the errors back, in the same manner as the signal propagation but in the opposite direction, i.e., from the output to the input layer, hence the term backpropagation; and, finally, re-adjusting all the weights according to the error (each weight is modified in proportion to its value). This process is repeated iteratively until the average (or total) error across the training set is below a specified maximum. Each such iteration is known as an epoch. The main advantages of the ANNs are:

(i) there is no need to assume an underlying data distribution, as it is usually the case in parametric modelling (methodologies described in the previous sections);

(ii) they are applicable to multivariate linear and non-linear problems (sometimes the latter are difficult to handle with other approaches);

(iii) high tolerance to noise;

(iv) ability to classify patterns on which they have not been trained previously;

(v) high adaptability, which means that they auto-organize themselves to learn how to get some outputs from a given set of inputs;

(vi) no specific formal equations have to be defined for each problem.

Nevertheless, they also present several disadvantages that difficult their application, among them:

(i) they are so good at learning that overfitting is a common problem and avoiding it requires a great number of tests (where a good validation sample set is required);

(ii) in general, the relationship between the predictors and the concentration cannot be interpreted chemically so that the model tends to be a “black-box” approach without a clear meaning;

(iii) the sample size has to be large, and three sets are needed to develop a proper model (calibration, testing and validation sets)—sometimes this increases workload;

(iv) ANN optimization requires changing the number of neurons in the hidden layers, the number of hidden layers, several parameters such as the learning rate (to avoid the net to be stacked on a local minimum), sometimes the transfer function, etc.—this makes optimization a laborious and iterative process where many tests have to be carried out before a satisfactory net is obtained;

(v) ANN have many advantages in clear non-linear systems but many times their behaviour cannot outperform that of typical linear methods (e.g.PLSR³⁹) when the problem is linear (or even when there are only minor non-linearities).

6. Applications of multivariate calibration in atomic spectrometry techniques

This section reviews those applications combining multivariate regression and atomic absorption spectrometry found in the 1990–2006 period. It is worth noting that, despite their relatively small quantity, they are more frequent on complex atomic measurements where information is difficult to extract (ICP and LIBS) and where analyte atomisation can be accompanied by complex concomitants (ETAAS). The papers cited hereinafter focus on the multivariate models explained above. Only minor references will be given to other methods (despite their being highly valuable), just to open new perspectives for more interested readers.

6.1. Atomic absorption techniques

Multiple linear regression (MOLSR) was applied as a natural extension of univariate ordinary least squares fit. In a pioneering work, Henrion et al.⁴⁰ found that MOLSR could treat analyte interferences as well as some more advanced methods in hydride generation AAS (HG-AAS). Later on, Torralba et al.⁴¹ compared MOLSR with Kalman filtering also in an HG-AAS application where continuous flow injection was employed. Results from three different approaches were compared by pair-wise F-test (instead of using ANOVA). Kalman filtering is beyond the scope of this tutorial and its basics can be found elsewhere.¹⁴ Majcen⁴² used absorbances at six different wavelengths plus the concentration of Ti to quantify Fe, Nb and Si (separately) in white pigments by FAAS in order to take account of spectral interferences that could not be addressed using standard addition.

Grotti et al.⁴³ combined MOLSR and experimental designs to correct for the (simultaneous) effects of Na, K, Mg and Ca nitrates on Mn atomisation from sea-water by ETAAS. The same authors extended their previous work by comparing MOLSR models with other classical alternatives such as matrix-matched standards and standard additions, which systematically yielded excess quantitations.⁴⁴ They drew conclusions from the different cross-product terms included in the regression models (e.g. an interaction between Mg and Ca). They addressed similar problems with Te⁴⁵ and the complex interferences of Cl^–, Ca²⁺, Na⁺, K⁺ and Mg²⁺ on Pb, Cd, Ni, Cr and Mn ETAAS determinations.⁴⁶

Despite MOLSR models being helpful and allowing much insight into the atomic measurements, several major experimental pitfalls can be underlined. First, as MOLSR needs to model all possible spectral and matrix effects⁴⁷ each standard and unknown sample must be “matched” so that the matrix composition is approximately the same.

Besides, in order to strictly apply the MOLSR equations the concentration of the concomitants in the unknowns should be known, which is not always the case, and this would imply too much analytical work. Nevertheless, when multi-elemental techniques can be used, such as ICP, this problem can be alleviated.⁴⁸

Some pioneering authors in ANNs on chemometrics⁴⁹ diagnosed calibration problems related to the use of AAS spectral lines. As they focused on classifying potential calibration lines, Kohonen neural networks were used instead of typical error back-propagation feed forward ANNs (BPN). Many times Kohonen nets are best suited to performing classification tasks, whereas BPN are preferred for calibration purposes, as explained in Section 5.

Despite PCR solving many of the statistical problems MOLSR possesses, it has scarcely been applied in atomic spectrometry. Some papers applied it as “another” option among several and, mainly, as a matter of comparison.^42,50,51

PLSR (partial least squares regression) seems by far the most popular multivariate regression tool employed by atomic spectroscopists. Flores et al.⁵² employed PLSR to quantify Cd in marine and river sediments measured by direct solid sampling flame atomic absorption spectrometry.

There are three pioneering works that, in our opinion, are a must for interested readers. Baxter and Ǒhman⁵³ discussed the fact that background correction in ETAAS has several problems and, so, incompletely corrects the interferences, and that such a problem can be overcome by PLSR. In order to do so, they also applied the generalised standard addition method (GSAM) to develop the calibration set and, then, the final model. Among the different studies, they combined signal averaging of the replicates and signal smoothing before implementing the PLSR model.

ETAAS was also combined with PLSR by Baxter et al.⁵⁴ to determine As in marine sediments. In this work, they demonstrated that classical standard additions methods do not correct for spectral interferences (their main problem) because of mutual interactions between the two analytes of interest (As and Al). PLSR-2 block was applied to quantify simultaneously both elements (PLSR-2 block is a PLSR procedure that predict several analytes simultaneously; it is not widely applied, except when the analytes are correlated).

Quite surprisingly, ETAAS has not attracted much attention with regard to PLSR. Except for the Baxter et al. paper^53,54 it was until Felipe-Sotelo et al.⁵⁵ that other work was found. These authors considered a problem where a major element (Fe) caused spectral and chemical interferences on a minor one (Cr), which had to be quantified in natural waters. They demonstrated that linear PLSR handled (eventually) non-linearities since polynomial PLSR and locally weighted regression (non-linear models) did not outperform its results. Furthermore, it was found that linear PLSR was able to model three typical effects which currently occur in ETAAS: peak-shift, peak enhancement (depletion) and random noise.

More complex is the situation where several major concomitants affect the atomic signal of the trace element(s) to be measured (whose concentrations are several orders of magnitude lower). PLSR was very recently demonstrated to give good results⁵⁶ when a proper experimental design was developed to quantify Sb in water samples by ETAAS. Instead of the traditional approach, where only an experimental design is deployed to establish the calibration (and validation) set, a saturated experimental design considering the concomitants was deployed at each of the concentration levels considered for the analyte. Once more, polynomial PLSR performed worse than or equal to linear PLSR, demonstrating that linear models are good enough. Further, multivariate figures-of-merit were calculated following IUPAC and ISO guidelines and, also, bracketing both the α- and β-errors to 5%. In these two later papers the authors studied graphically the factor loadings and regression coefficients to gain insight on how the models behave.

Very recently, Felipe-Sotelo et al.³⁹ modelled complex interfering effects on Sb when soil, sediments and fly ash samples were analysed by slurry sampling-ETAAS (SS-ETAAS). Sometimes, spectral and chemical interferences cannot be totally solved on slurries using chemical modifiers, ashing programs, etc., because of the absence of a sample pre-treatment step to eliminate/reduce the sample matrix. Hence, the molecular absorption signal is so high and structured that background correctors cannot be totally effective. In addition, alternative wavelengths may not be a solution due to their low sensitivity when trace levels are measured. In order to circumvent all these problems, the authors employed current PLSR, second-order polynomial PLSR and ANNs to develop predictive models on experimentally-designed calibration sets. Validation with five CRMs showed that the main limitations of the models were related to the SS-ETAAS technique, i.e., the mass/volume ratio and the low content of analyte of some solid matrices (which forced the introduction of too much sample matrix into the atomizer). Both PLSR and ANN gave good results since they could handle severe problems like peak displacement, peak enhancement/depletion and peak tailing. Nevertheless, PLSR was preferred because the loadings and correlation coefficients could be interpreted chemically. Moreover, this approach allowed a reduction on the laboratory workload to optimise the analytical procedure by around 50%.

In addition to the work from Felipe-Sotelo et al.³⁹ in which they employed the complete atomic peaks, other authors applied ANN as multivariate regression tools as well, although without using the overall information in the peaks.

Hernández-Caraballo et al.⁵⁷ applied BPNs and aqueous standards to develop a calibration model capable of enlarging the (typically) short linear dynamic range of Cd curves determined by ETAAS. They employed a univariate approach since only those absorbances at the maxima of the atomic peaks were regressed against Cd concentrations. Unfortunately, they did not apply the model to real samples and they did not consider that the atomic maxima could appear at slightly different times. In a later work⁵⁸ they compared BPNs to other mathematical functions, with good results for the BPNs.

6.2. Inductively coupled plasma

Inductively coupled plasma spectrometry, ICP, needs careful extraction of the relevant information to get satisfactory models and several chemometric studies were found. Indeed, many ICP spectroscopists applied multivariate regression and other multivariate methods to a number of problems. An excellent review has recently been published on chemometric modelling and applications of inductively coupled plasma optical emission spectrometry (ICP-OES).⁵⁹

Several papers can be traced back to the early 1990s: Glick et al.⁶⁰ compensated for spectral and stray light interferences in a ICP-OES-photodiode array spectrometer; Ivaldi et al.⁶¹ extracted ICP-OES information using least squares regression; Danzer et al. used PCR⁶² and multi-line PCR and PLS⁶³ on ICP-OES spectra. Two other applications are those from Van Veen et al.,⁶⁴ applying Kalman filtering to ICP-OES spectra; the same authors reviewed several procedures to perform background correction and multi-component analysis.⁶⁵ Sadler and Littlejohn⁶⁶ applied PLS to detect uncorrected additive interferences. Venth et al.⁶⁷ compared PLSR and canonical correlation analysis to solve isobaric and polyatomic ion interferences in Mo–Zr alloys measured by ICP-MS. Pimentel et al.⁶⁸ applied PLS and PCR to simultaneously measure five metals (Mn, Mo, Cr, Ni and Fe) in steel samples, using a low-resolution ICP with diode array detection.

Rupprecht and Probst⁶⁹ corrected ICP-MS spectral and non-spectral interferences by different multivariate regression methods. They studied MOLSR, PCR and PLSR and compared them with OLSR. Further, they tested different data pre-treatments, namely, mean centring, autoscaling, scaling 0 to 1 and internal standardization. The best model was developed using PLSR, mean centred data (also internal standard would be fine) and variable selection according to the regression coefficients (studied in a previous model). A method for the quantification of spectral interferences in ICP-MS, based on empirical modelling and experimental design, was developed by Grotti et al.⁷⁰ They used MOLSR to deduce the relationship between interfering effects and matrix composition. They applied a similar approach to study the interferences caused by complex matrices containing Na, K, Ca, Al and Fe⁴⁷ on ICP-AES measurements.

Moberg et al.⁷¹ used ICP-MS to determine Cd in fly ash and metal allows; severe spectral overlaps arose and multivariate regression outperformed other univariate approaches. They also studied whether day-to-day ICP-MS recalibration could be avoided so that the calibration set could be constructed on several runs.

Haaland et al.⁷² developed a so-called multi-window classical least squares for ICP-AES measurements (CCD, charge-coupled device, detector arrays). Essentially, it consisted in performing a classical least squares regression in each of the spectral windows which were measured and combining the concentration predictions (for a given analyte). The methodology was compared with PLSR and it proved superior and capable of handling interferences from several concomitants.

Griffiths et al.⁷³ quantified Pt, Pd and Rh in autocatalyst digests by ICP (CCD detector array). They compared univariate techniques (pure standards, pure standards with inter-element correction factors and matrix matched standards) and PLSR, the latter being superior in general although less effective at low concentrations due to spectral noise. They also studied the effect of using the gross signal or background corrected ones, being more successful the former option.

In a following work, Griffiths et al.⁷⁴ studied how to reduce the ICP-AES (segmented-array charge-coupled device detector) raw variables (5684 wavelenghts per spectrum). This application holds many similarities with classical molecular spectrometry from where they selected two advanced algorithms, applied in three steps: (i) application of an uninformative variable elimination PLSR algorithm (UVE-PLSR), which identifies variables with close-to-zero regression coefficients; (ii) application of an informative variable degradation-PLSR, which ranked variables using a ratio calculated as the regression coefficient divided by its estimated standard error; and (iii) selection of the variables according to that ratio. Interestingly, they must autoscale data instead of the more frequent mean centring pre-treatment.

Kola et al.⁴⁸ corrected spectral interferences on ICP measurements of S when Ca was present. They discussed that linear terms (each associated with a given wavelength) in the MOLSR equation and cross-product terms would account for matrix effects. In order to develop the regression equation they had to restrict the working range to concentration levels where correlation between S an Ca was negligible (a typical problem of MOLSR, as discussed in the corresponding section).

Other multivariate methods were applied to ICP spectra for quantitative measurements. As an example, they include: multi-component spectral fitting (which is incorporated in several commercial instrument softwares);⁶¹ matrix projection, which avoids measurement of background species;^75,76 generalised standard addition⁷⁷ and Bayesian analysis.⁷⁸

6.3. Laser-induced breakdown spectrometry

Laser-induced breakdown spectrometry, LIBS, required also multivariate regression to solve complex problems. Here, the first paper found dates back to 2000 and it was related to jewellery studies. Amador-Hernández et al.⁷⁹ showed that PLSR models were highly satisfactory for measuring Au and Ag in Au–Ag–Cu alloys. This study was further completed by Jurado-López and Luque de Castro,⁸⁰ who compared the “hybridised” LIBS-PLSR technique with analytical scanning microscopy, ICP-AES, FAAS and LIBS. Despite the accuracy of LIBS-PLSR did not outperform the official procedure: several characteristics made it highly appealing for routine work.

Two other papers presented routine LIBS applications, without too many details on the multivariate models.^81,82

Martín et al.⁸³ presented a recent work where LIBS was employed for the first time for wood-based materials where preservatives containing metals had to be determined. They applied PLSR-1 block and PLSR-2 block (because of the interdependence of the analytes) on multiplicative scattered-corrected data (a data pre-treatment option of most use when diffuse radiation is employed to get spectra). These authors studied the loadings of a PCA decomposition to identify the main chemical features that grouped samples. Unfortunately, they did not extend this study to the PLSR factors. However, they analysed the regression coefficients to determine the most important variables for some predictive models.

List of acronyms

a	Denote a number (scalar)
a	Bold font denotes a vector
A	Capital letter, bold font, denotes a matrix
E, e	Matrix and vector of random errors
C	The matrix of concentrations with k rows (= number of standards) and n columns (= absorbing species, i = 1, 2,…, n)
T	The scores matrix, with k rows (standards) and z columns (factors)
P	The loadings matrix, with z rows (factors) and j columns (variables, measuring times)
S	The matrix of the pure unit-concentration spectra or “regression coefficients” with n rows (= pure spectral atomic peak for each absorbing species, i = 1, 2,…, n) and j columns ( measuring times)
X, X-block	In PLS, the matrix of measured atomic peaks for all standards (analyte/s plus concomitant/s) (k rows and j columns)
Y , y, Y-block	In PLS, the matrix (or vector) with the concentrations of the analyte(s) for each standard (k rows)
W	In PLS, vector of weights
ANN	Artificial neural networks
BPNs	Backpropagation neural networks
CCD	Charge-couple device detectors
ETAAS	Electrothermal atomic absorption spectrometry
FAAS	Flame atomic absorption spectrometry
GSAM	Generalised standard addition method
HG-AAS	Hydride generation atomic absorption spectrometry
ICP	Inductively coupled plasma
ICP-AES	Inductively coupled plasma atomic emission spectrometry
ICP-OES	Inductively coupled plasma optical emission spectrometry
ICP-MS	Inductively coupled plasma mass spectrometry
LIBS	Laser-induced breakdown spectrometry
MOLSR	Multiple ordinary linear least squares regression
OLSR	Ordinary least squares regression
PC	Principal component
PCA	Principal components analysis
PCR	Principal components regression
PLSR	Partial least squares regression
SS-ETAAS	Slurry-sampling-electrothermal atomic absorption spectrometry
UVE-PLSR	Uninformative variable elimination partial least squares regression algorithm

Acknowledgements

Two anonymous referees are thanked because of their useful suggestions to improve the original manuscript.

References

1. L. Ebdon, E. H. Evans, A. Fisher and S. J. Hill, An introduction to analytical atomic spectrometry, John Wiley & Sons, Chichester, 1998.
2. M. J. Cal-Prieto, M. Felipe-Sotelo, A. Carlosena, J. M. Andrade, P. López-Mahía, S. Muniategui and D. Prada, Talanta, 2002, 56, 1.
3. K. Danzer and Ll. A. Curie, Pure Appl. Chem., 1998, 70, 993.
4. H. Mark, Principles an Practice of Spectroscopic Calibration, John Wiley & Sons, New York, 1991.
5. M. Meloun, J. Militký, M. Hill and R. G. Brereton, Analyst, 2002, 127, 433.
6. R. G. Brereton, Analyst, 2000, 125, 2125.
7. R. Boqué and J. Ferré, LC-GC Eur., 2004, 17(7), 402.
8. A. C. Olivieri, N. Faber, J. Ferré, R. Boqué, J. H. Kalivas and H. Mark, Pure Appl. Chem., 2006, 78(3), 633.
9. H. Martens and M. Martens, Multivariate Analysis of Quality: An Introduction, John Wiley & Sons, New York, 2001.
10. T. Naes, T. Isaksson, T. Fearn and T. Davies, A User-friendly Guide to Multivariate Calibration and Classification, NIR Publications, Chichester, UK, 2002.
11. D. C. MacTaggart and S. O. Farwell, J. AOAC Int., 1992, 75(4), 608.
12. A. Martínez, F. J. del Río, J. Ríu and F. X. Rius, Chemom. Intell. Lab. Syst., 1999, 49, 179.
13. A. Martínez, J. Riu and F. X. Rius, J. Chemom., 2002, 16, 189.
14. D. L. Massart, B. G. M. Vandeginste, L. M. C. Buydens, S. de Jong, P. J. Lewi and J. Smeyers-Verbeke, Handbook of Chemometrics and Qualimetrics, Elsevier, 1997.
15. R. Caulcutt, Statistics in Research and Development, Chapman and Hall, London, 2nd edn., 1991.
16. B. M. Wise and N. B. Gallagher, PLS-Toolbox for use with MATLAB, Eigenvector Technologies, 1998.
17. P. Geladi, Spectrochim. Acta, Part B, 2003, 58, 767.
18. P. Geladi, B. Sethson, J. Nyström, T. Lillhonga, T. Lestander and J. Burger, Spectrochim. Acta, Part B, 2004, 59, 1347.
19. S. Wold, M. Sjöström and L. Eriksson, Chemom. Intell. Lab. Syst., 2001, 58, 109.
20. P. Geladi and B. R. Kowalski, Anal. Chim. Acta, 1986, 185, 1.
21. J. M. Sutter, J. H. Kalivas and P. M. Lang, J. Chemom., 1992, 6, 217.
22. H. Wold, Estimation of principal components and related models by iterative least squares, in Multivariate Analysis, ed. P. R. Krishnaiah, Academic Press, New York, 1966.
23. H. Wold, Nonlinear Iterative Partial Least Squares (NIPALS) Modelling: Some Current Developments, in Multivariate Analysis, ed. P. R. Krishnaiah, Academic Press, New York, 1973.
24. H. Wold, Path models with latent variables: the NIPALS approach, in Quantitative Sociology International Perspectives on Mathematical and Statistical Model Building, ed. H. M. Blalock, Academic Press, New York, 1975.
25. H. Martens, Chemom. Intell. Lab. Syst., 2001, 58(2), 85.
26. S. Wold, Chemom. Intell. Lab. Syst., 2001, 58(2), 83.
27. I. E. Frank and J. H. Friedman, Technometrics, 1993, 35, 109.
28. P. H. Garthwaite, J. Am. Stat. Assoc., 1994, 89, 122.
29. F. McLennan and B. R. Kowalski, Process Analytical Chemistry, Blackie Academic & Professional, Edinburgh, 1995.
30. M. P. Gómez-Carracedo, J. M. Andrade, D. N. Rutledge and K. Faber, Anal. Chim. Acta, 2007, 585(2), 253.
31. C. A. L. Bailer-Jones, R. Gupta and H. P. Singh, An introduction to artificial neural networks, in Automated Data Analysis in Astronomy, eds. R. Gupta, H. P. Singh and C. A. L. Bailer-Jones, Narosa Publishing House, New Delhi, India, 2001.
32. J. Zupan and J. Gasteiger, Neural Networks in Chemistry and Drug Design, John Wiley & Sons, New York, 1999.
33. X. Yao, Proc. IEEE, 1999, 87(9), 1423.
34. X. Shi, L. Wang, N. Kariuki, J. Luo, C.-J. Zhong and S. Lu, Sens. Actuators, B, 2006, 117, 65.
35. S. Duan, Z. Shi, H. Feng, Z. Duan and Z. Mao, Biochem. Eng. J., 2006, 30, 88.
36. S. Dragovic and A. Onjia, Appl. Radiat. Isot., 2007, 65, 218.
37. F. Despagne and D. L. Massart, Analyst, 1998, 123, 157R.
38. D. E. Rumelhart, G. E. Hinton and R. J. Williams, Nature, 1986, 323, 533.
39. M. Felipe-Sotelo, M. J. Cal-Prieto, M. P. Gómez-Carracedo, J. M. Andrade, A. Carlosena and D. Prada, Anal. Chim. Acta, 2006, 571, 315.
40. G. Henrion, R. Genrion, R. Hebisch and B. Boeden, Anal. Chim. Acta, 1992, 268(1), 115.
41. R. Torralba, M. Bonilla, L. V. Pérez-Arribas, M. A. Palacios and C. Cámara, Mikrochim. Acta, 1997, 126(3–4), 257.
42. N. Majcen, Fresenius’ J. Anal. Chem., 1996, 355, 315.
43. M. Grotti, R. Leardi, C. Gnecco and R. Frache, Spectrochim. Acta, Part B, 1999, 54, 845.
44. M. Grotti, M. L. Abelmoschi, F. Soggia, Ch. Tiberiade and R. Frache, Spectrochim. Acta, Part B, 2000, 55, 1847.
45. M. Grotti, E. Magi and R. Leardi, Anal. Chim. Acta, 1996, 327(1), 47.
46. M. Grotti, R. Leardi and R. Frache, Anal. Chim. Acta, 1998, 376(3), 293.
47. M. Grotti, E. Magi and R. Frache, J. Anal. At. Spectrom., 2000, 15, 89.
48. H. Kola, P. Perämäki and I. Välimäki, J. Anal. At. Spectrom., 2002, 17, 104.
49. Y. Vander Heyden, P. Vankeerberghen, M. Novic, J. Zupan and D. L. Massart, Talanta, 2000, 51, 455.
50. M. Rupprecht and T. Probst, Anal. Chim. Acta, 1998, 358, 205.
51. A. Donachie, A. D. Walmsley and S. J. Haswell, Anal. Chim. Acta, 1999, 378, 235.
52. E. M. M. Flores, J. N. G. Paniz, A. P. F. Saidelles, E. I. Müller and A. B. da Costa, J. Anal. At. Spectrom., 2003, 18, 769.
53. D. C. Baxter and J. Ǒhman, Spectrochim. Acta, Part B, 1990, 45(4–5), 481.
54. D. C. Baxter, W. Frech and I. Berglund, J. Anal. At. Spectrom., 1991, 6, 109.
55. M. Felipe-Sotelo, J. M. Andrade, A. Carlosena and D. Prada, Anal. Chem., 2003, 75(19), 5254.
56. M. Felipe-Sotelo, M. J. Cal-Prieto, J. Ferré, R. Boqué, J. M. Andrade and A. Carlosena, J. Anal. At. Spectrom., 2006, 21, 61.
57. E. A. Hernández-Caraballo, R. M. Avila-Gómez, F. Rivas, M. Burguera and J. L. Burguera, Talanta, 2004, 63, 425.
58. E. A. Hernández-Caraballo, F. Rivas and R. M. Ávila de Hernández, Anal. Bioanal. Chem., 2005, 381, 788.
59. M. Grotti, Ann. Chim., 2004, 94, 1.
60. M. Glick, K. R. Brushwyler and G. M. Hieftje, Appl. Spectrosc., 1991, 45, 328.
61. J. C. Ivaldi, D. Tracy, T. W. Barnard and W. Slavin, Spectrochim. Acta, Part B, 1992, 47, 1361.
62. K. Danzer and M. Wagner, Fresenius’ J. Anal. Chem., 1993, 346, 520.
63. K. Danzer and K. Venth, Fresenius’ J. Anal. Chem., 1994, 350, 339.
64. E. H. Van Veen, S. Bosch and M. T. C. De Loos-Vollebregt, Spectrochim. Acta, Part B, 1994, 49(8), 829.
65. E. H. Van Veen and M. T. C. De Loos-Vollebregt, Spectrochim. Acta, Part B, 1998, 53(5), 639.
66. D. A. Sadler and D. Littlejohn, J. Anal. At. Spectrom., 1996, 11, 1105.
67. K. Venth, K. Danzer, G. Kundermann and K.-H. Blaufuss, Fresenius’ J. Anal. Chem., 1996, 354(7–8), 811.
68. M. F. Pimentel, B. De Narros Neto, M. C. Ugulino de Araujo and C. Pasquini, Spectrochim. Acta, Part B, 1997, 52, 2151.
69. M. Rupprecht and T. Probst, Anal. Chim. Acta, 1998, 358(3), 205.
70. M. Grotti, C. Gnecco and F. Bonfiglioli, J. Anal. At. Spectrom., 1999, 14, 1171.
71. L. Moberg, K. Pettersson, I. Gustavsson and B. Karlberg, J. Anal. At. Spectrom., 1999, 14(7), 1055.
72. D. M. Haaland, W. B. Chambers, M. R. Keenan and D. K. Melgaard, Appl. Spectrosc., 2000, 54(9), 1291.
73. M. L. Griffiths, D. Svozil, P. J. Worsfold, S. Denham and E. H. Evans, J. Anal. At. Spectrom., 2000, 15, 967.
74. M. L. Griffiths, D. Svozil, P. Worsfold, S. Denham and E. H. Evans, J. Anal. At. Spectrom., 2002, 17, 800.
75. P. Zhang, D. Littlejohn and P. Neal, Spectrochim. Acta, Part B, 1993, 48(12), 1517.
76. P. Zhang and D. Littlejohn, Spectrochim. Acta, Part B, 1995, 50(10), 1263.
77. S. Luan, H. Pang and R. S. Houk, Spectrochim. Acta, Part B, 1995, 50(8), 791.
78. B. L. Sharp, A. S. Bashammakh, Ch. M. Thung, J. Skilling and M. Baxter, J. Anal. At. Spectrom., 2002, 17, 459.
79. J. Amador-Hernández, L. E. García-Ayuso, J. M. Fernández-Romero and M. D. Luque de Castro, J. Anal. At. Spectrom., 2000, 15, 587.
80. A. Jurado-López and M. D. Luque de Castro, Anal. Bioanal. Chem., 2002, 372, 109.
81. J. L. Luque-García, R. Soto-Ayala and M. D. Luque de Castro, Microchem. J., 2002, 73, 355.
82. A. Jurado-López and M. D. Luque de Castro, Talanta, 2003, 59, 409.
83. M. Z. Martín, N. Labbé, T. G. Rials and S. D. Wullschleger, Spectrochim. Acta, Part B, 2005, 60, 1179.

---