A kinetic model for microbial decontamination of water based on a modified Fenton reaction
Received
3rd April 2008
, Accepted 4th July 2008
First published on
24th July 2008
Abstract
In a water treatment process, microbial decontamination prevents the introduction of pathogenic microorganisms in natural water bodies. There are numerous processes used for microbial decontamination which are, however, technologically intensive. The need exists for simpler treatment processes that are cost effective and do not generate toxic by-products. We have recently proposed the use of a heterogeneous catalyst based treatment system for microbial decontamination of water. The system is based on the generation of hydroxyl radicals through reaction of resin-bound copper with hydrogen peroxide. This paper proposes and validates a mathematical model for the decontamination of Escherichia coli from wastewater. A reaction mechanism based on elementary steps is proposed and experimental data of E. coli concentration in the wastewater under different operating conditions were used. Rate parameters were estimated through nonlinear optimization techniques and the model was experimentally validated.
1. Introduction
For microbial decontamination of water such as swimming pools, industrial effluents that contain microorganisms as main pollutants or other similar water bodies, the five most widely used disinfection agents are free chlorine, combined chlorine (chlorine combined with ammonia), ozone, chlorine dioxide and UV light in combination with ozone and/or hydrogen peroxide. Of the five, by far the most commonly used agent is free chlorine. The advantage of this method is the ease of treatment and its effectiveness against microorganisms. However, with increasing concern over the conversion of organic compounds to chlorinated carcinogenic molecules, focus is now on alternative methods of microbial decontamination.1 Advanced oxidation processes (AOPs) provide an attractive alternative to chlorine based treatments as the dominant oxidizing species in these processes are hydroxyl radicals (˙OH). Advantages of ˙OH over chlorine as oxidizing agents include higher oxidation potential, higher rates of oxidation and non-toxic end products.2 Ozone and UV based microbial decontamination treatment processes are examples of AOPs. However, these processes are technologically intensive and require extensive capital investment for infrastructure development and maintenance. The need exists for simple treatment processes that could be operated by non-technical personnel, are cost effective and do not generate toxic by-products.
AOPs that are based on Fenton's reaction are widely used in water treatment to destroy organic compounds.3 Fenton's reaction processes are applicable in environments where traditional technologies are not effective. For example, if water is turbid or contains colored compounds, it would interfere with UV/H2O2 methods. Capital equipment costs for application of Fenton's reaction can be expected to be much lower than for UV/H2O2 processes. Moreover, Fenton's reaction has lower operation and maintenance costs compared to the ozonation methods, because the operating costs for Fenton's reaction depend primarily on reagents concentrations and have very low energy requirements, as opposed to the high energy requirements for ozonation.4 However, currently no commercially viable process is available for microbial decontamination of water that is based on Fenton's reaction.
Earlier we had described several copper based Fenton-like metal/ligand systems for homogeneous catalytic decomposition of hydrogen peroxide and production of hydroxyl radicals. The system employing ligands such as succinic acid and glucaric acid and copper metal were shown to be highly effective in decolorizing textile dyes.5,6 Homogenous catalytic systems however are not suitable for treatment of waste water as it requires secondary processes for removal of catalysts from the water. These processes are technically and/or economically unfeasible.7 Later, we demonstrated that a Fenton's like reaction employing a heterogeneous catalyst system was capable of microbially decontaminating the water.8 Experimental results have shown that the system was successful in reducing the microbial load in water by more than 99% in 15 min and was effective against all microorganisms tested.8 In the developed method, copper is first immobilized on a commercial ion-exchange resin, Amberlite IRC 148, to create a polymer–metal complex. This complex acts as a catalyst for the decontamination process. The catalyst is brought in contact with microbially contaminated water and hydrogen peroxide added. The system generates hydroxyl radicals through a series of reactions in which hydrogen peroxide reacts with a ligand-bound transition metal, in this case copper. However, unlike classical Fenton's reaction, hydroxyl radicals do not diffuse freely into the water but remain bound to the catalyst to form polymer–metal–radical complex. This complex reacts with E. coli and kills it. The main advantage of copper-mediated decomposition of hydrogen peroxide compared to other transition metals such as iron is the fact that copper reacts with hydrogen peroxide both as CuII and CuI and hydroxyl radicals are produced in both cases.5 Also, copper mediated Fenton's reaction is independent of pH of the water.
The objective of this paper is to propose and validate a mathematical model for the kinetics of decontamination of E. coli from water using the polymer–catalyst–peroxide treatment system proposed by Shah et al.8 This information is vital before proceeding with the design and scale-up of the process.
The paper is organized as follows: section 2 presents the experimental methodology, while section 3 shows the proposed mechanisms and mathematical models for these reactions. Results of the simulations for parameter estimation as well as for model validation; sensitivity analysis and optimal concentration are presented in section 4. Finally section 6 concludes this work.
2. Experimental
The experimental protocol described in Shah et al.8 was followed for the decontamination process. In brief, a loopful of E. coli ATCC 33625 culture was inoculated in nutrient broth and incubated overnight at 200 rpm and 30 °C. 1 mL of approximately diluted overnight culture was added to the catalyst and hydrogen peroxide added. Incubation was carried out at 25 °C at various time intervals; 10 μL of the liquid was withdrawn at various time intervals and after serial dilution plated on nutrient agar. The plates were incubated overnight and the colonies were counted the next day. The copper content in decontaminated water was measured following standard protocol SW-846 (method 6010 and 7000 series analysis respectively).9 Measurements were carried out using inductively coupled plasma mass spectrometry.
3. Proposed mechanisms and models
Baldrian et al.7 proposed a reaction mechanism for the degradation of polycyclic aromatic hydrocarbons by hydrogen peroxide catalyzed by polymeric metal chelates. The main equations for the reaction mechanisms are as follows:| | 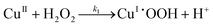 | (I.1) |
| | 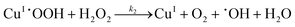 | (I.2) |
| | 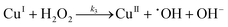 | (I.3) |
It could be seen that hydroxyl radicals are formed in reactions (I.2) and (I.3). In reaction (I.1) copper and hydrogen peroxide form a reactive complex, which in turn reacts with hydrogen peroxide to generate a reactive hydroxyl radical. Hydroxyl radicals are proposed by Baldrian et al.7 to be responsible for the degradation of hydrocarbons.
In the developed treatment system, copper is immobilized on an ion-exchange resin (Amberlite IRC748) and a polymer–copper complex (PCuII) is formed. The first reaction mechanism proposed consists of the following reactions:
Mechanism 1
| |

| (II.1) |
| |

| (II.2) |
| |

| (II.3) |
| |
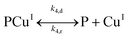
| (II.4) |
In reaction (II.1), the polymer–copper complex reacts with peroxide to generate reactive radicals that remain bound to a polymer–copper complex along with hydroxyl ion.8 Microbial decontamination occurs in reaction (II.2) when E. coli reacts with the reactive complex (PCuI˙OH). Subsequently PCuI˙OH breaks down to water and a new polymer–copper complex (PCuI). It should be noted that the reaction described in eqn (II.1) occurs in a two-step process. In the first step PCuII reacts with peroxide to form PCuI˙OOH and in the second step PCuI˙OOH reacts with peroxide to form PCuI˙OH. The two steps are similar to eqn (I.1) and (I.2). However, as they are zero order with respect to hydrogen peroxide concentration, they can be combined to yield eqn (II.1). Leaching of copper into water can occur from PCuI.
Taking into account that the experiments take place in batch mode and in liquid phase, mass balances are developed for each component in mechanism 1. It is assumed that the mechanism follows homogeneous kinetics and elementary reaction steps. For the dimensions of the rate constants to be consistent, the units of copper leaching and peroxide must be converted respectively to their corresponding mass values before proceeding with the mass balances. The rate laws for mechanism 1 are shown under model 1.
Model 1
| |
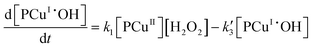
| (III.1) |
| |

| (III.2) |
| |

| (III.3) |
| |

| (III.4) |
| |

| (III.5) |
| |

| (III.6) |
It can be noted that E. coli decay rate (III.4) follows a complex kinetics because it depends on its concentration as well as on the one of PCuI˙OH, which in turn follows nonlinear kinetics. The proposed model is rather different than the Chick–Watson model and its variants.10
Since the main advantage of using copper-mediated compounds with respect to other transition metals is the ability of CuI and CuII to react with peroxide to form hydroxyl radicals, a second mechanism is proposed that accounts for the reaction of the PCuI with hydrogen peroxide to produce a second hydroxyl radical complex (PCuII˙OH). Two reversible reactions account for the decomposition of both polymer–catalysts (reactions (IV.4) and (IV.8)).
Mechanism 2
| |

| (IV.1) |
| |

| (IV.2) |
| |
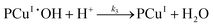
| (IV.3) |
| |

| (IV.4) |
| |

| (IV.5) |
| |

| (IV.6) |
| |
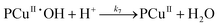
| (IV.7) |
| |
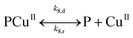
| (IV.8) |
Applying elementary steps to mechanism 2, the following differential equations are obtained:
Model 2
| |

| (V.1) |
| |

| (V.2) |
| |
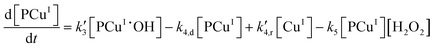
| (V.3) |
| |

| (V.4) |
| |
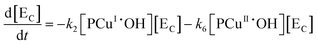
| (V.5) |
| |
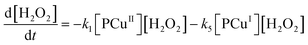
| (V.6) |
| |

| (V.7) |
| |
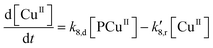
| (V.8) |
Eqn (III.1) to (III.6) form a system of nonlinear first order differential equations. The same holds for the system in (V.1) to (V.8). In both mechanisms 1 and 2 the rate constants in reactions II.3, II.4, IV.3, IV.4, IV.6 and IV.8 have been simplified to k3[H+] ≡ k′3; k4,r[P] ≡ k′4,r, k7[H+] ≡ k′7 and k8,r[P] ≡ k′8,r because concentrations of polymer and hydrogen ions remain constant in the system. Also, in comparison to reactions (I.1) and (I.2) from Baldrian's proposed mechanism, it is assumed that hydroxyl radicals are formed in a single step (reactions (II.1), IV.1 and IV.5). The reason for this assumption is the lack of information available for the steps involved in the formation of hydroxyl radicals through the reaction of polymer–copper complex and hydrogen peroxide. Thus, k1 and k5 in all proposed mechanisms represent the combined rate constant of all the reactions that might be involved in the generation of hydroxyl radicals.
A typical simplification assumed in models such as the ones presented in this paper is the Pseudo Steady State Hypothesis (PSSH), as discussed in Fogler.11 The main idea of the hypothesis is that reaction complexes have very fast dynamics and therefore behave as in the steady state. Specifically, PCuI˙OH in Model 1, and PCuI˙OH and PCuII˙OH in Model 2 are considered active species. If the PSSH holds, eqn (V.1) and (V.2) of the model can be simplified accordingly.
After simplification and representing the rate constants as (k1k2)/k′3 = kα and (k5k6)/k′7 = kβ, model 1 and model 2 can be reduce to PSSH 1 and PSSH 2, respectively:
Model PSSH 1
| |
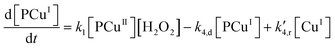
| (VI.1) |
| |

| (VI.2) |
| |

| (VI.3) |
| |

| (VI.4) |
| |

| (VI.5) |
Model PSSH 2
| |

| (VII.1) |
| |

| (VII.2) |
| |

| (VII.3) |
| |

| (VII.4) |
| |

| (VII.5) |
| |

| (VII.6) |
4. Results and discussion
Table 1 shows the results of E. coli load in contaminated water as a function of time and varying concentration of hydrogen peroxide and catalyst. These results will be used simultaneously to estimate the reaction rate constants and optimize the microbial decontamination system. Experiments with polymer–catalyst concentrations below 20 mg or hydrogen peroxide concentrations below 5 μL did not show any significant reduction in the bacterial load and are not shown in Table 1. Also, polymer–catalyst controls and hydrogen peroxide controls were carried out for all the concentrations mentioned in Table 1. No significant decrease in E. coli concentration was observed in any of the control experiments. Copper leaching was measured at the end of the experiments. Results described in Table 2 were used to validate the developed models. The copper leaching value for the data of Table 2 is estimated based on results from previous experiments as 149 ppm. All experiments were carried out in triplicates and the deviation was not more than 5% in any case.
| Initial concentrations |
| Case |
A |
B |
C |
D |
| PCuII/mg |
30 |
40 |
50 |
50 |
| H2O2./μL |
25 |
50 |
25 |
25 |
| Time/min |
E. coli load/cells mL−1 |
E. coli load/cells mL−1 |
E. coli load/cells mL−1 |
E. coli load/cells mL−1 |
| 0 |
1.01 × 109 |
1.01 × 109 |
1.01 × 109 |
1.01 × 109 |
| 20 |
5.00 × 105 |
2.00 × 105 |
5.00 × 105 |
5.00 × 105 |
| 40 |
4.00 × 105 |
1.00 × 104 |
1.50 × 105 |
1.00 × 105 |
| 60 |
2.00 × 105 |
1.00 × 103 |
1.50 × 105 |
1.50 × 105 |
| 80 |
2.00 × 104 |
0 |
2.00 × 104 |
1.50 × 104 |
| Initial concentration |
| PCuII/mg |
40 |
| H2O2/μL |
50 |
| Time/min |
E. coli load/cells mL−1 |
| 0 |
1.60 × 109 |
| 2 |
2.00 × 106 |
| 4 |
2.00 × 106 |
| 6 |
2.00 × 106 |
| 8 |
2.00 × 106 |
| 10 |
6.00 × 106 |
| 15 |
1.60 × 105 |
| 20 |
1.32 × 105 |
| 40 |
2.00 × 104 |
| 60 |
1.00 × 103 |
| 80 |
0 |
| 100 |
0 |
| 120 |
0 |
Parameter estimation
The models proposed in the previous section present sets of parameters that must be estimated. These are (k1, k2, k′3, k4,d and k′4,r) for model 1; (k1, k2, k′3, k4,d, k′4,r, k5, k6, k′7, k8,d and k′8,r) for model 2; (k1, kα, k4,d and k′4,r) for PSSH 1; (k1, kα, k4,d, k′4,r, k5, kβ, k8,d and k′8,r) for PSSH 2.
Parameter estimation is done using data presented in Table 1. Model parameters are optimized to generate values for their respective reaction rate constants and the log transformed dependent variables are used, including the organism concentration remaining. The estimation is done with Matlab® and the procedure is as follows: The nonlinear optimization function (lsqnonlin) minimizes the sum of squares of an objective function (Fmin). Fmin denotes the overall error from E. coli load and amount of copper leached that exists between the experimental and calculated concentrations while taking into account their normalized values with a weighted function. The objective function depends on a vector k, which contains guessed values for each parameter. Fmin evaluates a third function (ode_fun) at k with a solver for stiff ordinary differential equations (ode15s) that uses the Rosenbrock method and integrates the system of ordinary differential equations at every optimization step.
Fig. 1 is generated from case B of Table 1. Fig. 1 contains three time-dependent plots for all mechanisms. Fig. 1-A and 1-B represents the theoretical and experimental values for the E. coli load in water and for copper leaching, respectively. Fig. 1-C illustrates the predicted values for the concentrations of the reactive complexes.
 |
| | Fig. 1 Model behavior using data from Table 1 case B. (A) E. coli; (B) copper leached; and (C) reactive complexes. | |
E. coli concentration calculated for all models in Fig. 1-A follows a pattern similar to the corresponding experimental data, as evidenced by the last row of Table 3. In the next subsection each model will be validated with a different set of data (not used in the parameter estimation).
Table 3 Estimated parameters for all proposed models
| Parameters |
Model 1 |
PSSH 1 |
Model 2 |
PSSH 2 |
|
k
1/mg−1 min−1 |
9.9 × 10−4 |
9.8 × 10−4 |
2.2 × 10−3 |
7.4 × 10−4 |
|
k
2/mg−1 min−1 |
5.4 × 101 |
|
5.6 × 101 |
|
|
k′3/min−1 |
4.5 × 100 |
|
4.8 × 100 |
|
|
k
4,d/min−1 |
3.3 × 10−3 |
3.4 × 10−3 |
3.7 × 10−5 |
2.7 × 10−2 |
|
k′4,r/min−1 |
3.2 × 10−3 |
4.3 × 10−3 |
4.1 × 100 |
1.1 × 10−2 |
|
k
5/mg−1 min−1 |
|
|
6.5 × 10−1 |
1.1 × 10−1 |
|
k
6/mg−1 min−1 |
|
|
1.7 × 10−1 |
|
|
k′/min−1 |
|
|
3.4 × 10−14 |
|
|
k
8,d/min−1 |
|
|
1.6 × 10−4 |
9.3 × 10−14 |
|
k′8,r/min−1 |
|
|
4.0 × 10−2 |
6.3 × 10−1 |
|
k
α
/mg−2 min−1 |
|
1.2 × 10−2 |
|
1.3 × 10−2 |
|
k
β
/mg−2 min−1 |
|
|
|
1.7 × 10−12 |
|
R
2
|
0.669458 |
0.664907 |
0.312553 |
0.390275 |
In Fig. 1-B, the copper concentrations are plotted for all models. In the case of model 2 and PSSH 2; the parameters are estimated such that the overall copper concentration (CuI and CuII) fits the experimental data value at the end of the experiment. Since model 1 and PSSH 1 rely only on CuI, the estimation procedure minimizes the difference of this species with respect to the final measured copper concentration.
PSSH models 1 and 2 do not have any reactive complexes and therefore are not represented in Fig. 1-C. The reactive complex for model 2 is given by the sum of PCuI˙OH and PCuII˙OH, whereas model 1 has only PCuI˙OH. Fig. 1-C shows that PCuI˙OH increases quickly within the first 20 min then gradually decreases for the remaining 60 min for model 1 while model 2 remains approximately constant for the remaining time at about 1 mg. This indicates that if the PSSH was to be implemented, it will be effective after 20 min for model 2 and this is 25% of the entire reaction time. More evidence in the next subsection will support the fact that the PSSH models do not hold true for this system.
Model validation
Fig. 2 was generated and it is based on data from Table 2. Besides the plots presented in Fig. 1, plots of the concentration profile of the reactants are added to Fig. 2. Semi-log plots A and B show the concentration profiles of PCuII and H2O2, respectively. Figs. 2-C, D and E represent the concentrations of E. coli, copper leached and reactive complexes in that order. The concentration profiles of the reactants show a sharp decrease within the first 5 to 10 min, and H2O2 is depleted but the polymer–catalyst reactant does not readily decompose.
The final concentration of copper leached matches the experimental value for all models. Moreover, the reactive complexes increase in less than 5 min then steadily decrease for model 1 and the overall concentration (PCuI˙OH and PCuII˙OH) remains almost constant at about 1 mg for model 2, similar to the plot in Fig. 1-C.
The component with more experimental data points is E. coli, so plot C will be the main one in determining the applicability of each model. It shows the theoretical and experimental values for each mechanism from time 0 to 120 min. Moreover, the theoretical values were extrapolated from 120 min to 240 min in Fig. 2-C and it can be noted that model 1, PSSH 1 and PSSH 2 remain constant after extrapolation. Only model 2 continues to decontaminate the remaining E. coli in the system, which is what is observed experimentally. Therefore, it can be concluded that model 2 best fits the present treatment system. Finally, the statistical Fmax test was applied to model 2 with respect to model 1, which showed the non-homogeneity of the variances or the statistical significance of model 2.12 Hence model 2 will be used to optimize the process, as shown in the next subsections.
Sensitivity analysis
To investigate which parameters most affect the three major components (E. coli, copper leached and reactive complexes) of this system, a parameter sensitivity analysis was carried out. As previously mentioned, the parameters used are those from model 2. All ten parameters were changed by up to ±20% each. The effect on the final values of the three components was then compared to their corresponding base case values, which is when no change in the parameters occurs. Fig. 3 shows three plots with the effect of parameter variation on the three component concentrations.
 |
| | Fig. 3 Model 2 parameter sensitivity analysis. Effect on (A) E. coli; (B) copper leached and (C) reactive complex. | |
The parameters that most influence the final E. coli concentration are k2, k3, and k6, followed by k1 and k5. This result indicates that several factors influence the decontamination rate. Copper leached is strongly influenced by k8,d and k′8,r, and hence the reversible reaction IV.8 plays a main role in the toxicity of this process. Lastly, the reactive complex is affected by k1 and k5, which are the rates of formation of the reactive complexes (reactions IV.1 and IV.5).
Optimal initial concentrations of reactants
Fig. 4 contains three-dimensional plots of a combination of the final concentration of E. coli, and copper leaching as functions of the initial concentrations of polymer–catalyst and hydrogen peroxide. These plots confirm the experimental observation that no change in microbial load is observed when H2O2 concentration is below 5 μL or when PCuII is below 20 mg. This analysis also makes it possible to evaluate the dependence of copper leaching on the initial conditions (H2O2 and PCuII).
![Analysis of the initial concentration of PCuII [0–60 mg] and H2O2 [0–60 μL]. (A) E. coli. (B) Copper leached.](/image/article/2008/EE/b805642k/b805642k-f4.gif) |
| | Fig. 4 Analysis of the initial concentration of PCuII [0–60 mg] and H2O2 [0–60 μL]. (A) E. coli. (B) Copper leached. | |
The initial concentration of the E. coli colony is 1.60 × 109 cells mL−1, which is identical to that of Table 2. Fig. 4-A shows that PCuII hardly affects the bacterial load; however, if PCuII is present at a sufficiently low value, microbial decontamination ceases. The concentration of H2O2 strongly affects the bacterial load and brings it from a concentration level of 108 to 1 cell mL−1 for concentrations of 5 to 45 μL, respectively. In contrast, Fig. 4-B shows that copper leached hardly changes with respect to H2O2 and linearly increases with PCuII concentration. Note that the initial reactant concentrations that resulted in the lowest E. coli final value are PCuII at 50 mg and H2O2 at 60 μL; and the ones for the minimum copper leaching are PCuII at 20 mg and H2O2 at 60 μL.
Throughout this paper we have developed a mechanistic-based mathematical model for the decontamination of E. coli from wastewater based on a modified Fenton reaction. Currently experiments are under way in our laboratory involving the dynamic optimization of the process, as well as its scale up.
Nomenclature
| Notation |
Symbol |
| Total copper leached out of the system |
Cu |
| Copper I leached out of the system |
CuI |
| Copper II leached out of the system |
CuII |
| Baldrian's reactive complex |
CuI˙OOH |
|
E. coli present in the system |
EC |
|
E. coli remaining in the system |
EC,D |
| Experimental data |
Exp. |
| Hydrogen Ion |
H+ |
| Water |
H2O |
| Hydrogen peroxide |
H2O2 |
| Hydroxyl radical |
OH− |
| Reactive radical |
˙OH |
| Polymer |
P |
| Pseudo Steady State Hypothesis 1 |
PSSH 1 |
| Pseudo Steady State Hypothesis 2 |
PSSH 2 |
| Polymer–catalyst I |
PCuI |
| Polymer–catalyst II |
PCuII |
| Polymer–catalyst I bound to a hydroxyl radical |
PCuI˙OH |
| Polymer–catalyst II bound to a hydroxyl radical |
PCuII˙OH |
Acknowledgements
Financial support from the National Science Foundation (Grant CBET-0647137) is gratefully acknowledged. JMP also acknowledges H. Wechsler.
References
- K. Nakano, K. Suyama, H. Fukazawa, M. Uchida, K. Wakabayashi, T. Shiozawa and Y. Terao, Chlorination of harman and norharman with sodium hypochlorite and co-mutagenicity of the chlorinated products, Mutat. Res., 2000, 470, 141–146 CAS.
-
J. C. Crittenden, R. R. Trussell, D. W. Hand, K. J. Howe and G. Tchobanoglous, in Water treatment: Principles and design, John Wiley & Sons, NJ, 2005, pp. 583–586 Search PubMed.
- W. Glaze, J. -W. Kang and D. H. Chapin, Chemistry of water treatment processes involving ozone, hydrogen peroxide and ultraviolet radiation, Ozone Sci. Eng., 1987, 9, 3335–352.
-
W. Z. Tang, Physicochemical treatment of hazardous wastes, CRC Press, FL, 2004, pp. 165–227 Search PubMed.
- V. Shah, P. Verma, P. Stopka, J. Gabriel, P. Baldrian and F. Nerud, Decolorization of dyes with copper(II)/organic acid/hydrogen peroxide systems, Appl. Catal., B, 2003, 46, 287–292 CrossRef CAS.
- P. Verma, V. Shah, P. Baldrian, J. Gabriel, P. Stopka, T. Trnka and F. Nerud, Decolorization of synthetic dyes using a copper complex with glucaric acid, Chemosphere, 2004, 54, 291–295 CrossRef CAS.
- P. Baldrian, T. Cajthaml, V. Merhautova, J. Gabriel, F. Nerud, P. Stopka, M. Hruby and M. J. Benes, Degradation of polycyclic aromatic hydrocarbons by hydrogen peroxide catalyzed by heterogeneous polymeric metal chelates, Appl. Catal., B, 2005, 59, 267–274 CrossRef CAS.
- S. Shah, B. Dzikovski and V. Shah, Development of a new approach for microbial decontamination of water using modified Fenton's reaction, Environ. Pollut., 2007, 148, 674–678 CrossRef CAS.
- EPA SW-846, Test Methods for Evaluating Solid Waste, Vol 1A, 1B, 1C: Laboratory Manual Physical/Chemical Methods, and Vol 2: Field Manual Physical/Chemical Methods, U.S. Environmental Protection Agency, Office of Solid Waste and Emergency Response, Washington, DC, 3rd edn, 1986 Search PubMed.
- M. Cho, H. Chung and J. Yoon, Disinfection of water containing natural organic matter by using ozone-initiated radical reactions, Appl. Environ. Microbiol., 2003, 69(4), 2284–2291 CrossRef CAS.
-
S. Fogler, Elements of Chemical Reaction Engineering, Prentice Hall, Upper Saddle River, NJ, 4th edn, 2006 Search PubMed.
-
D. Sheskin, Handbook of Parametric and Nonparametric Statistical Procedures, Chapman and Hall, Boca Raton, FL, 3rd edn, 2004 Search PubMed.
Footnote |
| † Current address: Praxair Inc., 39 Old Ridgebury Road, Danbury, CT 06810, USA. |
|
| This journal is © The Royal Society of Chemistry 2008 |
Click here to see how this site uses Cookies. View our privacy policy here. 
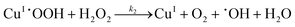
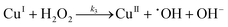




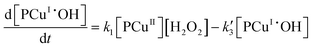







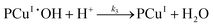



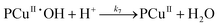



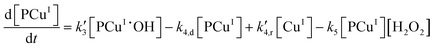

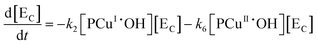
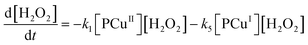

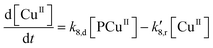
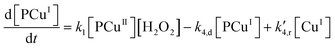













![Analysis of the initial concentration of PCuII [0–60 mg] and H2O2 [0–60 μL]. (A) E. coli. (B) Copper leached.](/image/article/2008/EE/b805642k/b805642k-f4.gif)


