View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/B712704A (Paper) Phys. Chem. Chem. Phys., 2008, 10, 114-120

From nanostrips to nanorings: the elastic properties of gold-glued polyauronaphthyridines and polyacenes

Pekka Pyykkö * and Patryk Zaleski-Ejgierd
Department of Chemistry, University of Helsinki, POB 55 (A. I. Virtasen aukio 1), 00014, Helsinki, Finland. E-mail: Pekka.Pyykko@helsinki.fi

Received 17th August 2007 , Accepted 3rd October 2007

First published on 23rd October 2007

Abstract

The previously proposed flat 2,6-diauro-1,5-naphthyridine polymers were bent to closed rings with up to 12 monomers. Their bending energies and lowest in-plane deformation frequencies were calculated at the DFT level using quasirelativistic pseudopotentials for gold. The ring-formation energies were compared with those for polyacene rings and found to be of the same order of magnitude, suggesting sufficient stability for the predicted polyauronaphthyridines. As function of the ring radius, r, the frequencies and deformation energies were shown to behave as r−2 and r−1, respectively. The molecules thus behave as classical elastic bodies.

1. Introduction

Gold atoms can act as an intermolecular glue, coupling (hetero)aromatic rings, typically through C–Au ← N bonds. We have recently predicted the possible existence of such poly(triaurotriazine) sheets,1 their Cu and Ag analogues2 and infinite nanostrips based on monomers such as naphthyridine.3

While there are chemically stable dimers and oligomers of such a type,4,5 no corresponding infinite polymers are yet experimentally known. We therefore here try to get a feeling for their mechanical rigidity by bending our nanostrips to rings and comparing that bending energy with the one for the corresponding polyacene rings, which have been considered before.6

The predicted rings may also exhibit interesting dispersion interactions with atoms or molecules inside them. The London-type theory of such interactions was just formulated.7

Apart from the energy needed to create the ring from a linear strip, we also use the in-plane deformation vibrational frequencies as a criterion for rigidity. The mathematical theory of such vibrations was already considered by Hoppe8 and later by Love.9 Note that we then treat molecules as elastic bodies.

A similar approach using the Hoppe solution for rings was used by Ceulemans and Vos to discuss the ring vibrations of benzene.10 The approach was also extended to spheres, modelling icosahedral fullerenes.10,11

2. Methods

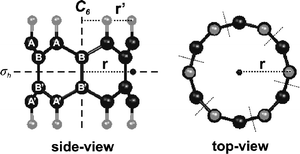
In our previous work we studied the structural and electronic properties of various infinite strips and sheets, composed from (hetero)aromatic rings coupled by C–Au–C, C–Au ← N and N → Au ← N bonds. To do so, we applied periodic boundary conditions and used the Vienna ab initio Simulation Package VASP.12–14 Here we study finite strips or strings and used instead mainly the TURBOMOLE package.15

In this paper we consider two families of rings. The first one consists of rings, composed from monomeric 2,6-diauro-1,5-naphthyridine units, ’glued’ together by C–Au ← N bonds. The second one consists of polyacene rings, composed from six-membered carbon-rings fused together. In both cases the number of monomeric units, N, ranged from 4 to 12.

We have also performed calculations for corresponding finite flat strips. For the gold-glued strips we calculated an isolated 2,6-diauro-1,5-naphthyridine molecule, and its oligomers, see Fig. 1. For the polyacene strips we started from the benzene molecule, adding C4H2 blocks, thus obtaining naphthalene, anthracene, etc., see Fig. 2.


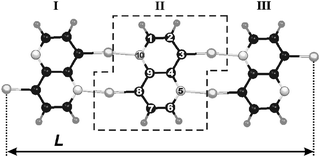The polynaphthyridine strip with N = 3. The dashed frame encircles a 2,6-diauro-1,5-naphthyridine monomer. All considered strips belong to the C2h symmetry point group. L defines a strip length.
Fig. 1 The polynaphthyridine strip with N = 3. The dashed frame encircles a 2,6-diauro-1,5-naphthyridine monomer. All considered strips belong to the C2h symmetry point group. L defines a strip length.

Examples on polyacene strips with an odd and even number, N, of six-membered carbon rings. All systems have a D2h symmetry. The dashed frame encircles a [C4H2] building unit. The distance L is taken as the polyacene length.
Fig. 2 Examples on polyacene strips with an odd and even number, N, of six-membered carbon rings. All systems have a D2h symmetry. The dashed frame encircles a [C4H2] building unit. The distance L is taken as the polyacene length.

2.1 Ab initio calculations

As mentioned, all currently considered systems were treated as isolated molecules. Ab initio calculations were performed within density functional theory (DFT)16,17 in combination with the resolution of identity (RI) technique18 as implemented in the TURBOMOLE V5.9 package. The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional with a generalized gradient-approximation (GGA)19,20 was employed. The structures were optimized with TZVPP basis sets on all atoms. All electrons were correlated in case of light elements. For the heavy, Au atoms, 19 valence electrons were treated explicitly, while the remaining inner ones were described by the latest Stuttgart pseudopotential,21 thereby accounting for scalar relativistic effects. All discussed structures were optimized with the symmetry constraints, explained in detail in section 3.1.

Our gold nanostrips and rings have relatively short Au⋯Au distances, imposed by the rest of the system. While those covalent interactions are well described by DFT, the dispersion interactions between the gold atoms are not.22 Therefore it may not be useful to extend the present basis, because other factors form the accuracy bottleneck.

We have also checked that the obtained results are not affected if a hybrid, B3-LYP exchange–correlation functional is used. Both the geometries and the energy differences obtained for a few test cases were close to the PBE results.

The presented structures and results correspond to closed shell singlets, for both rings and strips. In case of the longer polyacenes, the possibility of a diradical singlet state has been mentioned in the past. The latest studies show that a finite gap persists even for infinite polymers.23 We did find a decreasing HOMO–LUMO gap trend with increasing N.

2.2 Molecules as elastic bodies

For understanding the connection between the elastic deformation energies of the present ring systems and the vibrational frequencies of both the finite strips and the rings, it is useful to describe their classical counterparts, outlined in Fig. 3. Consider first a bar segment, as in Fig. 3A, B. The potential energy contribution due to bending is then (ref. 24, p. 190):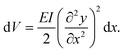
 
ugraphic, filename = b712704a-t1.gif(1)
Here EI has the SI dimension of N m2. For a macroscopic bar, made of a certain material with Young’s modulus E, [E] = N m−2, I is the cross-sectional inertia and [I] = m4. These we obviously cannot introduce for a molecule.
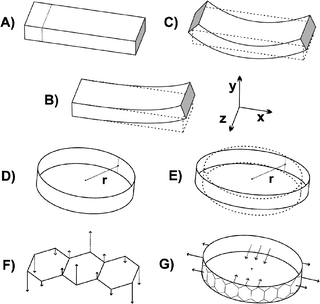Schematic illustration for the bar-type (A–C) and the ring-type (D–E) systems. Examples on the considered vibration modes are depicted in F and G.
Fig. 3 Schematic illustration for the bar-type (A–C) and the ring-type (D–E) systems. Examples on the considered vibration modes are depicted in F and G.

For a ring of radius r:

 
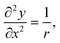ugraphic, filename = b712704a-t2.gif(2)
hence the total bending energy of the ring,

 
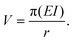
ugraphic, filename = b712704a-t3.gif (3)
The lowest vibrational angular frequency of a “free–free bar” is:24
 
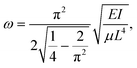ugraphic, filename = b712704a-t4.gif(4)
where L is the length, m the mass and μ = m/L the mass per unit length of the bar. Note that ω behaves as L−2. For arbitrary vibrational mode of a ring of radius r in its own plane, the results of Hoppe8 and Love,9 together with eqn (3), yield:
 
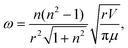ugraphic, filename = b712704a-t5.gif(5)
where n≥ 2 is the number of wavelengths along the ring. This yields a consistency check between V and ω:
 
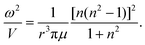ugraphic, filename = b712704a-t6.gif(6)
For the lowest, n = 2, mode of the in-plane ring vibration:
 
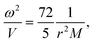ugraphic, filename = b712704a-t7.gif(7)
where M is the total mass of the ring. Finally, comparing eqn (4) and (5) (for n = 2), one finds that the ring of radius r has the same lowest frequency as a bar of length L for:
 
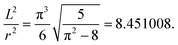ugraphic, filename = b712704a-t8.gif(8)
This corresponds to L/r = 2.90706 or L≈πr, half the ring perimeter.

The key conclusions from this subchapter are that, as function of the system size, the discussed vibrational frequencies should behave as L−2 and r−2 for the slabs and rings, respectively. The total bending energy of the system to a ring of radius r should go as r−1 for a given monomer. These laws can be used to analyze the quantum chemical results.

3 Results and discussion

3.1 Geometries

3.1.1 Polyacene rings and strips. We considered nine polyacene ring-type structures with N varying from 4 to 12. All systems were relaxed under Dnh symmetry. The radius, r, of each ring is defined as the distance from the molecular centre of symmetry to the midpoint between carbon atoms, CA–CA′, as depicted in Fig. 4. The corresponding radii and bond lengths are given in Table 1. While the A–B distances are almost constant, the B–B′ distances show an even–odd alternation (cf. ref. 25). For rings with even N, the distance CB–CB′ is slightly increasing with N, while for odd N it is almost constant. The C–H bond length is practically invariant. In the smallest ring (N = 4), the H atoms are bent outside the ring, so that the distance, r′, from each H atom to the main symmetry axis, Cn, is slightly larger than r.
An example on a polyacene ring. The black spheres stand for carbon and the gray spheres for hydrogen atoms. The radius of the ring, r, lies in a σh plane of symmetry and is defined as the distance from the center of symmetry to the HC ⋯ CH midpoint, given as a black dot). Each ring is composed of N C4H2 building blocks. All rings considered have Dnh symmetry.
Fig. 4 An example on a polyacene ring. The black spheres stand for carbon and the gray spheres for hydrogen atoms. The radius of the ring, r, lies in a σh plane of symmetry and is defined as the distance from the center of symmetry to the HC ⋯ CH midpoint, given as a black dot). Each ring is composed of N C4H2 building blocks. All rings considered have Dnh symmetry.
Table 1 Optimized ring radii (r, r′) and bond lengths for polyacene rings. The distances are defined as in Fig. 4. N is the number of [C4H2] building blocks. All values in pm
N r r′ CA–CB CB–CB′ CA–H
4 171.7 173.7 141.3 144.7 109.1
5 202.4 196.2 142.2 147.4 109.2
6 241.9 238.8 141.3 145.0 109.3
7 278.4 273.5 141.3 147.2 109.3
8 318.1 315.5 141.2 145.8 109.2
9 355.7 351.8 141.0 147.0 109.2
10 395.3 393.0 140.9 146.2 109.3
11 433.4 430.1 140.9 147.0 109.2
12 472.9 470.9 140.8 146.4 109.3

Already for N = 5, the hydrogen atoms start to turn towards the principal symmetry axis, Cn, so that r′ < r. For N > 5, r′→r and the CA–H bonds become closely parallel to the mentioned Cn axis.

In addition to rings, we have carried out calculations for several strip-type structures. The simplest ‘strip’ corresponds to the benzene molecule. It was optimized under D6h symmetry, while the larger systems with N > 1, were optimized under D2h symmetry. The length of a strip, L, is defined as the distance between the outermost symmetrically equivalent hydrogen atoms, see Fig. 2.

Our initial structures were fully symmetrical, with all C–C bonds set equal. After geometry optimization we found two types of C–C bond length alternations. The first one affects the ’vertical’ C–C contacts. The innermost, C1–C1′ bond length (see Fig. 2) was always the longest one, each following one decreasing in length. The second type of alternation refers to the ‘tilted’–C–C–C–C– bonds. The central part of the strips exhibits a lower degree of alternation. For details, see Table 2. A vibrational analysis revealed no imaginaries for the singlet states studied.

Table 2 Calculated bond lengths and the length, L, for polyacene strips (for the atom numbering, see Fig. 2). All values in pm
Length N 1 2 3 4 5 6 7 8 9 10
C0–C1 139.7 — 140.2 — 140.4 — 140.4 — 140.5 —
C1–C2 — 142.0 142.8 141.1 141.3 140.7 140.9 140.6 140.7 140.3
C2–C3 — 137.9 137.4 139.6 139.3 140.1 139.9 140.3 140.2 141.3
C3–C4 — — — 143.1 143.2 141.5 141.6 141.0 141.0 139.4
C4–C5 — — — 137.1 137.0 139.1 139.1 139.9 139.9 142.0
C5–C6 — — — — — 143.3 143.3 141.6 141.6 139.2
C6–C7 — — — — — 136.9 136.9 139.0 139.0 142.0
C7–C8 — — — — — — — 143.3 143.3 139.9
C8–C9 — — — — — — — 136.9 136.9 140.9
C9–C10 — — — — — — — — — 142.2
C11–C10 — — — — — — — — — 138.0
C1–C1′ 139.7 143.7 144.8 145.5 145.9 146.3 146.5 146.7 146.8 146.2
C3–C3′ — 141.6 142.4 145.3 145.6 146.2 146.3 146.6 146.7 146.2
C5–C5′ — — — 142.7 142.9 145.8 145.8 146.3 146.4 145.9
C7–C7′ — — — — — 143.0 143.1 145.9 145.9 145.3
C9–C9′ — — — — — — — 143.1 143.1 144.5
C11–C11′ — — — — — — — — — 141.7
L 431.0 676.9 922.5 1168.3 1414.2 1660.2 1906.2 2152.2 2398.4 2649.9

3.1.2 Naphthyridine rings and strips. Six poly-naphthyridine rings were considered, with the number of [Au2C8N2H4] units, N, varying from 4 to 10. All systems were relaxed with fixed Dn symmetry, starting from flat, fully symmetrical 2,6-diauro-1,5-naphthyridine units. The radius, r, is now defined as the distance from the molecular centre of symmetry to the Au–Au bond midpoint, as shown in Fig. 5. The corresponding radii and bond lengths are given in Table 3.
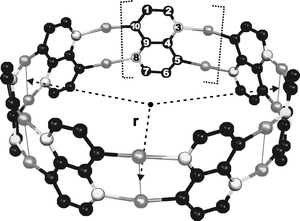The polynaphthyridine ring with N = 7. The black spheres are the carbon atoms, the gray spheres the gold atoms and the white spheres with a black border the nitrogen atoms. Each ring can be seen as N naphthyridine units, ‘glued’ together by Au atoms. The hydrogen atoms were removed for readability. All systems considered belong to Dn point groups.
Fig. 5 The polynaphthyridine ring with N = 7. The black spheres are the carbon atoms, the gray spheres the gold atoms and the white spheres with a black border the nitrogen atoms. Each ring can be seen as N naphthyridine units, ‘glued’ together by Au atoms. The hydrogen atoms were removed for readability. All systems considered belong to Dn point groups.
Table 3 Calculated bond lengths and radius, r, for polynaphthyridine rings. For the atom notation, see Fig. 5. All values in pm
Length/N 4 5 6 7 8 9 10
C1–C2 139.9 139.8 139.7 139.7 139.7 139.6 139.6
C2–N3 133.7 133.6 133.5 133.5 133.4 133.4 133.4
N3–C4 138.7 138.8 138.8 138.8 133.9 138.9 139.0
C4–C5 144.4 144.4 144.4 144.4 144.4 144.4 144.4
C5–C6 139.2 139.2 139.1 139.1 139.1 139.1 139.1
C6–C7 139.9 139.8 139.7 139.7 139.7 139.7 139.7
C7–N8 133.7 133.6 133.5 133.5 139.4 133.4 133.4
N8–C9 138.7 138.8 138.8 138.8 138.9 138.9 139.0
C9–C4 144.0 144.1 144.2 144.2 144.3 144.3 144.3
C9–C10 144.4 144.4 144.4 144.4 144.4 144.4 144.4
C10–C1 139.2 139.2 139.1 139.1 139.1 139.1 139.1
N3–Au 214.6 213.5 213.3 213.0 212.9 212.8 212.7
C5–Au 200.6 200.4 200.4 200.4 200.4 200.4 200.4
Au–Au 274.4 272.8 272.4 271.7 271.4 271.2 271.1
R 442.4 553.4 641.1 775.9 871.1 998.5 —

In contrast to polyacene rings, there is no alternation between the rings with odd and even N. While the coupled aromatic rings of a polyacene form a single aromatic system, the present (hetero)aromatic monomers are simply ‘glued’ together by σ-bonded gold atoms. Interestingly, the N → Au and the Au–Au bond lengths decrease slightly for larger systems, while the Au–C distances remain practically the same.

The simplest member of the corresponding strip family is the 2,6-diauro-1,5-naphthyridine molecule. Like the longer strips, it was optimized with C2h symmetry. The length of a strip, L, is defined as in Fig. 1. The geometry optimizations did not reveal any significant bond length alternation. The results are collected in Table 4. A vibrational analysis shows only real frequencies.

Table 4 Bond lengths and strip lengths, L, calculated for selected flat polynaphthyridine systems (for the monomer notation and bond description, see Fig. 1)
  N = 1 N = 2 N = 3 N = 4
Length I I II I II III I II III IV
C1–C2 141.8 141.0 140.4 140.9 139.6 140.4 141.0 139.6 139.6 140.4
C2–C3 137.9 139.1 137.9 139.1 139.0 138.0 139.1 139.0 139.0 138.0
C3–C4 142.6 144.2 142.5 144.2 144.5 142.6 144.2 144.5 144.5 142.6
C4–N5 136.0 138.8 136.1 138.8 138.8 136.1 138.9 138.9 138.8 136.1
N5–C6 131.9 133.3 132.0 133.3 133.3 132.1 133.3 133.3 133.3 132.1
C6–C7 141.8 140.4 141.0 140.4 139.6 140.9 140.4 139.6 139.6 141.0
C7–C8 137.9 137.9 139.1 138.0 139.0 139.1 138.0 139.0 139.0 139.1
C8–C9 142.6 142.5 144.2 142.6 144.5 144.2 142.6 144.5 144.5 144.2
C9–C4 144.7 144.4 144.4 144.4 144.5 144.4 144.4 144.4 144.4 144.4
C9–N10 136.0 136.1 138.8 136.1 138.8 138.8 136.1 138.8 138.9 138.9
C3–Au 197.9 200.7 197.7 200.6 200.5 197.7 200.6 200.4 200.5 197.7
C8–Au 197.9 197.7 200.7 197.7 200.5 200.6 197.7 200.5 200.4 200.6
N5–Au — 212.8 — 212.7 212.8 — 212.7 212.6 212.8 —
N10–Au — — 212.8 — 212.8 212.7 — 212.8 212.6 212.7
N 1 2 3 4 5 6 7 8 9 10
L 678.7 1376.6 1675.0 2772.9 3870.8 4968.7 6066.6 7164.5 8262.4 9360.3

3.2 Vibrational analysis

The vibrational frequencies were calculated for all the considered strip- and ring-type molecules. We focus on the energetically lowest-lying modes, corresponding to the macroscopic vibrational modes of a stiff slab and a ring in Fig. 3. When available, the experimental frequencies agree well with our results, see Table 5 and Table 6.
Table 5 Calculated frequencies of the out-of-plane vibrational modes for polyacene and polynaphthyridine strips. An example on the mode is shown in Fig. 3F
  Calculated frequencies/cm−1
  Polyacene strips Polynaphthyridine strips
N Type Calc. Exp. Type Calc.
a Ref. 26. b Ref. 27. c Ref. 28 (B3LYP/6-31-G, calculation).
1 e3u 400 398a au 39.33
2 b1u 170 176b au 11.20
3 b1u 95 108b au 7.40
4 b1u 59 57c au 4.17
5 b1u 47 — — —
6 b1u 42 — — —
7 b1u 28 — — —
8 b1u 22 — — —
9 b1u 19 — — —
10 b1u 17 — — —

Table 6 Calculated out-of-plane vibrational frequencies for polyacene and polynaphthyridine rings. Uncertain results are in italics. For illustration of the corresponding distortion, see Fig. 3G
  Calculated frequencies/cm−1
  Polyacene rings Polynaphtyrydine rings
N Type Calc. Type Calc.
4 b1u 255 au 24.19
5 b1u 206 au 14.71
6 b1u 147 au 12.06
7 b1u 110 au 6.51
8 b1u 81 au 5.89
9 b1u 69 au 6.75
10 b1u 48 au 7.81

An accurate determination of the frequency values for larger systems, especially for the polynaphthyridine strips, posed certain problems. Due to a symmetry, lower than for the rings, as well as to the large number of atoms and the fact that considered values are rather small, we do not expect the results for the largest systems to be reliable, and hence they were excluded from further consideration, see Table 5 and Table 6 for details.

We have also checked that the ω(L−2) relation is correct for two higher vibrational modes, corresponding to the n = 3 and n = 4, where n is given by eqn (5). Results are given in Fig. 7 and 9. The calculated ratios of slope coefficients: 1[thin space (1/6-em)]:[thin space (1/6-em)]2.32[thin space (1/6-em)]:[thin space (1/6-em)]4.21, are comparable to the theoretical values of 1[thin space (1/6-em)]:[thin space (1/6-em)]2.82[thin space (1/6-em)]:[thin space (1/6-em)]5.42 obtained from eqn (5). We found that for n = 3, the benzene ‘strip’, and for n = 4 also the naphthalene strip had to be excluded from further consideration. With a larger number of nodes those molecules were found to be too ‘short’ to reproduce the higher-order distortions in a reliable manner. Similar trends were observed for naphthyridine series.


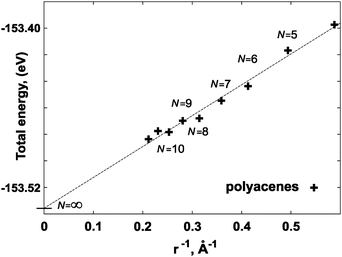Extrapolation scheme based on the polyacene case. The extrapolated value E∞Ring, at 1/r→ 0, corresponds to the energy of a monomer in the ring of an infinite radius, N→∞.
Fig. 6 Extrapolation scheme based on the polyacene case. The extrapolated value E∞Ring, at 1/r→ 0, corresponds to the energy of a monomer in the ring of an infinite radius, N→∞.

The main conclusion from Fig. 7, 8 and 9 is that, as function of system size, the considered vibrational frequencies indeed behave as predicted by the classical model, i.e. they are proportional to the length parameter r or L to the power of −2. The small deviations occurring for higher n values, could be related to the mentioned ‘length problem’ or the harmonic approximation. This is the first observation, to our knowledge, that a molecular sequence behaves in this respect as a series of elastic bodies.


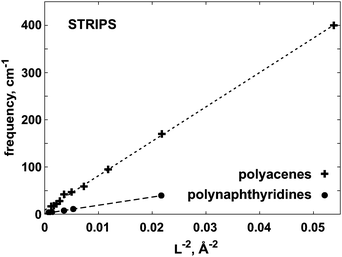The ω versus L−2 dependence for polyacene and polynaphthyridine strips. The frequency ω corresponds to the lowest ‘butterfly’ deformation of the strip, see Fig. 3F.
Fig. 7 The ω versus L−2 dependence for polyacene and polynaphthyridine strips. The frequency ω corresponds to the lowest ‘butterfly’ deformation of the strip, see Fig. 3F.

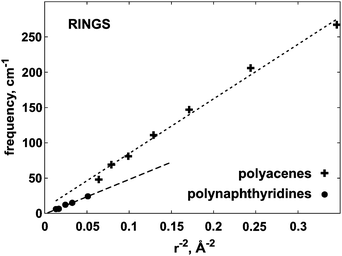The ω versus r−2 dependence for polyacene and polynaphthyridine rings. The frequency ω corresponds to the out-of-plane deformation, shown in Fig. 3G.
Fig. 8 The ω versus r−2 dependence for polyacene and polynaphthyridine rings. The frequency ω corresponds to the out-of-plane deformation, shown in Fig. 3G.

3.3 Bending energies of the rings

The unknown closing energy of the ring would impair attempts to determine the energy, required for bending a strip into a ring through their total energies for the polyacenes.

There is a difference of a [C2H4] block between the corresponding polyacene ring and strip, hence the different number of atoms makes this kind of direct comparison impossible.

For the naphthyridines, the rings are indeed just bent strips with the same general formula, (Au2C8N2H4)n, but an extra complexation energy would still arise.

Therefore an alternative reference for the energy of a flat, infinite polymer was obtained by letting the ring radius approach infinity, first verifying the r−1 behavior of the deformation energy, see Fig. 6. The extrapolated energy value E∞Ring, is the energy per monomer in a ring of infinite diameter.


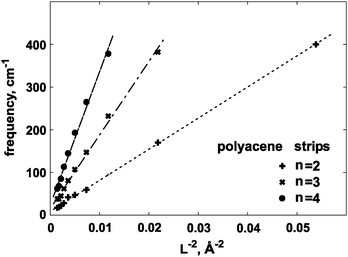Calculated out-of-plane vibrational frequencies for the polyacene strips, for the three lowest n values, as a function of L−2. Here, n is defined in eqn (5).
Fig. 9 Calculated out-of-plane vibrational frequencies for the polyacene strips, for the three lowest n values, as a function of L−2. Here, n is defined in eqn (5).

The energy of bending the strips into rings is then defined by:

 
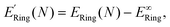ugraphic, filename = b712704a-t9.gif(9)
where ERing(N) is the total energy of one monomer and E′Ring(N) is the excess energy per one monomer, see Table 7.

Table 7 Calculated bending energy (kJ mol−1), for polyacene and naphthyridine rings, per one unit N. All values were calculated according to eqn (9)
  Bending energy
N Polyacene ring Polynaphthyridine ring
4 240.9 86.5
5 190.2 55.4
6 119.3 38.5
7 90.6 28.2
8 56.0 21.6
9 50.7 17.0
10 28.6 13.7
11 30.8 —
12 14.5 —

A further consistency check between the calculated vibrational frequencies and bonding energies was performed using eqn (7). This relation combines the energetic properties, ω and E′Ring(N), with the physical parameters, M and r. The computationally calculated results are consistent with theoretically expected values, see the caption of Fig. 10. The linear dependence provides further support to the model and shows that the polyacene and polynaphthyridine rings behave in a similar fashion.


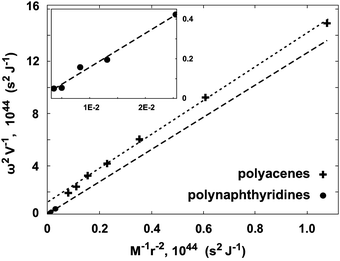The consistency check according to eqn (7). The two sets of data correspond to polyacene, +, and polynaphthyridine,●, structures. The fitted slopes of the two lines are 14.32 and 13.64 for the two systems, respectively. These can be compared to the slope of 72/5 = 14.4, predicted by eqn (7).
Fig. 10 The consistency check according to eqn (7). The two sets of data correspond to polyacene, +, and polynaphthyridine,●, structures. The fitted slopes of the two lines are 14.32 and 13.64 for the two systems, respectively. These can be compared to the slope of 72/5 = 14.4, predicted by eqn (7).

Based on eqn (3), we now can also define deformation energy as:

 
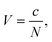ugraphic, filename = b712704a-t10.gif(10)
whose coefficient, c (kJ mol−1), is one possible measure of the relative stiffness of the two families of polymers. The coefficients cPAC and cPNP, for the polyacene and polynaphthyridine ring families, respectively, are given in Table 8.

Table 8 Comparison of the constants; πEI, as in eq. (3) and c, as in eqn (10), for the polyacene (PA) and polyauronaphthyridine (PAN) rings
System πEI/kJ mol−1Å c/kJ mol−1
PA 2152 4889
PAN 1555 1386
PA/PAN 1.38 3.51

4 Conclusions

We have shown that the polymer strips and rings of the present type have deformation energies and frequencies that behave as x−1 and x−2, respectively, where x is a size parameter (length or radius) of a particular oligomer. This corresponds exactly to the behavior expected for a classical elastic body.

The corresponding pre-coefficients for our proposed polyauronaphthyridine systems are not drastically smaller than those for the experimentally known polyacene systems. Therefore the proposed systems with “gold as intermolecular glue” may also be sufficiently stable for experimental synthesis and further study.

Acknowledgements

We belong to the Finnish Center of Excellence in Computational Molecular Science (2006–2011). The Center of Scientific Computing (CSC, Espoo Finland) is acknowledged for providing computer resources.

References

  1. M. O. Hakala and P. Pyykkö, Chem. Commun., 2006, 2006, 2890 RSC.
  2. P. Zaleski-Ejgierd, M. O. Hakala and P. Pyykkö, Phys. Rev. B, 2007, 76, 094104 CrossRef.
  3. P. Pyykkö, M. O. Hakala and P. Zaleski-Ejgierd, Phys. Chem. Chem. Phys., 2007, 9, 3025 RSC.
  4. L. G. Vaughan, J. Am. Chem. Soc., 1970, 92, 730 CrossRef CAS.
  5. L. G. Vaughan, J. Organomet. Chem., 1980, 190, C56 CrossRef.
  6. J. M. André, B. Champagne, E. A. Perpète and M. Guillaume, Int. J. Quantum Chem., 2001, 84, 607 CrossRef CAS.
  7. P. Pyykkö, C. Wang, M. Straka and J. Vaara, Phys. Chem. Chem. Phys., 2007, 9, 2954 RSC.
  8. R. Hoppe, J. Reine Angew. Math., 1871, 73, 158 Search PubMed.
  9. A. E. H. Love, Proc. London Math. Soc., 1893, 24, 118 Search PubMed.
  10. A. Ceulemans and I. Vos, Mol. Phys., 1991, 72, 1051 CrossRef CAS.
  11. A. Ceulemans, P. W. Fowler and I. Vos, J. Chem. Phys., 1994, 100, 5491 CrossRef.
  12. G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558 CrossRef CAS.
  13. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
  14. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS.
  15. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165 CrossRef CAS.
  16. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864 CrossRef.
  17. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133 CrossRef.
  18. M. Sierka, A. Hogekamp and R. Ahlrichs, J. Chem. Phys., 2003, 118, 9136 CrossRef CAS.
  19. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B, 1992, 46, 6671 CrossRef CAS.
  20. A. D. Becke, J. Chem. Phys., 1992, 97, 9173 CrossRef CAS.
  21. D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227 CrossRef CAS.
  22. S. Kristyán and P. Pulay, Chem. Phys. Lett., 1994, 229, 175 CrossRef CAS.
  23. J. Hachmann, J. J. Dorando, M. Avilés and G. K.-L. Chan, J. Chem. Phys., 2007, 127, 134309 CrossRef.
  24. J. P. Den Hartog, Mechanical Vibrations, McGraw-Hill, New York, London, 1947 Search PubMed.
  25. H.-S. Choi and K.-S. Kim, Angew. Chem., Int. Ed., 1999, 38, 2256 CrossRef CAS.
  26. K. V. Berezin and E. K. Kosterina, J. Appl. Spectrosc., 1998, 65, 196 CrossRef CAS.
  27. L. M. Sverdlow, M. A. Kovner and E. P. Krainov, Vibrational Spectra of Polyatomic Molecules, Nauka, Moscow, 1970 Search PubMed.
  28. A. M. Pivovar, J. E. Curtis, J. B. Leao, R. J. Chesterfield and C. D. Frisbie, Chem. Phys., 2006, 325, 138 CrossRef CAS.
This journal is © the Owner Societies 2008