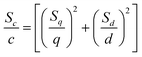Direct analysis of clay and refractory materials slurries by inductively coupled plasma optical emission spectrometry with axial viewing using the simplified generalized standard additions method

Abstract

The feasibility of clays and refractory materials analysis by direct introduction of slurries in an inductively coupled plasma optical emission spectrometry (ICP-OES) with axial viewing using the simplified generalized standard additions method (GSAM) was evaluated. The adopted approach is a multivariate extension of the conventional standard additions method, and uses two independent variables for determination of the analytes’ concentrations (the sample masses and the volumes of reference solutions added) and one dependent variable, the response. The relationship between the sample mass, volume of the reference solution added and the signal intensity is assumed to be linear. Concentrations of the analytes can be found either geometrically, from the slope of the two-dimensional response plane in a three-dimensional space, or mathematically from the ratio of the parameters estimated by multiple linear regression. Aluminium, Ca, Fe, K, Mg, Na, P, Si, and Ti were determined in clays and refractory materials slurries (10% v/v HNO₃) of certified reference materials. The software “Teach/Me” was used to fit the data. Aluminium oxide was detected in the 0.36–73.0%, CaO in the 0.03–2.13%, Fe₂O₃ in the 0.56–3.39%, K₂O in the 0.03–3.58%, MgO in the 0.06–0.47%, Na₂O in the 0.01–0.45%, P₂O₅ in the 0.05–0.13%, SiO₂ in the 22.2–98.42% and TiO₂ in the 0.06–1.95% range. Applying a paired t-test it was shown that all results were in agreement at a 95% confidence level with certified values. The application of GSAM was demonstrated as an effective method for the analysis of clays and refractory materials slurries.

---

Introduction

Ceramic compounds include advanced materials of great importance in various fields of modern technology. The design of both structural and functional ceramics for industrial applications and electronic devices requires the development of methods in the analytical sciences.^1,2

Most analytical methods require that samples are converted in representative solutions prior to analysis. The decomposition of inorganic samples with high chemical resistance and low fusibility, such as refractory compounds, siliceous minerals and ceramics, generally involves fusion³ or acid digestion using concentrated acids, especially HF.⁴ The process of decomposition can lead to losses of volatile elements, contamination, dilution of analytes and incomplete dissolution of the sample.^5–7

Because of the problems encountered with sample decomposition procedures and an increase in the demand for new types of ceramic materials, the direct introduction of slurries into plasmas is an alternative to circumvent these difficulties and markedly reduce sample preparation time by combining matrix destruction and analyte atomization and excitation in a single step.^6,8 Analytical plasmas are, in general, higher temperature sources than conventional combustion flames, a prerequisite if complex solid matrices are to be efficiently atomized, ionized and excited.^6,8,9

In the direct analysis of slurries by ICP-OES it is necessary to control particle size distribution, density of particles, concentration of slurry, flow rate, geometry of spray chamber, diameter of the torch injector tube, radiofrequency power, viewing height, and dispersing agent medium because all these factors can influence signal intensities.

The careful control of these parameters and the requirement to obtain accurate results are strictly connected with three fundamental criteria: (a) transport efficiency of the sample slurry through the nebulization system towards the plasma; (b) incomplete atomization of the sample particles in the slurry; and (c) instability of the particles in the slurry.^10,11

Calibration of the instrument is one the most difficulty steps when analyzing inorganic materials slurries by ICP-OES. The major problems caused by the presence of solid particles in direct analysis of slurries by ICP-OES are: (1) the analyte from the slurry must be physically transported into the plasma with the same efficiency as in the solution; and (2) particle—plasma interactions give rise to interference effects that are influenced by the size, mineralogy, and chemical composition of solid particles.^9,12 The processes of the refractory mineral species in the slurry will not be the same as for an aqueous droplet in the plasma and the residence times are different.

Simple calibration using aqueous reference solutions is one of the main goals of researches in this field.^13–15 A slurry must produce atomization–excitation of analytes with the same efficiency shown by the calibrating solutions. The dissociation process for slurries and for solutions can be assumed to be similar, since the vast majority (99.9%) of the solution/slurry is solvent. Thus, in this kind of calibration, any differences between transportable slurries and solutions should arise in the processes in the plasma.¹³

In the slurry technique sometimes it is possible to calibrate by applying the standard additions method with aqueous reference solutions. However, the prerequisite is the identical behaviour of solutions and slurries in the ICP-OES. As a criterion for achievement of this aim, the ratio of the intensities of matrix line for the slurry and a solution containing the same amount of sample should be measured. Slurry nebulization in ICP-OES can be applied reliably when this ratio is equal to 1.^16–18

When the maximum intensity obtained for the slurry is different from that for a reference solution, four other different strategies can be applied to overcome this problem: (1) use of certified standard reference powders materials with physical and chemical characteristics as similar as possible to those of the materials to be analyzed; (2) use of correction factors, which may be promising if the processes in the plasma do not strongly depend on the elements; (3) use of an internal standard, which may compensate transport efficiencies and inefficient atomization of slurry; and (4) use of generalized standard additions method (GSAM).¹⁹

The GSAM uses multiple linear regression to process data obtained for multi-component samples in which the response/analyte concentration relationship is of some arbitrary polynomial.²⁰

The method of multiple linear regression treats all data simultaneously: it means that all individual information existing between the independent variables and the dependent variable, with that on the matrix and transport effects, can be corrected simultaneously by the model,²¹ since it establishes an existent mathematical relationship between sample mass and the volume of the reference solution that will be reflected in the intensity of the signal.

In the GSAM, determinations are based on the premise that the analyte concentration is a function of two independent variables, sample mass (x) and volume of reference solution added (y), and one dependent variable, the signal intensity (z). A linear relationship is assumed to exist between the variables:

z_i = a + bx_i + qcy_i + e_i (1)

i = 1, 2, …, N, where N is the number of points, a is the spectral background, b is the sensitivity (slope), c is analyte concentration in the sample, and e_i is an error term related to point i. It is assumed that error terms e_i of different observations are independent with zero mean. It can be assumed that b and q are the same for the sample mass and the reference solution and the model can be expressed by:

z_i = a + bx_i + dy_i (2)

where d = qbc. The unknown parameters to be estimated are a, b and d. The concentration c can be calculated from the ratio of parameters d and b: both can be estimated by linear multiple regression.

Geometrically, the simplified GSAM can be expressed as a two-dimensional response surface in a three-dimensional space. The two-dimensional surface is less sensitive to curvature than the response line in the conventional standard additions method.¹⁹ In the three-dimensional model (GSAM), the concentration is less sensitive to curvature than the response line in the conventional standard additions method (two-dimensional model).²⁰

Owing to the fact that the model presented here has a linear equation, it has some limitations concerning the non-linearity of the response plane:^19,20

(1) sensitivity (b) is constant under the conditions used (e.g., b does not depend on the concentration or the amount of matrix);

(2) non-specific response (background) is not a function of the amount of matrix;

(3) contamination is constant in all the experiments (points).

The conventional standard additions method is able to correct only for matrix effects affecting the slope of the calibration line, but nonspecific background signals are not eliminated. The GSAM also corrects for interferences caused by the matrix components and limited selectivity of the sensors used.²⁰

Kalivas and Kowalski investigated various types of interferences in ICP-OES. The authors verified that the GSAM in multi-component analysis provides a means of detecting the interference effects, quantifying the magnitude of the interferences, allowing the use of the most sensitive wavelengths for all analytes, and simultaneously determining analyte concentrations with adequate accuracy and precision.²²

The advantage of the GSAM over other multivariate methods is that both spectral interferences and matrix effects can be overcome simultaneously. Luan et al. verified the matrix effects in As–Cd–Na samples for determination of As and Cd by ICP-OES. The results were accurately corrected when GSAM was employed independent of the matrix utilized.²³

Recently, Marjanovic et al.¹⁹ used the simplified GSAM for the analysis of cement, gypsum and basic slurries by ICP-OES. Aluminium, Ca, Fe, Mg, Mn, S and Si were determined and the results were in agreement with the certified values, except for Ca in cement, Ca and Fe in gypsum samples and Al, Mg, and Mn in basic slag. All analytes were determined in the matrices as they are in the samples, so matrix effects and the need for closely-matched standards were also avoided.

The procedure proposed here was based on the use of simplified GSAM to analyse clays and refractory materials slurries by ICP-OES with axial viewing.

Experimental

Instrumentation

The analysis of clay and refractory materials was performed using a VISTA AX simultaneous ICP-OES with axial viewing configuration (Varian, Mulgrave, Australia). This equipment has a charge coupled detector that makes it possible to obtain a two-dimensional echellogram, which enables a faster detection of spectral interferences. The sample introduction system consisted of a reduced-volume Sturman–Masters type spray chamber made of polytetrafluorethylene (PTFE) and a V-groove nebulizer. The inner surface of the spray chamber has a rough surface to ensure proper drainage, an aspect relevant for the introduction of slurries. The operating parameters and analyte emission lines are listed in Table 1.

Table 1 Instrumentation and operating conditions for ICP OES with axial viewing

Operating parameters
Rf generator/MHz	40
Power/kW	1.3
Plasma gas flow rate/L min^−1	15
Auxiliary gas flow rate/L min^−1	1.5
Nebulizer gas flow rate/L min^−1	0.9
Replicates	3
Injector tube diameter/mm	2.4
Spray chamber	Sturman–Masters
Nebulizer	V-groove
Emission lines/nm	Al I 394.399
	Ca II 422.673
	Fe I 239.561
	K I 766.480
	Mg II 280.268
	Na I 589.592
	P I 213.618
	Si I 288.158
	Ti II 334.938

---

Samples and reagents

All reagents employed were of analytical grade. Nitric acid (Merck, Darmstadt, Germany) was used for slurry preparation. The slurries were prepared with Milli-Q water (Millipore, Bedford, MA, USA).

Clays (IPT-28, IPT-32 and IPT-42) and refractory certified reference materials (IPT-51, IPT-57 and IPT-63) prepared by the Instituto de Pesquisas Tecnológicas, São Paulo, SP, Brazil, were used.

Grinding step and particle size distribution determination

The samples were ground for 30 min in a high impact ball mill (SPEX 8000 CertPrep, Metuchen, NJ, USA) using a tungsten carbide receptacle and 2 balls (od 10 mm). Ground samples were screened through a 37 μm (400 mesh) Nylon sieve. Slurries were prepared using the sample fraction with particle sizes lower than 37 μm. Each sample was dried at 105 °C for 1 h after the grinding step.

The particle size distribution was determined using a Mastersizer Microplus MAF 5001 (Malvern, Worcestershire, UK) based on laser diffraction and Mie scattering polarization intensity differential scattering.

Preparation of slurries

Slurries were prepared by weighing a required mass of samples (60.0, 90.0 and 120.0 mg) and transferring it quantitatively to 100 mL volumetric flasks. After transferring the sample, a volume of multi-element reference solution was added by means of a pipette, and slurries were made up to the mark in a medium containing 10% v/v HNO₃. The slurries were placed in an ultrasonic bath (Unique Model 1400, SP, Brazil) for 5 min before the analysis to allow particle disaggregation. A vortex mixer (Maxi Mix II, Thermolyne, USA) was used to ensure homogeneity of slurry samples before introduction into the ICP-OES. This procedure was based on a procedure developed by Silva et al. for the analysis of clays.²⁴

The reference standard solution was prepared by additions of mono-element solutions of Al, Ca, Fe, K, Mg, Na, P, Si and Ti from stocks containing 1000 mg L⁻¹ of each analyte. For each one of masses used 1.0, 2.0 and 3.0 mL of the multi-element reference solution (450 mg L⁻¹ Si and Al; 10 mg L⁻¹ Ca, K, Mg, Na, and P; and 30 mg L⁻¹ Fe and Ti) were added (Table 2). Thus, the masses of suspended materials and volumes of reference solutions were simultaneously varied.

Table 2 Experimental parameters of the generalized standard additions method for the determination Al, Ca, Fe, K, Mg, Na, P, Si, and Ti in certified reference materials of clays and refractories slurries in 10% v/v HNO₃

Point	Sample mass/mg	Volume of reference solution/mL	Point	Sample mass/mg	Volume of reference solution/mL
A	0	0	I	0	2.0
B	60.0	0	J	60.0	2.0
C	90.0	0	K	90.0	2.0
D	120.0	0	L	120.0	2.0
E	0	1.0	M	0	3.0
F	60.0	1.0	N	60.0	3.0
G	90.0	1.0	O	90.0	3.0
H	120.0	1.0	P	120.0	3.0

---

The software “Teach/Me—Data Analysis” (developed by H. Lohninger, Vienna University of Technology) was used to fit the data in order to find the parameters a, b and d.²⁵

Results and discussion

The mean particle sizes for all certified reference materials varied from 6.1 to 12.8 μm and these values are superior to the ones recommended in literature (<5 μm) for slurry introduction in ICP-OES.^2,6,26 It was also observed that up to 76.1% of the particles were smaller than 19.3 μm.

The application of the simplified GSAM to ceramic slurries led to the results presented in Table 3.

Table 3 Analysis of clay (IPT-28, 32 and 42) and refractory (IPT-51, 57 and 63) slurries by ICP-OES. Certified and determined values (mean ± standard deviation, n = 3)

Element as oxide		IPT-28	IPT-32	IPT-42	IPT-51	IPT-57	IPT-63
a Correlation coefficient <0.5. b The determined values are close to 0.
Al2O3	Determined value (%)	37.8 ± 8.18	31.2 ± 2.8	32.1 ± 11.18	45.2 ± 10.6	73.0 ± 4.46	0.36 ± 0.11
	Certified value (%)	37.58 ± 0.22	28.5 ± 0.3	32.2 ± 0.1	40.3 ± 0.1	71.5 ± 0.2	0.48 ± 0.01
CaO	Determined value (%)	0.13 ± 0.02	0.18 ± 0.01	0.07 ± 0.16	0.07 ± 0.03	0.06 ± 0.01	2.13 ± 0.16
	Certified value (%)	0.10 ± 0.03	0.17 ± 0.03	0.06 ± 0.01	0.06 ± 0.01	0.05 ± 0.01	2.21 ± 0.03
Fe2O3	Determined value (%)	0.88 ± 0.14	3.39 ± 0.31	1.24 ± 0.99	0.99 ± 0.27	1.08 ± 0.18	0.56 ± 0.07
	Certified value (%)	0.83 ± 0.06	3.46 ± 0.10	1.09 ± 0.06	1.19 ± 0.03	1.25 ± 0.02	0.52 ± 0.02
K2O	Determined value (%)	0.03 ± 0.03	0.96 ± 0.05	3.58 ± 2.62	0.59 ± 0.11	0.75 ± 0.05	0.06 ± 0.05
	Certified value (%)	0.03 ± 0.01	0.80 ± 0.05	2.15	0.69 ± 0.03	0.83 ± 0.03	0.043 ± 0.003
MgO	Determined value (%)	0.06 ± 0.02	0.47 ± 0.04	—^a	0.23 ± 0.07	0.15 ± 0.02	0.17 ± 0.01
	Certified value (%)	0.04 ± 0.01	0.39 ± 0.07	0.39 ± 0.05	0.20 ± 0.01	0.13 ± 0.01	0.18 ± 0.01
Na2O	Determined value (%)	0.03 ± 0.03	0.14 ± 0.06	0.012 ± 0.008	—^a	0.45 ± 0.12	—^b
	Certified value (%)	0.02 ± 0.01	0.16 ± 0.02	0.02 ± 0.01	0.09 ± 0.02	0.35 ± 0.02	0.013 ± 0.002
P2O5	Determined value (%)	0.13 ± 0.02	0.09 ± 0.03	—^a	0.05 ± 0.03	0.08 ± 0.01	—^b
	Certified value (%)	0.15 ± 0.01	0.13 ± 0.01	0.07 ± 0.01	0.09 ± 0.01	0.05 ± 0.05	0.013 ± 0.002
SiO2	Determined value (%)	42.5 ± 2.6	55.4 ± 9.5	54.7 ± 4.3	58.9 ± 5.6	22.2 ± 2.0	98.42 ± 3.29
	Certified value (%)	45.14 ± 0.26	51.8 ± 0.03	51.9 ± 0.1	55.0 ± 0.1	24.3 ± 0.1	96.28 ± 0.04
TiO2	Determined value (%)	1.93 ± 0.35	1.68 ± 0.28	1.00 ± 0.01	1.95 ± 0.30	1.13 ± 0.10	0.06 ± 0.03
	Certified value (%)	2.04 ± 0.15	1.49 ± 0.05	0.96 ± 0.04	2.19 ± 0.03	1.19 ± 0.05	0.030 ± 0.002

---

The accuracy of the method was verified by comparing the results obtained with the certified values of the materials using the Student t-test. It was concluded that there was no significant difference at a 95% confidence level between the determined and certified values. The simplified GSAM is effective, because it uses all data information to model the concentration.

Standard deviations presented in Table 3 are deviations obtained from b and q on one set of standards and were calculated as follows:

where S_c is the standard deviation of c, S_d the standard deviation of d, and S_q the standard deviation of q.²⁷

The determinations were performed independently of any other methods and errors. All analytes were determined in the matrices as they are in the samples.

Conclusions

The simplified GSAM was successfully used for the analysis of clays and refractory materials slurries by ICP-OES with axial viewing. The model allows the simultaneous correction of matrix and transport slurries that affect slurry analysis. The procedure proposed represents a simple alternative to direct analysis of slurries without the critical limitations caused by calibration strategies and particle size distribution.

Acknowledgements

The authors wish to express their appreciation to Fundação de Amparo à Pesquisa do Estado de São Paulo (São Paulo, SP, Brazil) for financial support of this research (FAPESP, Processes 02/04473-6 and 03/04502-9). We would like to thank MSc Leandro Martins, MSc Ana Beatriz Neves Brito and Professor Dilson Cardoso (Department of Chemical Engineering, Universidade Federal de São Carlos, São Carlos, SP, Brazil) for particle size distribution analysis. The authors are also thankful to Dr. Sherlan G. Lemos for helping with the Teach Me software. J.A.N. expresses gratitude to Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, Brasília, DF, Brazil) for the researchship provided.

References

1. J. A. C. Broekaert, T. Graule, H. Jenett, G. Tölg and P. Tschöpel, Fresenius’ J. Anal. Chem., 1989, 332, 825.
2. J. A. C. Broekaert, C. Laten, R. Brandt, C. Pilger, D. Pollman, P. Tschöpel and G. Tölg, Fresenius’ J. Anal. Chem., 1994, 349, 20.
3. O. Lau, L. Lam and S. Luk, Talanta, 2000, 51, 1009.
4. D. McGrath, Talanta, 1998, 46, 439.
5. J. C. Fariñas, R. Moreno and J. M. Mermet, J. Anal. At. Spectrom., 1994, 9, 841.
6. L. Ebdon, M. Foulkes and K. Sutton, J. Anal. At. Spectrom., 1997, 12, 213.
7. L. Ebdon and J. R. Wilkinson, J. Anal. At. Spectrom., 1987, 2, 39.
8. H. Nickel and J. A. C. Broekaert, Fresenius’ J. Anal. Chem., 1999, 363, 145.
9. I. B. Brenner and A. Zander, Fresenius’ J. Anal. Chem., 1996, 355, 559.
10. O. Abollino, M. Braglia, C. Contardi, G. Dai, E. Mentasti, S. Mosso and C. Sarzanini, Anal. Chim. Acta, 1999, 383, 243.
11. J. Borszeki, P. Halmos and E. Gegus, Can. J. Anal. Sci. Spectrosc., 1997, 46, 165.
12. C. Chen and T. W. McCreary, Appl. Spectrosc., 1994, 48, 410.
13. M. B. Renfrow, J. M. Riley and J. T. Riley, Microchem. J., 1997, 56, 30.
14. C. S. Silva, T. Blanco and J. A. Nóbrega, Spectrochim. Acta, Part B, 2002, 57, 29.
15. Z. Wang, Z. M. Ni, D. Qiu, T. Y. Chen, G. Y. Tao and P. Y. Yang, J. Anal. At. Spectrom., 2004, 18, 273.
16. R. Lobinski, J. A. C. Broekaert, P. Tschopel and G. Tolg, Fresenius’ J. Anal. Chem., 1992, 342, 569.
17. J. H. Hyun, H. B. Lim and C. H. Lim, Anal. Chim. Acta, 1997, 342, 83.
18. K. E. Jarvis and J. G. Williams, Chem. Geol., 1989, 77, 53.
19. L. Marjanovic, R. I. McCrindle and B. M. Botha, Anal. Bioanal. Chem., 2004, 379, 104.
20. S. Piepponen, T. Alanko and P. Minkkinen, Anal. Chim. Acta, 1986, 191, 495.
21. L. Shen, H. M. Pang and R. S. Houk, Spectrochim. Acta, Part B, 1995, 50, 791.
22. J. H. Kalivas and B. R. Kowalski, Anal. Chem., 1981, 53, 2207.
23. S. Luan, H. M. Pang and R. S. Houk, Spectrochim. Acta, Part B, 1995, 50, 791.
24. C. S. Silva, T. Blanco and J. A. Nóbrega, Quim. Nova, 2002, 25, 1194.
25. H. Lohniger, Software Teach/Me Data Analysis 1.0, Developed by SDL Vienna, in cooperation with the Vienna University of Technology and the Austrian Federal Ministry of Education, Springer-Verlag, Heidelberg, Germany, 1999.
26. C. W. Fuller, R. C. Hutton and B. Preston, Analyst, 1981, 106, 913.
27. D. A. Skoog, D. M. West and F. J. Holler, Fundamentals of Analytical Chemistry, Saunders College Publishing, Philadelphia, USA, 7th edn., 1996.

---