Spider silk as archetypal protein elastomer
Fritz
Vollrath
* and
David
Porter
Department of Zoology, University of Oxford, South Parks Road, Oxford, OX1 3PS, United Kingdom. E-mail: fritz.vollrath@zoology.oxford.ac.uk; Fax: +44 (0) 1865 358221 Phone +44 (0) 1865 271216
First published on 29th March 2006
Abstract
We present an overview of the physical properties of spider silks, and introduce a model designed to study the energy absorbed by the material as it stretches before breaking. Of particular interest are the inter- and intramolecular hydrogen bonds as well as the role of water in modifying the material properties of silk. A solid understanding of this interaction is of paramount importance for any deeper insights into the mechanical properties of any biomaterial. Here we note that the typical biological material has evolved to function in the fully hydrated i.e. elastomeric state. We conclude that silk after its transformation from the hydrated feedstock to the dehydrated fibre state can in fact be analysed in great detail and interpreted as representative of a wide range of elastomeric proteins covering, inter alia, bone, keratins, elastin and collagen.
 Fritz Vollrath | Fritz Vollrath received his PhD from the Zoology Department at the University of Freiburg in Germany. After time at the Smithsonian Tropical Research Institution in Panama and the Zoology Departments at the Universities of Oxford UK, Basel CH and Aarhus DK he is now back at the Zoology Department in Oxford where he works primarily on spiders’ webs and silks. |
 David Porter | David Porter obtained his PhD in the Physics Department at Loughborough University and then worked for Dow Chemical on the modelling of polymer properties. He now works with Professor Vollrath at Oxford University on understanding structure–property relations in silk, and also works at QinetiQ in Farnborough, where he is a QinetiQ Fellow working on Materials Modelling of a wide range of materials. |
Introduction
What is silk? What is in the name? The English word ‘silk’ according to the Oxford Dictionary derives from a Baltic/Slavic precursor and as such would suggest an old trading name for a specific type of textile. Today, ‘silk’ defines primarily the fibre spun by the larva of the silk moth Bombyx mori and collected by unravelling the insect's pupal cocoon. But the name ‘silk’ encompasses other fibres with specific properties such as filaments produced by caddisflies, mites and spiders. Even filaments of the ears of corn are called ‘silk’; perhaps because of their ‘feel’ rather than any implied biophysical or biochemical similarity with the animal silks?These classic animal silks, such as the filaments spun by lepidoptera, hymenoptera, diptera, neuroptera, acarids and araneids, share many traits in their biophysical and biochemical make-up1 although there are a fair number of interesting differences.2 Nevertheless, the spider's formidable dragline silk thread (probably the most outstanding of all biological fibres) is not all that different, at least in its general structure and in its mechanical properties, from the commercial Bombyx silk produced in vast quantities worldwide. The ‘typical’ dragline spider silk is considerably stronger and significantly more extensible than any silkworm silk but both show high initial strength that, at a clear yield point, gives way to work hardening.3,4 Indeed, the difference in strength between silkworm and spider silk can be attributed more to periodic weak points generated during the figure-of-eight spinning motion of the silkworm, rather than intrinsic structural differences; and these weak spots can be avoided simply by pulling the silk thread away from the worm with a constant force during spinning5
Interestingly, people often seem surprised when told that the spider's fibre is a ‘silk’ just like the fibre of an insect such as the commercial silkworm. Clearly the public considers the silks of spiders and insects as different materials despite them sharing a name. And public perception has a point. Neither material is what it seems on the surface. For example, the spider makes many different ‘silks’ extruding from a veritable battery of nozzles near its anus6 while the insect lays just one thread through its mouth.7,8
Silkworm silk is a composite fibre (bave) and comprises a doublet of fibroin filaments (brins) surrounded by several thick layers of sericin coating.9,10 Both fibroin and sericin are proteins, but of very different composition and properties.10 The two brins, produced and coated in separate ducts, are pressed together while still inside the animal; the sericin hardens in air and typically on the cocoon to form the con-joining bave and tough cocoon wall composite. Spider silk also consists of two filaments, but they are extruded individually and remain easily separated. Their coating is much thinner and consists of a varied number of small molecules of non-protein compounds.11 This is the composition of ‘typical’ silk, i.e. the benchmark of spider silks, the dragline and frame silk of the orb weaving tribe of araneid spiders, such as the garden orb spider Araneus diadematus or the golden silk spider Nephila clavipes.
But both these species, as all other spiders, have more than one type of silk, with the dragline produced by the major ampullate (MAA) gland being only one of several different silks, each with specific properties that appear to be optimised to perform key functional roles. Orbweavers like Nephila also produce minor ampullate (MIA) silk to accompany the MAA silk in the web, as well as flagelliform silk that forms the core filaments of the orb web's capture thread. The capture thread filaments are coated by yet another ‘silk’ from the aggregate gland, which is not a hard filament but an aqueous solution of small and highly hygroscopic peptides as well as sticky glycoproteins. The web threads are anchored to the vegetation and affixed to one another by a silk cement originating in the pyriform glands. The eggs are encased in very fine silk filaments from the tubuliform or cylindriform and one type of aciniform gland, while another type of aciniform filament is used for a multitude of other purposes such as strengthening the cement matrix.
Despite this amazing multiplicity of silk types and silk uses, all spider silks, diverse as they are in both mechanical properties and chemical composition, can each and everyone without doubt be called a ‘spider silk’ because they all derive from one common type of ancestral silk gland. All these glands have a common origin, although over nearly 400 million years of evolution12 the selection for different functionalities has lead to diversification13,14 and hence to biochemical tuning15–18 as well as to mechanical specialisations3,19,20 and to temporary tensile adjustments.21,22 Thus, the diversity of spider silks shows us the huge variability that is possible for one natural elastomeric biomaterial on both the chemical (genetic) and the physical (mechanical) level. Spider silks therefore open a window into the structure–function relationships of many (perhaps even all) biological protein elastomers.
In the following we will explore the mechanical properties of silks and sketch our reasons for defining ‘silk’ as a model material to study protein elastomers. As we outline below, our hypothesis is based on a combination of biological, physical and chemical data represented by a wide range of measurements and observations of silk properties and processing over many decades.23–28 These data illuminate the relationship between composition, structure and properties and thus allow the evolution of a formal silk property model, based on the analysis of the energy management at the molecular level. After all, a biological elastomer has its properties because it has evolved in order to negotiate energy. In the spider's case this is kinetic energy originating from a prey hitting and struggling in the web.
Bio-elastomers typically function either inside the body or at the interface between body and environment. Spider silk is unusual in working away from the animal. Moreover, the typical silk has evolved to function in the dry or only partially hydrated state. For a biological elastomer this is highly unusual (if not unique) because in the body all materials are always bathed in water, and have evolved both functionality and molecular architecture for that fully hydrated stage.29 Spider silk, which in its natural state encounters a wide range of hydration, therefore provides an interesting (and rare) opportunity to study the importance of water on all levels of bio-elastomer function.
Structure–function relationships in silk
Most of our own work on silk has been the experimental measurements of physical properties from the spinning of the fibre to the final mechanical performance, which has been reviewed previously.30,31 However, recently this has led us to integrate the findings from other research groups working on the details of silk protein structure in order to develop a self-consistent set of models that relate silk constituents and properties to the apparently complex composition and microstructure of this intriguing material. These new models under development aim to identify the underlying processes that control chemico–physical properties as the design tools for most, perhaps all, natural biomaterials.Structure–function modelling allowed us to not only map but also to predict the generic space of mechanical properties that are possible in dry silk fibres in the form of stress–strain curves to failure, as illustrated in Fig. 1. To this end we deployed the evolutionary concept that in biology ‘energy’ is the primary ‘currency’ used by natural selection. Efficient energy management allows animals (and plants) to accumulate reserves, which can ultimately be converted into offspring (the secondary currency). While energy management starts with the basic chemical processes in the cells, it is also a crucial factor in the organism's functional morphology and behaviour. For the spider, web efficiency depends on optimal web engineering in the combination of architecture and silk materials, as well as the choice of a good building site that provides the flies for the spider to catch. These flies arrive with kinetic energy that needs to be distributed in the web not only effectively but also efficiently,32 since the silk is a protein that could be used for other critical functions such as enhanced offspring production.26
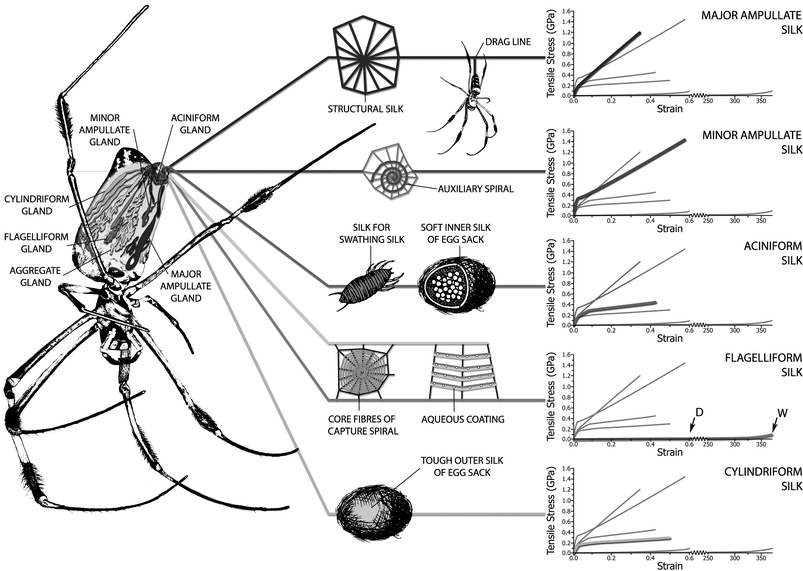 | ||
| Fig. 1 Nephila golden silk spider showing its silk glands as well as the use for each silk and its mechanical properties in the form of comparative experimental stress–strain plots, where the highlighted line in each graph is that of the graph label; the symbols D and W in the flagelliform graph are dry and wet respectively. We thank Chris Holland for the artwork. | ||
Silkworm silk is under rather different selection pressures compared to spider silk, as silkworm silk has evolved to make a tough composite and not a tough fibre, which requires a rather different structure–function relationship.5,33–36 Indeed, the functional requirements of the material in vivo must always be considered when studying any biological material, which is typically done in vitro. Spider silk provides the ideal biological material for detailed analysis as it must function ex vivo and thus is eminently accessible for detailed and highly relevant studies. Such experimental studies would either be very difficult or impossible for most other biomaterials, which are designed (by nature) to function in the complex context of a highly specific physiological environment. Feather keratin is also a biomaterial designed to function ex vivo but it is grown, rather than spun, which imposes other constraints on its study (as well as its commercial uses), as we shall discuss briefly later.
Returning to the spider's silks; in our model we link the biological rule of ‘energy management for survival’ to the macromolecular chemistry of silk proteins via the physics of storage and dissipation of mechanical energy at a molecular level. The model has been presented in detail elsewhere37 and is here only outlined in order to illustrate the elegance of design in natural proteins that allows major changes in property to be controlled by apparently small changes in structure. More recent work has allowed us to develop these models to understand how water changes the properties of silk and to give insights into the mechanical properties of other biological polymers that function in wet environments. These more recent models are introduced for the first time below to suggest how we might predict the full range of properties that are possible in most natural polymers.
The first problem encountered when attempting to model any protein is the need for a quantitative parameter describing its structure. The peptide sequences of many silks are known and a number of different secondary structure types are possible. However, no clear consensus has yet been established on the detailed crystallographic structures in the different silk types.32b,c,d Rather than define structure in terms of specific space groups, we chose to use ‘order’ and ‘disorder’ fractions of peptide segments to quantify the morphology of any specific silk.37 ‘Ordered’ segments are aligned sufficiently with neighbours to have two hydrogen bonds between amide groups. Similarly, ‘disordered’ segments have only one hydrogen bond per amide–amide interaction due to misalignment of adjacent chain segments. This radical simplification allows the role of complex secondary structures in determining mechanical properties to be assigned unambiguously.
To make quantitative predictions of mechanical properties, we chose an approach based upon group interaction modelling, since it had been validated for a wide range of synthetic polymers.38 With this approach, we can reduce the mechanical functions of the fibre studied to a balance between stiffness and strength that are determined by elastic energy storage, and between toughness and extensibility that are determined by energy dissipation. Fig. 2 shows the prediction of mechanical properties in graphical form for a typical major silk of Nephila clavipes with a model ordered fraction of 66% to illustrate the method.
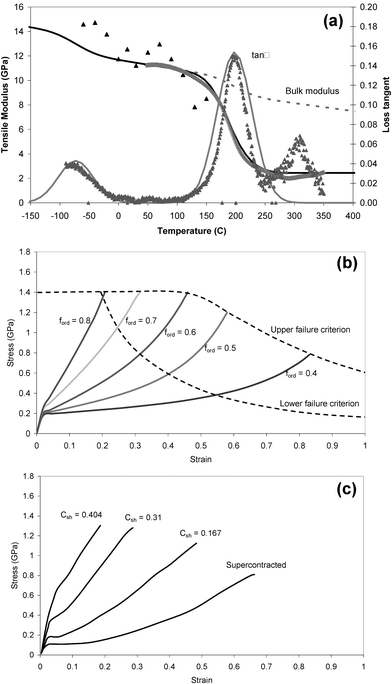 | ||
| Fig. 2 Model for the mechanical properties of silk: (a) shows a comparison of experimental dynamic mechanical analysis of elastic modulus and loss tangent (points) with model predictions (lines);37 (b) shows model predictions of stress–strain relations for a range of realistic ordered fractions in silk; (c) shows experimental stress–strain plots for a spider silk spun under different conditions.39–41 | ||
Elastic energy is stored as volumetric changes against the bulk modulus, B. Energy is dissipated while the polymer converts mechanical energy irreversibly to heat, mainly because the material goes through transition points such as the glass transitions in the disordered fraction, fdis. These transitions can be quantified by the parameter of loss tangent, tanδ, which is the ratio of energy lost to energy stored in a deformation cycle. As the polymer is heated or stretched uniaxially, more elastic energy is dissipated and the value of the tensile modulus, E, is reduced in proportion to the residual elastic energy.
In step one of our analysis,37 we calculate the bulk modulus, B, and loss tangent as a function of temperature. B is calculated using the cohesive energy density as a function of temperature from an ensemble average potential energy function for interactions between all molecular groups in the polymer. The loss tangent is dominated by the two relaxation peaks at around 200 and 470 K, which are treated as two different glass transition events in the disordered fraction; the upper peak is due to amide–amide interactions and the lower peak is due to interactions between the hydrocarbon side chain groups. The specific hydrogen bonding between the amide groups separates these two interactions into distinct relaxation events. The area under the loss tangent peaks (cumulative loss) is predicted using the model parameters for the two interactions, and the distribution is taken typically to be Gaussian with a standard deviation of about 30 degrees.
Step two is to calculate the tensile modulus by the cumulative dissipation through the temperature history in the disordered fraction, fdis ∫ tanδ dT, on B using a relation derived from the coupling of thermal and mechanical energy during deformation
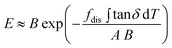 | (1) |
Step 3 is to calculate strain, ε, and stress, σ, in a self-consistent pair of equations using a dummy variable of temperature (that has a value Tε at a combination of ε and σ) and the linear thermal expansion coefficient, which is predicted to be β ≈ 0.0001 K−1.
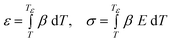 | (2) |
Fig. 2b shows the predicted stress–strain profiles for a number of values of ordered fraction that are typical within the range seen in spider silk fibres. Key features are the yield strain, εy ≈ 0.02, determined by the amide–amide relaxation peak temperature, and the post-yield strain hardening to failure, which is due to the transformation of the post-yield rubberlike states to crystal and glassy states until all the ductile material has been converted to a brittle form, at which point the fibre breaks. Fig. 2c shows experimental stress–strain plots for Nephila major fibres spun under different conditions in order to generate a broad range of mechanical properties for comparison with the model predictions.39
Thus, we can predict the full range of possible stress–strain profiles in dry silk simply by changing the fraction of ordered segments. Typical values of ordered fraction for different silk types are 0.85 for Bombyx mori cocoon silk, 0.66 for major dragline silk, and 0.2 for flagelliform. Generally, higher initial modulus (stiffness) gives a higher failure stress (strength) but lower strain to failure (elongation) and area under the stress–strain curve (toughness).
Water sensitivity and cyclical loading
An important characteristic of different silks is their sensitivity to water. Some silks shrink considerably upon exposure to water, which is called supercontraction.40,42–49 At the same time as shrinking, these silks also show a large drop in their elastic modulus and a commensurate increase in their strain to failure after they have been dried out again.50,51 Major silk is sensitive to water, whereas and minor silk from the same spider is not.45 Understanding this selective response to water is not only important scientifically in order to understand silk properties overall but may also be very useful commercially if one wants to deploy such silks as implantable biomaterials.The experimental stress–strain curves in Fig. 2c are major silks with different degrees of supercontraction strain, Csh, that are labelled on the curves. Inspection of the disordered fraction in the model curves of Fig. 2b and supercontraction strain in the experimental curves of Fig. 2c suggests a direct numerical relation between these parameters.
| Csh ≡ ford − 0.45 | (3) |
Although the precise numerical identity between Csh and the change in Δfdis is coincidence, the identity can be explained quantitatively by comparing the mechanical energy of the strain Csh at the yield stress with the energy to convert the fraction Δfdis of disordered states to ordered states above yield during strain hardening of a fibre. Thus, supercontraction is directly linked to the change (loss) of order in a silk on exposure to water and the fully supercontracted state has an ordered fraction of about 0.45. The maximum order inferred from the stiffest silk stress–strain curves suggests a minimum fdis ≈ 0.15.
When one first dries and then elongates supercontracted silk, a fraction of the elongation is retained in the fibre and can again be recovered by another exposure to water.40,50,52 The inset in Fig. 3 shows repeated cycles of strain applied to supercontracted major silk, with modulus increasing as the fibre length increases. This cyclical loading characteristic shows that some degree of order in major silk is reversible, and suggests that the ordered phase of a specific fraction of the peptide segments can be manipulated by exposure to water. In nature, this phenomenon may be useful, as dew condensation can lead to the tightening of webs that have sagged. In effect, this behaviour allows a specific silk (and by extension the web where it is deployed) to perform optimally under the full range of vapour pressures (ambient humidities) encountered from the desert to the rain forest and from the late night to the middle of the day53,54
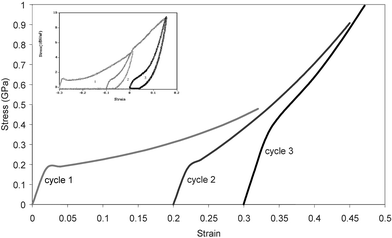 | ||
| Fig. 3 Cyclical loading plots; the main plots model predictions of experimental data50 shown in the inset (see text for details). | ||
Fig. 3 shows model plots of cyclical stress–strain loading of a fully supercontracted major silk, where each new loading starts with the origin in the strain axis shifted by the supercontraction strain predicted by the change in fdis during strain hardening in the previous cycle. Agreement with the experimental plots in the inset is good, and validates the general principle. We are currently modelling the rate of relaxation of strain at the end of each loading cycle by making the relaxation rate a function of the fraction of rubberlike states at each point in the relaxation process. This will allow the full loading–unloading profile to be predicted and also refine the model for stress–strain response around the yield point, where some dynamic stress relaxation is seen in the lower modulus fibres.
Model structure of major silk
Using the model for mechanical properties and water sensitivity, we are in a position to formulate a model structure for dragline MAA silk that is based on both the measured chemical composition (based on analytical studies) and the degree of order (deduced from the model stress–strain response). The response to water of the MAA (and other silks) makes it apparent that the rather simple parameters of order and disorder need to be refined more. Not least because a recent study on supercontraction and its effects on mechanical properties40,41 has demonstrated that some degree of order can be manipulated by a combination of spinning conditions and hydration.Major ampullate MAA silk is generally taken to be an alloy of Spidroins I and II, which we take here to have characteristic segment compositions,55–58
Spidroin I: GQG GYG GLG SQG A GRG GLG GQG A GAAAAAAAGG A
Spidroin II: GPGGY GPGQQ GPGGY GPGQQ GPGGY GPGQQ GPSGPGS AAAAAAAAAA
Taking a number average proline fraction of about 6% suggests a ratio of about 2 ∶ 1 for Spidroin I to Spidroin II segments, with a weight fraction of about 33% for Spidroin II.
The important feature of proline is that it is not intrinsically ‘ordered’, since the ring in the chain backbone twists the torsional angles away from any of the simple configurations that can be ordered and it has no amide group for two potential hydrogen bonds. Each proline group is associated with four other peptide groups in the pentamer sequence GPGXX, so these four groups are intrinsically ‘disordered’ by the proline. Nevertheless, they are potentially capable of ‘order’ under the correct set of packing conditions and an approximate calculation of the GGXX groups in the GPGXX pentamers suggests about 20% by volume/weight of the total major silk composition is in this state. Since each Spidroin II chain interacts in a pairwise manner with Spidroin I segments in the polymer alloy, this suggests that about 40% of the total amide–amide interactions in major silk are intrinsically disordered (defined by inter-amide hydrogen bonds), but with the potential for order.
Studies of molecular structure in silk have suggested that silk has a folded hairpin structure59,60,61 with about six peptide segments per fold, shown in a simplified form in Fig. 4. If we take the peptide segment at a turn of the hairpins as being unable to form ordered interchain hydrogen bonds, this suggests a fraction of about 0.17 of the segments as being permanently disordered. Using this simple argument, three types of material in the major silk can be suggested with approximate fractions in the hairpin-turn model for silk nanofibrils as a ‘string of beads’:
—permanent disorder: hairpin turns: about 0.15 fraction
—intrinsically disordered but with a potential for order under strain: about 0.4 fraction located between turns due to Spidroin II interactions
—permanent order: Spidroin I between turns: about 0.45 fraction.
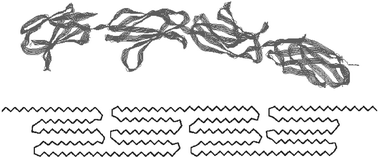 | ||
| Fig. 4 A fibroin folded chain backbone and a simplified hairpin fold morphology of spider silk. | ||
Thus, major MAA dragline silk has an underpinning set of mechanical properties that are determined by the permanent order and disorder fractions and are those of supercontracted fibres9,60,62–64. Further order can be forced into the structure by greater stress during the spinning process and gives the spider considerable flexibility in controlling mechanical properties. Minor MAI dragline silk does not contain proline65 and is not water sensitive,66 but we do not yet have enough structural information to allow us to model its properties in any detail.
Before moving on to more general aspects of other biomaterials, it is interesting to consider the properties of pure Spidroin II fibres with their high proline content. These are predicted here to have properties characteristic of flagelliform silk in the hydrated supercontracted state and potentially be almost as stiff as silkworm fibres in the fully ordered dry state, but with a high sensitivity to water and deformation conditions. Such fibres (Nexia ‘biosteel’ silk) were spun from recombinant silk ‘cloned’ from Spidroin II and indeed show67 the properties expected from our model.
Silk compared to other biopolymers
Since silks are produced by spinning, rather than by growth, they have a realistic potential for commercial bulk production. Of specific interest (because of the inherent biocompatibility of spidroin filaments) are fibres for medical applications such as tendon or ligament replacements, where a synthetic silk material should be gradually replaced in the body by natural collagenous protein fibres. The mechanical properties of the silk can be matched to those of tendons by using classical rope making skills,68 and the biodegradation rate will be determined largely by the hydration of the silk. Since mechanical properties and hydration both depend upon the fraction of disordered peptide segments, balancing all these aspects presents an interesting challenge. Silk has also been suggested as a template for bone growth, where hydroxyapatite grows around synthetic silk fibres with the natural tropocollagen–hydroxyapatite structure developing with time68Spiders do produce elastomeric (viscid) silk with a modulus of the order 1 MPa, which has the mechanical properties of a rubberlike polymer. This web capture-silk is a composite of a flagelliform (FLG) core fibre and an aggregate coating, with the latter providing hygroscopic components that keep the silk fully hydrated even under rather dry ambient conditions.43,53 The water of the coat penetrates and plasticizes the filament protein and reduces its glass transition temperature to below ambient and thus induces a rubberlike state in the polymer.69 Such deeply hydrated silk material (not only FLG but also MAA) has mechanical properties that compare with mammalian elastin. Elastin is an important biopolymer, with a range of biological functions, one of which (most importantly) keeps our blood-pressure in healthy range through its action in our arteries.29
Collagen is an equally important, and much more widely spread, biopolymer making up (in its hydrated form) over 80% of our body's weight and much of its functional morphology. Accordingly, silks with collagen-behaviour or conducive to collagen infiltration are of great interest to bio-medical silk-researchers. The structure and properties of such important bio-functional polypeptides as collagen, elastin and a range of others such as feather keratin and mussle byssus thread have been studied extensively for quite some time70,71 with many exciting developments in recent years.29,72,73 Nevertheless, at present their chemical composition and physical morphology still elude the full quantitative explanation and accurate prediction of mechanical properties. It would be very useful indeed if our studies on silks and the models of silk structure–function relations outlined above could guide us also to a better understanding of these other natural biomaterials. The materials have evolved to work fully hydrated and deep inside the body or as part of the body’s interface with the environment. And because of this interaction with the body physiology they are not easy to study quantitatively. Silk, in contrast, has evolved to work away from the body and thus can provide us with the experimental data required to establish it as the perfect general model for these other, more intractable, fibres and fibre composites.
Indeed, a full understanding of natural silks should lead to the design of ‘silk’ analogues of a wide range of other protein biopolymers with elastic properties ranging from the 20 GPa of bone to the MPa modulus of protein elastomers such as elastin and the kPa modulus of resilin at low strain. Of equal importance to forming the link from silk to other bio-fibres, perhaps, is to understand the highly nonlinear strain dependence of mechanical properties that are crucial for biological function; for example, the stiffening of collagen from 1 MPa to 1 GPa modulus after a few percent strain, or that of elastin at about 100% strain.
Quantifying the effects of water is a key step for modelling most structural proteins, as water is not only their natural environment, but it is also biology's principal plasticizing agent.74,75 We discussed above that water affects only disordered segments; and it is reasonable to assume that one water molecule can hydrogen bond to each disordered amide group, which is a weight fraction of 0.29 water in the water–amide pair. Using either the group interaction modelling relation or the Fox–Flory rule38 for calculating the glass transition temperature of the water–amide pairs (using Tg values of 160 and 473 K for water and disordered amide respectively) suggests Tg = 300 K for the hydrated segment.37 As more water hydrates a disordered protein at low water levels, then a greater fraction must operate above its upper glass transition temperature at normal body temperature and behave as a rubber. Of course, excess water is another matter, and we will consider this later.
Let us look at keratin first as it is also a biomaterial evolved to function outside the body and in the dry state. Keratin is a semi-crystalline composite material with about 0.3–0.4 fraction of ordered crystal fibrils dispersed in a disordered matrix.76 Using the silk model relation to predict the isotropic tensile modulus of dry keratin with this range of ordered segments gives an expected range of 5.5 to 6.5 GPa, and the yield strain of unhydrated segments is unchanged at 2%, which agrees with observation. As more water hydrates the disordered matrix fraction at increasing levels of relative humidity, a slightly more complex calculation to include the hydrated segments with a new contribution to loss at Tg = 300 K shows that the modulus reduces with increasing hydrated fraction, until a lower limit of between 0.5 and 1 GPa is reached when all the disordered segments have been hydrated at 100% RH. This is in line with the 0.5 GPa modulus measured for wet hoof keratin.77 We note that the hydrated modulus value is calculated at the glass transition temperature of 300 K, and infers that the material should have a very high damping capability while operating in the glass transition zone.
Collagen, unlike keratin, has evolved to work inside the body and in the wet state. But it is also a semi-crystalline composite material with comparable (to keratin) fractions of order and disorder. Bulk collagen consists of a left handed triple helix with a pitch of about 10 nm that contains about 35% glycine (every third segment to stabilise the helix) and 21% proline or hydroxyproline. Since the characteristic periodicity of the peptide chains is dominated by the glycine into trimer groups, a reasonable estimate for the degree of order in the structure is again about 0.35 from the likely hydrogen bonding with the small glycine groups in the helix and the disordering influence of proline. Like keratin, the predicted dry modulus is about 6 GPa, and the hydrated modulus is again about 1 GPa, as measured.77b Note that here we have not included the low initial modulus of the collagen due to proteoglycan coating of the collagen fibrils.78,79 Recently a discussion of collagen in bone has been published outlining how the polymer–mineral nanostructure of bone imparts its attractive combination of stiffness and toughness.37
Elastin, has an even more complex structure than collagen albeit being largely disordered.29,80–82 Its principal component—the (PGVGV) segment—takes a square wave form of β-turns forming a primary helix with a diameter of about 2.4 nm.83 This primary helix is then twisted again into a triple helix with a pitch of about 7.2 nm. We note the similarity of the elastin pentamer with Spidroin II. Hydrated elastin has excess water (about 35% by weight) above that required to hydrogen bond simply with the amide segments. This affects the glass transition temperature by reducing it well below operating conditions, such that elastin has a rubberlike modulus of about 1 MPa. Taking hydrated elastin to be fully disordered, the calculated bulk modulus of 3.5 GPa (with 35% water) and the usual cumulative loss of 45 through the glass transitions predict a tensile modulus of 1 MPa using the elastic modulus relation of eqn 1.
The range of mechanical properties provided by silk, keratin, collagen and elastin is extended upwards in modulus by mineralization in materials such as bone, which is a natural hybrid nanocomposite of hydroxyapatite mineral in a hydrated tropocollagen polymer matrix.84 These materials range from mineralised tendon, through various mineral fractions of bone, to tooth enamel from about 10 to 30 GPa modulus respectively.85 Porter37 has published a model for structure–property relations in bone that is consistent with the model for silk reviewed above, so the same underlying mechanisms operating in silk can be used as a general template for understanding a wide range of biomaterials.
Summary and challenges
The overview presented here shows not only why silk functions as it does, but also how silk can be used to provide insights into other important structural proteins at both a practical and a theoretical level. This leads us to conclude that silk can be considered as an ideal archetypal elastomeric protein. The range of mechanical properties that can be derived from silk-based proteins is enormous; from mineralised bone-like materials with a modulus of 20 GPa, through classical silks with a modulus 2–10 GPa, down to viscid elastin-like rubbers with only 1 MPa.The outlined combination of experimental work with analytical modelling shows the large range of mechanical properties that silk can assume with apparently small changes in chemical structure and processing. This makes silk an important analytical tool as well as an interesting biopolymer for a wide range of important applications. In this context silk can provide a valuable basis for complex protein composites. For example, subtle combinations of protein structures with other biopolymers can produce elegant materials such as peptidoglycans for the walls of bacterial cells, which are rigid impermeable polymers when dry, but swell by hydration of the protein segments between the disaccharides to form a tough semipermeable membrane; for example, murein as the walls of virus cells.86,87
Now that we have begun to understand the interaction of spinning and material properties in silk, as well as its underlying principles, it is the next great challenge to produce silk fibres and films in a biomimetic and environmentally benign manner from aqueous dope suspensions. Although silk fibres can without much difficulty be pulled straight from both spider and silkworm dope (our own observations), and fibres with good material properties can be spun relatively easily from regenerated silk.68 Yet making semi-natural fibres from natural, genetically modified or indeed synthetic feedstock with properties comparable to the natural fibre is far from solved.57,88–90 After all, the natural spinning process is a complex combination of material chemistry and rheological processing.24,91,92 Nevertheless, nature shows us how it could be done and by working on all aspects of understanding the biological spinning process in different species through to theoretical models for the complex viscoelastic properties of the dope we should have a good chance of success in our quest to unravel the secret of the spider's silk.
Acknowledgements
For funding we thank the British Research Councils EPSRC(grant GR/NO1538/01) and BBSRC (grant S12778), the European Commission (grants G5RD-CT-2002-00738 and EC-MTKD-CT-2004-014533) as well as the US-AFOSR (grant F49620-03-1-0111).References
- C. Craig, Annu. Rev. Entomol., 1997, 42, 231–267 CrossRef CAS
.
-
C. L. Craig, Spiderwebs and Silks: Tracing Evolution from Molecules to Genes to Phenotypes, Oxford University Press, New York, 2003 Search PubMed
.
-
M. W. Denny, in The Mechanical Properties of Biological Materials, ed. J. F. V. Vincent and J. D. Currey, 245–271, Cambridge University Press, Cambridge, UK, 1980 Search PubMed
.
- F. Vollrath and D. Porter, Appl. Phys. A: Solid Surf., 2006, 82, 205–212 CAS
.
- Z. Z. Shao and F. Vollrath, Nature, 2002, 418, 741–741 CrossRef CAS
.
- F. Vollrath, Spider Webs and Silks, Sci. Am., 1992, 70–76 CrossRef CAS
.
-
(a) H. Akai, Experientia, 1983, 39, 443–449 CrossRef
; (b) H. Akai, pp 219–253, in Microscopic Anatomy of Invertebrates, Wiley-Liss, New York, 1988 Search PubMed
.
-
J. Magoshi, Y. Magoshi and S. Nakamura, in Silk Polymers. Materials Science and Biotechnology, ed. D. Kaplan , W. W. Adams, B. Farmer and C. Viney, American Chemical Society, Washington, 1994, pp 292–310 Search PubMed
.
-
T. Asakura and D. L. Kaplan, Silk Production and Processing in Encyclopedia of Agricultural Science, C. J. Arntzen and E. M. Ritter, Academic Press, London, 1994, 4, 1––11 Search PubMed
.
- J. Perez-Rigueiro, C. Viney, J. Llorca and M. Elices, J. Appl. Polym. Sci., 2000, 75, 1270–1277 CrossRef CAS
.
- F. Vollrath, W. J. Fairbrother, R. J. P. Williams, E. K. Tillinghast, D. T. Bertstein, K. S. Gallagher and M. A. Townley, Nature, 1990, 345, 526–528 CrossRef CAS
.
- W. A. Shear, J. M. Palmer, J. A. Coddington and P. M. A. Bonamo, Science, 1989, 246, 479–481 CrossRef
.
- J. W. Shultz, Biol. Rev. Cambridge Philos. Soc., 1987, 62, 89–113 Search PubMed
.
- J. Gosline, P. Guerette and C. Ortlepp, Proc. SPIE-Int. Soc. Opt. Eng., 1996, 2716, 296–299 CAS
.
- C. Y. Hayashi and R. V. Lewis, Science, 2000, 287, 1477–1479 CrossRef CAS
.
-
(a) J. E. Garb and C. Y. Hayashi, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11379–11384 CrossRef CAS
; (b) J. Gatesy, C. Hayashi, D. Motrluk, J. Woods and R. Lewis, Science, 2001, 291, 2603–2605 CrossRef CAS
; (c) J. M. Gosline, P. A. Guerette, C. S. Ortlepp and K. N. Savage, J. Exp. Biol., 1999, 202, 3295–3303 Search PubMed
.
- M. Tian and R. V. Lewis, Biochemistry, 2005, 44, 8006–8012 CrossRef CAS
.
- A. E. Brooks, H. B. Steinkraus, S. R. Nelson and R. V. Lewis, Biomacromolecules, 2005, 6, 3095–3099 CrossRef CAS
.
- F. Vollrath and T. Köhler, J. Exp. Zool., 1995, 271, 1–17 Search PubMed
.
- F. Vollrath, B. Madsen and Z. Z. Shao, Phil. Trans. Roy. Soc. London Series B-Biol. Sci, 2001, 268, 2339–2346 Search PubMed
.
- B. Madsen, Z. Z. Shao and F. Vollrath, Int. J. Biol. Macromol., 1999, 24, 301–306 CrossRef CAS
.
- M. A. Garrido, M. Elices, C. Viney and J. Perez-Rigueiro, Polymer, 2002, 43, 4495–4502 CrossRef CAS
.
-
J. Gosline, M. Lillie, E. Carrington, P. Guerette, C. Ortlepp and K. Savage, in Elastomeric Proteins, ed. A. J. Bailey, Cambridge
University Press, Cambridge, 2005, 15–38 Search PubMed
.
- F. Vollrath and D. P. Knight, Nature, 2001, 410, 541–548 CrossRef CAS
.
-
F. Vollrath and D. Knight, in Biotechnology of Biopolymers; from Synthesis to Patents Volume 2, ed. A. Steinbuchel and Y. Doi, Wiley-VCH, Weinheim, 2005, 873–894 Search PubMed
.
-
C. L. Craig, Spiderwebs and Silks: Tracing Evolution from Molecules to Genes to Phenotypes, Oxford University Press, New York, 2003 Search PubMed
.
- S. Winkler and D. L. Kaplan, Rev. Mol. Biotechnol., 2000, 74, 85–93 CrossRef CAS
.
- A. Sponner, B. Schlott, F. Vollrath, E. Unger, F. Grosse and K. Weisshart, Biochemistry, 2005, 44, 4727–4736 CrossRef CAS
.
-
J. Gosline, M. Lillie, E. Carrington, P. Guerette, C. Ortlepp and K. Savage, in Elastomeric Proteins, ed. P. R. Shewry, A. S. Tatham and A. J. Bailey, Cambridge University Press, Cambridge, 2003, 15––38 Search PubMed
.
-
F. Vollrath and D. P. Knight, in Elastomeric Proteins, ed. P. R. Shewry, A. S. Tatham and A. J. Bailey, Cambridge University Press, Cambridge, 2003,152––174 Search PubMed
.
-
D. P. Knight and F. Vollrath, in Elastomeric Proteins, ed. P. R. Shewry, A. S. Tatham and A. J. Bailey, Cambridge University Press, Cambridge, 2003, 115––135 Search PubMed
.
-
(a) L. H. Lin, D. T. Edmonds and F. Vollrath, Nature, 1995, 373, 146–148 CrossRef CAS
; (b) C. Riekel, M. Müller and F. Vollrath, Macromolecules, 1999, 32, 4464–4466 CrossRef CAS
; (c) C. Riekel, B. Madsen, D. P. Knight and F. Vollrath, Biol. Macromol., 2000, 24, 179–186 Search PubMed
; (d) C. Riekel and F. Vollrath, Int. J. Biol. Macromol., 2001, 29, 203–210 CrossRef CAS
; (e) C. Riekel, M. Roessle, D. Sapede and F. Vollrath, Naturwissenschaften, 2004, 91, 30–33 CrossRef CAS
.
- J. Perez-Rigueiro, C. Viney, J. Llorca and M. Elices, J. Appl. Polym. Sci., 1998, 70, 2439–2447 CrossRef CAS
.
- J. Perez-Rigueiro, C. Viney, J. Llorca and M. Elices, Mechanical properties of single-brin silkworm silk, J. Appl. Polym. Sci., 2000, 75, 1270–127 CrossRef CAS
.
- J. Perez-Riguero, M. Elices, J. Llorca and C. Viney, J. Appl. Polym. Sci., 2001, 82, 2245–2251 CrossRef
.
- J. Perez-Rigueiro, M. Elices, J. Llorca and C. Viney, J. Appl. Polym. Sci., 2002, 84, 1431–1437 CrossRef CAS
.
- D. Porter, F. Vollrath and J. Z. Shao, Eur. Phys. J. E, 2005, 16, 199–206 CrossRef CAS
.
-
D. Porter, Group Interaction Modelling of Polymers, Marcel Dekker, New York, 1995 Search PubMed
.
- Y. Yang, X. Chen, Z. Z. Shao, P. Zhou, D. Porter, D. P. Knight and F. Vollrath, Adv. Mater., 2005, 17, 84–+ CAS
.
- Y. Liu, Z. Shao and F. Vollrath, Nat. Mater., 2005 Search PubMed
.
- Y. Liu, Z. Z. Shao and F. Vollrath, Chemical Commun., 2005, 19, 2489–2491 Search PubMed
.
- R. W. Work and N. A. Morosoff, Text. Res. J., 1982, 52, 349–356 Search PubMed
.
- F. Vollrath and D. T. Edmonds, Nature, 1989, 340, 305–307 CrossRef
.
- F. Vollrath, K. M. Bonthorne, B. K. Hunter and J. K. M. Sanders, Proc. R. Soc. London, Ser. B, 1992, 248, 141–144 CrossRef CAS
.
- F. Vollrath, T. Holtet, H. C. Thogersen and S. Frische, Proc. R. Soc. London, Ser. B, 1996, 263, 147–151 CrossRef
.
-
(a) D. T. Grubb, D. B. Jackrel and L. W. Jelinski, Chem. Abs., 1997, 214, 164 Search PubMed
; (b) D. T. Grubb and L. W. Jelinski, Macromolecules, 1997, 30, 2860–2867 CrossRef CAS
; (c) D. T. Grubb and J. Gending, Int. J. Biol. Macromol., 1999, 24, 203–210 CrossRef CAS
.
- Z. Yang, O. Liivak, A. Seidel, G. LaVerde, D. B. Zax and L. W. Jelinski, J. Am. Chem. Soc., 2000, 122, 9019–9025 CrossRef CAS
.
- F. I. Bell, I. J. McEwen and C. Viney, Nature, 2002, 416, 37–37 CrossRef CAS
.
- J. Perez-Rigueiro, M. Elices and G. V. Guinea, Polymer, 2003, 44, 3733–3736 CrossRef CAS
.
- Z. Z. Shao and F. Vollrath, Polymer, 1999, 40, 1799–1806 CrossRef CAS
.
- Z. Shao, F. Vollrath, J. Sirichaisit and R. J. Young, Polymer, 1999, 40, 2493–2500 CrossRef CAS
.
- P. T. Eles and C. A. Michal, Macromolecules, 2004, 37, 1342–1345 CrossRef CAS
.
- D. T. Edmonds and F. Vollrath, Proc. R. Soc. London, Ser. B, 1992, 248, 145–148 CrossRef
.
-
F. Vollrath, in Plastics in Automotive Engineering, ed. L. Vollrath, VDI Verlag, Düsseldorf, 1993, 1–16 Search PubMed
.
- R. V. Lewis, M. Hinman, S. Kothakota and M. J. Fournier, Protein Expression Purif., 1996, 7, 400–406 CrossRef CAS
.
- S. Winkler, S. Szela, P. Avtges, R. Valluzzi, D. A. Kirschner and D. Kaplan, Int. J. Biol. Macromol., 1999, 24, 265–270 CrossRef CAS
.
-
S. R. Fahnestock, in Biotechnology of Biopolymers; from Synthesis to Patents Volume 2, ed. A. Steinbuchel, and Y. Doi, 895–927, Wiley-VCH, Weinheim, 2005 Search PubMed
.
- J. P. O'Brien, S. R. Fahnestock, Y. Termonia and K. C. H. Gardner, Adv. Mater., 1998, 10, 1185–1195 CrossRef CAS
.
- A. H. Simmons, C. A. Michal and L. W. Jelinski, Science, 1996, 271, 84–87 CrossRef CAS
.
- C. Y. Hayashi, N. H. Shipley and R. V. Lewis, Int. J. Biol. Macromol., 1999, 24, 271–275 CrossRef CAS
.
- V. J. D. Beek, H. Hess, F. Vollrath and B. H. Meier, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 10266–10271 CrossRef
.
- R. Valluzzi and H. Y. Jin, Biomacromolecules, 2004, 5, 696–703 CrossRef CAS
.
- M. T. Krejchi, S. J. Cooper, Y Deguchi, E. D. T. Atkins, M. J. Fournier, T. L. Mason and D. A. Tirrell, Macromoecules, 1997, 30, 5012–5024 Search PubMed
.
- X. Peng, Z. Shao, X. Chen, D. P. Knight, P. Wu and F. Vollrath, Biomacromolecules, 2005, 6, 302–308 CrossRef CAS
.
- M. A. Colgin and R. V. Lewis, Protein Sci., 1998, 7, 667–672 CAS
.
- F. Vollrath and D. P. Knight, Int. J. Biol. Macromol., 1999, 24, 243–249 CrossRef CAS
.
- A. Lazaris, S. Arcidiacono, Y. Huang, J.-F. Zhou, F. Duguay, N Chretien, E. A. Welsh, J. W. Soares and C. N. Karatzas, Science, 2002, 295, 472–476 CrossRef CAS
.
- G. H. Altman, F. Diaz, C. Jakuba, T. Calabro, R. L. Horan, J. Chen, H. Lu, J. Richmond and D. L. Kaplan, Biomaterials, 2003, 24, 401–416 CrossRef CAS
.
-
(a) J. M. Gosline, M. W. Denny and M. E. Demont, Nature, 1984, 309, 551–552 CrossRef CAS
; (b) J. M. Gosline, C. C. Pollack, P. A. Guerette, A. Cheng, M. E. DeMont and M. W. Denny, in Silk Polymers. Materials Science and Biotechnology, ed. D. Kaplan , W. W. Adams, B. Farmer and C. VineyAmerican Chemical Society, Washington, 1994, 328–341 Search PubMed
.
-
J. F. V. Vincent, Biomechanics—Materials, Oxford University Press, Oxford, 1992 Search PubMed
.
-
J. F. V. Vincent, in Elastomeric Proteins, ed. P. R. Shewry, A. S. Tatham and A. J. Bailey, Cambridge University Press, Cambridge, 2003, 366–378 Search PubMed
.
-
P. R. Shewry, A. S. Tatham and A. J. Bailey, in Elastomeric Proteins, ed. P. R. Shewry, A. S. Tatham and A. J. Bailey, Cambridge University Press, Cambridge, 2003 Search PubMed
.
-
J. H. Waite, E. Vaccaro, C. Sun and J. Lucas, in Elastomeric Proteins, ed. P. R. Shewry, A. S. Tatham and A. J. Bailey, Cambridge University Press, Cambridge, 2003 Search PubMed
.
- L. S. Vincent, G. W. Frankie and J Kansas, Entomol. Soc., 1985, 58, 378–385 Search PubMed
.
- F. Franks, Biophys. Chem., 2002, 96, 117–127 CrossRef CAS
.
-
R. D. B. Fraser and T. P. Macrae, in The mechanical Properties of Biological Materials, ed. J. F. V. Vincent and J. D. Currey, Cambridge University Press, Cambridge, 1980, 211–246 Search PubMed
.
-
(a) J. E. Bertram and J. M. Gosline, J. Exp. Biol., 1986, 125, 29–47 Search PubMed
; (b) J. Vincent, Structural Biomaterials, Princeton University, Princeton, 1990 Search PubMed
.
- P. Fratzl, K. Misof, I. Zizak, G. Rapp, H. Amenitsch and S. Bernstorff, J. Struct. Biol., 1997, 122, 119–22
.
-
P. Fratzl, in Elastomeric Proteins, ed. P. R. Shewry, A. S. Tatham and A. J. Bailey, Cambridge University Press, Cambridge, 2003, 175–188 Search PubMed
.
- J. M. Gosline, Symp. Soc. Exp. Biol., 1980, 34, 332–57 Search PubMed
.
- B. B. Aaron and J. M. Gosline, Biopolymers, 1981, 20, 1247–1260 CrossRef CAS
.
-
C. M. Bellingham and F. W. Keeley, in Elastomeric Proteins, ed. P. R. Shewry, A. S. Tatham and A. J. Bailey, Cambridge University Press, Cambridge, 2003, 39–53 Search PubMed
.
- D. W. Urry, Ultrastruct. Pathol., 1983, 4, 227–51 CrossRef CAS
.
-
J. L. Katz, in The Mechanical Properties of Biological, ed. J. F. V. Vincent and J. D. Currey, Cambridge University Press, Cambridge, 1980, 137–168 Search PubMed
.
- J. D. Currey, Proc. R. Soc. London, Ser. B, 1984, 304, 509–18 CrossRef CAS
.
-
H. Rogers, H. R. Perkins and J. B. Ward, Microbial Cell Walls, Chapman and Hall, London, 1980, chapter 6 Search PubMed
.
- J. J. Thwaites and N. H. Mendelson, Int. J. Biol. Macromol., 1989, 11, 201–6 CrossRef CAS
.
-
J. Cappello and K. P. McGrath, in Silk Polymers. Materials Science and Biotechnology, ed. D. Kaplan, W. W. Adams, B. Farmer, and C. Viney, American Chemical Society, Washington, 1994, 311–327 Search PubMed
.
-
C. N. Karatzas, N. Cretien, F. Duguay, A. Bellemare, J. F. Zhou, A. Rodenhiser, S. A. Islam, C. Turcotte, Y. Huang and A. Lazaris, in Biotechnology of Biopolymers; from Synthesis to Patents Volume 2, ed. A. Steinbuchel and Y. Doi, Wiley-VCH, 2005, 945–965 Search PubMed
.
-
J. Scheller and U. Conrad, in Biotechnology of Biopolymers; from Synthesis to Patents Volume 2, ed. A. Steinbuchel and Y. Doi, Wiley-VCH, 2005, 929–943 Search PubMed
.
- D. P. Knight and F. Vollrath, Proc. R. Soc. London, Ser. B, 2002, 357, 155–163 CAS
.
- K. Kerkam, C. Viney, D. Kaplan and S. Lombardi, Nature, 1991, 349, 596–598 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2006 |
