The dynamics of proton transfer between adjacent sites

Abstract

The mechanism of proton transfer at the interface is the most prevalent reaction in the biosphere, yet its modeling at atomic level is still technically impossible. The difficulties emerge from the quantum mechanical nature of the proton, the modulation of the local electrostatic potential by the protein–water dielectric boundary and the formation of covalent bonds with proton binding sites whenever encounters take place. To circumvent some of these difficulties, and to identify the effect of the local electrostatic field, we present molecular dynamics simulations, where Na⁺ and Cl⁻ ions diffuse at the surface of a small model protein, the S6 of the bacterial ribosome. The analysis reveals the presence of a detained state, where an ion is located for a relatively long period within the immediate environment of certain attractor residues. In the detained state the ion retains its ability to diffuse, yet the local field deters it from leaving to the bulk. When an ion is detained inside a Coulomb cage, it has a high probability to be transferred between nearby attractors, thus forming a mechanism similar to that responsible for the proton collecting antenna present on proton proteins.

---

M. Gutman

Menachem Gutman educated as a clinical microbiologist, converted to biochemistry and evolved as an addicted mitochondriac, only to discover the beauty of proton transfer chemistry as model for kinetic analysis of complex-coupled reaction systems. Presently, M. G. is an emeritus professor in the Laser Laboratory for Fast Reactions in Biology, Department of Biochemistry, Tel-Aviv University.

E. Nachliel

Esther Nachliel graduated as a chemist from Tel Aviv University, she joined the Laser Laboratory for Fast Reactions and participated in introducing the Laser Induced Proton Pulse as a research tool. Presently, Dr Nachliel is leading the mathematical modeling team.

R. Friedman

Ran Friedman received his BSc degree in Biology from Tel Aviv University in 2001 and immediately joined the Laser Laboratory for Fast Reactions in Biology as a graduate student. His PhD thesis will deal with interactions between proteins and small solutes at the protein–solvent interface.

---

Proton propagation at interface

Of all reactions in the biosphere, the bulk-surface proton transfer is the most voluminous one. Each O₂ molecule generated by the chloroplasts is coupled with 20 moles of H₃O⁺ ions, which are sequentially taken up and released by membranal enzymes. Similarly, the mitochondrial oxidative phosphorylation operates by a coupled cross-membranal proton flux, which is comparable in magnitude to that of the photosynthesis process. This high proton flux has for long been a subject of intensive biochemical-biophysical research, and each level of its refinement generated a new set of experimental/theoretical uncertainties. The clarification of the process necessitates an understanding of the mechanism at the atomistic level. This demand calls for measuring the reaction with atomic resolution coupled with an analysis that is based on molecular details of the reaction space, which by itself is not a trivial problem.

The surface of a protein is irregular in shape, covered by a large number of charged residues that are unevenly distributed. Thus, there may be domains with high local electrostatic potential, while in others the positive and negative residues can cancel the charge. Yet at close quarters, within the first solvation shell of the protein, the local fields are not eliminated, mostly due to the amplification of the electrostatic potential caused by the special conditions that characterize the boundary zone between the aqueous phase and the low dielectric constant of the protein. In this narrow domain, only a few Ängströms from the interface, the image charges caused by the dielectric discontinuity almost double the electrostatic potential.¹ Besides these ‘static’ considerations, the dynamics of the protein should not be ignored. The relative motion of the charged residues on the protein's surface falls in the picosecond time frame, and is comparable with the time needed for a proton (D_H⁺ = 9.3 × 10⁻⁵ cm² s⁻¹) to propagate between two sites some 10 Å apart. Thus, the relative motion of the proton-exchanging residues is comparable with that of a proton on the protein–solvent interface. A combination of these requests amounts to very heavy computational demands that can hardly be carried out. The dynamics of the protein, together with the water and electrolyte, can be calculated by standard molecular dynamics simulation methods,² but once the proton diffusion is properly implemented, as in the Car–Parinnello simulation,³ the task is too heavy.

The need to introduce the atomistic mechanism of proton transfer emerges from the unique mode of the reaction. While the proton is a fully solvated ion, similar to Na⁺ or other small ions, its diffusion is not through a self diffusion reaction, where the mass and charge of the ion move in tandem, but through the Grotthuss mechanism (for comprehensive review see ref. 4). The reaction is a consequence of constant rearrangements of the hydrogen bond network in the water, with rapid transition between covalent and hydrogen bonds in the vicinity of the solvated proton. The modeling of the reaction necessitates a full quantum mechanical treatment.³ Molecular dynamics simulations are not suitable to observe and account for the formation of covalent bonds; thus, whenever a free proton is taken up by a reaction with a proton binding site simulation wise, it ‘vanishes’ from the solution for a time frame of microseconds to milliseconds (for residues with pK values of 4–7, respectively). These time intervals are orders of magnitude longer than the upper limit of molecular dynamics simulations. The binding of a proton to a site on a protein does not mean that it becomes immobile. Whenever a nearby acceptor residue, due to structural fluctuations, forms a temporary hydrogen bond with the bound proton, the shared proton may end up on a new location, when the hydrogen bond is broken. The collisional proton mechanism can contribute to the overall mobility of the proton on the surface, even though the proton is still hidden in a covalent bond. Thus, the propagation of a proton will be a series of ‘fly and perch’ events, rendering the overall process to be too complex for molecular simulation. The system can be fairly simplified by ignoring the quantum mechanical aspects of the proton propagation by looking at the dynamics of standard ions, like Na⁺ and Cl⁻, at the immediate vicinity of a protein,⁵ thus clarifying the effects of the local electrostatic potential and geometry of sites.

Proton transfer reaction on the protein surface

The reactions of a free proton with the protein surface were studied directly by use of the laser induced proton pulse technique.^6–9 In these studies, the proteins were dissolved or suspended in a solution containing photoacid. Photoacids are molecules whose pK_as are dramatically reduced when excited to their first electronic singlet state.^6,10–12 The excitation of the photoacid molecules led to a rapid proton release into the solution. Following the momentary acidification of the solution, surface groups such as histidine, aspartate and glutamate became transiently protonated. Using probe molecules attached to the protein, the kinetics of the proton transfer reactions on the protein surface could be analyzed. It was noted in these studies that residues which, according to the crystal structure of the protein are up to 10–15 Å apart, could form proton-attractive domains and could share the proton among them at a very fast rate, exceeding the upper limit of diffusion-controlled reactions as characterized by the Debye–Smoluchowski equation.^7,13–16 To account for the fast rate, it was suggested that random fluctuations of the protein generate transient configurations, in which the residues are sufficiently close to permit a proton transfer between them. What is more, the passage of the proton is accelerated by the electrostatic potentials that bias the diffusion of the proton between the donor–acceptor sites. It was also reasoned that, if such a mechanism is operative, it should be a general feature of the protein surfaces and not limited to a specific protein or to the nature of the charged particle.

The role of fixed proton binding sites in bulk-surface proton transfer

Proton transfer at the surface of an interface was measured by the scanning electrochemical microscopy technique.¹⁷ A microscopic electrode, placed few µm under Langmuir monolayer made by protonable lipids, was used to perturb the acid–base equilibrium through electroreduction of a soluble base. The experimental conditions are set so that a mobile buffer serves as a proton carrier between the electrode's surface and the proton reservoir of the protonated carboxylates on the surface. Under steady state conditions, the rate-limiting step of the system is the flux of protons on the surface, which funnel protons from remote sites towards the reducing electrode. The rate of this reaction is modulated by compression of the overall proton transfer monolayer, thus evaluating the contribution of the freedom of motion of the fixed proton binding sites on the overall proton transfer dynamics.

Using this method, Unwin and coworkers^17–19 observed that the fixed proton binding sites can move, one with respect to the other. This motion contributes to the propagation of the proton on the surface. The phospholipid surface, made exclusively of the zwitterionic phosphatidylcholine cannot support any lateral proton diffusion on the monolayer, reflecting the lack of proton binding sites on the surface. On the other hand, when the surface is made of stearic acid, the carboxylate residues can exchange protons among them, and a steady surface proton flux was recorded with a diffusion coefficient of ∼8 × 10⁻⁶ cm² s⁻¹, which is ∼10 times smaller than the diffusion coefficient in bulk. Condensation of the monolayer by application of a pressure exceeding, π = 25 mN m⁻¹, suppressed the motion of the carboxylates on the surface to such an extent that no lateral proton transfer could be recorded. These results clearly imply that evaluation of proton transfer at interface must explicitly consider the motion of the surface residues as an integral feature of the system. This observation can also be applied to proteins; their structural fluctuations cannot be ignored when proton transfer is under study. Considering the various aspects associated with proton propagation at interface, it is obvious that the molecular mechanism cannot be analyzed by a single comprehensive model; one must define a specific aspect of interest concerning proton transfer on the protein surface and then design the best model for this study. Thus, to avoid the complication of the quantum mechanical aspects associated with a free proton in aqueous solution, we replaced the proton by other ions, assuming that of the electrostatic forces affect ions through the same mechanism. Through this simplification we shall address the following problems.

(1) How fast is the equilibration between the ions in the bulk and the surface of a protein?

(2) How do the electrostatic forces affect the spatial and temporal distribution of an ion in the immediate vicinity of the protein?

(3) Can a collisional proton transfer between sites on a surface contribute significantly to the overall surface flux?

As will be described below, these questions were addressed through molecular dynamics simulations of a model protein in a dilute aqueous solution with a few explicit ions.⁵ In this case, the spatio–temporal follow up of the ions, either in respect to the protein or to certain attractor sites, can reveal the effects of local forces. The conclusions of these generalized considerations directly reflect on the properties of a free proton in the vicinity of a protein. On evaluation of the results presented below, it must be recalled that, unlike the proton, neither the Na⁺ nor the Cl⁻ ions can form a covalent bond with any of the sites on the protein. On the other hand, the diffusion coefficients of the ions are only ∼20% with respect to that of the proton. As a result, the encounters between the ions and the protein are slower than the reaction with the free proton, and the dwell time of the ions on the surface binding sites will be much shorter than that of a bound proton.

The spatial–temporal distribution of ions near a protein

Contacts between the ions and the protein

The interactions between the ions and the protein can be expressed, in a quantitative manner, by the relative location of the ions with respect to the protein surface. The description of ions near a planar membrane surface was based on the atomic densities and radial distribution functions.^20,21 However, because of the irregularity of the protein surface, these parameters are not informative for the study of such reactions. Moreover, the small number of ions results in large fluctuations of the calculated densities. For these reasons, the most suitable parameter is a follow up of the distance between each of the ions, either with the nearest site on the protein or to a certain attractor site selected by the investigator. For example, see ref. 22–25.

The protein selected as a model for ion–protein interactions⁵ was the S6 of the bacterial 30S ribosome central domain,²⁶ which has no physiological function associated with ion transport on its surface. S6 is a globular protein and all of its 101 amino acids are exposed to the water. The protein carries 32 charged residues, of which 16 are positive and 16 negative. For these properties, it was considered as a neutral target, suitable for testing whether the surface per-se and the charges it carries are sufficient to affect the spatio–temporal dynamics of the ions. The calculations were carried out with 4Na⁺ and 4Cl⁻ ions which, within the dimension of the simulations box, correspond with a 30 mM NaCl solution. Simulations carried out at higher salt concentration were deleterious: the high ionic strength masks most of the weak interactions and saturated the attractor sites with more ions than they could handle. Keeping in mind that our interest is in protons, it must be recalled that, under physiological conditions, the free proton concentration is very low and saturation of proton binding sites is never achieved.

The simulation was first tested by calculation of the diffusion coefficient of the ions in the reaction space. The derived values did not differ from the experimentally determined coefficients, indicating that the presence of the protein did not impede the motion of the ions.

The variations with time of the minimal distance between the protein and each of the Na⁺ ions during the simulation are presented in Fig. 1. The distance varies from a contact distance of ∼2 Å up to ∼31 Å. Yet, while some ions only collide with the protein and bounce back to the bulk (see the yellow and black traces), there are ions that appear to be attracted by the protein, spending as much as few hundreds of picoseconds at less than 6 Å from the surface (magenta and cyan tracings). The analysis of the Cl⁻-protein spatial–temporal distribution yielded a similar behavior (data not shown). A close inspection of the ion–protein distance traces reveals that, even when the ions are near the surface of the protein, their minimal distances with respect to the protein still exert fluctuation at high frequency and almost with the same amplitude, as if the ion attempts to diffuse from the surface, but some forces detain it at the interface. The fact that detained states appear well within the first ns of the simulation time implies that the equilibrium between the bulk ions and the surface is established in less than 1 ns.

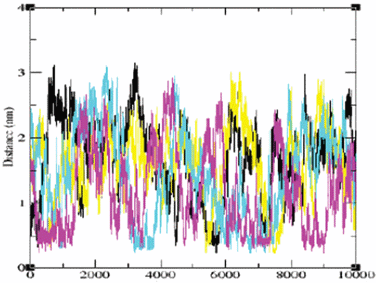Fig. 1 The minimal distance from the protein to each of the Na⁺ ions present in the simulation box (for each ion there is another color code) as it varies during the simulation. The distances are given in nm and the time in ns. The absolute minimal distance (∼0.2 nm) is dictated by the steric interferences between the van der Waals radii of the ions.

Molecular dynamics simulations of ions near a peptide molecule²² revealed that the ions can be attracted to a sufficiently close site, to form an inner-sphere complex. In these cases, the ion–site distance is shorter than the length of a water molecule and the frequency and amplitude of the spatial fluctuations are significantly different from those presented in Fig. 1. In the case of the S6 ribosomal protein the ions exhibit two kinds of fluctuations. The first one is of a free ion in the bulk, where it exhibits a normal random walk with a diffusion coefficient similar to the experimental value. The other kind of motion is of an ion that spends a long period, up to few hundreds of picoseconds, near the protein. In that state, the ion retains a high mobility yet its random motion is biased, thus keeping it close to the protein's surface. For this reason, these ions were termed ‘detained’.

Quantitative evaluation of the detained state

The detained state can be expressed by two quantitative parameters: the time averaged tendency to be detained and the duration of the detained state. To evaluate the probability of finding an ion within the 6 Å layer surrounding the protein, we first assume that the protein is totally inert with respect to the ions' distribution. Under this assumption, we can expect that the time averaged fraction of an ion within the detaining layer⁵ will be proportional to the ratio between the volume of the detainment layer (39.18 nm³) and the total aqueous phase of reaction simulation box (217.7 nm³) which, in the case investigated by Friedman et al., implied that the ions will spend 22% of the simulation time within the 6 Å layer around the S6. In practice, the values were 70.2% and 50.8% for the Cl⁻ and the Na⁺ respectively, well above the limit of confidence. Yet, in accordance with the non-homogeneous nature of the protein's surface, the average value is only indicative and the attractor sites should be identified and scaled according to their detainment capacity. The most attractive sites for the Na⁺ ion located on the surface of the S6 are presented in Table 1.

Table 1 The probability of finding the Na⁺ ions in a detained state, in which an ion is within 6 Å of the carboxylate oxygens of the C-terminus, aspartate or glutamate and the unprotonated imidazole nitrogen of his16, calculated over the simulation time; only residues associated with the protein during more than 10% of the simulation time, or discussed in the text, are included in the table

Residue	Probability	Detainment energy/kcal mol^−1
Asp15	0.06	−0.45
His16	0.03	−0.02
Glu31	0.07	−0.55
Glu41	0.08	−0.64
Glu42	0.005	1.07
Glu95	0.12	−0.90
Phe97 (CT)	0.08	−0.64

---

The inspection of the attractor sites reveals a very large variation between similar residues. For example, glu41 detains a Na⁺ ion in its vicinity for 8% of the time, while its ‘next door neighbor’, glu42, detains it for only 0.5%. This large difference clearly implies that the attractor domain is a local property, determined by the charges and the geometry of the surface/surrounding.

In corollary with the spatial identification of the attractor, we can evaluate the time that an ion dwells inside a given detaining space. In the absence of electrostatic force, an ion at a contact distance (2 Å) from a neutral atom on the protein will take only ∼40 ps to diffuse and escape out of the 6 Å detainment range (τ = Δl²/2D; Δ = 4 Å). As seen in Fig. 1, there are time frames, extending up to few hundreds of ps, in which an ion appears to remain within the detained space. Thus, the attractivity of a site can be expressed by the sum of the dwell time of the ions that fell into the potential ‘trap’.

Assuming a two state system, where the ion can be either free or detained, the equilibrium constant for detainment (K_det) is calculated according to:^21,27

K_det = α/[(1 − α)C] (1)

where C is the concentration of the ions and α is the time fraction that the site is associated with an ion. Accordingly, the free energy associated with the detainment is given by the expression

ΔG_det = −RT ln K_det (2)

Some typical values are provided in Tables 1 and 2, where the α value and the detainment energy are given for few Cl⁻ and Na⁺ sites. The weak sites are hardly attractive, and the ions spend near them a time frame very similar to a random distribution in an inert space. The more attractive sites are characterized by few k_BT units. These values are significantly weaker than a covalent bond, yet strong enough to delay an ion inside a limited space. This makes the detainment a key feature when kinetics are considered.

Table 2 The probability of finding the Cl⁻ ions in a detained state, in which an ion is located within 6 Å of the terminal group hydrogens of the N-terminus, arginine or lysine, or the hydrogen from the OH group of tyrosine 50, calculated over the simulation time; only residues associated with the protein during more than 5% of the simulation time, or discussed in the text, are included in the table

Residue	Probability	Detainment energy/kcal mol^−1
Tyr50	0.11	−0.84
Arg80	0.28	−1.53
Arg87	0.24	−1.41

---

The dynamics of ions at the interface

The simulation of the S6 in the presence of 30 mM NaCl revealed that the ions were moving randomly in the solution, with a diffusion coefficient similar to the experimentally determined value. When the ions were next to the protein, the randomness was lost and, occasionally, anion was observed to move from one attractor site to the other. Two such cases are displayed in Fig. 2.

Fig. 2 (a) The distance between one of the chloride ions and the hydrogen atoms attached to the guanido group of arg47 (magenta) or the amino group of lys54 (black), as a function of simulation time. (b) The distance between one of the sodium ions and the carboxylate oxygens of glu31 (cyan), glu38 (black) and glu66 (magenta) as a function of simulation time.

Two different modes of detainment can be observed in the study model. The first one is an ion localized in a closed compartment, exemplified by the Cl⁻ near the S6,⁵ see Fig. 2 frame (a) or near a peptide.²² The second form of a detained ion is a rapid shuttling between nearby attractors, as a motion of the Na⁺ ion, demonstrated in Fig. 2 frame (b).

The figure depicts the minimal distance between a single ion and two attractor sites, as it varies with time. Whenever the ion is less than 6 Å from the attractors, it is in a detained state. Frame (a) depicts the dynamics of a Cl⁻ ion over ∼200 ps. During this time frame, the ion spent ∼50 ps, near residue R47 (the magenta trace in Fig. 2(a)). Then, for about 50 ps it diffused out of site to the detainment layer, only to be rearrested in the vicinity of K54 (indicated by black trace). It is of interest to point out that the Cl⁻ ion, having a lower charge density than the cation, is less hydrated and when interacting with the attractor, the minimal distance is in the range of 2–3 Å, representing an inner sphere complex. Frame (b) represents the same scenario for a Na⁺ ion. In this case, the ion rapidly shifts between three residues E31, E38 and E66. In the crystal structure the distance between the carboxylate of E31 and that of E66, is 13.25 Å and from E31 to E38 is 13.31 Å. The simulation reveals that the Na⁺ ion is detained in their vicinity for a considerable time, ∼0.5 ns. Within this time frame, the ion can be present simultaneously in the vicinity of both residues, indicating the contribution of the dynamics of the side chains to the ion's propagation.

Indeed, the diffusion coefficient of the proton and the mode of propagation in the bulk differ from those of the ions reported above, yet the electrostatic potential will bias its motion just as reported here for the Na⁺ or the Cl⁻ ions. For these reasons, we can look for the correlation between the trajectories of the ions and that of free proton near the surface of the proteins. The photocycle of Bacteriorhodopsin consists of a series of proton transfer reactions; some take place between residues located inside the protein, while others are between the bulk and the exit or entry sites of the proton transfer machinery. Examination of the time constants of the reactions reveals that the reuptake of free proton from the cytoplasmic space of the bacterium is faster than the expected random encounter between the free proton and the site. The enhancement was attributed to the fusion of a special structure, termed the ‘proton collecting antenna’^28–31 which utilizes the electrostatic attractivity of few carboxylates to fish the free proton from the bulk and deliver them to D36, which serves as a local proton reservoir next to the channel-entry. The antenna is made of three carboxylates between which a proton is rapidly shuttled in similarity with the Na⁺ dynamics presented in Fig. 2, frame (b), where the charged particle executes a biased diffusion under the umbrella of attractive electrostatic potential, thus enhancing its encounter with the nearby attractor sites.

The dynamics of the Cl⁻ ion, trapped in the vicinity of the positive residues (Fig. 2, frame (a)) are reminiscent of the behavior of the proton on the proton release site at the extra-cellular side of the Bacteriorhodopsin. The proton release site of the protein is made of two carboxylates (E194 and E294) that appear to share a proton between them, without forming a covalent bond.³² This situation is similar to the strong attractor domain for the Cl⁻, where three residues, each interacting with the ion by a rather weak force, detain the Cl⁻ ion in shallow trough.

The Coulomb cage around the protein

The tendency of the ions to shuttle between the attractor sites without leaving the detention distance reflects the presence of the local electrostatic potential, which can be visualized by the 1 k_BT surface calculated for the protein dissolved in aqueous solution containing 50 mM of 1 : 1 electrolyte (Fig. 3).

Fig. 3 The electrostatic potential surface around the protein. The three attractor sites between which the Na⁺ ions, were observed to shuttle (his16, glu41 and glu95), are all located under the positive Coulomb cage umbrella. The Coulomb cages for the positive (blue) and negative (red) domains are drawn at the distance where the electrostatic potential equals 1 k_BT/e.

The potential field consists of two main lobes, one positive and the other negative. The negative Coulomb cage is characterized by a linear array of attractors. During the molecular dynamics, the Na⁺ ion can be observed to be shuttled along the attractors. Such bind-and-release events are demonstrated on the animation, which is provided in the following web site: http://www.biophysj.org/content/vol0/issue2005/images/data/biophysj.105.058917/DC1/s6.AVI.

At the first frame of the movie (t = 700 ps), the ion is associated with E95. Within a short time, it escapes from the vicinity of E95 and diffuses into the bulk and at t = 890 ps it is re-attracted to the protein and becomes detained by E41. The ion's encounter with E41 is brief and after approximately 20 ps, it diffuses away, only to associate, within less than 100 ps, with the nitrogen atom of H16. Usually, histidine residues are not cation attractors. However, when the residue is located under the negative Coulombic umbrella (see Fig. 3), it can briefly detain the sodium ion (see Table 1). The ion is associated with H16 for a rather long time, ∼100 ps, indicating that under favoring electrostatic potential, even poor attractors become efficient. When the Na⁺ ion is released, it is re-detained by E41. Finally, the ion is driven into the bulk solvent, where it freely diffuses away from the protein surface.

In contrast, with the capacity of the Na⁺ ion to shuttle freely over the whole space under the (negative) electrostatic umbrella, the Cl⁻ seems to prefer a local domain, where it interacts successively with (mostly) three sites R80, R87, Y50 and, to a lesser extent, with K92. This suggests that the geometry of the site must be considered, not only the intensity of the electrostatic potential.

The effect of proximity between sites

In the crystal state, the three components of the Cl⁻ attractor site are well apart (Fig. 4). The nearest nitrogen atoms of the two arginines are 9.14 Å apart, and the distance between Y50 to the nitrogen of R87 is 5.57 Å. When the Cl⁻ ion is detained, the three sites reorient to form a clathrate, where the ion interacts, almost at inner sphere distance, with the hydrogen atoms of at least one of the ligands. Even though the configuration seems to restrict the ion, examination of the ion's dynamics reveals a high freedom of motion. The amplitude of the fluctuations alternates between occasional rigid binding (reflecting a stable inner-sphere complex) and a more prevalent state, where the ion exercises encounters with some of the ligands, while remaining within the detainment space. Apparently, the gain in potential energy, when a strong interaction between the ion and the positive ligand is established, is compensated by high entropic penalty, reflecting the loss of freedom of motion that characterized the detained state.

Fig. 4 The bound ions and their immediate vicinity. A chloride ion bound to residues arg80, arg87 and tyr50. The minimal distances between the ion and the residues were 2.24 Å, 2.86 Å and 2.02 Å for arg80, arg87 and tyr50, respectively.

Proton transfer between nearby sites

A surface of a protein carried a large number of proton binding sites which are as close as few Å. When one of these sites is protonated, the covalently bound proton is ‘out of the field’ with respect to free diffusing protons, yet it can be transferred among neighboring residues whenever they form a hydrogen bond between them. Such a state, where two residues are at a range suitable for a proton exchange between them, is presented in Fig. 5. The figure depicts two residues of the S6 protein, where one of them, E22, is protonated, while the other, D83, is not. During simulations of the protein, in a box of water and in the presence of 30 mM NaCl, two types of connections between the residues were recorded.³³ In one case, the interaction is through a direct hydrogen bond via the covalently bound proton (Fig. 5(a)), while in the other it is through a couple of water molecules (Fig. 5(b)). In both cases, the carboxylate residues did not protrude beyond the Coulombic umbrella. The length of molecular dynamics simulations can hardly exceed few tens of nanoseconds, a time frame that is too short for the bound proton to dissociate from a site with pK ≤ 4. Yet, when the two carboxylates form a hydrogen bond, and their pK values are comparable, the proton can propagate between the two sites within less than a picosecond.³⁴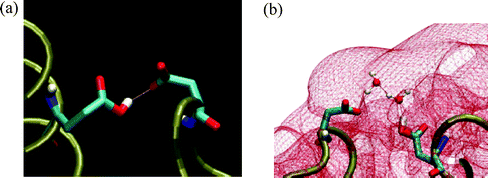

Fig. 5 A hydrogen bond structure between the protonated glu22 and the carboxylate of asp83, formed either by direct interaction (frame (a)) or through 2 interconnecting water molecules (frame (b)). Please note that the connection between the carboxylates is under the Coulombic umbrella (−1 k_BT) covering the protein (shown in red).

Thus, given the proper geometry and appropriate local electrostatic field, ions at the surface can propagate both as a self-diffusing particle or can be shared by the ligands when they come close enough during their random search of the conformation space.

Perspective

The study of proton transfer at interface is a hierarchical problem, ranging from the quantum mechanical level up to cell physiology; and at each level bears its own complications. In the present report, we addressed the motion of a charged particle at the molecular level; instead of investigating the chemistry of the proton, with all of the complications derived from its quantum mechanical properties, we investigated a stable charged particle such as the Na⁺ or the Cl⁻ ion. The replacement of the proton by salt ions generalizes the problem, posing it as a study of the properties of a charged particle near a protein. This substitution allows us to employ the ‘simple’ molecular dynamics formalism. The system was treated explicitly, but the mobile particles were Na⁺ and Cl⁻ ions rather than the solvated proton. This generalization permitted the evaluation of the trajectory of an ion, at a molecular level, while avoiding the complications caused by the covalent bond formed between a proton and the multitude of proton binding sites on the surface.

A detailed analysis of the ions' trajectories revealed states where the ions can be detained. In these states, the ion was free to diffuse, yet the local electrostatic potential restricted its motion to a limited space, defined by the geometry and the placement of charged residues. The temporal localization of the ion enhanced its encounter with the attractor sites, thus revealing events that are of low probability in dilute solutions like the interaction of Na⁺ ion with a histidine or Cl⁻ with the OH moiety of tyrosine. These reactions indicate how ‘poor binding sites’ can profit by the immediate environment.

Finally, considering the tendency to explore biochemical reactions at molecular-atomistic resolution, where experimental technologies can be less effective, the relative ease of molecular dynamics, without attempting the more demanding QM/MM simulation, can allow evaluation of ensemble properties of a domain and reflect the conclusions on similar reactions proceeding in the same space.

References

1. R. T. Mathias, G. J. Baldo, K. Mannivannan, S. McLaughlin, Discrete charges on biological membranes, in Electrified interfaces in physics chemistry and biology, ed. R. Guidelli, 1992, Kluwer academic publishers, pp. 473–490.
2. J. Norberg and L. Nilsson, Advances in biomolecular simulations: methodology and recent applications, Quart. Rev. Biophys., 2003, 36, 257–306.
3. R. Car and M. Parinnello, Unified approach for molecular dynamics and density-functional theory, Phys. Rev. Lett., 1985, 55(22), 2471–4.
4. N. Agmon, The Grotthuss mechanism, Chem. Phys. Lett., 1995, 244, 456–462.
5. R. Friedman, E. Nachliel and M. Gutman, Molecular Dynamics of a Protein Surface: Ion-Residues Interactions, Biophys. J., 2005, 89, 768–81.
6. M. Gutman and D. Huppert, Rapid pH and ΔμH⁺ jump by short laser pulse, J. Biochem. Biophys. Methods, 1979, 1(1), 9–19.
7. M. Gutman, The pH jump: probing of macromolecules and solutions by a laser-induced, ultrashort proton pulse-theory and applications in biochemistry, Methods Biochem. Anal., 1984, 30, 1–103.
8. M. Gutman and E. Nachliel, The dynamic aspects of proton transfer processes., Biochim. Biophys Acta, 1990, 1015, 391–414.
9. M. Gutman and E. Nachliel, Time resolved dynamics of proton transfer in proteinous systems., Annu. Rev. Phys. Chem., 1997, 48, 329–56.
10. A. Weller, Excited state proton transfer, Prog. React. Kinet., 1961, 1, 198–214.
11. T. H. Forster and S. Volker, Kinetics of proton transfer reation involving hydroxypyrene-trisulfonate in aqueous solution by nanosecond laser absorption spectroscopy, Chem. Phys. Lett., 1975, 34, 1–5.
12. T. H. Tran-Thi, T. Gustavsson, C. Prayer, S. Pommeret and J. T. Hynes, Primary ultrafast events preceding the photoinduced proton transfer from pyranine to water, Chem. Phys. Lett., 2000, 329(5–6), 421–30.
13. M. von-Smoluchowski, Z. Physik, 1916, 17, 557–585.
14. N. Agmon, Geminate recombination in proton-transfer reactions. III. Kinetics and equilibrium inside a finite sphere, J. Chem. Phys., 1988, 88(9), 5639–42.
15. E. Nachliel, Z. Ophir and M. Gutman, Kinetic analysis of fast alkalinization transient by photoexited hetrocyclic compounds: pOH jump, J. Am. Chem. Soc., 1987, 109, 1342–1345.
16. B. Cohen, D. Huppert, K. M. Solntsev, Y. Tsfadia, E. Nachliel and M. Gutman, Excited state proton transfer in reverse micelles, J. Am. Chem. Soc., 2002, 124(25), 7539–47.
17. Z. Jie and P. R. Unwin, Scanning electrochemical microscopy (SECM) feedback approach for measuring lateral proton diffusion in Langmuir monolayers: theory and application, Phys. Chem. Chem. Phys., 2002, 4(15), 3814–19.
18. C. J. Selevia and P. R. Unwin, lateral proton diffusion rates along stearic monolayer, J. Am. Chem. Soc., 2000, 122, 2597–2602.
19. J. Zhang and P. R. Unwin, Proton diffusion at phospholipid assemblies, J. Am. Chem. Soc., 2002, 124(10), 2379–83.
20. P. Mukhopadhyay, L. Monticelli and D. P. Tieleman, Molecular dynamics simulation of a palmitoyl-oleoyl phosphatidylserine bilayer with Na⁺ counterions and NaCl, Biophys. J., 2004, 86, 1601–9.
21. S. A. Pandit, D. Bostic and M. L. Berkowitz, Molecular Dynamics Simulation of a Dipalmitoylphosphatidylcholine Bilayer with NaCl, Biophys. J., 2003, 84, 3743–3750.
22. P. E. Smith and B. M. Pettitt, Effects of Salt on the Structure and Dynamics of the Bis(Penicillamine) Enkephalin Zwitterion- a Simulation Study, J. Am. Chem. Soc., 1991, 113(16), 6029–6037.
23. P. E. Smith, G. E. Marlow and B. M. Pettitt, Peptides in Ionic-Solutions - a Simulation Study of a Bis(Penicillamine) Enkephalin in Sodium-Acetate Solution, J. Am. Chem. Soc., 1993, 115(16), 7493–8.
24. G. E. Marlow and B. M. Pettitt, Simulations of the bis-penicillamine enkephalin in sodium chloride solution: a parameter study, Biopolymers, 2001, 60, 134–52.
25. G. E. Marlow and B. M. Pettitt, Simulation of the bis-(penicillamine) enkephalin in ammonium chloride solution: a comparison with sodium chloride, Biopolymers, 2003, 68, 192–209.
26. S. C. Agalarov, G. S. Prasad, P. M. Funke, C. D. Stout and J. R. Williamson, Structure of the S15,S6,S18-rRNA Complex: Assembly of the 30S Ribosome Central Domain, Science, 2000, 288, 107–112.
27. P. M. Macdonald and J. Seelig, Anion binding to neutral and positively charged lipid membranes, Biochemistry, 1988, 27, 6769–6775.
28. S. Checover, Y. Marantz, E. Nachliel, M. Gutman, M. Pfeiffer, J. Tittor, D. Oesterhelt and N. A. Dencher, Dynamics of the proton transfer reaction on the cytoplasmic surface of bacteriorhodopsin, Biochemistry, 2001, 40(14), 4281–92.
29. E. Nachliel, M. Gutman, J. Tittor and D. Oesterhelt, Proton Transfer Dynamics on the Surface of the Late M State of Bacteriorhodopsin, Biophys. J., 2002, 83(4), 416–426.
30. S. Yaniv-Checover, Structure function relationship of proton transfer system on the surface of Bacteriorhodopsin, PhD Thesis, Tel Aviv University, Israel, 2002.
31. B. Schatzler, N. A. Dencher, J. Tittor, D. Oesterhelt, S. Yaniv-Checover, E. Nachliel and M. Gutman, Subsecond proton-hole propagation in bacteriorhodopsin, Biophys. J., 2003, 84(1), 671–86.
32. V. Z. Spassov, H. Luecke, K. Gerwert and D. Bashford, pK(a) Calculations suggest storage of an excess proton in a hydrogen-bonded water network in bacteriorhodopsin, J. Mol. Biol., 2001, 312(1), 203–19.
33. R. Friedman, E. Nachliel and M. Gutman, Application of classical molecular dynamics for evaluation of proton transfer mechanism on a protein, Biophys. Biochim. Acta, 1710(2–3), 67–77.
34. M. Rini, B. Z. Magnes, E. Pines and E. T. Nibbering, Real-time observation of bimodal proton transfer in acid–base pairs in water, Science, 2003, 301(5631), 349–52.

---

Footnote

† This paper was published as part of the special issue on Proton Transfer in Biological Systems.

---