Ceramic microreactors for on-site hydrogen production from high temperature steam reforming of propane

Abstract

The steam reforming of hydrocarbon fuels is a promising method for the production of hydrogen for portable electrical power sources. A suitable reactor for this application, however, must be compatible with temperatures above 800 °C to avoid coking of the catalytic structures during the reforming process. Here, ceramic microreactors comprising high surface area, tailored macroporous SiC porous monoliths coated with ruthenium (Ru) catalyst and integrated within high-density alumina reactor housings were used for the steam reforming of propane into hydrogen at temperatures between 800 and 1000 °C. We characterized these microreactors by studying C₃H₈ conversion, H₂ selectivity, and product stream composition as a function of the total inlet flow rate, steam-to-carbon ratio (S/C), and temperature. As much as 18.2 sccm H₂, or 3.3 × 10⁴ sccm H₂ per cm³ of monolith volume, was obtained from a 3.5 sccm entering stream of C₃H₈ at a S/C of 1.095 and temperatures greater than 900 °C. Operating at a S/C close to 1 reduces the energy required to heat excess steam to the reaction temperature and improves the overall thermal efficiency of the fuel processor. Kinetic analysis using a power law model showed reaction orders of 0.50 and −0.23 with respect to propane and steam, respectively, indicating that the rate limiting step in the steam reforming reaction is the dissociative adsorption of propane on the Ru catalyst. The performance of the microreactor was not affected after exposure to more than 15 thermal cycles at temperatures as high as 1000 °C, and no catalyst deactivation was observed after more than 120 h of continuous operation at 800 °C, making these ceramic microreactors promising for efficient on-site hydrogen production from hydrocarbons for use in polymer electrolyte membrane (PEM) fuel cells.

---

Introduction

An attractive option to obtain electrical power sources with high energy densities is the use of highly efficient hydrogen fuel cells, typically referred to as polymer electrolyte membrane (PEM) fuel cells.^1,2 The use of PEM fuel cells in electronic devices lacking access to wired electrical power, such as vehicles, portable electronics, and electrical equipment in remote locations, requires either storage of compressed H₂ or on-site production of H₂, for example by the reforming of liquid hydrocarbons or alcohols.^3–5 Safety issues related to the distribution and storage of compressed H₂, however, have made the on-site generation of H₂ from liquid fuels a preferred solution.

Currently, typical technologies for producing H₂ from hydrocarbons include steam reforming,⁶ partial oxidation,⁷ and autothermal reforming.^5,8 While each technology has its advantages and disadvantages,⁹ steam reforming was chosen in this study because the highest H₂ concentration in the product stream is obtained, thus reducing the size of subsequent purification units to obtain high-purity H₂ for introduction into a PEM fuel cell. In addition to a sulfur removal unit and vaporizers for the feed gas prior to entering the reformer, a typical fuel processor includes water gas shift reactors, preferential oxidation reactors, and/or membrane separators to obtain a high-purity H₂ stream and to avoid CO poisoning of the fuel cell catalyst.^10,11 Other direct and simple routes to producing H₂, such as the decomposition of ammonia (energy density ∼4 kW h l⁻¹), have been studied;^12,13 however, the reforming of liquid hydrocarbons is highly desirable due to their high energy densities (e.g. 7.0, 9.7, and 10.7 kW h l⁻¹ for propane, gasoline, and diesel, respectively) and the fact that an infrastructure for their storage and distribution already exists. Recently, others have reported a preliminary study on the production of H₂ by the reforming of biomass-derived hydrocarbons to eliminate the use of non-renewable fossil fuels;¹⁴ however, this technology is still in the early stages of development.

To date, several microreactors for on-site production of H₂ from several alcohols and a few hydrocarbons have been developed^4,15–18 to exploit advantages of performing catalytic steam reforming at the microscale. Mass and heat transfer fluxes are much larger at the microscale than those at the macroscale as a result of the larger surface area-to-volume ratios and the shorter transport distances, resulting in steeper concentration and temperature gradients.¹⁹ At the macroscale, limitations in the rate of heat transfer to the reactants lead to a reduced operating temperature, and therefore a reduced equilibrium conversion and reaction rate. These heat transfer issues while performing endothermic steam reforming can be avoided in microscale reactors. For example, integrated microsystems for H₂ production consisting of burner, vaporizer, and reformer units have been made from stainless steel for the steam reforming of methanol.^2,4,16 Also, micro-electro-mechanical-system (MEMS) fabrication methods have been used to develop silicon-based microreactors for methanol reforming.¹⁷ Additionally, stainless steel microreactors for the steam reforming of propane have been reported earlier.^15,18 Although these microreactor systems can achieve high conversion of methanol and propane into H₂, they are not stable for continuous operation above 800 °C, the minimum temperature required to eliminate coking of the catalyst during the steam reforming of higher hydrocarbons.²⁰ Stainless steel and silicon oxidize in the presence of steam above 800 °C and can corrode to a significant extent, and are thus not suitable for prolonged high temperature operation.

A few studies have shown that ceramic-based microreactors show promise for applications involving high temperature reactions due to their high thermal and chemical resistance.²¹ In fact, a microreactor comprising suspended silicon nitride tubes for fuel processing up to 825 °C has been demonstrated.²² The use of catalytic wash-coats or packed beds of loose catalytic particles in these tube reactors may lead to passing of the reactants through the system without reacting. Wash coat-based layers crack and packed particles settle as a result of vibrations and shock that are commonly encountered in portable devices, causing the flow of reactants to be diverted around the active catalytic sites and reducing the reactor efficiency.²³ This phenomenon, known as channeling, is avoided when using a monolithic catalyst support.

Recently, we have reported on the synthesis of silicon carbide (SiC) and silicon carbonitride (SiCN) inverted beaded monoliths,²⁴ prepared via the micromolding in capillary (MIMIC)-based templating method used previously for the preparation of porous oxide materials.²⁵ These porous monolithic structures are stable up to 1200 °C in air, have high surface areas (up to 7.4 × 10⁷ m² m⁻³), and have a ∼2 orders of magnitude lower pressure drop (∼74% porosity) than a packed beaded structure (26% porosity) for the same geometric surface area.²⁶ We have further demonstrated the capability of these porous monoliths as catalyst supports for high temperature reactions by coating them with ruthenium (Ru) catalyst and integrating them within high-density alumina housings, followed by testing the integrated ceramic microreactors using the decomposition of ammonia (NH₃) up to 1000 °C.²⁶

In this paper, we study the steam reforming of propane (eqn (1)) at temperatures between 800 and 1000 °C in these integrated ceramic microreactors to validate their promise for on-site production of H₂ for PEM fuel cells via the reforming of liquid hydrocarbons:

C₃H₈ + 3H₂O ↔ 3CO + 7H₂ (1)

The high energy density, relatively easy storage, and the availability in high purity (eliminating the need of, for example, a desulfurization pretreatment) through established infrastructure makes propane a promising hydrocarbon source for the production of high quality hydrogen for fuel cell applications with a power requirement of up to several kilowatts.

Experimental

Synthesis and characterization of porous catalytic monoliths

The synthesis of SiC porous monoliths was performed using procedures described earlier.^24,26 Porous monoliths with typical dimensions of 350 µm width, 100 µm height, and 3 mm length were obtained, as shown in Fig. 1a. The size of the windows connecting adjacent pores is approximately one-fifth of the pore diameter of the SiC structures. We suspect that varying the temperature and time of the pyrolysis step may change the size of the pore windows; however, we have not studied this relationship.

Fig. 1 (a) SEM micrograph of fracture profile of an inverted beaded SiC monolith with 7.2 µm pore size (inset: an optical micrograph of an entire SiC porous monolith) after heating at 1200 °C for 6 h in air. The black spots are the windows that connect adjacent pores in these close packed structures. The bits of debris are due to cutting of the samples prior to SEM analysis. (b) SEM micrograph of fracture profile of a Ru-coated SiC porous catalytic monolith. The arrows indicate the position of pore windows. (c) Optical micrograph of an integrated ceramic microreactor composed of an alumina housing structure with five SiC porous monoliths, an alumina lid, and alumina inlet and outlet tubes.

Ruthenium (Ru) catalyst was deposited on these SiC porous monoliths by wet impregnation with 14.72 wt% (0.67 M) RuCl₃ (Aldrich) in a mixture of 10 vol.% DI water in acetone, similar to a method described by others.²⁷Fig. 1b shows a scanning electron microscopy (SEM) image of Ru particles covering the walls of the SiC porous structures. An energy dispersive X-ray spectroscopy (EDS) analysis confirmed that these particles are Ru catalyst. SEM micrographs were taken using either a JEOL 6060-LV (Fig. 1a) or a Hitachi S-4700 (Fig. 1b) scanning electron microscope.

Full characterization of the SiC porous monoliths (pore morphology, surface area, porosity, and thermal stability) and of the deposited Ru metal catalyst on these monolithic supports (Ru loading, dispersion, and surface area of active sites) has been described previously.²⁶

Design and fabrication of integrated ceramic microreactors

The integrated ceramic microreactors (Fig. 1c) are composed of an alumina housing structure with five SiC porous monoliths (Fig. 1a), an alumina lid, and alumina inlet and outlet tubes. In this study, the gelcasting forming method developed by Young et al. for mesoscale ceramic structures²⁸ was adapted and optimized for the fabrication of cm-scale high-density, non-porous alumina structures with sub-millimeter features for reactor housings and lids. Earlier, we reported a detailed description of the optimized gelcasting procedure to obtain alumina structures without cracking and deformation.²⁶ The alumina housing structure consists of five identical microchannels in parallel, each with typical dimensions of approximately 400 µm width, 150 µm height, and 1 or 3 mm length. The Ru-coated SiC porous catalytic monoliths were mounted in these microchannel slots within the high-density alumina housing using ceramic paste (Ceramabond 569, Aremco Products). After applying the paste and inserting the porous monoliths into the microchannels with tweezers, the housing was visually inspected under a stereozoom microscope (Leica MZ 12.5, up to 30×) to ensure a good fitting of the monoliths within the channels. The alumina lid and alumina tubes (0.063″ od and 0.031″ id, CoorsTek) were then integrated with the housing using the same ceramic paste.²⁶

Testing of the integrated ceramic microreactors

A schematic diagram of the experimental setup for the study of propane steam reforming is shown in Fig. 2. The flow of propane (ultra high purity, Matheson Tri-Gas) was controlled using a mass flow controller (1479A MassFlo^® Controller, MKS Instruments). Using a syringe pump (Model 55-4143, Harvard Apparatus) steam was introduced into the system by leading DI water through a steam generator at 180 °C prior to mixing with the other feed gases. The steam generator is a 12″ long stainless steel tube (0.5″ od and 0.444″ id, K & S Engineering) wrapped with heating tape (Type 45500, Thermolyne). The temperature of the steam generator was monitored by a K-type thermocouple (Omega) connected to a digital multimeter (179 True RMS, Fluke). The flow of helium (ultra high purity, S.J. Smith) was controlled using a mass flow controller (MC Series 16 Bit, Cole Parmer). Helium was used as an internal standard gas to enable direct measurement of the amount of H₂ in the product stream inside the GC apparatus. The flow rates of propane, steam, and helium used in this study are listed in Table 1.

Fig. 2 Schematic diagram of the experimental setup to study the steam reforming of propane in an integrated ceramic microreactor.

Table 1 Flow rates of propane, steam, and helium in the feed stream for different total inlet flow rates (Q_tot) and steam-to-carbon ratios (S/C)

Qtot (sccm)	S/C	C3H8 (sccm)	H2O (sccm)	He (sccm)
20	1.095	3.5	11.5	5
13.33	1.095	2.33	7.67	3.33
10	1.095	1.75	5.75	2.5
20	1.33	3	12	5
13.33	1.33	2	8	3.33
10	1.33	1.5	6	2.5
20	1.94	2.2	12.8	5
13.33	1.94	1.47	8.53	3.33
10	1.94	1.1	6.4	2.5

---

The temperature of the integrated ceramic microreactor was controlled by placing it inside a tube furnace (HTF5500 Series, Lindberg/Blue M), while feed and product streams were led into and out of the microreactor through alumina tubes that were attached to stainless steel tubing outside of the tube furnace with Swagelok^® connections. The product stream was then passed through a Drierite column (anhydrous calcium sulfate) to remove the remaining H₂O. The product gas composition, conversion of C₃H₈, and amount of H₂ produced were measured using gas chromatography with a thermal conductivity detector (TRACE DSQ, Thermo Finnigan). Separations were performed using a Hayesep D column (25 ft × 1/8″, stainless steel, 100/120 mesh, Supelco) with either helium or argon as the carrier gas. Helium (ultra high purity, S.J. Smith) was used as the carrier gas for the detection of CO, CO₂, unreacted C₃H₈, and side products (i.e., CH₄, C₂H₄, and C₃H₆), while argon (ultra high purity, S.J. Smith) was used for the detection of H₂ and the internal standard gas (i.e., helium). For each total inlet flow rate (Q_tot) and steam-to-carbon ratio (S/C), the product gas composition, C₃H₈ conversion, and amount of H₂ produced were measured as a function of temperature by increasing the temperature of the furnace from 800 to 1000 °C in 50 °C increments. The average values of the product gas composition, C₃H₈ conversion, and the amount of H₂ produced along with their standard deviations at a certain Q_tot, S/C, and temperature were calculated from at least three measurements after steady state was reached.

In this study, the H₂ selectivity was calculated using the following equation:

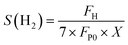where S(H₂) is the H₂ selectivity, F_H is the actual amount of H₂ produced as directly measured using a thermal conductivity detector with argon as the carrier gas, F_P0 is the inlet flow rate of C₃H₈, and X is the conversion of C₃H₈.

Kinetic analysis of propane steam reforming

In this study, an empirical power law model (eqn (3)) was used to represent the rate expression for the steam reforming of propane, although earlier work by others showed that the reforming of hydrocarbons most likely occurs by a Langmuir–Hinshelwood mechanism.^29,30 The power law model was used because of its simplicity, with only three parameters to extract from the limited set of data collected in this work. In addition, Praharso et al. used both a power law model and a Langmuir–Hinshelwood model to fit their experimental data for the steam reforming of iso-octane, and both models were in excellent agreement, justifying the use of the power law model.²⁹

r_P = k′C^α_PC^β_W (3)

where r_P is the molar rate of consumption of propane per unit of volume (in mol s⁻¹ m⁻³), C_P and C_W are the concentrations of propane and steam, respectively (in mol m⁻³), k′ is the observed rate constant in appropriate units (the units will depend on the values of α and β), and α and β represent the reaction orders with respect to the concentrations of propane and steam, respectively. This rate expression assumes that the rates of side reactions are negligible and that propane is consumed only by the steam reforming reaction.

A plug flow reactor (PFR) design equation was used to describe these integrated ceramic microreactors as justified earlier:²⁶

where V is the volume of SiC monoliths (in m³). The pressure along the microreactor was estimated using the Ergun equation,²³ described by the following differential equation:where P is the absolute pressure (in atm), G is the superficial mass velocity (in kg m⁻² s⁻¹), A_C is the cross-sectional area of the SiC monolith (in m²), ε is the void fraction, ρ is the density of the gas mixture (in kg m⁻³), μ is the viscosity of the gas mixture (in kg m⁻¹ s⁻¹), and d_P is the pore diameter (in m).

Eqns (4) and (5) were then numerically integrated using MATLAB software, with the conditions of X = 0 at V = 0 and P = 1 atm at the outlet of the reactor. At each temperature, the experimental C₃H₈ conversion data were obtained at 3 different Q_tot and 3 different S/C. For each of these 9 data points, a value of k′ was calculated at given pairs of α and β such that the conversion of C₃H₈, given by the integration of eqns (4) and (5), matched the experimentally obtained conversion. After obtaining all 9 k′ values (one for each experimental data point) for given pairs of α and β, an average k′ (k_avg) and its standard deviation (k_sd) were obtained for each pair of α and β. Then, the quotient, Q = k_sd/k_avg, was calculated for each pair. The pair of α and β yielding the minimum value of Q was used as the best fit of the experimental data for the rate expression.

Results and discussion

Synthesis and characterization of porous catalytic monoliths

For the present study of the steam reforming of propane, we employ SiC porous monoliths that we used earlier to investigate the decomposition of NH₃.²⁶ Inverted beaded SiC porous monoliths with an average pore diameter of 7.2, 2.2, and 0.75 µm were obtained from packed beds of PS spheres as sacrificial templates with 10, 3.2, and 1.1 µm diameter, respectively, following a procedure that we reported previously.²⁴ This range of pore diameters was chosen to maximize the reactor performance (i.e., large surface area-to-volume ratio and high mass transfer coefficient) while maintaining a sustainable pressure drop across the microreactors.

We have also validated the physical and chemical stability of these SiC monoliths at temperatures as high as 1200 °C in an oxidative environment using previously reported tests.^24,26 Ru metal catalyst was deposited onto the SiC structures via wet impregnation, followed by calcination in air and reduction in H₂ (Fig. 1b). Ru was chosen as the catalyst due to its high activity toward the steam reforming of hydrocarbons and its low carbon formation rate.³¹

Table 2 lists the actual surface area of the SiC porous monoliths as measured with BET analysis, the dispersion of the active Ru metal phase, and the Ru loading for the SiC structures used in this study. The calculated geometric surface areas of these monoliths are 6.2 × 10⁵, 2.0 × 10⁶, and 5.9 × 10⁶ m² m⁻³ for pore diameters of 7.2, 2.2, and 0.75 µm, respectively. Therefore, the actual surface areas are 3.2 and 12.5 times larger than the geometric surface areas for 2.2 and 0.75 µm SiC structures, respectively, indicating the presence of surface roughness and microporosity in these monolithic catalyst supports. A reliable analysis for the actual surface area of the 7.2 µm SiC porous structure could not be performed due to the low surface area-to-volume ratio. The dispersion of active Ru metal and Ru loading, 20–31% and 4.5–5.8 wt%, as determined from pulsed CO and H₂ chemisorption and inductively coupled plasma (ICP) spectrometry, respectively, are within the range of values reported in the literature.^13,32 The resulting values of the surface area of active catalytic sites per gram of Ru for each SiC porous monolith, 250–400 m² g⁻¹, are comparable to the values found in the literature for Ru/SiO₂ and Ru/Al₂O₃.^13,32

Table 2 Dispersion of active metal phase and catalyst loading for Ru-coated SiC porous monoliths with pore diameters of 7.2, 2.2, and 0.75 µm

Pore diameter/µm (SEM)	Surface area/m^2 m^−3 (BET)	Ru dispersion (%, chemisorption)	Surface area of active catalytic sites per g Ru/m^2 g^−1^b	Ru loading (wt%, ICP)
a Surface area-to-volume ratio is not sufficiently large for a reliable analysis.b Calculated using the Ru dispersion data obtained with CO chemisorption.
7.2	∼10^6^a	19.7 (CO) 20.7 (H2)	250	4.5
2.2	6.4 × 10^6	29.3 (CO) 31.1 (H2)	370	5.3
0.75	7.4 × 10^7	—	—	5.8

---

Assembly and testing of integrated ceramic microreactors

The Ru-coated SiC porous monoliths were mounted in the microchannels of an alumina housing using ceramic paste. The high-density, non-porous alumina housing structure, consisting of five identical channels in parallel that are each 400 µm wide, 150 µm high, and 3 mm long, and its matching alumina lid, were obtained after modification of the drying and sintering steps²⁶ of the gelcasting procedure developed previously by Young et al.²⁸ for the fabrication of ceramic structures with much larger feature sizes. The lid, with alumina inlet and outlet tubes attached using ceramic paste, was finally mounted on top of the housing using the same paste and an integrated ceramic microreactor was obtained after curing of the paste (Fig. 1c).

In a previous study, we used these integrated ceramic microreactors, comprising Ru-coated SiC catalytic monoliths, for the decomposition of NH₃ to produce up to 54 sccm of H₂ (∼9.8 × 10⁴ sccm H₂ produced per cm³ of monolith).²⁶ We showed that the microreactors did not fail after more than 15 thermal cycles and that catalyst deactivation did not occur at temperatures as high as 1000 °C.²⁶ In this study, we used the same microreactors, 0.55 mm³ in total SiC monolith volume with different pore sizes, for on-site H₂ production by the steam reforming of propane. We characterized the performance of these microreactors by studying the conversion of C₃H₈ and the selectivity toward H₂ as a function of the total inlet flow rate (Q_tot), the steam-to-carbon ratio (S/C), and temperature. The flow rates of C₃H₈, steam, and helium in the feed stream for different Q_tot and S/C are listed in Table 1.

The dried product stream consisted mainly of H₂ and CO (up to 69 and 25 vol.% on a dry basis, respectively) as shown in Fig. 3, obtained using 7.2 µm SiC porous monoliths at a Q_tot of 20 sccm and a S/C of 1.33. The remaining gases were unreacted C₃H₈ (as low as 0.01 vol.% at 1000 °C), CO₂, and small amounts of the side products CH₄, C₂H₄, and C₃H₆. The product gas composition in Fig. 3 is representative of the composition over the different Q_tot, S/C, and SiC pore sizes used in this study. Table 3 lists the corresponding values of the product gas composition from Fig. 3 at 800, 900, and 1000 °C. The presence of side products indicates that reactions such as the decomposition of C₃H₈ are also occurring. The amounts of these side products can be reduced by reducing the residence time to prevent the homogeneous decomposition of C₃H₈, and by using a catalyst with a higher selectivity toward H₂ formation (eqn (1)). The product gas contains two major side products (Table 3): about 1.8 vol.% of CO₂, which may be formed by the water gas shift (WGS) reaction (eqn (6));³³ and up to 4.3 vol.% of CH₄, which may be produced by the methanation of CO (eqn (7))^18,34 and the homogeneous decomposition of C₃H₈.

CO + H₂O ↔ CO₂ + H₂ (6)

CO + 3H₂ ↔ CH₄ + H₂O (7)

Fig. 3 Product gas composition (dry basis) of the effluent stream as a function of temperature obtained using a microreactor with a Ru-coated SiC porous monoliths with 7.2 µm pore size for Q_tot = 20 sccm and S/C = 1.33. The corresponding values of the product gas composition at 800, 900, and 1000 °C are listed in Table 3.

Table 3 Product gas composition (vol.%, dry basis) of the effluent stream after removal of the remaining H₂O at 800, 900, and 1000 °C obtained using Ru-coated SiC porous monoliths with 7.2 µm pore size for Q_tot = 20 sccm and S/C = 1.33

Temp./°C	H2	CO	CO2	C3H8	CH4	C2H4	C3H6
800	62.1 ± 0.3	21.2 ± 0.3	1.8 ± 0.2	8.9 ± 0.4	3.9 ± 0.3	1.1 ± 0.1	1.0 ± 0.1
900	68.8 ± 0.1	23.7 ± 0.1	1.9 ± 0.1	0.17 ± 0.02	4.3 ± 0.1	0.92 ± 0.05	0.14 ± 0.03
1000	68.4 ± 0.1	25.2 ± 0.1	1.8 ± 0.1	0.01 ± 0.01	3.1 ± 0.1	1.4 ± 0.1	0.02 ± 0.01

---

The amount of CO, as high as 25 vol.% (dry basis) in the product stream, can be reduced by the addition of WGS and preferential oxidation reactors following the reformer. For a typical PEM fuel cell, the amount of CO in the H₂ feed stream has to be less than 20 ppm to avoid CO poisoning of the fuel cell catalyst.⁴

In this study, the minimum S/C was set at 1.095 so that C₃H₈ is always the limiting reactant, and the highest S/C was fixed at 1.94 to obtain a larger quantity of H₂ in the product stream. Many studies have used S/C values that are greater than 2 to minimize coking of the catalyst during the steam reforming of hydrocarbons while operating at temperatures below 800 °C;^29,30,35 however, the present study avoids using a high S/C by operating above 800 °C. Here, at a S/C of 1.94, a maximum of only 12.5 sccm H₂ was produced, which was about 30% lower than the 18.2 sccm H₂ produced at a S/C of 1.095. Operating at a lower S/C is also desirable since less energy is required to heat the excess water to the reaction temperature. In other words, the parasitic losses to a complete PEM fuel cells-based power source system with an integrated fuel reformer are reduced.

Fig. 4 shows the C₃H₈ conversion and the H₂ selectivity as a function of temperature over the range of 800 to 1000 °C for Q_tot between 10 and 20 sccm and S/C between 1.095 and 1.94, obtained using Ru-coated SiC porous monoliths having pore diameters of 7.2, 2.2, and 0.75 µm. The H₂ selectivity is defined as the ratio between the actual amount of H₂ produced and the amount of H₂ that would have been produced in the absence of side reactions. Here, the lowest operating temperature was fixed at 800 °C to eliminate coking of the catalyst, while the maximum temperature was set at 1000 °C as limited by the use of Ru metal catalyst. Although the ceramic microreactor should be able to operate without structural failure at temperatures up to 1200 °C in air, the operating temperature needs to be kept below ∼0.5 times the melting point of metal catalyst (T_m for Ru is 2600 K) to minimize sintering of the Ru catalyst into the ceramic substrate.²³

Fig. 4 C₃H₈ conversion and H₂ selectivity as a function of temperature obtained for microreactors with Ru-coated SiC porous monoliths (volume = 0.55 mm³) for: (a) and (b) different total inlet flow rates (Q_tot) at a steam-to-carbon ratio (S/C) of 1.095 using 7.2 µm pores; (c) and (d) different S/C at Q_tot = 20 sccm using 7.2 µm pores; and (e) and (f) different pore sizes at Q_tot = 20 sccm and S/C = 1.095. The lines fitting the conversion data below 900 °C in (a), (c), and (e) are obtained from the power law model while the lines between 900 and 1000 °C are added to guide the eye. The dashed lines (— – —) at 100% conversion represent the equilibrium conversion for the steam reforming of propane as a function of temperature and S/C (different S/C used here give similar equilibrium conversion values). The lines connecting the H₂ selectivity data points in (b), (d), and (f) are added to guide the eye.

The lines in Fig. 4a, 4c, and 4e were obtained from a nonlinear regression of the C₃H₈ conversion data using a power law kinetic model (eqn (3)) with a plug flow reactor (PFR) design equation (eqn (4)), assuming constant temperature across the reactor. A maximum temperature drop of only 3.7 °C (endothermic reaction) was estimated using Fourier's law of conduction for a maximum Q_tot of 20 sccm and C₃H₈ flow rate of 3.5 sccm at 800 °C, justifying this assumption. The pressure along the reactor was estimated using the Ergun equation (eqn (5)). A detailed kinetic analysis can be found in the next sub-section.

Fig. 4a and 4b show the C₃H₈ conversion and the H₂ selectivity, respectively, as a function of temperature for different Q_tot at a S/C of 1.095 obtained using the 7.2 µm SiC porous monoliths. As expected, the C₃H₈ conversion increased with increasing temperature and with longer residence time (lower Q_tot). The H₂ selectivity initially increased with increasing temperature, and then reached a constant value of about 74% for all Q_tot used. A lower H₂ selectivity is expected at lower temperatures since the formation of CH₄ is thermodynamically favored, while the increasing H₂ selectivity observed at 800 °C with increasing residence time may be due to the formation of H₂ and CO₂via the WGS reaction. At higher temperatures, the H₂ selectivity is independent of Q_tot since the equilibrium of the WGS reaction is shifted completely toward the formation of CO and H₂O. Here, for Q_tot between 10 and 20 sccm, complete conversion of C₃H₈ (i.e., >99.9%) was reached above 950 °C. High C₃H₈ conversion can still be obtained even with relatively low residence times, ranging from 1.65 to 3.3 ms, due to the high operating temperature.

The C₃H₈ conversion and the H₂ selectivity as a function of temperature for different S/C at a Q_tot of 20 sccm obtained with the 7.2 µm SiC porous monoliths are shown in Fig. 4c and 4d, respectively. Here, the C₃H₈ conversion also increased with increasing temperature and with higher S/C, as expected. At a higher S/C, less C₃H₈ is present in the feed stream for a given Q_tot, resulting in a higher residence time with respect to C₃H₈ (1/F_P0 in eqn (4)) and thus a higher C₃H₈ conversion. Similarly, the H₂ selectivity increased with increasing S/C for the entire range of temperatures as expected. A larger amount of steam in the feed gas mixture favors the steam reforming reaction while suppressing side reactions, such as the homogeneous decomposition of C₃H₈ and the methanation of CO. Moreover, the excess amount of steam contributes to the formation of CO₂ and even more H₂via the WGS reaction,³³ especially at lower temperatures.

Fig. 4e and 4f show C₃H₈ conversion and H₂ selectivity, respectively, as a function of temperature obtained using SiC monoliths with different pore sizes at a Q_tot of 20 sccm and a S/C of 1.095. The C₃H₈ conversion initially increased when decreasing the SiC pore diameter from 7.2 to 2.2 µm, but then it decreased again as the SiC pore diameter was further reduced to 0.75 µm, to a level slightly higher than that for the 7.2 µm reactor. The H₂ selectivity, on the other hand, decreased with decreasing SiC pore size for the entire range of temperature. This discrepancy probably is the result of having a worse Ru coverage on the SiC surface in monoliths with smaller pore diameter: the total surface area of active Ru sites for 2.2 µm SiC porous monoliths is only 1.75 times larger than that for 7.2 µm SiC structures although the geometric surface area is 3.2 times greater (see Table 2). This indicates the presence of surface area within the SiC porous monoliths that is not covered with Ru catalyst, which reduces the reactor efficiency toward the catalytic steam reforming reaction and favors the homogeneous decomposition of C₃H₈, thus reducing the selectivity toward H₂. In the future, this issue could be mitigated by repeated impregnation of the structures with the RuCl₃ solution to obtain a better Ru coverage within the SiC monoliths with smaller pore diameters.

One of the key desired characteristics for fuel reformers is the retention of structural integrity and catalytic activity over prolonged periods of time while operating at a high temperature. Here, the integrated ceramic microreactors did not show any signs of failure after exposure to more than 15 thermal cycles of about 10 h each at temperatures as high as 1000 °C. Furthermore, no catalyst deactivation was observed after exposing the microreactor continuously to 3 sccm C₃H₈ and 12 sccm steam at 800 °C (Fig. 5). Fig. 5a shows the C₃H₈ conversion and the H₂ selectivity, while Fig. 5b shows the product gas composition, as a function of time over a 48 h period of continuous operation, obtained using the 7.2 µm SiC porous monoliths prior to any thermal cycles. Both the C₃H₈ conversion and the H₂ selectivity remained constant at 59% and 71%, respectively, and the product gas composition did not change over time. Additionally, using the 7.2 µm SiC porous monoliths that have been exposed to more than 15 thermal cycles, the C₃H₈ conversion, H₂ selectivity, and product gas composition did not change over time during the second catalyst deactivation study over 126 h of continuous operation (Fig. 5c and 5d). The conversion and selectivity values were all identical to those obtained during the initial study (Fig. 5a and 5b). The activity and selectivity of the Ru-coated SiC porous catalytic monoliths are, therefore, stable during the steam reforming of propane at temperatures as high as 1000 °C, and the promise of these integrated ceramic microreactors for on-site H₂ production via the high temperature (i.e., >800 °C to avoid the catalyst coking) reforming of liquid hydrocarbons is validated.

Fig. 5 C₃H₈ conversion, H₂ selectivity, and product gas composition (dry basis) as a function of time obtained using Ru-coated SiC porous monoliths with 7.2 µm pore size during continuous operation at T = 800 °C, Q_tot = 20 sccm, and S/C = 1.33 for: (a) and (b) the microreactor prior to exposure to any thermal cycles and (c) and (d) the microreactor after exposure to more than 15 thermal cycles of about 10 h each at temperatures as high as 1000 °C. The dashed line (– – –) in (a) and (c) indicates the equilibrium conversion for the steam reforming of propane at 800 °C and S/C = 1.33.

We obtained a maximum production of 18.2 sccm H₂, corresponding to 3.3 × 10⁴ sccm H₂ produced per cm³ of monolith volume, using these microreactors. This H₂ production rate is only limited by the maximum inlet flow rate possible before excessive pressure may induce mechanical failure of the microreactor. The amount of H₂ produced per cm³ of overall reactor volume (equals 1.05 cm³) is only 17.3 sccm per cm³, a value that can be increased significantly by reducing the wall thickness of the alumina reactor housing as well as by increasing the number of SiC catalytic monoliths within the reactors. This work is ongoing.

Kinetic analysis of propane steam reforming

To better understand the effects of temperature, flow rate, and inlet gas composition (S/C) on the microreactor performance during the steam reforming of propane, a kinetic analysis of the C₃H₈ conversion data was performed. Previous work using these ceramic microreactors demonstrated that they can be modeled as plug flow reactors (PFR).²⁶ We therefore used the design equation for a PFR to model the steam reforming of propane in this study. Eqns (4) and (5), which represent the change in C₃H₈ conversion and the change in pressure with respect to the SiC monolith volume, respectively, were solved simultaneously using MATLAB software. The adjustable parameters for this set of differential equations are: k′ (the observed rate constant), α (the reaction order with respect to propane), β (the reaction order with respect to steam), and P₀ (the inlet pressure).

The conversion data at 800 °C for the SiC monoliths with 7.2 µm pores were modeled with the set of differential equations to determine the values of α and β that best fit the power rate law for the steam reforming of propane. The analysis resulted in a value of 0.50 for α and a value of −0.23 for β. The value of 0.50 for α is consistent with other kinetic studies of the steam reforming of hydrocarbons,^29,36 indicating a mechanism with dissociative adsorption of propane on the Ru active sites. The β value equal to −0.23 indicates that steam actually inhibits the steam reforming reaction due to the competition between steam and propane for active sites on the Ru surface, which has been observed previously.^35,37 On first sight, this outcome seems to contradict the experimental data that show conversion increases with increasing S/C at a constant temperature and Q_tot, but this data is actually consistent with the design equation since the molar rate of production of H₂ is lower at the higher S/C due to the smaller amount of C₃H₈ entering the reactor.

Using these values of α and β, and the experimentally obtained C₃H₈ conversion data at 3 different Q_tot and 3 different S/C, the observed rate constants k′ at temperatures of 800, 850, and 900 °C were calculated for SiC monoliths with different pore sizes by solving eqns (4) and (5) simultaneously. These k′ values were then used to generate curves to fit the experimental data for each temperature, Q_tot, S/C, and SiC pore diameter, indicated by the lines in Fig. 4a, 4c, and 4e. The kinetic analysis at temperatures above 900 °C was not performed since the experimentally obtained conversion values all approached 100%, introducing more uncertainty into the fitting of the data with the power law model.

In general, the fit of the power rate law in a PFR to the conversion data obtained at 850 and 900 °C is poorer than that for the data obtained at 800 °C. This discrepancy occurs since the values of α and β, 0.50 and −0.23, respectively, were derived using the data at 800 °C, while α and β may have changed with temperature. Although previous work has shown that a power law model fits the steam reforming data obtained at different temperatures, the temperature range in those studies was less than 50 °C,²⁹ whereas here it was 100 °C.

The observed rate constant, k′, normalized with respect to the surface area of active Ru sites, was 2.95 × 10⁻⁴ mol^0.73 s⁻¹ m^−1.19 for 7.2 µm SiC porous monoliths at 800 °C, and an apparent activation energy (E_a) of 51 kJ mol⁻¹ was calculated from the data obtained between 800 and 900 °C. Additionally, the k′ values at 800 °C obtained for the microreactors comprising 2.2 and 0.75 µm SiC porous structures were 4.38 × 10⁻⁴ and 3.64 × 10⁻⁴ mol^0.73 s⁻¹ m^−1.19, respectively, with activation energies of 35 and 40 kJ mol⁻¹. The k′ value obtained for the microreactor composed of 0.75 µm structures was estimated based on a 5.8 wt% Ru loading and an assumption of 36% Ru dispersion. These E_a values fall within the range of values reported by others for the steam reforming of light hydrocarbons over Ni- and Pd-based catalysts.^36,38 To our knowledge, this is the first study that reports the E_a for the steam reforming of propane over a Ru-based catalyst.

We studied the presence of mass transfer limitations during the steam reforming of propane in these ceramic microreactors by comparing the observed rate constants k′ for SiC structures with pore diameters of 2.2 and 7.2 µm. Assuming that mass and heat transfer limitations can be neglected, k′ depends only on the reaction temperature; therefore, the ratio of k′ values for the 2.2 µm reactor and for the 7.2 µm reactor at a given temperature should have a constant value of 1. The k′ ratio, however, changes as a function of temperature, as shown in Table 4. Here, the k′ ratio is equal to 1.5 at 800 °C, then decreases to 1.2 at 850 °C, and finally increases slightly at 900 °C. The effects of mass transfer on reaction rate intensify with increasing temperature since the gas diffusion coefficient increases more slowly with temperature (D ∝ Tⁿ, where n is ∼2) than does the rate constant, k ∝ exp{−E_a/RT}, where k is the intrinsic rate constant. As temperature increases, mass transfer limitations first affect the observed reaction rate for the SiC structures with a larger pore diameter (7.2 µm), and then affect the rate for the 2.2 µm SiC porous monoliths, resulting in a k′ ratio that is greater than 1. As the temperature is increased from 800 to 900 °C, the k′ ratio decreases to a value closer to 1, indicating that mass transfer limitations start to dominate the reaction rates for both reactors. A slight increase of the k′ ratio when increasing the temperature from 850 to 900 °C may be due to uncertainty in the k′ values derived from the fitting of the data at 900 °C since some of the measured conversion values were very close to 100%.

Table 4 Observed reaction rate constants k′ derived using the power law model at different temperatures for SiC porous monoliths with pore diameters of 7.2 and 2.2 µm

	800 °C	850 °C	900 °C
k′ (7.2 µm)/mol^0.73 s^−1 m^−1.19	2.95 × 10^−4	4.29 × 10^−4	4.79 × 10^−4
k′ (2.2 µm)/mol^0.73 s^−1 m^−1.19	4.38 × 10^−4	5.01 × 10^−4	6.11 × 10^−4
k′ (2.2 µm)/k′ (7.2 µm)	1.49	1.17	1.28

---

Conclusions

For the first time, ceramic microreactors with integrated SiC porous monoliths have been studied for the on-site production of H₂via the steam reforming of propane at temperatures between 800 and 1000 °C. The use of these macroporous SiC porous monoliths combines the properties of high surface area catalyst support structures, high thermal stability, and sustainable pressure drop across the microreactor. We were able to avoid coking of the catalyst while maintaining a S/C close to 1 by operating at temperatures above 800 °C. Being able to perform steam reforming at a lower S/C has several advantages. First, less energy input is required to heat the excess steam to the reaction temperature. Second, kinetic analysis of the conversion data showed that the reaction order with respect to steam is −0.23, indicating that the process is inhibited by steam due to the competition between propane and steam for active sites on the Ru surface. Thus, the production rate of H₂ can be increased by using a lower S/C value. The kinetic analysis also revealed that the reaction order with respect to propane is 0.50, which indicates that the rate limiting step in the steam reforming of propane studied here is the dissociative adsorption of propane on the Ru catalyst.

At 900 °C and a S/C of 1.095, 99% conversion of C₃H₈ was achieved with a H₂ selectivity of 74%, and no drop in reactor performance was seen over time, even after more than 15 thermal cycles at temperatures as high as 1000 °C. Currently, up to 25 vol.% (dry basis) of CO exited the reactor along with ∼18.2 sccm of H₂, while a typical PEM fuel cell can only tolerate up to 20 ppm of CO in the H₂ feed stream. In a complete fuel reforming unit, most of this CO would be converted into additional hydrogen in a WGS reactor following the reformer. Any remaining CO would then be removed from the effluent stream using reactors to selectively oxidize CO to CO₂, or using a membrane separator.¹¹ Work to create an integrated fuel processor for propane steam reforming followed by a WGS reactor is in progress.

These ceramic microreactors show promise for the steam reforming of propane or higher hydrocarbons to produce H₂ on-site for use in PEM fuel cells. To our knowledge, this is the first study that utilizes microreactors to perform the steam reforming of propane at temperatures above 800 °C, with S/C as low as 1.095 and yet no signs of coking or catalyst deactivation have been observed. Additionally, the demonstrated stability of these ceramic microreactors at high temperatures in the presence of oxygen²⁶ and steam makes them promising for other high-temperature reactions occurring under harsh chemical conditions, such as the partial oxidation of hydrocarbons.

Acknowledgements

This work was supported by the Department of Defense (DoD) Multidisciplinary University Research Initiative (MURI) program administered by the Army Research Office (ARO) under Contract DAAD19-01-1-0582 and by the campus research board of the University of Illinois. M.M. gratefully acknowledges NSF for a graduate fellowship. Christian gratefully acknowledges support of an H.G. Drickamer Fellowship from the Department of Chemical & Biomolecular Engineering at UIUC. SEM was carried out in the Center for Microanalysis of Materials, UIUC, which is partially supported by DOE grant DEFG02-91-ER45439. We acknowledge Dr Dong-Pyo Kim of Chungnam National University, Daejeon, Korea for his help on the fabrication and characterization of the SiC structures. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the authors and do not necessarily reflect the views of the DoD or the ARO.

References

1. M. L. Perry and T. F. Fuller, J. Electrochem. Soc., 2002, 149, S59; A. S. Patil, T. G. Dubois, N. Sifer, E. Bostic, K. Gardner, M. Quah and C. Bolton, J. Power Sources, 2004, 136, 220.
2. D. R. Palo, J. D. Holladay, R. T. Rozmiarek, C. E. Guzman-Leong, Y. Wang, J. Hu, Y.-H. Chin, R. A. Dagle and E. G. Baker, J. Power Sources, 2002, 108, 28.
3. J. R. Rostrup-Nielsen, Phys. Chem. Chem. Phys., 2001, 3, 283; S. Springmann, G. Friedrich, M. Himmen, M. Sommer and G. Eigenberger, Appl. Catal., A, 2002, 235, 101.
4. J. D. Holladay, E. O. Jones, M. Phelps and J. Hu, J. Power Sources, 2002, 108, 21.
5. K. Geissler, E. Newson, F. Vogel, T.-B. Truong, P. Hottinger and A. Wokaun, Phys. Chem. Chem. Phys., 2001, 3, 289.
6. R. Craciun, B. Shereck and R. J. Gorte, Catal. Lett., 1998, 51, 149; Q. Ming, T. Healey, L. Allen and P. Irving, Catal. Today, 2002, 77, 51.
7. E. C. Wanat, B. Suman and L. D. Schmidt, J. Catal., 2005, 235, 18.
8. S. Ayabe, H. Omoto, T. Utaka, R. Kikuchi, K. Sasaki, Y. Teraoka and K. Eguchi, Appl. Catal., A, 2003, 241, 261.
9. Fuel Cell Systems, ed. L. J. M. J. Blomen and M. N. Mugerwa, Plenum Press, New York, 1993.
10. J. N. Armor, Appl. Catal., A, 1999, 176, 159.
11. A. J. Franz, K. F. Jensen and M. A. Schmidt, IEEE: Technical Digest 12th International Conference on MicroElectroMechanical Systems, 1999, p. 382.
12. A. S. Chellappa, C. M. Fischer and W. J. Thomson, Appl. Catal., A, 2002, 227, 231; T. V. Choudhary, C. Sivadinarayana and D. W. Goodman, Catal. Lett., 2001, 72, 197.
13. J. C. Ganley, E. G. Seebauer and R. I. Masel, J. Power Sources, 2004, 137, 53.
14. G. W. Huber, J. W. Shabaker and J. A. Dumesic, Science, 2003, 300, 2075; R. R. Davda and J. A. Dumesic, Chem. Commun., 2004, 36; G. A. Deluga, J. R. Salge, L. D. Schmidt and X. E. Verykios, Science, 2004, 303, 993.
15. S. Natesakhawat, R. B. Watson, X. Wang and U. S. Ozkan, J. Catal., 2005, 234, 496.
16. W. Wiese, B. Emonts and R. Peters, J. Power Sources, 1999, 84, 187.
17. A. V. Pattekar and M. V. Kothare, J. Microelectromech. Syst., 2004, 13, 7.
18. G. Kolb, R. Zapf, V. Hessel and H. Löwe, Appl. Catal., A, 2004, 277, 155.
19. T. A. Ameel, R. O. Warrington, R. S. Wegeng and M. K. Drost, Energy Convers. Manage., 1997, 38, 969; K. F. Jensen, AIChE J., 1999, 45, 2051.
20. J. N. Armor and D. J. Martenak, Appl. Catal., A, 2001, 206, 231.
21. R. Knitter and M. A. Liauw, Lab Chip, 2004, 4, 378; R. M. Tiggelaar, J. W. Berenschot, J. H. de Boer, R. G. P. Sanders, J. G. E. Gardeniers, R. E. Oosterbroek, A. van den Berg and M. C. Elwenspoek, Lab Chip, 2005, 5, 326.
22. L. R. Arana, S. B. Schaevitz, A. J. Franz, M. A. Schmidt and K. F. Jensen, J. Microelectromech. Syst., 2003, 12, 600.
23. H. S. Fogler, Elements of Chemical Reaction Engineering, Prentice Hall PTR, Upper Saddle River, 1999.
24. I.-K. Sung, Christian, M. Mitchell, D.-P. Kim and P. J. A. Kenis, Adv. Funct. Mater., 2005, 15, 1336.
25. E. Kim, Y. Xia and G. M. Whitesides, J. Am. Chem. Soc., 1996, 118, 5722.
26. Christian, M. Mitchell, D.-P. Kim and P. J. A. Kenis, J. Catal., 2006, 241, 235.
27. J. C. Ganley, K. L. Riechmann, E. G. Seebauer and R. I. Masel, J. Catal., 2004, 227, 26.
28. A. C. Young, O. O. Omatete, M. A. Janney and P. A. Menchhofer, J. Am. Ceram. Soc., 1991, 74, 612; O. O. Omatete, M. A. Janney and R. A. Strehlow, Am. Ceram. Soc. Bull., 1991, 70, 1641.
29. Praharso, A. A. Adesina, D. L. Trimm and N. W. Cant, Chem. Eng. J., 2004, 99, 131.
30. K. Hou and R. Hughes, Chem. Eng. J., 2001, 82, 311.
31. J. R. Rostrup-Nielsen and J.-H. B. Hansen, J. Catal., 1993, 144, 38; T. Suzuki, H. Iwanami and T. Yoshinari, Int. J. Hydrogen Energy, 2000, 25, 119.
32. X.-K. Li, W.-J. Ji, J. Zhao, S.-J. Wang and C.-T. Au, J. Catal., 2005, 236, 181.
33. M. Levent, Int. J. Hydrogen Energy, 2001, 26, 551; A. G. Ghenciu, Curr. Opin. Solid State Mater. Sci., 2002, 6, 389.
34. M. S. Batista, E. I. Santiago, E. M. Assaf and E. A. Ticianelli, J. Power Sources, 2005, 145, 50.
35. C. K. Acharya, A. M. Lane and T. R. Krause, Catal. Lett., 2006, 106, 41.
36. K. M. Hardiman, T. T. Ying, A. A. Adesina, E. M. Kennedy and B. Z. Dlugogorski, Chem. Eng. J., 2004, 102, 119.
37. A. Berman, R. K. Karn and M. Epstein, Appl. Catal., A, 2005, 282, 73.
38. J. R. Rostrup-Nielsen, J. Catal., 1973, 31, 173; C. Resini, M. C. H. Delgado, L. Arrighi, L. J. Alemany, R. Marazza and G. Busca, Catal. Commun., 2005, 6, 441; X. Wang and R. J. Gorte, Catal. Lett., 2001, 73, 15.

---

Footnote

† Electronic supplementary information (ESI) available: Derivation of appropriate equations for the kinetic analysis of the steam reforming of propane in this study. See DOI: 10.1039/b607552e

---