Single DNA molecule stretching in sudden mixed shear and elongational microflows
Jonathan W.
Larson
*,
Gregory R.
Yantz
,
Qun
Zhong
,
Rebecca
Charnas
,
Christina M.
D’Antoni
,
Michael V.
Gallo
,
Kimberly A.
Gillis
,
Lori A.
Neely
,
Kevin M.
Phillips
,
Gordon G.
Wong
,
Steven R.
Gullans
and
Rudolf
Gilmanshin
U.S. Genomics, Inc., Woburn, MA 01801
First published on 7th July 2006
Abstract
High-throughput stretching and monitoring of single DNA molecules in continuous elongational flow offers compelling advantages for biotechnology applications such as DNA mapping. However, the polymer dynamics in common microfluidic implementations are typically complicated by shear interactions. These effects were investigated by observation of fluorescently labeled 185 kb bacterial artificial chromosomes in sudden mixed shear and elongational microflows generated in funneled microfluidic channels. The extension of individual free DNA molecules was studied as a function of accumulated fluid strain and strain rate. Under constant or gradually changing strain rate conditions, stretching by the sudden elongational component proceeded as previously described for an ideal elongational flow (T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016): first, increased accumulated fluid strain and increased strain rate produced higher stretching efficiencies, despite the complications of shear interactions; and second, the results were consistent with unstretched molecules predominantly in hairpin conformations. More abrupt strain rate profiles did not deliver a uniform population of highly extended molecules, highlighting the importance of balance between shear and elongational components in the microfluidic environment for DNA stretching applications. DNA sizing with up to 10% resolution was demonstrated. Overall, the device delivered 1000 stretched DNA molecules per minute in a method compatible with diffraction-limited optical sequence motif mapping and without requiring laborious chemical modifications of the DNA or the chip surface. Thus, the method is especially well suited for genetic characterization of DNA mixtures such as in pathogen fingerprinting amidst high levels of background DNA.
Introduction
The past decade has witnessed an extraordinary growth in the knowledge of both DNA mechanical properties and its polymeric behavior. It has been shown that double-stranded DNA, henceforth referred to simply as DNA, exhibits extensible wormlike chain elasticity,1,2 and that it undergoes a cooperative state change under high tension involving a disruption of the B-form double helix.3,4 DNA stretching dynamics in elongational and shear flows have been measured on single molecules.5,6 And although some initial random coil conformations can be elongated almost as quickly as the carrier solvent at high strain rates (affine stretching), others, such as hairpin conformations, require much greater accumulated fluid strain for full extension.5,7 These and other discoveries in DNA polymer physics provide a solid framework for the development of microfluidic devices capable of manipulating long DNA polymers for genomic analysis.The ability to stretch and spatially interrogate individual DNA molecules has significant advantages for genomic analyses such as DNA mapping.8,9 However, routine practical application of DNA stretching for mapping has been hindered by unwieldy technical constraints and/or low throughputs, such as with optical/magnetic tweezers and DNA combing.8 Micro- and nanofluidic approaches to DNA stretching are particularly advantageous because no cumbersome DNA or surface modifications are required. For example, mere confinement of DNA inside nanochannels almost as small as the DNA persistence length can produce partial extensions.10 This confinement method was used to restriction map partially linearized long single 61 kb molecules in under a one minute time.11 In the method described here, very high throughputs approaching 1000 fully extended single 185 kb sized DNA molecules per minute were achieved by linearization in a sudden elongational microflow. Such high throughputs are particularly advantageous for large scale screening applications of heterogeneous samples, such as for pathogen identification in human diagnostics or for biowarfare agent detection.
Typical microfluidic devices, such as the device described here (Fig. 1), produce combinations of different flow types. It remains an open question to what extent the polymer behavior observed in isolated pure flow types, as highlighted above, can predict or explain behavior in complicated flows. For example, does shear-induced DNA tumbling limit device efficiency? In the present study the stretching behavior of long DNA molecules was explored in shear flow combined with sudden fixed duration elongational flow. A number of microfluidic devices were constructed and tested to characterize DNA stretching in a variety of mixed microflows. It will be shown that the general behavior predicted by the current body of knowledge carries over to this more complicated case. Additionally, the technology developed in performing these studies will be shown to be enabling for a variety of high throughput single molecule genomic applications.
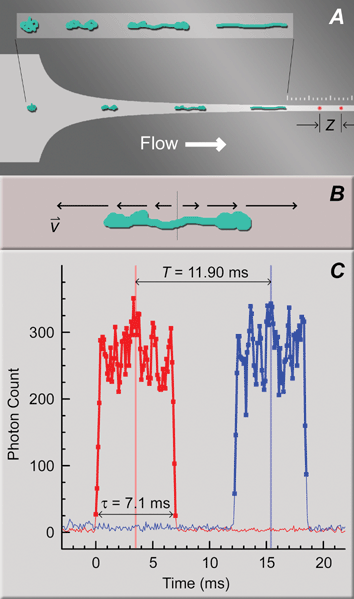 | ||
| Fig. 1 Two-spot system for interrogating DNA conformations after stretching in mixed microflows. (A) CAD drawing of a funnel for high strain rate flows similar to those used in this study (constant strain rate design, wi = 50 µm, wf = 2.5 µm, lF = 125 µm, see Table 1), with a superimposed cartoon of DNA responding to the elongational component of the flow. The inset is provided for clarity. The constant width exit channel begins at the first tick mark on the ruler etched above the funnel (10 µm and 2 µm between major and minor tick marks, respectively). The two confocal spots for DNA fluorescence detection (red spots in the exit channel), separated by a distance, Z, are aligned at one contour length of the longest polymer in a mixture away from the end of the funnel. (B) Cartoon of DNA stretching in a pure elongational flow with a strong velocity gradient (equivalently, strain rate) along the polymer. (C) Example single DNA molecule detection event. Two similar fluorescence bursts from the separate confocal detection spots (red and blue traces for the first and second spots away from the funnel, respectively), with CMs marked as vertical lines, were separated by time T, indicating DNA velocity. Thick lines with symbols denote the contiguous region above a threshold value. The burst duration, τ, reveals the length of the molecule in the projection of flow. Z = 28 µm for this example. | ||
Initial microflow design criteria and development of hypotheses
Our mixed microflow designs for DNA stretching were based on guidelines derived from DNA stretching in pure flows. These starting design principles are reviewed in brief, as follows, concluding with the development of the specific hypotheses that were tested in the present study.Fig. 1A shows an example quasi-2-dimensional microfluidic funnel of the type used in this study to stretch DNA in an elongational shear flow. A pressure drop applied across the device drives fluorescently stained DNA from the loading port and through the funnel in hydrodynamic flow (left-to-right direction in Fig. 1A). Flow is laminar due to the confined microfluidic environment: the smallest characteristic distance (the uniform 1 µm etch depth of the channel) and the slow flow velocities (at most ∼10 µm ms−1) produce a low Reynolds number (∼0.01). As described in detail below, DNA molecules are expected to arrive at the funnel in unrelaxed “prestretched” conformations arising from shearing between the channel floor and ceiling. The initial conformation shown in Fig. 1A represents the worst case resembling a random coil. Pure elongational flow drives all molecules toward a uniform steady-state extension.5 Elongational flow in the microfluidic funnel combines with shear flow that can cause the DNA to tumble, and the two influences compete. We will demonstrate that elongational flow can dominate over the very short duration of DNA excursion through the funnel, with stretching progressing roughly as diagrammed in the inset of Fig. 1A, ultimately yielding a significant fraction of uniformly stretched molecules.
As stated above, DNA molecules are expected to arrive at the funnel somewhat prestretched by shearing. Preconditioning by shearing before elongational flow has been predicted to increase stretching efficiency.12 The polymer sizes in this study range from 9 to 185 kb, thus the largest polymers, with average end-to-end distances of ∼2 µm are an extreme case because they can never completely relax when confined to a 1 µm space along one dimension.† More importantly, upstream from the funnel the entrance channel is much wider than it is deep (50 µm × 1 µm in the figure), and therefore even the smaller polymers are sheared in Poiseuille flow between the channel floor and ceiling. DNA molecules tethered to a surface on one end have been shown to exhibit vacillating stretching and relaxation behavior in shear flow as the free end diffuses in and out of faster regions of flow away from the surface.16 So too, completely free DNA molecules can stretch and tumble in shear flow,17 especially as the ends diffuse in and out of the slow regions of flow near chip surfaces. While such polymer responses have been examined thoroughly on a single molecule basis in constant shear environments, expectations for Poiseuille flow must be approximated. The average DNA extension under constant shear grows asymptotically to approximately 50% of the contour length at very high Weissenberg numbers (wi > 150), where wi equals the strain rate perpendicular to flow,  , multiplied by the longest polymer relaxation time, trelax.18 The strain rate is a device property and, for purposes of roughly estimating wi, is the same on average for all DNA sizes,‡ whereas the relaxation time grows with increasing DNA size. Consequently longer polymers, like the ∼50 and 185 kb DNA used here, are expected to tumble up to the funnel in a mixture of partially extended states. For example, 48.5 kb λ-phage DNA relaxes exponentially with at least a 150 ms time constant in a confined microfluidic environment,§ and the average strain rate is ∼2 ms−1 (velocity gradient of ∼1 µm ms−1 over a 0.5 µm distance from surface to center), yielding an estimated Weissenberg number of (150 ms)(2 ms−1) ≈ 300. It will be shown that a significant fraction of the longer molecules used in this study were indeed extended before the funnels, and the influence of this prestretching on downstream events will be discussed.
, multiplied by the longest polymer relaxation time, trelax.18 The strain rate is a device property and, for purposes of roughly estimating wi, is the same on average for all DNA sizes,‡ whereas the relaxation time grows with increasing DNA size. Consequently longer polymers, like the ∼50 and 185 kb DNA used here, are expected to tumble up to the funnel in a mixture of partially extended states. For example, 48.5 kb λ-phage DNA relaxes exponentially with at least a 150 ms time constant in a confined microfluidic environment,§ and the average strain rate is ∼2 ms−1 (velocity gradient of ∼1 µm ms−1 over a 0.5 µm distance from surface to center), yielding an estimated Weissenberg number of (150 ms)(2 ms−1) ≈ 300. It will be shown that a significant fraction of the longer molecules used in this study were indeed extended before the funnels, and the influence of this prestretching on downstream events will be discussed.
On entering the funnel, elongation of the fluid elements drives the population of polymers toward a uniform distribution of extended conformations.5 As cartooned in Fig. 1B, the center of the polymer (vertical line in the figure) moves at the same velocity as the surrounding fluid, and if the velocity gradient along the polymer is sufficiently high, then hydrodynamic drag forces will pull the leading and lagging segments away from the center in opposite directions. Geometrically, the funnel can be thought of as squeezing the fluid elements in the direction perpendicular to flow as the channel narrows moving into the funnel. The aqueous carrier fluid is incompressible and therefore slips along the polymers in both directions parallel to flow as the fluid elements lengthen to conserve volume. After sufficient residence time under strain, polymers stretch uniformly in response to the hydrodynamic drag force produced by slipping.5
In pure elongational flow, the average steady-state extension in a population of polymers approaches the full polymer contour length asymptotically as a function of the strain rate.5 This phenomenon is attributed in part to the drop in hydrodynamically induced tension along the polymer from the middle to the ends because the tension on each polymer segment is the accumulation of the drag forces on all other adjacent segments toward the nearest end. The middle segment has the most segments separating it from the ends, and therefore the highest tension, whereas the end segments have nothing pulling on them and therefore zero tension. As an outcome of the variable tension, DNA polymers are most easily stretched in the middle, and only at very high strain rates can they be stretched to the ends.
Yet despite the variable tension along DNA polymers in hydrodynamic flow, uniform stretching over most of the contour length can be achieved due to the DNA’s wormlike chain elasticity. Maximizing the fraction of DNA fully stretched is critical for genomic applications to unlock the most information from each molecule; only the stretched regions can be “read” easily by linear scanning. In brief, DNA pulled apart from the ends can be stretched to ∼85% of the contour length at relatively low tension (∼1 pN).2 However, DNA becomes quite resistant to stretching nearing full extension over a wide range of applied tensions: varying tension from approximately 5 to 60 pN produces less than 10% variation in stretching.2 Above ∼60 pN DNA overstretches to 1.7 times the contour length in a cooperative process involving an unraveling of the double helix and requiring little increase in tension throughout the transition.3,4 Consequently, our general strategy for genomics applications is to apply the highest strain rates possible, without overstretching the middle, to raise tensions as far as possible toward the ends above the ∼5 pN threshold for invariant stretching.
Although it is conceptually useful to think about polymer stretching in terms of tension, more often hydrodynamic stretching is described as a balance between the fluid strain rate and the polymer relaxation rate. Similar to wi for polymer shearing, the Deborah number equals the strain rate parallel to flow,  , multiplied by the longest polymer relaxation rate, with a critical value of
, multiplied by the longest polymer relaxation rate, with a critical value of  for the coil-to-stretch transition for isolated DNA molecules.5 Both parameters describing the Deborah number are immediately accessible in our system. The longest relaxation time can be measured directly, or extrapolated based on length (trelax scales as L3/2, where L is the contour length).22,23 The average strain rate of a funnel device is dictated by flow speed and funnel geometry according to
for the coil-to-stretch transition for isolated DNA molecules.5 Both parameters describing the Deborah number are immediately accessible in our system. The longest relaxation time can be measured directly, or extrapolated based on length (trelax scales as L3/2, where L is the contour length).22,23 The average strain rate of a funnel device is dictated by flow speed and funnel geometry according to
 | (1) |
 ).
).
Although the strain rate is sufficient to characterize the average steady-state extension in a population of polymers, and also to predict the onset of the coil-to-stretch transition, it is insufficient to describe the efficiency of stretching, that is the percent of molecules arriving at the steady-state extension in a fixed duration elongational flow. Certain DNA random coil conformations are more difficult to stretch than others.5,7 For example, molecules entering elongational flow mid-section first can be rapidly extended in transient hairpin conformations with both ends pulled tightly behind a leading middle section. These require a relatively long residence time under strain to reach steady-state extension. Conversely, other conformations, such as those entering end first and adopting transient “dumbbell” conformations during stretching, elongate at rates almost as fast as the fluid elements. The combined strain rate and the residence time, tres, expressed as a product,  , is the accumulated fluid strain, or simply the strain. The stretching efficiency was shown to depend strongly on the accumulated fluid strain.5 In funnel devices, the accumulated fluid strain is related geometrically to the natural logarithm of the funnel reduction ratio, the ratio of entrance to exit width. Therefore high reduction ratio funnels are predicted to achieve the highest stretching efficiencies based on a purely elongational flow model. The validity of this reduction ratio hypothesis for a mixed flow environment is tested here specifically.
, is the accumulated fluid strain, or simply the strain. The stretching efficiency was shown to depend strongly on the accumulated fluid strain.5 In funnel devices, the accumulated fluid strain is related geometrically to the natural logarithm of the funnel reduction ratio, the ratio of entrance to exit width. Therefore high reduction ratio funnels are predicted to achieve the highest stretching efficiencies based on a purely elongational flow model. The validity of this reduction ratio hypothesis for a mixed flow environment is tested here specifically.
In summary, the expectations developed from polymer studies in pure flow environments drive our hypothesis that the following three key parameters determine the DNA stretching efficiency in sudden elongational shear flows generated by tapered microfluidic channels: shear-induced prestretching before the tapered flow, the strain rate, and the fluid strain.
Experimental
DNA isolation and staining
Unmethylated λ-phage DNA (D1251, Promega, Madison, WI) was used without further purification, and a bacterial artificial chromosome (BAC) clone (12M9), from the human male BAC library RPC1-11, was obtained from the BAC/PAC resource center at Children’s Hospital Oakland Research Institute. This BAC contains a region of chromosome 22 cloned into the EcoRI sites of the BAC vector pBAC e3.6 (GenBank accession number AL080243). Agarose stabs of cells bearing 12M9 were incubated overnight at 37 °C and the cells were streaked for isolation on Luria Bertani (LB) chloramphenicol (20 µg mL−1) media. Individual colonies were inoculated into 2 mL of LB chloramphenicol and grown for 4 hours at 37 °C. The feeder cultures were subcultured into 2 L of LB chloramphenicol media and incubated overnight at 37 °C. Mid-log phase cells were harvested by centrifugation at 4 °C. BAC DNA was isolated using modifications of the standard plasmid alkaline lysis protocol.24 The isolated BAC DNA was then subjected to ultra centrifugation through three cesium chloride gradients to minimize contamination by nicked BAC, linear, or chromosomal DNA. Negatively supercoiled BAC DNA was then either linearized by digestion with the homing endonuclease PI-SceI, or fragmented by digestion with the restriction endonuclease NotI (R0696 and R0189, respectively, New England Biolabs, Beverly, MA).DNA was intercalated with ToTo-3 at a 5 ∶ 1 base pair to intercalator ratio (T3604, Molecular Probes, Eugene, OR) for fluorescence visualization. In general, DNA backbone staining with this family of bis-cyanine intercalating dyes extends the DNA contour length, however relatively little is known about the effect of ToTo-3 on DNA mechanical properties. We observed from measurements with magnetic tweezers, average DNA backbone signals, and comparative studies with YoYo-1 as a reference, that ToTo-3 can, at most, extend the DNA contour length ∼10% at the highest binding densities. Additionally, under the conditions used here the binding density appeared less than saturating most likely due to non-specific adsorption of unbound intercalator to container surfaces.
Microfluidics
2D microfluidic structures were etched 1 ± 0.1 µm into quartz substrates by standard photolithography (Dupont, Ichon, Korea; Micralyne, Edmonton, Canada) and sealed either in-house with Kasil® coated standard #1 coverslips, cleaned by sonication in FL-70 detergent at 80 °C, or by fusion bonding a quartz cover (Micralyne). Funnel patterns, such as in Fig. 1A, were deliberately rounded to a 0.1 µm grid matching the maximum photomask resolution to guarantee accurate production of the intended design. As a consequence of rounding, the true instantaneous strain rate is pulsed toward the funnel ends rather than continuous. This effect is most pronounced for long funnels with narrow exit channels, and cannot be avoided for resolution-limited structures. In general, stretched or partially extended molecules span across multiple pulses in most designs and therefore this non-ideality was ignored.As shown in Fig. 1A, the end of the funnel is marked by the beginning tick of a ruler etched just above the constant width exit channel (major ticks every 10 µm, and minor ticks every 2 µm). The ruler assisted in aligning the confocal spots (red dots in Fig. 1A) in the exit channel, as described below.
Funnel shapes yielding various strain rate profiles were designed according to Table 1 on the simplifying assumption that velocity is inversely proportional to channel width. Computational fluid dynamic models revealed that the strain rate profile depends on the streamline position lateral to flow, but for a given funnel shape, the strain rate profile along each streamline is generally reflective of the ideal case without the no-slip boundary conditions.
| Funnel name | Funnel equation | Funnel shape |
|---|---|---|
| a Symbols: entrance width, wi; exit width, wf; funnel length, lF. | ||
| Sudden finish (linear) | w(x) = mx + B, m = (wf − wi)/lF, B = wi |

|
| Sudden onset (constant acceleration) |

|

|
| Increasing strain rate |

|

|
| Constant strain rate |

|

|
Instrumentation
Extended DNA conformations were analyzed in the constant width exit channel after the funnel by a two-spot confocal microscope system described in detail previously.9 In brief, two confocal spots from separate 633 nm lasers (#31-2140-000, Coherent, Santa Clara, CA) were positioned a known distance apart within the exit channel (red spots in Fig. 1A). To avoid acceleration during measurement, the spot closest to the funnel—called the first spot—was positioned no closer to the exit than the longest contour length in a DNA sample mixture. The ruler above the exit channel assisted these alignments. Fluorescence emission from each spot was focused into separate fiber-coupled APD photon counting modules (SPCM-AQR-12-FC, PerkinElmer Optoelectronics, Fremont, CA), and signals were collected at 10 kHz rates by event counters (PCI-6602, National Instruments, Austin, TX).The two-spot system was specifically designed for high throughput microfluidic applications and especially for high resolution DNA sequence motif mapping. To independently validate our 2-spot system of DNA length measurement, we imaged PoPo-3 intercalated λ-phage DNA with broad-field 532 nm excitation (defocused 50 mW CW Nd:YAG laser epi-lumination) with very short 50 µs exposure times to avoid image streaking (DiCamPRO iCCD camera, Cooke Corporation, Auburn Hills, MI). DNA extensions under optimized flow conditions were evaluated after threshold-based black and white image conversion by standard blob analysis, and extensions similar to the two-spot system were obtained (data not shown).
Shear-induced extension before the funnel was measured using a wide-field epi-fluorescence microscope that integrated a 532 nm diode pumped Nd:YLF laser (Millennia, Spectra Physics, Mountain View, CA), a 60× objective lens (NA = 1.4, Nikon), and a CCD camera (SensiCam QE, Cooke Corp, Romulus, MI). The laser beam was expanded 9×, shaped by two slit apertures, then collimated onto the sample plane to yield a uniform intensity profile across the CCD viewing area at a power density of about several microwatts per µm2. The laser beam was chopped by an electromechanical shutter (Newport Corp-Oriel, Stratford, CT), and synchronized with the CCD exposure to minimize DNA photodamage. All images were acquired using BAC 12m9 DNA that was intercalated with PoPo-3 (Molecular Probes, Eugene, OR) at a 1 ∶ 5 dye/bp ratio. Typical exposures times were 1 ms with a frame rate of ∼20 fps. DNA extension was evaluated by standard blob analysis after threshold-based image conversion. Intact BAC DNA molecules were selected based on integrated fluorescence intensity.25,26 DNA length was approximated as the major axis of the best fit ellipse to identified DNA objects, and lengths were corrected for a small amount of streaking at the highest velocities. Velocities were obtained by tracking DNA molecules through the field-of-view across multiple exposures.
Data processing
Fig. 1C shows the fluorescence signature of a single extended λ-phage DNA molecule detected with the two spot system (red trace, first spot; blue trace, second spot). The sharp increase in fluorescence at time t = 0 ms corresponds to the arrival of the leading edge of an extended DNA molecule into the first spot. The fluorescence plateaued throughout residence of the molecule in the first spot, and abruptly returned to the baseline level as the lagging end departed. A similar feature appeared in the second spot after a delay for the molecule to transit between spots, T. DNA events were interpreted as pairs of similar photon burst features delayed between spots by a time consistent with the expected flow velocity. Events were defined as a contiguous set of photon counts (square symbols connected by thick lines in Fig. 1C) above a threshold level determined from the average and the standard deviation of the baseline.The delay time between spots, T, was calculated as the difference between the center-of-mass (CM) times for each individual event (vertical red and blue lines in Fig. 1C). CM times are the weighted average of the discrete count times (bin times),
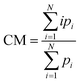 | (2) |
 | (3) |
Technically, X is the projection of the molecule in the direction of flow, but for simplicity is called “length” from this point forward.
DNA events were subsequently filtered by three physical criteria before inclusion in subsequent statistical analyses: velocity, similarity between fluorescence profiles in each spot, and general consistency of DNA size and fluorescence. Flow was laminar and steady throughout experimental runs, and consequently a characteristic velocity range could be identified (for example, see Fig. 3A) and outliers were excluded on that basis. Most outliers occurred when close proximity between two molecules confused the identification algorithm. Low DNA concentrations were used to minimize such coincident events (500 pg µL−1). Event similarity was also asserted to eliminate other misidentifications on the grounds that the molecules could not significantly change conformations between spots, because polymer relaxation times greatly exceeded the transit time. Similarity in both length and total integrated intensity (burst size) was imposed, although this is not generally necessary for sequence motif mapping (for example see ref. 9). Lastly, a minimum occupancy time of 0.3 ms was asserted to eliminate coincident noise spikes, or other sources of brief low intensity signal otherwise inconsistent with intercalated DNA.
Despite extra efforts to purify only intact BAC DNA, quantitative photometric analysis of pulsed field gel electrophoregrams revealed a significant fraction of fragmented DNA in the purified and linearized samples used in these experiments. Therefore an intensity-based approach was further used to subselect intact BAC DNA from the fragments and other miscellaneous detritus. Shown in Fig. 2 is a two-dimensional histogram (heat map) of the average fluorescence intensity per unit time vs. the observed length. Intact molecules of a particular size line up along the same hyperbola, shown in pink in this representation. Intuitively this can be understood by considering a few simple DNA conformations. Because the intercalator molecules are distributed uniformly along the DNA, the fluorescence intensity is proportional to the density of DNA in the confocal spot.25,26 In other words, incompletely stretched DNA is “brighter” because there are more intercalators per unit length. Fully stretched DNA yields the lowest signal. If the fully stretched DNA is folded in half, then there is twice the intensity; in quarters, four times the intensity; and so on. Technically, the product of the average signal (y-coordinate) and the length (x-coordinate) is equivalent to the burst size, known to be proportional to DNA size for uniformly stained molecules.25,26 We find this statistical representation useful because all fully stretched molecules cluster along the same horizontal line in a DNA size mixture (3 × 103 photons in Fig. 2, also see the red line Fig. 6A), and the signal strength is immediately discernable from the vertical position of this line.
 | ||
| Fig. 2 Example “comet” diagram of DNA stretching in a sudden elongational shear microflow analyzed by the two-spot system, and showing a hyperbolic selection of intact molecules for further analysis (pink shaded region; selected data shown in Fig. 3B, green plot). The comet diagram is a two dimensional histogram of the average DNA fluorescence intensity (as photon counts) per unit time vs. measured length, and is plotted as a heat map (legend: molecules per pixel, i.e., hotter colors for higher occupancies). Experimental conditions: increasing strain rate design, wi = 167 µm, wf = 2 µm, and lF = 200 µm. | ||
 | ||
| Fig. 3 BAC 12m9 DNA stretching at varying fluid strain rates and total fluid strains. Only intact molecules were selected for analysis, as shown in Fig. 2 and as described in the text. (A) DNA velocity histograms at varying pressure in the high fluid strain funnel (see below). (B) Length histograms in the high fluid strain funnel, corresponding to velocity histograms in (A) (matching colors and symbols). (C) Length histograms in the low fluid strain funnel at corresponding pressures to (A) (matching colors and symbols). Funnels drawn to scale with corresponding results (gray inserts in panels (B) and (C)). High fluid strain funnel: increasing strain rate design, wi = 167 µm, wf = 2 µm, and lF = 200 µm. Low fluid strain funnel: identical to the high strain design, except wi = 20 µm. | ||
The shaded area in Fig. 2 shows a hyperbolic subselection of intact DNA events, centered around the strong cluster of highly stretched events. Although the intact DNA events were discernable by eye from the separated population of fragments and detritus, in general the two populations overlapped sufficiently such that an unbiased selection procedure based on, for example, Gaussian peak fitting of a one dimensional burst size histogram could not be performed adequately. This difficulty arises, in part, because the distribution of intact events is only approximated by a hyperbola. As can be seen in Fig. 2, the average intensities do not rise at shorter lengths as fast as the simple hyperbola. This systematic deviation from the ideal hyperbola resulted in a broadening of the burst size histogram. As an aside, it is expected that incompletely stretched molecules would yield lower integrated intensities, on average, because the unstretched positions can span the full confocal volume, always likely to occupy, in part, some portion of the peripheral confocal volume where the detection efficiency is lower. In contrast, stretched molecules follow a particular fixed trajectory through the confocal spot, and therefore the resulting average intensities are a direct reflection of the distribution of detection efficiencies.
Intact DNA events were therefore selected manually “by eye”, centering the selection region on the obvious stretched cluster and understanding that this process introduced a potential bias in the results toward an overestimation of the stretching efficiency. Nevertheless, the main purpose of subselection of intact events was to monitor changes in stretching efficiency induced by varying flow parameters, and for this comparative purpose the method was quite adequate.
Results
Strain rate and fluid strain
Fig. 3A shows histograms of DNA velocities at varying fluid drive pressures in the high strain rate funnel. Individual velocities were calculated for each DNA event, and the distributions clearly shifted toward higher velocities with increased pressure. The asymmetry in the velocity distributions is characteristic of Poiseuille flow, and the peak positions indicated the fastest flow speed in the center of the channel. The peak velocities were proportional to pressure (2 µm ms−1 per psi for the high reduction ratio funnel). Comparable velocity distributions were also observed for the low reduction ratio funnel (data not shown), as expected because the hydrodynamic resistance was dominated by the same 2 µm wide exit channel found in both designs.
The high fluid strain funnel extended the vast majority of molecules into either linear or significantly extended conformations (Fig. 3B), even at the lowest velocities yielding the lowest fluid strain rates. A prominent fraction of uniformly and highly stretched molecules was observed under all except the highest strain rate conditions. These highly stretched conformations are consistent with fully stretched DNA (61 µm observed, green trace in Fig. 3B, vs. 63 µm expected, see Discussion), and are readily usable for genomic analysis.
At the lowest strain rate (black plot in Fig. 3B), the high fluid strain funnel produced a prominent fraction of extended molecules centered around 57 µm and comprising 40% of the intact events selected, based on Gaussian peak fitting. Few molecules stretched beyond the 63 µm contour length, consistent with B-form DNA mechanical properties. Increasing the strain rate improved the efficiency of stretching DNA (black to red to green plots in Fig. 3B). The fraction of highly extended molecules rose from 40 to 50% on increasing pressure from 3 to 8 psi, and the average length of the extended conformation shifted from 57 to 61 µm.
DNA overstretching was observed at the highest strain rates. The trend in stretching toward a uniform extension approaching the 63 µm DNA contour length was broken between 8 and 13 psi. DNA overstretching to ∼80 µm was observed at 13 psi (blue plot in Fig. 3B), coinciding with the complete disappearance of the group of uniformly stretched molecules near the full contour length. In contrast, the length distribution of the understretched molecules remained largely unchanged, indicating that only the most extended molecules underwent the B-form to S-form DNA state transition at a critical strain rate produced between 8 and 13 psi in the high fluid strain rate device.3,4 The distribution of the overstretched molecule lengths varied from run to run, suggesting that the S-forms might not have reached steady-state extension upon measurement.
The drag coefficient for DNA in aqueous buffer can be estimated from the critical velocity of the overstretching transition. It is presumed that the observed overstretching transition coincided with a rise in the peak tension at the center of the fully extended molecules above the critical ∼60 pN tension for the B-state to S-state transition.3,4 For this estimation, the average strain rate according to eqn (1) is used, and the highly extended DNA conformation is modeled as a simple thin rod. Each DNA segment away from the center contributes ζ||(ν(s) −
ν(0)) ds to the peak tension; where ζ|| is the parallel drag coefficient per unit length; s is the distance from the molecule center; v is the velocity of the fluid in the polymer reference frame, equal to 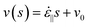 ; and it is assumed that the center moves at the same velocity as the surrounding fluid (i.e., ν0 = 0). Integrating along one-half of the polymer yields the peak tension, Tmax, and after rearrangement,
; and it is assumed that the center moves at the same velocity as the surrounding fluid (i.e., ν0 = 0). Integrating along one-half of the polymer yields the peak tension, Tmax, and after rearrangement,
 | (4) |
 | (5) |
Most molecules stretched longer than 20 µm in the high fluid strain funnel (Fig. 3). Of course, as mentioned in the Experimental section, the intact molecule selection shown in Fig. 3 is probably biased against the unstretched conformations. However, the complete distributions, like that shown in Fig. 2, were similarly unoccupied at short lengths for any reasonable average intensity vs. length trajectory (like the pink shaded region in Fig. 2). In other words, few short and bright DNAs with average photon counts above 6 × 103 ms−1 were observed that would be consistent with a mostly unstretched conformation.
What is most unusual about the results in the low strain rate funnel is the fact that the highly extended conformations were observed at all; the DNA molecules, if extended from random coil conformations, elongated farther than the fluid elements. The initial end-to-end distance is 1.8 µm for the random coil, with a final extended length of 61 µm. Thus, the DNA apparently elongated by a factor of 34, whereas the fluid elements only elongated by a factor of ten based on the funnel geometry. Of course, this is not possible. As confirmed in the next section, the simplest explanation is that the DNA arrived at the funnel entrance significantly extended and aligned with flow from shear interactions at the channel surfaces.
Thus, with regard to the performance in these funnel devices, DNA stretching behavior in a mixed elongational shear flow can exhibit the same trends as a pure elongational flow, with respect to strain rate and fluid strain, despite the clear influence of shear interactions before the funnel. Within the funnel, the sudden onset of fluid strain is quite complicated three-dimensionally, including shear components in both directions parallel to flow (floor-to-ceiling, and side-to-side), plus the elongational component parallel to flow. Unraveling the separate influences of each component goes beyond the scope of this work, but the clear ability of the device to drive a DNA population toward a uniform extended conformation attests to the strong influence of the elongational component.
DNA shearing in a confined microfluidic environment
Upstream from the DNA stretching funnel, shearing prestretched the molecules considerably under all flow conditions tested. The extensions of hundreds of individual molecules were measured by wide-field microscopy, and a clear trend toward increased extension with increased shear rate was observed (Fig. 4A–D) over the relevant range of flow velocities used in the preceding section, confirming that upstream DNA shearing enhanced device performance. Average flow velocities were obtained by tracking a small number of individual DNA molecules under each flow condition, and shear-induced extension was quantified by standard blob analysis. An asymptotic rise in the average extension was observed over the entire range of flow velocities examined (Fig. 4E), consistent with prior findings for simple linear shear flow profiles.16,17 | ||
| Fig. 4 Shear-induced DNA prestretching in a confined two-dimensional microfluidic environment. (A–D) Images of BAC 12m9 DNA in a shallow and wide channel (1 μm high by >50 μm wide) at average flow rates of 0.0, 0.1, 0.5, and 1.6 μm ms−1, respectively. (E) Average DNA fractional extension as a function of flow rate. Grey rectangle: highlighting upstream flow conditions in Fig. 3. Red line: best fitting line for velocities slower than 0.4 μm ms−1 (y-intercept = 0.09 ± 0.01, slope = 0.23 ± 0.06, uncertainties based on fit). | ||
The prestretching implicated by complete DNA stretching in the low total fluid strain funnel in Fig. 3C was clearly evident with an average upstream fractional extension of 0.3 at ∼2.5 µm ms−1 flow velocity (see Fig. 4E, with the upstream flow velocity estimated as the flow velocity in the interrogation channel divided by the funnel reduction ratio, or 25 µm ms−1 ÷ 10). Furthermore, a significant rise in upstream extension was observed across the range of flow velocities explored in the high reduction ratio funnel in Fig. 3B (velocity range highlighted with a gray box, Fig. 4E). Without a good theoretical model describing DNA extension in this complicated shear flow, the statistical significance of changes in upstream extension over the relatively narrow range of velocities explored in the high reduction ratio funnel was gauged by simple linear analysis in the derivative approximation (red line in Fig. 4E). The average upstream fractional extension rose from 0.11 ± 0.01 to 0.16 ± 0.02 (uncertainties based on fit), a statistically significant increase that likely accompanied decreases in DNA conformational complexity. Therefore upstream DNA shearing was strongly implicated as an important component of the improvement in stretching efficiency observed with increased velocity in the high reduction ratio funnel (Fig. 3B).
Strain rate profile
The shape of the microfluidic funnel taper proved critical for efficient DNA stretching, indicating that the time dependence of the fluid strain is an important funnel microflow design criterion. Four different funnel shapes were designed to examine the influence of the strain rate profile on DNA stretching (Table 1). Each funnel contained the same entrance width, exit width, and funnel length, and differed only by the shape of the taper (wi = 50 µm, wf = 0.6 µm, and lF = 200 µm). Funnels were placed in parallel on the same chip to avoid variations in etch depth. BAC 12m9 was stretched over a range of velocities spanning the overstretching transition, and the best results—defined as the highest fraction of molecules fully stretched—for each funnel are shown in Fig. 5 as length histograms, offset vertically for visibility. All runs were performed on the same day with the same BAC preparation and on the same chip.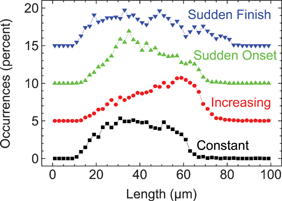 | ||
| Fig. 5 BAC 12m9 DNA stretching under different strain rate profiles. Strain rate was optimized for highest stretching efficiency in each case. Intact molecules were selected for analysis, as shown in Fig. 2 and as described in the text. The y-axis was offset in 5% increments for clarity. Funnel designs: each design in Table 1, with wi = 50 µm, wf = 0.6 µm, and lF = 200 µm. | ||
The “sudden finish” funnel consistently performed the worst, always yielding a wide and featureless length distribution ranging from quite understretched (15 µm) to overstretched (80 µm), and never driving the DNA population toward any significant uniform conformation. The “sudden onset” funnel was not much better. Although a recognizable small ledge appeared near the DNA contour length, the majority of molecules were heterogeneously understretched. The “increasing” strain rate funnel performed as described earlier, yielding a most probable highly extended conformation. The “constant” strain rate funnel always slightly underperformed in comparison to the increasing strain rate funnel, but was otherwise qualitatively quite similar.
DNA sizing and separation
The Fig. 6A “comet plot” shows a separation of four different DNA sizes in a mixture (9, 47, 129, and 185 kb, or 3, 16, 44, and 63 µm respectively) after stretching in the linearly increasing strain rate funnel used previously. Combining integrated intensity with physical DNA length measurement improved our system’s DNA sizing resolution. Except for the smallest fragment that was not completely resolved (small teal-colored cluster at ∼3 µm length), each DNA size fell along a different isolated hyperbola that terminated abruptly near its full contour length. The average number of photon counts, per unit time, was size independent for highly extended DNAs (red line in Fig. 6A), as expected for long uniformly stained DNA molecules that span many confocal diameters when stretched. The deviation from this trend at smaller DNA sizes arose from the increasing influence of low photon counts on the edges of individual DNA traces (for example, at times 0 to 0.3 and 6.7 to 7 ms in Fig. 1C). | ||
| Fig. 6 DNA size separation. (A) “Comet” plot presentation of BAC 12m9 fragment length separation after digestion with restriction enzyme NotI (9, 47, 129, and 185 kb fragment lengths, undigested DNA added separately). Red line: DNA size-independent average photon counts per unit time for fully stretched molecules (estimated position “by-eye”). Funnel design: increasing strain rate, wi = 50 µm, wf = 0.6 µm, and lF = 200 µm. (B) λ-phage DNA stretching in a shorter length, higher strain rate funnel (increasing strain rate, wi = 50 µm, wf = 0.6 µm, lF = 25 µm) and with 68% glycerol (10× higher viscosity). | ||
The strain rate was optimized for stretching the longest molecules, and consequently the stretching efficiencies were lower for the smaller, faster relaxing molecules. Especially evident was the loss of the distinctive highly stretched cluster, or “comet head” at shorter lengths. For instance, the 47 kb fragment stretched to the expected contour length of 16 µm, but with a relatively uniform probability distribution between 8 and 16 µm. In contrast, under conditions optimized for this DNA size that included a higher strain rate, 40% of similarly sized λ-phage DNA molecules stretched uniformly to 16.4 µm (Fig. 6B). Therefore, it can be concluded that a single set of experimental conditions (i.e. funnel shape, velocity, and spot positions relative to the end of the funnel) has a somewhat limited dynamic range for DNA size separation based on length alone. Similarly, with confocal optics, size separation based on intensity alone suffered from peak broadening, as discussed in the Experimental section. However, 2D combined histograms of length and intensity, such as the comet plot, overcame the shortcomings of the individual approaches for DNA size separation. For instance, for genomics applications highly extended DNA molecules can be identified first on an intensity basis (region above and below the red line in Fig. 6A). Otherwise, on a length basis alone it is difficult to distinguish short stretched molecules from longer unstretched ones. Subsequent length selection separates the differently sized molecules.
The size resolution was 30% for the longest molecules in Fig. 6A, estimated from Gaussian peak fitting of the length histogram of the highly extended molecules (region above and below the red line in Fig. 6A), and taken as the full width at half maximum of the best fit, compared to the center. The size resolution worsened at shorter lengths; the width of the hyperbolic cluster remained roughly constant while the length dropped. Therefore, although the 2D histogram approach expanded the dynamic range considerably for size separation, for optimal resolution the strain rates should be tuned for particular DNA lengths of interest. As an aside, better resolution for the longer sized molecules was obtained under more highly optimized conditions. For example, 14% resolution was estimated for the best stretched DNA in Fig. 3B (green plot).
A low viscosity, high throughput buffer was used for all of the BAC DNA stretching experiments in this work. However, better size resolution can be obtained by viscosification due to improved photon counting statistics. Fig. 6B shows λ-phage DNA stretching at 10-fold higher viscosity and at a strain rate optimized for this molecule size (68% glycerol solution, 25 µm “increasing” strain rate funnel, and νf ≈ 2.4 µm ms−1). These conditions attained a 10% resolution, based on Gaussian peak fitting of the corresponding one-dimensional length histogram (as above).
Discussion
In the present study we detailed for the first time a method for efficiently and quickly linearizing long individual DNA molecules of significant genetic interest by microfluidics. This work establishes the microfluidic and polymer dynamics underpinnings for the genomic DNA sequence motif mapping technique begun by Chan et al. on small λ-phage viral DNA genomes,9 and continued very recently by Phillips et al. on significantly longer BAC molecules with a cloned genetic sequence of human origin.28 Overall, by microfluidic manipulation of individual BAC-sized DNA molecules, we report stretching efficiencies of up to 50%, complete stretching for most practical intents and purposes in genomic analysis (see below), and very high throughput rates exceeding one thousand molecules per minute.Throughput
Very high throughput is the primary distinguishing advantage of the DNA linearization method described here. For example, thousands of molecules were analyzed in standard five minute runs in determining the DNA stretching efficiencies presented in Fig. 3. At optimal flow velocities of 15 µm ms−1, a single 185 kb sized DNA molecule was analyzed in ∼4 ms. Allowing ample 15 ms gaps between molecules on average to avoid overlap, and accounting for 50% stretching efficiencies, a maximum of 1500 molecules were analyzed per minute. Recent improvements in stretching efficiency, higher flow velocity designs, and instrument parallelization have increased our current capabilities to greater than 2000 molecules per second (manuscripts in preparation).DNA stretching in mixed type microflows
The microfluidic structures used in the present study were designed by criteria derived from DNA stretching properties in pure flow types. It was demonstrated, in various mixed flow environments with both shear and elongational components, that the funnel reduction ratio and the flow velocity (equivalently, fluid strain and strain rate) influence the DNA stretching similarly to the pure elongational flow environment. An open question had remained whether bursts of elongational fluid strain could drive full polymer stretching efficiently in the presence of extra shear interactions. Specifically, a concern existed that shear-induced polymer tumbling in the tapered funnel region would diminish stretching efficiency: poor stretching performance was observed in mixed flows with equivalent elongational and shearing components,29 and in our devices the shearing component was expected to dominate the flow characteristics (see Introduction). However, it was also thought that upstream shear interactions might increase the stretching efficiency by minimizing the conformational complexity in the prestretched DNA conformations arriving at the stretching funnel.5 The high λ-phage DNA stretching efficiency exhibited in Fig. 6B, with an average extension of X/L = 0.87 (assuming little intercalator-induced DNA lengthening, see the Experimental section), actually exceeded the performance of a pure elongational flow,5 for the same accumulated fluid strain albeit with a ten-fold higher Deborah number in this study. Therefore, the stretching efficiencies may have been enhanced by upstream shear interactions more than they were hindered by tumbling in the funnel.The analysis of different funnel tapers (equivalently, strain rate profiles) revealed extra complexity in DNA stretching beyond the simple model based on fluid stain and average strain rate alone. Each funnel shape produced a continuum of different strain rate profiles dependent on the streamline position lateral to flow, and, for rigorous analysis, each profile should be described by the appropriate three dimensional strain rate tensor as a function of position along the streamline. Such analysis goes beyond the scope of this work, however, the funnel shape comparison emphasized the need for such analysis in understanding polymer behavior in complex microflows. While it is possible to design mixed flows, like the increasing strain rate funnel, that mimic polymer behavior in pure flows, such behavior hinges on a balance among shear and elongational flow components throughout DNA excursion through the funnel. Therefore, the basic design principles of high fluid strain and high strain rate are necessary, but not sufficient to achieve uniform DNA stretching in a mixed flow microfluidic environment.
Upstream DNA prestretching by shearing was readily apparent, confirming that mere flow in a confined environment is an important component of device function. However the average extension was significantly smaller than predicted based on simple comparison to pure shear flow. In the pure flow, fractional extensions exceeding 0.4 were observed at Weissenberg numbers as low as 80.17 However, in our device fractional extensions did not exceed 0.3 even at much higher estimated Weissenberg numbers (see Introduction). Insight into the greater stretching efficiency in the pure shear flow environment over DNA shearing in a confined environment can be gained by considering the two chip surfaces as competing influences on DNA stretching. The large polymers used here typically spanned the narrow height of the channels, experiencing rotational flow in opposing directions simultaneously, above and below the center of the channel. The conflicting influences of opposed rotational flows likely frustrated shear-induced extension in comparison to the pure shear environment (P. Doyle, Massachusetts Institute of Technology, personal communication, 2005).
Prestretching with post fields
Previously we reported stretching shorter λ-phage DNA molecules (48.5 kb) in similar tapered microfluidic structures, but with a post field array immediately preceding the stretching funnel.9 Ostensibly the posts were to aid in prestretching by transiently tethering the molecules. However, based on the results presented here, it is now understood that the post fields were probably ineffective because the DNA molecules were already sufficiently prestretched such that they readily slipped in between the posts. Indeed, in a later controlled study of DNA stretching efficiency with and without posts using longer BAC 12m9 DNA, no benefit from posts was discernable within experimental uncertainty (data not shown). 1 × 1 µm2 square posts spaced apart 2.5 µm center-to-center were used in these studies. Smaller and more tightly packed posts might yield improvements in prestretching, but at the cost of shifting to sub-micron fabrication techniques and possibly necessitating shallower channels to protect the fine post field features. In support of post field miniaturization, Randall et al. recently improvised a diffuse photopatterned gel for prestretching DNA in an analogous electrophoretic DNA stretching microdevice.30 Ensemble fractional extensions improved substantially (up to 0.95) with this approach for similarly sized 169 kb T4 DNA. Another promising approach of prestretching by two-dimensional hydrodynamic flow focusing has improved stretching efficiency up to 80% for BAC-sized molecules.31DNA extension
The DNA length measurements reported here using the two spot system were both accurate and precise within experimental uncertainty compared to expectations based on the 3.4 Å axial rise per base pair of the B-form double helix determined by crystallography (16.4 µm, from Fig. 6B, and 61 µm, from the green plot in Fig. 3B, vs. 16.4 and 63 µm for λ-phage and BAC 12m9 respectively).14,15 However, as discussed below, this empirical agreement is insufficient evidence to conclude that the highly extended DNA conformations observed here are nearly 100% stretched. Nevertheless, as will be argued, the simplifying assumption of 100% stretching is valid within experimental uncertainty for purposes of genetic analysis.There are two reasons to suspect that the highly extended DNA molecules in this study might not be fully stretched. First, at high tensions just below the B-state to S-state transition—achieved here at the highest strain rates not producing overstretching—DNA overextends to 110% of its full contour length.4 Although entropy driven relaxation from partially extended states has been characterized thoroughly,32,33 the fastest components of relaxation at higher extensions (greater than 90% of the contour length) and overextension have never been examined thoroughly. Overextension involves deformation of the B-state, with an accompanying increase in enthalpy. Consequently, unlike the entropic relaxation, driven by thermal fluctuations that begin at the ends and work inward—the stem and flower model32,33—enthalpy-driven relaxation is a deterministic action at a distance along the polymer and therefore can potentially occur relatively quickly. A small insight into the kinetics of polymer relaxation at high extension or overextension can be gained from the two-spot system by comparing the DNA lengths determined from the separate spots. Invariably, the lengths calculated from the second spot were shorter. Varying the distance between spots revealed a very approximate 10% relaxation component in the millisecond time domain for 185 kb DNA, and while our investigation of fast relaxation remains as an interesting work in progress in its early stages, it can be concluded that the long DNA molecules in this study did relax to some extent during measurement. Therefore the expected stretched length is somewhat uncertain within approximately ±10% of the full contour length. The second reason to suspect that the DNA is not fully stretched regards intercalator-induced extension of the contour length. As mentioned in the Experimental section, a variety of evidence including magnetic tweezers measurements suggests that ToTo-3 intercalation perturbs the DNA structure significantly less than other common DNA stains, yet still producing as much as a 10% increase in contour length.
In summary, without further investigation the possibility cannot be excluded that the combined effects of relaxation and overextension/intercalation coincidently offset each other yielding apparently fully stretched DNA. Nevertheless, within experimental uncertainty the data is also consistent with a simpler model that holds that the highly extended molecules are lightly intercalated and completely stretched, and that any overextension relaxes quickly on the measurement time scale such that it can be ignored to a first order approximation. This model was used successfully by Chan et al. for sequence motif mapping,9 where it was found that both the DNA length and the sequence positions were consistent with the 3.4 Å bp−1 axial rise of the double helix. In conclusion, for mapping applications using the two-spot system with ToTo-3, it can safely and simply be assumed that DNA stretches fully under the optimized conditions recommended here.
Partially stretched DNA molecules
DNA molecules emerged from the stretching funnel in both stretched and unstretched conformations. It is consistent with our observations that single-bend hairpins are the most abundant unstretched conformations at high strain rates for longer BAC molecules: almost all of the molecules stretched to at least one-half of the length of the highly extended conformation at the highest strain rate not producing overstretching (green trace in Fig. 3B). Single-bend hairpins were previously identified as the most transiently stable unstretched conformation for shorter λ-phage DNA molecules,5,7 although it was also noted that multiple bends were evident in longer molecules.5 A larger fraction of molecules too short for fully extended single-bend hairpins appeared at the lower strain rates in our study (black and red traces in Fig. 3B), and these molecules may contain multiple bends.While not the ideal linearized structures, single-bend DNA hairpins are the second most highly ordered conformations and can be mined for genomic information. De novo DNA mapping applications that benefit the most from linear molecules are waning in significance in today’s high throughput sequencing environment in favor of applications that focus on the differences between known sequences, such as in haplotyping and pathogen fingerprinting (for a thorough survey of the potential applications of the method described here, see ref. 28). For this growing set of genome difference studies, the linear information content of single-hairpin molecules may often suffice.
DNA sizing
DNA sizing resolutions of up to 10 and 14% were demonstrated for 48.5 and 185 kb molecules (λ-phage and BAC 12m9 respectively) using a combined approach of physical length determination and integrated fluorescence intensity. In comparison, better than 5% resolutions have been measured by fluorescence intensity alone in microfluidic systems optimized for this purpose.25,26 Resolution can be improved in our device in two primary ways: application of uniform illumination across the detection zone, and longer observation times. The latter involves a fundamental trade-off between throughput and resolution that can be tuned to the individual application.Acknowledgements
We thank John Marko, Dunja Skoko, and Jie Yan for assistance evaluating ToTo-3 intercalator-induced DNA lengthening, and John Marko and Pat Doyle for critical review of this manuscript. This research was partially funded by grant DMI-0213876 from the National Science Foundation.References
- C. Bustamante, J. F. Marko, E. D. Siggia and S. Smith, Science, 1994, 265, 1599–1600 CrossRef CAS.
- S. B. Smith, L. Finzi and C. Bustamante, Science, 1992, 258, 1122–1126 CrossRef CAS.
- P. Cluzel, A. Lebrun, C. Heller, R. Lavery, J.-L. Viovy, D. Chatenay and F. Caron, Science, 1996, 271, 792–794 CrossRef CAS.
- S. B. Smith, Y. Cui and C. Bustamante, Science, 1996, 271, 795–799 CrossRef CAS.
- T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016–2021 CrossRef CAS.
- P. K. Wong, Y.-K. Lee and C.-M. Ho, J. Fluid Mech., 2003, 497, 55–65 Search PubMed.
- D. E. Smith and S. Chu, Science, 1998, 281, 1335–1340 CrossRef CAS.
- C. Aston, C. Hiort and D. C. Schwartz, Methods Enzymol., 1999, 303, 55–73 CAS.
- E. Y. Chan, N. M. Goncalves, R. A. Haeusler, A. J. Hatch, J. W. Larson, A. M. Maletta, G. R. Yantz, E. D. Carstea, M. Fuchs, G. G. Wong, S. R. Gullans and R. Gilmanshin, Genome Res., 2004, 14, 1137–1146 CrossRef CAS.
- J. O. Tegenfeldt, C. Prinz, H. Cao, S. Chou, W. W. Reisner, R. Riehn, Y. M. Wang, E. C. Cox, J. C. Sturm, P. Silberzan and R. H. Austin, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 10979–10983 CrossRef CAS.
- R. Riehn, M. Lu, Y.-M. Wang, S. F. Lim, E. C. Cox and R. H. Austin, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10012–10016 CrossRef CAS.
- R. G. Larson, J. Non-Newtonian Fluid Mech., 2000, 94, 37–45 Search PubMed.
- J. R. Wenner, M. C. Williams, I. Rouzina and V. A. Bloomfield, Biophys. J., 2002, 82, 3160–3169 CrossRef CAS.
- R. Langridge, D. A. Marvin, W. E. Seeds, H. R. Wilson and L. D. Hamilton, J. Mol. Biol., 1960, 2, 38–64 CrossRef CAS.
- R. R. Sinden, DNA Structure and Function, Academic Press, San Diego, CA, 1994 Search PubMed.
- P. S. Doyle, B. Ladoux and J.-L. Viovy, Phys. Rev. Lett., 2000, 84, 4769–4772 CrossRef CAS.
- D. E. Smith, H. P. Babcock and S. Chu, Science, 1999, 283, 1724–1727 CrossRef CAS.
- R. Duggal and M. Pasquali, J. Rheol., 2004, 48, 745–764 CrossRef CAS.
- O. B. Bakajin, T. A. J. Duke, C. F. Chou, S. S. Chan, R. H. Austin and E. C. Cox, Phys. Rev. Lett., 1998, 80, 2737–2740 CrossRef CAS.
- Y.-L. Chen, M. D. Graham, J. J. de Pablo, G. C. Randall, M. Gupta and P. S. Doyle, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2004, 70, 060901(R).
- G. C. Randall and P. S. Doyle, Macromolecules, 2005, 38, 2410–2418 CrossRef CAS.
- B. H. Zimm, J. Chem. Phys., 1956, 24, 269–278 CrossRef CAS.
- T. T. Perkins, S. R. Quake, D. E. Smith and S. Chu, Science, 1994, 164, 822–826 CrossRef.
- J. Sambrook and R. W. Russell, Molecular Cloning: A Laboratory Manual, Cold Spring Harbor Laboratory Press, Cold Spring, NY, 3rd edn, 2001 Search PubMed.
- H.-P. Chou, C. Spence, A. Scherer and S. R. Quake, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 11–13 CrossRef CAS.
- M. Foquet, J. Korlach, W. Zipfel, W. W. Webb and H. G. Craighead, Anal. Chem., 2002, 74, 1415–1422 CrossRef CAS.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, Oxford, 1986 Search PubMed.
- K. M. Phillips, J. W. Larson, G. R. Yantz, C. M. D’Antoni, M. V. Gallo, K. A. Gillis, N. M. Goncalves, L. A. Neely, S. R. Gullans and R. Gilmanshin, Nucleic Acids Res., 2005, 33, 5829–5837 CrossRef CAS.
- H. P. Babcock, R. E. Teixeira, J. S. Hur, E. S. G. Shaqfeh and S. Chu, Macromolecules, 2003, 36, 4544–4548 CrossRef CAS.
- G. C. Randall, K. M. Schultz and P. S. Doyle, Lab Chip, 2006, 6, 516–525 RSC.
- G. Yantz, R. Gilmanshin and J. W. Larson, Biophysical Society Conference Abstracts, Long Beach, CA, 2005, http://www.biophysics.org/abstracts, presentation number 3269-Pos Search PubMed.
- S. Manneville, P. Cluzel, J.-L. Viovy, D. Chatenay and F. Caron, Europhys. Lett., 1996, 36, 413–418 CrossRef CAS.
- T. T. Perkins, D. E. Smith, R. G. Larson and S. Chu, Science, 1995, 268, 83–87 CrossRef CAS.
Footnotes |
† 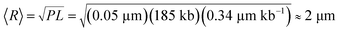 , where P
≈ 50 nm is the persistence length indicative of polymer stiffness,13 and L is the contour length calculated from the crystallographically determined axial rise per base pair.14,15 , where P
≈ 50 nm is the persistence length indicative of polymer stiffness,13 and L is the contour length calculated from the crystallographically determined axial rise per base pair.14,15 |
| ‡ For the purpose of roughly estimating the Weissenberg number, it is assumed that the velocity gradient is constant from the channel center to the chip surface. Of course, the velocity profile is parabolic in Poiseuille flow and smaller polymers can experience greater strain rates as they can diffuse more readily to the surfaces. |
| § The no-slip boundary condition retards the fluid rearrangement that accompanies polymer relaxation near surfaces.19,20 Relaxation in 2 µm high channels has been measured at 150 ms (scaled to the viscosity of water)21 as compared to 60 ms in the bulk phase.5 Therefore the relaxation in the 1 µm high channels used here can be expected to be even slower. |
| This journal is © The Royal Society of Chemistry 2006 |
