FTIR-monitoring of a fast setting brushite bone cement: effect of intermediate phases
Michael P.
Hofmann
*a,
Anne M.
Young
b,
Uwe
Gbureck
c,
Showan N.
Nazhat
b and
Jake E.
Barralet
d
aBiomaterials Unit, School of Dentistry, University of Birmingham, Birmingham, UK B4 6NN. E-mail: m.p.hofmann@bham.ac.uk
bDivision of Biomaterials and Tissue Engineering, UCL Eastman Dental Institute, 256 Gray's Inn Road, London, UK WC1X 8LD
cDepartment of Functional Materials in Medicine and Dentistry, University of Wurzburg, 97070 Wurzburg, Germany
dFaculty of Dentistry, McGill University, Montréal, Québec, Canada H3A 2B2
First published on 22nd June 2006
Abstract
The setting reaction of an equimolar β-tricalcium phosphate/monocalcium phosphate monohydrate (β-TCP/MCPM) cement was monitored in real time with ATR-FTIR at 23 and 37 °C using powder to liquid ratios (PLRs) of 2.0 and 3.3 g ml−1 and aqueous retardant citric acid concentrations of 800, 1000 and 1500 mM. The final set products, for PLRs of 2.0 to 3.3 g ml−1 and citric acid concentrations of 300 to 1500 mM, were characterised with regard to phase composition, compressive strength, density and relative porosity. FTIR provided evidence for the formation of an intermediate dicalcium phosphate–citrate complex (DCPC). As the concentration of citric acid in solution increased so did the maximum level of citrate intermediate. Decreasing the PLR reduced the rate of citrate removal, but had no effect on its rate of formation or maximum level. FTIR also indicated a time delay before formation of any observable dicalcium phosphate (DCP) in solution. This delay increased as the citric acid solution concentration was raised or the temperature reduced, but was less affected by the PLR. There was then an additional delay between DCP formation in solution and its precipitation. Both Rietveld analysis of XRD patterns and density measurements 24 h after setting confirmed that the final product was primarily dicalcium phosphate dihydrate (DCPD or brushite) when the citric acid concentration was less than 1000 mM, irrespective of temperature or PLR. On the other hand, with 1500 mM citric acid significant levels of dicalcium phosphate anhydrous (DCPA or monetite) also present, this led to increased porosity and a dramatic decline in strength. As the levels of the intermediate phase increased, the final wet compressive strength of the resulting cements also deteriorated. It is therefore proposed that strength reduction may be due to formation of the intermediate at early stages of setting or DCPA formation in the final product, both causing increased material inhomogeneity. This study thereby illustrates that real time ATR-FTIR monitoring of a setting reaction clearly indicates that there is an upper limit to the use of citric acid as a setting retardant for a fast setting brushite-forming cement system, a limit that can also be expected for the use of other setting retardants, and that ATR-FTIR monitoring comprises a useful complement to the traditional before–after investigations.
Introduction
Calcium phosphate cements (CPCs) are in widespread use as bone substitutes, and are set in aqueous conditions to form a solid structure.1–6 At cement slurry pH values of less than 4, brushite is formed which is degradable in vivo.7 Inherent disadvantages of brushite-forming systems, however, are very short setting times, accompanied by low mechanical strength.8 Setting times can be increased to workable lengths by the use of either a low powder to liquid ratio (PLR), leading to higher porosity and therefore lower strength, or a high setting retardant concentration in the cement paste.8–10Bohner et al. investigated the effect of sulfuric acid, sodium pyrophosphate and up to 0.1 M sodium citrate solutions as setting retardants in a one powder reactant β-tricalcium phosphate-liquid phase (phosphoric acid) on the performance of a brushite-forming cement system.8,11 It was found that increasing the retardant concentration led to an increased setting time and an improvement in mechanical strength due to the smaller precipitated crystals. In contrast, it has recently been shown that high concentrations (up to 1 M) of citric acid retardant in a brushite-forming β-tricalcium phosphate/monocalcium phosphate monohydrate (β-TCP/MCPM) system may lead to extended setting times and improved injectability and strength, but it was also indicated that very high retardant concentrations of 1 M might decrease mechanical strength.9 The addition of citric acid salt to the β-TCP/MCPM powder mixtures has also been proven to increase the shelf life of these bone cement mixtures up to one year by preventing the conversion of the reactants to dicalcium phosphate anhydrous (DCPA or monetite) which is known to decrease strength.11,12
The fast setting of any cement system provides a challenge when attempting to monitor the reaction kinetics. Mechanical methods of monitoring setting, e.g. the Gillmore needles technique, generally only measure the point in time when the cement paste hardens (initial setting time) or is almost completely set (final setting time) and are known to be subjective.13 User-independent techniques, such as ultrasonics14,15 and oscillating rheometry,16 have been used to monitor the setting times in CPCs, but require rather complex non standard experimental setups and evaluation techniques. Differential scanning calorimetry (DSC) has been used to monitor the setting of CPCs17 but it is intrinsically insensitive to non-endothermic and non-exothermic processes.
With the above techniques, however, the rates, types and extent of reactions occurring are only inferred. X-Ray powder diffraction (XRD) has been used to monitor the chemical setting kinetics of a brushite cement using a time series of quenched samples.18 Limits of quenching techniques, however, can include the long times between sampling points but this problem can be overcome through the use of continuous XRD monitoring.19 XRD, though, is mostly limited to crystalline component detection. It has recently been shown, however, that the fast setting reactions in dental restorative materials can be readily monitored using diamond ATR-FTIR. With this technique, spectral changes that are characteristic and proportional to the level of reaction taking place can be generated every few seconds from within ca. 30 s from the start of cement mixing. Using this method very small changes in absorbance due to reactions can be accurately measured, enabling different chemical processes occurring simultaneously to be monitored separately.20
In this study the use of ATR-FTIR has been extended to evaluate for the first time the effect of PLR and citric acid retardant concentration on the setting kinetics and the course of the setting reaction of a brushite-forming cement system on a time scale of seconds. The FTIR data are correlated with mechanical, density, and porosity data, and phase composition of the set cement.
Experimental
Materials
The reactants for the cement powder mixture were phase pure sintered β-TCP, prepared as described previously21 and monocalcium phosphate monohydrate (MCPM) powder (Rhodia, Birmingham, UK) with median particle sizes of 11 and 62 µm, respectively (as determined by laser diffraction particle sizing). β-TCP was prepared by sintering a 2 ∶ 1 molar mixture of DCPA (Mallinckrodt-Baker, Griesheim, Germany) and calcium carbonate (Merck, Darmstadt, Germany) at 1050 °C for 24 h. The β-TCP sinter cake was crushed in a mortar until it passed through a 355 µm sieve and afterwards was dry milled for 1 h in a planetary ball mill (PM400 Retsch, Haan, Germany) unidirectionally at 200 rpm in 500 ml agate jars with a load of 125 g β-TCP and four agate balls (30 mm).Equimolar amounts of the two cement powders were mixed in a vibrating unit prior to addition to the aqueous phase, which was a 300, 500, 800, 1000 or 1500 mM aqueous citric acid solution (Fisher, Loughborough, UK). To ensure homogeneous mixing of the paste, 500 mg of the powder mixture was mixed for 30 s with an amount of the aqueous phase, corresponding to powder to liquid ratios (PLRs) of 2.0, 2.5, and 3.3 g ml−1, in order to start the reaction. In the presence of water, the two phases reacted to form a brushite cement, according to eqn. (1)22
| β-Ca3(PO4)2 + Ca(H2PO4)2·H2O + 7H2O → 4CaHPO4·2H2O | (1) |
Compressive strength and density measurements
For compressive mechanical testing, the hand mixed slurries made with the different PLRs and citric acid concentrations were cast into a polytetrafluoroethylene mould to produce cylindrical samples with 12 mm height and 6 mm diameter. After 24 h immersion in water at 37 °C the wet compressive strength of the cement samples (n ≥ 6) was measured with a Universal testing machine (Instron 5544, High Wycombe Bucks, UK) at a crosshead speed of 1 mm min−1. To test the significance of the mean values a one-way ANOVA was performed on the raw data followed by a Tukey post hoc test with SPSS 10.0.0 for Windows (SPSS Inc, Chicago, USA).The strut densities of the dried cement samples were measured by helium pycnometry (Accupyc 1330, Micromeritics, Norcross, USA). These results and apparent wet and dry densities were used to calculate relative porosities.
Rietveld analysis of XRD patterns
X-Ray diffraction patterns of the set cements with a PLR of 3.3 g ml−1 were recorded on a D5005 diffractometer (Siemens, Karlsruhe, Germany). Data sets were collected from 2θ = 20–40° with a step size of 0.02° and the count time was normalised to 1 s/step. The phase composition was checked by means of ICDD reference patterns for β-TCP (PDF Ref. 09-0169), dicalcium phosphate dihydrate (DCPD) (PDF Ref. 09-0077), hydroxyapatite (HA) (PDF Ref. 09-0432) and DCPA (PDF Ref. 09-0080). The phase composition of partially set samples was calculated on the basis of XRD patterns by means of Rietveld analysis with TOPAS software (Bruker AXS, Karlsuhe, Germany).Kinetic investigations with FTIR
For kinetic investigations at time zero, equimolar mixtures of the powder reactants were hand-mixed for 30 s with 800, 1000 or 1500 mM citric acid solution at PLRs of 2.0 and 3.3 g ml−1 and placed on the diamond of an ATR-FTIR Perkin Elmer Series 2000 spectrometer temperature controlled at 37 °C (Perkin-Elmer Beaconsfield, UK with Timebase software). Additionally, studies were performed at 23 °C with 800 mM citric acid solution; spectra were obtained with a resolution of 4 cm−1, every 12 s from 60 s until spectral absorbance changes became minimal.To aid peak assignment, reference spectra of citric acid (sharp intense C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O peaks at 1752, 1719 and 1681 cm−1), calcium citrate (broad intense COO asymmetric stretch at 1554 cm−1 and symmetric stretch at 1397 cm−1), β-TCP (broad PO stretch at 1000 cm−1) and MCPM (sharp PO stretch peaks at 1075, 955 and 850 cm−1) were also generated. To identify the products, final spectra were compared with those of DCPA (monetite) and DCPD (brushite) from the literature.23,24 Both these dicalcium phosphates (DCPs) have four sharp distinctive PO/P–O(H) stretch peaks at comparable wavenumbers between 1150 and 870 cm−1, but whereas with DCPD all are strong, with DCPA the two between 870 and 1000 cm−1 are only of medium strength. Four sharp peaks between 3000 and 3600 cm−1 (OH stretches) and one around 1650 cm−1 (H2O bend) are also present in the spectrum of DCPD but not the anhydrous form, DCPA.23,24
O peaks at 1752, 1719 and 1681 cm−1), calcium citrate (broad intense COO asymmetric stretch at 1554 cm−1 and symmetric stretch at 1397 cm−1), β-TCP (broad PO stretch at 1000 cm−1) and MCPM (sharp PO stretch peaks at 1075, 955 and 850 cm−1) were also generated. To identify the products, final spectra were compared with those of DCPA (monetite) and DCPD (brushite) from the literature.23,24 Both these dicalcium phosphates (DCPs) have four sharp distinctive PO/P–O(H) stretch peaks at comparable wavenumbers between 1150 and 870 cm−1, but whereas with DCPD all are strong, with DCPA the two between 870 and 1000 cm−1 are only of medium strength. Four sharp peaks between 3000 and 3600 cm−1 (OH stretches) and one around 1650 cm−1 (H2O bend) are also present in the spectrum of DCPD but not the anhydrous form, DCPA.23,24
Generally, diamond ATR-FTIR spectra of liquids and solutions give reproducible absolute absorbance but those of solids vary with particle size and the pressure applied by the ATR unit. The spectrum of an “ideal” mixture or solution will be the sum of the spectra of all the pure components weighted by their volume fractions in contact with the ATR diamond. Since the technique only penetrates a few microns into the sample surface the absorbance from solid particles of several microns in a cement can be weak relative to the surrounding fluid phase, due to their low contact with the diamond. With cements that set on the diamond, provided they do not detach, the absolute absorbance of both the initial fluid and final solid spectra can be reproducible.20 With crystallising cements it should be noted, however, that the size and shape of the crystals (finer particles will have higher contact with the diamond) as well as the chemical composition may affect the absolute absorbance of the final spectrum.
Results
Compressive strengths and densities
The compressive strengths, strut densities, and porosities for set cement samples of the investigated PLR–citric acid concentration combinations are presented in Table 1. The results for low retardant concentrations could not be obtained for some PLRs, especially the highest ones, as the cement pastes set during mixing, preventing sample preparation and investigation. For a PLR of 3.3 g ml−1, however, with the lowest feasible citric acid concentrations (500 and 800 mM), the measured strengths of 23–24 MPa were significantly higher than for any other PLR (p < 0.01). For higher retardant concentrations, 500 and 800 mM at PLR 2.0 g ml−1 and 800 and 1000 mM at PLR 2.5 g ml−1, there was a significant deterioration in strength (p < 0.01) compared to the lowest retardant concentration at the same PLR. On raising the citric acid concentration to 1500 mM, however, a more dramatic deterioration in mechanical strength occurred for all PLRs.| PLR/g ml−1 | Citric acid concentration/mM | Compressive strength/MPa | Strut density/g cm−3 | Relative porosity (%) |
|---|---|---|---|---|
| 2.0 | 300 | 10.9 ± 1.1 | 2.35 ± 0.05 | 41 ± 1 |
| 500 | 6.4 ± 1.5 | 2.37 ± 0.05 | 41 ± 1 | |
| 800 | 6.2 ± 0.4 | 2.35 ± 0.05 | 43 ± 1 | |
| 1500 | 1.3 ± 0.1 | 2.50 ± 0.05 | 52 ± 1 | |
| 2.5 | 500 | 18.5 ± 2.4 | 2.36 ± 0.05 | 35 ± 1 |
| 800 | 9.8 ± 2.4 | 2.35 ± 0.05 | 36 ± 1 | |
| 1000 | 8.6 ± 0.9 | 2.34 ± 0.05 | 36 ± 1 | |
| 1500 | 2.9 ± 0.5 | 2.50 ± 0.05 | 48 ± 1 | |
| 3.3 | 500 | 23.5 ± 2.7 | 2.39 ± 0.05 | 26 ± 1 |
| 800 | 23.1 ± 1.2 | 2.37 ± 0.05 | 27 ± 1 | |
| 1000 | 17.2 ± 2.7 | 2.37 ± 0.05 | 30 ± 1 | |
| 1500 | 6.1 ± 0.9 | 2.49 ± 0.05 | 37 ± 1 |
The relative porosity of the set cement was at a maximum of 52% for a PLR of 2.0 g ml−1 and a citric acid concentration of 1500 mM, and at a minimum of 26% with a PLR of 3.3 g ml−1 and a citric acid concentration of 500 mM. Strut density had an average value of around 2.36 g cm−3 for citric acid concentrations of 1000 mM and lower, which increased to around 2.50 g cm−3 for citric acid concentrations of 1500 mM.
Phase identification by XRD
The phase composition of a completely set cement for a PLR of 3.3 g ml−1 did not change for retardant concentrations from 500 to 1000 mM. The DCPA (monetite) content was between 7 and 10% and the DCPD (brushite) content was between 90 and 93% (see Table 2). At a retardant concentration of 1500 mM however, the DCPA content increased dramatically to around 33% with only 67% brushite in the set cement. Unreacted MCPM and β-TCP were not detected in the cement at all retardant concentrations investigated (see Table 2).| Citric acid concentration/mM | Brushite (DCPD) (%) | Monetite (DCPA) (%) | β-TCP (%) | R wp factor (%) |
|---|---|---|---|---|
| 500 | 93 ± 1 | 7 ± 1 | <1 | 9.8 |
| 800 | 92 ± 1 | 7 ± 1 | <1 | 9.1 |
| 1000 | 90 ± 1 | 10 ± 1 | <1 | 10.4 |
| 1500 | 67 ± 1 | 33 ± 1 | <1 | 12.1 |
FTIR kinetic investigations: absorbance spectra
Time-dependent absorbance spectra for cements with a PLR of 3.3 g ml−1 and an 800 mM citric acid concentration at 37 °C are given in Fig. 1a. The early FTIR cement spectra were comparable with combined MCPM, β-TCP and water spectra, with the peaks stemming from citric acid being masked by the higher concentrations of the other components. With time, five sharp OH peaks associated with DCPD formation appeared as expected at 3550, 3465, 3255, 3160 (data not shown) and 1640 cm−1 on top of the broad “free” water bands. Additional sharp PO peaks developed at 1110, 1050, 980 and 860 cm−1, consistent with dicalcium phosphate (DCP) formation (either DCPD or DCPA) (see Fig. 1a). | ||
| Fig. 1 Development of FTIR spectra with time for cements at PLR of 3.3 g ml−1 at 37 °C, prepared with citric acid concentrations of (a) 800 mM and (b) 1500 mM. | ||
Examples of absorbance spectra for cements with a PLR of 3.3 g ml−1 and a 1500 mM citric acid concentration at 37 °C are given in Fig. 1b. In this case, there is initially limited change in the broad water bands around 3200 and 1640 cm−1 or the P–O(H) peak at 980 cm−1 despite a significant increase in intensity of the DCP peaks at 1110 and 1050 cm−1. Instead, additional peaks at 1555, 1410 and 1010 cm−1 appear (see Fig. 2b). Those peaks at 1555 and 1410 cm−1 are comparable in shape and position to the most intense peaks in the calcium citrate spectra, but that at 1010 cm−1 is in none of the reference spectra discussed above. The 1010 cm−1 peak is most likely, however, a PO stretch of an intermediate dicalcium phosphate–citrate (DCPC) complex stabilized in solution. After the initial period, the DCP peaks at 1110 and 1050 cm−1 reached their maximum values, but the 1555, 1410 and 1010 cm−1 intermediate peaks were then slowly replaced by the 980 cm−1 peak from the final product DCP (see Fig. 1b) and sharp DCPD OH peaks at 3530, 3465, 3255, 3160 and 1640 cm−1. These results suggest that the peak at 1050 cm−1 is due to both DCP dissolved in the aqueous phase and in any crystalline state, but that at 980 cm−1 only appears upon crystallization and is expected to correspond with the setting of the cement.
 | ||
| Fig. 2 Effect of time on difference spectra (calculated by subtraction of spectra at 100 s) for cements at 37 °C prepared using a PLR of 3.3 g ml−1 and citric acid concentrations of (a) 800 mM and (b) 1500 mM. | ||
Corresponding difference spectra for Fig. 1 obtained by subtracting the spectra at 100 s from those at later times are provided in Fig. 2. All difference spectra in Fig. 2a and that at the latest time in Fig. 2b exhibit comparable profiles as expected if the same overall process is occurring. Those at intermediate times and higher citric acid concentrations, however, vary with time (see Fig. 2b)
On reducing the PLR from 3.3 to 2.0 g ml−1, whilst keeping citric acid concentrations constant, spectral changes were largely similar to those discussed above. On reducing the temperature, the major effect was on the reaction rates. Effects of PLR and temperature are compared in more detail below, using absorbance profiles at 1050 and 980 cm−1 where the greatest absorbance change occurs during reaction, and also at 1555 cm−1 where changes are due only to the formation or loss of the citrate which forms intermediately. Absorbance changes at 1050 and 980 cm−1 will provide an indication of the relative rates of formation and crystallization of DCP, respectively.
FTIR kinetic investigations: absorbance profiles
After a delay period, the absorbances at 1050 and 980 cm−1 increase to a maximum final value, whereas at 1555 cm−1 it increases to a peak value before declining towards its original level (see Fig. 3). The maximum absorbance change, ΔAmax, at each wavenumber is provided in Fig. 4a for all samples investigated. Comparing values provides an indication of the relative maximum concentrations of products and intermediates in contact with the FTIR diamond. From repeat measurements the standard deviation was found to be around 10%.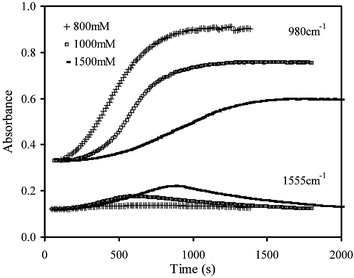 | ||
| Fig. 3 Absorbance profiles at 980 and 1555 cm−1 for cements prepared using 800, 1000 and 1500 mM citric acid concentrations at 37 °C with a PLR of 3.3 g ml−1. | ||
 | ||
| Fig. 4 Effect of citric acid concentration, PLR and temperature at different wavenumbers on (a) maximum absorbance change ΔAmax, (b) time to half maximum absorbance change, t1/2 and (c) the apparent rate constant ΔAmax/t1/2. | ||
At 1050 cm−1, ΔAmax was observed to decline by average factors of 0.8 and 0.7 when reducing PLR or raising citric acid concentration from 800 to 1500 mM respectively, but was less affected by temperature (see Fig. 4a) as the effect of temperature was within the errors of the experiment. The ΔAmax value is expected to be proportional to the maximum concentration of DCP (both in solution and in crystallized form) that comes into contact with the FTIR diamond. A reduction in ΔAmax at 1050 cm−1 could therefore be due either to less complete reaction or to the formation of a different product with either poorer contact with the FTIR diamond or weaker absorbance at this wavenumber.
The ratio of ΔAmax at 980 cm−1 to that at 1050 cm−1 also decreased by, on average, by a further factor of 0.7 upon either reducing the PLR or raising the citric acid level, but the temperature change had no observable effect as experimental error variations with temperature were not significant. A reduction in this ratio is expected if, at equilibrium, a higher fraction of the DCP remains stabilized in solution, or if the final product contains a higher level of DCPA relative to DCPD, since the former has a weaker peak at 980 cm−1.
The ΔAmax at 1555 cm−1 was too small to be determined at 23 °C, and on average was not significantly affected by PLR at 37 °C. It did, however, increase by an average factor of 3.0 when raising the citric acid concentration from 800 to 1500 mM (see Fig. 4a), indicating that higher maximum levels of citrate are formed in solution.
To compare the rates of intermediate and product formation, the normalised absorbance change ζ was calculated using
 | (2) |
where A0 and At represent the absorbance at the initial time and time t. The time of half maximum absorbance change, t1/2, for all samples is given in Fig. 4b. When ζ is plotted against the normalised time, t divided by t1/2, all curves overlap up to ζ = 0.8 irrespective of time, citric acid concentration (Fig. 5a), wavenumber or PLR (Fig. 5b), and even temperature. Beyond ζ = 0.8, ζ values at 980, 1050 and 1555 cm−1 all tend to unity as the normalised time t/t1/2 approaches 1.5, whereas after this time ζ remains largely constant at 980 and 1050 cm−1, but at 1555 cm−1 it declines at a rate that increases with the raised citric acid concentration or PLR (see Fig. 5b).
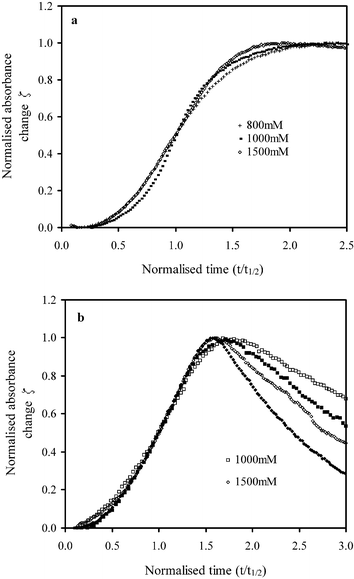 | ||
| Fig. 5 Normalised absorbance profiles at 37 °C at a wavenumber of (a) 980 cm−1 for cements with 800 mM citric acid and PLR of 3.3 g ml−1 and (b) 1555 cm−1 for cements prepared using 1000 and 1500 mM citric acid with PLR of 2.0 g ml−1 (□, ◇) or 3.3 g ml−1 (■, ◆). | ||
For 0.2 < ζ < 0.6 the normalised curves could all be fitted by an expression of the form
 | (3) |
Eqn. (3) indicates a time delay of 0.4t1/2 before formation of detectable levels of either intermediates or products. The t1/2 values in Fig. 4b show that delay times at 37 °C and 1555 cm−1 (dependent upon citrate formation) are on average only slightly shorter than those at 1050 cm−1 (due to DCP formation) but much smaller than those at 980 cm−1 (arising with DCP crystallization). Also t1/2 was not noticably affected by the PLR, but increased by an average factor of 1.7 on raising citric acid concentration from 800 to 1500 mM at all wavenumbers. At 23 °C with 800 mM citric acid it was difficult to assess t1/2 at 1555 cm−1, but at both 1050 and 980 cm−1t1/2 is more than doubled with lowering the temperature from 37 to 23 °C.
Combining eqn. (2) with the differential of eqn. (3) provides an equation that is proportional to the reaction rate after the delay period
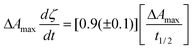 | (4) |
In this expression ΔAmax/t1/2 can be taken as an apparent rate constant and is provided in Fig. 4c. This apparent rate constant for the 1050 cm−1 peak decreased on average by factors of 0.8, 0.5 and 0.5 on reducing the PLR, raising the citric acid concentration from 800 to 1500 mM, or reducing the temperature from 37 to 23 °C, respectively. Corresponding average factors for the 980 cm−1 peak were 0.6 (reducing PLR), 0.3 (raising citric acid concentration) and 0.5 (reducing temperature). Neither PLR nor citric acid concentration, however, had a significant effect on the average rate constant for the intermediate 1555 cm−1 peak (see Fig. 4c). Greater maximum build up of the citrate concentration on raising the citric acid concentration is therefore not due to faster formation of citrate, but its slower conversion back to citric acid.
Discussion
Mechanical and density studies
It has been shown in several studies that the compressive strength of cement is connected to porosity and flaw size.25–27 The wet compressive strengths of the cement in this study were reduced significantly with lower PLRs and/or at high citric acid concentrations. This deterioration could not, however, be entirely explained by increasing porosity as changes in density with citric acid concentration variation were relatively minor for 500 to 1000 mM citric acid (see Table 1). Conversely, between 1000 and 1500 mM citric acid the porosity of the set cement increased dramatically, e.g. from 30 to 37% for a PLR of 3.3 g ml−1, see Table 1.Several XRD studies on slow setting hydroxyapatite-forming calcium phosphate cements have also shown that the final mechanical strength is directly correlated with the degree of reaction.28,29 Set cement densities attained by helium pycnometry in this study (Table 1) were typical of brushite (ρ ≈ 2.3 g cm−3) for all PLRs and citric acid concentrations from 500 to 1000 mM and quite different from the original cement powder mixture density (ρ = 2.71 g cm−3). This indicated a consistently high degree of conversion of the reactants for all PLR–citric acid concentration combinations and also excluded an extensive generation of DCPA (monetite, ρ ≈ 2.9 g cm−3), the only other crystalline calcium phosphate with a calcium to phosphate ratio of 1. At a citric acid concentration of 1500 mM, however, the strut density of set cements increased to around 2.5 g cm−3.
XRD studies
The quantitative Rietveld analysis of XRD patterns for a PLR of 3.3 g cm−3 confirmed that, for 500 to 1000 mM, the DCPA content was around 7–10%, with the rest being brushite which is consistent with earlier findings of our group where the brushite content of this cement system using citric acid as a retardant was found to be over 95%.9 For 1500 mM citric acid and a PLR of 3.3 g cm−3 the DCPA content in the set cement jumped to 33%. The latter finding is in accordance with the findings of Bohner et al. where the deterioration in strength of a brushite cement was explained by the presence of DCPA in the final product.11 The high DCPA content in the set cement can also explain the significant increase in relative porosity at 1500 mM citric acid, see Table 1. As more DCPA was formed, less water was consumed in the setting reaction to form brushite, see eqn. (1), and therefore more residual water was present, generating porosity and thus leading to the dramatic deterioration in strength at 1500 mM for all PLRs. The deterioration in strength at 800 and 1000 mM, most noticeably at PLRs of 2.0 and 2.5 g ml−1, where DCPA content and resulting relative porosity in the set samples were similar, could not, however, be explained by radically increased DCPA content in the final product.FTIR studies
The observation of various isosbestic points (no absorbance change with time) and identical FTIR difference spectra for the 800 mM citric acid cements at PLRs of 3.3 g ml−1 irrespective of time suggests that any reactive intermediates that may be formed are quickly converted to the final products. The peak positions are consistent in both position and relative intensity with that of pure brushite (DCPD),23,24,30 and therefore in agreement with XRD and density studies after 24 h. The low absorbance of the PO peaks of the reactant particles relative to those of the products could be, in part, due to their initially larger size that limits contact with the flat ATR-FTIR diamond. It is known that the presence of even small citric acid concentrations during brushite precipitation makes brushite crystals smaller and rounder, i.e. less blade-like.8 Due to the limited range of citric acid concentrations in this study it is considered unlikely that changes in crystallite size or orientation with cement paste composition are causing the variations in maximum absorbance levels.On raising the citric acid concentration, the difference spectra changed due to the formation of increasing levels of reactive intermediates. The observation of peaks at 1555 and 1410 cm−1 are consistent with the formation of CO2− symmetric and asymmetric stretching peaks of calcium citrate intermediates. The appearance of these at the same time as other sharp peaks at 1110, 1050 and 1010 cm−1, but none initially at 980, 1640 or 3300 cm−1, suggests a DCPC. The high level of absorbance change with intermediate formation suggests that the DCPC is likely to be well dispersed throughout the aqueous phase, rather than on the original particles (which can make only limited contact with the ATR diamond due to their size of 10–60 µm).
On raising the citric acid concentration, both ΔAmax at 1050 cm−1 and the ratio of ΔAmax values at 980 cm−1 divided by those at 1050 cm−1 decline (Fig. 4a). Comparison with the XRD and porosity data indicate this to be due to greater formation of DCPA compared with DCPD. The reduction in ΔAmax at 1050 cm−1 upon lowering the PLR, however, is more likely to be due to changes in cement porosity. From the cement porosities (see Table 1), the ratio of the final volume occupied by the solid at PLR 2.0 g ml−1 divided by that at 3.3 g ml−1 for a given citric acid concentration was on average 0.8. This was equal to the average level of reduction in ΔAmax at 1050 cm−1 observed upon lowering the PLR. Since greater DCPA formation is not expected from XRD and density investigations, the decline in the ΔAmax value at 980 cm−1 divided by that at 1050 cm−1 with reduction in PLR may be due to higher levels of DCPC being stabilised in solution at equilibrium.
From ΔAmax at 1555 cm−1 (Fig. 4a) it can be seen that the maximum level of citrate formed increased with citric acid concentration, but not significantly with the PLR. This citrate was converted back to citric acid more slowly if the PLR was lower (see Fig. 5b). It is therefore thought possible that on storing the cement samples in water for 24 h (after which compressive strength measurements were performed and the fragments dried) the citric acid might have slowly diffused out of the cement, thereby allowing greater conversion of previously solution stabilised DCP to precipitate into DCPD and thus leading to a more inhomogeneous and therefore weaker structure. This would then explain the strength deterioration at 800 and 1000 mM citric acid concentrations, despite the 24 h DCPA content being as low as in samples made with 500 mM citric acid (see Table 2).
It is thought possible that citric acid may be interacting with the surface of the β-TCP particles, thereby delaying their dissolution and DCP formation in solution. This could then explain the rise in the delay time and t1/2 at 1050 cm−1 with increasing citric acid concentration. The value of t1/2 at 980 cm−1 is expected to be related to the delay time before the cement begins to crystallize and set. Smaller values of t1/2 at 1050 compared with 980 cm−1, particularly at high citric acid concentrations, suggest a further delay between formation of DCP in solution and its precipitation. This might be explained if the citrate is additionally complexed with, and is stabilizing, the DCP in solution.
The levels of reduction in the apparent rate constant at 1050 and 980 cm−1 with both increase in citric acid concentration (by a factor of 1.9) and reduction in the PLR suggest that formation of DCPC and DCPD are approximately inversely proportional to the citric acid concentration and to the square of the citric acid concentration, respectively. This provides further evidence that the initial formation of DCP is inhibited by citric acid, but then precipitation is further inhibited by DCP association with the citrate in solution. The apparent rate constants for the 1555 cm−1 peak further demonstrate that raised levels of citrate in the cements with increased citric acid concentration or reduced PLRs are due to slower removal of the citrate in solution rather than faster initial formation. Finally, a reduction in temperature largely affects only the rate of reaction, not the final product or maximum levels of citrate intermediate.
Conclusions
The study presented shows that in a brushite-forming β-TCP/MCPM system with citric acid as a setting retardant, mechanical strength deteriorated on raising the citric acid concentration. ATR-FTIR spectroscopy indicated that, as the citric acid concentration was raised, increasing levels of an intermediate DCP complex are formed, which increased a time delay before any DCP precipitation. Kinetic analysis of the FTIR data also suggested that citric acid may additionally interact with the β-TCP particles, thereby slowing the formation of the DCP complex in solution. These results provide evidence for alternative mechanisms of setting retardation in addition to the suggestion that retardation by citric acid is due to its ability to chelate calcium ions.31 Reducing the temperature from 37 to 23°C led to a slightly larger increase in the time delay before DCP precipitation than raising citric acid concentration from 800 to 1500mM, but altering PLR had little effect. Increasing the citric acid concentration was the only factor found to noticeably raise the maximum level of citrate intermediate but reducing the PLR did decrease its rate of removal. FTIR also provided evidence that with raised citric acid concentrations some DCPA could precipitate instead of DCPD. From XRD and density measurements after 24 h, only samples with high citric acid concentrations (1500 mM) had significant levels of DCPA. The study suggests that the presence of DCPA in the final set cement reduces the material strength by raising porosity. Significant citrate formation as an intermediate is also thought to reduce strength by increasing cement inhomogeneity.This study thereby clarified two things: (a) there is an upper limit to the use of citric acid as a setting retardant for a fast setting cement, a limit that can also be expected for the use of other setting retardants, and (b) real time ATR-FTIR monitoring of a setting reaction comprises a useful complement to the traditional before–after investigations.
Acknowledgements
We acknowledge the financial support of the EU by the FP 6 Mobility 5 Marie Curie Fellowship 500694 (M. P. H.).References
- M. Bohner, Injury, 2000, 31, 37–47.
- M. Bohner, F. Theiss, D. Apelt, W. Hirsiger, R. Houriet, G. Rizzoli, E. Gnos, C. Frei, J. A. Auer and B. von Reichenberg, Biomaterials, 2003, 24, 3463–3474 CrossRef CAS.
- C. D. Friedman, P. D. Constantino, S. Takagi and L. C. Chow, J. Biomed. Mater. Res., 1998, 43, 428–432 CrossRef CAS.
- D. Knaack, M. E. P. Goad, M. Aiolova, C. Rey, A. Tofighi, P. Chakravarthy and D. D. Lee, J. Biomed. Mater. Res., 1998, 43, 399–409 CrossRef CAS.
- U. Gbureck, J. E. Barralet, K. Spatz, L. M. Grover and R. Thull, Biomaterials, 2004, 25, 2187–2195 CrossRef CAS.
- D. Apelt, F. Theiss, A. O. El-Warrak, K. Zlinszky, R. Bettschart-Wolfisberger, M. Bohner, S. Matter, J. A. Auer and B. von Rechenberg, Biomaterials, 2004, 25, 1439–1451 CrossRef CAS.
- A. A. Mirtchi, J. Lemaitre and N. Terao, Biomaterials, 1989, 10, 475–480 CrossRef CAS.
- M. Bohner, J. Lemaitre and T. A. Ring, J. Am. Ceram. Soc., 1996, 79, 1427–1434 CrossRef CAS.
- J. E. Barralet, L. M. Grover and U. Gbureck, Biomaterials, 2004, 25, 2197–2203 CrossRef CAS.
- C. Pittet and J. Lemaître, J. Biomed. Mater. Res. A, 2000, 53, 769–780 Search PubMed.
- M. Bohner, H. P. Merkle, P. van Landuyt, G. Trophardy and J. Lemaitre, J. Mater. Sci., 2000, 11, 111–116 CrossRef CAS.
- U. Gbureck, S. Dembski, R. Thull and J. E. Barralet, Biomaterials, 2005, 26, 3691–3697 CrossRef CAS.
- ASTM C 266-99, ASTM International, 2002 Search PubMed.
- A. M. Viano, J. A. Auwarter, J. Y. Rho and B. K. Hoffmeister, J. Biomed. Mater. Res., 2001, 56, 593–599 CrossRef CAS.
- J. Carlson, M. Nilson, E. Fernandez and J. A. Planell, Biomaterials, 2003, 24, 71–77 CrossRef CAS.
- G. J. P. Fleming, A. A. Farooq and J. E. Barralet, Biomaterials, 2003, 24, 4173–4179 CrossRef CAS.
- M. P. Hofmann, S. N. Nazhat, U. Gbureck and J. E. Barralet, J. Biomed. Mater. Res., Part B, 2006 DOI:10.1002/jbm.b.30550.
- M. P. Ginebra, F. C. M. Driessens and J. A. Planell, Biomaterials, 2004, 25, 3453–3462 CrossRef CAS.
- L. M. Grover, U. Gbureck, A. M. Young, A. J. Wright and J. E. Barralet, J. Mater. Chem., 2005, 15, 4955–4962 RSC.
- A. M. Young, S. A. Rafeeka and J. A. Howlett, Biomaterials, 2004, 25, 823–833 CrossRef CAS.
- U. Gbureck, O. Grolms, J. E. Barralet, L. M. Grover and R. Thull, Biomaterials, 2003, 24, 4123–4131 CrossRef CAS.
- J. Lemaitre, A. Mirtchi and A. Mortier, Silic. Ind., 1987, 9–10, 141–146 Search PubMed.
- J. Xu, I. S. Butler and D. F. R. Gilson, Spectrochim. Acta, Part A, 1999, 55, 2801–2809 CrossRef.
- L. Tortet, J. R. Gavarri, G. Nihoul and A. J. Dianoux, J. Solid State Chem., 1997, 132, 6–16 CrossRef CAS.
- K. Ishikawa and K. Asaoka, J. Biomed. Mater. Res., 1995, 29, 1537–1543 CrossRef CAS.
- J. E. Barralet, M. Hofmann, L. M. Grover and U. Gbureck, Adv. Mater., 2003, 15, 2091–2094 CrossRef CAS.
- T. Takahashi, M. Yamamoto, K. Ioku and S. Goto, Adv. Cem. Res., 1997, 9, 25–30 Search PubMed.
- S. Sarda, E. Fernandez, M. Nilsson, M. Balcells and J. A. Planell, J. Biomed. Mater. Res., 2002, 61, 653–659 CrossRef CAS.
- E. Fernandez, M. P. Ginebra, M. G. Boltong, F. C. M. Driessens, J. Ginebra, E. A. P. de Maeyer, R. M. H. Verbeeck and J. A. Planell, J. Biomed. Mater. Res., 1996, 32, 367–374 CrossRef CAS.
- S. M. Arifuzzaman and S. Rohani, J. Cryst. Growth, 2004, 267, 624–634 CrossRef CAS.
- K. S. Tenhuisen and P. W. Brown, J. Mater. Sci.: Mater. Med., 1994, 5, 291–298 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2006 |
