Thermal gating of the single molecule conductance of alkanedithiols

Abstract

The temperature dependence of the single molecule conductance (SMC) of α,ω-alkanedithiols has been investigated using a scanning tunnelling microscopy (STM) method. This is based on trapping molecules between a gold STM tip and a gold substrate and measuring directly the current across the molecule under different applied potentials. A pronounced temperature dependence of the conductance, which scales logarithmically with T⁻¹, is observed in the temperature range between 293 and 353 K. It is proposed that the origin of this dependence is the change in distribution between molecular conformers rather than changes in either the conduction mechanism or the electronic structure of the molecule. For alkanedithiols the time averaged conformer distribution shifts to less elongated conformers at higher temperatures thus giving rise to higher conductance across the molecular bridges. This is analysed by first calculating energy differences between different conformers and then calculating their partition distribution. A simple tunnelling model is then used to calculate the temperature dependent conductance based on the conformer distribution. These findings demonstrate that charge transport through single organic molecules at ambient temperatures is a subtle and highly dynamic process that cannot be described by analysing only one molecular conformation corresponding to the lowest energy geometry of the molecule.

---

1. Introduction

The temperature dependence of the electrical properties of solids is understood in most instances in some detail. The same level of understanding has not been achieved yet for molecular devices and although there has been a substantial theoretical effort^1–3 it has only been recently possible to measure thermal effects in molecular junctions down to the single molecule level. In a recent publication, Selzer et al.⁴ have shown that it is possible to measure the temperature dependence of the current-voltage (I–V) response of a single molecule immobilised in a break junction. It was shown that electron transport in a “molecular wire’, characterised by a conjugated π system and having a relatively rigid-rod structure, could be switched from coherent superexchange tunnelling at low temperatures to incoherent temperature dependent hopping at higher temperatures.⁴ However, other important contributions to the temperature dependence of single molecule conductance such as molecular conformation have been generally neglected in the past, and this forms the motivation for the current manuscript. We show that thermal effects are highly significant at ambient temperatures and as such they would need to be considered in the design of future nano-electronic devices based on molecular electronics.

It has been previously shown that electrochemically gated electron transport across redox active molecules can be investigated in nanoscale structures^5–8 and that these measurements can be carried out for single molecules.^9–12 In the present work, it is shown that temperature can have a gating action in charge transfer across molecules through control of the molecular conformation. This has been investigated by measuring the temperature dependence of the molecular conductance for conformationally non-rigid alkanedithiol molecules. The observed behaviour is analysed in terms of the distribution of molecular conformers. The understanding of the effect of molecular conformation on the electrical characteristics of single molecules is of great importance in the emerging field of unimolecular electronics. As pointed out by Troisi and Ratner,^13,14 control of molecular conformation at the metal-molecule interface offers possibilities to realise molecular rectifiers through, for instance, electrical field or current driven switching between conformers. For instance, Donhauser et al.¹⁵ have observed conductance switching through thermal fluctuations at the single molecule level, while Gaudioso and Ho¹⁶ have demonstrated that in an STM, tunnelling electrons can be used to excite vibrations.

In order to analyse ambient temperature effects on single molecule conductance we have recorded and analyzed data over the temperature range between 293 and 353 K. The present work demonstrates the importance of conformational effects on molecular conductance in this temperature range and attempts to quantify these effects through single molecule measurements. We show that thermal effects are very significant at ambient temperatures and can be described in terms of the temperature dependence of conformer distribution and a tunnelling barrier model.

2. Methods

Several approaches have been described in the literature for measuring transport through either single or small groups of molecules, including mechanically formed break junctions,^17–20 break junctions formed by electromigration methods²¹ and a variety of scanning probe microscopy techniques based on either STM^22–24 or conducting AFM.^25,26 In this work an STM method recently described, based on trapping molecules between a gold STM tip and a gold substrate, has been used.⁹ Electrical contact between the target molecule and the gold probes was achieved by the use of thiol groups present at either end of an α,ω-alkanedithiol molecule. The spontaneous attachment and detachment of molecular wires was easily monitored by recording the tunnelling current as a function of time with the STM feedback loop disabled, the so called “I(t) method”.⁹ A Pico2000 system (Molecular Imaging) STM using the PicoScan 4.19 software was used for these measurements. The relevant tunnelling parameters are the tip potential (U_t) and the setpoint current (I₀). Following disengagement of the feedback loop the current jumps (I − I₀, I = tunnelling current) resulting from the spontaneous attachment and detachment of molecules between the tip and the substrate were recorded. The current jumps were then analysed as histograms in order to distinguish between single and multiple molecule attachment or detachment events. The conductance of the molecule in the gap was calculated from these characteristic histograms.

Gold films employed as substrates were prepared by the evaporation of 2 nm of chromium followed by 200 nm of gold onto Tempax® glass (Berliner Glas KG) under high vacuum. These were flame-annealed at approximately 800–1000 °C with a Bunsen burner immediately prior to use; a procedure that is known to result in atomically flat Au(111) terraces.²⁷

The I(t) method requires the attachment of the target molecule on the substrate at low coverage. This was achieved by immersion of the gold films in 0.05 mM methanolic solutions of the α,ω-alkanedithiols (Aldrich, reagent grade) for 15 s. After adsorption, the samples were thoroughly washed in ethanol and blown dry with nitrogen. It has been previously shown that such low exposures favour a flat-lying adsorbate orientation from which it is possible to form a molecular bridge between tip and substrate.^9,10 The Au tips were carefully flame-annealed prior to the experiments to remove any organic contamination. Measurements were carried out in air between 293 and 353 K.

The gold on glass samples were mounted on a metal plate that was heated with a variable temperature resistive heating source. The temperature was measured with two thermocouples simultaneously, one placed directly on the heating stage and the other pressed on top of the sample with a rubber seal ring. The thermocouples were calibrated with a precision thermometer.

Theoretical analyses in Section 4 were performed with SPARTAN PRO©. A MMFF basis set was used for the molecular modelling whereas a 6-31G* basis set was used for the Hartree–Fock calculations. The starting point for the H–F calculations for the alkanedithiols was the generation of the corresponding alkane conformers using molecular mechanics (e.g. HS-C₆H₁₂-SH was represented by C₈H₁₈). The outermost CH₃ groups were then replaced by S–H groups assuming a linear C–S–H geometry.

Structure optimisation at this level of theory for all possible conformers was outside the possibility of the computation facility available and for this reason single point energy calculations were then carried out after energy minimisation by freezing the symmetry of each conformer. The energies thus obtained were used to calculate the corresponding partition functions describing conformer distribution. Spatial and electronic boundary conditions imposed by the enclosing substrate and tip electrodes were not included in these computations. Focus is thus on the conductance properties of the molecules themselves.

3. Results

Fig. 1a shows a typical example of a current jump (current step = I_w) for 1,8-octanedithiol (ODT) on Au(111) at 65 °C obtained with the I(t) technique.⁹ The downwards current jump corresponds to a detachment event. These events were statistically analysed as histogram plots (Fig. 1b). The shape of the histograms obtained at 65 °C (Fig. 1b) was similar to those obtained at room temperature and allowed the determination of the molecular conductance (σ_M) with a standard deviation of 10 to 20%. The current jumps were not dependent on the tunnelling current for I₀ > I_w (see Fig. 1c) and I_w (height of the current jump) scaled linearly with the applied voltage for measurements at 0.2, 0.3 and 0.4 V. The behaviour of the system was very similar to that previously observed for room temperature measurements.⁹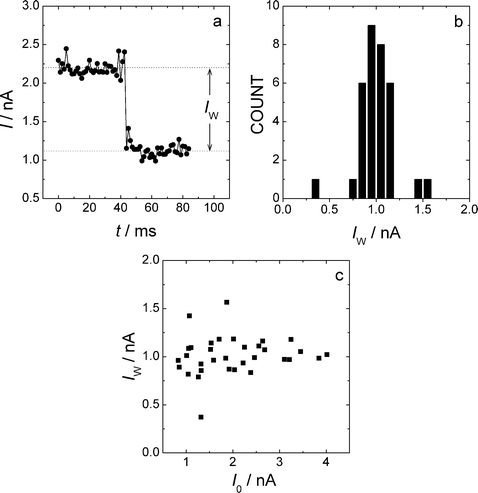

Fig. 1 I(t) measurements at elevated temperatures; 1,8-octanedithiol, 65 °C, U_t = +0.2 V. (a) Typical current jump (height = I_w); (b) Histogram of I(t) current jumps. (c) Plot of the jump height as a function of set-point current I₀.

A pronounced increase of conductance at elevated temperatures was found for all the alkanedithiols studied. For example, the conductance of nonanedithiol (NDT) increased from (0.52 ± 0.09) nS at 20 °C to (2.90 ± 0.37) nS at 67 °C. The logarithm of σ_M is linearly dependent on the inverse absolute temperature as can be clearly seen in Fig. 2. This Figure also shows that the temperature dependence of σ_M decreases with the length of the molecule. The slopes of the linear fits in Fig. 2 will formally be referred to here as a thermal gating activation energy (E_g) although this quantity does not represent an energy barrier that electrons have to overcome during their transport through the molecule. This assertion will be justified later in the manuscript where it is shown that the thermal gating effect is related to the temperature dependent distribution of conformers.

Fig. 2 Logarithmic plot of the single molecule conductance of several alkanedithiols as a function of the inverse temperature (T range: 20–70 °C); dashed lines are linear fits; NDT: 1,9-nonanedithiol, slope: −(3533 ± 71) K; ODT = 1,8-octanedithiol, slope: −(3271 ± 118) K; HDT = 1,6-hexanedithiol, slope: −(2325 ± 104) K; PDT = 1,5-pentanedithiol, slope: −(1774 ± 6) K; measurements were taken in air at U_t = +0.2 and +0.4 V; error bars = ±sd.

The dependence of E_g on the number of C–C bonds in the alkanedithiol molecule is shown in Fig. 3. An almost linear relation is found from which E_g per C–C bond can be determined, E_C−C = (39 ± 2) meV. It is remarkable that the linear fit in Fig. 3 intercepts the y-axis very close to zero (intercept = 0.04 ± 0.08). E_g scales directly with the number of C–C bonds and it is suggested that this is a consequence of the number of conformer-creating bonds.

Fig. 3 Dependence of E_g (in meV) on the number of C–C bonds in the molecule; error bars = ±sd. Note that the linear fit (dotted line) crosses the y-axes close to 0.

Further evidence for the participation of different conformers in the charge transport through alkanedithiols was obtained from conductance measurements performed at large tip-sample separations (i.e. small tunnelling currents). This was achieved by altering the set point current I₀. Larger values of I₀ result in a smaller tip-sample separation. It was expected that only at relatively short tip-sample separations all the conformers would contribute to the observed current. Fig. 4 shows the dependence of the current jump values for pentanedithiol (PDT) on I₀. If I₀ is smaller than a critical current (I_c), that is to say the tip-sample separation (s) exceeds a critical distance (s_c), the value of the current jumps is significantly reduced, probably because for s > s_c, not all the conformers can bridge the tunnelling gap. Importantly, as will be discussed further on, the short conformers that would be expected to exhibit a large conductance cannot contribute to the measured current. In contrast, for s < s_c, the current jumps showed little dependence on I₀ for values up to 30 times that of I_w. It is proposed, therefore, that for s < s_c the different conformers of a molecule present in the gap can establish chemical contact across the two contacts and therefore, all conformers can contribute to I_w for this condition. It has been previously shown that only molecules establishing chemical contact between the metal probes contribute significantly to the observed current.²⁵

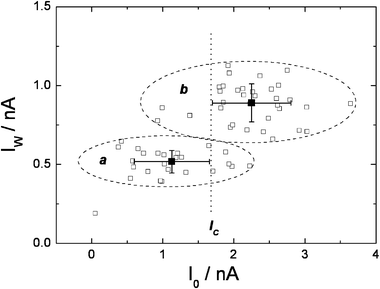Fig. 4 Dependence of the current jumps in the I(t) spectra of 1,5-pentanedithiol, on the set-point tunnelling current (I₀); T = 24 °C; U_t = +0.2 V; group a: I_w = (518 ± 71) pA at I₀ = (1127 ± 529); group b: I_w = (890 ± 120) pA at I₀ = (2250 ± 553) pA.

4. Theoretical aspects of the temperature dependence of single molecule conductance

The temperature dependence of the conformer distribution and its influence on electron transport through molecules will be discussed first for pentane as a simple example to describe the computational strategy. Fig. 5 shows ball and stick models of the four energetically different conformers of pentane. These structures correspond to energy minima obtained from a molecular modelling calculation. It is assumed that tunnelling occurs across a barrier the width of which is related to the distance between the terminal groups. In this approximation temperature affects tunnelling through the temperature dependent distribution of conformers. However, the tunnelling probability will also depend on conformation through changes with temperature of the energy of the HOMO and LUMO. This question is discussed further on.

Fig. 5 Ball and stick models of four energetically different pentane conformers; numbering from 1 (all trans) to 4 (all gauche) as in Tables 1 and 2. The lower diagram shows the effective barrier model, where the conformers are replaced by a medium with the barrier width (s_x) being determined by the length of the conformer (the distance between C₁ and C₅ in this case).

In what follows, a qualitative discussion of these contributions is presented. Alkanethiols do not have a low lying LUMO that can be temporarily populated or depopulated by electron transfer and therefore, the temperature dependence of the single-molecule conductance cannot originate from multiphonon electron transfer steps such as those observed for single-molecule electronic conductance where low-lying redox centres are involved as electronic relays. Sequential electron transfer through localized redox centres operates in the STM tunnelling mechanism of the viologen-based redox bridge molecule studied recently.^7–11 The redox transmitter group used in that work was linked to the substrate and tip electrodes by thiol-linker groups similar to those addressed here. Bridge group molecules based on transition metal complexes are other systems which also exploit redox transmitter groups.^28,29

The temperature dependence of tunnelling through a polymethylene chain can be regarded as an example of “gated” electron tunnelling through the alkanedithiol molecules (“gated” in this context means regulating the flow of current across the molecular wire by changing the temperature and hence, by controlling the population of different molecular conformations). This implies that a nuclear equilibrium configuration of minimum energy exists alongside a distribution of other configurations at thermally accessible energies. Tunnelling through the minimum energy configuration is feasible but it is unfavourable compared to higher energy conformations, which can offer more facile tunnelling routes due to lower effective barrier widths. An increase in temperature would result in a change in population of molecules with different tunnelling properties. Thus, thermal activation of the nuclear conformational system prior to electron tunnelling would lead to more facile electron tunnelling than tunnelling through the lowest energy conformer. Gated electron tunnelling is therefore most likely to involve thermal activation of the conformer distribution and the observed apparent activation energy would reflect this pre-organisation. In this model, the apparent activation energy observed is then a consequence of the changes in the distribution of the structural identity of the molecules involved in tunnelling.

The influence of temperature on molecular dimensions is discussed in what follows. For the purposes of illustration the conformers of pentane shown in Fig. 5 are discussed. Conformer 1 in Fig. 5 is the all trans form with the largest separation between terminal groups, while conformer 4 is the most folded with the smallest separation between terminal groups. For the purposes of our calculations we make the simplest approximation that the barrier width for tunnelling between the terminal groups is related to the separation between the two terminal groups. Hence, our approximation is that conformer 1 will have the largest barrier width, while conformer 4 has the smallest. It is proposed to the first approximation that the conductance scales with the barrier width according to a simple 1-D tunnelling barrier model (see below). Using this assumption each conformer is replaced by a barrier of effective width s_x (where x refers to conformer x), while the other barrier properties such as barrier height remain unchanged. Hence the effective barrier medium for all 4 conformers is assumed to be the same, with the width progressively decreasing from conformer 1 to 4. This model is also illustrated in the lower half of Fig. 5 for each of the conformers.

The influence of temperature on conformer distribution and tunnelling probability was estimated by calculating first the energy of the conformers relative to the conformation of lowest energy. Fig. 6 shows the results of such calculations. The relative energy (E − E₀) increases when the distance between C₁ and C₅ decreases. Qualitatively, it can be seen that the average length of the molecule is reduced notably upon an increase of temperature and hence the tunnelling probability from C₁ to C₅ should increase significantly with increasing temperature. To quantify the influence of this effect, the partition function for the conformers was determined using a statistical mechanics formulation: A molecular state with relative energy ε_j and degeneracy g_j has a probability P_j to be occupied at a temperature T given by:³⁰

with the molecular partition function q given by:ε_j is the energy of the molecule in the quantum state j. Table 1 shows the probability of the molecule to be present as a particular conformer (eqn. (1)) for 20 and 70 °C and the corresponding molecular dimensions. The probability for a molecule to be present as a conformer of higher energy, with a resulting decrease of average length, increases significantly in this temperature range. As schematically shown in Fig. 5 and in Table 1, the coiled conformations dominate as the temperature is raised. The observed temperature dependence would therefore most likely arise from increasing contributions from more contracted conformers.

Fig. 6 Dependence of the distance between C₁ and C₅ on the relative energy for the four energetically different conformers of pentane. Molecular modelling calculations (circles) are compared with Hartree–Fock calculations (squares); the conformer number shown next to the symbols relates to the geometry of the molecule shown in Fig. 5 and Tables 1 and 2.

Table 1 Dependence of the relative energy (E_x − E₁) on length change (d_x − d₁) of the four energetically different pentane conformers determined from molecular mechanics calculations. The energy increases with decreasing length of the molecule. d_x denotes the distance between the two outermost C atoms in conformer x. P denotes the probability distribution of the conformers calculated from the partition function, taking into account the degeneracy (Deg.)

Conformer number	Deg.	E x − E1/meV	d x − d1/Å	d x /Å	P/% 20 °C	P/% 70 °C
1 (a,a)	1	0	0	5.04	46.7	41.0
2 (g,a)	4	36	−0.50	4.54	45.0	48.5
3 (g,g)	2	62	−1.28	3.76	8.13	10.2
4 (g,g)	2	160	−1.61	3.43	0.16	0.36

---

The tunnelling process can be described by a simple model, assuming one-dimensional tunnelling through a rectangular barrier, where the exponential decay of the wave function in the barrier is characterised by the decay constant κ (in nm⁻¹) with

andwhere h is Planck’s constant, ϕ is the effective barrier height (in J) and m_e* is the effective electron mass. If ϕ is expressed in meV, κ in nm⁻¹ and m* is taken as the rest mass of the electron then eqn. (2) transforms into the simple expression:A change of the separation between the ends of the molecule attached to the contacts, Δs = s_x − s₁ consequently results in a change of the tunnelling current given by:where the subscript “1” denotes the lowest energy conformer and “x” corresponds to conformer x. I_x then refers to the current through conformer x and I₁ is the current through the lowest energy conformer.

Assuming ϕ_x = ϕ₁ = 5 eV (valid for small applied potentials) and m_e* = m_e, (m_e = rest mass of the electron) eqn. (3) yields:

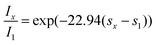with s in nm. From eqn. (4), the relative current (I_x/I₁) for the different conformers can be calculated. For the lowest energy conformation (conformer 1; all anti) I_x/I₁ = 1. The total tunnelling current (I_T) is given by

I_T ∝ ∑ (P_xI_x/I₁) (5)

The sum over all conformers of the probability-weighted currents ∑(P_xI_x/I₁) is a measure of the temperature dependent tunnelling probability. Table 2 shows numerical values of the quantities described above for tunnelling between C₁ and C₅ in a pentane molecule.

Table 2 Relative currents (I_x/I₁) for tunnelling between the outermost C atoms of pentane calculated from eqn. (4) for the four different pentane conformers. The sum of the probability-weighted currents (∑(P_xI_x/I₁)) shown at the bottom of columns 6 (for 20 °C) and 7 (for 70 °C) is a measure of the tunnelling probability between C₁ and C₅. Its value increases by approximately 15% upon an increase of temperature from 20 to 70 °C

Conformer number	d x − d1 /Å	I x /I1	P x /% 20 °C	Px/% 70 °C	P x I x /I1 20 °C	P x I x /I1 70 °C	I fra/% 20 °C	I fra/% 70 °C
d x is the length of conformer x. Px is the probability (%) of the molecule to be present as conformer x. Ix is the current through conformer x, while I1 is the current through conformer 1, the ground state. Ifra are the percentage current fractions for the different conformers.
1 (a,a)	0	1	46.73	40.95	0.47	0.410	13.5	10.3
2 (a,g)	−0.50	3.12	44.98	48.51	1.40	1.514	40.7	38.2
3 (g,g)	−1.28	18.7	8.12	10.16	1.52	1.897	43.9	47.8
4 (g,g)	−1.61	40.4	0.16	0.36	0.07	0.146	1.9	3.7
Sum:			100	100	3.45	3.97	100	100

---

Table 2 also shows the percentage current fractions (I_fra) for the different conformers. It is interesting to note that the energetically higher lying conformers 2 and 3 (compare with the results in Table 1) give the largest contributions to the tunnelling current. It is important to notice that the transition between the different conformers of alkanes (at least in the gas phase) is very fast since these involve rotations of C–C bonds.³¹ Therefore, in STM experiments, where the tunnelling current through a molecule is measured in a time scale of milliseconds, the probability-weighted average of the conductivities of the different conformers is measured. For these reasons σ_M should be seen as the time average of the conductance of an ensemble of conformers in thermal equilibrium.

To study the chain length dependence of d(ln(∑(P_xI_x/I₁))/dT⁻¹ calculations of ∑(P_xI_x/I₁) as a function of temperature have been carried out for hexane and octane (Fig. 7). The results of these calculations are in broad agreement with the experimental results (Fig. 2), since ln(∑(P_xI_x/I₁)) and hence ln(σ_M) scales linearly with 1/T and the slope of d(ln(∑(P_xI_x/I₁))/dT⁻¹ increases with increasing chain length. To enable direct comparison between theory and experiment, calculations have also been carried out for propanedithiol, butanedithiol and pentanedithiol, where a realistic value of the barrier height (1.2 eV ³²) and an effective electron mass (m_e* = 0.4m_e,³²) have been used (Fig. 8). The numerical results for the slope in Fig. 8 were similar for different calculation methods for the case of the simple propanedithiol molecule, whereas the results for the more complex butanedithiol and pentanedithiol molecules on the other hand, were strongly dependent on the particular choice of the computational method (Hartree–Fock, molecular mechanics or DFT) used to calculate the conformer geometry and its corresponding single point energy. If all possible conformers, including those resulting from the rotation of the terminal H atoms, were taken into account, unrealistic values were calculated due to a wide variance of the different conformer energies of similar length. To avoid these problems the number of conformers was reduced by assuming a linear geometry for the C–S–H groups for each different conformation of the S–(CH₂)_n–S skeleton. Hence the calculations proceeded from a straight C–S–H bond.

Fig. 7 (a) Dependence of the relative energy (E_x − E₁) on length change (Δd) of 66 different octane conformers determined from systematic molecular mechanics calculations. The energy of the conformers increases with decreasing length of the molecule. (b) Relative conductance (I_x/I₁) of the conformers of octane. (c) Probability of occupation for 20 °C (filled squares) and 70 °C (open squares) for octane. (d) T-dependence of ln(σ_M) for both hexane and octane; the value of ∑(PI_x/I₁) has been normalised with respect to its value at 20 °C. The logarithm of the conductance scales linearly with 1/T and the slope increases with increasing chain length.

Fig. 8 (a) The dependence of the logarithm of the calculated tunnelling probability on T⁻¹ for different alkanedithiols: 1,3-propanedithiol (circles; slope = −46 K), 1,4-butanedithiol (squares; slope = −124 K) and 1,5-pentanedithiol (triangles; slope = −201 K); the lines are linear fits. Hartree–Fock methods were used for the calculations of the tunnelling probability between the two terminal sulfur atoms. Note that the conductance scales linearly with 1/T in the temperature range between 290 and 350 K and the slope increases with increasing chain length as was found in the experimental study. For each molecule, the value of ∑(P_x × I_x/I₁) has been normalised with respect to its value at 20 °C. (b) Hartree–Fock calculations for 1,3-Propanedithiol covering a wider temperature range; the numbers next to the symbols correspond to the temperature in °C. The value of ∑(P_xI_x/I₁) has been normalised with respect to its value at 0 K.

Fig. 8a shows the dependence of the current predicted from eqn. (4) in the temperature range between 290 and 350 K. The results of these calculations are in qualitative agreement with the experimental results in the temperature range between 293 and 353 K (Fig. 2). Fig. 8(b) shows that, for 1,3-propanedithiol as an example, the relationship between ln(∑(P_x × I_x/I₁)) and 1/T is non-linear over a wider temperature range (not accessible in our experiments). Therefore at low temperatures where the ground state conformer is the main state populated, the temperature dependent gating is much weaker.

The calculated slope of d(ln(∑(P_xI_x/I₁))/dT⁻¹ for tunnelling between the two sulfur atoms³³ in pentanedithiol (201 K; see Fig. 8(a)) differs from the experimental value of d(ln(σ_M))/dT⁻¹ (1774 K; see Fig. 2). The difference can be attributed to a breakdown of the effective barrier height at small substrate–tip distances, a phenomenon which has been observed at metal–vacuum–metal³⁴ and metal–water–metal tunnelling junctions.³⁵ A decrease of the effective barrier height at small separations will increase the slope of d(ln(∑(I_x/I₁))/dT⁻¹ since shorter conformers are more prevalent at higher temperatures (vide infra).

The model and calculations above represent straightforwardly tunnelling through a temperature dependent barrier width and the strong temperature dependence clearly indicates the gated nature of the conduction mechanism; i.e. shorter conformers present a narrower barrier width. However, through bond tunnelling would also include a gating element, considering the structural dependence of the energetics and electronic overlaps in the appropriate HOMO’s or LUMO’s. The temperature dependence of these effects might be significant but are not expected to be nearly as strong as the effective barrier width considerations, as the bonds contributing to the HOMO and LUMO remain the same in different conformations. The effects can be illuminated by the following simple calculation. The effective barrier height for through-bond tunnelling in a symmetric metal-molecule-metal junction is given by half the difference between the HOMO and the LUMO energy if the Fermi level of the metal is placed half way between the energy of these molecular orbitals.³⁶ The tunnelling probability for the different conformers is then influenced by a change in barrier height (Δϕ) relative to the barrier height of the lowest energy conformation (ϕ₁). Eqns. (2b) and (3) and ϕ_x = ϕ₁ + Δϕ yield:

I₁ = I(ϕ₁) = exp(−2d(ϕ₁/38)^1/2) (6)

I_x = I(ϕ₁ + Δϕ) = exp(−2d((ϕ₁ + Δϕ)/38)^1/2) (7)

From eqns. (6) and (7), the current ratio is given by

I_x/I₁ = exp(−2d(((ϕ₁ + Δϕ)/38)^1/2) − (ϕ₁/38)^1/2)) (8)

Table 3 shows numerical results calculated from eqn. (8) for pentane using the P values from Table 1 and assuming ϕ₁ = 5 eV and d = 0.6 nm = constant. Δϕ has been calculated for the various conformers from the HUMO and LUMO energies. The current increases only by 0.6% for an increase of temperature from 20 to 70 °C. The increase is small. This conclusion should, however, be substantiated by ‘ab initio’ calculations for the situation encountered in the experiments, i.e. with the alkanedithiols incorporated between two suitably represented gold electrodes and including all the different conformers and different adsorption geometries. Such computations are feasible but beyond the scope of the present work.

Table 3 Influence of the effective barrier height on the temperature dependent tunnelling probability (P_xI_x/I₁) in propane; see text for details

Conformer number	Δϕ/meV	I x /I1	P x (%) 20 °C	P x (%) 70 °C	P x I x /I1 20 °C	P x I x /I1 70 °C
1 (a,a)	0	1	46.73	40.96	46.73	40.95
2 (g,a)	−23	1.03	44.98	48.52	46.42	50.07
3 (g,g)	−145	1.22	8.125	10.17	9.936	12.43
4 (g,g)	−129	1.20	0.163	0.361	0.195	0.432
Sum			100	100	1.033	1.039

---

The analysis presented in this section has demonstrated that conformational changes are the most likely reason for the pronounced temperature dependence observed for single molecule conductance of alkanedithiols. The molecule trapped between tip and support has freedom to adopt many conformations. In support of the proposed mechanism, it is noteworthy that the conductance of self assembled monolayers of alkanedithiols sandwiched between two metal electrodes show only little temperature dependence.³² This is probably a result of the absence of conformational freedom for molecules present in a densely packed layer.

5. Conclusions

The pronounced temperature dependence of the conductance of single alkanedithiol molecules observed experimentally can be understood semi-quantitatively by taking into account the temperature dependent conformer distribution and its influence on the tunnelling probability in a simple barrier tunnelling model. This model also predicts a pronounced increase of the temperature dependence of σ_M with increasing chain length, which was observed experimentally. These findings demonstrate that charge transport through organic molecules at ambient temperatures is a subtle and highly dynamic process, which cannot be described by the analysis of only one conformation locked in the lowest energy geometry.

The model presented is a simplification of a complex problem in gated tunnelling since the interplay between through-bond and through-space tunnelling requires a more extensive analysis. The main point of this work, however, is to have demonstrated that single molecule conductance is strongly temperature dependent whereas the energies of the HOMO and LUMO are not. The implications of these observations are that we are dealing here mainly with conformation effects, which have been generally neglected in the past.

Acknowledgements

This work was carried out with financial support from the EPSRC under grants GR/R07684/01 (Scanning Tunneling Spectroscopy of Nanoscale Structures) and EP/C00678X01 (Mechanisms of Single Molecule Conductance) and the European Union (SUSANA project (HvZ), Human Potential Program (HPRN-CT-2002-00185)).

References

1. D. Segal and A. Nitzan, Chem. Phys., 2002, 281, 235.
2. A. Nitzan, Annu. Rev. Phys. Chem., 2001, 52, 681.
3. D. Segal, A. Nitzan, M. Ratner and W. B. Davis, J. Phys. Chem. B, 2000, 104, 2790.
4. Y. Selzer, M. A. Cabassi, T. S. Mayer and D. L. Allara, J. Am. Chem. Soc., 2004, 126, 4052.
5. D. I. Gittins, D. Bethell, R. J. Nichols and D. J. Schiffrin, Adv. Mater., 1999, 11, 737.
6. D. I. Gittins, D. Bethell, R. J. Nichols and D. J. Schiffrin, J. Mater. Chem., 2000, 10, 79.
7. D. I. Gittins, D. Bethell, D. J. Schiffrin and R. J. Nichols, Nature, 2000, 408, 67.
8. W. Haiss, R. J. Nichols, S. J. Higgins, D. Bethell, H. Hobenreich and D. J. Schiffrin, Faraday Discuss., 2004, 125, 179.
9. W. Haiss, R. J. Nichols, H. van Zalinge, S. J. Higgins, D. Bethell and D. J. Schiffrin, Phys. Chem. Chem. Phys., 2004, 6, 4330.
10. W. Haiss, H. van Zalinge, S. J. Higgins, D. Bethell, H. Hobenreich, D. J. Schiffrin and R. J. Nichols, J. Am. Chem. Soc., 2003, 125, 15294.
11. W. Haiss, H. van Zalinge, H. Hobenreich, D. Bethell, D. J. Schiffrin, S. J. Higgins and R. J. Nichols, Langmuir, 2004, 20, 7694.
12. B. Q. Xu, X. Y. Xiao, X. M. Yang, L. Zang and N. J. Tao, J. Am. Chem. Soc., 2005, 127, 2386.
13. A. Troisi and M. A. Ratner, Nano Lett., 2004, 4, 591.
14. A. Troisi and M. A. Ratner, J. Am. Chem. Soc., 2002, 124, 14528.
15. Z. J. Donhauser, B. A. Mantooth, K. F. Kelly, L. A. Bumm, J. D. Monnell, J. J. Stapleton, D. W. Price, A. M. Rawlett, D. L. Allara, J. M. Tour and P. S. Weiss, Science, 2001, 292, 2303.
16. J. Gaudioso and W. Ho, J. Am. Chem. Soc., 2001, 123, 10095.
17. M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252.
18. C. Kergueris, J. P. Bourgoin, S. Palacin, D. Esteve, C. Urbina, M. Magoga and C. Joachim, Phys. Rev. B, 1999, 59, 12505.
19. H. B. Weber, J. Reichert, R. Ochs, D. Beckmann, M. Mayor and H. von Lohneysen, Physica E, 2003, 18, 231.
20. J. Reichert, R. Ochs, D. Beckmann, H. B. Weber, M. Mayor and H. von Lohneysen, Phys. Rev. Lett., 2002, 88, 176804.
21. H. Park, A. K. L. Lim, A. P. Alivisatos, J. Park and P. L. McEuen, Appl. Phys. Lett., 1999, 75, 301.
22. A. Yazdani, D. M. Eigler and N. D. Lang, Science, 1996, 272, 1921.
23. B. Q. Xu and N. J. J. Tao, Science, 2003, 301, 1221.
24. M. Dorogi, J. Gomez, R. Osifchin, R. P. Andres and R. Reifenberger, Phys. Rev. B, 1995, 52, 9071.
25. X. D. Cui, A. Primak, X. Zarate, J. Tomfohr, O. F. Sankey, A. L. Moore, T. A. Moore, D. Gust, G. Harris and S. M. Lindsay, Science, 2001, 294, 571.
26. G. Leatherman, E. N. Durantini, D. Gust, T. A. Moore, A. L. Moore, S. Stone, Z. Zhou, P. Rez, Y. Z. Liu and S. M. Lindsay, J. Phys. Chem. B, 1999, 103, 4006.
27. W. Haiss, D. Lackey, J. K. Sass and K. H. Besocke, J. Chem. Phys., 1991, 95, 2193.
28. T. Albrecht, A. Guckian, J. Ulstrup and J. G. Vos, Trans. IEEE Nanotechnol., 2005 , in press.
29. T. Albrecht, A. Guckian, J. Ulstrup and J. G. Vos, Nano Lett., 2005 , in press.
30. P. W. Atkins, Physical Chemistry, Oxford University Press, Oxford, 1st edn., 1978.
31. P. Y. Bruice, in Organic Chemistry, Prentice Hall, Englewood Cliffs, NJ, 2004.
32. W. Y. Wang, T. Lee and M. A. Reed, J. Phys. Chem. B, 2004, 108, 18398.
33. For completeness it should be mentioned that d(ln(∑(P_xI_x/I₁))/dT⁻¹ is similar for other pairs of atoms.
34. S. Yagyu and M. Yoshitake, Surf. Interface Anal., 2004, 36, 1110.
35. J. R. Hahn, Y. A. Hong and H. Kang, Appl. Phys. A, 1998, 66, S467.
36. X. D. Cui, A. Primak, X. Zarate, J. Tomfohr, O. F. Sankey, A. L. Moore, T. A. Moore, D. Gust, L. A. Nagahara and S. M. Lindsay, J. Phys. Chem. B, 2002, 106, 8609.

---