Controlling charge transport in single molecules using electrochemical gate

Abstract

We have studied charge transport through single molecules covalently bound to two gold electrodes in electrolytes by applying a voltage between the two electrodes and a reference electrode (gate). This electrochemical gating can effectively control the current through the molecules, depending on the electronic properties of the molecules. For electrochemically inactive molecules, such as 4,4′-bipyridine and 1,4′-benzenedithiol, the gate voltage influences the transport current only slightly (less than 30%). This lack of significant gate effect is attributed to the large LUMO–HOMO gaps of the molecules and the screening of the gate field by the two electrodes. For nitro-oligo(phenylene ethynylene) (OPE-NO₂), which undergoes multiple irreversible reductions at negative gate voltages, the current through the molecules can be modulated several folds by the gate. This gate effect is irreversible and associated with the reduction of the NO₂ group to different products that have different electron withdrawing capabilities from the conjugate backbone of the molecule. The most interesting molecules are perylene tetracarboxylic diimide compounds (PTCDI), which exhibit fully reversible redox reactions. The current through PTCDI can be reversibly varied and controlled over three orders of magnitude with the gate. Such a large gate effect is related to a redox state-mediated electron transport process.

---

1. Introduction

The building blocks of silicon-based microelectronics are field effect transistors (FET) whose basic function is to control electrical current between two electrodes (source and drain) with a third electrode (gate). The ability to control electron transport through a single molecule is thus considered to be a crucial task in the development of molecular electronic devices.^1–3 This ability also provides one with a rather unique opportunity to study charge transport, a phenomenon that plays vital roles in many chemical, electrochemical and biological processes, on a single molecule basis. Most works in molecular electronics to date have focused on two-terminal devices.^4–7 A three-terminal FET-like device is highly desired, because it provides power gain, an essential requirement for large-scale integrated circuits. FET-like behavior has been demonstrated in carbon nanotubes^8,9 and semiconductor nanowires.¹⁰ Interesting Coulomb blockade^11–14 and Kondo effects^12,13 have also been observed in molecular systems using a back gate at low temperatures. Theoretical models have predicted that the conductance of a single molecule can be modulated with a gate electrode in a fashion of conventional FET.^15,16 However, experimental demonstration of this FET behavior at single molecule level has been a challenge due to the following reasons:

First, the gate electrode has to be placed within a few angstroms distance from the molecule in order to achieve a large enough gate field, which is not an easy task using conventional solid-state device configurations. One method to overcome this difficulty is to use electrochemical gate in which the molecular junction is immersed in an electrolyte and the source and drain potentials are biased with respect to a reference electrode inserted in the electrolyte. This reference electrode is called electrochemical gate. An applied gate voltage falls across the double layer at the reference electrode–electrolyte interface, the electrolyte between the gate electrode and the source/drain electrodes, as well as the double layer at the electrolyte-source (drain) electrode interface. Since the current between the gate and the source/drain electrode is negligible, the voltage drop in the electrolyte is practically zero. The effective gate–molecule distance is thus determined by the double layer thickness at the electrode–electrolyte interfaces, which is of the order of the size of a few solvated ions. This allows the electrochemical gate to create a rather large field in the molecule. Such a electrochemical gating method has been applied to control charge transport in conducting polymer films^17,18 and nanojunctions,^19,20 metal oxide semiconductors,²¹ carbon nanotubes^22,23 and molecular junctions.^24–29

Second, the screening of gate field by the source and drain electrodes must be minimized. This screening effect becomes serious when the distance between source and drain electrodes is small in comparison to the distance between the molecule and the gate electrode. For a molecular FET, the source–drain distance is determined by the molecule size, and thus it is a challenge to avoid the screening problem for small molecules using the solid state device configurations. Even for the electrochemical gate approach, the molecule used has to be longer than the thickness of the double layer. One obvious solution to this problem is to choose relatively long molecules. However, since the conductance of a molecule often decreases exponentially with its length, highly conductive conjugated molecules are clearly among the best choice.

Finally, a reliable method is needed to measure electron transport in single molecules connected to the source and drain electrodes. To date, many experimental methods have been developed, but most methods measure either a large or unknown number of molecules. A scanning tunneling microscope (STM) can perform electrical measurements on single molecules, but the measured conductance is complicated by the uncertain contact between the molecule and the STM tip. Nevertheless, these measurements, together with theoretical efforts, have provided the bulk of our current knowledge about electron transport in molecules. In order to reliably measure the conductance of a single molecule, one must: (1) provide reproducible contacts between the molecule and two probing electrodes,^30–33 (2) identify a “signature” that the measured conductance is due to not only the sample molecules but also a single sample molecule, and (3) perform statistical analysis, which is required because of the sensitive dependence of the molecular conductance on the microscopic details of the molecule–electrode contacts.

In this paper, we discuss electrochemical gating effects on the charge transport through single molecules covalently bound to two metal electrodes. We focus on three types of molecules: electrochemically inactive molecules, electroactive molecules that undergo irreversible redox reactions, and electroactive molecules that undergo reversible redox reactions. These molecular systems exhibit rather different electrochemical gating behaviors.

2. Experimental method

The experimental method used in this work is based on statistical analysis of many individual molecular junctions.³⁴ The individual molecular junctions are created using a modified scanning tunneling microscope (STM) which repeatedly moves a Au tip (source electrode) into and out of contact with a Au substrate (drain electrode) in a solution containing sample molecules (Fig. 1). The sample molecule chosen has two terminal groups that can bind strongly to Au electrodes, and thus has a chance to bridge the two electrodes and form a well defined molecular junction during the separation of the tip and the substrate electrode.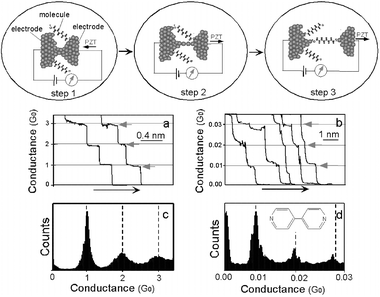

Fig. 1 Measurement of single molecule conductance. Step 1: A piezoelectric transducer (PZT) drives an electrode into contact with another electrode in a solution containing sample molecules. Step 2: The first electrode is then pulled back to form an atomic-scale neck between the two electrodes, which is signaled by conductance quantization (a,c). Step 3: After breaking the atomic-scale neck, the sample molecules start to bridge the two electrodes via chemical bonds. Further pulling breaks the individual molecules, which leads to a new series of steps in the conductance (b). Conductance histogram (d) constructed from more than a thousand measurements reveals well-defined peaks near integer multiples of a fundamental value (0.01G₀ for 4,4′-bipyridine shown here), which is identified as the conductance of a single molecule.

The process can be divided into three steps.

(1) A piezoelectric transducer drives the STM tip into contact with the substrate electrode.

(2) The tip is then pulled away from the substrate, during which a small Au neck forms between the tip and the substrate due to large metallic cohesion. The neck becomes thinner and thinner, and eventually approaches atomic scale. The conductance monitored during the pulling process decreases in discrete steps near integer multiples of a fundamental constant, G₀ = 2e²/h = 77.4 μS, where e is the electron charge and h is the Planck constant (Fig. 1a and 1c). This phenomenon, called conductance quantization, occurs only when the neck is decreased to atomic scale.^35–41 As such, it is a useful indicator of when the tip and the substrate are connected by only a few Au atoms.⁴²

(3) The tip is pulled further away to break the atomically thin neck, after which a new sequence of steps with much lower conductance values appears (Fig. 1b). In the case of 4,4′-bipyridine, a molecule with two nitrogen terminals that can bind to Au electrodes, the steps are near 0.01G₀, 0.02G₀, 0.03G₀,…, two orders of magnitude lower than those due to the conductance quantization. We ascribe the new conductance steps that appear after breaking STM tip–substrate contact to the formation of molecular junctions, and the corresponding peaks in the histogram (Fig. 1d) to one, two and three molecules in the junctions.

This interpretation is supported by simultaneous measurement of the conductance and the force using a modified conducting atomic force microscope (AFM).⁴³ The measurement shows that each stepwise decrease in the conductance is accompanied by an abrupt drop in the force, corresponding to the breaking of contact between a molecule and the electrodes. Like the conductance histogram described above, the force histogram also reveals well-defined peaks at integer multiples of a fundamental force quantum, which corresponds to the force required to break a single molecule at the junction. For dithiol molecules that are bound to Au electrodes via S–Au bonds, the force is 1.5 nN. This force is the same as that required to break a Au–Au bond under the same conditions,⁴⁴ which indicates that the breakdown takes place likely at the Au–Au bond. The force to break a 4,4′-bipyridine obtained with the same pulling rate is only 0.8 nN, corresponding to the breakdown of a N–Au bond. In addition to AFM, several other control experiments also support the above conclusion. First, in the absence of molecules, no peaks below G₀ appear in the histogram. Second, in the presence of 2,2-bipyridine or alkanemonothiol molecules which cannot simultaneously bind to two electrodes, there are no well defined peaks in the conductance histogram either. Third, the peaks are located at different conductance values for different molecules. For instance, the conductance of alkanedithiol decreases exponentially with the molecule length.³⁴

The histogram analysis shown in Fig. 1d provides an unambiguous determination of single molecule conductance averaged over a large number of measurements. Once the conductance of a single molecule is determined, pull the source and drain electrodes apart until the conductance drops to the lowest step, corresponding to the value of a single molecule conductance. We then freeze the electrodes and record the current (I_sd) while sweeping the source–drain voltage (V_sd) or gate voltage (V_g) (Fig. 2). We refer to these procedures as the pull–hold–measure method. This approach is useful but requires good STM stability. We have been able to routinely hold the tip for many seconds to a few minutes using our setup.

Fig. 2 Schematic illustration of a single molecule transistor with an electrochemical gate (a reference electrode in electrolyte). The gate and the source–drain bias voltages are controlled with a bipotentiostat (a Pt counter electrode not shown for clarity). Note that the gate voltage, V_g, cited here is the potential of the source electrode with respect to the reference electrode, so the sign convention is opposite to the solid state FET.

The electrochemical gate was controlled by either a homemade or commercial bipotentiostat (PicoStat, Molecular Imaging Co.) using a Pt wire as counter electrode and a Ag wire as quasi-reference electrode (Fig. 2). The quasi reference electrode was calibrated against the more commonly used Ag/AgCl (in 3.5 M KCl) reference electrode. The substrate was prepared by thermally evaporating 100 nm gold on mica in a UHV chamber. Prior to each experiment, the substrate was briefly annealed in a hydrogen flame. The STM tip was prepared by cutting a 0.25 mm gold wire (99.999%), which was then coated with Apiezon wax in order to reduce ionic conduction and polarization currents. The leakage current, due to ionic conduction and polarization, was on the order of picoamperes. The STM cell was cleaned with piranha solution (98% H₂SO₄: 30% H₂O₂ = 3 : 1, v/v) and then sonicated in 18 MΩ water three times (Caution: piranha solution reacts violently with most organic materials and must be handled with extreme care). The electrochemical experiment was conducted in an argon atmosphere.

3. Results and discussion

3.1. Electrochemically inactive molecules

We have studied 4,4′-bipyridine and benzenedithiol molecules, both are electrochemically inactive within the potential windows studied here. These molecules can bind to two Au electrodes and form molecular junctions via N–Au and S–Au bonds, respectively. We have measured cyclic voltammograms of the two molecules adsorbed on Au electrodes in aqueous electrolytes, and found no electrochemical reactions within the potential windows studied here. The upper limit of the windows is fixed by the oxidation potential of gold, which is about 0.5 V, and the lower limit is determined by the desorption of the molecules, which is −0.5 V for 4,4′-bipyridine and −0.9 V for the thiol compounds.

To measure the gate effect of 4,4′-bipyridine, we first obtained a 4,4′-bipyridine molecular junction in 50 mM NaClO₄ supporting electrolyte and then we swept the electrochemical gate voltage while maintaining a constant bias voltage between the source and drain electrodes at 0.1 V. Fig. 3a is a typical source–drain current (I_sd) vs. gate voltage (V_g) curve. It shows a ∼25% increase in the source–drain current as the gate voltage was swept negatively. To examine the reproducibility of the observation, we performed the same measurement on different molecular junctions prepared under the same conditions. Fig. 3b plots the histogram of the gate-induced current change, showing that the small gate effect is reproducibly observed despite of the run-to-run variations. We have performed the measurement by sweeping the gate voltage at different rates, and found no obvious dependence of the source–drain current on the sweep rate, which indicates that the gate effect is not due to a capacitive charging process. We can also rule out ionic leakage current as a possible cause for the gate effect because it is much smaller than the conduction current through the molecular junction.

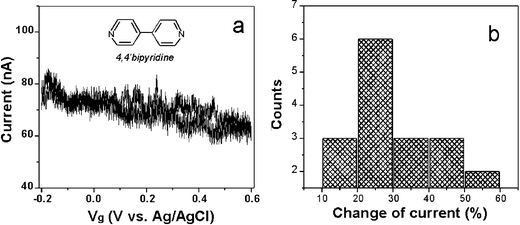Fig. 3 (a) A typical source–drain current (I_sd) vs. gate voltage (V_g) curve of a 4,4′-bipyridine molecular junction in 0.05 M NaClO₄. The gate voltage is swept from −0.2 V to +0.6 V. (b) Statistic of the current change of 17 individual curves shown in (a). The source–drain bias is fixed at 0.1 V.

We have also studied the electrochemical gate effect on the conductance of benzenedithiol in a similar way. This molecule was used initially in the theoretical modeling of molecular FET.^15,16 The conductance of a single benzenedithiol bound to Au electrodes was previously determined in our lab using the STM break junction approach.⁴⁵ A typical source–drain current vs. gate voltage curve is plotted in Fig. 4. Within the electrochemical gate voltage window, the current through the benzenedithiol molecule changes only slightly (∼5%) with the gate voltage.

Fig. 4 A typical source–drain current (I_sd) vs. gate voltage (V_g) curve of a benzenedithiol molecular junction in 0.05 M NaClO₄.

The lack of significant gate effect on the conductance of 4,4′-bipyridine and benzenedithiol are not fully understood yet. A possible reason is that both HOMOs and LUMOs of the two molecules are far away from the Fermi levels of the Au electrodes, and the applied gate voltage is not enough to shift the HOMOs or LUMOs close to the Fermi levels. This argument is consistent with the lack of electrochemical activity of these molecules. Another possible reason is the screening effect. In order to achieve effective gate control with a single gate electrode, the gate thickness has to be much smaller than the molecular length.¹⁶ In the case of electrochemical gating, the gate thickness is given by the double layer thickness, which is comparable with the lengths of 4,4′-bipyridine and benzenedithiol (∼0.7 nm). This may result in substantial screening of the gate field.

3.2. Molecules with irreversible redox reactions

We have extended the above electrochemical gating measurement to oligo(phenylene ethynylene) (OPE) dithiolated molecules. In contrast to benzenedithiol and 4,4′-bipyridine, the OPE molecules are much longer and electroactive in their nitro-substituted form, which should lead to a large gate effect according to the above argument. Fig. 5a shows the cyclic voltammogram of nitro-substituted OPE (OPE-NO₂) on a gold electrode in anhydrous acetonitrile containing TBAP as supporting electrolyte (with a small amount of aqueous NaOH solution to remove the protection groups). It resolves three reduction peaks located near −0.5 (C1), −1.1(C2)⁴⁶ and −1.16 V (C3), respectively. The peaks, C₁ and C₂ are assigned to the electrochemical reduction of the nitro group, while third peak C₃ is, however, due to the reductive desorption of the adsorbed molecules because it diminishes with potential cycles.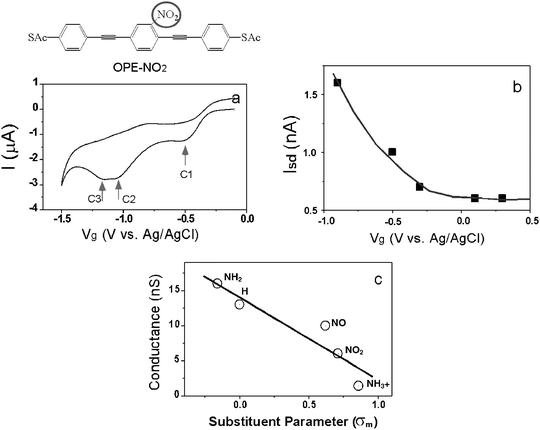

Fig. 5 (a) Cyclic voltammogram of thiol-deprotected OPE-NO₂ in MeCN/H₂O containing 0.1 M TBAP and 0.001 M NaOH solution. (b) Source–drain current (I_sd) vs. gate voltage (V_g) for single OPE-NO₂. (c) Conductance vs. Hammett parameter (σ) plot. The location of the substituent is indicated with red circle in the structure of OPE-NO₂.

Because the reduction of the OPE-NO₂ molecule is irreversible, we could not record the source–drain current by repeatedly sweeping the gate voltage. In order to study the gate effect, we determined the conductance histograms by holding the gate voltage at different values between −0.9 V and 0.3 V, starting at a positive gate voltage. We extracted the source–drain current vs. gate voltage by plotting the position of the lowest peak in the conductance histograms as a function of the gate voltage (Fig. 5b). Unlike 4,4′-bipyridine and benzenedithiol, the conductance of OPE-NO₂ is sensitive to the applied gate voltage. In 0.1 M NaOH, it increases from ∼0.6 nA at 0.1 V to ∼1.6 nA at −0.9 V (Fig. 5b). This gate effect depends on the pH of the electrolyte. We have measured the gate effect in 0.1 M NaClO₄ and 0.1 M NH₄Ac, both have much lower pH than 0.1 M NaOH. When holding the gate voltage above the reduction potentials, the conductance is the same in different electrolytes. However, if lowering the gate voltage below the reduction potentials, the conductance first increases and then decreases, which is different from that in NaOH solutions. This difference is related to the protonation of the amine group (reduced from the nitro group) in NaClO₄ and NH₄Ac.

We believe that the change in the conductance of OPE-NO₂ upon irreversible electrochemical reduction is due to the substituent effect on the central benzene ring based on the following considerations. The reduction processes in aqueous solution can be described as the following steps:

–NO₂ → –NO → –NH(OH) → –NH₂.

The substituent group changes with the successive reductions. The chemical nature of a substituent can shift the frontier molecular orbital, and thus alter the electron transport efficiency through the molecule.^1,47Fig. 5c shows that the measured conductance decreases linearly with the Hammett substituent parameter (σ), which is in good agreement with theoretical estimation by Vedova-Brook et al.⁴⁸ The decrease of the conductance with σ is expected because a larger σ corresponds to a higher electron withdrawing capability of the substituent.⁴⁹

3.3. Molecules with reversible redox reactions

The gate effect observed in OPE-NO₂ is related to the electrochemical reductions of the NO₂ group, but the reactions are not reversible. Perylene tetracarboxylic diimide (PTCDI) is known to exhibit reversible redox reactions. To wire the molecule to two gold electrodes, we have synthesized two PTCDI derivatives, one is terminated with two thiol groups (PTCDI-dithiol) and the other with two pyridine groups (PTCDI-bipyridine). Both terminals can spontaneously bind to gold electrodes (Fig. 6a). The energy gap between LUMO and HOMO is only 2.5 eV. Such an energy gap implies a semiconductor-like molecule.

Fig. 6 (a) Molecular structure of pyridine-terminated PTCDI and thiol-terminated PTCDI. (b) Cyclic voltammogram of thiol terminated PTCDI molecules adsorbed on gold electrode in DMF containing 0.1 M TBAP (red) and in 0.1 M NaClO₄ aqueous solution (black). To avoid reductive desorption of the molecule, the lower limit of the potential was kept at −0.8 V in aqueous solution. The arrows point reduction and re-oxidation peaks of two redox processes. (c) Source–drain current (I_sd) vs. gate voltage (V_g) for single molecule transistors consisted of pyridine-terminated PTCDI and thiol-terminated PTCDI. The squares were determined from the peak position of the conductance histograms and the solid lines were obtained by directly recording the source–drain current while sweeping the gate voltage. (d) Sweeping the gate voltage to more negative values, the current through the thiol-terminated PTCDI increases by several orders of magnitude.

The cyclic voltammogram (Fig. 6b) of PTCDI-dithiol bound on gold electrodes shows two pairs of peaks at −0.55 V and −0.8 V, respectively, corresponding to two reversible reduction processes, so the levels of the empty molecular states are close to the Fermi level. The redox behavior of the surface bound molecule is similar to that in bulk solution, which indicates that the strong molecule-electrode binding does not significantly alter the molecular electronic states. The nominal lengths of the rigid molecules are about 2.3 nm, much greater than the gate thickness (∼0.7 nm), so the screening of gate field due to the proximity of source and drain electrodes is significantly reduced, compared to the cases of 4,4′-bipyridine and benzenedithiol. These attributes make PTCDI an excellent candidate for molecular FET.

The conductance of the thiol-terminated PTCDI determined by the STM-break junction method is ∼1.2 × 10⁻⁵G₀, while the conductance of the pyridine-terminated PTCDI is ∼5 × 10⁻⁵G₀. The difference between the two derivatives may be attributed to the shorter length of the pyridine-terminated PTCDI. Although pyridine-terminated PTCDI molecule has same linkers as 4,4′-bipyridine does, the magnitude of the conductance is three orders lower than that of the latter. This indicates the molecular conductance does depend on the length. The ring structure in the middle of PTCDI molecule dominates the molecular resistivity. On the other hand, the charge transport through PTCDI molecule shows strong dependence on gate with the ring structure in PTCDI molecule. Fig. 6c plots the source–drain current vs. the gate voltage for both the thiol- and pyridine-terminated PTCDI in 0.1 M NaClO₄. Despite the run-to-run variations, all the curves reveal a rapid increase in I_sd when V_g is decreased below −0.1 V. Unfortunately, the pyridine-terminated PTCDI desorbs from gold electrodes below ∼−0.5 V, which prevents us from studying the gate effect below −0.5 V. For thiol-PTCDI, however, we were able to continuously record I_sd–V_g curves down to ∼−0.8 V (Fig. 6c). It reveals a large gate effect on the conductance of the molecule. For example, the conductance increases to 5 × 10⁻³G₀ at V_g = −0.8 V, which is ∼500 times greater than that at 0 V. It also reveals a peak at V_g ∼ −0.65 V.

The large gate effect obtained with these redox molecules resembles the n-type solid state FET (the gate sign convention here is opposite to that in solid state electronics), but the mechanisms are different. The current peak observed here is located at V_g ∼ −0.65 V, close to the redox potential of the molecule. This leads us to believe that the current enhancement is due to an empty molecular state-mediated electron transport process.⁵⁰ One mechanism is resonant tunneling which predicts that the current reaches a peak when the empty state is shifted to the Fermi level by the gate (inset of Fig. 6d).^15,24,51 Since the V_sd is 0.1 V, the potential of the redox center is ∼−0.6 V at the resonance if considering the symmetry of the molecular junction. This potential is close to the first reduction potential (∼−0.55 V) of PTCDI adsorbed on gold electrodes (Fig. 6b). By considering the stochastic dynamics of solvent polarization and internal vibration modes, Kuznetsov and Schmickler⁵² have shown recently that the resonant enhancement in the current through a redox molecule reaches the maximum near the redox potential, which supports the interpretation above. An alternative mechanism that predicts a maximum current near the reduction potential is a two-step electron transport in which an electron from one electrode tunnels into the empty state to reduce the molecule and then tunnel out into the second electrode.⁵³

The on–off current ratio observed in the present system is ∼10³. The peak current is determined by the coupling of the empty states to the vibration modes and polarization of the surrounding environment.⁵⁴ So by designing a molecule to minimize the coupling, one may achieve higher on–off current ratio. Another way to further increase the on-off ratio is to decrease the off-resonance conductance by increasing the linker group length between the redox center and the source/drain electrodes.

4. Summary

In summary, we have measured electrochemical gate effect on single molecules covalently bound to gold electrodes using two methods. The first one is to create individual molecular junctions by repeatedly bringing a gold STM tip (source electrode) into and out of contact with a gold substrate (drain electrode) in the presence of molecules terminated either with two thiols or two pyridines. The conductance decreases in a stepwise fashion when pulling the source–drain electrodes apart, which is attributed to the breakdown of individual molecules from contact with the electrodes. The conductance histograms constructed from many individual measurements reveal pronounced peaks near integer multiples of a fundamental conductance value, which is assigned to the conductance of the single molecule. By performing the measurement at various gate voltages, the molecular conductance vs. gate voltage is determined. The second method is built upon the first one. It starts by bringing the tip electrode into contact with the substrate electrode, and then pulling the tip out of contact with the substrate during which the conductance (current) is continuously monitored. We freeze the tip as soon as the conductance drops to the last step, corresponding to a single molecular junction, and record the conductance as we sweep the gate voltage.

Using the two methods, we have studied the gate effect on three types of molecules: electrochemically inactive (4,4′-bipyridine and benzenedithiol), electrochemically active but with irreversible redox reactions (OPE-NO₂), and electrochemically active with fully reversible redox reactions (PTCDI). The gate effects on the first type of molecules are rather small. We attribute this weak gate effect to two possible reasons. The first one is that the LUMO and HOMO of these molecules are far away from Fermi energy levels of the drain and source electrodes. The second reason is the screening of the gate field from the proximity of the source and drain electrodes since both 4,4′ bipyridine and benzenedithiol are small in comparison to the double layer thickness. In the case of the second type of molecules, the conductance changes irreversibly by several folds, which is correlated with the irreversible reduction of the NO₂ moiety. The conductance decreases linearly with the Hammett parameter which describes the electron withdrawing capability from the conjugated backbone of the molecule. The third type of molecules is most interesting since the conductance can be reversibly controlled over nearly three orders of magnitude. The conductance also reaches a peak that resembles resonant tunneling via the empty state of the molecule. While the resonant tunneling model seems to explain qualitatively the experimental observation, more sophisticated theories are needed for a complete understanding of the large gate effect.

Acknowledgements

We thank Mark Ratner, Wolfgang Schmickler, Stuart Lindsay, Larry Nagahara and Salah Boussaad for helpful discussions, Nguyen Ly and Jin He for sample preparations, and DOE(DE-FG03-01ER45943) (Xu) and NSF(CHE-0243423) (Li and Xiao).

References

1. A. Aviram and M. Ratner, Chem. Phys. Lett., 1974, 29, 277–283.
2. R. l. Carroll and C. B. Gorman, Angew. Chem., Int. Ed., 2002, 41, 4379–4399.
3. C. Joachim, J. K. Gimzewski and A. Aviram, Nature, 2000, 408, 541–548.
4. J. Chen, M. A. Reed, A. M. Rawlett and J. M. Tour, Science, 1999, 286, 1550–1552.
5. C. P. Collier, E. W. Wong, M. Belohradsky, F. M. Raymo, J. F. Stoddart, P. J. Kuekes, R. S. Williams and J. R. Heath, Science, 1999, 285, 391–394.
6. S. Datta, W. D. Tian, S. H. Hong, R. Reifenberger, J. I. Henderson and C. P. Kubiak, Phys. Rev. Lett., 1997, 79, 2530–2533.
7. R. M. Metzger, Chem. Rev., 2003, 103, 3803–3834.
8. S. J. Tans, A. R. M. Verschueren and C. Dekker, Nature, 1998, 393, 49–52.
9. P. C. Collins, M. S. Arnold and P. Avouris, Science, 2001, 292, 706.
10. Y. Cui and C. Lieber, Science, 2001, 291, 851–853.
11. H. Park, J. Park, A. K. L. Lim, E. H. Anderson, A. P. Alivisatos and P. L. McEuen, Nature, 2000, 407, 57–60.
12. J. Park, A. N. Pasupathy, J. L. Goldsmith, C. Chang, Y. Yaish, J. R. Petta, M. Rinkoski, J. P. Sethna, H. D. Abruna, P. L. McEuen and D. C. Ralph, Nature, 2002, 417, 722–725.
13. W. J. Liang, M. Shores, M. Bockrath, J. R. Long and H. Park, Nature, 2002, 417, 725–729.
14. S. Kubatkin, A. Danilov, M. Hjort, J. Cornil, J.-L. Bredas, N. Stuhr-Hansen, P. Hedegard and T. Bjornholm, Nature, 2003, 425, 698–701.
15. M. Di Ventra, S. T. Pantelides and N. D. Lang, Appl. Phys. Lett., 2000, 76, 3448–3450.
16. P. Damle, T. Rakshit, M. Paulsson and S. Datta, IEEE Trans. Nanotechnol., 2002, 1, 145–1153.
17. E. W. Paul, A. J. Ricco and M. S. Wrighton, J. Phys. Chem., 1985, 89, 1441–1447.
18. H. S. White, G. P. Kittlesen and M. S. Wrighton, J. Am. Chem. Soc., 1984, 106, 5375.
19. H. X. He, C. Z. Li and N. J. Tao, Appl. Phys. Lett., 2001, 78, 811–813.
20. H. X. He, X. L. Li, N. J. Tao, L. A. Nagahara, I. Amlani and R. Tsui, Phys. Rev. B, 2003, 68, 45302-1.
21. E. A. Meulenkamp, J. Phys. Chem. B, 1999, 103, 7831–7838.
22. M. Krüger, M. R. Buitelaar, T. Nussbaumer, C. Schönenberger and L. Forró, Appl. Phys. Lett., 2001, 78, 1291-3.
23. S. Rosenblatt, Y. P. Yaish, Jiwoong, Gore, Jeff, V. Sazonova and P. L. McEuen, Nano Lett., 2002, 2, 869–872.
24. N. J. Tao, Phys. Rev. Lett., 1996, 76, 4066–4069.
25. D. I. Gittins, D. Bethell, D. J. Schiffrin and R. J. Nichols, Nature, 2000, 408, 67–69.
26. E. Tran, M. A. Rampi and G. M. Whitesides, Angew. Chem., Int. Ed., 2004, 43, 3835–3839.
27. W. Haiss, H. Van Zalinge, S. J. Higgins, D. Bethell, H. Hoebenreich, D. J. Schiffrin and R. J. Nichols, J. Am. Chem. Soc., 2003, 125, 15294–15295.
28. F. Chen, J. He, C. Nuckolls, T. Roberts, J. E. Klare and S. Lindsay, Nano Lett., 2005, 5, 503–506.
29. B. Xu, X. Xiao, X. Yang, L. Zang and N. Tao, J. Am. Chem. Soc., 2005, 127, 2386–2387.
30. X. D. Cui, A. Primak, X. Zarate, J. Tomfohr, O. F. Sankey, A. L. Moore, T. A. Moore, D. Gust, G. Harris and S. M. Lindsay, Science, 2001, 294, 571–574.
31. M. Magoga and C. Joachim, Phys. Rev. B, 1997, 56, 4722–4729.
32. S. N. Yaliraki, M. Kemp and M. A. J. Ratner, J. Am. Chem. Soc., 1999, 121, 3428–3434.
33. F. Moresco, L. Gross, M. Alemani, K. H. Rieder, H. Tang, A. Gourdon and C. Joachim, Phys. Rev. Lett., 2003, 91, 36601.
34. B. Q. Xu and N. J. Tao, Science, 2003, 301, 1221–1223.
35. J. K. Gimzewski and R. Moller, Phys. Rev. B, 1987, 36, 1284–1287.
36. J. I. Pascual, J. Mendez, J. Gomez-Herrero, A. M. Baro, N. Garcia and V. T. Binh, Phys. Rev. Lett., 1993, 71, 1852–1855.
37. J. M. Krans, J. M. v. Ruitenbeek, V. V. Fisun, I. K. Yanson and L. J. d. Jongh, Nature, 1995, 375, 767–769.
38. U. Landman, W. D. Luedtke, B. E. Salisbury and R. L. Whetten, Phys. Rev. Lett., 1996, 77, 1362–1365.
39. H. Hakkinen, R. N. Barnett and U. Landman, J. Phys. Chem. B, 1999, 103, 8814–8817.
40. N. Agrait, J. G. Rodrigo and S. Vieira, Phys. Rev. B, 1993, 47, 12345–12348.
41. A. I. Yanson, G. Rubio Bollinger, H. E. van den Brom, N. Agrait and J. M. van Ruitenbeek, Nature, 1998, 395, 783–785.
42. H. Ohnishi, Y. Kondo and K. Takayanagi, Nature, 1998, 395, 780–783.
43. B. Q. Xu, X. Y. Xiao and N. J. Tao, J. Am. Chem. Soc., 2003, 125, 16164–16165.
44. G. Rubio-Bolliger, S. R. Bahn, N. Agrait, K. W. Jacobsen and S. Vieira, Phys. Rev. Lett., 2001, 87, 26101.
45. X. Y. Xiao, B. Q. Xu and N. J. Tao, Nano Lett., 2004, 4, 267–271.
46. J. Chen, W. Wang, M. A. Reed, A. M. Rawlett, D. W. Price and J. M. Tour, Appl. Phys. Lett., 2000, 77, 1224–1226.
47. Y. Luo, C. P. Collier, J. O. Jeppesen, K. A. Nielsen, E. Delonno, G. Ho, J. Perkins, H. R. Tseng, T. Yamamoto, J. F. Stoddart and J. R. Heath, ChemPhysChem, 2002, 3, 519.
48. N. Vedova-Brook, N. Matsunaga and K. Sohlberg, Chem. Phys., 2004, 299, 89–95.
49. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195.
50. L. Scudiero, D. E. Barlow, U. Mazur and K. W. Hipps, J. Am. Chem. Soc., 2001, 123, 4073–4080.
51. W. Schmickler and C. Widrig, J. Electroanal. Chem., 1992, 336, 213–221.
52. A. N. Kuznetsov and W. Schmickler, Chem. Phys., 2002, 282, 371–377.
53. A. M. Kuznetsov and J. Ulstrup, J. Phys. Chem. A, 2000, 104, 11531–11540.
54. X. H. Qiu, G. V. Nazin and W. Ho, Phys. Rev. Lett., 2004, 92, 206102.

---