DOI:
10.1039/B602392D
(Paper)
Dalton Trans., 2006, 2647-2660
Encapsulation of labile trivalent lanthanides into a homobimetallic chromium(III)-containing triple-stranded helicate. Synthesis, characterization, and divergent intramolecular energy transfers†
Received
17th February 2006
, Accepted 20th March 2006
First published on 4th April 2006
Abstract
The segmental bidentate–tridentate–bidentate ligand L2 reacts with MII (M = Cr, Zn) and LnIII (Ln = La, Eu, Gd, Tb, Lu) to give the heterotrimetallic triple-stranded helicates [MLnM(L2)3]7+. For M = ZnII, the isolated complexes [ZnLnZn(L2)3](CF3SO3)7 (Ln = Eu, Tb) display only lanthanide-centred luminescence arising from the pseudo-tricapped trigonal prismatic LnN9 coordination site. For M = CrII, rapid air oxidation provides CrIII and leads to the isolation of inert [CrLnCr(L2)3](CF3SO3)9 (Ln = Eu, Tb) complexes, in which divergent intramolecular Ln → Cr energy transfers can be evidenced. Taking [ZnEuZn(L2)3]7+ as a luminescent standard for Eu-centred emission, a quantitative treatment of the energy migration processes indicates that the rate constant characterizing the Eu → Cr energy transfer is more efficient in the trimetallic system, than in the analogous simple bimetallic edifice. Particular attention is focused on potential control of directional energy transfer processes in Cr–Ln pairs.
Introduction
Due to its high positive charge (+3), small ionic radius (61.5 pm) and considerable ligand-field stabilization energy,1 trivalent chromium, CrIII, mainly exists in coordination chemistry as kinetically inert pseudo-octahedral complexes displaying strong metal–ligand bonds.2 Moreover, the peculiar orbitally non-degenerate quartet ground state, corresponding to the open shell (t2g)3 electronic configuration of octahedral CrIII (4A2g in Oh symmetry), prevents efficient associative pathways for ligand exchanges processes.1–3 Consequently, CrIII complexes combine extreme kinetic inertness (the rate of water exchange in [Cr(H2O)6]3+ amounts to k(298 K) = 2.4 × 10−6 s−1),1,4 with predictable pseudo-octahedral geometries, which makes them ideal coordination models for the refinement of theoretical inorganic kinetic mechanisms3,5 and electronic spectroscopy.6 More recently, some interest has been focussed on the design of sophisticated polymetallic networks with predictable two-dimension and three-dimension organization based on inert negatively charged tris-oxalato [Cr(ox)3]3−,7 or mixed oxalato-bipyridine [Cr(ox)2(bipy)]− building blocks.8 Interestingly, lanthanides have been used as counter-cations in these infinite architectures,8,9 thus producing heterometallic Cr–Ln interactions, but only weak magnetic coupling results from the minute expansion of the 4f orbitals,9 which restricts the design of single molecular magnets (SMM) to extremely low temperatures.10 According to a functional point of view, the Cr–Ln association is more attractive for its optical properties because resonant intermetallic energy transfers depend on the spectral overlap integral ΩDA between the absorption spectrum of the acceptor A, and the emission spectrum of the donor D. They can be thus operative over long distances, if the perturbation operator H′ is of electrostatic origin (Fermi's golden rule, eqn (1), WDA is the probability of the energy transfer).11| | | WDA = (2π/ℏ)|〈DA*|H′|D*A〉|2ΩDA | (1) |
Assuming the common approximation, which limits the electrostatic multipolar series to dipole–dipole interactions, Förster's theory predicts a (RDA)−6 dependence on the separation between the donor and the acceptor (eqn (19), vide infra).12 Applying this treatment to Cr–Ln pairs gives critical distances for 50% energy transfer extending on the nanometric scale with REuCr0 = 11.5 Å,13RTbCr0
≥ 20.1 Å,13RCrNd0 = 12.8 Å14 and RCrYb0 = 9.1 Å at 10 K.14 When strong field α,α’-diimines are coordinated to CrIII as in [Cr(2,2′-bipyridine)3]3+ or [Cr(2-benzimidazol-pyridine)3]3+, the integral overlap ΩLnCr (or ΩCrLn) mainly involves the low-lying excited Cr-centred excited states 2E and 2T1,15 and some adequate Ln-centred levels.13,14 For Ln = Eu and Tb, which possess high-energy emitting levels in the visible range, CrIII may act as an acceptor and Ln → Cr energy transfers, followed by Cr(2E) luminescence, are evidenced.13,16 Conversely, Ln = Nd, Ho, Er, Tm and Yb possess low-energy excited electronic states. CrIII thus acts as a donor, and Cr → Ln energy transfers result in the sensitization of Ln-centred near infrared (NIR) emission.14,17 Although the significant spectral overlap between the transitions of the d-block donor (Cr(4T2g
→
4A2g) and/or Cr(2E →
4A2g)) and specific Ln-centred intra-configurational 4f → 4f absorption bands of NIR Ln-emitters has prompted the introduction of CrIII in weak-field garnets (Al2O3) for sensitizing LnIII (Ln = Nd, Er, Tm) via Cr → Ln energy transfers,18 only a few discrete heterometallic Cr–Ln pairs have been designed for unravelling the mechanism of intramolecular intermetallic optical communication. A first example [(acac)2Cr(µ-ox)Ln(HBpz3)2] (Fig. 1a) has been shown by Kaizaki and co-workers to display intramolecular Ln → Cr (Ln = Eu, Tb) energy transfer processes, which completely quench Ln-centred emission,16b or more interestingly Cr → Ln (Ln = Nd, Ho, Er, Tm, Yb) energy migrations responsible for the dual metal-centred emission of the sensitized LnIII emitter, together with the residual phosphorescence of the Cr(2E) donor level.17c According to a synthetic point of view, the latter heterobimetallic complexes are obtained by the simultaneous complexation of inert [Cr(acac)2(ox)]− and [HBpz3]− to LnIII.17 An alternative strategy uses the labile CrII precursor (the rate of methanol exchange in [Cr(CH3OH)6]2+ amounts to k(298 K) = 1.2 × 108 s−1),19 for producing the self-assembled bimetallic helicate [CrLn(L1)3]5+, which is further oxidized to give the inert CrIII–Ln pair in [CrLn(L1)3]6+ (Fig. 1b, see Fig. 3 for the structures of the ligands).13
![Structures of discrete bimetallic CrLn complexes a) [(acac)2Cr(ox)Ln(HBpz3)2]16b,17 and b) [CrLn(L1)3]6+,13,14 in which intramolecular intermetallic energy transfers have been evidenced.](/image/article/2006/DT/b602392d/b602392d-f1.gif) |
| | Fig. 1 Structures of discrete bimetallic CrLn complexes a) [(acac)2Cr(ox)Ln(HBpz3)2]16b,17 and b) [CrLn(L1)3]6+,13,14 in which intramolecular intermetallic energy transfers have been evidenced. | |
Both intramolecular Ln → Cr (Ln = Eu, Tb)13 and Cr → Ln (Ln = Nd, Yb)14 energy transfers have been evidenced in [CrLn(L1)3]6+, and a quantitative treatment of the energy migration processes according to the simple mechanism shown in Fig. 2 demonstrates that, except for Tb → Cr (kTb,CrET > 3.5 × 104 s−1),13 the rate constants of energy transfers kLn,CrET or kCr,LnET are rather slow and fall within the range 102–103 s−1 for intermetallic Cr⋯Ln separations around 9.0–9.3 Å, taken as acceptable approximations for the donor–acceptor distances RDA.13,14 Therefore, when CrIII is used as a donor for short-lived NIR lanthanide emitters (kLnLum
≈ 104–105 s−1) in these complexes, the combination of the long-lived Cr(2E) level (kCrLum
≈ 300 s−1) with the slow energy transfer process (kCr,LnET
≈ 200 s−1) results in kCrLum
+
kCr,LnET
≪
kLnLum, and the de-excitation of the lanthanide emitter mirrors the long lifetime of the Cr donor (Fig. 2).14 The resulting extended NIR lifetime occurring within the millisecond range (instead of the usual microsecond regime) may greatly help in time-resolved analyses of NIR emitters involved in homogeneous fluoroimmunoassays.20 However, this attractive property is obtained at the cost of the existence of poorly efficient energy transfer processes, and thus a poor sensitization of the NIR lanthanide probe. The only way for improving sensitivity of the NIR emission process without affecting the energy migration regime requires the connection of several [Cr(2-benzimidazol-pyridine)3]3+ donors (similar to that found in [CrLn(L1)3]6+, Fig. 1b) about a central LnIII coordination site, with all Cr⋯Ln distances being fixed at 9.0–9.3 Å.
![Kinetic model for the deactivation and communication between d- and f-block-centred excited levels in [CrLn(L1)3]6+ (Ln = Nd, Eu, Tb, Yb).13,14](/image/article/2006/DT/b602392d/b602392d-f2.gif) |
| | Fig. 2 Kinetic model for the deactivation and communication between d- and f-block-centred excited levels in [CrLn(L1)3]6+ (Ln = Nd, Eu, Tb, Yb).13,14 | |
As a first step toward this goal, we report here on the encapsulation of the tricapped trigonal prismatic LnN9 site between two inert facial [Cr(2-benzimidazol-pyridine)3]3+ stoppers located at ca. 9 Å in the heterotrimetallic triple-stranded helicates [CrLnCr(L2)3]9+ (Fig. 6). Moreover, the LnN9 lanthanide coordination sphere produced in the latter trimetallic helicate is different from LnN6O3 found in [CrLn(L1)3]6+, and we thus focus in this contribution on the thermodynamic, structural and photophysical consequences of this change in the highly charged helicate [CrLnCr(L2)3]9+.
 |
| | Fig. 3 Structures of the ligands L1–L4. | |
Results and discussion
Synthetic and thermodynamic aspects
Self-assembly of [ZnLnZn(L2)3]7+, [CrLnCr(L2)3]7+ and [CrLnCr(L2)3]9+ in solution.
The segmental bidentate–tridentate–bidentate ligand L2 is obtained by the simultaneous reductive cyclization of four ortho-nitroamide groups in the precursor 1 (Scheme 1).21 The 1H NMR spectrum displays 15 signals, which reflect the dynamically average C2v-symmetry of L2 on the NMR time scale (Fig. 4a and Table 1). Although paramagnetic low-spin CrII (S = 1) possesses a fast electronic relaxation time (τe
≈ 10−12 s)22 combined with minor delocalization of the unpaired electrons,23 the increased nuclear relaxation induced for 1H nuclei in [CrLn(L1)3]5+ was shown to be large enough to significantly broaden and shift the signals of the bidentate units bound to CrII, thus preventing reliable assignment.13 The situation is more dramatic for [CrLnCr(L2)3]7+, since each proton undergoes the effect of two paramagnetic CrII centres via through-bond (contact) and through-space (dipolar) mechanisms (Fig. S4a, ESI†).24 We therefore decided to replace labile paramagnetic low-spin CrII with diamagnetic ZnII in order to prepare [ZnLnZn(L2)3]7+, which can be used as a structural model for NMR investigations. Moreover, ESI-MS can be reliably used as a guide for speciation in solution with ZnII, but not with air-sensitive CrII complexes.
Table 1
1H NMR shifts (in ppm with respect to TMS) for the ligand L2 in CDCl3 and its complexes [ZnLnZn(L2)3]7+ in CD3CN at 293 K (Ln = La, Eu, Tb, Lu, Y)
| |
L2 |
[ZnLaZn(L2)3]7+ |
[ZnLuZn(L2)3]7+ |
[ZnYZn(L2)3]7+ |
[ZnEuZn(L2)3]7+ |
[ZnTbZn(L2)3]7+ |
| H1 |
8.48 |
7.88 |
7.85 |
7.88 |
8.44 |
3.62 |
| H2 |
7.61 |
7.76 |
7.78 |
7.78 |
8.11 |
5.33 |
| H3 |
8.19 |
8.06 |
8.10 |
8.09 |
8.57 |
3.22 |
| H4 |
7.32 |
7.07 |
7.20 |
7.17 |
7.60 |
4.38 |
| H5 |
7.21 |
6.86 |
6.91 |
6.90 |
7.13 |
0.42 |
| H6 |
7.67 |
5.11 |
4.95 |
4.98 |
7.22 |
−12.55 |
| H7,H7′ |
4.25 |
3.62, 3.22 |
3.55, 3.26 |
3.56, 3.26 |
4.15, 3.53 |
4.09, 7.44 |
| H8 |
7.63 |
5.88 |
5.37 |
5.49 |
11.40 |
−49.0 |
| H9 |
7.19 |
7.23 |
7.14 |
7.17 |
7.32 |
4.34 |
| H10 |
7.30 |
7.61 |
7.54 |
7.56 |
5.93 |
8.63 |
| H11 |
8.33 |
7.89 |
7.83 |
7.88 |
3.62 |
15.98 |
| H12 |
7.98 |
8.07 |
7.83 |
7.88 |
5.49 |
15.43 |
| H13 |
2.37 |
2.14 |
2.15 |
2.15 |
2.40 |
−0.14 |
| H14 |
4.19 |
3.96 |
4.05 |
3.96 |
4.44 |
0.35 |
| H15 |
4.17 |
3.88 |
3.98 |
4.03 |
2.55 |
16.30 |
ESI-MS titrations of L2 (2 × 10−4 mol dm−3) with Zn(CF3SO3)2·6H2O and La(CF3SO3)3·3H2O in CHCl3/CH3CN (1 : 1) for various Zn : La : L2 ratios are dominated by the formation of homometallic complexes [Zn(L2)2]2+, [Znx(L2)x]2x+ (x = 1, 2) and [La(L2)(CF3SO3)2]+, together with traces of the heterometallic complex [ZnLa(L2)(CF3SO3)3]2+, but no peak corresponding to the target helicate [ZnxLa(L2)3](3 + 2x)+ could be detected (Fig. S1, ESI†). Increasing the total concentration of the ligand to millimolar concentration for the stoichiometric ratio La : Zn : L2 = 1 : 2 : 3 shows the appearance of two weak peaks at m/z = 599.5 and m/z = 786.8 corresponding to [ZnLaZn(L2)3(CF3SO3)2]5+ and [ZnLaZn(L2)3(CF3SO3)3]4+. This behaviour suggests that the highly charged heterotrimetallic helicate is poorly stable in acetonitrile/chloroform mixtures. Parallel titrations at higher concentrations (total ligand concentration 10−2 mol dm−3) have been followed by 1H NMR spectroscopy (Fig. 4b–d). The addition of 0.33 eq. of LaIII to a solution of L2 slightly affects the original spectrum of the free ligand, and new broad signals arise, which are diagnostic for the formation of flexible lanthanide complexes displaying intermediate exchange processes on the NMR time scale (Fig. 4b). The subsequent addition of 0.33 eq. of ZnII to the mixture drastically reduces the intensity of the signals of the free ligands, which are replaced with novel signals associated with the formation of a symmetrical species (Fig. 4c). The latter complex is quantitatively formed when a total amount of 0.66 eq. of ZnII has been added, which corresponds to the stoichiometry La : Zn : L2 = 1 : 2 : 3 expected for entropically maximizing the formation of the target helicate [ZnLaZn(L2)3]7+ in solution (Fig. 4d). We observe 16 signals characterizing one half of a ligand strand L2, which implies an average D3-symmetry. The transformation of the enantiotopic methylene protons H7–H7′ in the free ligand (C2v-symmetry, Fig. 4a) into diastereotopic protons in the final complex (Fig. 4d) confirms the wrapping of the ligand strands, and the removal of the symmetry planes. Finally, the detection of significant intrastrand H11–H15 and H3–H14 NOE effects indicates that both the tridentate and the bidentate binding units adopt the cisoid conformation (i.e. the lone pairs of the nitrogen atoms of the adjacent pyridine and benzimidazole rings point in the same direction) compatible with their chelation to the metal ions. Concomitantly, the coordination of the tridentate and bidentate binding units results in the splitting of the ligand-centred π
→
π* transitions, which allows the investigation of the complexation process by spectrophotometry.25 Titrations of L2 (2 ×10−4 mol dm−3) with Ln(CF3SO3)3·nH2O (Ln = La, Eu, Lu) for L2 : La = 0.1–2.5 : 1 (Fig. S2a and S2b, ESI†), or with Zn(CF3SO3)2·6H2O for L2 : Zn = 0.1–2.5 : 1 (Fig. S2c and S2d, ESI†), or titrations of [Ln(L2)3]3+ (Ln = La, Eu, Lu, total ligand concentration: 2 × 10−4 mol dm−3) with Zn(CF3SO3)2·6H2O for L2 : Zn = 0.1–2.5 : 1 (Fig. 5 and S3, ESI†) in CHCl3/CH3CN (1 : 1) show complicated variations of the absorption spectra. Detailed mathematical analyses by using factor analysis26 and evolving factor analysis27 indicate the existence of a minimum of nine absorbing species (the free ligand and eight complexes) for rationalizing the spectrophotometric data (equilibria 2–9).
| | | 3 L2 + Ln3+
⇌ [Ln(L2)3]3+ log(βLn,L213) | (2) |
| | | 3 L2 + 3 Ln3+
⇌ [Ln3(L2)3]9+ log(βLn,L233) | (3) |
| | | 3 L2 + 4 Ln3+
⇌ [Ln4(L2)3]12+ log(βLn,L243) | (4) |
| | | 2 L2 + Zn2+
⇌ [Zn(L2)2]2+ log(βZn,L212) | (5) |
| | | 2 L2 + 2 Zn2+
⇌ [Zn2(L2)2]4+ log(βZn,L222) | (6) |
| | | 2 L2 + 3 Zn2+
⇌ [Zn3(L2)2]6+ log(βZn,L232) | (7) |
| | | 3 L2 + Ln3+
+ Zn2+
⇌ [ZnLn(L2)3]5+ log(βZn,Ln,L2113) | (8) |
| | | 3 L2 + Ln3+
+ 2 Zn2+
⇌ [ZnLnZn(L2)3]7+ log(βZn,Ln,L2213) | (9) |
![a) Variation of absorption spectra observed for the spectrophotometric titration of [La(L2)3]3+ (total ligand concentration: 2 × 10−4 mol dm−3) with Zn(CF3SO3)2·6H2O at 293 K in CHCl3–CH3CN = 1 : 1 (Zn : L2 = 0.1–2.5 : 1). b) Corresponding variation of observed molar absorption at six different wavelengths.](/image/article/2006/DT/b602392d/b602392d-f5.gif) |
| | Fig. 5 a) Variation of absorption spectra observed for the spectrophotometric titration of [La(L2)3]3+ (total ligand concentration: 2 × 10−4 mol dm−3) with Zn(CF3SO3)2·6H2O at 293 K in CHCl3–CH3CN = 1 : 1 (Zn : L2 = 0.1–2.5 : 1). b) Corresponding variation of observed molar absorption at six different wavelengths. | |
We were however unable to simultaneously and reliably fit the eight stability constants to the experimental data, because the non-linear least-squares procedure showed significant instability. Nevertheless, we systematically observed two end points at Zn : L2 ≈ 0.3 and Zn : L2 ≈ 0.7 for the titrations of [Ln(L2)3]3+ (Ln = La, Eu, Lu) with Zn(CF3SO3)2·6H2O (Fig. 5 and S3, ESI†), in agreement with the successive formation of [ZnLn(L2)3]5+ and [ZnLnZn(L2)3]7+ complexes as the main species in solution under these conditions.
We conclude from the combination of ESI-MS, 1H NMR and spectrophotometric titrations that the target complexes [ZnLnZn(L2)3]7+ can be formed in solution as the major species under a strict stoichiometric ratio Zn : Ln : L2 = 2 : 1 : 3 and millimolar concentrations of the ligand (Fig. 6).
![Schematic representation of the complexation process leading to the triple-stranded helicate [MLnM(L2)3]7+ (M = ZnII, CrII). The structure of the complex corresponds to the optimized D3-symmetrical geometry constructed for [CrIIIEuCrIII(L2)3]9+ by using the crystal structure of [CrIIIEu(L1)3]6+ as model.](/image/article/2006/DT/b602392d/b602392d-f6.gif) |
| | Fig. 6 Schematic representation of the complexation process leading to the triple-stranded helicate [MLnM(L2)3]7+ (M = ZnII, CrII). The structure of the complex corresponds to the optimized D3-symmetrical geometry constructed for [CrIIIEuCrIII(L2)3]9+ by using the crystal structure of [CrIIIEu(L1)3]6+ as model. | |
As expected, the replacement of Zn(CF3SO3)2·6H2O with air-sensitive Cr(CF3SO3)2·H2O produces broad 1H NMR signals for [CrLaCr(L2)3]7+ under strict anaerobic conditions, which are typical of paramagnetic low-spin CrII cations (Fig. S4a, ESI†). We observe 16 signals spread over 70 ppm (−20 to 50 ppm, Fig. S4a, ESI†) compatible with D3-symmetry. Upon air oxidation, the fast colour change from deep green to orange is accompanied by a further drastic broadening of the 1H NMR signals, compatible with the formation of slow-relaxing CrIII (τe
≈ 10−9 s, Fig. S4b, ESI†).4 This CrII
→ CrIII oxidation is confirmed by the variation of the electronic absorption spectra recorded for [CrLnCr(L2)3]7+ and [CrLnCr(L2)3]9+ (Ln = Eu, Lu, Fig. 7 and Table 2). As previously discussed in detail for the absorption spectrum of [CrLn(L1)3]5+,13 the [CrLnCr(L2)3]7+ complexes show intense UV bands assigned to ligand-centred π
→
π* transitions, together with less intense LMCT transitions occurring at low energy (8280 cm−1, ε = 3250 M−1 cm−1; 9460 cm−1, ε = 1840 M−1 cm−1, Table 2), which compare well with those found in [Cr(2,2′-bipyridine)3]2+ (8700 cm−1, ε = 10000 M−1 cm−1; 9900 cm−1, ε = 2900 M−1 cm−1)28 and in [CrLn(L1)3]5+ (8300 cm−1, ε = 4300 M−1 cm−1; 9090 cm−1, ε = 2900 M−1 cm−1).13 The series of poorly resolved bands in the range 11000–25000 cm−1 correspond to overlapping low-spin CrII-centred d–d transitions possessing significant CT character (a detailed assignment is given in Table 2).13
Table 2 Electronic spectral data for the heterometallic complexes [CrIILnCrII(L2)3]7+ and [CrIIILnCrIII(L2)3]9+ in acetonitrile at 293 Ka
| Compound |
π
→
π* |
d → d + CT |
Attribution |
|
Energies are given for the maximum of the band envelope in cm−1 and ε (in parentheses) in M−1 cm−1; sh = shoulder, CT = charge transfer, LMCT = ligand-to-metal charge transfer.
|
| L2 |
31150 (85800) |
|
|
| [CrEuCr(L2)3]7+ |
40490 (107100 sh) |
25550 (29550 sh) |
3T1
→
3T2(b) + CT |
| |
31150 (121490) |
20000 (3100 sh) |
3T1
→
3E(b) + CT |
| |
27550 (94150 sh) |
16640 (1720) |
3T1
→
3A1
+
3A2
+ CT |
| |
|
14184 (1460) |
3T1
→
3T1(a) +
3T2(a)+ CT |
| |
|
11450 (1530) |
3T1
→
3E(a) + CT |
| |
|
9460 (1840 sh) |
LMCT |
| |
|
8280 (3250) |
LMCT |
| [CrLuCr(L2)3]7+ |
40650 (130500 sh) |
25400 (49500 sh) |
3T1
→
3T2(b) + CT |
| |
31150 (149800) |
20000 (4630 sh) |
3T1
→
3E(b) + CT |
| |
27300 (86700 sh) |
16690 (2370) |
3T1
→
3A1
+
3A2
+ CT |
| |
|
14200 (2700) |
3T1
→
3T1(a) +
3T2(a) + CT |
| |
|
11765 (3140) |
3T1
→
3E(a) + CT |
| |
|
10225 (2700) |
LMCT |
| |
|
8300 (4290) |
LMCT |
| [CrEuCr(L2)3]9+ |
40160 (109400 sh) |
27250 (85740) |
4A2
→
4T1
+ CT |
| |
31350 (136550) |
20000 (1460) |
4A2
→
4T2
+ CT |
| |
27250 (85740) |
|
|
| [CrLuCr(L2)3]9+ |
40160 (100630 sh) |
27100 (68000) |
4A2
→
4T1
+ CT |
| |
31350 (131900) |
20000 (2680 sh) |
4A2
→
4T2
+ CT |
| |
27100 (68000) |
|
|
Upon air oxidation, the low-energy L2 → CrII LMCT and the spin-allowed CrII-centred transition responsible for the deep green colour of [CrLnCr(L2)3]7+ are replaced by a shoulder on the low-energy side of the ligand-centred π
→
π* transitions (Fig. 7), which is assigned to the novel spin-allowed CrIII-centred 4A2
→
4T2 and 4A2
→
4T1 transitions (in Oh symmetry), mixed with MLCT bands in the orange complex [CrLnCr(L2)3]9+. Obviously, the oxidized CrLnCr complexes are stable enough to be analyzed with ESI-MS, and the resulting spectra show the exclusive formation of [CrLnCr(L2)3]9+ characterized by a series of adducts [CrLnCr(L2)3(CF3SO3)x](9−x)+ (x = 0–7, Fig. S5, ESI†).
Isolation and characterization of of [ZnLnZn(L2)3](CF3SO3)7 and [CrLnCr(L2)3](CF3SO3)9 (Ln = La, Eu, Gd, Tb, Lu).
Stoichiometric mixing of L2, Ln(CF3SO3)3·nH2O (Ln = La, Eu, Gd, Tb, Lu) and Zn(CF3SO3)2·6H2O (3 : 1 : 2) in dichloromethane/acetonitrile (1 : 1) followed by slow diffusion of diethyl ether yields 70–82% of microcrystalline needles of [ZnLnZn(L2)3](CF3SO3)7·nH2O (Ln = La, n = 5; Ln = Eu, n = 7; Ln = Gd, n = 8; Ln = Tb, n = 6; Ln = Lu, n = 6, Table S1, ESI†). Replacement of Zn(CF3SO3)2·6H2O with Cr(CF3SO3)2·H2O13 under nitrogen atmosphere provides deep green solutions of [CrLnCr(L2)3]7+. Air oxidation combined with the addition of nBu4N(CF3SO3) (2 eq.) in acetonitrile followed by fractional crystallization with diethyl ether give 73–88% of yellow microcrystalline solids, whose elemental analyses correspond to [CrLnCr(L2)3](CF3SO3)9·nH2O·pnBu4N(CF3SO3) (Ln = La, n = 12, p = 0.1; Ln = Eu, n = 8, p = 0.1; Ln = Gd, n = 9, p = 0.3; Ln = Tb, n = 7, p = 0.3; Ln = Lu, n = 10, p = 0.3, Table S1, ESI†). The presence of small amounts of co-crystallized nBu4N(CF3SO3) in the final CrLnCr complexes has been confirmed by 1H NMR spectroscopy. Re-dissolution of all complexes in CH3CN at millimolar concentrations provides 1H NMR, ESI-MS and electronic absorption spectra identical to those obtained during the investigation of the self-assembly process occurring in solution. For simplifying the rest of the discussions, the solid [ZnLnZn(L2)3](CF3SO3)7·nH2O and [CrLnCr(L2)3](CF3SO3)9·nH2O·pnBu4N(CF3SO3) complexes will be termed ZnLnZn and CrLnCr, respectively.
Structural aspects
X-Ray diffraction study of CrEuCr.
Despite numerous attempts for re-crystallizing ZnLnZn or CrLnCr complexes, we were unable to obtain single crystals of sufficient quality for high-resolution X-ray diffraction studies. However, diffusion of di-isopropylether into a nitromethane solution of [CrEuCr(L2)3]9+ provides prisms, for which a monoclinic unit cell with a = 28.79 Å, b = 16.63 Å, c = 43.86 Å, β = 104.8° and V = 20300 Å3 can be determined. The volume of the unit cell compares well with V = 25888 Å3 (monoclinic, P21/c, Z = 4) found for a closely related heterotrimetallic triple-stranded helical complex [EuLaEu(L′)3](CF3SO3)9(CH3NO2)9, in which the ligand L′ is identical to L2, except for the replacement of the two terminal 5-methylpyridine groups with 6-(N,N′-diethylcarboxy)pyridine groups.29
High-resolution emission spectroscopy of ZnEuZn and CrEuCr.
In the absence of X-ray crystal structure data, the nature and geometry of the lanthanide coordination site in ZnLnZn and CrLnCr have been addressed by using EuIII as a structural probe and high-resolution emission spectroscopy.30 The excitation spectrum of ZnEuZn recorded upon monitoring the Eu(5D0
→
7F2) transition displays ligand-centred π
→
π* absorptions, together with specific narrow peaks typical for Eu-centred intra-configurational 4f → 4f absorptions (Fig. S6a, ESI†). The high-resolution excitation profile of the Eu(5D0
←
7F0) transition in ZnEuZn at 10 K shows a single and symmetrical band (full width at half height, fwhh = 19.8 cm−1) indicating the existence of a single EuIII coordination site in a polycrystalline material (Fig. 8a).30 The energy of the Eu(5D0
←
7F0) transition at 295 K (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) in cm−1) can be correlated with the ability of the coordinated atoms to produce a nephelauxetic effect according to eqn (10)31
in cm−1) can be correlated with the ability of the coordinated atoms to produce a nephelauxetic effect according to eqn (10)31| |  | (10) |
(CCN is an empirical parameter depending on the coordination number of EuIII, CCN = 1 for nine-coordinate sites, ni is the number of i-type atoms in the coordination sphere, δi is the ability of atom i to accept electronic delocalization from the metal with δi = −15.3 cm−1 for heterocyclic nitrogen atoms,32,33 and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0 = 17374 cm−1 is the energy of Eu(7F0
→
5D0) for the free ion). For the pseudo-tricapped trigonal EuN9 site proposed in the model of ZnEuZn (Fig. 6), we calculate
0 = 17374 cm−1 is the energy of Eu(7F0
→
5D0) for the free ion). For the pseudo-tricapped trigonal EuN9 site proposed in the model of ZnEuZn (Fig. 6), we calculate ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 17236 cm−1 at 295 K, which translates into
= 17236 cm−1 at 295 K, which translates into ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 17224 cm−1 at 10 K (assuming the accepted 1 cm−1/24 K dependence of the energy of the Eu(5D0
←
7F0) transition with temperature).30 This prediction matches fairly well the experimental value found for ZnEuZn (17221 cm−1 at 10 K, Table 3), and those previously reported for [ZnEu(L3)3]5+ (17224 cm−1 at 10 K, Table 3)32 and [Eu(L4)3]3+ (17223 cm−1 at 10 K, Table 3),34 in which the existence of the pseudo-tricapped trigonal prismatic EuN9 site has been unambiguously evidenced in the associated X-ray crystal structures.
= 17224 cm−1 at 10 K (assuming the accepted 1 cm−1/24 K dependence of the energy of the Eu(5D0
←
7F0) transition with temperature).30 This prediction matches fairly well the experimental value found for ZnEuZn (17221 cm−1 at 10 K, Table 3), and those previously reported for [ZnEu(L3)3]5+ (17224 cm−1 at 10 K, Table 3)32 and [Eu(L4)3]3+ (17223 cm−1 at 10 K, Table 3),34 in which the existence of the pseudo-tricapped trigonal prismatic EuN9 site has been unambiguously evidenced in the associated X-ray crystal structures.
Table 3 Energy (cm−1) of the identified crystal-field sublevels of the Eu(7FJ) manifold (J = 1–4) and Eu(5D0) in [ZnEuZn(L2)3](CF3SO3)7(H2O)7, [ZnEu(L3)3](ClO4)5(H2O)4,32 [Eu(L4)3](ClO4)3,34 [ZnEu(L1)3](CF3SO3)4(ClO4)(CH3CN)4,33 [CrEuCr(L2)3](CF3SO3)9(H2O)8(nBu4NCF3SO3)0.1 and [CrEu(L1)3](CF3SO3)5(H2O)413 as determined from excitation and emission spectra in the solid state at 10 K; 7F0 is taken as the origin
| Compound |
[ZnEuZn(L2)3]7+ |
[ZnEu(L3)3]5+ |
[Eu(L4)3]3+ |
[ZnEu(L1)3]5+ |
[CrEuCr(L2)3]9+ |
[CrEu(L1)3]6+ |
| Site |
EuN9 |
EuN9 |
EuN9 |
EuN6O3 |
EuN9 |
EuN6O3 |
| Ref. |
This work |
32 |
34 |
33 |
This work |
13 |
|
7F0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
7F1 |
312 |
315 |
300 |
294 |
326 |
320 |
| |
394 |
387 |
410 |
411 |
389 |
368 |
| |
426 |
430 |
427 |
432 |
423 |
444 |
|
7F2 |
990 |
987 |
986 |
984 |
989 |
980 |
| |
1011 |
1027 |
1009 |
1002 |
1015 |
997 |
| |
1071 |
1067 |
1077 |
1043 |
1068 |
1053 |
| |
1095 |
1097 |
1089 |
1085 |
1083 |
1113 |
|
7F3 |
1825 |
1825 |
1819 |
1824 |
1824 |
1829 |
|
7F4 |
2692 |
2694 |
2693 |
2706 |
2692 |
2697 |
| |
2714 |
2717 |
2715 |
2717 |
2713 |
2724 |
| |
2772 |
2774 |
2754 |
2799 |
2780 |
2806 |
| |
2841 |
2843 |
2785 |
2860 |
2838 |
2846 |
| |
2872 |
2874 |
2876 |
2888 |
2869 |
2894 |
| |
2980 |
2981 |
2981 |
2990 |
2981 |
2983 |
|
5D0 |
17221 |
17224 |
17223 |
17220 |
17218 |
17216 |
The detailed analysis of the crystal-field splitting of the Eu(5D0
→
7FJ) (J = 0–6, Table 3) in the emission spectrum of ZnEuZn (Fig. 8b) is diagnostic for a distorted trigonal symmetry around EuIII. The Eu(5D0
→
7F0), which is forbidden in D3 by symmetry-related selection rules, but allowed in C3 point group, is extremely weak. The magnetically-allowed Eu(5D0
→
7F1) transition is split into one singlet (A1
→ A2, 312 cm−1 above 7F0, Table 3) and one doublet (A1
→ E, barycentre 410 cm−1 above 7F0, Table 3), with ΔEA–E = 98 cm−1; further splitting of the A1
→ E component (ΔEE–E = 32 cm−1) is assigned to deviation from ideal trigonal symmetry.34 Interestingly, a point charge electrostatic model predicts that the energetic separation ΔEA–E between the 7F1(A) and 7F1(E) sublevels is proportional to the absolute magnitude of the second-rank crystal-field parameter |B20|, while deviation from trigonal symmetry involves the additional second-rank crystal-field parameter |B22|, which is proportional to the splitting of the 7F1(E) sublevel (ΔEE–E).35 We thus deduce that the symmetry of the EuN9 site is very similar in ZnEuZn (ΔEA–E = 98 cm−1, ΔEE–E = 32 cm−1, Table 3), and in the analogous heterobimetallic complex [ZnEu(L3)3]5+ (ΔEA–E = 94 cm−1, ΔEE–E = 43 cm−1, Table 3),32 but slightly more distorted than in the less constrained monometallic complex [Eu(L4)3]3+ (ΔEA–E = 119 cm−1, ΔEE–E = 17 cm−1, Table 3).34 The forced electric dipole Eu(5D0
→
7F2) transition comprises two main bands, assigned to the allowed A1
→ E components in D3 symmetry, which are further split into two components each (ΔEE–E = 21–24 cm−1, Table 3). We could not unambiguously detect the A1
→ A1 transition, which is forbidden in D3-symmetry, but allowed in C3-symmetry, thus confirming a minor distortion from tricapped trigonal prismatic microsymmetry around EuIII. Again close similarity of the crystals field splitting of the Eu(7FJ) levels (J = 0–6, Table 3) observed in ZnEuZn, with those reported for [ZnEu(L3)3]5+32 and [Eu(L4)3]3+34 indicates very similar EuN9 sites in the three complexes. The long Eu(5D0) lifetime determined for ZnEuZn at 10 K (1.94–2.05 ms, Table 4 and Table S2, ESI†) also agrees with similar measurements performed for [ZnEu(L3)3]5+ (1.96(7) ms)32 and [Eu(L4)3]3+ (1.87(4) ms).34 Moreover, the typical fast decrease of the Eu(5D0) lifetime with increasing temperature (Fig. S7, ESI†) is the signature of the existence of a low-lying LMCT state, which efficiently quenches Eu(5D0) emission at room temperature.36 This effect has been investigated in details for [Eu(L4)3]3+,36 and it arises from the coordination of nine heterocyclic nitrogen atoms to EuIII, which favours the EuIII
→ EuII reduction process.
Table 4 Emission Eu(5D0) lifetimes and associated rate constants for the complexes [ZnEuZn(L2)3]7+, [CrEuCr(L2)3]9+, [ZnEu(L1)3]5+,33 and [CrEu(L1)3]6+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13
13
| Compound |
T/K |
τ
MEuMobs/ms |
k
MEuMobs/ms−1 |
η
CrEuCrglobal
a (%) |
k
Eu,CrET
b/ms−1 |
R
EuCr0
c/Å |
Reference |
|
Calculated with eqn (14).
Calculated with eqn (17).
Calculated with eqn (19).
10−3 mol dm−3 in acetonitrile solution.
|
| [ZnEuZn(L2)3]7+ |
10 |
1.96(1) |
0.510(3) |
|
|
|
This work |
| |
295 |
0.69(4) |
1.45(9) |
|
|
|
This work |
| |
10d |
2.21(5) |
0.45(1) |
|
|
|
This work |
| |
295d |
1.48(1) |
0.680(5) |
|
|
|
This work |
| [CrEuCr(L2)3]9+ |
10 |
0.20(1) |
5.0(3) |
90(4) |
2.2(1) |
11.9(2) |
This work |
| |
295 |
0.10(1) |
10(1) |
86(8) |
4.3(4) |
11.2(4) |
This work |
| |
10d |
0.24(1) |
4.2(2) |
89(6) |
1.9(1) |
11.8(2) |
This work |
| |
295d |
0.076(1) |
13.2(2) |
95(8) |
6.2(5) |
13.5(3) |
This work |
| Compound |
T/K |
τ
EuMobs/ms |
k
EuMobs/ms−1 |
η
EuCr (%) |
k
Eu,CrET
b/ms−1 |
R
EuCr0/Å |
Reference |
| [EuZn(L1)3]5+ |
10 |
2.53(1) |
0.400(2) |
|
|
|
33
|
| |
295 |
1.67(2) |
0.60(2) |
|
|
|
33
|
| [CrEu(L1)3]6+ |
10 |
0.55(4) |
1.8(1) |
78(5) |
1.42(9) |
11.5(1) |
13
|
| |
295 |
0.59(1) |
1.69(3) |
65(4) |
1.10(7) |
10.3(1) |
13
|
For CrEuCr, the excitation spectrum recorded upon monitoring the Eu(5D0
→
7F2) transition mainly shows the ligand-centred π
→
π* absorption as previously described for ZnEuZn (Fig. S6b, ESI†). When the analysis wavelength is set on the Cr(2E →
4A2) transition, the excitation profile is completed by direct sensitization of the spin-allowed Cr-centred 4A2
→
4T2 transition at 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 (Fig. S6b, ESI†). Upon excitation of the π
→
π* transitions, the emission spectrum displays the narrow Eu(5D0
→
7FJ) transitions (J = 0–4), together with Cr(2E →
4A2) transitions, the latter masking the weaker Eu(5D0
→
7FJ) (J = 5–6) emission bands (Fig. 8c). Both the energy (13245 cm−1 at 10 K, Table S2, ESI†) of the Cr(2E →
4A2) transition and the associated Cr(2E) lifetime (2.08–2.10 ms, Table S2, ESI†) are comparable with those reported for [CrEu(L1)3]6+ (13301 cm−1 at 10 K, τ = 3.46 ms),13 in agreement with the existence of similar terminal trigonally distorted [Cr(2-benzimidazol-pyridine)3]3+ chromophores in the bi- and trimetallic complexes. The crystal-field splitting of the Eu-centred transitions in CrEuCr is almost identical to that obtained for ZnEuZn (Table 3), thus pointing to very similar EuN9 coordination sites in both trimetallic complexes (from the splitting of the Eu(5D0
→
7F1) transition, we calculate ΔEA–E = 80 cm−1, ΔEE–E = 34 cm−1, Table 3). It is worth noting that Cr-centred excitation at 21470 cm−1 (Cr(4A2
→
4T2)) results in the exclusive detection of the Cr(2E →
4A2) emission, in line with the absence of intramolecular Cr → Eu energy transfer processes. However, the reverse situation is found upon Eu-centred excitation (i.e observation of the luminescence of both Eu-centred and Cr-centred emission), which implies the existence of a partial Eu → Cr energy transfer (Fig. 10, vide infra) responsible for the reduced Eu(5D0) lifetime measured in CrEuCr (τ = 0.20–0.24 ms at 10 K, Tables 4 and S2, ESI†). We can therefore safely conclude from the X-ray diffraction and high-resolution emission studies that (i) ZnEuZn and CrEuCr exhibit very similar structures, (ii) the terminal d-block ions are pseudo-octahedrally coordinated by three bidentate 2-benzimidazolpyridine units and (iii) europium is encapsulated within a slightly distorted tricapped trigonal prismatic EuN9 site provided by the three wrapped central tridentate 2,6-bis(benzimidazol-2-yl)pyridine units, as found in the D3-symmetrical complex [Eu(L4)3]3+. All these characteristics are compatible with the structural model shown in Fig. 6.
500 cm−1 (Fig. S6b, ESI†). Upon excitation of the π
→
π* transitions, the emission spectrum displays the narrow Eu(5D0
→
7FJ) transitions (J = 0–4), together with Cr(2E →
4A2) transitions, the latter masking the weaker Eu(5D0
→
7FJ) (J = 5–6) emission bands (Fig. 8c). Both the energy (13245 cm−1 at 10 K, Table S2, ESI†) of the Cr(2E →
4A2) transition and the associated Cr(2E) lifetime (2.08–2.10 ms, Table S2, ESI†) are comparable with those reported for [CrEu(L1)3]6+ (13301 cm−1 at 10 K, τ = 3.46 ms),13 in agreement with the existence of similar terminal trigonally distorted [Cr(2-benzimidazol-pyridine)3]3+ chromophores in the bi- and trimetallic complexes. The crystal-field splitting of the Eu-centred transitions in CrEuCr is almost identical to that obtained for ZnEuZn (Table 3), thus pointing to very similar EuN9 coordination sites in both trimetallic complexes (from the splitting of the Eu(5D0
→
7F1) transition, we calculate ΔEA–E = 80 cm−1, ΔEE–E = 34 cm−1, Table 3). It is worth noting that Cr-centred excitation at 21470 cm−1 (Cr(4A2
→
4T2)) results in the exclusive detection of the Cr(2E →
4A2) emission, in line with the absence of intramolecular Cr → Eu energy transfer processes. However, the reverse situation is found upon Eu-centred excitation (i.e observation of the luminescence of both Eu-centred and Cr-centred emission), which implies the existence of a partial Eu → Cr energy transfer (Fig. 10, vide infra) responsible for the reduced Eu(5D0) lifetime measured in CrEuCr (τ = 0.20–0.24 ms at 10 K, Tables 4 and S2, ESI†). We can therefore safely conclude from the X-ray diffraction and high-resolution emission studies that (i) ZnEuZn and CrEuCr exhibit very similar structures, (ii) the terminal d-block ions are pseudo-octahedrally coordinated by three bidentate 2-benzimidazolpyridine units and (iii) europium is encapsulated within a slightly distorted tricapped trigonal prismatic EuN9 site provided by the three wrapped central tridentate 2,6-bis(benzimidazol-2-yl)pyridine units, as found in the D3-symmetrical complex [Eu(L4)3]3+. All these characteristics are compatible with the structural model shown in Fig. 6.
![Correlation between Ln⋯Hi distances observed in the crystal structure of [ZnEu(L1)3]5+,33 and those determined by paramagnetic 1H NMR in acetonitrile with eqn (13) for [ZnTbZn(L2)3]7+ (H6 is used as a reference, see text).](/image/article/2006/DT/b602392d/b602392d-f9.gif) |
| | Fig. 9 Correlation between Ln⋯Hi distances observed in the crystal structure of [ZnEu(L1)3]5+,33 and those determined by paramagnetic 1H NMR in acetonitrile with eqn (13) for [ZnTbZn(L2)3]7+ (H6 is used as a reference, see text). | |
![Kinetic model for the deactivation and communication of f-block and d-block-centred excited levels in [MLnM(L2)3]9+ (M = Cr, Ln = Eu, Tb).](/image/article/2006/DT/b602392d/b602392d-f10.gif) |
| | Fig. 10 Kinetic model for the deactivation and communication of f-block and d-block-centred excited levels in [MLnM(L2)3]9+ (M = Cr, Ln = Eu, Tb). | |
1H NMR spectroscopy of ZnLnZn in solution (Ln = La, Eu, Tb, Lu, Y).
Although the emission spectra become broader in solution, the conservation of both crystal-field splitting patterns and lifetimes for Eu- and Cr-centred luminescence, observed when dissolving microcrystals of ZnEuZn in acetonitrile (10−3 mol dm−3, Table S2, ESI†), demonstrates that the solid-state structure is maintained in solution, as previously established for [ZnEu(L3)3]5+32 and [ZnEu(L1)3]5+.33 The 1H NMR spectra of [ZnLnZn(L2)3]7+ (Ln = La, Eu, Tb, Lu, Y) systematically show eleven aromatic C–Hi signals (i = 1–6 and 8–12, numbering in Fig. 4), together with AB spin systems for the diastereotopic methylene protons H7,H7′, which implies dynamically averaged D3-symmetry for the trimetallic complexes in solution (Table 1 and Fig. 4d). The unusual shielding of H6 and H8 in the diamagnetic complexes [ZnLnZn(L2)3]7+ (Ln = La, Lu, Y, Table 1) is diagnostic for the wrapping of the three strands about the metal ions, which puts these protons in the shielding region of the benzimidazole ring of an adjacent strand (Fig. 6), as previously established for the analogous bimetallic triple-helical complexes [ZnEu(L3)3]5+ (δH6 = 5.02 ppm, δH8 = 5.42 ppm),32 and [ZnEu(L1)3]5+ (δH6 = 5.34 ppm, δH8 = 5.44 ppm).33 In order to obtain intramolecular Ln⋯Hi distances in [ZnLnZn(L2)3]7+, we have resorted to the extra nuclear relaxation induced by the lanthanide electronic spin. For fast-relaxing paramagnetic lanthanides (Ln = Ce–Yb, except Gd), the increase of the longitudinal nuclear relaxation rate for a proton Hi| | | 1/Tparali = 1/Texpli
− 1/Tdiali | (11) |
is dominated by dipolar electron–nucleus interactions modelled with eqn (12), whereby the constants have their usual meaning, µeff is the electronic effective magnetic moment, H0 is the magnetic field, τr and τe are the rotational and electronic correlation times, and ri is the Ln⋯Hi distance.24| |  | (12) |
Since both transient and static (i.e. Curie spin) dipolar contributions depend on r−6i for a given complex at fixed temperature, we deduce that 1/Tparali is simply proportional to r−6i with a scaling factor Ej, which is maximum for lanthanide cations possessing a large magnetic momentum (µeff is maximum) at high magnetic fields (H0 is maximum). When a reference Ln⋯Hi distance, rref, is accessible in a lanthanide paramagnetic complex, all the remaining Ln⋯Hi distances can be easily determined from the measurement of the paramagnetic longitudinal relaxation rates with eqn (13).24
| |  | (13) |
Because TbIII complexes possess large electronic magnetic momenta,24 we have focused on [ZnTbZn(L2)3]7+, for which the experimental characteristic longitudinal relaxation times Texpli have been determined by 1H NMR spectroscopy (Table S3, ESI†). After correcting for the diamagnetic contribution Tdiali measured in [ZnLuZn(L2)3]7+ (eqn (11) and Table S3, ESI†), the resulting paramagnetic contributions Tparali have been used to compute ri with eqn (13). Since the diamagnetic shifts of H6 are almost identical in [ZnLu(L1)3]5+, [ZnLu(L3)3]5+ and in [ZnLuZn(L2)3]7+ despite their extreme sensitivity to the exact wrapping of the strands, we can safely conclude that H6 occupy very similar positions in the three complexes, and the Eu⋯H6 distance observed in the crystal structure of [ZnEu(L1)3](CF3SO3)4(ClO4)(CH3CN)4 has been used as reference (rref = 6.7 Å).33 The Tb⋯Hi distances calculated for [ZnTbZn(L2)3]7+ with eqn (13) are collected in Table S3 (i = 1–5 and 8–2, ESI†), and they closely match those found in the crystal structure of [ZnEu(L1)3]5+ (Fig. 9). We conclude that the triple-helical organization of the strands about the Zn⋯Ln axis is very similar in [ZnEu(L1)3]5+ and in [ZnTbZn(L2)3]7+, which further justifies the model proposed in Fig. 6 for the heterotrimetallic complexes [MLnM(L2)3]7/9+ (M = Cr, Ln). Moreover, the crystal structure of [ZnEu(L1)3]5+,33 which is almost superimposable with that of [CrEu(L1)3]6+,13 can be used as a reliable structural model for the ‘asymmetric unit’ of the D3-symmetrical trimetallic complexes [MLnM(L2)3]7/9+ (M = Cr, Ln).
Functional aspects
Indirect sensitization processes involving ligand-to-metal energy transfer processes in ZnLnZn and CrLnCr (Ln = Eu, Gd).
In the absence of L2 → metal transfer in ZnGdZn (i.e. neither ZnII nor GdIII possess accessible excited states for accepting energy from L(ππ*)), the coordinated tritopic ligand L2 shows a broad and poorly structured emission band in the 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800–16
800–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range (
000 cm−1 range (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) max = 18
max = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1). Its associated lifetime is bi-exponential with τ1 = 2.45 ms (86%) and τ2 = 0.49 ms (14%), which is typical for emissions arising from the L2(3ππ*) excited states located on different parts of the ligand, due to the isolating effects of the methylene spacers.32,33 At 295 K, efficient thermally-activated non-radiative processes reduce L2(3ππ*) lifetimes to τ1 = 42 µs (64%) and τ2 = 6 µs (36%). Upon replacement of ZnII with CrIII in CrGdCr, the L2(3ππ*) band is shifted by approximately 5500 cm−1 toward higher energy (26
900 cm−1). Its associated lifetime is bi-exponential with τ1 = 2.45 ms (86%) and τ2 = 0.49 ms (14%), which is typical for emissions arising from the L2(3ππ*) excited states located on different parts of the ligand, due to the isolating effects of the methylene spacers.32,33 At 295 K, efficient thermally-activated non-radiative processes reduce L2(3ππ*) lifetimes to τ1 = 42 µs (64%) and τ2 = 6 µs (36%). Upon replacement of ZnII with CrIII in CrGdCr, the L2(3ππ*) band is shifted by approximately 5500 cm−1 toward higher energy (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–20
000–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range,
000 cm−1 range, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) max = 24
max = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 cm−1 at 10 K), while its lifetimes are only marginally reduced with respect to those measured in ZnGdZn (Table S4, ESI†). This suggests that (i) the bidentate binding units co-ordinated to the d-block ion strongly contributes to the ligand-centred 3ππ* emission and (ii) the L2(3ππ*) → CrIII transfer is poorly efficient. Conversely, only a faint residual ligand-centred 3ππ* emission is detected in the emission spectra of ZnEuZn and CrEuCr, which points to an efficient L2(3ππ*) → EuIII sensitization process, as similarly reported for [ZnEu(L3)3]5+,32 [ZnEu(L1)3]5+33 and [CrEu(L1)3]6+.13 We conclude that the energy of L2(3ππ*) in the complexes MLnM is more adequate for resonant energy transfer processes with EuIII than with CrIII.
450 cm−1 at 10 K), while its lifetimes are only marginally reduced with respect to those measured in ZnGdZn (Table S4, ESI†). This suggests that (i) the bidentate binding units co-ordinated to the d-block ion strongly contributes to the ligand-centred 3ππ* emission and (ii) the L2(3ππ*) → CrIII transfer is poorly efficient. Conversely, only a faint residual ligand-centred 3ππ* emission is detected in the emission spectra of ZnEuZn and CrEuCr, which points to an efficient L2(3ππ*) → EuIII sensitization process, as similarly reported for [ZnEu(L3)3]5+,32 [ZnEu(L1)3]5+33 and [CrEu(L1)3]6+.13 We conclude that the energy of L2(3ππ*) in the complexes MLnM is more adequate for resonant energy transfer processes with EuIII than with CrIII.
Cr-centred luminescence in [CrLnCr(L2)3](CF3SO3)9 (Ln = Eu, Gd, Tb).
Excitation through the ligand-centred ππ* (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exc = 28170 cm−1) or via CrIII-centred 4A2
→
4T2 (
exc = 28170 cm−1) or via CrIII-centred 4A2
→
4T2 (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exc = 20492 cm−1, Fig. S6d†) in CrGdCr produces identical emission spectra displaying the characteristic Cr(2E →
4A2) transition at 13
exc = 20492 cm−1, Fig. S6d†) in CrGdCr produces identical emission spectra displaying the characteristic Cr(2E →
4A2) transition at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 245 cm−1, combined with weak Stokes phonon side bands (13
245 cm−1, combined with weak Stokes phonon side bands (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100–12
100–12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1, Fig. S8, ESI†), in good agreement with a similar behaviour reported for [CrGd(L3)3]6+ (13
900 cm−1, Fig. S8, ESI†), in good agreement with a similar behaviour reported for [CrGd(L3)3]6+ (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301 cm−1).33 The Cr(2E) lifetime at 10 K is long (2.27(1) ms, Table S2, ESI†) and points to only minor non-radiative processes affecting the CrIII-centred emission. However, both intensity (Fig. S8, ESI†) and lifetime of the Cr(2E) emission in CrGdCr dramatically decrease at higher temperature (τ295 K = 0.031 ms, Table S2, ESI†), which is tentatively attributed to thermally-activated energy migration processes, as previously discussed for [CrGd(L1)3]6+.13,37 Moreover, the maximum of the Cr(2E →
4A2) emission band shifts from 13
301 cm−1).33 The Cr(2E) lifetime at 10 K is long (2.27(1) ms, Table S2, ESI†) and points to only minor non-radiative processes affecting the CrIII-centred emission. However, both intensity (Fig. S8, ESI†) and lifetime of the Cr(2E) emission in CrGdCr dramatically decrease at higher temperature (τ295 K = 0.031 ms, Table S2, ESI†), which is tentatively attributed to thermally-activated energy migration processes, as previously discussed for [CrGd(L1)3]6+.13,37 Moreover, the maximum of the Cr(2E →
4A2) emission band shifts from 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 245 cm−1 at 10 K to 13
245 cm−1 at 10 K to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316 cm−1 at 295 K (ΔE = 71 cm−1, Fig. S8, ESI†), a change in energy much larger than ΔE = 15 cm−1 expected for the splitting of the Cr(2E) level by trigonal symmetry, which accounts for the hot band emission in the model complex [Cr(2,2′-bipyridine)3]3+.37b We thus suspect that the long-lived luminescence observed at 10 K indeed originates from pseudo-octahedral CrN6 chromophores found in CrGdCr. At room temperature, fast energy migration processes combined with the existence of small amounts of killer sites provided by minor crystal defects and/or photochemical degradations are responsible for the short shifted Cr(2E →
4A2) emission. For CrEuCr and CrTbCr, the long-lived CrIII-centred emission is strictly maintained at 10 K, whatever the origin of the sensitization process, i.e. via ligand-centred or Ln-centred excited states (Fig. 8b, Table S2, ESI†), consistent with no Cr → Eu energy transfer.
316 cm−1 at 295 K (ΔE = 71 cm−1, Fig. S8, ESI†), a change in energy much larger than ΔE = 15 cm−1 expected for the splitting of the Cr(2E) level by trigonal symmetry, which accounts for the hot band emission in the model complex [Cr(2,2′-bipyridine)3]3+.37b We thus suspect that the long-lived luminescence observed at 10 K indeed originates from pseudo-octahedral CrN6 chromophores found in CrGdCr. At room temperature, fast energy migration processes combined with the existence of small amounts of killer sites provided by minor crystal defects and/or photochemical degradations are responsible for the short shifted Cr(2E →
4A2) emission. For CrEuCr and CrTbCr, the long-lived CrIII-centred emission is strictly maintained at 10 K, whatever the origin of the sensitization process, i.e. via ligand-centred or Ln-centred excited states (Fig. 8b, Table S2, ESI†), consistent with no Cr → Eu energy transfer.
Intramolecular Ln → Cr communication in CrLnCr (Ln = Eu, Tb).
Upon irradiation of the ligand-centred ππ* excited states at 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 cm−1 in CrEuCr, we observe the dual metal-centred emission of Eu(5D0
→
7FJ) (J = 0–4) and Cr(2E →
4A2) (Fig. 8c). At 10 K, the deep red Cr-centred emission dominates (89% of the total luminescence), but reduces to 68% at 295 K. Compared with ZnEuZn, the Eu(5D0) lifetime in CrEuCr is dramatically shortened (Table 4) as a result of the occurrence of Eu → Cr energy transfer processes. The intramolecular origin of the latter energy transfers is demonstrated by related dynamic measurements obtained for [CrEuCr(L2)3]9+ in acetonitrile, which closely mirror those obtained in the solid state (Table 4). We can therefore analyse the Eu → Cr intermetallic communication according to the simple scheme shown in Fig. 10, and for which the global efficiency of the energy transfer processes in CrEuCr is given in eqn (14).
170 cm−1 in CrEuCr, we observe the dual metal-centred emission of Eu(5D0
→
7FJ) (J = 0–4) and Cr(2E →
4A2) (Fig. 8c). At 10 K, the deep red Cr-centred emission dominates (89% of the total luminescence), but reduces to 68% at 295 K. Compared with ZnEuZn, the Eu(5D0) lifetime in CrEuCr is dramatically shortened (Table 4) as a result of the occurrence of Eu → Cr energy transfer processes. The intramolecular origin of the latter energy transfers is demonstrated by related dynamic measurements obtained for [CrEuCr(L2)3]9+ in acetonitrile, which closely mirror those obtained in the solid state (Table 4). We can therefore analyse the Eu → Cr intermetallic communication according to the simple scheme shown in Fig. 10, and for which the global efficiency of the energy transfer processes in CrEuCr is given in eqn (14).| |  | (14) |
Assuming that kEuLum is identical in ZnEuZn and CrEuCr, we can write
| | | kEuLum = kZnEuZnLum = (τZnEuZnobs)−1 | (15) |
| | | kEuLum
+ 2kEu,CrET = kCrEuCrobs = (τCrEuCrobs)−1 | (16) |
Substituting eqn (15) into eqn (16) allows the calculation of the rate of intermetallic energy transfer (eqn (17)), while parallel substitution of eqn (15) and (16) into eqn (14) gives the well-known eqn (18), which is commonly used for estimating the efficiency of energy transfer processes.30
| | 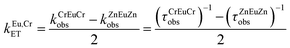 | (17) |
| | 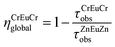 | (18) |
From the experimental lifetimes measured for ZnEuZn and CrEuCr, we calculate with eqn (18) that ηCrEuCrglobal
≈ 90% at 10 and 295 K, in the solid state and in solution (Table 4). As expected from the existence of two CrIII acceptors in CrEuCr, the contribution of the intramolecular Eu → Cr energy transfers to the quenching of Eu(5D0) luminescence is larger than that previously reported for [CrEu(L1)3]6+ (ηCrEu = 65–78%, Table 4).13 The individual rate constants kEu,CrET in CrEuCr and in [CrEu(L1)3]6+ can be directly compared in order to quantify the relative efficiency of the Eu → Cr communication in the two complexes. From eqn (17), we calculate kEu,CrET(CrEuCr) > kEu,CrET (CrEu),13 thus leading to the ratios kEu,CrET (CrEuCr)/kEu,CrET (CrEu) = 1.6(2) at 10 K and kEu,CrET (CrEuCr)/kEu,CrET (CrEu) = 3.9(6) at 295 K (Table 4). Modelling the Eu → Cr energy transfer with a simple dipole–dipole mechanism (eqn 19)12 is reasonable according to (i) the large Eu⋯Cr intermetallic separation measured in the crystal structure of [CrEu(L1)3]6+(REuCr = 9.32 Å),13 which is expected to be very similar in CrEuCr, and (ii) the minute expansion of the 4f orbitals.30
| |  | (19) |
Taking the rate constants collected in Table 4, we calculate with eqn (19) the critical distances for 50% energy transfer REuCr0 = 11.2–13.5 Å, which are in the nanometric range (Table 4). Theoretically, REuCr0 can be estimated with eqn (20), in which κ2 is an orientation factor having an isotropic limit of 2/3, ϕF is the quantum yield of the donor luminescence in the absence of acceptor (i.e. the europium quantum yield measured in ZnEuZn), n is the refractive index of the intermetallic medium and J is the overlap integral between the emission spectrum of the donor (EuIII) and the absorption spectrum of the acceptor (CrIII) in cm6 mol−1.30
| | | (REuCr0)6 = 8.75 × 10−25
×
κ2
×
ϕL
×
n−4
×
J [cm6] | (20) |
Surprisingly, the critical distances REuCr0 measured in the trimetallic CrEuCr complex are marginally larger than those found in the bimetallic analogue [CrEu(L1)3]6+ (Table 4), despite the considerable decrease of the donor quantum yield when going from a EuN6O3 site in [ZnEu(L1)3]5+ (ϕL = 0.34%, 10−4 mol dm−3 in acetonitrile at 293 K)13 to the less luminescent EuN9 site in [ZnEuZn(L2)3]7+ (ϕL = 0.002%, 10−4 mol dm−3 in acetonitrile at 293 K). This ratio ϕEuL (EuZnEu)/ϕEuL (EuZn) = 0.0059 translates into REuCr0 (CrEuCr)/REuCr0 (CrEu) = 0.42 by using eqn (20). The experimental data REuCr0 (CrEuCr)/REuCr0 (CrEu) = 1.03(2) at 10 K and 1.08(3) at 295 K (Table 4) imply that κ2
×
n−4
×
J (CrEuCr)/κ2
×
n−4
×
J (CrEu) ≈ 2.5. Since both the orientation factor κ2 and the local refractive index separating EuIII and CrIII can be reasonably assumed to be similar in the two analogous triple-stranded helicates, we tentatively assign this compensation effect to an increase of the overlap integral J in CrEuCr. To understand this, one has to realize that the EuIII emission intensity is quite small in both bimetallic and trimetallic helicates, so that minute changes in the crystal-field splitting or in the transition probabilities associated with the various sub-levels, may generate large changes in J.
When TbIII is used as the donor in CrTbCr, we calculate ηCrTbCrglobal
≥ 99.9% with eqn (18) at 10 K (lifetimes taken from Table S2, ESI†), which points to a quantitative Tb → Cr energy transfer process, as previously reported for [CrTb(L1)3]6+.13 An efficient thermally-activated Tb(4D4) →
3ππ* energy back transfer operates in CrTbCr and ZnTbZn, as previously described for [ZnTb(L3)3]5+,32 [ZnTb(L1)3]5+,33 and [Tb(L4)3]3+,34 which prevents the detection of residual TbIII-centred emissions at room temperature.
Conclusion
The idea of exploiting the chiral macrobicyclic cavity produced by the wrapping of the three ligand strands about two terminal pseudo-octahedral d-block cations in a triple helicate was suggested in 1997,38 and experimentally demonstrated by Albrecht and co-workers for TiIV and GaIII metallocryptates, in which negatively charged oxygen atoms can bind alkali cations in the internal cavity.39 In parallel work, Chaudhuri and collaborators introduced the concept of using inert pseudo-octahedral CrIII stoppers for producing kinetically stable macrobicyclic cavities, in which labile alkaline earth and 3d-block cations in different oxidation states can be encapsulated.40 However, to the best of our knowledge, the complexes [CrLnCr(L2)3]9+ represent the first examples, in which both aspects are combined to produce a triple-helical nine-coordinate macrobicyclic cavity adapted for the complexation of labile trivalent lanthanides. Interestingly, the seminal contributions of Albrecht39 and Chaudhuri40 focused on negatively charged ligand strands, which limit short-distance intermetallic repulsion thanks to charge compensation. In [ZnLnZn(L2)3]7+ and [CrLnCr(L2)3]9+, the intermetallic separation is large enough to allow the quantitative formation of the highly charged complexes in solution at millimolar concentrations, that is we are able to kinetically control the incorporation of LnIII ions in self-assembled macrobicyclic cavities. Moreover, the replacement of the terminal N2O tridentate biding site in L1 with a central N3 binding unit in L2 for complexing LnIII was initially thought to be deleterious for both stability constants41 and LnIII-centred luminescence (Ln = Eu, Tb).36 We indeed detect a considerable decrease of the Eu-centred luminescent quantum yield in [ZnEuZn(L2)3]7+ compared with [ZnEu(L1)3]5+, but an unexpected compensation effect assigned to an increase of the spectral overlap integral leads to sizeable intramolecular intermetallic communication and light-conversion. In future work, we will address the potential use of convergent Cr → Ln transfers for efficiently sensitizing NIR emitters (Ln = Nd, Er, Yb) while simultaneously lengthening their apparent lifetime.
Experimental
Solvents and starting materials
These were purchased from Fluka AG (Buchs, Switzerland) and used without further purification unless otherwise stated. The segmental ligand L221 and the chromium(II) salt Cr(CF3SO3)2·H2O13 were obtained according to literature procedures. The triflate salts Ln(CF3SO3)3·nH2O (Ln = La, Eu, Gd, Tb, Lu, Y) were prepared from the corresponding oxides (Rhodia, 99.99%) and dried according to published procedures.42 The Ln content of the solid salts was determined by complexometric titrations with Titriplex III (Merck) in the presence of urotropine and xylene orange.43
Preparation of the complexes [ZnLnZn(L2)3](CF3SO3)7·nH2O (Ln = La, n = 5; Ln = Eu, n = 7; Ln = Gd, n = 8; Ln = Tb, n = 6; Ln = Lu, n = 6)
A solution of Ln(CF3SO3)3·nH2O (Ln = La, Eu, Gd, Tb, Lu; 0.017 mmol) in acetonitrile (2 cm3) was added to a solution of L2 (41.3 mg, 0.051 mmol) in acetonitrile–dichloromethane (12 cm3 : 12 cm3). After stirring for 2 h at rt, a solution of Zn(CF3SO3)2·6H2O (12.3 mg, 0.034 mmol) was added in acetonitrile (2 cm3). After stirring for 1 h at rt, the solvent was evaporated and the pale yellow residue was dissolved in a minimum of acetonitrile. Slow diffusion of diethyl ether (3 days) provided 70–82% of microcrystalline needles of [ZnLnZn(L2)3](CF3SO3)7·nH2O (Ln = La, n = 5; Ln = Eu, n = 7; Ln = Gd, n = 8; Ln = Tb, n = 6; Ln = Lu, n = 6). All the complexes were characterized by their IR spectra and gave satisfactory elemental analyses (Table S1, ESI†).
Preparation of the complexes [CrLnCr(L2)3](CF3SO3)9·nH2O·pnBu4N(CF3SO3) (Ln = La, n = 12, p = 0.1; Ln = Eu, n = 8, p = 0.1; Ln = Gd, n = 9, p = 0.3; Ln = Tb, n = 7, p = 0.3; Ln = Lu, n = 10, p = 0.3)
A solution of Ln(CF3SO3)3·nH2O (Ln = La, Eu, Gd, Tb, Lu; 0.017 mmol) in acetonitrile (2 cm3) was added to a solution of L2 (41.3 mg, 0.051 mmol) in acetonitrile/dichloromethane (12 cm3 : 12 cm3). After stirring for 2 h at rt, the solvent was removed under vacuum and the residue transferred into a glove box under an inert atmosphere. Dissolution into degassed acetonitrile (25 cm3), followed by the addition of a deep blue solution of Cr(CF3SO3)2·H2O (12.6 mg, 0.034 mmol) in acetonitrile (1 cm3) produced a deep green mixture, which was stirred for one night under an inert atmosphere. nBu4N(CF3SO3) (13.3 mg, 0.034 mmol) was added, followed by slow bubbling of air for two hours. The solution turned orange, the solvent was removed, and the solid residue dissolved in acetonitrile. Fractional crystallization by using slow diffusion of diethyl ether provided 73–88% of orange microcrystalline powders of [CrLnCr(L2)3](CF3SO3)9·nH2O·pnBu4N(CF3SO3) (Ln = La, n = 12, p = 0.1; Ln = Eu, n = 8, p = 0.1; Ln = Gd, n = 9, p = 0.3; Ln = Tb, n = 7, p = 0.3; Ln = Lu, n = 10, p = 0.3, Table S1, ESI†). All the complexes were characterized by their IR spectra and gave satisfactory elemental analyses (Table S1, ESI†).
Spectroscopic and analytical measurements
Electronic spectra in the UV-Vis region were recorded at 293 K from solutions in MeCN with a Perkin-Elmer Lambda 900 spectrometer using quartz cells of 0.1 and 1 mm path length. Spectrophotometric titrations were performed with a J & M diode array spectrometer (Tidas series) connected to an external computer. In a typical experiment, 50 cm3 of L2 in acetonitrile/chloroform (1 : 1; 2 × 10−4 mol dm−3) were titrated at 20 °C with an equimolar solution of Ln(CF3SO3)3·nH2O (10−3 mol dm−3) or Zn(CF3SO3)3·nH2O (10−3 mol dm−3) in acetonitrile/chloroform (1 : 1) under an inert atmosphere. After each addition of 0.20 ml, the absorbance was recorded using Hellma optrodes (optical path length 0.1 cm) immersed in the thermostated titration vessel and connected to the spectrometer. Mathematical treatment of the spectrophotometric titrations was performed with factor analysis26 and with the SPECFIT program.27 IR spectra were obtained from KBr pellets with a FT-IR Perkin-Elmer Spectrum One. 1H NMR spectra were recorded at 25 °C on a Bruker Avance 400 MHz spectrometer. Chemical shifts are given in ppm with respect to TMS. The determination of longitudinal relaxation times (T1) used the inversion–recovery technique. Pneumatically-assisted electrospray (ESI-MS) mass spectra were recorded on a Finnigan SSQ7000 instrument. The equipment and experimental procedures for luminescence measurements in the visible range were published previously.44 Excitation of the finely powdered samples was achieved by a 450 W xenon high-pressure lamp coupled with a monochromator or a Coherent Innova Argon laser. The emitted light was analyzed at 90° with a Spex 1404 double monochromator with holographic gratings (band-path used 0.01–0.2 nm). Light intensity was measured by a RCA 31034 photomultiplier with a cooled S-20 photocathode (−20 °C), coupled to a Lecroy linear amplifier (500 MHz) and a Stanford Research SR-400 double photon counter. The emission spectra were corrected for the instrumental function. The excitation spectra were corrected for the emission of the Xenon lamp. Luminescent lifetimes were measured using excitation provided by a Quantum Brillant Nd:YAG laser equipped with frequency doubler, tripler and quadrupler as well as with an OPOTEK MagicPrismTM OPO crystal. The output signal of the photomultiplier was fed into a Stanford Research SR-430 multichannel scaler and transferred to a PC. Lifetimes are averages of 3 independent determinations. Quantum yields were determined using a Perkin Elmer LS50B fluorimeter. The quantum yields were calculated using the equation ϕx/ϕr = [Ar(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ×
Ir(
) ×
Ir(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ×
n2x
×
Dx]/[Ax(
) ×
n2x
×
Dx]/[Ax(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ×
Ix(
) ×
Ix(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ×
n2r
×
Dr], where x refers to the sample and r to the reference; A is the absorbance,
) ×
n2r
×
Dr], where x refers to the sample and r to the reference; A is the absorbance, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) the excitation wavenumber used, I the intensity of the excitation light at this energy, n the refractive index (n = 1.341 for acetonitrile solution and n = 1.330 for 0.1 mol dm−3 aqueous Tris-buffer solution) and D the integrated emitted intensity. Cs3[Eu(2,6-pyridinedicarboxylic acid)3] (ϕ = 9.5% in 0.1 mol dm−3 aqueous Tris-buffer solution) was used as reference.45 Elemental analyses were performed by Dr H. Eder from the Microchemical Laboratory of the University of Geneva.
the excitation wavenumber used, I the intensity of the excitation light at this energy, n the refractive index (n = 1.341 for acetonitrile solution and n = 1.330 for 0.1 mol dm−3 aqueous Tris-buffer solution) and D the integrated emitted intensity. Cs3[Eu(2,6-pyridinedicarboxylic acid)3] (ϕ = 9.5% in 0.1 mol dm−3 aqueous Tris-buffer solution) was used as reference.45 Elemental analyses were performed by Dr H. Eder from the Microchemical Laboratory of the University of Geneva.
Acknowledgements
We thank Mr J. Mercier for his contribution to the initial stage of this project, and Prof. A. Hauser and Dr D. Imbert for fruitful discussions. Financial support from the Swiss National Science Foundation is gratefully acknowledged.
References
-
(a)
K. F. Purcell and J. C. Kotz, Inorganic Chemistry, W.B. Saunders Company, Philadephia, London, Toronto, 1977, pp. 550 and 719 Search PubMed;
(b)
N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, Pergamon Press, Oxford, 1984, p. 1196 Search PubMed.
-
(a) S. F. Lincoln and A. E. Merbach, Adv. Inorg. Chem., 1995, 42, 1 CrossRef CAS;
(b) S. F. Lincoln, Helv. Chim. Acta, 2005, 88, 523 CrossRef CAS.
-
R. G. Wilkins, Kinetics and Mechanisms of Reaction of Transition Metal Complexes,VCH, Weinheim-New York-Basel-Cambridge, 2nd edn, 1991, p. 201 Search PubMed.
- I. Bertini, M. Fragai, C. Luchinat and G. Parigi, Inorg. Chem., 2001, 40, 4030 CrossRef CAS.
-
(a) D. T. Richens, Chem. Rev., 2005, 105, 1961 CrossRef CAS;
(b) L. Helm and A. E. Merbach, Chem. Rev., 2005, 105, 1923 CrossRef CAS.
-
A. B. P. Lever, Electronic Spectroscopy, Elsevier, Amsterdam, 2nd edn., 1984, p. 417 Search PubMed.
- S. Decurtins, H. W. Schmalle, R. Pellaux, P. Schneuwly and A. Hauser, Inorg. Chem., 1996, 35, 1451 CrossRef CAS.
- X. Zhang, Y. Cui, F. Zheng and J. Huang, Chem. Lett., 1999, 1111 CrossRef CAS.
- S. Decurtins, M. Gross, H. W. Schmalle and S. Ferlay, Inorg. Chem., 1998, 37, 2443 CrossRef CAS.
- J.-P. Costes, F. Dahan and W. Wernsdorfer, Inorg. Chem., 2006, 45, 5 CrossRef CAS.
-
B. Henderson and G. F. Imbusch, Optical Spectroscopy of Inorganic Solids, Clarendon Press, Oxford, 1989 Search PubMed.
- T. Förster, Ann. Phys., 1948, 55 Search PubMed; T. Förster, Discuss. Faraday Soc., 1959, 27, 7 RSC.
- M. Cantuel, G. Bernardinelli, D. Imbert, J.-C. G. Bünzli, G. Hopfgartner and C. Piguet, J. Chem. Soc., Dalton Trans., 2002, 1929 RSC.
- S. Torelli, D. Imbert, M. Cantuel, G. Bernardinelli, S. Delahaye, A. Hauser, J.-C. G. Bünzli and C. Piguet, Chem. Eur. J., 2005, 11, 3228 CrossRef CAS.
-
(a) N. Serpone and M. Z. Hoffmann, J. Chem. Educ., 1983, 60, 853 CrossRef CAS;
(b) A. D. Kirk, Chem. Rev., 1999, 99, 1607 CrossRef CAS.
-
(a) P. A. Brayshaw, J.-C. G. Bünzli, P. Froidevaux, J. M. Harrowfield, Y. Kim and A. N. Sobolev, Inorg. Chem., 1995, 34, 2068 CrossRef CAS;
(b) T. Sanada, T. Suzuki, T. Yoshida and S. Kaizaki, Inorg. Chem., 1998, 37, 4712 CrossRef CAS.
-
(a) M. A. Subhan, T. Suzuki and S. Kaizaki, J. Chem. Soc., Dalton Trans., 2001, 492 RSC;
(b) M. A. Subhan, T. Suzuki and S. Kaizaki, J. Chem. Soc., Dalton Trans., 2002, 1416 RSC;
(c) M. A. Subhan, H. Nakata, T. Suzuki, J.-H. Choi and S. Kaizaki, J. Lumin., 2003, 101, 307 CrossRef.
-
(a) Y. Shen, T. Riedener and K. L. Bray, Phys. Rev. B., 2000, 61, 11460 CrossRef CAS;
(b) S. Heer, M. Wermuth, K. Krämer, D. Ehrentraut and H. U. Güdel, J. Lumin., 2001, 94–95, 337 CrossRef.
- L. Chong and R. B. Jordan, Inorg. Chem., 1987, 26, 3855 CrossRef.
- D. Imbert, M. Cantuel, J.-C. G. Bünzli, G. Bernardinelli and C. Piguet, J. Am. Chem. Soc., 2003, 125, 15698 CrossRef CAS.
- C. Piguet, B. Bocquet and G. Hopfgartner, Helv. Chim. Acta, 1994, 77, 931 CrossRef CAS.
- G. N. La Mar and G. R. van Hecke, J. Chem. Phys., 1970, 52, 5676 CrossRef CAS.
- G. N. La Mar and G. R. van Hecke, J. Am. Chem. Soc., 1969, 91, 3442 CrossRef CAS.
-
(a) I. Bertini and C. Luchinat, Coord. Chem. Rev., 1996, 150, 1 CrossRef CAS;
(b) J. A. Peters, J. Huskens and D. J. Raber, Prog. Nucl. Magn. Reson. Spectrosc., 1996, 28, 283 CrossRef CAS;
(c)
C. Piguet and C. F. G. C. Geraldes, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, Jr., J.-C. G. Bünzli and V. K. Pecharsky, Elsevier Science, Amsterdam, 2003, vol. 33, ch. 215, p. 353 Search PubMed.
- C. Piguet, G. Hopfgartner, B. Bocquet, O. Schaad and A. F. Williams, J. Am. Chem. Soc., 1994, 116, 9092 CrossRef CAS.
-
E. R. Malinowski and D. G. Howery, Factor Analysis in Chemistry, Wiley, New York, Chichester, 1980 Search PubMed.
-
(a) H. Gampp, M. Maeder, C. J. Meyer and A. D. Zuberbühler, Talanta, 1986, 33, 943 CrossRef CAS;
(b) H. Gampp, M. Maeder, C. J. Meyer and A. D. Zuberbühler, Talanta, 1985, 23, 133.
- E. König and S. Herzog, J. Inorg. Nucl. Chem., 1970, 32, 585 CrossRef.
- S. Floquet, M. Borkovec, G. Bernardinelli, A. Pinto, L.-A. Leuthold, G. Hopfgartner, D. Imbert, J.-C. G. Bünzli and C. Piguet, Chem. Eur. J., 2004, 10, 1091 CrossRef CAS.
-
J.-C. G. Bünzli, in Lanthanide Probes in Life, Chemical and Earth Sciences, ed. J.-C. G. Bünzli and G. R. Choppin, Elsevier, Amsterdam, 1989, ch. 7 Search PubMed.
- S. T. Frey and W. deW. Horrocks, Inorg. Chim. Acta, 1995, 228, 383 CrossRef.
- C. Piguet, E. Rivara-Minten, G. Hopfgartner and J.-C. G. Bünzli, Helv. Chim. Acta, 1995, 78, 1541 CrossRef CAS.
- C. Piguet, J.-C. G. Bünzli, G. Bernardinelli, G. Hopfgartner, S. Petoud and O. Schaad, J. Am. Chem. Soc., 1996, 118, 6681 CrossRef CAS.
- C. Piguet, J.-C. G. Bünzli, G. Bernardinelli and A. F. Williams, Inorg. Chem., 1993, 32, 4139 CrossRef CAS.
-
(a) K. Binnemans and C. Görller-Walrand, Chem. Phys. Lett., 1995, 245, 75 CrossRef CAS;
(b)
C. Görller-Walrand and K. Binnemans, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, Jr. and L. Eyring, North-Holland Publishing Company, Amsterdam, 1996, vol. 23, p. 121 Search PubMed.
- S. Petoud, J.-C. G. Bünzli, C. Piguet, Q. Xiang and R. Thummel, J. Lumin., 1999, 82, 69 CrossRef CAS.
-
(a) V. S. Langford, M. E. von Arx and A. Hauser, J. Phys. Chem. A, 1999, 103, 7161 CrossRef CAS;
(b) A. Hauser, M. E. von Arx, V. S. Langford, U. Oetliker, S. Kairouani and A. Pillonet, Top. Curr. Chem., 2004, 241, 65 CAS.
- C. Piguet, G. Bernardinelli and G. Hopfgartner, Chem. Rev., 1997, 97, 2005 CrossRef CAS.
-
(a) M. Albrecht, M. Schneider and H. Röttele, Angew. Chem., Int. Ed., 1999, 38, 557 CrossRef CAS;
(b) M. Albrecht, O. Blau and R. Fröhlich, Chem. Eur. J., 1999, 5, 48 CrossRef CAS;
(c) M. Albrecht, O. Blau, E. Wegelius and K. Rissanen, New J. Chem., 1999, 23, 667 RSC;
(d) For an exhaustive review see: M. Albrecht, Chem. Rev., 2001, 101, 3457 Search PubMed.
- D. Burdinski, F. Birkelbach, T. Weyermüller, U. Flörke, H.-J. Haupt, M. Lengen, A. X. Trautwein, E. Bill, K. Wieghardt and P. Chaudhuri, Inorg. Chem., 1998, 37, 1009 CrossRef CAS.
- T. Le Borgne, P. Altmann, N. André, J.-C. G. Bünzli, G. Bernardinelli, P.-Y. Morgantini, J. Weber and C. Piguet, Dalton Trans., 2004, 723 RSC.
-
J. F. Desreux, in Lanthanide Probes in Life, Chemical and Earth Sciences, ed. J.-C. G. Bünzli and G. R. Choppin, Elsevier, Amsterdam, 1989, ch. 2, p. 43 Search PubMed.
-
G. Schwarzenbach, Complexometric Titrations, Chapman & Hall, London, 1957, p. 8 Search PubMed.
- R. Rodriguez-Cortinas, F. Avecilla, C. Platas-Iglesias, D. Imbert, J.-C. G. Bünzli, A. de Blas and T. Rodriguez-Blas, Inorg. Chem., 2002, 41, 5336 CrossRef CAS.
- A.-S. Chauvin, F. Gumy, D. Imbert and J.-C. G. Bünzli, Spectrosc. Lett., 2004, 37, 517 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tables of elemental analyses (Table S1), luminescence data for [ZnLnZn(L2)3]7+ and [CrLnCr(L2)3]9+ (Ln = Eu, Gd, Tb, Table S2), and longitudinal nuclear relaxation times for [ZnLnZn(L2)3]7+ (Ln = Tb, Lu) (Table S3). Figures showing ESI-MS (Figure S1), spectrophotometric (Figures S2 and S3) and 1H NMR (Figure S4) titrations. Figures showing ESI-MS (Figure S5), excitation (Figure S6) and emission (Figure S8) spectra of isolated [MLnM(L2)3]7/9+ complexes. Figure S7 shows the temperature dependence of Eu(5D0) lifetime in [ZnEuZn(L2)3]7+. See DOI: 10.1039/b602392d |
|
| This journal is © The Royal Society of Chemistry 2006 |
Click here to see how this site uses Cookies. View our privacy policy here. ![Structures of discrete bimetallic CrLn complexes a) [(acac)2Cr(ox)Ln(HBpz3)2]16b,17 and b) [CrLn(L1)3]6+,13,14 in which intramolecular intermetallic energy transfers have been evidenced.](/image/article/2006/DT/b602392d/b602392d-f1.gif)
![Kinetic model for the deactivation and communication between d- and f-block-centred excited levels in [CrLn(L1)3]6+ (Ln = Nd, Eu, Tb, Yb).13,14](/image/article/2006/DT/b602392d/b602392d-f2.gif)


![a) Variation of absorption spectra observed for the spectrophotometric titration of [La(L2)3]3+ (total ligand concentration: 2 × 10−4 mol dm−3) with Zn(CF3SO3)2·6H2O at 293 K in CHCl3–CH3CN = 1 : 1 (Zn : L2 = 0.1–2.5 : 1). b) Corresponding variation of observed molar absorption at six different wavelengths.](/image/article/2006/DT/b602392d/b602392d-f5.gif)
![Schematic representation of the complexation process leading to the triple-stranded helicate [MLnM(L2)3]7+ (M = ZnII, CrII). The structure of the complex corresponds to the optimized D3-symmetrical geometry constructed for [CrIIIEuCrIII(L2)3]9+ by using the crystal structure of [CrIIIEu(L1)3]6+ as model.](/image/article/2006/DT/b602392d/b602392d-f6.gif)
![Absorption spectra of a) [CrIILnCrII(L2)3]7+ (black trace) and b) [CrIIILnCrIII(L2)3]9+ (grey trace) in acetonitrile (2.1 × 10−3 mol dm−3).](/image/article/2006/DT/b602392d/b602392d-f7.gif)
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) in cm−1) can be correlated with the ability of the coordinated atoms to produce a nephelauxetic effect according to eqn (10)31
in cm−1) can be correlated with the ability of the coordinated atoms to produce a nephelauxetic effect according to eqn (10)31
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0 = 17374 cm−1 is the energy of Eu(7F0
→
5D0) for the free ion). For the pseudo-tricapped trigonal EuN9 site proposed in the model of ZnEuZn (Fig. 6), we calculate
0 = 17374 cm−1 is the energy of Eu(7F0
→
5D0) for the free ion). For the pseudo-tricapped trigonal EuN9 site proposed in the model of ZnEuZn (Fig. 6), we calculate ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 17236 cm−1 at 295 K, which translates into
= 17236 cm−1 at 295 K, which translates into ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = 17224 cm−1 at 10 K (assuming the accepted 1 cm−1/24 K dependence of the energy of the Eu(5D0
←
7F0) transition with temperature).30 This prediction matches fairly well the experimental value found for ZnEuZn (17221 cm−1 at 10 K, Table 3), and those previously reported for [ZnEu(L3)3]5+ (17224 cm−1 at 10 K, Table 3)32 and [Eu(L4)3]3+ (17223 cm−1 at 10 K, Table 3),34 in which the existence of the pseudo-tricapped trigonal prismatic EuN9 site has been unambiguously evidenced in the associated X-ray crystal structures.
= 17224 cm−1 at 10 K (assuming the accepted 1 cm−1/24 K dependence of the energy of the Eu(5D0
←
7F0) transition with temperature).30 This prediction matches fairly well the experimental value found for ZnEuZn (17221 cm−1 at 10 K, Table 3), and those previously reported for [ZnEu(L3)3]5+ (17224 cm−1 at 10 K, Table 3)32 and [Eu(L4)3]3+ (17223 cm−1 at 10 K, Table 3),34 in which the existence of the pseudo-tricapped trigonal prismatic EuN9 site has been unambiguously evidenced in the associated X-ray crystal structures.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13
13
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 (Fig. S6b, ESI†). Upon excitation of the π
→
π* transitions, the emission spectrum displays the narrow Eu(5D0
→
7FJ) transitions (J = 0–4), together with Cr(2E →
4A2) transitions, the latter masking the weaker Eu(5D0
→
7FJ) (J = 5–6) emission bands (Fig. 8c). Both the energy (13245 cm−1 at 10 K, Table S2, ESI†) of the Cr(2E →
4A2) transition and the associated Cr(2E) lifetime (2.08–2.10 ms, Table S2, ESI†) are comparable with those reported for [CrEu(L1)3]6+ (13301 cm−1 at 10 K, τ = 3.46 ms),13 in agreement with the existence of similar terminal trigonally distorted [Cr(2-benzimidazol-pyridine)3]3+ chromophores in the bi- and trimetallic complexes. The crystal-field splitting of the Eu-centred transitions in CrEuCr is almost identical to that obtained for ZnEuZn (Table 3), thus pointing to very similar EuN9 coordination sites in both trimetallic complexes (from the splitting of the Eu(5D0
→
7F1) transition, we calculate ΔEA–E = 80 cm−1, ΔEE–E = 34 cm−1, Table 3). It is worth noting that Cr-centred excitation at 21470 cm−1 (Cr(4A2
→
4T2)) results in the exclusive detection of the Cr(2E →
4A2) emission, in line with the absence of intramolecular Cr → Eu energy transfer processes. However, the reverse situation is found upon Eu-centred excitation (i.e observation of the luminescence of both Eu-centred and Cr-centred emission), which implies the existence of a partial Eu → Cr energy transfer (Fig. 10, vide infra) responsible for the reduced Eu(5D0) lifetime measured in CrEuCr (τ = 0.20–0.24 ms at 10 K, Tables 4 and S2, ESI†). We can therefore safely conclude from the X-ray diffraction and high-resolution emission studies that (i) ZnEuZn and CrEuCr exhibit very similar structures, (ii) the terminal d-block ions are pseudo-octahedrally coordinated by three bidentate 2-benzimidazolpyridine units and (iii) europium is encapsulated within a slightly distorted tricapped trigonal prismatic EuN9 site provided by the three wrapped central tridentate 2,6-bis(benzimidazol-2-yl)pyridine units, as found in the D3-symmetrical complex [Eu(L4)3]3+. All these characteristics are compatible with the structural model shown in Fig. 6.
500 cm−1 (Fig. S6b, ESI†). Upon excitation of the π
→
π* transitions, the emission spectrum displays the narrow Eu(5D0
→
7FJ) transitions (J = 0–4), together with Cr(2E →
4A2) transitions, the latter masking the weaker Eu(5D0
→
7FJ) (J = 5–6) emission bands (Fig. 8c). Both the energy (13245 cm−1 at 10 K, Table S2, ESI†) of the Cr(2E →
4A2) transition and the associated Cr(2E) lifetime (2.08–2.10 ms, Table S2, ESI†) are comparable with those reported for [CrEu(L1)3]6+ (13301 cm−1 at 10 K, τ = 3.46 ms),13 in agreement with the existence of similar terminal trigonally distorted [Cr(2-benzimidazol-pyridine)3]3+ chromophores in the bi- and trimetallic complexes. The crystal-field splitting of the Eu-centred transitions in CrEuCr is almost identical to that obtained for ZnEuZn (Table 3), thus pointing to very similar EuN9 coordination sites in both trimetallic complexes (from the splitting of the Eu(5D0
→
7F1) transition, we calculate ΔEA–E = 80 cm−1, ΔEE–E = 34 cm−1, Table 3). It is worth noting that Cr-centred excitation at 21470 cm−1 (Cr(4A2
→
4T2)) results in the exclusive detection of the Cr(2E →
4A2) emission, in line with the absence of intramolecular Cr → Eu energy transfer processes. However, the reverse situation is found upon Eu-centred excitation (i.e observation of the luminescence of both Eu-centred and Cr-centred emission), which implies the existence of a partial Eu → Cr energy transfer (Fig. 10, vide infra) responsible for the reduced Eu(5D0) lifetime measured in CrEuCr (τ = 0.20–0.24 ms at 10 K, Tables 4 and S2, ESI†). We can therefore safely conclude from the X-ray diffraction and high-resolution emission studies that (i) ZnEuZn and CrEuCr exhibit very similar structures, (ii) the terminal d-block ions are pseudo-octahedrally coordinated by three bidentate 2-benzimidazolpyridine units and (iii) europium is encapsulated within a slightly distorted tricapped trigonal prismatic EuN9 site provided by the three wrapped central tridentate 2,6-bis(benzimidazol-2-yl)pyridine units, as found in the D3-symmetrical complex [Eu(L4)3]3+. All these characteristics are compatible with the structural model shown in Fig. 6.![Correlation between Ln⋯Hi distances observed in the crystal structure of [ZnEu(L1)3]5+,33 and those determined by paramagnetic 1H NMR in acetonitrile with eqn (13) for [ZnTbZn(L2)3]7+ (H6 is used as a reference, see text).](/image/article/2006/DT/b602392d/b602392d-f9.gif)
![Kinetic model for the deactivation and communication of f-block and d-block-centred excited levels in [MLnM(L2)3]9+ (M = Cr, Ln = Eu, Tb).](/image/article/2006/DT/b602392d/b602392d-f10.gif)


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800–16
800–16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range (
000 cm−1 range (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) max = 18
max = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1). Its associated lifetime is bi-exponential with τ1 = 2.45 ms (86%) and τ2 = 0.49 ms (14%), which is typical for emissions arising from the L2(3ππ*) excited states located on different parts of the ligand, due to the isolating effects of the methylene spacers.32,33 At 295 K, efficient thermally-activated non-radiative processes reduce L2(3ππ*) lifetimes to τ1 = 42 µs (64%) and τ2 = 6 µs (36%). Upon replacement of ZnII with CrIII in CrGdCr, the L2(3ππ*) band is shifted by approximately 5500 cm−1 toward higher energy (26
900 cm−1). Its associated lifetime is bi-exponential with τ1 = 2.45 ms (86%) and τ2 = 0.49 ms (14%), which is typical for emissions arising from the L2(3ππ*) excited states located on different parts of the ligand, due to the isolating effects of the methylene spacers.32,33 At 295 K, efficient thermally-activated non-radiative processes reduce L2(3ππ*) lifetimes to τ1 = 42 µs (64%) and τ2 = 6 µs (36%). Upon replacement of ZnII with CrIII in CrGdCr, the L2(3ππ*) band is shifted by approximately 5500 cm−1 toward higher energy (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–20
000–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range,
000 cm−1 range, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) max = 24
max = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 cm−1 at 10 K), while its lifetimes are only marginally reduced with respect to those measured in ZnGdZn (Table S4, ESI†). This suggests that (i) the bidentate binding units co-ordinated to the d-block ion strongly contributes to the ligand-centred 3ππ* emission and (ii) the L2(3ππ*) → CrIII transfer is poorly efficient. Conversely, only a faint residual ligand-centred 3ππ* emission is detected in the emission spectra of ZnEuZn and CrEuCr, which points to an efficient L2(3ππ*) → EuIII sensitization process, as similarly reported for [ZnEu(L3)3]5+,32 [ZnEu(L1)3]5+33 and [CrEu(L1)3]6+.13 We conclude that the energy of L2(3ππ*) in the complexes MLnM is more adequate for resonant energy transfer processes with EuIII than with CrIII.
450 cm−1 at 10 K), while its lifetimes are only marginally reduced with respect to those measured in ZnGdZn (Table S4, ESI†). This suggests that (i) the bidentate binding units co-ordinated to the d-block ion strongly contributes to the ligand-centred 3ππ* emission and (ii) the L2(3ππ*) → CrIII transfer is poorly efficient. Conversely, only a faint residual ligand-centred 3ππ* emission is detected in the emission spectra of ZnEuZn and CrEuCr, which points to an efficient L2(3ππ*) → EuIII sensitization process, as similarly reported for [ZnEu(L3)3]5+,32 [ZnEu(L1)3]5+33 and [CrEu(L1)3]6+.13 We conclude that the energy of L2(3ππ*) in the complexes MLnM is more adequate for resonant energy transfer processes with EuIII than with CrIII.
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exc = 28170 cm−1) or via CrIII-centred 4A2
→
4T2 (
exc = 28170 cm−1) or via CrIII-centred 4A2
→
4T2 (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) exc = 20492 cm−1, Fig. S6d†) in CrGdCr produces identical emission spectra displaying the characteristic Cr(2E →
4A2) transition at 13
exc = 20492 cm−1, Fig. S6d†) in CrGdCr produces identical emission spectra displaying the characteristic Cr(2E →
4A2) transition at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 245 cm−1, combined with weak Stokes phonon side bands (13
245 cm−1, combined with weak Stokes phonon side bands (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100–12
100–12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1, Fig. S8, ESI†), in good agreement with a similar behaviour reported for [CrGd(L3)3]6+ (13
900 cm−1, Fig. S8, ESI†), in good agreement with a similar behaviour reported for [CrGd(L3)3]6+ (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 301 cm−1).33 The Cr(2E) lifetime at 10 K is long (2.27(1) ms, Table S2, ESI†) and points to only minor non-radiative processes affecting the CrIII-centred emission. However, both intensity (Fig. S8, ESI†) and lifetime of the Cr(2E) emission in CrGdCr dramatically decrease at higher temperature (τ295 K = 0.031 ms, Table S2, ESI†), which is tentatively attributed to thermally-activated energy migration processes, as previously discussed for [CrGd(L1)3]6+.13,37 Moreover, the maximum of the Cr(2E →
4A2) emission band shifts from 13
301 cm−1).33 The Cr(2E) lifetime at 10 K is long (2.27(1) ms, Table S2, ESI†) and points to only minor non-radiative processes affecting the CrIII-centred emission. However, both intensity (Fig. S8, ESI†) and lifetime of the Cr(2E) emission in CrGdCr dramatically decrease at higher temperature (τ295 K = 0.031 ms, Table S2, ESI†), which is tentatively attributed to thermally-activated energy migration processes, as previously discussed for [CrGd(L1)3]6+.13,37 Moreover, the maximum of the Cr(2E →
4A2) emission band shifts from 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 245 cm−1 at 10 K to 13
245 cm−1 at 10 K to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 316 cm−1 at 295 K (ΔE = 71 cm−1, Fig. S8, ESI†), a change in energy much larger than ΔE = 15 cm−1 expected for the splitting of the Cr(2E) level by trigonal symmetry, which accounts for the hot band emission in the model complex [Cr(2,2′-bipyridine)3]3+.37b We thus suspect that the long-lived luminescence observed at 10 K indeed originates from pseudo-octahedral CrN6 chromophores found in CrGdCr. At room temperature, fast energy migration processes combined with the existence of small amounts of killer sites provided by minor crystal defects and/or photochemical degradations are responsible for the short shifted Cr(2E →
4A2) emission. For CrEuCr and CrTbCr, the long-lived CrIII-centred emission is strictly maintained at 10 K, whatever the origin of the sensitization process, i.e. via ligand-centred or Ln-centred excited states (Fig. 8b, Table S2, ESI†), consistent with no Cr → Eu energy transfer.
316 cm−1 at 295 K (ΔE = 71 cm−1, Fig. S8, ESI†), a change in energy much larger than ΔE = 15 cm−1 expected for the splitting of the Cr(2E) level by trigonal symmetry, which accounts for the hot band emission in the model complex [Cr(2,2′-bipyridine)3]3+.37b We thus suspect that the long-lived luminescence observed at 10 K indeed originates from pseudo-octahedral CrN6 chromophores found in CrGdCr. At room temperature, fast energy migration processes combined with the existence of small amounts of killer sites provided by minor crystal defects and/or photochemical degradations are responsible for the short shifted Cr(2E →
4A2) emission. For CrEuCr and CrTbCr, the long-lived CrIII-centred emission is strictly maintained at 10 K, whatever the origin of the sensitization process, i.e. via ligand-centred or Ln-centred excited states (Fig. 8b, Table S2, ESI†), consistent with no Cr → Eu energy transfer.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 cm−1 in CrEuCr, we observe the dual metal-centred emission of Eu(5D0
→
7FJ) (J = 0–4) and Cr(2E →
4A2) (Fig. 8c). At 10 K, the deep red Cr-centred emission dominates (89% of the total luminescence), but reduces to 68% at 295 K. Compared with ZnEuZn, the Eu(5D0) lifetime in CrEuCr is dramatically shortened (Table 4) as a result of the occurrence of Eu → Cr energy transfer processes. The intramolecular origin of the latter energy transfers is demonstrated by related dynamic measurements obtained for [CrEuCr(L2)3]9+ in acetonitrile, which closely mirror those obtained in the solid state (Table 4). We can therefore analyse the Eu → Cr intermetallic communication according to the simple scheme shown in Fig. 10, and for which the global efficiency of the energy transfer processes in CrEuCr is given in eqn (14).
170 cm−1 in CrEuCr, we observe the dual metal-centred emission of Eu(5D0
→
7FJ) (J = 0–4) and Cr(2E →
4A2) (Fig. 8c). At 10 K, the deep red Cr-centred emission dominates (89% of the total luminescence), but reduces to 68% at 295 K. Compared with ZnEuZn, the Eu(5D0) lifetime in CrEuCr is dramatically shortened (Table 4) as a result of the occurrence of Eu → Cr energy transfer processes. The intramolecular origin of the latter energy transfers is demonstrated by related dynamic measurements obtained for [CrEuCr(L2)3]9+ in acetonitrile, which closely mirror those obtained in the solid state (Table 4). We can therefore analyse the Eu → Cr intermetallic communication according to the simple scheme shown in Fig. 10, and for which the global efficiency of the energy transfer processes in CrEuCr is given in eqn (14).
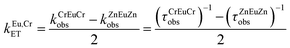
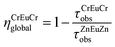

![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ×
Ir(
) ×
Ir(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ×
n2x
×
Dx]/[Ax(
) ×
n2x
×
Dx]/[Ax(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ×
Ix(
) ×
Ix(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) ×
n2r
×
Dr], where x refers to the sample and r to the reference; A is the absorbance,
) ×
n2r
×
Dr], where x refers to the sample and r to the reference; A is the absorbance, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) the excitation wavenumber used, I the intensity of the excitation light at this energy, n the refractive index (n = 1.341 for acetonitrile solution and n = 1.330 for 0.1 mol dm−3 aqueous Tris-buffer solution) and D the integrated emitted intensity. Cs3[Eu(2,6-pyridinedicarboxylic acid)3] (ϕ = 9.5% in 0.1 mol dm−3 aqueous Tris-buffer solution) was used as reference.45 Elemental analyses were performed by Dr H. Eder from the Microchemical Laboratory of the University of Geneva.
the excitation wavenumber used, I the intensity of the excitation light at this energy, n the refractive index (n = 1.341 for acetonitrile solution and n = 1.330 for 0.1 mol dm−3 aqueous Tris-buffer solution) and D the integrated emitted intensity. Cs3[Eu(2,6-pyridinedicarboxylic acid)3] (ϕ = 9.5% in 0.1 mol dm−3 aqueous Tris-buffer solution) was used as reference.45 Elemental analyses were performed by Dr H. Eder from the Microchemical Laboratory of the University of Geneva.

