The relative stabilities of 11-vertex nido- and 12-vertex closo-heteroboranes and -borates: facile estimation by structural or connection increments

Abstract

The relative thermodynamic stabilities of ortho-, meta- and para-isomers of 12-vertex closo-heteroboranes and -borates with different p-block heteroatoms were determined using density functional theory. More electronegative (smaller) heteroatoms tend to occupy non-adjacent, whereas less electronegative (larger) heteroatoms tend to occupy adjacent vertices in the thermodynamically most stable closo-diheterododecaborane isomers. The computed relative stabilities agree perfectly with experimental observations. The energy differences of para- and meta- relative to ortho-isomers of 12-vertex closo-heteroboranes generally depend on the extent of electron localization by a given heteroatom and show highly periodic trends, i.e. increase along the period and decrease down the group. The energy penalties for the HetHet structural feature (two heteroatoms adjacent to each other) for the 12-vertex closo-cluster are apparently significantly different from those for the 11-vertex nido-cluster. Reformulating two 11-vertex nido-structural features, i.e. Het_5k(2) and HetHet, in terms of connection increments along with the additional structural feature HetHet_m give the relative stabilities of various isomeric 11-vertex nido- as well as 12-vertex closo-heteroboranes and -borates, using one unique set of increments.

---

1 Introduction

Beside their potential use in medical applications,^1,2 heteroboranes are of interest due to their unusual non-classical structure and their key role in stimulating new concepts and a general picture of chemical bonding.³ Simple qualitative rules presented by Williams^4–6 and Wade^7,8 are helpful for both understanding the building principles and to identify possible synthetic targets. More sophisticated quantitative rules also called structural increments arising due to disfavoring structural features in heteroboranes^3,9–12 have also been presented. The additive nature of these structural increments, i.e. their ability to accurately reproduce the DFT computed relative stabilities is now proven to be generally true for various nido-heteroboranes and -borates with diverse numbers, connectivities and types of heteroatoms. Sets of structural features and corresponding energy penalties were reported for 6-,⁹ 10-¹⁰ and 11-vertex nido-heteroboranes and -borates.^3,11,12 They allow to easily derive the relative stabilities of various isomers with good accuracy, once corresponding energy increments “penalties” are assigned to relevant structural features based on DFT results computed for a selected set of structures. The energy penalties for the structural features HetHet (two adjacent heteroatoms) and HetC (a heteroatom adjacent to a carbon atom) possess periodic trends (increase along the period and decrease down the group) for various p-block heteroatoms in 11-vertex nido-heteroboranes and -borates.³ Here, we extend the study of HetHet and HetC structural features to the 12-vertex closo-cluster for comparison with those from the 11-vertex nido-cluster. Both clusters have identical numbers of skeletal electrons (26) and hence have allied cluster shapes: the 11-vertex nido-cluster is derived from the 12-vertex closo-icosahedron by elimination of one vertex. Therefore, the influence of heteroatoms can be expected to be similar in both cases, particularly the positions of various heteroatoms relative to each other. For closo-compounds the number of possible isomers is very limited due to the high symmetry of the spherical cluster shapes. In 12-vertex closo-diheteroboranes, each structural feature is present only in one isomer (e.g. 1,2-C₂B₁₀H₁₂ has ortho carbon atoms, its 1,7- and 1,12-isomers have carbon atoms in meta and para positions, respectively). On the basis of these, it is therefore impossible to decide if the destabilization due to certain structural features is special for one isomer or has a general meaning. For the 11-vertex nido-clusters, the number of possible isomeric structures is vast due to the less symmetric cluster shape and due to the presence of additional hydrogen atoms. It has already been shown that the relative energies can, nevertheless, be estimated quite accurately by a small number of energy penalties related to certain structural features. Here we try to find quantitative rules that apply both for 12-vertex closo- and 11-vertex nido-compounds.

2 Computational details

All structures were optimized at the RB3LYP^13,14/LANL2DZ level of density functional theory using the Gaussian 03 program¹⁵ with d-type polarization functions¹⁶ for B (ζ = 0.388), Al (ζ = 0.198), Ga (ζ = 0.207), In (ζ = 0.160), Tl (ζ = 0.146), C (ζ = 0.600), Si (ζ = 0.262), Ge (ζ = 0.207), Sn (ζ = 0.183), Pb (ζ = 0.164), N (ζ = 0.864), P (ζ = 0.340), As (ζ = 0.293), Sb (ζ = 0.211) and Bi (ζ = 0.185) followed by frequency calculations and zero-point energy calculations at the same level. Single-point energies of the optimized geometries were computed at the RB3LYP/SDD level with additional d-type polarization functions (see above), p-type polarization function for hydrogen atoms (ζ = 1.000) and an sp set of diffuse functions for B, C and N (ζ = 0.0315, 0.0438 and 0.0639, respectively),¹⁷ for Al, Si and P (0.0318, 0.0331 and 0.0348, respectively)¹⁸ and for Ga, Ge, As, In, Sn, Sb, Tl, Pb and Bi (0.0205, 0.0222, 0.0287, 0.0223, 0.0231, 0.0259, 0.0170, 0.0171 and 0.0215, respectively).¹⁹ The relative energies reported for isomeric structures correspond to the RB3LYP/SDD//RB3LYP/LANL2DZ + ZPE level.

3 Results and discussion

3.1 Periodic trends of heteroatom energy penalties for the 12-vertex closo-cluster

Thermodynamic stabilities of Het₂B₁₀H₁₀ isomers have been determined where Het = two-electron donating group 13 heterogroup, i.e. H–Al, H–Ga, H–In, H–Tl, three-electron donating exo-substituted group 14 heteroatoms, i.e. H–C, H–Si, H–Ge, H–Sn and H–Pb, and three-electron donating group 15 heteroatoms, i.e. N, P, As, Sb and Bi. The thermodynamic stabilities of the diheterododecaboranes and -borates depend on the position of the heteroatoms relative to each other and can be expressed in the following terms: HetHet_o is the energy difference of the ortho (1,2)- with respect to the para (1,12)-isomer (Fig. 1) while HetHet_m is the energy difference of the meta (1,7)- with respect to the para (1,12)-isomer. HetHet_{m → o}, the energy difference of the ortho (1,2)- with respect to the meta (1,7)-isomer results as the difference of HetHet_m and HetHet_o (Chart 1). Generally, HetHet_o and HetHet_{m → o} have larger values than HetHet_m for diheteroboranes and -borates. The thermodynamic stabilities of the diheterododecaboranes and -borates also depend upon the position of heteroatoms in the Periodic Table. Energy penalties for HetHet_o (two heteroatoms adjacent to each other) decrease down the group. For example, among group 14 heteroatoms (Fig. 2, Chart 1), preference of paravs.ortho of C₂B₁₀H₁₂ (+18 kcal mol⁻¹) is diminished in Si₂B₁₀H₁₂ (+4 kcal mol⁻¹) and reversed for the Ge homolog (−2.4 kcal mol⁻¹). The ortho preference is even more pronounced for Sn (−13 kcal mol⁻¹) and Pb (−26.2 kcal mol⁻¹). The same trend is observed for N (+25.0 kcal mol⁻¹) → Bi (−12.6 kcal mol⁻¹). Among exo-substituted group 13 heteroatoms, aluminium has the largest HetHet_o energy penalties while thalium has the smallest.

Fig. 1 Structural features HetHet′_o, HetHet′_m and HetHet′_{m → o} for 12-vertex closo-HetHet′B₁₀H₁₀.

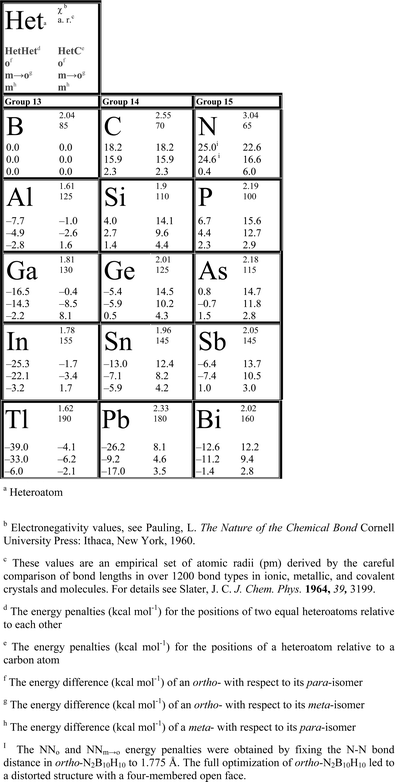
Fig. 2 HetHet_o energy penalties for 12-vertex closo-clusters generally decrease down the group and increase along the period. The energy penalty for NN_o (included in parenthesis) was obtained by fixing the N–N bond distance to be 1.775 Å in the ortho-N₂B₁₀H₁₀ isomer because an icosahedral structure without fixed bond distances did not survive geometry optimization.

Chart 1 Periodic trends of HetHet and HetC energy penalties in 12-vertex closo-hetero(carba)boranes and -borates.

HetHet_o energy penalties generally increase (become more positive) along one period; e.g. along the second period, energy penalties increase from zero (for two adjacent boron atoms) to 15.9 kcal mol⁻¹ for two adjacent carbon atoms. The energy penalty for NN (two adjacent nitrogen atoms) was obtained by fixing N–N bond distance in the ortho isomer to be 1.775 Å, as otherwise the cluster distorted upon full optimization to have a four-membered open face. HetHet_o energy penalties increase along Al to P in the 3rd period, Ga to As in the 4th, In to Sb in the 5th and Tl to Bi in the 6th period (Fig. 2, Chart 1).

Thermodynamic stabilities of HetCB₁₀H₁₁ isomers (where Het = heteroatom) were also computed and corresponding values for the relative placement of a heteroatom adjacent to a carbon atom (HetC_o) are also included in Chart 1 (also see Appendix I, ESI†). The energy range of HetC_o energy penalties is much smaller and the values generally diminish down the 13th, 14th and 15th group, although the trends are less strictly followed. For example, Ga has a higher energy penalty than Al in group 13, and Ge has a higher HetC_o energy penalty than Si in group 14. HetC_o values, however, always become more positive along the 3rd, 4th, 5th and 6th period, without any exception.

HetHet_{m → o} and HetC_{m → o} energy penalties for 12-vertex closo-Het₂B₁₀H₁₀ and HetCB₁₀H₁₁ clusters also decrease down the group and increase along the period (Chart 1).

Periodic trends of energy penalties can be explained on the basis of the extent of electron localization due to a heteroatom. Within the same group, all heteroatoms formally donate the same number of electrons to the cluster. However, the larger electronegativities of smaller heteroatoms, generally result in enhanced electron localization and hence larger energy penalties. There is a steady increase in HetHet and HetC energy penalties of group 14 members as compared to group 13 members but a less pronounced increase is observed for group 15 members (see the HetHet_o and HetC_o curves in Fig. 2 and Appendix I of ESI†). This is because group 13 heteroatoms formally localize two electrons at one vertex but group 14 and 15 heteroatoms localize three electrons. The increase in energy penalties for group 15 heteroatoms as compared to group 14 heteroatoms is, however, due to higher electronegativity, that further enhances the extent of electron localization.

3.2 Redefining Het_5k(2) and HetHet in terms of connection increments

The HetHet_{m → o} energy penalties for group 14 heteroatoms in 11-vertex nido- and equivalent HetHet_{m → o} in 12-vertex closo-clusters are listed next to each other in Table 1 (also see Fig. 3). The CC_{m → o} energy penalty for two neighboring carbon atoms is very similar for both closo- and nido-clusters. For all other heteroatoms, HetHet_{m → o} values are surprisingly smaller for the 12-vertex closo-cluster as compared to HetHet_{m → o} for the 11-vertex nido-cluster. HetHet_{m → o} values reported for the nido-cluster are all positive (meaning heteroatoms apart are generally more favorable) but a number of heteroatoms (especially large ones) have negative HetHet_{m → o} (and also HetHet_o) values for the 12-vertex closo-cluster (meaning ortho isomers are more stable). Furthermore, the difference of HetHet_{m → o} energy penalties between the 11-vertex nido- and 12-vertex closo-cluster (Δ) increases with the size of the heteroatom (Sn > Ge > Si > C, Fig. 3). HetHet energy penalties are also significantly different for the 11-vertex nido- and the 12-vertex closo-cluster for group 15 heteroatoms (Table 1, Fig. 3). The difference of energy penalties of a given heteroatom for the two clusters increases from P to Sb (Fig. 3). This apparently means different energy penalties for the same structural features in 11-vertex nido- and 12-vertex closo-cluster, in spite of very similar cluster structure and the same electronic requirement of 13 skeletal electron pairs for each cluster. This prompted us to consider increments for individual “bonds” (or better bonding connections) rather than for structural features for a universal treatment of both cluster types.

Table 1 Direct comparison of HetHet energy penalties (kcal mol⁻¹) for exo-substituted group 14 heteroatoms in 12-vertex closo- and 11-vertex nido-clusters

Heteroatom	12-Vertex closo-	11-Vertex nido-^a	Δ
Group 13 heteroatoms
H–C	16	16	0
H–Si	3	9	6
H–Ge	−3	4	7
H–Sn	−7	3	10

---

Group 14 heteroatoms
a Values taken from ref. 12. b The NNm → o energy penalty was obtained by fixing the N–N bond distance in ortho-N2B10H10 to 1.775 Å. The full optimization of ortho-N2B10H10 led to a distorted structure with a four-membered open face where the nitrogen atoms occupy opposite sites (reminiscent of a diamond–square–diamond intermediate).
N^b	25	41	32
P	4	11	7
As	−1	7	8
Sb	−7	4	11

---

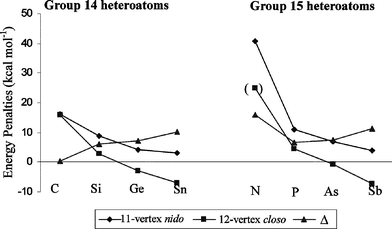Fig. 3 HetHet_{m → o} energy penalties for 11-vertex nido- and 12-vertex closo-clusters of group 14 and 15 heteroatoms. The energy penalties for NN_{m → o} (included in parenthesis) was obtained by fixing the N–N bond distance to be 1.775 Å in ortho-N₂B₁₀H₁₀ isomer as an icosahedral structure without fixed bond distances did not survive geometry optimization.

Fig. 4(a) shows two isomeric [CB₁₀H₁₁]³⁻ structures, i.e. 7-[CB₁₀H₁₁]³⁻ (A) and 2-[CB₁₀H₁₁]³⁻ (B). The former has a carbon atom at the open face while the latter has the carbon atom at an unfavorable five-coordinate vertex (vertex number 2). Hence, the difference may be described by the disfavoring structural feature C_5k(2) with an increment of 28 kcal mol⁻¹ in the latter (B), while the former (A) is a structure without any disfavoring structural feature (carbon at the lowest possible coordinated vertex).¹¹ The first structure, 7-[CB₁₀H₁₁]³⁻, described in terms of heteroatom cluster connections has four C–B bonding connections while the latter has five C–B bonding connections. The presence of one additional C–B connection in B as compared to A has to reflect the stability difference of 28 kcal mol⁻¹. Hence, the C–B connection increment is attributed a (destabilizing) value of 28 kcal mol⁻¹.²⁰

Fig. 4 Comparison of (a) 7-[CB₁₀H₁₁]³⁻ and 2-[CB₁₀H₁₁]³⁻ as well as (b) 7,9-[C₂B₉H₁₁]²⁻ and 7,8-[C₂B₉H₁₁]²⁻ using (I) the structural increment approach and (II) the connection increment approach (all energy values in kcal mol⁻¹). The values reported in Table 2 are slightly different due to statistical fitting procedure.

The 16 kcal mol⁻¹ energy difference of 7,9-[C₂B₉H₁₁]²⁻ (C) and 7,8-[C₂B₉H₁₁]²⁻ (D) (Fig. 4(b)) is due to the presence of adjacent carbon atoms (structural feature CC) in the latter with an energy penalty of 16 kcal mol⁻¹.¹¹ These two structures can also be distinguished on the basis of connection increments: 7,9-[C₂B₉H₁₁]²⁻ has eight C–B bonding connections while 7,8-[C₂B₉H₁₁]²⁻ has six C–B bonding connections in addition to one C–C bonding connection. 7,9-[C₂B₉H₁₁]²⁻ accumulates 224 kcal mol⁻¹ due to eight C–B (8 × 28) and is 16 kcal mol⁻¹ less stable than the 7,8-isomer. In order to reproduce the relative energy, the latter must have a total of 240 kcal mol⁻¹ of connection increment energy. Six C–B contribute 168 kcal mol⁻¹, the remaining 72 kcal mol⁻¹ are deduced as connection increment for C–C.

Two structures differing in para and meta positions of two carbon atoms may be differentiated on the basis of CC_m (Fig. 5). It cannot be treated in terms of connection increments, due to the same number of C–B connections in the para- and meta-isomers (Fig. 5). However, this structural feature has a very small energy penalty (2 kcal mol⁻¹) for both 11-vertex nido- and 12-vertex closo-clusters.²¹ Both 2,9-[C₂B₉H₁₁]²⁻ (E) and 2,8-[C₂B₉H₁₁]²⁻ (F) have nine C–B connections. Four C–B connections are due to a carbon atom at the open face and the remaining five C–B connections involve a carbon atom in the middle belt. Likewise closo-C₂B₁₀H₁₂ has ten C–B connections for both the para (G) and the meta-isomer (H).

Fig. 5 Structural feature CC_m differentiates between 2,9- (E) and 2,8-[C₂B₉H₁₁]²⁻ (F) and 1,12- (G) and 1,7-C₂B₁₀H₁₂ (H) (all values in kcal mol⁻¹).

Upon statistical fitting to E_calc of the isomers reported in Table 2, the energy penalties for C–B, C–C and CC_m change slightly to 27, 71 and 1 kcal mol⁻¹, respectively. These energy penalties suffice to reproduce the relative energies of various 11-vertex nido-carborates and 12-vertex closo-carboranes and -borates (Table 2). For instance, 7,8,10-[C₃B₈H₁₁]⁻ has ten C–B connections, one C–C connection and twice the structural feature CC_m. ∑E_inc (the sum of increments) is 343 kcal mol⁻¹. 7,8,9-[C₃B₈H₁₁]⁻ has eight C–B connections, two C–C connections and one CC_m structural feature. The sum of increments (∑E_inc) is 359 kcal mol⁻¹ with E_inc^rel (the relative energy of the 7,8,9-isomer as compared to the 7,8,10-isomer) is 16 kcal mol⁻¹ as predicted by the increment scheme. E_calc (the DFT computed relative energy) comes out to be 19 kcal mol⁻¹ for the 7,8,9-isomer as compared to the 7,8,10-isomer. The difference in relative energy between the two methods is 3 kcal mol⁻¹. The same set of increments has been applied to 11-vertex nido-carborates with one, two and three carbon atoms and also to closo-carboranes with two and three carbon atoms (Table 2).

Table 2 The relative stabilities (kcal mol⁻¹) of 11-vertex nido-^a and 12-vertex closo-carborane isomers based on a common set of increments (values in kcal mol⁻¹ are specified in the column headers)

		C–B	C–C	CCm
	Formula	27	71	1	∑Einc	E inc ^rel	E calc ^b	ΔE^c
a If endo-hydrogen atoms are present, additional increments as reported in ref. 11 may be needed. These can be used together with the bonding connection increments reported here. b Computed relative energies for 11-vertex nido-carboranes and -borates are taken from ref. 11. c ΔE is the energy difference of Einc^rel and Ecalc.
nido	7-[CB10H11]^3−	4			108	0	0	0
	2-[CB10H11]^3−	5			135	28	26	2
	7,9-[C2B9H11]^2−	8		1	136	0	0	0
	7,8-[C2B9H11]^2−	6	1		216	14	16	−2
	2,9-[C2B9H11]^2−	9			233	26	27	−1
	2,8-[C2B9H11]^2−	9		1	260	28	29	−1
	2,7-[C2B9H11]^2−	7	1		244	42	43	−1
	7,8,10-[C3B8H11]^−	10	1	2	343	0	0	0
	7,8,9-[C3B8H11]^−	8	2	1	359	16	19	−3
closo	1,12-C2B10H12	10			270	0	0	0
	1,7-C2B10H12	10		1	270	1	2	−1
	1,2-C2B10H12	8	1		287	17	18	−1
	1,7,9-[C3B9H12]^+	15		3	408	0	0	0
	1,2,12-[C3B9H12]^+	13	1	1	423	15	14	1
	1,2,8-[C3B9H12]^+	13	1	2	424	16	17	−1
	1,2,4-[C3B9H12]^+	11	2	1	440	32	33	−1
	1,2,3-[C3B9H12]^+	9	3		456	48	49	−1

---

Following the same approach, the relative stabilities of various other 11-vertex nido- and 12-vertex closo-heteroboranes and -borates (Appendices II through V, ESI†) can successfully be estimated by a single set of increments.

This connection increment approach can be further expanded to 11-vertex nido- and 12-vertex closo-heterocarbaboranes and -borates with two different heteroatoms (i.e. Het and C). Table 3 indicates how the relative stabilities of germaboranes and -borates, germacarbaboranes and -borates can be reproduced using the additional connection increments, Ge–C, Ge–B, Ge–Ge, and structural increments CGe_m and GeGe_m. The method can be used to get the relative stabilities of other heterocarbaboranes and -borates.

Table 3 The relative stabilities (kcal mol⁻¹) of 11-vertex nido- and 12-vertex closo-germaborane and germacarbaborane isomers based on a common set of increments (values in kcal mol⁻¹ are specified in the column headers)

		C–B	Ge–B	Ge–Ge	GeGem	Ge–C	GeCm
	Formula	28	44	90	2	82	1	∑Einc	E inc ^rel	E calc ^a	ΔE
a E calc values for 11-vertex nido-germaboranes and -borates and germacarbaboranes and -borates are taken from ref. 12.
nido	7-[GeB10H11]^3−		4					176	0	0	0
	2-[GeB10H11]^3−		5					220	44	44	0
	7,9-[Ge2B9H11]^2−		8		1			354	0	0	0
	7,8-[Ge2B9H11]^2−		6	1				354	1	4	−4
	7,9-[GeCB9H11]^2−		4				1	289	0	0	0
	7,8-[GeCB9H11]^2−		3			1		298	9	8	1
closo	1,12-GeCB10H12	5	5					360	0	0	0
	1,7-GeCB10H12	5	5				1	361	1	4	−3
	1,2-GeCB10H12	4	4			1		370	10	15	−5
	1,12-Ge2B10H12		10					440	0	0	0
	1,7-Ge2B10H12		10		1			442	2	0	1
	1,2-Ge2B10H12		8	1				442	2	−2	4

---

Some 11-vertex nido-heteroboranes and -borates like 2-[NB₁₀H₁₁]²⁻,³ 2-[SnB₁₀H₁₁]³⁻ and 2-[AsB₁₀H₁₁]²⁻,¹² did not optimize to a regular 11-vertex nido-cluster due to cluster distortion.³ Likewise differences of the estimated against the DFT computed relative energy larger than 5 kcal mol⁻¹ result for 2,7-, 2,8- and 2,9-[Sn₂B₉H₁₁]²⁻ structures. They all have a tin atom at vertex number 2 and show significant cluster distortion (Appendix VII, ESI†).

The strength of bonding interaction of one heteroatom with its cluster neighbors should depend on its overall connectivity. Bond increments therefore should also depend on the connectivity. However, as we see here, at least for fourfold vs. fivefold cluster connections, the difference seems to be small enough for the approach to work well.

3.3 Heavy heteroatoms at adjacent positions in the thermodynamically most stable 12-vertex closo-isomer; a phenomenon supported by experimental results

The qualitative heteroatom placement rules of Williams^4–6 have long remained the only theoretical tool to quickly determine the positions of heteroatoms in the thermodynamically most stable heteroboranes and -borates. These rules suggest least connected, non-adjacent vertices for heteroatoms in the thermodynamically most stable heteroborane isomers. DFT computations coupled with our quantitative structural increment approach, however, helped to rationalize the presence of heteroatoms at highly connected vertices in the thermodynamically most stable isomers for a number of structures in 10-¹⁰ and 11-vertex nido-heteroboranes and -borates.^11,3 Here, our computations demonstrate that if equivalently connected vertices are available (as in the 12-vertex closo-cluster), heavy heteroatoms tend to occupy adjacent vertices in the thermodynamically most stable isomer. Chart 1 shows larger (more positive) HetHet energy penalties for smaller heteroatoms. As a consequence, they rearrange to the more stable meta and para isomers upon heating (Fig. 6) as is known from experiments.²² For example, 2,1-PCB₁₀H₁₁ undergoes thermal rearrangement at 485 °C to form the 1,7-isomer,²³ while at higher temperature (650 °C) significant amounts of the 1,12-isomer are formed.²⁴ However, numerous experimental structures were reported with two heavy heteroatoms in the ortho position such as 1,2-As₂B₁₀H₁₀,²⁵ 1,2-Sb₂B₁₀H₁₀,^25,26 1,2-SbAsB₁₀H₁₀²⁶ or 1,2-HetBiB₁₀H₁₀ (Het = P, As, Sb, Bi)²⁷ but no meta or para-rearrangements were reported. As seen from smaller (more negative) HetHet energy values, the ortho-isomers are favored as compared to meta- and para-isomers for larger heteroatoms (Fig. 6) and no isomerization takes place upon heating the ortho compounds.

Fig. 6 (a) ortho-2,1-PCB₁₀H₁₁ undergoes thermal rearrangement to give meta and para isomers due to a PC_o energy penalty of 15.6 kcal mol⁻¹. (b) ortho-Bi₂B₁₀H₁₀ does not undergo any rearrangement: it is the most stable isomer as reflected by a negative BiBi_o energy penalty (−12.6 kcal mol⁻¹).

The stability order of para > meta > ortho is not generally valid! Chart 1 shows that this is only the case for Het = C, Si, N, P.

Note that in the third column in Chart 1 (group 14 members) there is no parallel trend of para → ortho and meta → ortho quantitatively, i.e., both become more negative when going down, but para → ortho much more. As a consequence para → meta becomes really significant. In all other cases, it remains small.

4 Conclusion

A single connection increment scheme is presented that can give the relative stabilities of 11-vertex nido- as well as 12-vertex closo-clusters with different heteroatom substitution patterns. The Het_5k and HetHet structural increments proposed for the 11-vertex nido-cluster^3,11 may be transformed to bonding connection increments that can be used for 12-vertex closo-clusters. Connection increments are still applicable to 11-vertex nido-heteroboranes and -borates along with other structural features. Hence, for the 11-vertex nido-cluster, the resulting estimated relative energies have exactly the previously reported values. The energy differences between para- to ortho-, and meta- to ortho-12-vertex closo-diheteroborane clusters follow strictly periodic trends. Smaller heteroatoms tend to occupy non-adjacent, while larger heteroatoms tend to occupy adjacent vertices in thermodynamically most stable diheteroborane isomers.

Acknowledgements

Financial support by DFG is gratefully acknowledged.

References and notes

1. M. F. Hawthorne and A. Maderna, Chem. Rev., 1999, 99, 3421–3434.
2. E. A. Mizusawa, H. L. Dahlman, S. J. Bennet and M. F. Hawthorne, Proc. Natl. Acad. Sci. USA, 1982, 79, 3011–3014.
3. F. A. Kiani and M. Hofmann, Inorg. Chem., 2005, 44, 3746-3754.
4. R. E. Williams, J. Am. Chem. Soc., 1965, 87, 3513–3515.
5. R. E. Williams, in Progress in Boron Chemistry, ed. R. J. Brotherton and H. Steinberg, Pergamon Press, England, 1970, vol. 2, ch. 2, p. 57.
6. R. E. Williams, Chem. Rev., 1992, 92, 177–207 and references therein.
7. K. Wade, Adv. Inorg. Chem. Radiochem., 1976, 18, 1–66.
8. K. Wade, in Metal Interactions with Boron Clusters, ed. R. N. Grimes, Plenum Press, New York, 1982, ch. 1, pp. 1–41.
9. M. Hofmann, M. A. Fox, R. Greatrex, P. v. R. Schleyer and R. E. Williams, Inorg. Chem., 2001, 40, 1790–1801.
10. F. A. Kiani and M. Hofmann, Eur. J. Inorg. Chem., 2005, 12, 2545–2553.
11. F. A. Kiani and M. Hofmann, Inorg. Chem., 2004, 43, 8561–8571.
12. F. A. Kiani and M. Hofmann, J. Mol. Model., 2005 DOI:10.1007/s00894-005-0037-3.
13. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
14. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
15. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03 (Revision C.02), Gaussian, Inc., Wallingford, CT, 2004.
16. S. Huzinaga and J. Andzelm, Gaussian Basis Sets for Molecular Calculations, Elsevier, Amsterdam, 1984, pp. 23–25.
17. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. v. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
18. G. W. Spitznagel, Diplomarbeit, Erlangen, 1982.
19. These values were optimized for the atomic ground state anion, using ROHF with a flexible ECP basis set, by Ted Packwood at NDSU. Diffuse functions for these and other heteroatoms may be found at the website: http://phoenix.liu.edu/%E2%88%BCnmatsuna/gamess/refs/basis.refs.html.
20. As there are no classical 2c–2e bonds in the clusters considered we use bonding “connection increments” rather than bond increments to refer to bonding connections in clusters.
21. As the preference of para over meta positions is only minor and in order to make the overall structural increment scheme simpler, a CC_m increment was not included for the 11-vertex nido-cluster.
22. B. Stibr, Collect. Czech. Chem. Commun., 2002, 67, 843–868 and references therein.
23. J. L. Little, J. T. Moran and L. J. Todd, J. Am. Chem. Soc., 1967, 89, 5495–5496.
24. L. J. Todd, J. L. Little and H. T. Silverstein, Inorg. Chem., 1969, 8, 1698–1703.
25. X. L. R. Fontaine, J. D. Kennedy, M. McGrath and T. R. Spalding, Magn. Reson. Chem., 1991, 29, 711–720.
26. J. L. Little, Inorg. Chem., 1979, 18, 1598–1600.
27. J. L. Little, M. A. Whitesell, J. G. Kester, K. Folting and L. J. Todd, Inorg. Chem., 1990, 29, 804–808.

---

Footnote

† Electronic supplementary information (ESI) available: A plot of HetC_o energy penalties for 12-vertex closo-clusters (Appendix I), a comparison of relative thermodynamic stabilities of various stanna-, phospha-, arsa- and stibaboranes and -borates (Appendices II–V), Cartesian coordinates from RB3LYP/SDD//LANL2DZ optimizations of various Het₂B₁₀H₁₀ and HetCB₁₀H₁₁ structures (Appendix VI) and optimized geometries of three 11-vertex nido distannaboranes, i.e., 2,7-, 2,8- and 2,9-isomers of [Sn₂B₉H₁₁]²⁻ (which distorted upon optimization, Appendix VII). See DOI: 10.1039/b512700a

---