Excited state dynamics and fragmentation channels of the protonated dipeptide H₂N-Leu-Trp-COOH

Abstract

The excited state dynamics of the isolated and protonated peptide H₂N-Leu-Trp-COOH are analyzed by fs pump–probe spectroscopy. The peptides are brought into the gas phase by electrospray ionization, and fs pump–probe excitation is detected by fragment ion formation. The pump laser addressed the excited ππ* state of the indole chromophore of the amino acid tryptophan. The subsequent excited state dynamics agreed with a biexponential decay with time constants of 500 fs and 10 ps. This is considerably shorter than the lifetime of neutral tryptophan in solution and in proteins, but similar to isolated, protonated tryptophan. Several models are discussed to explain the experimental results but the detailed quenching mechanism remains unresolved.

---

1. Introduction

The fluorescence of proteins is often dominated by tryptophan (Trp), which absorbs at the longest wavelength of all amino acids and displays the largest extinction coefficient. The excited state behavior of Trp in solutions or in proteins is complex, extensively investigated and reviewed.^1–5 All excited state properties, such as absorption and fluorescence wavelengths, fluorescence quantum yield and anisotropy, as well as excited state lifetime, strongly depend on the Trp environment. Polarities of the environment,¹ specific solvent effects⁶ and different pH values^7,8 influence the excited state properties of Trp. For example the excited state lifetime is 19 ns at pH 11⁹ and 0.5 ns and 3.1 ns at pH 7 (double exponential).^9,10 At pH 11 the amine site is neutral and at pH 7 Trp exists as a zwitterion with a protonated amino group. It seems that the protonated amino group may be responsible for the pH dependency of the excited state lifetime and quench the fluorescence in Trp itself and in Trp-containing peptides.¹¹ Due to this sensitivity to the environment the fluorescence of Trp is often used as probe for structural changes in proteins.

Investigations of biological molecules in bulk are clearly of high biological relevance, but suffer from several drawbacks: the bulk spectra are very broad and products or intermediates such as radicals, radical anions and radical cations cannot be properly distinguished. We therefore investigate isolated molecules of biological relevance in the gas phase.

Here we study the excited state dynamics of protonated Trp and of a protonated, Trp-containing dipeptide by two-photon photoinduced dissociation. There are several advantages to this approach: mass selection before and after photoexcitation can exactly determine the molecular species under investigation and the formed photoproducts. Also, the intrinsic properties of the isolated molecules can be directly compared to theory. This concept can provide new insights into the photodynamics of isolated molecules of biological interest and may help to understand their complex behavior in bulk.

Early photodissociation experiments (PID) on radical cations of small model peptides were performed by laser desorption, laser ionization and laser dissociation with ns^12–14 and fs¹⁵ laser pulses. The photoinduced dissociation of closed shell ions from an electrospray source was pioneered with a fixed wavelength by Williams et al.¹⁶ and continued by others.^13–20 Frequency resolved spectra of closed shell ions of biological relevance were recorded by Andersen and co-workers^21–23 (visible wavelength range) and later Nolting et al.^24,25 (UV wavelength range). The spectra, however, were broad, presumably due to lifetime and temperature effects. Recently Rizzo and co-workers achieved efficient cooling of protonated species in a trap. The resulting UV spectrum was well resolved for tyrosine, but spectra for Trp were still unresolved presumably due to lifetime-broadening.²⁶

Jouvet and co-workers pioneered the time-resolved fs measurements of protonated species using PID. They investigated the protonated amino acids Trp (TrpH⁺),^20,27 tyrosine (TyrH⁺),²⁷ the amino acid analogue tryptamine (TrypH⁺)²⁸ and the dipeptide H₂N-Trp-Leu-COOH (WLH⁺).²⁹ For TrpH⁺ they found two components with a short (400 fs) and a longer (15 ps) lifetime of the optically excited state.²⁰ The fast dynamics were attributed to a charge transfer from the initially excited ππ* state to a state where the excited electron is at the protonated amine site. First, this charge transfer (CT) state has a Rydberg-like character but evolves to a πσ* state when the NH bond is stretched. In this coordinate a conical intersection with the ground state is reached, leading either to internal conversion (IC) back to the ground state or to H loss. The two different lifetimes were tentatively attributed to a coexistence of two different conformers in the ion beam.^20,30

For the dipeptide WLH⁺, Jouvet and co-workers found dynamics similar to those for TrpH⁺.²⁹ This agreed with the expectation that the excited state properties are dominated by the interaction of the indole moiety and the protonated amino group and the Leu only plays the role of a spectator.

In this work we investigate the complementary peptide H₂N-Leu-Trp-COOH (LWH⁺, Fig. 1). We expect that the proton is attached to the terminal amine and may influence the Trp excited state lifetime in LWH⁺ in a different way than in TrpH⁺.

Fig. 1 Lewis structure of protonated Leu-Trp.

2. Experimental

2.1. Experimental set-up

The experimental set-up consisted of a modified commercial mass spectrometer coupled to a fs laser system. The mass spectrometer (Esquire 3000, Bruker Daltonik) was equipped with an electrospray ionization source and uses a Paul trap for ion trapping and mass analysis. The mass spectrometer and the modifications are described in detail elsewhere.²⁴

The fs laser system was a commercial (Clark MXR) Ti:sapphire laser/amplifier operating at 1 kHz. The fundamental wavelength was set to 800 nm with a pulse width of 120 fs. The third harmonic (266 nm) with an average pulse energy of 750 nJ was used as pump pulse and the fundamental with 100 μJ probed the excited states dynamic. The laser pulses were focused into the center of the Paul trap using a focusing mirror with a focal length of 60 cm resulting in an approximate intensity of 2 × 10¹⁰ W cm⁻² for the pump pulse.

500 pump–probe laser pulses interacted with the same trapped ion ensemble. Hence, we could work with very low excitation densities and we typically observed a rate of fragmentation of about 2% per 500 pump–probe pulses. This ensured single-photon pump excitation and avoided dissociation of fragments by subsequent laser pulses. A pulse energy of 100 μJ for the probe pulse gave optimal signal to noise ratios for the pump–probe signal. The IR pulse alone is far detuned from any molecular resonances and generated no fragments.

For each measurement ∼500 mass selected ions were accumulated within the Paul trap. The number of ions was controlled by the time during which ions coming from the ion source were allowed to enter the trap. After ion accumulation, 500 pump–probe laser pulses interacted with the ion ensemble. The following mass analysis was performed in the Paul trap. The detector signal was discriminated and single ions were counted with a 2 GHz multiscaler (Model 7886, Fast ComTech). 50 measurements were summed for one mass spectrum. For recording transient mass spectra the delay time between pump and probe pulse was scanned with an optical delay line. For scanning long delays the step size was increased with increasing distance to the time-zero delay. The delay steps then ranged from a step width of 40 fs close to zero delay to a step width of 1 ps for delays larger than 5 ps.

The time-zero delay and cross correlation were measured using two-color multiphoton ionization of neutral furan. The procedure was similar to the one described above, but only ions generated by photo-ionization inside the Paul trap were accumulated and detected. The S₁ state of neutral furan is at 5.8 eV (214 nm).³¹ Multiphoton ionization is therefore a non-resonant 1 + 3′ photon process and the measured ion signal resembles a higher order cross correlation, allowing a precise measurement of the time-zero delay. The cross correlation was measured by scanning the delay line with equidistant steps of 20 fs. All transients were fitted by mono-, bi- and tri-exponential fitting routines based on the nonlinear Levenberg–Marquardt algorithm.

Laser–ion interaction in an ion trap has the advantage that fragments stemming from fast and slow fragmentation channels are detected with similar detection probability. Unfortunately fragment ion masses below m/z 50 were lost due to the lower mass cut-off of the ion trap.

2.2. Detection scheme

A common detection scheme for pump–probe spectroscopy in the gas phase uses multiphoton ionization. The pump laser excites a higher electronic state and the probe laser ionizes from the excited state. Although applicable for many systems, this scheme fails for small cationic species. The ion already carries a positive charge, hence it is difficult to overcome the second ionization potential.

The detection scheme used here utilizes the changes of the fragmentation pattern as a function of the internal energy of the ion. As shown in Fig. 2, the pump laser excites the ion to a higher electronic state and facilitates the resonant absorption of one or several probe photons from the excited state. Thus, ions which have absorbed a pump photon end up with the same charge but with lower internal energy than ions which have absorbed pump and probe photons. The different internal energies result in different rel. intensities of the fragments in the mass spectrum. The transients of the rel. intensities can therefore be used to probe the excited state dynamics. The processes responsible for the change in the rates of fragmentation are discussed in detail in section 1 and 2.

Fig. 2 Scheme of detection. The ion is excited to the first electronically excited state S₁via a pump photon. Resonant excited state absorption of probe photon(s) into higher electronic states S_m, S_n increases the internal energy of the ion. After internal conversion the ion fragments. The rate of fragmentation into specific fragments Frag 1, 2 and 3 (thicker arrows indicate higher rates) depends on the internal energy. Thus the rel. intensities of fragments change with the number of absorbed photons.

Recently, Kang et al. applied this detection scheme successfully to TrypH⁺ and TrpH⁺.^20,28 With our set-up we could fully reproduce these results. This shows that our laser intensities and the interaction of multiple laser shots with the same ion ensemble does not cause problems. Fig. 3 shows the transient mass spectra of protonated Trp. The fragments m/z 188 and 130 gain intensity (analogous to fragments 2 and 3 in Fig. 2) whereas the fragment m/z 146 loses intensity (analogous to fragment 1 in Fig. 2). The transients were fitted with mono- and biexponential decay functions. As described in the Introduction, theoretical investigations showed that a CT leads to conical intersections with the initially excited state and the ground state, causing the observed short excited state lifetime.³⁰

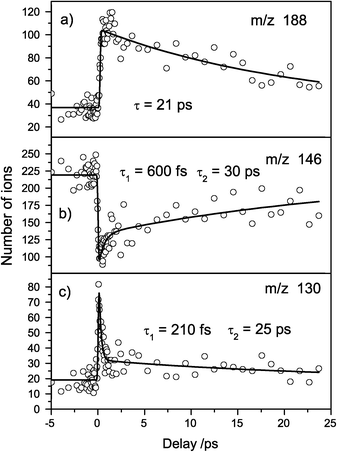Fig. 3 Transient mass spectra of protonated Trp. (a) Fragment m/z 188 shows a mono-exponential decay of 21 ps. (b) Fragment m/z 146 exhibits a biexponential decay with 600 fs and 30 fs. (c) Fragment m/z 130 also shows a biexponential decay with time constants 210 fs and 25 ps.

2.3. Chemicals

The samples Trp and Leu-Trp were purchased by Sigma and used without further purification. For electrospray ionization they were dissolved in a mixture of acetonitrile, water and acetic acid (66, 33, 1%). All solvents were of highest purity and purchased from Merck.

3. Results

3.1. Collision induced dissociation of LWH⁺

The collision induced dissociation (CID) mass spectrum of mass-selected LWH⁺ is shown in Fig. 4. Fragments from assigned loss channels are summarized in Table 1. The most prominent fragmentation channel is the formation of the y₁ fragment, i.e. protonated Trp (m/z 205). The ions m/z 188, 159, 146, 132 and 130 are known CID fragments of protonated Trp.^32,33 Thus the fragmentation is dominated by C-terminal ions. Only the minor signals m/z 274 and 141 could be assigned to N-terminal ions.

Fig. 4 CID mass spectrum of LWH⁺. The favored fragmentation pathway is the formation of protonated Trp (m/z 205) and its fragments (m/z 188, 159, 146, 132, 130). The loss of ammonia (m/z 301) and the decarboxylation (m/z 274) are of minor importance.

Table 1 Neutral fragments lost in CID of LWH⁺

Fragment ions (m/z)	Neutrals lost
301	NH3
274	CO2
205	Leu
188	Leu, NH3
159	Leu, CO, H2O
146	Leu, NH3, CH2CO
141	Skatole, CO, H2O
132	Leu, H2O, CO, HCN
130	Leu, H2O, CO, HCN, H2

---

3.2. Photoinduced dissociation of LWH⁺

The photoinduced dissociation (PID) mass spectrum of LWH⁺ at 266 nm is shown in Fig. 5a. The fragmentation was similar to that for CID (Fig. 4). Again, the most favored fragmentation pathway was the formation of the y₁ ion, i.e. protonated Trp (m/z 205). The loss of ammonia (m/z 301) was hardly observable, as was the decarboxylation (m/z 274). The fragments m/z 188, 159, 146, 132 and 130 are already known from PID of TrpH⁺.^19,24,34 The ion m/z 237 could not be assigned unambiguously. It was neither observed in the CID nor in the background PID spectrum and exhibited a very long lifetime. Therefore we attribute this ion to an unknown gas phase reaction.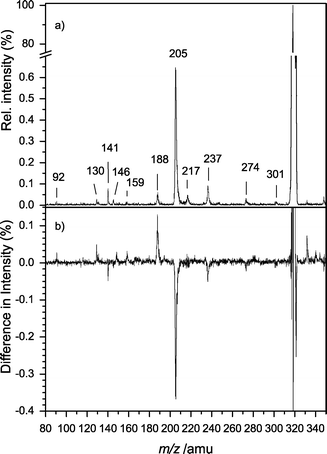

Fig. 5 (a) PID mass spectrum at 266 nm. The fragmentation pattern is dominated by C-terminal fragments. Most prominent is the y₁ fragment Trp (m/z 205). Most smaller masses (m/z 188, 159, 146, 132, 130) are known fragments of protonated Trp. (b) Difference mass spectrum of protonated LW. The mass spectrum at negative delays was subtracted from the mass spectrum at a delay of 200 fs. The intensity of nearly all fragments is affected by the pump–probe delay.

The relative intensities of the fragments depend on the internal energy of the ions. Thus the fragment intensities are different for absorption of one UV photon or one UV photon and subsequently one or several IR photons. Because the pump–probe excitation scheme only works for positive delays the fragment intensities are dependent on the pump–probe delay. Fig. 5b shows the difference spectrum: the mass spectrum for negative delays was subtracted from the mass spectrum at Δt = 500 fs. Negative intensities correspond to a decrease in the ion signal for positive delay times and positive intensities correspond to an increase in the ion signal. Most higher masses (m/z 301, 274 and 205) tend to decrease whereas the Trp fragments gain intensity.

3.3. Femtosecond transients of LWH⁺

Nearly all fragments were affected by excited-state (probe-) absorption of the resonantly excited (pumped) state as seen in the difference mass spectrum (Fig. 5b). The evolution of the fragment signals as a function of the pump–probe delay therefore reflects the temporal evolution of the excited state. We show the transients for m/z 205, 188, 130 and the integrated fragment signal in Fig. 6a–d.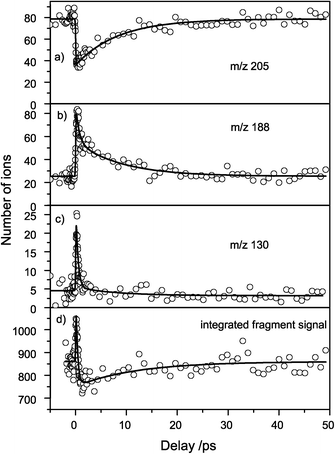

Fig. 6 Femtosecond transients of fragment ion intensities. (a) The most intense peak (m/z) is depleted with a 9 ps lifetime. The fragments m/z 188 (b) and m/z 130 (c) gain in intensity and show a biexponential decay with ≈0.5 ps and ≈9 ps life time. The integrated fragment signal (d) shows an increase of the total number of fragments with a ≈0.3 ps time constant and a depletion with a ≈11.9 ps time constant.

IR probe excitation resulted in a transient depletion of the TrpH⁺ fragment ion signal (Fig. 6a), whereas the smaller fragments m/z 188 and 130 showed a step-like rise at the pump–probe delay time zero, followed by a decay (Fig. 6b and c). The depletion of m/z 205 by the probe laser pulse by 50% shows that the probe excitation is very efficient and close to saturation. The high probe laser pulse intensity, however, also makes multiphoton IR excitation probable, leading to different dissociation channels and thus spreading out the dynamics over different fragment ions. Note that the depletion in the TrpH⁺ signal did not correspond to the increase in the smaller fragment intensities: for delays longer than 1 ps the integrated fragment signal (Fig. 6d) dropped below the initial value for negative delays, presumably due to the loss of small fragments with m/z < 50.

The transients exhibit two distinct time constants which were analyzed by a biexponential fit. The depletion of m/z 205 was dominated by a time constant of 9 ps whereas the formation of the fragment m/z 130 showed a time constant of 430 fs. For the transient of m/z 188, both time constants were observed and the data could be fitted biexponentially with time constants of 550 fs and 8 ps. All other fragments showed time constants close to 500 fs and 11 ps, but the signal to noise ratio was very poor. The fitted time constants are summarized in Table 2.

Table 2 Fitted time constants

Fragment ions (m/z)	Short time constant/ps	Long time constant/ps
Sum	0.3	11.9
205	—	8.3
188	0.7	8.9
159	0.5	9.5
141	—	11.5
130	0.4	8.2
92	0.4	—

---

The integrated fragment signals also showed two time constants of 360 fs and 11 ps. The short-lived component had a positive amplitude, i.e. the total number of fragments for small delays increased, whereas the longer-lived component had a negative amplitude, i.e. the total number of fragments for longer delays decreased.

For the following discussion it is necessary to remember that a fast (360–500 fs) and a relatively slow (8–11 ps) decay time constant are found in all signals, although with varying amplitudes. Note also that the observed time-dependent increase and loss in the total fragment intensity carries the same two time scales and is interpreted as a change in probe absorption cross section and hence also a signature of the excited-state dynamics.

4. Discussion

Our detection scheme for probing excited state dynamics relied on differences between the fragmentation patterns for pump and pump–probe photoabsorption. The temporal evolution of fragment intensities is shown in Fig. 6a–c and discussed in section 4.2. The integrated fragment ion signal in Fig. 6d shows the evolution of the total number of detected fragment ions. Whereas the temporal evolution for a given fragment reflects the excited state process intrinsic to the molecule, the change in the total number of ions is due to our experimental set-up and is therefore discussed separately in section 4.1.

4.1. Fragmentation and detection efficiency

In this chapter, we discuss two experimental artifacts which cause minor distortions of the observed signals: the influence of the He buffer gas in the trap on the fragmentation efficiency and the loss of small masses from the trap.

In general, the absorption of an UV photon provides enough energy for fragmentation in the excited or the ground state. Hence, all parent ions which absorb an UV photon should dissociate. The probe laser alone is not absorbed by ground state molecules and does not produce fragments despite its high intensity. Nevertheless we observe a 15% increase of the total fragment ion signal at pump–probe delays close to zero (Fig. 6d). This increase shows that not all UV-excited ions undergo dissociation. Otherwise, the increase in internal energy by excited state absorption would not increase the overall number of fragments.

There are several pathways to remove the energy introduced by the photons out of the parent ions before dissociation could take place: (i) UV fluorescence from the excited states, (ii) IR emission out of the hot ground state after IC or (iii) cooling by collisions with the He buffer gas which is constantly present in the trap. We think not all reasons play a role in our experiment:

(i) Fluorescence cannot compete with the short relaxation lifetimes observed in our experiment and can be ruled out.

(ii) IR emission after IC to the hot ground state can cool and thus stabilize the parent ion. Typical IR emissions take place on ms time scales and are not expected to compete with dissociation times in relatively small systems such as dipeptides.

(iii) The Paul trap is filled with He (p_He ≈ 0.1 mbar) to cool translational motion of the ions by collisions during the trapping and the isolation processes. These collisions with He can also cool internal degrees of freedom of the ions. Due to the high uncertainty in the He pressure in the trap as well as the uncertainty of the collisional cross section of the peptide ions it is very difficult to estimate dissociation quenching rates. Experimentally, we observed a notable quenching of the UV photodissociation of TrpH⁺ only at very high, pulsed He pressures.

At the pressure conditions of the fs experiments, the quenching of the dissociation by He collisions can be assumed to be relatively small. This is in agreement with the small increase in the total fragment yield when the probe laser is added (pump–probe delay zero). The cooling rate is constant for all ions, but the dissociation rate depends strongly on the internal energy. Thus a higher internal energy leads to a higher fragmentation probability. Therefore an excited state absorption (pump + probe) should increase the total number of fragments compared to one photon absorption (pump only) as observed in the integrated fragment signal (Fig. 6d).

At pump–probe delays longer than 1 ps, the integrated fragment ion signal drops below the initial value at negative pump–probe delays and recovers with a time constant of 9 ps. As the number of fragments should always increase upon multiphoton absorption, this can only mean that we are not able to detect all fragments. Possible reasons are: (i) a high kinetic energy release into the translational motion, leading to an escape of the fragment ions out of the trap or (ii) the detection threshold of the mass spectrometer for fragments masses below m/z 50 causes the loss of small ions.

The remaining question is, why the decrease of the total fragment ion intensity varies with the pump–probe delay. A possible explanation for this are time-dependent cross sections for multiphoton IR excitation. Preliminary calculations for Trp at the ground state geometry yield a significantly higher oscillator strength for excited state absorption from the CT than from L_b.³⁵ The long lived state absorbs more IR photons than the short lived state. This opens a fragmentation channel to a highly energetic fragment, which cannot be detected. This could for example mean that the excited state absorption cross section for the first IR photon changes with time after UV excitation. Such a change in the cross section at a probe wavelength of 800 nm can be explained either by changes of the Franck–Condon factors during the vibrational wave packet motion in the excited state, or an electronic state decay, e.g. a decay of the L_a state to the L_b state in Trp.

The change of the multiphoton IR cross section could also be explained by a scenario where two different intermediates are formed which have different IR absorption cross sections for the subsequent IR photoexcitations. Such intermediates could be closed or open shell species which have very different chemical and optical properties.

To summarize, the fragmentation efficiency is due to one photon absorption of the UV pump pulse, enhanced by additional excited state absorption of IR probe photons and quenched by collisional cooling with helium. The loss of small fragments (m/z < 50), or fast fragments from the trap artificially reduces the observed fragmentation yield at longer pump–probe delays.

4.2. Statistical and excited state dissociation

Two mechanisms can explain the changing rates of fragmentation for the individual fragment ions: non-statistical fragmentation from specific excited states accessible by one or multiphoton excitation respectively, or statistical fragmentation from the hot ground state after IC.

Some electronically excited states are dissociative and can fragment before IC takes place. This can happen from the resonantly excited state accessed by pump-only excitation or from higher lying states after multiphoton absorption of pump + probe. Experimentally, fragments unique to excited state dissociation can be identified by comparison of PID and CID mass spectra: CID is a statistical process from the ground state and will lack the fragments formed by excited state dissociation.

A competing mechanism to excited state fragmentation is IC to the ground state, followed by statistical fragmentation. Even if excited state dissociation is predominant the statistical fragmentation is not completely suppressed.²⁸ For the statistical dissociation process after IC two cases can occur:

(i) The activation energy for some fragments may be higher than the one UV photon energy (E = 4.66 eV), but smaller than the energy of one UV plus one or more IR photons (E ≥ 6.12 eV). This would result in fragments which are only observed for multiphoton absorption at positive delays within the lifetime of the UV excited state. This situation was found for adenine.³⁶

(ii) All fragments can be accessed with pump-only and pump–probe processes but different fragmentation channels have different activation energies. The statistical fragmentation can then be described via RRKM theory, which states that the rate constants for the different channels is a function of the internal energy. Typically channels with higher activation energy become more prominent with increased internal energy. In energy resolved CID mass spectrometry this is commonly used to estimate the relative stabilities of fragments.^33,37,38 In our case, we expect that small, charged fragments will gain intensity at the cost of bigger ones, if the internal energy is increased by excited state absorption in a pump–probe process.

The CID (Fig. 4) as well as the PID (Fig. 5a) mass spectra of LWH⁺ show essentially the same fragmentation pattern. As all fragments appear in both mass spectra, none of the fragments can be unambiguously assigned to excited state dissociation. Upon pump–probe absorption bigger fragments tend to lose intensity whereas the smaller fragments gain intensity (Fig. 5a–c). This is an indication for a statistical fragmentation, which we assume to be the dominating mechanism for the PID of LWH⁺.

For TrypH⁺,²⁸ TrpH⁺³⁴ and WLH⁺,²⁹ hydrogen loss could be assigned to excited state dissociation. For these systems, the indole ring is in direct vicinity of the protonated amino group. For LWH⁺ the Leu acts as a spacer between the chromophore and a charge transfer should be suppressed or delayed.

4.3. Excited state deactivating pathways

All conformers of neutral Trp in the gas phase show mono-exponential decays of 10–13 ns at their origin transitions.³⁹ The isolated neutral Trp analogue molecules tryptamine, 3-indolepropionic acid and N-acetylTrp ethyl ester also show single exponential decays with time constants of 10–13 ns for all conformers at their origin transitions.^39,40 This indicates that the presence of a charge in our experiments shortens the excited state lifetime by a factor of ≈1000 whereas in neutral molecules the different conformations seem to have a small effect.

From our experimental results alone, it is very difficult to derive a specific deactivation mechanism. Only theoretical calculations of the involved excited states can provide indications for possible pathways. This is, however, very difficult because different conformers and tautomers and even transformations between them have to be considered. The position of the charge with respect to the chromophore and its orientation may particularly influence the energetic positions of the chromophore excited states.³⁰ This holds true, especially for the polar L_a state in indole and presumably the CT state found in TrpH⁺ and TyrH⁺ where the excited electron moves to the protonated amine.

In small protonated model peptides consisting of glycine^41–43 and alanine,⁴³ the number of calculated conformers is relatively high. The calculated preferred protonation site is the N terminus. The second and third protonation sites are situated at the amide oxygen atoms, but are energetically unfavorable by >1750 cm⁻¹ than protonation at the N terminus. They should not be accessible at temperatures slightly above room temperature, as expected in the ESI Paul trap configuration. Nevertheless, conformers with and without charge-to-chromophore contacts may coexist or may be able to interconvert.

For Trp, two excited states L_b (S₁) and L_a (S₂) are known to have similar energies and cross sections and the energy of the pump photon is sufficient to reach both states. The L_a state has a high dipole moment and protonation accordingly causes a blue shift of L_a whereas L_b is hardly affected.²⁴ In LWH⁺ we expect similar electronic state energies as in the neutral indole chromophore, and the 266 nm UV pump excitation should be able to address both states directly.

According to theoretical investigations, protonation creates a πσ* state in tryptamine and Trp leading to CT. Recent investigations show that this πσ* is similar in energy to L_a and L_b and the ordering of the three states is very sensitive to the conformation.³⁰ The observed hydrogen loss and fast deactivation is assigned to this πσ* state. As a result, the excited state dynamics of TrpH⁺ and TrypH⁺ would be very sensitive to the conformation in contrast to the neutral species.

From our biexponential decay data, it is not possible to distinguish between a sequential decay, two parallel decays (Fig. 7a), or even a mixture of both (Fig. 7b). In LWH⁺, a sequential decay processes could be observed, for example, if all indole chromophores would be selectively excited to the L_a state (local S₂). L_a (with a lifetime ≈ 500 fs) then could decay to L_b (S₁) and subsequently (with a lifetime ≈ 10 ps) to the ground state. Alternatively the L_a could decay to the CT state, leading either to H loss or IC back to the ground state. We consider this scenario improbable, because both states can be energetically accessed and have similar excitation cross sections.

Fig. 7 Excitation scheme for LWH⁺. Without further excitation (pump only) the ion m/z 205 is the most prominent (thicker horizontal arrows mark higher rates). (a) The pump pulse addresses two conformers which have different life times. In this case, the observed biexponential decay is a superposition of two mono-exponential decays. Different conformers have different cross sections (thicker vertical arrows mark larger cross sections) for excited state absorption (pump + probe), leading to the growth and decay of fragment signals. (b) The pump pulse addresses two electronically excited states. The S₂ decays with 500 fs to the S₁ state. The S₁ has a much higher cross section for 800 nm than S₂. The S₁ decays with a time constant of 9 ps.

In LWH⁺, parallel decay processes (Fig. 7a) would be observed if two or more conformers or tautomers coexists in the ensemble of investigated molecules. Each conformer or tautomer ensemble is photoexcited and decays with a characteristic time scale. In our measurement we then see the superposition of the two ensemble decays. We think this possibility is very likely, because we work at room temperature and must assume that several conformers coexist.

Even a combination of the parallel and sequential decay is possible (Fig. 7b). If in a molecular ensemble a part of the molecules is excited to L_a (S₁) and another part to L_b (S₂), we would observe the decay cascade of S₂ to S₁ for the molecules excited to S₂, superimposed with the mono-exponential decay of the molecules excited to S₁. As discussed in section 1, the cross sections for excited state absorption should be different for the two states observed in our experiments. We could assume a moderate cross section of S₂ for 800 nm. Excited state absorption of S₂ to an unassigned state S_x results in smaller ions and the total number of fragments increases. The S₁ has a high cross section for the probe pulse leading to multiple photon absorption into a state S_y and smaller fragments are formed which cannot be detected. In this model the fast S₂ → S₁ IC creates the measured short-lived component of 500 fs. The S₁ returns with a time constant of 9 ps to the S₀. The measured biexponential decay is therefore the sum of two simultaneously excited states. This model could be further complicated with the assumption of different conformers, resulting in a very complicated interpretation. Time resolved measurements at different wavelengths and different temperatures may clarify this point in the future.

5. Conclusion

The excited state dynamics and fragmentation channels of the protonated, isolated dipeptide LWH⁺ were studied. With time-resolved multiphoton dissociation we could distinguish a short time constant of 500 fs and a longer time constant of ≈ 10 ps. The dynamics are very similar to those of TrpH⁺ (τ₁ = 400 fs, τ₂ = 15 ps)²⁰ and WLH⁺ (τ₁ = 1 ps, τ₂ = 10 ps). In the gas phase, the excited state dynamics of the protonated species differ significantly from neutral Trp and Trp analogue molecules which show single exponential decays with long lifetimes (τ₁ = 10–13 ps).^39,40 In solution, the lifetime behavior of Trp and its derivatives show a similar charge effect: the lifetime of Trp_(aq) is 19 ns at pH 11 (neutral amino group)⁹ and 0.5 ns and 3.1 ns (double exponential) at pH 7 (protonated amino group in the zwitterionic structure).^9,10 In addition, the lifetime components are also strongly correlated with the conformation.^11,44 It would be nice to understand the influence of charges on the photophysics of chromophores with biological relevance in more detail. For this conformer-selective measurements at well defined temperatures will be very important.

References

1. Principles of Fluorescence Spectroscopy, ed. J. R. Lakowicz, Kluwer Academic/Plenum Publishers, New York, 1999.
2. Luminescent Spectroscopy of Proteins, ed. E. Permyakov, CRC Press, Boca Raton, FL, 1992.
3. Ultraviolet Spectroscopy of Proteins, ed. A. P. Demchenko, Springer Verlag, New York, 1981.
4. Fluorescence and Phosphorescence of Proteins and Nucleic Acids, ed. S. V. Konev, Plenum Press, New York, 1967.
5. I. Weinryb and R. Steiner, The luminescence of the aromatic amino acids, in Excited States of Proteins and Nucleic Acids, ed. I. Weinryb and R. F. Steiner, Plenum Press, New York, 1971, pp. 277–318.
6. I. Gryczynski, W. Wiczk, M. L. Johnson and J. R. Lakowicz, Biophys. Chem., 1988, 32, 173.
7. W. W. E. Gudgin and R. Lopez-Delgado, Can. J. Chem., 1980, 59, 1037.
8. D. Jameson and G. Weber, J. Phys. Chem., 1981, 85, 953.
9. R. J. Robbins, G. R. Fleming, G. S. Beddard, G. W. Robinson, P. J. Thistlethwaite and G. J. Woolfe, J. Am. Chem. Soc., 1980, 102, 6271.
10. A. G. Szabo and D. M. Rayner, J. Am. Soc. Mass Spectrom., 1980, 102, 554.
11. R. F. Chen, J. R. Knutson, H. Ziffer and D. Porter, Biochemistry, 1991, 30, 5184.
12. R. Tembreull and D. M. Lubman, Anal. Chem., 1987, 59, 1003.
13. K. Walter, J. Lindner and J. Grotemeyer, Chem. Phys., 1988, 125, 155.
14. R. Weinkauf, P. Schanen, D. Yang, S. Soukara and E. W. Schlag, J. Phys. Chem., 1995, 99, 11255.
15. R. Weinkauf, P. Aicher, G. Wesley, J. Grotemeyer and E. W. Schlag, J. Phys. Chem., 1994, 98, 8381.
16. E. R. Williams, J. J. P. Furlong and F. W. McLafferty, J. Am. Soc. Mass Spectrom., 1990, 1, 288.
17. Z. Guan, N. L. Kelleher, P. B. O’Connor, D. J. Aaserud, D. P. Little and F. W. McLafferty, Int. J. Mass Spectrom. Ion Processes, 1996, 158, 357.
18. W. Gabryelski and L. Li, Rev. Sci. Instrum., 1999, 70, 4192.
19. F. O. Talbot, T. Tabarin, R. Antoine, M. Broyer and P. Dugourd, J. Chem. Phys., 2005, 122, 74310.
20. H. Kang, C. Dedonder-Lardeux, C. Jouvet, G. Grégoire, C. Desfrançoise, J.-P. Schermann, M. Barat and J. A. Fayeton, J. Phys. Chem. A, 2005, 109, 2417.
21. L. H. Andersen, A. Lapierre, S. Brønstedt Nielsenan, I. B. Nielsen, S. U. Pedersen, U. V. Pedersen and S. Tomita, Eur. Phys. J. D, 2002, 20, 597.
22. S. Brønstedt Nielsen, A. Lapierre, J. U. Anderson, U. V. Pedersen, S. Tomita and L. H. Andersen, Phys. Rev. Lett., 2001, 87, 228102.
23. L. H. Andersen, I. B. Nielsen, M. B. Kristensen, M. O. A. E. Ghazaly and S. Haacke, J. Am. Chem. Soc., 2005, 127, 12347.
24. D. Nolting, C. Marian and R. Weinkauf, Phys. Chem. Chem. Phys., 2004, 6(10), 2633.
25. C. Marian, D. Nolting and R. Weinkauf, Phys. Chem. Chem. Phys., 2005, 7, 3306.
26. O. V. Boyarkin, S. R. Mercier, A. Kamariotis and T. R. Rizzo, J. Am. Chem. Soc., 2006, 128, 2816.
27. H. Kang, C. Jouvet, C. Dedonder-Lardeux, S. Martrenchard, G. Grégoire, C. Desfrançoise, J.-P. Schermann, M. Barat and J. A. Fayeton, Phys. Chem. Chem. Phys., 2005, 7(2), 394.
28. H. Kang, C. Jouvet, C. Dedonder-Lardeux, S. Martrenchard, C. Charrière, G. Grégoire, C. Desfrançoise, J. Schermann, M. Barat and J. A. Fayeton, J. Chem. Phys., 2005, 122, 084307.
29. G. Grégoire, H. Kang, C. Dedonder-Lardeux, C. Jouvet, C. Desfrançoise, S. Martrenchard, D. Onidas, V. Lepere and J. A. Fayeton, Phys. Chem. Chem. Phys., 2006, 8, 122.
30. G. Grégoire, C. Jouvet, C. Dedonder and A. Sobolewski, Chem. Phys., 2006, 324, 398.
31. M. H. Palmer, I. C. Walker, C. C. Ballard and M. F. Guest, Chem. Phys., 1995, 192, 111.
32. H. Lioe and R. A. J. O’Hair, J. Am. Soc. Mass Spectrom., 2004, 15, 65.
33. H. el Aribi, G. Orlova, A. C. Hopkins and K. W. M. Siu, J. Phys. Chem. A, 2004, 108, 3844.
34. H. Kang, C. Dedonder-Lardeux, C. Jouvet, S. Martrenchard, G. Grégoire, C. Desfrançoise, J.-P. Schermann, M. Barat and J. A. Fayeton, Phys. Chem. Chem. Phys., 2004, 6(10), 2628.
35. C. Marian, private communication.
36. D. Nolting, R. Weinkauf, I. V. Hertel and T. Schultz, J. Am. Chem. Soc., submitted.
37. A. G. Harrison, Rapid Commun. Mass Spectrom., 1999, 13, 1663.
38. V. Gabelica and E. De Pauw, Mass Spectrom. Rev., 2005, 24, 566.
39. L. A. Philips, S. P. Webb, S. J. Martinez, G. R. Fleming and D. H. Levy, J. Am. Chem. Soc., 1988, 110, 1352.
40. J. Sipior, M. Sulkes, R. Auerbach and M. Boivineau, J. Phys. Chem., 1987, 91, 2016.
41. J. Wu and C. B. Lebrilla, J. Am. Chem. Soc., 1993, 115, 3270.
42. K. Zhang, C. J. Cassady and A. Chung-Phillips, J. Am. Chem. Soc., 1994, 116, 11512.
43. C. J. Cassady, S. R. Cam, K. Zhang and A. Chung-Phillips, J. Org. Chem., 1995, 60, 1704.
44. J. T. Vivian and P. R. Callis, Biophys. J., 2001, 80, 2093.

---