Probing the intrinsic features and environmental stabilization of multiply charged anions†
William E.
Boxford
and
Caroline E. H.
Dessent
*
Department of Chemistry, University of York, Heslington, York, UK YO10 5DD. E-mail: ced5@york.ac.uk.; Fax: +44 1904 432516; Tel: +44 1904 434092
First published on 21st September 2006
Abstract
Multiply charged anions (MCAs) represent exotic, highly energetic species in the gas-phase due to their propensity to undergo unimolecular decay via electron loss or ionic fragmentation. There is considerable fundamental interest in these systems since they display novel potential energy surfaces that are characterized by Coulomb barriers. Over recent years, considerable progress has been made in understanding the factors that affect the stability, decay pathways and reactivity of gas-phase MCAs, mainly as a result of the application of electrospray ionization as a generic technique for transferring solution-phase MCAs into the gas-phase for detailed characterization. We review contemporary work in this field, focusing on the factors that control the intrinsic stability of MCAs, both as isolated gas-phase ions, and on their complexation with solvent molecules and counter-ions. While studies of MCAs are primarily of fundamental interest, several classes of important biological ions are commonly observed as MCAs in the gas-phase (e.g. oligonucleotides, sugars). Recent results for biologically relevant ions are emphasised, since a fundamental understanding of the properties of gas-phase MCAs will be highly valuable for developing further analytical methods to study these important systems.
I. Introduction
There has been considerable recent interest in the properties of gas-phase multiply charged ions as a result of new experimental developments that allow their detailed characterization using techniques such as laser spectroscopy.1 Small and medium sized multiply charged ions represent highly energetic species in the gas-phase due to the strong, repulsive Coulomb interaction that exists between the excess charges.2–8 Multiply charged ions are therefore highly susceptible to decay via fragmentation into two ionic moieties.In this review, we highlight the results of recent experimental and theoretical studies that aim to characterize the intrinsic properties of multiply charged anions (MCAs) through the study of isolated gas-phase ions. MCAs are regarded as being generally less stable than their cationic analogues due to their propensity to decay by electron loss via tunnelling. Fundamental studies of MCAs were hampered for many years by the lack of a broadly applicable technique for generating the gas-phase species. The introduction of electrospray ionization (ESI),9 has however, revolutionised this area since it allows robust quantities of MCAs to be transferred directly from bulk solutions into the gas-phase for experimental interrogation. Over the last ten years, considerable progress has subsequently been made in understanding the factors that affect the stability, decay pathways and reactivity of isolated MCAs.
Although MCAs (e.g. SO2−4, PtCl2−6, etc.) can reasonably be regarded as exotic, metastable species in the gas-phase, they are common components of polar solutions and ionic solids. Within a condensed phase environment, the solvent or counter-ions act to stabilize the excess charges and reduce the extent of Coulombic repulsion via dielectric screening. A primary focus for contemporary studies of MCAs is therefore the investigation of molecular clusters of MCAs with solvent molecules (e.g. IrCl3−6·(H2O)n n = 1–10).10–16 These studies explore the effect of sequential solvation on the intrinsic properties of the MCA, with the aim of understanding how an intrinsically unstable gaseous MCA evolves into a stable condensed-phase species. A smaller number of studies have addressed the issue of counter-ion stabilization through studies of clusters involving MCAs and cations.17–21 We review the recent work in this field to provide an overview of the factors that control the intrinsic stability of MCAs, both as isolated species and in condensed phase environments.
Gas-phase MCAs are mainly prone to decay by either electron detachment or via ionic fragmentation (also termed Coulombic explosion and thermodynamic decay) with production of two charged particles (Fig. 1a and b). Fig. 1c illustrates the third possible decay channel, neutral loss, which occurs for only a small number of MCAs. The most striking characteristic of the surfaces for electron detachment and ionic fragmentation (Fig. 1a and b) is the presence of repulsive Coulomb barriers (RCBs). These features arise from the combination of the short range binding force with the purely repulsive long range Coulombic interaction, and can be considered to result from the intersection of two diabatic curves.2 We note that the term “repulsive Coulomb barrier” is somewhat misleading since although the barrier is repulsive at long range, at short range (inside the barrier) the overall potential is attractive.2 In this review we use the phrase RCB since it has been adopted in most publications in this area.1,3,10,15,21
 | ||
| Fig. 1 Schematic potential energy curves for decay pathways of a dianion illustrating (a) electron detachment, (b) ionic fragmentation and (c) loss of a neutral atomic or molecular fragment. The RCBed (repulsive Coulomb barrier to electron detachment), RCBif (repulsive Coulomb barrier to ionic fragmentation, and Ediss (threshold dissociation energy) are illustrated. | ||
The existence of the RCB is of crucial importance in determining the intrinsic stability of an MCA, since it can confer metastability even when the system is exothermic with respect to electron detachment or fragmentation. Fig. 2 illustrates the two possible situations for the case of electron detachment, where the MCA is either intrinsically stable (Fig. 2a) or intrinsically unstable (Fig. 2b) against electron loss. While the RCB confers metastability on electronically unstable MCAs (Fig. 2b), a non-zero electron tunnelling rate will occur if the total energy of the system is above the electron detachment asymptote.23–26 In contrast, tunnelling behaviour is typically not observed on ionic fragmentation surfaces due to the considerably higher mass of atomic and molecular anions, resulting in such systems remaining metastable.
 | ||
| Fig. 2 Electron detachment potential energy curves for an MCA that is (a) stable and (b) metastable with respect to electron detachment. The inner and outer sections of the RCB are illustrated.22 | ||
While studies of gas-phase MCAs are of considerable fundamental interest due to the novel potential energy surfaces involved, it is worth noting that they also represent an important class of biological ions that are commonly observed in the gas-phase during mass spectrometric analysis. For example, oligonucleotides are generally electrosprayed as MCAs for sequence analysis, while important sugars such as heparin also preferentially ionize as MCAs.27–30 A fundamental understanding of the properties of gas-phase MCAs is therefore highly valuable for developing further analytical methods to study these important systems. For these medium or larger sized MCAs, ionic fragmentation is frequently the dominant decay mechanism rather than spontaneous electron loss. While most previous reviews of MCAs have focused on the electron detachment surfaces,1–3,5 we emphasise ionic fragmentation in this review, partly due to its relevance to biomolecular ions, but also because it is only recently that ionic fragmentation pathways have begun to be studied in depth.31,32
II. Intrinsic stability of molecular dianions
A. Electron detachment
The pioneering photodetachment studies conducted by Lai Sheng Wang and co-workers provided the first detailed information on the potential energy surfaces of MCAs.33–35 By combining an ESI source with a magnetic bottle time-of-flight photoelectron spectrometer,36 Wang produced a powerful instrument that was able to generate and characterize a wide range of MCAs from small, prototypical ions such as S2O2−8 through to biologically relevant ions such as copper phthalocyanine 3,4,4,4-tetrasulfonate.37,38 The instrument employed laser photodetachment spectroscopy, and hence directly probed the electron detachment propensity of the MCAs under spectral interrogation.A number of important results arose from the early photodetachment studies, including the first direct observation of an RCB. The photoelectron spectra (PES) of the citrate dianion (CA2−), revealed a striking photon-energy dependence.33 At a high photon energy of 4.661 eV, the PES consisted of two spectral bands, which could be assigned to the X and A electronic states of CA− (having electronic affinities of 1.0 and 1.6 eV, respectively).33 At the lower detachment energy of 3.496 eV only a single band occurred, whereas at the lowest detachment energy of 2.331 eV no photoelectron signals were observed, despite the fact that this photon energy was higher than the binding energies of the X and A states. These unique observations can be readily explained by invoking the presence of the RCB illustrated on Fig. 3. The high energy photon exceeds the X and A state RCBed(inner),22 so that both bands are observable in the 4.661 eV PES. In contrast, at the lowest detachment energy, the photon energy is below both RCBs. The intermediate photon therefore lies above the RCB on the X surface, but below the RCB on the A surface.
 | ||
| Fig. 3 Schematic potential energy curves illustrating the RCBs for electron detachment from the citrate dianion, CA2−, leading to the X and A states of the monoanion, CA−. Adiabatic binding energies are shown. The minimum energy structure of CA2− (HF/6-31G*) displayed illustrates the positions of the excess charges. Adapted from ref. 33. | ||
From the photon-energy dependent PES, it was possible to estimate the magnitude of the CA2− RCBed(outer) as 1.9–2.5 eV.22,33 The citrate excess negative charges (Fig. 3) are localized ∼6.14 Å apart, a distance which corresponds to a Coulomb repulsion energy of about 2.3 eV. This result suggested that the magnitude of RCBed(outer) is related to the intramolecular Coulomb repulsion energy. Indeed, a subsequent study of −O2C–(CH2)n–CO2− dianions (n = 3–10) revealed that the magnitude of RCBed(outer) in MCAs is exactly equal to the intramolecular Coulomb repulsion, while RCBed(inner) is equivalent to the binding energy of an electron to a carboxyl group.34 These important conclusions provided a basis for understanding the electron detachment surfaces of all MCAs.
Since these initial measurements, the presence of RCBed has been observed in many MCAs using photodetachment spectroscopy, both in further studies by the Wang group and in experiments performed by Weber and co-workers.1,39–42 Direct evidence for electron tunnelling decay of MCAs has come from a number of experiments: An early example was provided by Compton and co-workers who used a hybrid magnetic sector/quadrupole mass spectrometer to estimate the electron loss lifetime of C2−84.26 A similar approach has been used in more recent Fourier transform ion cyclotron resonance (FT-ICR) mass spectrometry measurements on the PtCl2−4, PtCl3Br2− and C2−70 dianions.23,24 Tunnelling effects have been observed in the 355 nm photoelectron spectra of the −O2C–(CH2)n–CO2− (n = 3–10) dianions,34 and also in laser photodetachment scans of PtBr2−4 at energies below the RCB.43
The description of the MCA electron detachment surfaces in terms of the electron binding energy and intramolecular Coulomb repulsion provides a highly useful model. Dreuw and Cederbaum have noted that the accurate calculation of the electron detachment surfaces, and the RCB in particular, is challenging.44 They developed a formally exact theory for calculating RCBed based on the Green’s function formalism of scattering. While electrostatic forces dominate the appearance of the RCBed in compact dianions, the RCB is a complicated non-local and energy dependent potential. We refer the reader to ref. 44 for a fuller discussion of this model.
B. Ionic fragmentation
The vast majority of experimental and theoretical studies of isolated MCAs to date have focused on the ions’ stability with respect to electron detachment, while studies exploring ionic fragmentation are relatively sparse. This situation has largely arisen due to the predominance of the photodetachment spectroscopy measurements described above.Friedrich et al. recently employed electronic photodissociation spectroscopy of IrBr2−6 to investigate whether it is stable with respect to fragmentation.32 Photodissociation produced Br− and IrBr5−, with fragment formation measurements providing an estimate of the RCBif(inner) as 1.6 ± 0.2, and kinetic energy release data yielding a value for the RCBif(outer) of 2.2 ± 0.2 eV.22 Since RCBed(inner) had previously been estimated as ∼3.0 eV,45 IrBr2−6 therefore represents the only dianion for which both RCBif(inner) and RCBed(inner) are known. The fact that RCBif(inner) < RCBed(inner) was notable as it demonstrated that ionic fragmentation would be the lowest energy unimolecular decay pathway for IrBr2−6. The issue of whether RCBif is generally lower than RCBed for dianions was subsequently addressed in our group using resonance excitation of dianions isolated in a quadrupole ion-trap.31 This approach provides a convenient and economical alternative to laser spectroscopy for determining the lowest energy decomposition pathway, and is therefore ideal for investigating the relative heights of RCBif(inner) and RCBed(inner).
Fig. 4 illustrates the process involved in quadrupole ion-trap resonance excitation. Ions of a chosen m/z value are isolated in the trap by the application of a tailored notched waveform to the entrance end-cap electrode.46 The ions are then cooled through collisions with the helium buffer gas, and assume a Boltzmann distribution of internal energies. Upon application of a resonance excitation signal to the endcap electrodes, the ions are accelerated and decelerated, causing their trajectories of motion to enlarge and resulting in multiple collisions with the buffer gas. These collisions raise the ions’ internal energy, and once the lowest energy barrier for decay is reached, they undergo unimolecular decay. Typically, this process can involve greater than 100 individual collision events, each with average energies of ∼0.1 eV.46
 | ||
| Fig. 4 Schematic illustrating movement and internal energies of ions in a quadrupole ion trap during (a) the trapping process and (b) the application of a resonance excitation signal. See text for further details. | ||
Quadrupole ion trap resonance excitation can therefore lead to the unambiguous identification of the lowest energy decay pathway for a system. In this respect, the technique has a clear advantage over other collision induced dissociation (CID) techniques such as dissociation within a triple quadrupole mass spectrometer, where several decay pathways can be accessed simultaneously.47 (Note that all CID ion-trap experiments are distinct from FT-ICR mass spectrometry experiments, where spontaneous ion decay is monitored in a collision-free environment.46) It is difficult to quantify dissociation thresholds using resonance excitation,48 although for ions of similar mass and charge, the dissociation threshold is linearly proportional to the observed onset for decay.49
Fig. 5a displays a typical electrospray ionization mass spectrum (ESI-MS) of the potassium salt of IrBr2−6 in which the parent dianion appears prominently along with IrBr−5, IrBr−4 and K+·IrBr2−6. No IrBr−6 is evident in the mass spectrum, an observation that is significant given the widespread view that small dianions are primarily unstable with respect to electron detachment. Fig. 5b displays the MS obtained upon isolation of IrBr2−6 within the quadrupole ion trap, while Fig. 5c presents the CID mass spectrum of IrBr2−6 at 6% collision energy, illustrating fragmentation of IrBr2−6 to IrBr−5.50 The IrBr−5 product ion is attributed to decay of the dianion via ionic fragmentation (Fig. 1b), leading to the conclusion that RCBif(inner) lies below RCBed(inner), in agreement with the laser photodissociation measurement. This result appears to be general for this class of dianions, as similar results were obtained for OsCl2−6, ReCl2−6, IrCl2−6 and PtBr2−6. Fig. 6 illustrates % fragmentation curves for OsCl2−6, ReCl2−6 and IrCl2−6. These curves indicate that RCBif(inner) ReCl2−6 > IrCl2−6 > OsCl2−6.31
 | ||
| Fig. 5 (a) Negative ion ESI-MS of the potassium salt of IrBr2−6 obtained by optimizing the m/z 333 signal. (b) Isolation of IrBr2−6 in the quadrupole ion trap at 0% collision energy.50 (c) CID mass spectrum of IrBr2−6 at 6% collision energy, illustrating fragmentation of IrBr2−6 to IrBr2−5. | ||
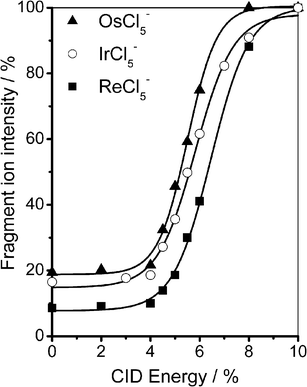 | ||
| Fig. 6 % fragmentation curves for production of the IrCl−5, OsCl−5 and ReCl−5 product ions from the decay of the IrCl2−6, OsCl2−6 and ReCl2−6 parent dianions.31,50 Reprinted from Chem. Phys. Lett., Vol. 399, W. E. Boxford, J. K. Pearce and C. E. H. Dessent, Ionic fragmentation versus electron detachment in isolated transition metal complex dianions, Pages No. 465–470, Copyright 2004, with permission from Elsevier. | ||
It is instructive to consider the physical origin of the observation RCBif(inner) < RCBed(inner). As discussed above, RCBed(inner) can be attributed to the purely attractive binding energy of an electron to the respective monoanion.34 RCBed(outer) was attributed to the intramolecular Coulomb repulsion. By analogy, we proposed that RCBif(inner) for an MX2−6 dianion should be associated with the purely attractive binding energy of an X− ion to the MX−5 moiety, i.e.
 | (1) |
Table 1 lists RCBed(inner) and RCBed(outer) for the IrCl2−6, OsCl2−6, ReCl2−6, IrBr2−6 and PtBr2−6 dianions obtained from photoelectron spectroscopy.45 We suggest that the intramolecular Coulomb repulsion for a dianion will be the same on the ionic fragmentation and electron detachment surfaces. The experimental value of RCBed(outer) for IrBr2−6 obtained from photoelectron spectroscopy, ≤2.0 eV,45 and the value of RCBif(outer) gained from photofragmentation spectroscopy, 2.2 ± 0.2 eV,32 are indeed in good agreement. The measured RCBed(outer) values can therefore be combined with ab initio calculated fragmentation reaction energies (Table 1) to obtain estimates of RCBif(inner). It is noteworthy that the RCBif(inner) value obtained for IrBr2−6 ≤ 1.75 eV (Table 1), agrees well with the photofragmentation measurement (1.6 ± 0.2 eV).32 Furthermore, the RCBif(inner) value for IrCl2−6 is somewhat lower than the RCBif(inner) for ReCl2−6, in line with the respective % fragmentation curves displayed in Fig. 6.
The results presented in Table 1 illustrate the generality of RCBif being lower than RCBed for transition metal complex dianions. Using a similar approach we have also identified RCBif < RCBed in other inorganic dianions: a further example is provided by H3P3O2−10, where the dianion fragments into the PO−3 and H3P2O−7 product ions upon resonance excitation.51 Other examples such as [Fe4S4X4]2− and adenosine diphosphate2− also exist in the literature.51,52These results suggest that more experimental and theoretical focus should be placed on the ionic fragmentation of gas-phase MCAs since it appears to represent the dominant thermally or collisionally activated decay pathway for dianions that can fragment to produce two stable singly charged anions.
Finally, we note that novel measurements of RCBif(outer) have come from Nielsen and co-workers who observed spontaneous ionic fragmentation decay of the Cr(SCN)2−4 and Au(N3)2−4 dianionic complexes in experiments where electrons are attached to the respective monoanionic metal complexes via collision with sodium vapour.53,54 Measurement of the kinetic energy release associated with the ionic fragmentation process provides values for RCBif(outer) of 3.2 ± 0.4 and 2.6 ± 0.5 eV, respectively.
C. Neutral loss
While the intrinsic Coulombic repulsion of a multiply charged anion generally makes it susceptible to decay into two negatively charged fragments, there are a small class of dianions for which the lowest energy surfaces for decay correspond to loss of a neutral moiety (Fig. 1c). An example is provided by the Pt(CN)2−6 transition metal complex dianion.55 Resonance excitation of Pt(CN)2−6 within a quadrupole ion trap (Fig. 7a) leads to decay of the parent ion into Pt(CN)2−4, i.e. fragmentation proceeds with loss of two CN groups. Fig. 7b displays the % fragmentation curve for production of the Pt(CN)2−4 product ion from decay of Pt(CN)2−6. | ||
| Fig. 7 (a) CID mass spectrum of Pt(CN)2−6 at 9% collision energy illustrating fragmentation to Pt(CN)2−4. (b) % fragmentation curve for decay of the Pt(CN)2−6 parent dianion into the Pt(CN)2−4 product ion.50 | ||
Fig. 8 compares ab initio calculations for decay of Pt(CN)2−6via (a) ionic fragmentation into Pt(CN)2−5 and CN−, and (b) neutral loss of (CN)2 from the dianion. Both the final asymptote and the barrier to fragmentation lie lower on the neutral loss channel. The calculations indicate that the neutral loss channel is favoured due to the high bond strength of the cyanogen product (6.270 eV at the B3LYP/LANL2DZ level). The amount of Coulomb repulsion in Pt(CN)2−6 is also somewhat reduced compared to other complex dianions due to charge delocalisation along the CN− ligands.
 | ||
| Fig. 8 Diagram illustrating the energetics of the reactants, transition state and products (B3LYP/LANL2DZ) for decay of Pt(CN)2−6via (A) ionic fragmentation into Pt(CN)−5 and CN− and (B) loss of (CN)2. The energy axis is scaled so that 0 eV corresponds to the global minima of each complex. | ||
Dicarboxylates represent another important class of MCAs that routinely decay with loss of a neutral molecule, e.g.56,57
 | (2) |
Neutral loss channels can be expected to feature prominently on the excited state surfaces of MCAs. The excited state surfaces are currently almost entirely uncharacterized, although high-energy CID experiments have provided a primary insight into the decay pathways available from electronically excited MCAs. For Pt(CN)2−6, high energy CID results in production of Pt(CN)2−5 as well as Pt(CN)2−4.55 Intriguingly, IrCl2−5 is absent from the high energy CID of the IrCl2−6 parent dianion, indicating that alternative decay mechanisms are operative for the smaller hexa-halide complex compared to the larger hexa-cyano transition metal dianions.58
III. Trianions, tetraanions and higher analogues
The majority of work conducted on MCAs to date has focused on molecular dianions, with studies of small highly charged systems being sparse. A recent computational study compared IrCl2−6 with IrCl3−6 to systematically explore the intrinsic stability of a dianion versus a trianion.10 Both IrCl2−6 and IrCl3−6 are stable ions in the condensed phase, but their properties differ significantly in the gas-phase.IrCl2−6 has a positive electron binding energy, and is predicted to lie on the edge of stability with respect to ionic fragmentation. In contrast, IrCl3−6 is predicted to be both electronically and thermodynamically unstable. Fig. 9 illustrates the electron detachment surfaces for the two ions. From the ground state of IrCl2−6 (Fig. 9a), electron emission via tunnelling though RCBed cannot occur as the electron detachment asymptote lies higher in energy than the dianion at its global minimum. Electron tunnelling will, however, occur for IrCl3−6 (Fig. 9b) with a predicted lifetime of ∼2.4 × 10−13 s. A similar change occurs in the shape of RCBif when going from IrCl2−6 to IrCl3−6, with RCBif(inner) dramatically decreasing in height, and the ionic fragmentation asymptote becoming more exothermic. Due to rapid electron tunnelling decay, the trianion would therefore be undetectable using conventional mass spectrometric techniques. These results illustrate a general point regarding the stability of small, highly charged MCAs. As the excess charge increases, the ion will become less stable with respect to both electron loss and ionic fragmentation.37,38,59,60 However, more highly charged ions will be particularly prone to decay via spontaneous electron loss due to rapid electron tunnelling.
 | ||
| Fig. 9 Two-dimensional shape of RCBed calculated using a point charge model for (a) IrCl2−6 and (b) IrCl3−6 along the xy plane of the complex as defined in (c).5,10 The energy axis is scaled so that 0 eV corresponds to the global minima of the parent ions. | ||
Some direct experimental evidence for the intrinsic instability of small molecular trianions has been provided by novel experiments exploring electron scattering of a corresponding dianion, e.g. Pt(CN)2−6.61 The scattered electron is only temporarily trapped in a short-lived resonance, demonstrating that the trianion is unstable with respect to electron detachment.
Gas-phase oligonucleotides represent a somewhat different class of highly multiply charged anions.62–66 These ions are of considerable current interest due to their importance in biological mass spectrometry. It is possible to generate high charge states of oligonucleotides via ESI, e.g. [dT5-4H]4−, since the charge carrying phosphate groups are interdispersed with the nucleic acid bases, which can stabilize the excess charges via dielectric screening or hydrogen bonding interactions (see Section VC). In a recent study, Weber et al. obtained photoelectron spectra of the [dA5-4H]4− and [dT5-4H]4− oligonucleotides.39 The study revealed an unexpected dependence of the detachment energies on base composition. Several explanations for this phenomenon are possible, since the oligonucleotides could display different geometric structures, deprotonation sites, or degrees of HOMO localization. This experiment illustrates the importance of developing accurate but economical theoretical methods for interpreting the spectroscopic data that are now available for medium sized biomolecular ions. To this end, we have recently developed a systematic methodology for obtaining global minima structures of such systems.51Fig. 10 displays a minimum energy structure for [dT5-4H]4−, illustrating the complex pattern of intramolecular interactions that occur in this ion. In this case, the HOMO is localised on a deprotonated phosphate group, although this situation may change as a function of deprotonation site, nucleobase or overall charge.
![Structure of [dT5-4H]4− where deprotonation occurs on the phosphate groups, calculated using a simulated annealing molecular dynamics protocol utilising the Amber Parm99 force field.67 The HOMO from a subsequent single point B3LYP/6-31G* calculation is shown.](/image/article/2006/CP/b609123g/b609123g-f10.gif) | ||
| Fig. 10 Structure of [dT5-4H]4− where deprotonation occurs on the phosphate groups, calculated using a simulated annealing molecular dynamics protocol utilising the Amber Parm99 force field.67 The HOMO from a subsequent single point B3LYP/6-31G* calculation is shown. | ||
IV. Bimolecular reactivity of multiply charged anions
Little work has been conducted to date on bimolecular reactions of gas-phase MCAs. (In contrast, the gas-phase reactivity of multiply charged cations is well understood.4,7,68–73) We briefly discuss the results of two studies which illustrate how the novel potential energy surfaces influence the chemical reactivity of an MCA.FT-ICR mass spectrometry has recently been employed to monitor the kinetics of electron transfer collisions between the fullerene dianions C2−76, C2−78, C2−84 and SF6, compared with collisions for the corresponding monoanions,74e.g.
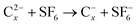 | (3) |
The reactions of dicarboxylates with alkyl halides have been studied by Flores and Gronert to investigate the competition between substitution and elimination reactions.75 Subsequent ab initio calculations compared the SN2 potential energy surfaces for the reaction of bromomethane with the acetate monoanion [4a] and linear dicarboxylates [4b]:76
 | (4a) |
 | (4b) |
Both studies indicate that MCA reactions can be very energetically favourable due to the release of Coulombic repulsion, although the presence of an RCB may introduce a kinetic barrier. Much more work is clearly desirable in this stimulating area.
V. Environmental stabilization
In this section, we explore the phenomena that can lead to stabilization of MCAs against the decay pathways and reactive surfaces described above.A. Solvation
The influence of solvent molecules on the electronic structure is a key issue for understanding how the intrinsic properties of an isolated MCA evolve into the condensed phase analogue. A number of experimental and theoretical studies of MCA–water clusters have revealed that the ions are gradually stabilized with respect to electron detachment upon sequential solvation.10–16,77 Early ESI mass spectrometry studies by Blades and Kebarle lead to the identification of a number of stable gas-phase dianions, including S2O2−6 and S2O2−8, and their hydrated clusters.13 When SO2−4 salt solutions were electrosprayed, however, no SO2−4 could be observed leading to the conclusion that SO2−4 is electronically unstable, an observation in line with theoretical predictions.78 Furthermore, while n = 3 SO2−4·(H2O)n clusters were present in the ESI-MS, the n = 1, 2 systems were absent, indicating that SO2−4 requires microsolvation by three water molecules to become electronically stable. Photodetachment photoelectron spectroscopy was subsequently employed to directly measure the sequential electronic stabilization of SO2−4 (and other dianions) by water molecules.15,16 For the SO2−4·(H2O)n clusters, the adiabatic detachment energy (ADE) increased from a value of 0.4 eV for the n = 3 cluster to 5.73 eV for the n = 40 cluster. This increase was accompanied by a corresponding rise of RCBed(inner).The nature of solvent-induced electronic stabilization of MCAs was recently explored in a computational study of IrCl3−6·(H2O)n n = 1–12.10 The solvation motifs of the trianion were studied in detail, leading to the identification of two classes of microsolvated clusters (A and B) illustrated in Fig. 11. Water binding energies and detachment energies for the IrCl3−6·(H2O)n n = 1–12 clusters are displayed in Table 2. The results illustrate that as n increases, the VDEs and ADEs increase, indicating that water binding has a stabilising effect. For series A, the n = 10 cluster is the first to exhibit electronic stability, whilst n = 12 marks the onset of stability for series B.
 | ||
| Fig. 11 Structure of (a) series A and (b) series B IrCl3−6·(H2O)10 clusters calculated at the B3LYP/LANL2DZ level.10 Hydrogen bonds are illustrated by dashed lines. Adapted from ref. 10. | ||
| n | Series Aa | Series Bb | ||||
|---|---|---|---|---|---|---|
| VDE/eV | ADEa /eV | BEc /eV | VDE/eV | ADEa /eV | BEc /eV | |
| a Minimum energy isomer where water is bound exclusively via bifurcated hydrogen bonds. b Minimum energy isomer where the number of binding motifs in which a bifurcated hydrogen bonded water molecule acts as an acceptor to another water molecule is maximised. c BE = E(IrCl3−6·(H2O)n) − E(IrCl3−6·(H2O)n−1 + H2O). | ||||||
| 1 | −3.437 | −3.617 | 1.328 | — | — | — |
| 2 | −2.912 | −3.072 | 1.276 | −3.029 | −3.221 | 1.332 |
| 3 | −2.362 | −2.582 | −1.203 | −2.549 | −2.817 | −1.216 |
| 4 | −1.898 | −2.113 | 1.077 | −2.163 | −2.381 | 1.230 |
| 5 | −1.570 | −1.793 | 0.993 | −1.722 | −1.939 | 1.051 |
| 6 | −1.202 | −1.356 | 0.949 | −1.374 | −1.161 | 1.144 |
| 7 | −0.741 | −1.070 | 0.833 | −0.901 | −1.232 | 0.949 |
| 8 | −0.490 | −0.613 | 0.780 | −0.693 | −0.995 | 1.013 |
| 9 | −0.087 | −0.327 | 0.725 | −0.388 | −0.693 | 0.762 |
| 10 | 0.263 | 0.009 | 0.672 | −0.007 | −0.473 | 0.726 |
Fig. 12 illustrates two-dimensional cuts through the minimum energy path for electron detachment. The increase in RCBed(inner) with increasing solvent coordination number is clearly illustrated, along with the accompanying reduction in RCBed(outer).10 These results support the conclusions drawn from the photodetachment study of SO2−4·(H2O)n.16 The impact of increasing hydration on the ionic fragmentation surface of IrCl3−6 was also investigated, since this issue has been largely ignored for MCAs. Fig. 13 displays potential energy scans for ionic fragmentation of selected IrCl3−6·(H2O)n clusters. The magnitude of RCBif(inner) is shown to increase with increasing solvation, in line with the situation for RCBed. This is an important result as it demonstrates that an MCA will generally be stabilized towards decay by ionic fragmentation, as well as decay by electron detachment, upon sequential solvation.
 | ||
| Fig. 12 The lowest energy sections through RCBed of the IrCl3−6·(H2O)n, n = 1, 5 and 10, series A clusters, calculated using a point charge model at the B3LYP/LANL2DZ level.5,10 In each case, the surface shown corresponds to removal of an electron from the least solvated side of the ion. The energy axis is scaled so that 0 eV corresponds to the global minima of the clusters. Adapted from ref. 10. | ||
 | ||
| Fig. 13 Potential energy curves (B3LYP/LANL2DZ) for ionic fragmentation (loss of Cl−) of the IrCl3−6·(H2O)n, n = 1, 2, 5 and 10 series A clusters.10 The surfaces shown are due to the loss of one of the least solvated chlorine ligands. The energy axis is scaled so that 0 eV corresponds to the global minimum of each complex. Adapted from ref. 10. | ||
By invoking the model discussed in section IIB, the effects of increasing solvation on RCBed and RCBif can be rationalised. (The outer RCB was found to be associated with the intramolecular Coulomb repulsion, whereas the magnitude of the inner RCB reflects the purely attractive binding energy of the electron or ion.) RCBed/if(outer) reduces with increasing solvation due to the increasing dielectric screening of the solvation shell reducing the intramolecular Coulombic repulsion. The purely attractive binding energy between a Cl− ion and the IrCl2−5·(H2O)n cluster increases with n due to the presence of additional favourable water–Cl− interactions, thus increasing RCBif(inner). Similarly, the rise in RCBed(inner) with increasing solvation can be traced to the increase in the purely attractive binding energy of an electron to IrCl2−5·(H2O)n.
In addition to decay via electron loss or ionic fragmentation, a third reactive decay channel is possible for water clusters of protic MCAs, i.e.
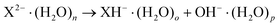 | (5) |
 | (6a) |
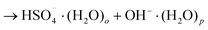 | (6b) |
B. Counter-ion complexation
Whereas numerous studies have explored the effect of solvation on the stability of gas-phase MCAs, relatively little attention has been paid to the effect of counter-ion complexation. The most important study to date involved photoelectron spectroscopy of the alkali metal sulfate ion-pair complexes, M+·SO2−4 where M = Na, K.17 A strong similarity was observed between the electronic features of the Na+/K+ ion-pair complexes, which correlated well with the MO energy levels of isolated SO2−4. The complexes could therefore be viewed as somewhat distorted isolated SO2−4 ions interacting electrostatically with the metal cations, as in bulk solids. Similar results were obtained in a photoelectron study of the Li+·B2−6 system.18 The only other experimental studies we are aware of are collision induced dissociation (CID) measurements for Cs+·C2−9 and alkali metal salts of terephthalic acid.19,20,57 However, neither of these studies specifically focused on the effect of the counter-ion on the MCA.Ab initio calculations can provide some insight into the effect of counter-ion complexation on MCAs. Dreuw and Cederbaum have investigated the structures of the Cs+·C2−9 and Cs+·C2−7 clusters, and found that the structures of the C2−9 and C2−7 dianions are largely retained with the cation simply electrostatically stabilizing them.21 Another example is provided by the Pt(CN)2−4 dianion and the K+·Pt(CN)2−4 ion-pair.80Fig. 14 displays the global minimum structures of the dianion and ion-pair obtained at the B3LYP/LANL2DZ level. K+·Pt(CN)2−4 corresponds to a bidentate C2v structure where the cation binds to two CN− ligands. Counter-ion complexation induces only modest structural changes in the MCA, primarily via tilting of the adjacent CN− ligands towards the metal ion.
 | ||
| Fig. 14 Global minimum structures of (a) PtCN2−4 and (b) K+·Pt(CN)2−4 obtained at the B3LYP/LANL2DZ level. Adapted from ref. 80. | ||
A simplified molecular orbital diagram for K+·Pt(CN)2−4 is shown in Fig. 15. The left hand side shows the valence orbitals of the unperturbed Pt(CN)2−4 dianion, which correspond to the classic MO scheme for a tetrahedral transition metal complex,81 while the central column displays the MOs of K+·Pt(CN)2−4. Inspection of Fig. 15 reveals that the orbital energies are shifted downwards upon complexation, while the reduction in symmetry from D4h to C2v lifts the orbital degeneracies. As the electrons of the K+ cation are extremely strongly bound, there is little interaction between the occupied orbitals of the dianion and the counter-ion, although the cation virtual orbitals are seen to interact with the corresponding metal complex orbitals. Overall, the modest structural and electronic changes observed upon counter-ion complexation suggest that K+·Pt(CN)2−4 can be viewed as a contact ion-pair where the metal ion only weakly perturbs the MCA. This result agrees well with previous ab initio calculations on other systems.17,21,82
 | ||
| Fig. 15 Molecular orbitals (B3LYP/LANL2DZ) of the Pt(CN)2−4 dianion, the K+·Pt(CN)2−4 ion-pair, and the K+ cation. Selected molecular orbitals are illustrated. | ||
Resonance excitation measurements of the K+·Pt(CN)2−6 and K+·Pt(CN)2−4 complexes, have been used to investigate how counter-ion complexation affects the propensity of the MCAs to decay by either electron detachment or ionic fragmentation.80 These experiments directly probe the effect of the counter-ion on the ground state potential energy surface of the MCA. Fig. 16a displays the CID mass spectrum obtained when the Pt(CN)2−4 dianion is subjected to resonance excitation. The dianion fragments with production of Pt(CN)−3, characteristic of decay via ionic fragmentation,
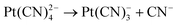 | (7) |
 | ||
| Fig. 16 (a) CID mass spectrum of Pt(CN)2−4 at 8% collision energy illustrating formation of Pt(CN)3−. (b) CID mass spectrum of K+·Pt(CN)2−4 at 8% collision energy illustrating formation of Pt(CN)3−. (c) % fragmentation curves for decay of Pt(CN)2−4 and K+·Pt(CN)2−4 with production of Pt(CN)−3.50 | ||
The ejection of K+ and CN− upon decay of K+·Pt(CN)2−4 is surprising in light of the DFT results which indicated that the MCA is only weakly perturbed by counter-ion complexation. On this basis, the ion-pair should have decayed with loss of CN− from the dianion with concomitant production of K+·Pt(CN)3− (i.e., the parent ion would decay, but no daughter ions would have been detected in our instrument). Other ion-pairs of transition metal complex dianions display similar behaviour with K+·IrBr2−6 decaying with production of IrBr−5, and Rb+·PtCl2−4 decaying to PtCl−3. Indeed, other types of cation–dianion ion-pairs have also been observed to fragment in a similar manner with K+·S2O82−, for example, decaying to SO4− as the sole ionic product upon resonance excitation.
To understand the fragmentation behaviour of K+·Pt(CN)2−4, DFT calculations were performed to determine the qualitative shape of the ground state potential energy surface. Fig. 17 displays the calculated potential energy surfaces for cleavage of a Pt–CN bond for both the bare Pt(CN)2−4 dianion, and the contact ion-pair. The dianion surface displays the expected repulsive Coulomb barrier, peaking at RPt−CN = 4.43 Å. The singly charged ion-pair K+·Pt(CN)2−4 unsurprisingly exists on a potential energy surface that lacks the long range repulsive character of the dianion. Intriguingly, however, the MCA ion-pair surface still displays a barrier in the same region as the original RCB suggesting that an RCB-like feature is retained at short range. This barrier feature evolves towards a local minimum at RPt−CN ∼ 9.64 Å corresponding to formation of an ion-dipole exit-channel complex, where the dipolar KCN moiety is bound to the Pt(CN)−3 anion. Fragmentation of K+·Pt(CN)2−4 can therefore be seen to involve initial “ionic fragmentation” of the dianion core with loss of CN−. The ligand is subsequently trapped in the long range electrostatic potential of the K+ counter-ion to form a K+CN−⋯Pt(CN)−3 exit channel complex, which decays upon further excitation into KCN and Pt(CN)−3. Further experimental and theoretical studies are certainly warranted to fully characterize these novel and fundamentally important systems.
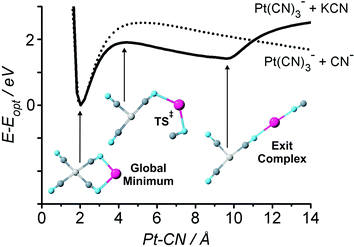 | ||
| Fig. 17 Calculated ground state potential energy surfaces (B3LYP/LANL2DZ) of Pt(CN)2−4 and K+·Pt(CN)2−4 as a function of RPt–CN. The energy axis is scaled so that 0 eV corresponds to the global minimum of each complex. The global minimum, the exit channel complex and the corresponding transition state are illustrated on the diagram. Reprinted with permission from J. Chem. Phys., Vol. 125, R. M. Burke, W. E. Boxford and C. E. H. Dessent, Counter-ion perturbation of the fragmentation pathways of multiply charged anions: Evidence for exit channel complexes on the fragmentation potential energy surfaces, Pages No. 21105–21109, Copyright 2006, American Institute of Physics. | ||
C. Intramolecular stabilization
As discussed above, small, energetic MCAs can be stabilized in the gas-phase through the formation of molecular clusters with solvent molecules or counter-ions. However, it is also possible for the excess negative charges in some MCAs to be stabilized intramolecularly through non-covalent interactions with different parts of the molecule.85 This type of stabilization is likely to be particularly important in contributing to the gas-phase stability of multiply charged biomolecular ions.28–30,62–66 We have explored intramolecular stabilization by probing the intrinsic stability of the [adenosine 5′-triphosphate-2H]2− ([ATP-2H]2−) and [adenosine 5′-diphosphate-2H]2− ([ADP-2H]2−) dianions, compared to the triphosphate, H3P3O2−10.51Fig. 18 illustrates the chemical structures of the fully protonated forms of these ions. We used the triphosphate, ADP, and ATP anions since they represent an ideal chemical system for exploring how the stability of an MCA evolves across a series of closely related molecular ions.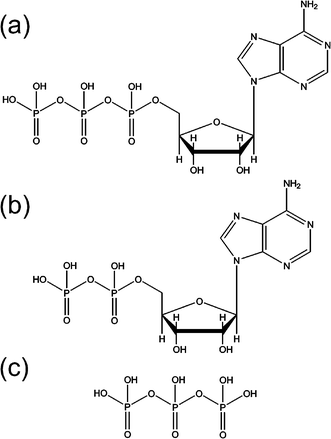 | ||
| Fig. 18 Chemical structures of the fully protonated forms of (a) ATP, (b) ADP and (c) H5P3O10. Reprinted with permission from J. Phys. Chem. A, Vol. 109, R. M. Burke, J. K. Pearce, W. E. Boxford, A. Bruckmann and C. E. H. Dessent, Stabilization of excess charge in isolated adenosine 5’-triphosphate and adenosine 5’-diphosphate multiply and singly charged anions, Pages No. 9775–9785, Copyright 2005, American Chemical Society. | ||
Both the ESI-MS and CID 100% fragmentation values of [ATP-2H]2−, [ADP-2H]2− and H3P3O2−10 indicate that the multiply charged H3P3O2−10 phosphate moiety is strongly stabilized by the presence of the adenosine group, and the stability of the dianions increases in the order H3P3O2−10 < [ADP-2H]2− < [ATP-2H]2−.51 Initially, this was a rather unsurprising result because we had anticipated that the molecular size would control the relative stabilities. In the larger ions, the excess charges can be positioned further apart, thus reducing the intramolecular Coulomb repulsion. However, fully optimized DFT calculations revealed that the lowest energy tautomers of the [ADP-2H]2− and [ATP-2H]2− dianions corresponded to structures where the excess charges occupied adjacent phosphate groups, producing very similar quantities of Coulomb repulsion. Global minimum energy structures (B3LYP/6-31+G*) of [ATP-2H]2− and [ADP-2H]2− along with the phosphate dianion are displayed in Fig. 19. The structures illustrate that the excess charges are stabilized by intramolecular hydrogen bonding either within the phosphate chain, or between the phosphate and the adenosine.
![Minimum energy structures of (a) [ATP-2H]2−, (b) [ADP-2H]2− and (c) H3P3O2−10 calculated at the B3LYP/6-31+G* level. Typical hydrogen bonds (<3 Å, 180 ± 25°) are indicated as dashed lines and loose “hydrogen-bond like” interactions (<3.5 Å, 180 ± 50°) as dotted lines.51 Adapted from ref. 51.](/image/article/2006/CP/b609123g/b609123g-f19.gif) | ||
| Fig. 19 Minimum energy structures of (a) [ATP-2H]2−, (b) [ADP-2H]2− and (c) H3P3O2−10 calculated at the B3LYP/6-31+G* level. Typical hydrogen bonds (<3 Å, 180 ± 25°) are indicated as dashed lines and loose “hydrogen-bond like” interactions (<3.5 Å, 180 ± 50°) as dotted lines.51 Adapted from ref. 51. | ||
In section IIB, we presented a model to illustrate the physical origin of the RCBif for an MX2−6 dianion.31 RCBif(inner) was found to be associated with the purely attractive binding energy of the monoanions (eqn (1)). Extending this model to the dianions studied here, RCBif(inner) will be given by
 | (8) |
The origin of the relative stability of [ATP-2H]2− compared to [ADP-2H]2− can therefore be traced to differences in the intramolecular non-covalent interactions present in the minimum energy structures, along with any differences in the charge–dielectric interaction. Comparing the structures displayed in Fig. 19a and b, the intramolecular interactions within [ATP-2H]2− and [ADP-2H]2− will be dominated by hydrogen bonds, and while [ATP-2H]2− possesses two typical and three loose hydrogen bonds (as defined in the figure captions), [ADP-2H]2− possesses only two typical and one loose hydrogen bond. The presence of two additional hydrogen-bonding type interactions in [ATP-2H]2− increases the magnitude of RCBif(inner), making this dianion intrinsically more stable than [ADP-2H]2−. Similarly, the minimum energy H3P3O2−10 structure (Fig. 19c) possesses a single typical hydrogen bond, along with two loose hydrogen bonds, consistent with its reduced stability compared to both [ATP-2H]2− and [ADP-2H]2−.
The relative stabilities of the phosphate dianions can therefore be rationalized with reference to the extent and strength of intramolecular hydrogen bonding within the ions. This mirrors the known stabilization of MCAs with respect to both ionic fragmentation and electron detachment via sequential solvation with water molecules.10–16 We note that the intrinsic stability of the dianions studied will also be affected by the extent of dielectric screening that exists between the excess charges (implicitly included within the third term of [8]), although this effect is expected to be small.86
The results discussed for [ATP-2H]2−, [ADP-2H]2− and H3P3O2−10 provide a preliminary insight into the effect of intramolecular stabilization of excess negative charges in gas-phase MCAs. Laser photodetachment-photoelectron spectroscopy would be highly useful to quantify the effects discussed here, since photodetachment measurements of [ATP-2H]2−, [ADP-2H]2− and H3P3O2−10 would give a spectroscopic measurement of the intramolecular Coulomb repulsion [i.e. RCBed(outer) = RCBif(outer)],1,32 and hence quantify the effect of dielectric stabilization of the excess charges. Complementary laser scans across the region of RCBif(inner)32 would similarly quantify the extent of the intramolecular stabilization of excess charge through non-covalent interactions.
VI. Concluding remarks
The wide range of new experimental data available on gas-phase MCAs has provided considerable insight into the intrinsic properties of these novel systems. Complementary cluster studies have revealed details of the nature of stabilization that occurs when MCAs are transferred into condensed phase environments. Descriptive models are now available that allow us to understand both the electron detachment and ionic fragmentation surfaces of MCAs in terms of molecular binding energies and the intramolecular Coulomb repulsion. These models have also been applied to provide a quantitative description of how solvent molecules mediate stabilization of MCAs. The new experimental results, combined with current theoretical models and ab initio calculations provide an excellent basis for understanding the intrinsic properties of small prototypical MCAs.Despite recent progress, there are a number of areas where further work is desirable. While IR vibration-predissociation spectroscopy has provided detailed information on the geometric structures of microsolvated clusters of singly charged anions and multiply charged cations,87–89 similar data for MCAs are currently conspicuously unavailable. Indeed, some controversy exists over the structure of even simple solvated MCA–water clusters e.g.−O2C(CH2)4CO2−·(H2O)2.11,35,90 One of the important considerations for performing such IR vibration–predissociation experiments is controlling the internal temperature of the MCA–solvent clusters, since temperature effects can seriously compromise the quality of data acquired. Cryogenically cooled ion traps should represent a suitable environment for conducting such studies,91 and efforts towards this end are currently under way in this laboratory. Another area where our current knowledge is poor is in relation to the MCA excited state surfaces. Experimental and theoretical progress in this area is highly desirable as a precursor to high resolution spectroscopy of MCAs. Finally, our understanding of the chemical reactivity of gas-phase MCAs is limited, although further work in this field could provide useful information for developing methodologies for analytical chemistry.
Perhaps one of the most interesting areas for future studies of gas-phase MCAs is extension of the paradigms deduced for small MCAs to medium and larger sized systems. Of particular importance in this respect will be investigations of biological ions that are MCAs. There is considerable current interest in the area of gas-phase biological molecules, due to the fact that spectroscopic studies can provide detailed structural information for comparison with high-level computational work.92,93 Moreover, such work also provides fundamental information to support the development of gas-phase analytical techniques, for instance in the sequencing of oligosaccharides.94 To date, the vast majority of spectroscopic studies of gas-phase biomolecules have been conducted on neutral systems,95 but since many important biological species exist as multiply charged anions it is clearly important to extend these techniques to MCAs.
Note added in proof
The reader may also be interested in the following publications which appeared during production of the manuscript.96,97Acknowledgements
CEHD thanks the Royal Society for support from a University Research Fellowship, the Leverhulme Trust for support from grant F00224K, and the EPSRC for support from EP/C51212X/1. We are also grateful for the award of computer time at the Rutherford Appleton Laboratories under the auspices of the Computational Chemistry Working Party. Finally, we thank Julie K. Pearce for early contributions to the work presented, and Ruth M. Burke for proof reading the manuscript.References
- For example: X. B. Wang, X. Yang and L. S. Wang, Int. Rev. Phys. Chem., 2002, 21, 473 Search PubMed . Further examples are given later in the manuscript.
- M. K. Scheller, R. N. Compton and L. S. Cederbaum, Science, 1995, 270, 1160 CrossRef CAS.
- I. Boldyrev, M. Gutowski and J. Simons, Acc. Chem. Res., 1996, 29, 497 CrossRef CAS.
- D. Schröder and H. Schwartz, J. Phys. Chem. A, 1999, 103, 7385 CrossRef.
- A. Dreuw and L. S. Cederbaum, Chem. Rev., 2002, 102, 181 CrossRef CAS.
- D. Schröder, Angew. Chem., Int. Ed., 2004, 43, 1329 CrossRef.
- S. D. Price, Phys. Chem. Chem. Phys., 2003, 5, 1717 RSC.
- S. G. Cox, A. D. J. Critchley, P. S. Kreynin, I. R. McNab, R. C. Shiell and F. E. Smith, Phys. Chem. Chem. Phys., 2003, 5, 663 RSC.
- J. B. Fenn, M. Mann, C. K. Meng, S. F. Wong and C. M. Whitehouse, Science, 1989, 246, 64 CrossRef CAS.
- W. E. Boxford and C. E. H. Dessent, J. Phys. Chem. A, 2005, 109, 5836 CrossRef CAS.
- C. E. H. Dessent and C. Rigby, Chem. Phys. Lett., 2003, 370, 52 CrossRef CAS.
- R. L. Wong and E. R. Williams, J. Phys. Chem. A, 2003, 107, 10976 CrossRef CAS.
- A. T. Blades and P. Kebarle, J. Am. Chem. Soc., 1994, 116, 10761 CrossRef CAS.
- S. Kambalapalli and J. V. Ortiz, J. Phys. Chem. A, 2003, 107, 10360 CrossRef CAS.
- X. B. Wang, X. Yang, J. B. Nicholas and L. S. Wang, J. Chem. Phys., 2003, 119, 3631 CrossRef CAS.
- X. Yang, X. B. Wang and L. S. Wang, J. Phys. Chem. A, 2002, 106, 7607 CrossRef CAS.
- X. B. Wang, C. F. Ding, J. B. Nicholas, D. A. Dixon and L. S. Wang, J. Phys. Chem. A, 1999, 103, 3423 CrossRef CAS.
- A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, J. Chem. Phys., 2005, 122, 54313 CrossRef.
- R. Vandenbosch, D. I. Will, C. Cooper, B. Henry and J. F. Liang, Chem. Phys. Lett., 1997, 274, 112 CrossRef CAS.
- K. Gupta and M. Krishnamurthy, Phys. Rev. A, 2003, 67, 23201 CrossRef.
- A. Dreuw and L. S. Cederbaum, J. Chem. Phys., 1999, 111, 1467 CrossRef CAS.
- RCB(inner) and RCB(outer) are used to refer to the magnitudes of the “inner” and “outer” halves of the RCB. The inner RCB is the barrier measured from the MCA minimum energy structure, while the outer RCB is the barrier measured from the dissociative asymptote. RCB (inner) and RCB(outer) are illustrated for electron detachment on Fig. 2, being referred to as RCBed(inner) and RCBed(outer), respectively. Similar definitions are used for ionic fragmentation surfaces, where RCBif replaces RCBed.
- P. Weis, O. Hampe, S. Gilb and M. M. Kappes, Chem. Phys. Lett., 2000, 321, 426 CrossRef CAS.
- M. N. Blom, O. Hampe, S. Gilb, P. Weis and M. M. Kappes, J. Chem. Phys., 2001, 115, 3690 CrossRef CAS.
- X. B. Wang, C. F. Ding and L. S. Wang, Chem. Phys. Lett., 1999, 307, 391 CrossRef CAS.
- R. N. Compton, A. A. Tuinman and C. E. Klots, Phys. Rev. Lett., 1997, 78, 4367 CrossRef CAS.
- S. A. McLuckey and G. Vaidyanathan, Int. J. Mass Spectrom., 1997, 162, 1 CrossRef CAS.
- J. H. Banoub, R. P. Newton, E. Esmans, D. F. Ewing and G. Mackenzie, Chem. Rev., 2005, 105, 1869 CrossRef CAS.
- J. Zaia, Mass Spectrom. Rev., 2004, 23, 161 CrossRef CAS.
- E. F. Naggar, C. E. Costello and J. Zaia, J. Am. Soc. Mass Spectrom., 2004, 15, 1534 CrossRef CAS.
- W. E. Boxford, J. K. Pearce and C. E. H. Dessent, Chem. Phys. Lett., 2004, 399, 465 CrossRef CAS.
- J. Friedrich, S. Glib, O. T. Ehrler, A. Behrendt and M. M. Kappes, J. Chem. Phys., 2002, 117, 2635 CrossRef CAS.
- X. B. Wang, C. F. Ding and L. S. Wang, Phys. Rev. Lett., 1998, 81, 3351 CrossRef CAS.
- L. S. Wang, C. F. Ding, X. B. Wang, J. B. Nicholas and B. Nicholas, Phys. Rev. Lett., 1998, 81, 2667 CrossRef CAS.
- C. F. Ding, X. B. Wang and L. S. Wang, J. Phys. Chem. A, 1998, 102, 8633 CrossRef CAS.
- L. S. Wang, C. F. Ding, X. B. Wang and S. E. Barlow, Rev. Sci. Instrum., 1999, 70, 1957 CrossRef CAS.
- C. F. Ding, X. B. Wang and L. S. Wang, J. Chem. Phys., 1999, 110, 3635 CrossRef CAS.
- X. B. Wang and L. S. Wang, Nature, 1999, 400, 245 CrossRef CAS.
- J. M. Weber, I. N. Ioffe, K. M. Berndt, D. Loffler, J. Friedrich, O. T. Ehrler, A. S. Danell, J. H. Parks and M. M. Kappes, J. Am. Chem. Soc., 2004, 126, 8585 CrossRef CAS.
- O. T. Ehrler, F. Furche, J. M. Weber and M. M. Kappes, J. Chem. Phys., 2005, 122, 94321 CrossRef.
- O. T. Ehrler, J. M. Weber, F. Furche and M. M. Kappes, Phys. Rev. Lett., 2003, 91, 113006 CrossRef.
- X. B. Wang and L. S. Wang, Phys. Rev. Lett., 1999, 83, 3402 CrossRef CAS.
- D. Loffler, J. M. Weber and M. M. Kappes, J. Chem. Phys., 2005, 123, 224308 CrossRef CAS.
- A. Dreuw and L. S. Cederbaum, Phys. Rev. A, 2000, 63, 12501 CrossRef.
- X. B. Wang and L. S. Wang, J. Chem. Phys., 1999, 111, 4497 CrossRef CAS.
- S. A. McLuckey and D. E. Goeringer, J. Mass Spectrom., 1997, 32, 461 CrossRef CAS.
- P. B. Armentrout, J. Am. Soc. Mass Spectrom., 2002, 13, 419 CrossRef CAS.
- W. R. Plass and R. G. Cooks, J. Am. Soc. Mass Spectrom., 2003, 14, 1348 CrossRef CAS.
- M. Satterfield and J. S. Brodbelt, Inorg. Chem., 2001, 40, 5393 CrossRef CAS.
- Collision energies are quoted as a percentage of 2.5 V resonance excitation voltage.
- R. M. Burke, J. K. Pearce, W. E. Boxford, A. Bruckmann and C. E. H. Dessent, J. Phys. Chem. A, 2005, 109, 9775 CrossRef CAS.
- X. Yang, X. B. Wang and L. S. Wang, Int. J. Mass Spectrom., 2003, 228, 797 CrossRef CAS.
- A. B. Nielsen, P. Hvelplund, B. Liu, S. Brøndsted Nielsen and S. Tomita, J. Am. Chem. Soc., 2003, 125, 9592 CrossRef CAS.
- K. Drenck, P. Hvelplund, C. J. McKenzie and S. Brøndsted Nielsen, Int. J. Mass Spectrom., 2005, 244, 144 CrossRef CAS.
- G. Bojesen, P. Hvelplund, T. J. D. Jørgensen and S. Brøndsted Nielsen, J. Chem. Phys., 2000, 113, 6608 CrossRef CAS.
- K. W. M. Siu, G. J. Gardner and S. S. Berman, Org. Mass Spectrom., 1989, 24, 931 CAS.
- S. M. Bachrach, M. Hare and S. R. Kass, J. Am. Chem. Soc., 1998, 120, 12646 CrossRef CAS.
- W. E. Boxford, M. O. A. El Ghazaly, C. E. H. Dessent and S. Brøndsted Nielsen, Int. J. Mass Spectrom., 2005, 244, 60 CrossRef CAS.
- A. V. Streletskiy, P. Hvelplund, S. Brøndsted Nielsen, B. Liu, S. Tomita, A. Goryunkov and O. V. Boltalina, J. Chem. Phys., 2006, 124, 144306 CrossRef.
- S. Feuerbacher and L. S. Cederbaum, J. Phys. Chem. A, 2005, 109, 11401 CrossRef CAS.
- M. A. O. El Ghazaly, A. Svendsen, H. Bluhme, A. B. Nielsen, S. Brøndsted Nielsen and L. H. Andersen, Phys. Rev. Lett., 2004, 93, 203201 CrossRef CAS.
- M. T. Rodgers, S. Campbell, E. M. Marzluff and J. L. Beauchamp, Int. J. Mass Spectrom. Ion Processes, 1994, 137, 121 CrossRef CAS.
- C. S. Hoaglund, Y. Liu, A. D. Ellington, M. Pagel and D. E. Clemmer, J. Am. Chem. Soc., 1997, 119, 9051 CrossRef CAS.
- A. S. Danell and J. H. Parks, J. Am. Soc. Mass Spectrom., 2003, 14, 1330 CrossRef CAS.
- J. S. Klassen, P. D. Schnier and E. R. Williams, J. Am. Soc. Mass Spectrom., 1998, 9, 1117 CrossRef CAS.
- A. Favre, F. Gonner and J. C. Tabet, Eur. J. Mass Spectrom., 2000, 6, 389 CrossRef CAS.
- E. S. Baker, J. Gidden, A. Ferzoco and M. T. Bowers, Phys. Chem. Chem. Phys., 2004, 6, 2786 RSC.
- J. Roithová, Z. Herman, D. Schröder and H. Schwarz, Chem.–Eur. J., 2006, 12, 2465 CrossRef CAS.
- O. Hadjer, D. Ascenzi, D. Bassi, P. Franceshi, M. Sabido and P. Tosi, Chem. Phys. Lett., 2004, 400, 476 CrossRef.
- O. Abu-Haija, E. Y. Kamber and D. Mathur, Chem. Phys. Lett., 2005, 408, 5 CrossRef CAS.
- M. S. Deleuze, J. P. Francois and E. S. Kryachko, J. Am. Chem. Soc., 2005, 127, 16824 CrossRef CAS.
- N. Lambert, N. Kaltsoyannis, S. D. Price, J. Zabka and Z. Herman, J. Phys. Chem. A, 2006, 110, 2898 CrossRef CAS.
- D. Ascenzi, P. Franceschi, P. Tosi, D. Bassi, M. Kaczorowska and J. N. Harvey, J. Chem. Phys., 2003, 118, 2159 CrossRef CAS.
- M. Neumaier, O. Hampe and M. M. Kappes, J. Chem. Phys., 2005, 123, 074318 CrossRef.
- A. E. Flores and S. Gronert, J. Am. Chem. Soc., 1999, 121, 2627 CrossRef CAS.
- S. Gronert and L. M. Fong, Int. J. Mass Spectrom., 1999, 192, 185 CrossRef CAS.
- D. V. Stefanovich, A. I. Boldyrev, T. N. Truong and J. Simons, J. Phys. Chem. B, 1998, 102, 4205 CrossRef.
- A. Whitehead, R. Barrios and J. Simons, J. Chem. Phys., 2002, 116, 2848 CrossRef CAS.
- B. Gao and Z. F. Liu, J. Chem. Phys., 2005, 123, 224302 CrossRef.
- R. M. Burke, W. E. Boxford and C. E. H. Dessent, J. Chem. Phys., 2006, 125, 21105 CrossRef.
- H. Basch and H. Gray, Inorg. Chem., 1967, 6, 365 CrossRef CAS.
- V. V. Murashov and J. Leszczyniski, THEOCHEM, 2000, 529, 1 CrossRef CAS.
- The % fragmentation curves for the ion-pair and the dianion are not directly comparable due to the different charges carried by the two complexes. The doubly charged dianion will experience higher single collision energies,84 thus leading it to fragment at lower % CID energy than the singly charged ion-pair. The relationship between the collision energy and charge is not simple,84 however, leading us to conclude that the difference between the ion-pair and dianion % fragmentation curves can be partially attributed to a higher barrier height for fragmentation of the ion-pair.
- D. E. Goeringer and S. A. McLuckey, Rapid Commun. Mass Spectrom., 1996, 10, 328 CrossRef CAS.
- A. T. Blades, Y. Ho and P. Kebarle, J. Phys. Chem., 1996, 100, 2443 CrossRef CAS.
- D. S. Gross and E. R. Williams, J. Phys. Chem. A, 1995, 99, 4034 Search PubMed.
- W. H. Robertson and M. A. Johnson, Annu. Rev. Phys. Chem., 2003, 54, 173 CrossRef CAS.
- M. A. Duncan, Int. Rev. Phys. Chem., 2003, 22, 407 CrossRef CAS.
- C. J. Thompson, K. P. Faherty, K. L. Stringer and R. B. Metz, Phys. Chem. Chem. Phys., 2005, 7, 814 RSC.
- P. Jungwirth, J. E. Curtis and D. J. Tobias, Chem. Phys. Lett., 2003, 367, 704 CrossRef CAS.
- H. Hess, K. R. Asmis, T. Leisner and L. Wöste, Eur. Phys. J. D, 2001, 16, 145 CrossRef CAS.
- P. Jurecka, J. Sponer, J. Cerny and P. Hobza, Phys. Chem. Chem. Phys., 2006, 8, 1985 RSC.
- Y. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2005, 7, 2701 RSC.
- J. L. Seymour, C. E. Costello and J. Zaia, J. Am. Soc. Mass Spectrom., 2006, 17, 844 CrossRef CAS.
- P. Çarçabal, R. T. Kroemer, L. C. Snoek, J. P. Simons, J. M. Bakker, I. Compagnon, G. Meijer and G. von Helden, Phys. Chem. Chem. Phys., 2004, 6, 4546 RSC.
- N. Mirsaleh-Kohan, S. Ard, A. A. Tuinman, R. N. Compton, P. Weis and M. M. Kappes, Chem. Phys. DOI:10.1016/j.chemphys.2006.07.017 , in press.
- S. Y. Ovchinnikov, J. Macek, A. A. Tuinman, J. D. Steill, R. N. Compton, P. Hvelplund, A. I. S. Holm, S. Brøndsted Nielsen and M. Brøndsted Nielsen, Phys. Rev. A, 2006, 73, 64704 CrossRef.
Footnote |
| † The HTML version of this article has been enhanced with colour images. |
| This journal is © the Owner Societies 2006 |
