Large molecular aggregates: from atmospheric aerosols to drug nanoparticles
George
Firanescu
,
Dana
Hermsdorf
,
Roman
Ueberschaer
and
Ruth
Signorell
*
Department of Chemistry, University of British Columbia, 2036 Main Mall, Vancouver, BC, Canada V6T 1Z1. E-mail: signorell@chem.ubc.ca; Fax: +1 604 822-2847
First published on 3rd August 2006
Abstract
Large molecular aggregates with sizes ranging from subnanometers to microns are ubiquitous. As atmospheric aerosols they influence our climate, in interstellar space they are discussed as reactive sites, and in medicine small particles are considered as promising candidates to achieve a targeted drug delivery. The present contribution is focused on the characterization of the physical–chemical properties of these particles and on their targeted generation. One of the greatest challenges is to understand the properties of these aggregates on a molecular level. The latter point is discussed in detail focussing on the vibrational dynamics of these particles.
1. Introduction
The role of weakly bound molecular aggregates in atmospheric processes, as drug delivery systems in medicine, and as potential players in interstellar chemistry has become an increasingly important issue in the past years. The size of the aggregates of interest varies over a wide range from subnanometer aggregates to micron sized particles. This means that the particles typically contain from some tens up to billions of molecules. In the atmosphere, the most familiar representatives of this type of matter are water aggregates, water droplets, and water ice particles. Water, however, is only one possible component of atmospheric aerosol particles.1,2 In general the latter consist of a wide variety of different substances ranging from organic acids to hydrocarbons. Atmospheric aerosols influence climate processes and are responsible for air pollution and thus affect our health. Large molecular aggregates also play a role in interstellar dust.3 A topical question here is how complex molecules can be formed at the surface of dust particles. The knowledge of the properties of molecular particles is also central for the targeted generation of micro- and nanoparticles of pharmaceutics and cosmetics. Micronization of pharmaceutics, for example, is considered as a promising way to increase the bioavailability of these substances.4,5All these particles have in common that they are held together by weak intermolecular forces (van der Waals forces, hydrogen bonds) which are in general weaker than typical chemical bonds by about two orders of magnitude. Of course, this determines the particle’s properties in a crucial way. Dealing with particles, among the most interesting properties are certainly intrinsic particles properties, such as particle size, shape, and architecture. All three can strongly influence the reactivity of the aggregates, their phase behavior, and their spectroscopic properties. Nowadays, however, not much is known or really understood about the influence of intrinsic particle properties on any of these physical–chemical properties. There is definitely a lack of good experimental data, and where experimental data are available the interpretation of these data on a fundamental level remains a real challenge. The reason lies in the complexity of these systems with their large number of degrees of freedom.
The aim of the present contribution is to elucidate the more fundamental relations between microscopic or molecular properties and intrinsic particle properties. Given the scope of the field we limit our review to the spectroscopic properties in the mid-infrared region, i.e. on the vibrational dynamics of these aggregates. As demonstrated in the following the vibrational spectra of these aggregates contain a wealth of information about their composition, structure, size, and shape. It is our goal to show that at least for certain spectroscopic properties a deeper understanding in terms of molecular properties can indeed be obtained. We start in section 2 with the discussion of some aspects of particle generation and characterization. A targeted particle formation is the crucial step to obtain useful experimental data. The particle characterization methods used here complement the infrared spectroscopic investigations in situ. Section 3 deals with different models to describe the vibrational dynamics of the aggregates considered. These models are the prerequisite for understanding the influence of size, shape, and architecture of model particles on a fundamental level as discussed in sections 4 and 5. We conclude in section 6 with a discussion of the benefit of such fundamental studies for investigations of atmospheric aerosols, interstellar ice particles, and drug particles.
2. Experimental approaches
Laboratory investigations of large molecular aggregates require the combination of diverse experimental methods both for the characterization of the particles and for their generation. Substantial effort goes into the particle formation. It is the wide variety of substances held together by intermolecular forces of different type and strength which makes particle generation a challenging task. A major point here is the targeted preparation of samples with well-defined sizes and shapes. In general, this is still an unsolved problem and substantial improvement of existing preparation methods and in particular ideas for new ways to form large molecular aggregates are required to advance here. In section 2.1, we shortly summarize the particle generation methods used in our lab which encompass most of the techniques used nowadays to investigate submicron sized molecular aggregates.A wide variety of standard methods are available for particle characterization. Some of them and the information they can provide for particle characterization are described in section 2.2. For a comprehensive understanding of particle properties it is often important to combine many different methods. In the present contribution, our focus lies on the spectroscopic characterization in the mid-infrared region. It is important to note here that standard spectroscopic methods are often insufficient and thus cannot be used without further modifications to characterize particulate systems. One reason can be insufficient sensitivity. These methods are thus helpful only after major adaptations and extensions which require special effort and knowledge. In addition, the spectroscopy of these complex systems and their understanding are still in their infancy. There exists only a limited amount of laboratory data for these complex systems and even less is known about the explanation of the spectroscopic features observed.
2.1. Particle generation
In the following, the focus lies on four particle generation methods that are ideal for submicron sized particles, i.e. collisional cooling, jet expansion techniques, rapid expansion of supercritical solutions (RESS), and electrospraying. The formation of larger particles is in general much more standard and will not be discussed further here. Collisional cooling6–19 and jet expansion techniques20–37 are useful for substances which are more or less volatile under ambient conditions, whereas RESS38–42 and electrospraying43–46 are used to form aggregates of non-volatile compounds. | ||
| Fig. 1 Scheme of the collisional cooling setup. | ||
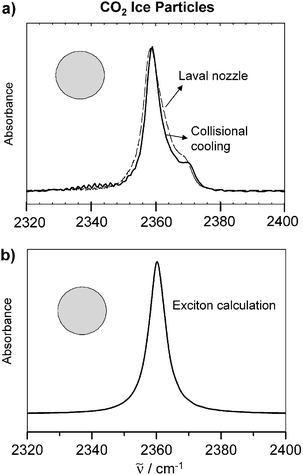 | ||
Fig. 2 (a) Experimental infrared spectra of spherical CO2 particles with radii around 20 nm. Depicted is the region of the antisymmetric stretching vibration. Dashed line: supersonic cooling in a Laval nozzle. Full line: collisional cooling. (b) Exciton calculations for spherical CO2 particles (see section 3). For the calculations we assumed a molecular transition wave number of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) M = 2355 cm−1 and a molecular transition dipole moment of δμ = 〈0|μ|1〉 = 0.32 D.47 M = 2355 cm−1 and a molecular transition dipole moment of δμ = 〈0|μ|1〉 = 0.32 D.47![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the transition wavenumber. is the transition wavenumber. | ||
 | ||
Fig. 3 Experimental infrared spectra in the region of the NO stretching-vibration of N2O ice particles with a radius of about 1.4 nm. Upper trace: spectrum recorded in a slit nozzle expansion.33,34 Lower trace: spectrum recorded in a collisional cooling cell. ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the transition wavenumber. is the transition wavenumber. | ||
A scheme of our RESS apparatus together with the expansion chamber, the different characterization methods, and the pumping system is shown in Fig. 4.18,42,50 Gaseous CO2 is liquefied by the cryostat, pressurized (pneumatic pump 1) and heated to the desired pressure (pext) and temperature (Text) in the extractor. The supercritical solution is formed in the extractor which is packed with the solute. After passing the extractor the supercritical solution enters the heated (Tres) high-pressure reservoir (pres). The reservoir serves to keep constant pressure during the pulsed expansion. This is achieved by a movable piston connected to the pneumatic pump 2. The expansion of the solution takes place through the pinhole nozzle (diameter ≥20 μm) located in the expansion chamber. The nozzle can be displaced by up to 30 cm relative to the position of the spectroscopic investigations. This allows us to observe processes before and after the Mach disk. The expansion chamber together with the buffer volume forms a continuous vacuum chamber. The buffer volume serves to limit the pressure increase during the expansion. Vacuum is maintained by two rotary piston pumps (350 m3 h−1). The different characterization methods (see section 2.2) are connected to the expansion chamber as depicted in Fig. 4.
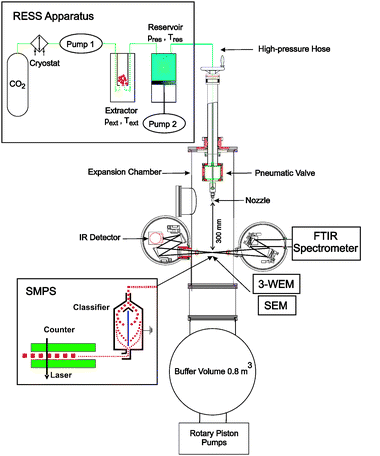 | ||
| Fig. 4 Scheme of the RESS apparatus with expansion chamber, characterization methods, and pumping system. | ||
2.2. Particle characterization
The two remaining size characterization methods, SMPS and SEM, can only be used for non-volatile molecular aggregates. In the SMPS the particles are first classified according to their mobility in an electric field and are afterwards counted optically.43,54 The size distributions obtained are very detailed and accurate (see Fig. 5c). However, SMPS measurements are much slower than 3-WEM and infrared spectroscopy. Typical acquisition times lie around 2 min. As implied in Fig. 4 the SMPS can be used for on-line measurements in the RESS expansion chamber. In comparison with the SMPS, the off-line size characterization with scanning electron microscopy results in only approximate size distributions.50 This method requires the particles to be collected first, which often leads to agglomeration. SEM, however, can be very helpful to visualize the shape of nanoparticles and their degree of agglomeration (see Fig. 5d and 6).
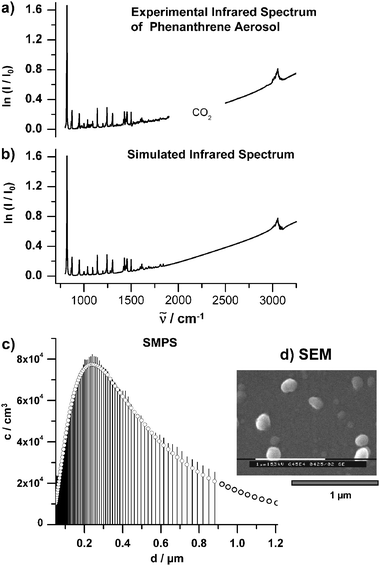 | ||
| Fig. 5 (a) Experimental infrared spectrum of phenathrene aerosol particles with sizes between 50 nm and 1.2 μm. The particles were generated with the RESS apparatus shown in Fig. 4. The region between 2000–2500 cm−1 where the absorptions of the solvent CO2 appear are excluded. (b) Simulated infrared spectrum (see section 4). (c) Number size distribution of the particles measured on-line with the SMPS (see section 2.2). c is the number concentration per logarithmic sampling interval. (d) Typical SEM image of the particles. | ||
 | ||
| Fig. 6 SEM images of ibuprofen particles. (a) Pure ibuprofen. The primary particles are strongly agglomerated and coagulated. (b) Mixed ibuprofen/PLA particles. The addition of polymer reduces agglomeration and coagulation. | ||
In addition to the methods mentioned above other standard characterization methods, such as X-ray diffraction or differential scanning calorimetry, can provide useful information on particle properties. X-ray powder diffraction leads to more accurate structural information than infrared spectroscopy. These data are, for instance, important to know for drug particles since the degree of crystallinity can influence the bioavailability of the substances. Some structural information and information about the composition of mixed drug particles can also be provided by differential scanning calorimetry.5,52
3. Modelling
Modelling plays a key function in the understanding of the spectroscopic features of these complex systems with their many degrees of freedom. Since this point is so important here we summarize in the following some of the methods which help us to get a deeper insight into the vibrational dynamics of such large molecular aggregates.3.1. Infrared extinction spectra
All infrared spectra discussed in this contribution are extinction spectra, i.e. the light source, the sample (particles in the form of an aerosol), and the detector were collinearly arranged. Extinction spectra of particles consist of two contributions, elastic scattering and absorption. Elastic scattering has a strong influence only when the size of the particles and the wavelength of the light are comparable. In the mid-infrared region this applies for particles with radii above about 50 nm. Characteristic scattering patterns in infrared extinction spectra are the slanted baseline and the dispersion shape of the absorption bands (see the example given in section 4). Absorption, by contrast, dominates all particle spectra independently of the size of the particles. As illustrated by several examples in sections 4 to 6, absorption bands are not only characteristic for the chemical composition and the phase of the particles, but they can also depend on the size, the shape, and the architecture of the aggregates.Infrared spectra of large molecular aggregates can be modelled either by classical scattering theory55–57 or by quantum chemical calculations.6,15,24,58–66 It is not possible to obtain a comprehensive understanding of the various spectroscopic features observed using one particular method alone. One goal of the present contribution is to demonstrate that the combination of the different methods helps us to improve our understanding of various phenomena observed in particle spectra. In the mid-infrared region, classical scattering theory can only be applied to particles with sizes above about 10 nm. Below this size range it is no longer suitable to describe infrared spectra since the molecular structure of the aggregates starts to dominate them.15,18,37,48,49,62–66 Classical scattering theory is particularly useful to describe infrared spectra of large particles (r > 100 nm) which exhibit in addition to characteristic absorption bands pronounced features due to elastic scattering of the light by the particles. A big disadvantage of this method is the need for independent optical data as input. These can be provided in the form of refractive index data, which have to be obtained from independent experimental investigations. Such data, however, are often not available and if available often not very accurate. Because of the inaccuracy in the input data, it can become difficult or even impossible to explain any of the details observed in the infrared spectra with classical scattering theory. Generally, classical scattering theory is more useful as an analytical tool, for example to determine rough particle size distributions (see sections 4 and 6). It is, however, not capable of providing detailed information about particle shape, or architecture, nor of the properties of very small aggregates (r < 10 nm) through band shape analysis. In particular it does not provide any insight into the microscopic origin of the phenomena observed.
Explanations on a molecular level can be obtained from quantum chemical calculations which take into account the inter- and intramolecular forces acting in the aggregates. The fact, however, that particles with radii of 10 nm can already contain more than 105 molecules makes it clear that it is in general impossible, at least nowadays, to model particle spectra on the basis of all these fundamental interactions. With available computer programs for standard quantum chemical calculations58 it is in some special cases possible to model infrared spectra of aggregates with sizes up to about 1–2 nm,63 but there appears to be no way to extend this approach to the simulation of shape or size effects in infrared spectra of much larger particles. For large systems the approach has to be simplified by reducing it to the dominant contributions as has been done, e.g. for water ice particles, ammonia ice particles, and CO2.15,37,60,62,65,66 The size of these particles, however, still lies in the lower nanometer range. Another important case are vibrational bands that are dominated by exciton coupling.6,10,24,47,49,59,61,67,68 For these bands it is even a single interaction, i.e. resonant transition dipole coupling, that determines the appearance of the bands. Recently, we have extended the vibrational exciton approach to treat large particles consisting of many thousands of molecules.47,49,61,67,68 Following this approach we could demonstrate that it is resonant dipole coupling which causes pronounced shape, and in some cases also size effects, in particle spectra. We were thus able to provide the first microscopic explanation of the origin of such intrinsic particle properties.
Not all spectral signatures arise from the interaction of all the molecules in a particle as it is the case for the exciton coupling. Local interactions within molecules in a particle and between neighboring molecules, such as Fermi resonances and hydrogen bonds, can also lead to characteristic features in infrared particle spectra. Some of these signatures can be understood by quantum chemical calculations using small oligomers as model systems.45,46,51
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) can then be determined from the calculated absorption cross sections Cabs,j and scattering cross section Csca,j by eqn (1). j labels the different types of particles in an ensemble and
) can then be determined from the calculated absorption cross sections Cabs,j and scattering cross section Csca,j by eqn (1). j labels the different types of particles in an ensemble and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the wavenumber.
is the wavenumber. | (1) |
In section 6 we extract refractive index data of particulate systems from experimental infrared extinction spectra and measured particle size distributions by following two alternative approaches, the Kramers–Kronig inversion and a Lorentz model fit.46,55,69–71, In both cases, the refractive index data are determined from a nonlinear least-squares fit of the calculated extinction in eqn (1) to the experimentally measured extinction. In the cases considered here, the particles were spheres to a good approximation so that we could employ Mie theory for spherical particles to calculate the spectra.55
A first approach to determine the complex index of refraction n + ik is to exploit the Kramers–Kronig relation between its real part n and its imaginary part k69–71 as given in eqn (2). In order to use eqn (2) the knowledge of the real index of refraction at some reference point ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) r is required.46 The Kramers–Kronig relation constitutes an inversion of the experimental spectrum and is not based on any model assumption about the optical data.
r is required.46 The Kramers–Kronig relation constitutes an inversion of the experimental spectrum and is not based on any model assumption about the optical data.
 | (2) |
 | (3) |
 | (4) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) s, their reduced oscillator strength fs, and their damping width γs. The parameter εe is the value of the dielectric function (assumed to be constant) at high frequencies compared with the vibrational excitations considered.
s, their reduced oscillator strength fs, and their damping width γs. The parameter εe is the value of the dielectric function (assumed to be constant) at high frequencies compared with the vibrational excitations considered.
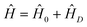 | (5) |
 | (6) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij is the distance between the centers of mass of the molecules labelled i and j and
ij is the distance between the centers of mass of the molecules labelled i and j and ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) is the dipole moment operator. The vibrational eigenfunction ψn and vibrational eigenvalues νn are found by solving the Schrödinger equation with Ĥ. The infrared spectrum (A(νn)) can then be calculated from these quantities as described in ref. 61. In its simplest form the model contains only two parameters for each type of molecule. One is the transition wave number of the uncoupled molecule
is the dipole moment operator. The vibrational eigenfunction ψn and vibrational eigenvalues νn are found by solving the Schrödinger equation with Ĥ. The infrared spectrum (A(νn)) can then be calculated from these quantities as described in ref. 61. In its simplest form the model contains only two parameters for each type of molecule. One is the transition wave number of the uncoupled molecule ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) M and the other is the transition dipole moment of the uncoupled molecule δμ = 〈0|μ|1〉. These parameters can be extracted from gas phase measurements67 or from ab initio calculations.68,49 This simplest case applies for instance for pure, large homogeneous crystalline particles (see section 5). To model spectra of smaller aggregates with a non-homogeneous structure throughout the particle (see section 4), we use the so-called extended exciton approach.62 It is based on the use of individual transition frequencies and transition dipole moments for each single molecule in the particle since each molecule is located in a somewhat different environment and thus has its individual values for these parameters. The transition frequencies for each molecule are found by local normal coordinate analysis after the structure optimization with molecular dynamics (section 3.2). Local transition dipoles are calculated within the double harmonic approximation, i.e. as derivatives of the dipole moment with respect to the local normal coordinate.
M and the other is the transition dipole moment of the uncoupled molecule δμ = 〈0|μ|1〉. These parameters can be extracted from gas phase measurements67 or from ab initio calculations.68,49 This simplest case applies for instance for pure, large homogeneous crystalline particles (see section 5). To model spectra of smaller aggregates with a non-homogeneous structure throughout the particle (see section 4), we use the so-called extended exciton approach.62 It is based on the use of individual transition frequencies and transition dipole moments for each single molecule in the particle since each molecule is located in a somewhat different environment and thus has its individual values for these parameters. The transition frequencies for each molecule are found by local normal coordinate analysis after the structure optimization with molecular dynamics (section 3.2). Local transition dipoles are calculated within the double harmonic approximation, i.e. as derivatives of the dipole moment with respect to the local normal coordinate.
To illustrate the contribution of individual radial shells to the overall absorption spectrum in Fig. 7 and 8 we introduce the radial transition moment
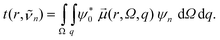 | (7) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) the dipole moment operator, and q the set of intramolecular vibrational coordinates. ψ0 is the vibrational ground state wavefunction and ψn is the exciton level with wavenumber
the dipole moment operator, and q the set of intramolecular vibrational coordinates. ψ0 is the vibrational ground state wavefunction and ψn is the exciton level with wavenumber ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) n. The radial transition density is given by
n. The radial transition density is given by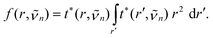 | (8) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) n) corresponds to the contribution of the shell at radius r to the overall absorbance at wavenumber
n) corresponds to the contribution of the shell at radius r to the overall absorbance at wavenumber ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) n, so that the total absorption spectrum A(
n, so that the total absorption spectrum A(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) n) is proportional to
n) is proportional to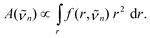 | (9) |
 | ||
| Fig. 7 Upper trace: Calculated infrared spectrum of a spherical CO2 ice particle. Lower trace: corresponding radial transition density as defined in eqn (8). The transition density decreases from red to yellow. | ||
 | ||
Fig. 8 Upper panel: calculated infrared spectrum of a N2O/CO2 core-shell particle. The ratio of the two substances amounts to 1 : 1. Lower trace: corresponding radial transition density as defined in eqn (8). The transition density decreases from dark blue to light blue. ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the transition wavenumber. is the transition wavenumber. | ||
3.2. Structure determination
The inner structure of the aggregates (amorphous, crystalline, partially crystalline, type of hydrogen bond network) is of course also reflected in their spectroscopic properties. For small particles (<10 nm) the high portion of surface area plays an important role in this context. Due to the altered interactions in the boundary region between surface and surrounding medium, the surface region has different structural and thus spectroscopic properties than the core of the particles. The inner structure thus becomes non-homogeneous throughout the particles. Such structural aspects can be modelled by molecular dynamics.15,29,59,62,64,66For the ammonia nanoparticles in section 4 we used a Verlet algorithm and simulated annealing to optimize the structure. Kinetic energy was distributed in the particles corresponding to an initial temperature of 100 K and then gradually removed by 0.1% of the remaining energy every 0.1 fs for a total simulation time of 5 ps. Due to the high number of degrees of freedoms (>105 for the largest particles), a simple potential was required. To describe the intramolecular interactions we used a modified version of the quadratic valence force field of Diraison et al.73 The modifications correct for the wrong inversion barrier and the wrong stretching and bending frequencies of the monomer. The intermolecular potential is a modified version of Impey and Klein.74 It contains pairwise Lennard-Jones interactions between the atoms of different molecules as well as electrostatic interactions modelled by four point charges on different sites. The modifications ensure that the potential describes the molecular transition dipole of the umbrella vibration correctly. The potentials and their modifications will be further described in ref. 62
4. Spectroscopic identification of size effects
This section gives a survey over the different size effects found in infrared spectra of aggregates in the size range from one micron to less than one nanometer. As explained in section 2.1, collisional cooling represents an ideal method to generate molecular aggregates of volatile substances over this whole size range. For nanosized particles, jet expansions represent complementary methods to collisional cooling. RESS and electrospraying are particularly suitable to form particles of non-volatile substances. The former leads often to larger particles (>50–100 nm) than the latter (<50–100 nm). For the sake of clarity we consider exclusively spherical particles in this section.4.1. Size range above 100 nm
The most prominent size effect in infrared spectra results from elastic scattering of the light by the particles. This phenomenon is observed for all types of particles no matter what composition or shape.11,14,17,19,50,75–77 The only condition for the occurrence of strong scattering effects in extinction spectra is that the wavelength of the light be comparable with the size of the particles. In the mid-infrared region this means that the radius of the particles must be larger than about 100 nm. Elastic scattering leads to the characteristic slanted baseline and to the dispersion shape of the absorption bands as illustrated in Fig. 5 for the example of phenanthrene (C14H10) aerosol particles. The experimental infrared spectrum is shown in trace a) together with the simulated spectrum in trace b). The slanted baseline can easily be seen, but the dispersion shape of the absorption peaks does not appear very prominent on this scale. Both features become the more pronounced the larger the particles are. For the calculation we have used classical scattering theory assuming spherical particles (see eqn (1)), the refractive index data from ref. 42, and the measured size distribution depicted in trace c). The image from electron microscopy in trace d) confirms that it is reasonable to treat these particles as spheres.4.2. Size range between 5–100 nm
In the intermediate size range, i.e. between about 5–100 nm (∼104–107 molecules per particle), the contribution from elastic scattering becomes negligible. In this size range the infrared spectra are dominated by absorption bands. The characteristic here is that the band structure and the band width for a certain absorption band remain almost constant over this whole size range provided that the shape of the particle remains the same. (As discussed in section 5, the particle shape has a strong influence on the structure of absorption bands if strong transition dipole coupling is important.) The only quantity which changes in this intermediate size range is the absolute value of the extinction. It scales with the particle density in the aerosol and approximately with the number of molecules per particle. For a spherical particle one expects a single unstructured absorption band if the molecular vibrational transition is non-degenerate.37,49,55,67,78 This is illustrated in Fig. 2 for crystalline CO2 particles.37 Trace a) shows two experimental spectra recorded in a Laval nozzle expansion36 and in a collisional cooling cell. The comparison with the exciton calculations shown in trace b) clearly reveals that particles with an almost spherical shape dominate the experimental infrared spectra.67With classical scattering theory the stability of the spectra in this intermediate size range between 5–100 nm can be understood as follows:55 In this region the particle size is always smaller than the infrared wavelength. Therefore, at any instant, the electromagnetic field to which the particle is exposed is more or less constant over the extension of the particle and the particle behaves like an oscillating electric dipole. Since the corresponding absorption cross section has no component that depends simultaneously on radius and frequency (see Cabs,j in eqn (1) and ref. 55) the band widths and the band structure are size independent. A microscopic explanation of the same phenomenon is provided by the exciton model.61 For the calculations (see trace b) in Fig. 2) all CO2 molecules in the crystalline particle were assumed to have the same transition wavenumber and the same transition dipole. In this size range this is a good approximation because the vast majority of molecules are located in the core of the particle and the contribution from the surface can thus be neglected. All core molecules experience approximately the same environment and show the same coupling scheme with other molecules. They thus have the same transition wavenumbers and transition dipoles.
4.3. Size range below 5–10 nm
The influence of the surface on infrared spectra can no longer be neglected if the particle radius drops below 5–10 nm because the fraction of the surface amounts to more than 15% for a 10 nm particle and incorporates almost the whole volume (90%) of a 1 nm aggregate. Even if the particle’s structure remains crystalline surface molecules can have a different absorption frequency due to the altered environment near the boundary.18,21,33,34,48,61,63 In addition, for vibrational bands which are dominated by exciton coupling, the surface molecules have a different coupling scheme with neighboring molecules compared with molecules inside the particles. Both phenomena can lead to characteristic surface features in the spectra as depicted for N2O aggregates in Fig. 9 for the NO stretching-vibration.48 The size of the particles decreases from top to bottom from about 10 nm to about 0.8 nm. With decreasing size the absorption band shifts continuously to lower wavenumbers. This spectral evolution with decreasing size nicely mirrors the increasing surface fraction.34,48,63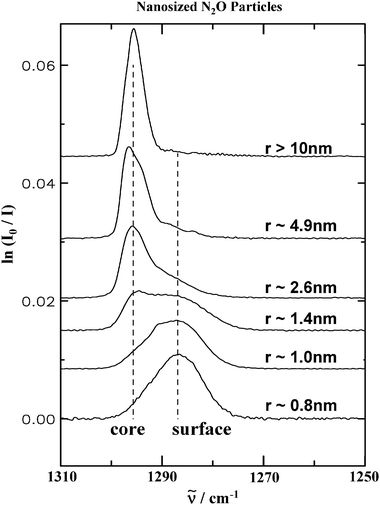 | ||
Fig. 9 Experimental infrared spectra in the region of the NO stretching-vibration of N2O ice particles for decreasing particle size. From top to bottom the particle radius changes from about 10 nm to about 0.8 nm. The sizes have been estimated from a band shape analysis which determines the surface contribution and, for a given thickness of the surface layer, the size.48![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) , is the transition wavenumber. , is the transition wavenumber. | ||
The small N2O particles in Fig. 9 have been generated by collisional cooling using liquid helium as a cooling agent. Another possibility is supersonic expansion in Laval or slit nozzles.33,34,36,42Fig. 3 compares a spectrum recorded in the expansion of a specially designed slit nozzle33,34 with a collisional cooling spectrum. Compared with the spectrum obtained by collisional cooling the jet spectrum (upper trace) has a worse signal to noise ratio and due to residual gas phase in the jet it shows additional sharp absorption peaks superimposed on the broad absorption of the particles. Apart from these minor differences, however, the good overall agreement between the two spectra is striking. It shows that the two very different generation techniques produce the same particles. Since jet expansion is the appropriate method to form even smaller aggregates down to dimers and collisional cooling allows us to generate larger particles, the combination of both methods opens the possibility to study molecular aggregates systematically from dimers to micron sized particles.
The boundary between particle and surrounding medium can also cause another type of size effect in small particles (1–5 nm). The boundary can lead to structural changes in the surface layer compared with the core region of the particles. Infrared patterns arising from the inner structure of ice particles were studied by Devlin, Buch, and co-workers for small supported water ice particles15 and in our research group for ammonia ice aerosols.49,62 The influence of structural changes in the surface on infrared spectra is illustrated for the umbrella vibration of ammonia particles in Fig. 10. The two spectra on the left show in trace a) a spectrum for a spherical aggregate with a size around 2 nm and in trace b) a spectrum for a spherical particle with a radius of about 20 nm. The influence of size shows up very prominently in these spectra. With decreasing size the spectrum becomes much broader. More insight into the microscopic origin of this behavior can be obtained from the calculated spectra depicted on the right hand sides in Fig. 10. For the calculation in trace d) we have assumed that the 20 nm particle is completely crystalline49 and that the band shape is mainly determined by exciton coupling (see eqn (6)). The comparison between experiment (trace b)) and calculation (trace d)) confirms that this is indeed a very good assumption. 20 nm particles of course do have a surface layer with a structure different from that of a perfect crystal. But these deviations from crystallinity in the surface layer cannot be detected in the infrared spectrum because the portion of the surface is negligible for these large particles. For the 2 nm particle (trace a)), by contrast, the calculation (trace c)) and Fig. 11 reveals that only the core is crystalline whereas the shell is amorphous. This is shown in Fig. 11. The bold line measures the deviation from crystallinity as a function of the particle radius r for the 2 nm particle after structure optimization by simulated annealing (see section 3). Zero means crystalline and a value around 1 Å represents amorphous structures. One can see that the amorphous layer amounts to about 80% of the total particle volume. The calculated infrared spectrum in trace c) of Fig. 10 shows that it is this amorphous part which makes the absorption band that broad. For these vibrational calculations we have used the extended exciton model described in section 3.
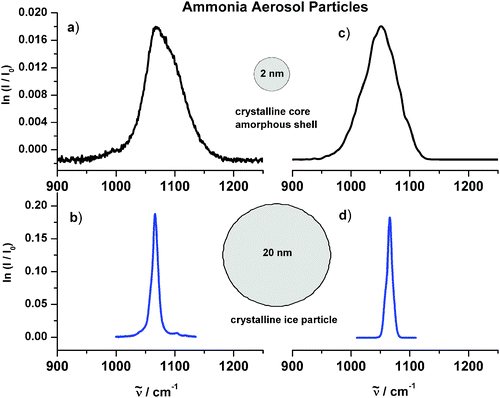 | ||
Fig. 10 Infrared spectra of ammonia aerosol particles in the region of the umbrella vibration. (a) Experimental spectrum of 2 nm particles. (b) Experimental spectrum of 20 nm particles. (c) Calculated spectrum of 2 nm particles. The infrared spectrum was calculated with the extended exciton approach after the particle’s structure had been optimized by simulated annealing (see section 3). (d) Calculated spectrum of 20 nm particles. For these exciton calculations we assumed a molecular transition wave number of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) M = 1060 cm−1 and a molecular transition dipole moment of δμ = 〈0|μ|1〉 = 0.23 D.49 M = 1060 cm−1 and a molecular transition dipole moment of δμ = 〈0|μ|1〉 = 0.23 D.49![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the transition wavenumber. is the transition wavenumber. | ||
 | ||
| Fig. 11 Structure of a 2 nm ammonia ice particle after structure optimization by simulated annealing (see section 3). Solid curve: deviation from crystallinity as a function of the particle’s radius. This deviation from crystallinity represents a mean deviation for every atom with respect to the crystalline structure.62 A value of zero means crystalline and a value around 1 Å indicates an amorphous region. | ||
Finally, the calculated spectra in Fig. 12 are meant to illustrate what happens with infrared spectra for even smaller aggregates, i.e. with sizes in the subnanometer range. All spectra show the umbrella vibration for crystalline ammonia aggregates.62 The number of molecules per particle ranges from 104 to 25. A general trend is that the band shape becomes more complex and spread out with decreasing cluster size. The reason for this is that in small aggregates every single molecule feels a slightly different environment and thus absorbs at a somewhat different wavenumber. Exceptions to this trend can occur for clusters with higher symmetry.65 As mentioned already supersonic expansion33,34,36,37,64,79,80 is more suitable to generate the very small aggregates than collisional cooling. Using collisional cooling one has to deal with very dilute samples. Thus impurities and low particle concentrations strongly affect the quality of the spectra. The most severe problem in investigating this size range, however, is the fact that detailed measurements must be made on size selected clusters. In ensemble measurements the spectral features are wiped out since many different cluster sizes contribute to the spectrum. Buck and coworkers have introduced a method that allows the investigation of size selected clusters.79,81,82
 | ||
Fig. 12 Calculated infrared spectra of ammonia aggregates in the subnanometer region. For small aggregates the infrared spectrum is more spread-out than for larger aggregates. ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the transition wavenumber. is the transition wavenumber. | ||
5. Infrared patterns of particle shape and architecture
5.1. Particle shape
As demonstrated in the previous section, the size of the particles can have a strong influence on infrared spectra and can thus be exploited, for instance, to determine the size of aerosol particles as outlined in section 6. Similar to the size, the shape also leaves its characteristic fingerprint in the spectra. To study pure shape effects we have to focus on the size range between 10–100 nm because size effects on band shapes can be excluded in this region as we have seen in the previous section.Fig. 2 and 13 compare the structure of the antisymmetric stretching band of CO2 particles for two different particle shapes: For mainly spherical particles in Fig. 2 and for predominantly elongated particles in Fig. 13.67 The difference in shape manifests itself very prominently. With the increasing fraction of elongated particles the band becomes much broader and the structure shows three maxima instead of the single maximum observed for pure spherical particles. Analogous shape effects have also been found for other ice particles such as N2O, NH3, SF6etc.9,10,13,17,49,67,78,83 The interesting observation, however, was that for a given substance only certain absorption bands show shape effects while others do not. This led to the question what exactly the criteria are for the occurrence of shape effects in infrared spectra and how this phenomenon can be understood in terms of molecular properties. As a result we have found the following points to be important:51,61,67,68 The molecular transition dipole moment of the vibrational transition under consideration must be strong (transition dipoles >0.1–0.2 D) and the next nearest neighbor molecules in the particles have to be separated by small distances (rij < 5–7 Å) (see eqn (6)). This configuration leads to strong resonant transition dipole coupling between all molecules in a particle. This coupling lifts the degeneracy of the uncoupled molecular energy levels and leads in this way to band structures which are characteristic for a certain particle shape. That exciton coupling is indeed the molecular origin of shape effects and is proven by the almost perfect agreement of experimental spectra in traces a) of Fig. 2 and 13 with corresponding predictions from exciton calculations depicted in traces b).
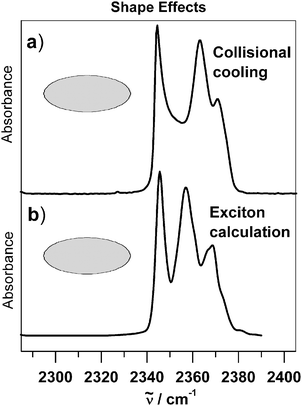 | ||
Fig. 13 (a) Experimental infrared spectra of predominantly elongated CO2 particles in the region of the antisymmetric stretching vibration. The particles were generated by collisional cooling. (b) Corresponding exciton calculations (see section 3 and ref. 67). The radius of the particles lies around 50 nm. ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the transition wavenumber. is the transition wavenumber. | ||
As the exciton coupling lifts the degeneracy of the uncoupled vibrational states it leads to eigenfunctions that are delocalized over the whole particle. It is this delocalization which explains the distinct shape sensitivity of the exciton states. This can be best visualized by inspecting the vibrational wave functions of these particles. For a spherical particle this is illustrated in Fig. 7. The upper trace again shows the calculated spectrum of a spherical CO2 ice particle and the lower trace depicts the radial transition density f(r,![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) n) as a function of the wavenumber and the radius as defined in eqn (8). The transition density demonstrates that the vibrational eigenfunctions are indeed delocalized over the whole particle. For a spherical particle this means delocalized over the whole radius thus explaining, as just mentioned, the shape sensitivity.
n) as a function of the wavenumber and the radius as defined in eqn (8). The transition density demonstrates that the vibrational eigenfunctions are indeed delocalized over the whole particle. For a spherical particle this means delocalized over the whole radius thus explaining, as just mentioned, the shape sensitivity.
One important parameter for the occurrence of strong exciton coupling is the distance rij between neighboring resonant molecular oscillators (see eqn (6)). The larger this distance the less prominent is the influence of exciton coupling and thus of shape effects on infrared spectra. In particles which consist of homogeneous mixtures of different substances this distance is reduced on average compared with a one-component aggregate. It is thus to be expected that shape effects in infrared spectra of mixed particles are altered compared with those of pure aggregates. To clarify this point we have investigated statistically mixed particles with CO2 as one of the components. The other component was the isotopomer 13CO2. For the antisymmetric stretching vibration of CO2, the influence on the band structure for particles with different amounts of CO2 is shown in Fig. 14. In all three cases the particles have the same shape, i.e. the ensemble consists of elongated aggregates as in Fig. 13. The percentage of CO2 decreases from top to bottom from 100 to about 20%. With increasing dilution the fine structure caused by the particle shape gradually vanishes. This means nothing else than that the information about the particle shape is lost in spectra of statistically mixed particles. The exciton calculations depicted below the respective experimental spectra in Fig. 14 fully confirm these experimental findings.47,49,67 As further outlined in section 6, this result has direct implications on the spectroscopic identification of interstellar dust particles as well as atmospheric aerosols.
 | ||
Fig. 14 Experimental infrared spectra of statistically mixed particles with predominantly elongated shape. The spectra show the region of the antisymmetric stretching vibration of CO2. The percentage of CO2 decreases continuously from top to bottom. (a) 100% CO2, (b) 78% CO2, and (c) 18% CO2. The characteristic signatures of the particle’s shape disappear with increasing dilution of CO2. ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the transition wavenumber. is the transition wavenumber. | ||
5.2. Architecture
Not only the shape but also the architecture of the particles can lead to characteristic spectroscopic features. As is the case for the shape of the particles, this effect is pronounced only for strong absorption bands which are dominated by exciton coupling. Core-shell particles represent a very simple example of a special particle architecture.47,84,85 This type of particles can be formed, for instance, if two substances with different volatility condense together. With collisional cooling it is possible to form core-shell particles of two substances in a controlled fashion even if their respective volatility is very similar47,84. This is realized experimentally by introducing two different sample pulses into the cooling cell within a short time delay.47,86 As an example Fig. 8 shows in the upper panel the infrared signatures of a spherical particle with N2O in the core and CO2 in the shell. The ratio of the two substances is 1 : 1. The characteristic spectral feature of these core-shell particles is the split band of the shell. The lower panel illustrates the behavior of the corresponding vibrational eigenfunctions. As in Fig. 7, the transition density is depicted as a function of the wavenumber and of the radius (see eqn (8)). The transition density is no longer delocalized over the whole particle as was the case for pure particles in Fig. 7. Rather it now features two separate components confined to the shell region and the core region, respectively.At temperatures around 80 K in the cooling cell, core-shell particles of CO2 and N2O do not remain stable. As can be seen from the infrared spectra depicted in Fig. 15, core-shell particles turn into statistically mixed particles in the course of increasing time. Trace a) shows the spectrum of core-shell particles with N2O in the shell (portion 25%) and CO2 in the core (portion 75%). The most characteristic feature is again the split band of the shell around 2240 cm−1 (see also Fig. 8). With increasing time the splitting of this band becomes increasingly blurred (trace b)) and disappears completely after 145 s (trace c)). This is clear spectroscopic evidence that the particles convert from core-shell particles to statistically mixed aggregates with their characteristic broad unstructured bands already found in Fig. 14c. The process by which this happens is not clear yet. Diffusion in the particles, as suggested in ref. 84 as well as evaporation and recondensation of the particle ensemble are likely to contribute to this dynamical behavior.
 | ||
Fig. 15 Experimental infrared spectra of two-component particles consisting of 25% N2O (shell) and 75%CO2 (core). (a) Immediately after the formation the particles have a core-shell structure. (b) After 60 s the two substances form statistically mixed regions either through diffusion in the particles or through evaporation and recondensation in the cell. (c) After 145 s the particles have completely turned into statistical mixtures. The small band at 2282 cm−1 arises from 13CO2 in natural abundance. ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the transition wavenumber. is the transition wavenumber. | ||
6. Atmospheric aerosols, interstellar ice particles, and drug particles
What is the benefit of the fundamental findings about size and shape effects in infrared spectra discussed in the two previous sections? One can quite generally say that only such fundamental studies allow us to correctly interpret and understand spectroscopic data obtained and used in many applications. They are the prerequisite for setting up databases of high quality. In the context of molecular particles, fundamental understanding finally means uncovering the relation between spectroscopic signatures and molecular properties, i.e. intra- and intermolecular forces acting in the particles. The systems to be considered nowadays, however, are very complex. With their huge number of individual molecules it is evidently difficult to arrive at a fundamental understanding of their behavior for most of the systems. In many cases it might not even be possible at all. Not only the theoretical approach, but also the experimental methods need to be improved. In the two preceding chapters we have tried to shed some light on several fundamental aspects. In this chapter we consider the usefulness of these findings in present day applications.6.1. Size
The knowledge of the size is central for the characterization of atmospheric aerosols, interstellar ice particles, and drug particles since the size can significantly influence the chemical and physical properties of the aggregates.1–4,55 For example, the size influences the reactivity of the particles, determines their residence time in the air and their bioavailability in case of drug particles, and it defines their spectroscopic properties. All these properties have a significant impact on our climate as well as on health issues. The characterization of small particles (<10 nm) is of particular interest because their role in the context of atmospheric processes and health issues (air pollution) is not yet satisfactorily clarified. As outlined in section 4 for small molecular aggregates one expects to retrieve characteristic features in infrared spectra which are associated with the increasing fraction of surface for decreasing particle size. As we have demonstrated these phenomena can be related to structural changes in the surface or they can simply arise from the fact that surface molecules are located in a different environment than molecules in the core of the particle. As explained in ref. 37, characteristic size effects can almost disappear when the measurement is performed on an ensemble of particles comprising different sizes. This point is important for field measurements which very often have to deal with particle ensembles. In addition, these particles are often composite particles which can consist of very different compounds. Size characterization of particles with a complex chemical composition poses an even greater challenge than for pure particles. So far, however, infrared spectra of only very few one-component systems have been investigated in more detail (see section 4). These studies clearly show that neither the experimental nor the theoretical methods available nowadays can provide reliable technical standards, for instance to create databases for the size characterization of nanosized aggregates. At this stage infrared spectroscopic techniques cannot yet be exploited as a standard technique for the size characterization in this size range. Both experimental and theoretical methods still need major development to attain this goal.In contrast to the situation for small particles, size characterization with infrared is to some extent standard for larger particles (>100 nm). The standard procedure here is to use classical scattering theory (section 3) with refractive index data as input data available from different databases.87–90 For several reasons, however, this standard procedure often produces no more than a rough estimate of the size distribution of a particle ensemble. One reason for this is the influence of the particle shape. This information is needed for accurate scattering calculations,55–57 but in most cases it is not available for the particle ensemble under consideration. As an approximation, Mie theory for spherical particles is often used with the justification that the influence of the shape is minor or averages out in an ensemble—a statement which is clearly not correct at all in general.55 A second problem, which has major impact on the accuracy of the derived size distributions, arises from the use of tabulated refractive index data. It is a difficult task to derive accurate optical data from experimental investigations.11,14,19,46,68,50,76,77 The reason is the lack of experimental information, for instance on the particle number, size, and shape when optical data are derived directly from particle measurements, or about the layer thickness in case they are obtained from thin film measurements. All these factors lead to inaccuracies in the tabulated values. In addition, there is only limited data available for certain compounds and for certain experimental conditions (e.g. temperature). In particular, it is often not possible to find optical data for multi-component particles of a specific composition. It is sometimes assumed that refractive index data of mixed aggregates can simply be obtained by combining the known refractive index data of the pure compounds. This assumption, however, is in general wrong for molecular particles. With changing composition the intermolecular forces in the particles alter which in turn changes their spectroscopic properties and thus their refractive index data in a non-trivial manner. Fig. 16 illustrates this point for mixed formic acid/water ice aerosols. The finely structured absorption bands of pure formic acid particles in trace a) gradually disappear with increasing fraction of water ice in the particles (traces b) to c)) due to the altered intermolecular forces. The same happens for the strong ice absorption around 3200 cm−1 when going from pure ice in trace d) to more dilute ice in traces c) and b). Thus, each mixture has its unique set of refractive index data which cannot be obtained from a simple combination of the data for pure particles.
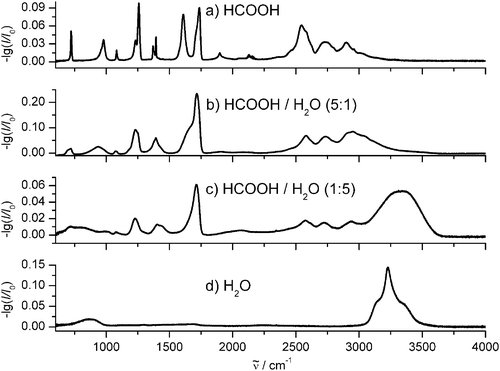 | ||
Fig. 16 Experimental infrared spectra of different aerosol particles. (a) Formic acid. (b) Mixture of formic acid and water ice with a ratio of 5 : 1. (c) Mixture of formic acid and water ice with a ratio of 1 : 5. (d) Water ice. ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the transition wavenumber. is the transition wavenumber. | ||
As an example, Fig. 17 shows infrared refractive index data for phenanthrene particles derived from aerosol measurements. Like carboxylic acid/water aerosols91 particles consisting of polycyclic aromatic hydrocarbons occur as pollutants in the atmosphere.2,92 They have also been discussed as carriers of the “unidentified” infrared bands in astrophysics.93,94 For the derivation of the data in Fig. 17, independent information about the size distribution and the shape of the particles were available from SMPS measurements and SEM measurements, respectively, as shown in Fig. 5c and d). This is an ideal situation which makes it possible to extract comparatively accurate optical data from measured aerosol spectra. In many other cases, however, independent experimental data about size and shape do not exist. These data are nearly always missing for volatile aerosol particles because in this case neither accurate size classifiers nor microscopic methods can be used. Different methods, which all rely on additional assumptions, have been implemented to derive refractive index data also in these cases.11,14,19,46,68,76,77 Recent examples are data for liquid sulfuric acid/water aerosols,14 which are relevant to the upper troposphere and lower stratosphere, or atmospherically relevant organic acid particles.19,90 Although the assumptions mentioned lead to inaccuracies in the data it is very important for applications to have at least approximate values. They are also helpful as references for further improvements of the data in future studies. It would be useful here if data were provided with their uncertainty quantified. Unfortunately this happens very rarely.90
 | ||
| Fig. 17 Refractive index data of phenanthrene aerosol particles (see Fig. 5). n is the real part of the complex index of refraction. k is the imaginary part of the complex index of refraction. | ||
6.2. Shape
Some fundamentals of shape effects in infrared spectra of molecular particles were addressed in section 5. The main merit of these findings for applications is that for the first time they provide a clear criterion when pronounced shape effects are expected to be important. Shortly summarized, this is the case for absorption bands with strong molecular transition dipoles and only if the particles consist of one major component, i.e. when other substances contribute less than 10–20%. Atmospheric aerosol particles often consist of many different components so that shape effects on band structures in the infrared are of minor importance here. Moreover, these systems can consist of an ensemble of particles comprising different shapes further complicating their spectra. In other words infrared spectroscopy is not an adequate method to obtain information about the particles shape for the vast majority of atmospheric aerosols. There are of course exceptions in some special cases when more or less pure particles of a certain shape are predominant. The same statement is probably true for interstellar dust particles. It has often been speculated that band structures observed in the spectra of atmospheric aerosols or interstellar ice particles could arise from shape effects. At this point we can conclude that these speculations were in general wrong. In most cases, the origin of unusual band structures in infrared spectra of mixed particles goes back to local effects within the particles, i.e. to special intermolecular interactions with neighboring molecules.49,51,95 Although these rules apply in general, reference spectra obtained from laboratory measurements are still the only possibility to clarify the influence of shape effects for individual cases. With the current experimental methods it is, however, a challenge to obtain reference spectra for different particles shapes so that there is a strong need for improvements here as well.6.3. Drug particles
As a last example, let us consider the benefit of infrared extinction spectroscopy for drug particle formation by rapid expansion of supercritical CO2/drug solutions (RESS). The principle of RESS is described in section 2.1. With the experimental setup depicted in Fig. 4, extinction spectra can be recorded in situ during the particle formation within ms. This allows us to analyze and control the properties of drug particles, such as size and composition, during the particle formation. For the micronization of thermally labile drugs, supercritical CO2 is a particularly suitable solvent because it has low critical data and it can easily be separated from the product after the particle formation. The idea behind the micronization of pharmaceutical substances is to improve their bioavalability.4,5,41 Small particles as opposed to bulk substance have a much larger surface and thus show an improved solubility even in media in which the bulk substance hardly dissolves.A main problem with RESS, however, is the fact that the small primary drug particles often agglomerate and coagulate, thus reducing the active surface area. This is illustrated for the painkiller ibuprofen (C13H18O2) by the SEM-images in Fig. 6a.96,97 The inset shows a detailed view of agglomerated and coagulated primary particles with a primary particle size of about 100–300 nm. The main panel of Fig. 6 (a) demonstrates on a larger scale that these agglomerates form very long branched chains. Our recent in situ investigations with rapid-scan infrared spectroscopy and 3-wavelengths-extinction measurements reveal that agglomeration and coagulation of these drugs already happens at and directly after the Mach disk, i.e. before the particles are collected in the form of powders.42,52 One way to prevent particle growth through coagulation and agglomeration is to spray the supercritical solutions directly into an aqueous surfactant solution (RESSAS,41,98–100). Another strategy is to mix or coat the particles with a second substance less prone to coagulation, for instance a biodegradable polymer such as Eudragit© or poly-lactic-acid (PLA). This can be achieved by rapid expansion of a ternary supercritical mixture which results in co-precipitation of the two solutes (CORESS,5,101–107). Encapsulation of drug particles is not only of interest for stabilizing primary particles. By tuning the property of the polymer it can also be a promising way for controlled drug delivery in the body. Fig. 6b shows a SEM-image of ibuprofen/PLA particles generated by co-precipitation of an ibuprofen/PLA/CO2 solution. Compared with pure ibuprofen particles in section (a), the composite particles are clearly less agglomerated.
We have found that the degree of agglomeration strongly depends on the amount of polymer in the particles. It is thus crucial here to have a method which allows us to determine and control the amount of polymer already during the particle formation. As Fig. 18 illustrates rapid-scan infrared spectroscopy in situ, as explained further in section 2, is the ideal method to achieve this. The fraction of drug and polymer can be easily determined by their characteristic carbonyl bands around 1723 and 1758 cm−1, respectively. The advantage of infrared extinction spectroscopy over other methods is obvious here: Compared with off-line methods for chemical analysis it allows the control during the particle formation process and compared with other spectroscopic methods infrared spectroscopy is very selective for these types of substances.
 | ||
Fig. 18 Experimental infrared spectra of ibuprofen particles. (a) Pure ibuprofen. Ibuprofen molecules form dimers in the particles as implied by the molecular structure shown. (b) Mixed ibuprofen/PLA. ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) is the transition wavenumber. is the transition wavenumber. | ||
7. Summary
The combination of different particle generation and characterization methods provides a wealth of information about large weakly bound molecular aggregates over the whole size range from subnanometers to microns. The central aspect of this contribution was to study the influence of characteristic particle properties, such as size, shape, and architecture, on the vibrational dynamics of these aggregates. Our combination of experimental data with modelling shows that the corresponding infrared spectroscopic signatures can indeed be understood on a microscopic level and that they can even be predicted from molecular properties. These fundamental investigations are the prerequisite for a better understanding of atmospheric aerosols, interstellar dust particles, and drug particles. They lay the foundation for the setup of reference data bases for particulate systems and help us to optimize and control particle formation processes. The present investigations, however, also demonstrate that studies on such a fundamental level are still in their infancy leaving a lot of room for improvements both on the experimental and on the theoretical side.Acknowledgements
We gratefully acknowledge the collaboration with PD Dr Michael Türk, Professor Dr Robert Georges, Professor Dr Martin A. Suhm, and Dr Sigurd Bauerecker. This project was supported by funds from the Natural Sciences and Engineering Research Council of Canada, from the Deutsche Forschungsgemeinschaft (grant Nr. SI 833/1–2, SFB 602, and GRK 782) and from the German Fonds der Chemischen Industrie.References
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics, Wiley & Sons, New York, 1998 Search PubMed.
- B. J. Finlayson-Pitts and J. N. Pitts, Chemistry of the Upper and Lower Atmosphere, Academic Press, San Diego, 2000 Search PubMed.
- P. Ehrenfreund and S. B. Charnley, Annu. Rev. Astron. Astrophys., 2000, 38, 427–483 CrossRef CAS.
- T. L. Rogers, K. P. Johnston and R. O. Williams, Drug Dev. Ind. Pharm., 2001, 27, 1003–1015 CrossRef CAS.
- M. Türk, P. Hils, K. Hussein and M. Wahl, Utilization of supercritical fluid technology for the preparation of innovative carriers loaded with nanoparticular drugs, in Produktgestaltung in der Partikeltechnologie, ed. U. Teipel, Fraunhofer IRB Verlag, Stuttgart, 2004, pp. 373–386 Search PubMed.
- F. Fleyfel and J. P. Devlin, J. Phys. Chem., 1989, 93, 7292–7294 CrossRef CAS.
- T. Dunder and R. E. Miller, J. Chem. Phys., 1990, 93, 3693–3703 CrossRef CAS.
- J. A. Barnes, T. E. Gough and M. Stoer, Rev. Sci. Instrum., 1989, 60, 406–409 CrossRef CAS.
- J. A. Barnes, T. E. Gough and M. Stoer, J. Chem. Phys., 1991, 95, 4840–4844 CrossRef CAS.
- R. Disselkamp and G. E. Ewing, J. Chem. Phys., 1993, 99, 2439–2448 CrossRef CAS.
- M. L. Clapp, R. E. Miller and D. R. Worsnop, J. Phys. Chem., 1995, 99, 6317–6326 CrossRef CAS.
- D. Newnham, J. Ballard and M. Page, Rev. Sci. Instrum., 1995, 66, 4475–4481 CrossRef CAS.
- T. E. Gough and T. Wang, J. Chem. Phys., 1996, 105, 4899–4904 CrossRef CAS.
- R. F. Niedziela, M. L. Norman, C. L. DeForest, R. E. Miller and D. R. Worsnop, J. Phys. Chem. A, 1999, 103, 8030–8040 CrossRef CAS.
- J. P. Devlin, C. Joyce and V. Buch, J. Phys. Chem. A, 2000, 104, 1974–1977 CrossRef CAS.
- S. Bauerecker, M. Taraschewski, C. Weitkamp and H. K. Cammenga, Rev. Sci. Instrum., 2001, 72, 3946–3955 CrossRef CAS.
- M. K. Kunzmann, R. Signorell, M. Taraschewski and S. Bauerecker, Phys. Chem. Chem. Phys., 2001, 3, 3742–3749 RSC.
- R. Signorell, Mol. Phys., 2003, 101, 3385–3399 CrossRef CAS.
- M. T. Dohm, A. M. Potscavage and R. F. Niedziela, J. Phys. Chem. A, 2004, 108, 5365–5376 CrossRef CAS.
- O. Abraham, S.-S. Kim and G. D. Stein, J. Chem. Phys., 1981, 75, 402–411 CrossRef CAS.
- R. E. Miller, R. O. Watts and A. Ding, Chem. Phys., 1984, 83, 155–169 CrossRef CAS.
- L. S. Bartell, Chem. Rev., 1986, 86, 491–505 CrossRef CAS.
- L. S. Bartell, L. Harsanyi and E. J. Valente, J. Phys. Chem., 1989, 93, 6201–6205 CrossRef CAS.
- J. A. Barnes and T. E. Gough, J. Chem. Phys., 1987, 86, 6012–6017 CrossRef CAS.
- M. Gauthier, J. Chem. Phys., 1988, 88, 5439–5449 CrossRef CAS.
- H.-D. Barth and F. Huisken, Chem. Phys. Lett., 1990, 169, 198–203 CrossRef CAS.
- J. Huang and L. S. Bartell, J. Phys. Chem., 1994, 98, 4543–4550 CrossRef CAS.
- J. Huang and L. S. Bartell, J. Phys. Chem., 1995, 99, 3924–3931 CrossRef CAS.
- G. Torchet, M.-F. de Feraudy, A. Boutin and A. H. Fuchs, J. Chem. Phys., 1996, 105, 3671–3678 CrossRef CAS.
- S. Tanimura, Y. Okada and K. Takeuchi, J. Phys. Chem., 1996, 100, 2842–2848 CrossRef CAS.
- U. Buck, R. Krohne and S. Schütte, J. Chem. Phys., 1997, 106, 109–115 CrossRef CAS.
- J. Brudermann, P. Lohbrandt, U. Buck and V. Buch, Phys. Rev. Lett., 1998, 80, 2821–2824 CrossRef CAS.
- Th. Häber, U. Schmitt and M. A. Suhm, Phys. Chem. Chem. Phys., 1999, 1, 5573–5582 RSC.
- Th. Häber, U. Schmitt, C. Emmeluth and M. A. Suhm, Faraday Discuss., 2001, 118, 331–359 RSC.
- K. A. Streletzky, Y. Zvinevich, B. E. Wyslouzil and R. Strey, J. Chem. Phys., 2002, 116, 4058–4070 CrossRef CAS.
- A. Bonnamy, R. Georges, A. Benidar, J. Boissoles, A. Canosa and B. R. Rowe, J. Chem. Phys., 2003, 118, 3612–3621 CrossRef CAS.
- A. Bonnamy, R. Georges, E. Hugo and R. Signorell, Phys. Chem. Chem. Phys., 2005, 7, 963–969 RSC.
- D. W. Matson, J. L. Fulton, R. C. Petersen and R. D. Smith, Ind. Eng. Chem. Res., 1987, 26, 2298–2306 CrossRef.
- J. W. Tom and P. G. Debenedetti, J. Aerosol Sci., 1991, 22, 555–584 CrossRef CAS.
- J. Jung and M. Perrut, J. Supercrit. Fluids, 2001, 20, 179–219 CrossRef CAS.
- M. Türk, P. Hils, B. Helfgen, K. Schaber, H.-J. Martin and M. A. Wahl, J. Supercrit. Fluids, 2002, 22, 75–84 CrossRef CAS.
- A. Bonnamy, D. Hermsdorf, R. Ueberschaer and R. Signorell, Rev. Sci. Instrum., 2005, 76, 053904 CrossRef.
- S. L. Kaufman, R. Caldow, F. D. Dorman, K. D. Irwin and A. Pöcher, J. Aerosol Sci., 1999, 30, S373–S374 CrossRef.
- R. Signorell, M. K. Kunzmann and M. A. Suhm, Chem. Phys. Lett., 2000, 329, 52–60 CrossRef CAS.
- M. Jetzki and R. Signorell, J. Chem. Phys., 2002, 117, 8063–8073 CrossRef CAS.
- R. Signorell and D. Luckhaus, J. Phys. Chem. A, 2002, 106, 4855–4867 CrossRef CAS.
- R. Signorell, M. Jetzki, M. Kunzmann and R. Ueberschaer, J. Phys. Chem. A, 2006, 110, 2890–2897 CrossRef CAS.
- M. K. Kunzmann, S. Bauerecker, M. A. Suhm and R. Signorell, Spectrochim. Acta, Part A, 2003, 59, 2855–2865 CrossRef CAS.
- M. Jetzki, A. Bonnamy and R. Signorell, J. Chem. Phys., 2004, 120, 11775–11784 CrossRef CAS.
- D. Hermsdorf, A. Bonnamy, M. A. Suhm and R. Signorell, Phys. Chem. Chem. Phys., 2004, 6, 4652–4657 RSC.
- M. Jetzki, D. Luckhaus and R. Signorell, Can. J. Chem., 2004, 82, 915–924 CrossRef CAS.
- M. Türk and R. Signorell, In situ characterization of drug nanoparticles by FTIR spectroscopy, in Nanotechnologies for the Life Sciences, Vol. 3 Nanosystem Characterization Tools in the Life Sciences, ed. Ch. Kumar, Wiley-VCH, Weinheim, 2005, pp. 208–240 Search PubMed.
- J. Meyer, M. Katzer, E. Schmidt, S. Cihlar and M. Türk, Comparative particle size measurements in lab-scale nanoparticle production processes, Proceedings of the World Congress on Particle Technology 3, Institute of Chemical Engineers, July 6–9, 1998, Brighton, UK Search PubMed.
- D.-R. Chen, D. Y. H. Pui and S. L. Kaufman, J. Aerosol Sci., 1995, 26, 963–977 CrossRef CAS.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, Wiley-Interscience, New York, 1998 Search PubMed.
- H. C. van de Hulst, Light Scattering by Small Particles, Dover Publications Inc., New York, 1981 Search PubMed.
- M. I. Mishchenko, J. W. Hovenier and L. D. Travis, Light Scattering by Nonspherical Particles, Academic Press, San Diego, 2000 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98, volume Revision A.7, 1998 Search PubMed.
- G. Cardini, V. Schettino and M. L. Klein, J. Chem. Phys., 1989, 90, 4441–4449 CrossRef CAS.
- R. Disselkamp and G. E. Ewing, J. Chem. Soc., Faraday Trans., 1990, 86, 2369–2373 RSC.
- R. Signorell, J. Chem. Phys., 2003, 118, 2707–2715 CrossRef CAS.
- G. Firanescu, D. Luckhaus and R. Signorell, J. Chem. Phys., 2006, Search PubMed submitted.
- Th. Häber, R. Kevorkiants, W. Thiel and M. A. Suhm, Phys. Chem. Chem. Phys., 2004, 6, 4939–4949 RSC.
- C. Steinbach, P. Andersson, J. K. Kazimirski, U. Buck, V. Buch and T. A. Beu, J. Phys. Chem. A, 2004, 108, 6165–6174 CrossRef CAS.
- T. A. Beu and U. Buck, J. Chem. Phys., 2001, 114, 7853–7858 CrossRef CAS.
- T. A. Beu, C. Steinbach and U. Buck, J. Chem. Phys., 2002, 117, 3149–3159 CrossRef CAS.
- R. Signorell and M. K. Kunzmann, Chem. Phys. Lett., 2003, 371, 260–266 CrossRef CAS.
- A. Bonnamy, M. Jetzki and R. Signorell, Chem. Phys. Lett., 2003, 382, 547–552 CrossRef CAS.
- R. Z. Bachrach and F. C. Brown, Phys. Rev. B, 1970, 1, 818–831 CrossRef.
- R. K. Ahrenkiel, J. Opt. Soc. Am., 1971, 61, 1651–1655 Search PubMed.
- J. P. Hawranek, P. Neelakantan, R. P. Young and R. N. Jones, Spectrochim. Acta, Part A, 1976, 32, 85–98 CrossRef.
- R. M. Hexter, J. Chem. Phys., 1960, 33, 1833–1841 CAS.
- M. Diraison, G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 111, 1096–1103 CrossRef CAS.
- R. W. Impey and M. L. Klein, Chem. Phys. Lett., 1984, 104, 579–582 CrossRef CAS.
- J. A. Barnes, T. E. Gough and M. Stoer, J. Phys. Chem., 1993, 97, 5495–5498 CrossRef CAS.
- R. F. Niedziela, R. E. Miller and D. R. Worsnop, J. Phys. Chem. A, 1998, 102, 6477–6484 CrossRef CAS.
- R. Wagner, S. Benz, O. Möhler, H. Saathoff, M. Schaiter and U. Schurath, J. Phys. Chem. A, 2005, 109, 7099–7112 CrossRef CAS.
- M. L. Clapp and R. E. Miller, Icarus, 1993, 105, 529–536 CrossRef.
- M. Fárník, C. Steinbach, M. Weimann, U. Buck, N. Borho and M. Suhm, Phys. Chem. Chem. Phys., 2004, 6, 4614–4620 RSC.
- D. Zimmermann, Th. Häber, H. Schaal and M. Suhm, Mol. Phys., 2001, 99, 413–425 CrossRef CAS.
- U. Buck and H. Meyer, J. Chem. Phys., 1986, 84, 4854–4861 CrossRef CAS.
- U. Buck, J. Phys. Chem., 1994, 98, 5190–5200 CrossRef CAS.
- M. Jetzki, PhD thesis, Cuvillier Verlag, Göttingen, 2005.
- S. Bauerecker, Phys. Rev. Lett., 2005, 94, 033404 CrossRef.
- B. E. Wyslouzil, G. Wilemski, R. Strey, C. H. Heath and U. Dieregsweiler, Phys. Chem. Chem. Phys., 2006, 8, 54–57 RSC.
- M. K. Kunzmann, PhD thesis, Cuvillier Verlag, Göttingen, 2002.
- D. M. Hudgins, S. A. Sandford, L. J. Allamandola and A. G. G. M. Tielens, Astrophys. J., Suppl. Ser., 1993, 86, 713–870 CrossRef CAS.
- Th. Henning, V. B. Il’in, N. A. Krivova, B. Michel and N. V. Voshchinnikov, Astron. Astrophys., Suppl. Ser., 1999, 136, 405–406 CrossRef CAS.
- L. S. Rothman et al., The HITRAN molecular spectroscopic database and HAWKS (HITRAN Atmospheric Workstation), 1996 edn., J. Quant. Spectrosc. Radiat. Transfer, 1998, 60, 665–710 CrossRef CAS.
- http: //wwwuser.gwdg.de/∼rsignor/refindex.html .
- J. Sun and P. A. Ariya, Atmos. Environ., 2006, 40, 795–820 CrossRef CAS.
- H. Schönbuchner, G. Guggenberger, K. Peters, H. Bergmann and W. Zech, Water, Air, Soil Pollut., 2001, 128, 355–367 CrossRef CAS.
- A. Li and B. T. Draine, Astrophys. J., 2001, 554, 778–802 CrossRef CAS.
- M. Schnaiter, H. Mutschke, J. Dorschner, Th. Henning and F. Salama, Astrophys. J., 1998, 498, 486–496 CrossRef CAS.
- P. Ehrenfreund, A. C. A. Boogert, P. A. Gerakines, A. G. G. M. Tielens and E. F. van Dishoeck, Astron. Astrophys., 1997, 328, 649–669.
- D. Hermsdorf, S. Jauer and R. Signorell, 2006, in preparation.
- P. Pathak, M. J. Meziani, T. Desai and Y.-P. Sun, J. Supercrit. Fluids, 2006, 37, 279–286 CrossRef CAS.
- M. Türk, B. Helfgen, P. Hils, R. Lietzow and K. Schaber, Part. Part. Syst. Charact., 2002, 19, 327–335 CrossRef.
- M. Türk, Chem.-Ing.-Tech., 2003, 75, 792–795 CrossRef.
- M. Türk and R. Lietzow, AAPS PharmSciTech, 5, Article 56, 2004 Search PubMed.
- J. W. Tom and P. G. Debenedetti, Biotechnol. Prog., 1991, 7, 403–411 CrossRef CAS.
- J. W. Tom, G.-B. Lim, P. G. Debenedetti and R. K. Prud’homme, ACS Symp. Ser., 1993, 514, 238–257 CAS.
- J. W. Tom, P. G. Debenedetti and R. Jerome, J. Supercrit. Fluids, 1994, 7, 9–29 CrossRef CAS.
- J.-H. Kim, T. E. Paxton and D. L. Tomasko, Biotechnol. Prog., 1996, 12, 650–661 CrossRef CAS.
- M. Türk, Chem.-Ing.-Tech., 2004, 76, 835–838 CrossRef.
- M. Türk and M. Wahl. Utilization of supercritical fluid technology for the preparation of innovative carriers loaded with nanoparticular drugs, in Proceedings of the International Congress for Particle Technology, PARTEC 2004, Nürnberg, March 16–18, 2004 Search PubMed.
- Kh. Hussein, M. Türk and M. A. Wahl. Preparation and evaluation of drug/β-cyclodextrin solid inclusion complexes by supercritical fluid technology, Proceedings of the 9th Meeting on Supercritical Fluids, Trieste, Italy, June 13–16, 2004 Search PubMed.
| This journal is © the Owner Societies 2006 |
