Brilliant opportunities across the spectrum
John
Evans
ab
aSchool of Chemistry, University of Southampton, Southampton, UK SO17 1BJ. E-mail: je@soton.ac.uk
bDiamond Light Source, Diamond House, Chilton, Didcot, Oxfordshire, UK OX11 0DE. E-mail: john.evans@diamond.ac.uk
First published on 24th May 2006
Abstract
Third generation synchrotron light sources provide stable, tuneable light of energy up to the hard X-ray region. The gain of a trillion in brightness as compared to a conventional laboratory X-ray source transforms the opportunities for establishing structure–function relationships. The light may be quasi-continuous or pulsed, have controllable polarisation and have coherence lengths larger than the sample size. The high brightness provides a basis for adding time and spatial resolution to X-ray scattering and spectroscopy. It may also be used to identify very specific information about the magnetic properties of atoms within materials, element specific vibrations, and local structural descriptions identified with chemical speciation. More demanding scattering and diffraction problems can be solved such as weakly scattering materials, large unit cells and structural entities. The high collimation of the source also provides enhanced spectroscopic and diffraction resolution that gives more insight into molecular, extended and supramolecular structures. The length scales can be bridged from the atomic up to that of visible light microscopy and buried features within materials can be observed with the appropriate energy. With an increased emphasis on ease of use, such capabilities are open to exploitation for chemical challenges.
1. Introduction
Synchrotron radiation sources are now well established as tools for scientific investigation.1 Initially, light was extracted parasitically from accelerators, but the provision was far from optimised in terms of access periods, source design and stability. A second generation of light sources succeeded these. Such storage rings were designed and operated as dedicated light sources, giving great improvements in experimental access and stability. The light is emitted from the bending magnets that create the quasi-circular path for the high energy electrons at relativistic velocities. It follows a broad spectral band, which can span from the far infrared, or THz region, deep into the X-ray component of the electromagnetic spectrum. Such sources provided the bases for the wider expansion of synchrotron radiation into the chemical sciences.However, the distribution of radiation from the bending magnets (normally electromagnets) of a storage ring is around its critical energy, Ec, the equipartition energy, at which point the source is close to its maximum intensity. The critical energy is a function of the magnet field, B (in T), at the electron beam, and the energy of the electron, E (in GeV):
| Ec (keV) = 0.667BE2 | (1) |
Each of the poles of a wiggler acts as an independent light source, and so aligning N poles in series will increase the intensity of the light source N-fold. This is an operationally better solution than attempting to increase the current in the storage ring by a factor of N. The spectrum from such a device, called a multipole wiggler (MPW), also follows eqn (1), and provides an opportunity both to increase the intensity of light on a sample and to modify the spectrum from that of the parent bending magnet lattice.
A third type of device consists of an array of small magnets that cause a small lateral perturbation of the electron beam. In this case the light sources are not independent and their interference gives rise to increased output at a particular energy, the fundamental E1, and at higher harmonics (E2, etc.). The deflection factor, K, distinguishes these two types of device:
| K = 0.934BλU | (2) |
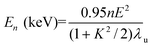 | (3) |
Major intensity gains at a sample are feasible if the insertion devices are installed; each storage ring can be fitted with a variety of these to provide a range of spectra at the facility overall. However, installing these devices has its own constraints on the design of the storage ring. Most obviously the straight sections should be sufficiently long to accommodate these IDs, thus increasing the required circumference of a storage ring. Also, to achieve the greatest benefit from an undulator source the electron beam size should be small and this path very consistent. This requires a well designed magnetic lattice with higher order focussing magnets, again increasing the optimal size of the storage ring. However, the spectral improvements are such that the present state of the art is one of these third generation sources, that is, one that is specifically designed for insertion devices (undulators or multipole wigglers). These storage rings also provide other properties of interest that go beyond merely increasing the flux on a sample of standard size. This review seeks to describe these benefits, and also their potential application to chemical sciences. It is timely, since new third generation sources will become available to user groups in the next few years: SOLEIL,2 Diamond,3 ALBA,4 INDUS2,5 SESAME,6 SuperSOR7 and the Australian Synchrotron.8
2. Characteristics of third generation storage ring light sources
The key spectral parameters for a synchrotron source are the output spectrum (flux vs photon energy), source size and divergence, time structure, polarisation and coherence.9,102.1. Output spectrum
Across the vacuum ultraviolet and soft X-ray regions, the flux plots of the SRS, as a second generation source, and existing (ESRF) and upcoming (Diamond) third generation sources are broadly similar (Fig. 1). Flux is defined as the output in photons s−1 0.1% bandwidth−1 mrad(h)−1, providing the density per milliradian of output fan extracted. Since a larger acceptance angle is normally achievable on a smaller ring, like the SRS, the three sources can provide very similar fluxes on many samples. As anticipated from eqn (1), the ring with the lowest electron energy (SRS, 2 GeV) will provide less flux at higher energies, hence the incorporation of two superconducting wigglers as wavelength shifters.11 In the infrared region, the flux is dependent only upon the beam current and is independent of the electron beam energy. | ||
| Fig. 1 Flux (photons s−1 mrad(h)−1 0.1% bandwidth−1) calculated from bending magnets on the SRS (green), ESRF (blue) and Diamond (red). Copyright Diamond Light Source Ltd, 2006. | ||
2.2. Beam size and divergence
The larger lattices of these two third generation sources create smaller electron beam emittances, ε (=σσ′). The small values of the electron beam sizes (σ) and angular divergences (σ′) result in a more tightly collimated photon beam, as reflected in the increased brightness. The brightness units used in Fig. 2 and 3 are also termed brilliance in some schools (photons s−1 mm−2 mrad−2 0.1% bandwidth−1); in those schools, brightness is presented in units of photons s−1 mrad−2 0.1% bandwidth−1. The brightness/brilliance of the three sources is presented in Fig 2. | ||
| Fig. 2 Brightness (photons s−1 mm−2 mrad−2 0.1% bandwidth−1) calculated from bending magnets on the SRS (green), ESRF (blue) and Diamond (red). Copyright Diamond Light Source Ltd, 2006. | ||
 | ||
| Fig. 3 Brightness (photons s−1 mm−2 mrad−2 0.1% bandwidth−1) calculated for insertion devices on Diamond. The undulator periodicities are shown in mm. Copyright Diamond Light Source Ltd, 2006. | ||
The effect of a multipole wiggler is to increase both flux and brightness, providing a smooth change in intensity with energy over a broad spectral range (Fig. 3). However, it can be seen that a gain of up to 106 in brightness can be derived from undulator outputs, which have very small photon beam divergences (∼10 μrad). The angular compression caused by an undulator is α 1/√N, where N is the number of periods and the intensity of the central cone of radiation down the axis of the undulator increases directly with N. The undulator plots are for varied gaps (the numbers given are the periods in mm), and the inverse relationship between energy and period is evident. The plots show the maximum brightness that can be achieved across the energy spectrum. There is an apparent discontinuity when the optimising intensity would require changing the harmonic number being tracked.
These brightness values may be compared to those displayed by laboratory sources, which spread from the order of ∼108 for a stationary anode through to ∼1010 for a rotating anode with microfocusing.10 The great increase in brightness provides for substantially increased spatial resolution in facetted samples and, in diffraction experiments, for increased resolution in interatomic distances.
2.3. Time structure
For most experiments, the light source is used in a quasi-continuous fashion. In a large storage ring like that at the ESRF (844 m circumference), the revolution time for a single bunch of electrons is ∼2.8 μs. Most filling patterns are termed multibunch, and so the light is actually received in packets of ∼20 ps duration received separated by several nanoseconds. So for measurement times in excess of 10−5 s, this is effectively a continuous source. Down to the time period of the orbital revolution, the time resolution achievable in an experiment is governed by sensitivity, detector characteristics and the intrinsic resolution of the sample initiation system (e.g. a gas pulse onto a catalyst bed or a stopped flow cell dead time).However, sources can also be operated with restricted numbers of electron bunches. For example, in its 16 bunch mode, the ESRF delivers a pulse width of 48 ps (RMS) every 176 ns. Then the bunch length provides the potential time resolution for an experiment.
2.4 Polarisation
The observer of the electron beam would see a linear oscillation of the electron path in the plane of the orbit. Accordingly, synchrotron light in the plane of the machine orbit has linear polarisation; above and below the plane the polarisation is elliptical, giving components of right and left circular polarisation.This is also the case for a conventional undulator which creates a linear oscillation. However by controlling the phasing of the magnetic arrays in an undulator (as in the helical undulator shown as HU64 in Fig. 3), then polarisation control spanning linear, circular and elliptical can be attained.
2.5. Coherence
Synchrotron sources, especially from undulators can be described as being partially coherent sources; the narrower band spread of an undulator harmonic and its narrow cone create a spread of parameter space that displays wave-like properties such as interference. The lateral (or transverse or spatial) coherence arises from the small beam size and divergence of undulator radiation. The fraction of the flux that is transversely coherent is ∝ λ2 and ∝ 1/εxεy.10 The longitudinal coherence length, lc, over which a wavelngth variation is not significant is given by lc = λ2/Δλ. The transverse coherence length is given by lt = λL/2σ, where L = distance between source and sample. Coherence lengths in the X-ray range of 10–100 μm are achievable.123. Applications to chemical systems
In addition to the improved spectral characteristics of modern storage ring sources, there are other important operational developments in accelarator physics that greatly ease the ability to carry out complicated experiments. The early second generation sources used the booster synchrotron to lift the energy of the electron beam to an intermediate level between that from the linear accelerator to that in the storage ring itself.11 So, once the full current was injected, the energy has to be ramped. This requires time and problems during ramping add to the down time to users. The current generation of sources achieve the full electron energy in the booster and so eliminate this extra step. Now also injection can be achieved without closing the shutters at the front ends at the beamlines, so injection is essentially a top-up process of one or two minutes restoring 10–20% of the current (at the ESRF).13 Then the optical elements do not have a period of cooling and rapid reheating during a cycle of beam dump and refill. This improves the stability and reproducibility of experiments, which is vital for time and spatially resolved experiments. The top-up mode has been taken a stage further at the advanced photon source14 where top-up occurs at frequencies of multiples of 2 min and a quasi-constant current is maintained. This does create an eccentric path for a few turns and allowance may be required for a few classes of time resolved experiments. The incorporation of beam position feedback systems has also dramatically improved beam stability.3.1 Spatial discrimination in complex materials
The tightly collimated beams emanating from the third generation sources may be used to provide conventional measurements on voxels within a complex sample. Hence 2- or 3-D images may be reconstructed to map elements, oxidation states, crystalline phases or molecular species. An array of focussing options is available to match the experiments in question, such mirrors, curved crystals, compound refractive lenses, capillaries and zone plates. Microprobes with micron resolution are attainable in the hard X-ray region, and a soft X-ray microscope with spatial resolution down to 15 nm has been reported.15Some synchrotron imaging experiments are extensions of laboratory instruments. For example, the enhanced brightness even in the infrared region provides a greatly improved measuring time at the diffraction limit of resolution.16 For example, with a 6 × 6 μm spot, the central medulla (5–10 μm) of a human hair (50–100 μm) could be spectroscopically characterised and imaged on its characteristic bands. Infrared microspectroscopy can be applied on very small samples under a controlled atmosphere. This is particularly important for the investigation of rare samples, for example of cultural heritage importance. An example is the study of skin fragments from the leg of an Egyptian mummified woman held at the anthropological museum of the Faculty of Medicine at the University of Athens.17 This showed that the best preserved part of the skin was the outer (20 μm) layer, which had some protein content. In some lower layers, spots of crystallised palmitic acid and others of calcium oxalate were detected.
Another laboratory technique, energy dispersive X-ray fluorescence can be enhanced by high brilliance sources. For example, the fluid inclusions from gold-quartz veins from the Italian Alps form an analytically challenging problem, as they are about 100 μm in size within the quartz and contain a mixture of trace elements. A Fresnel zone plate was used to focus radiation at 12.5 keV into a 2 × 7 μm spot delivering ∼1010 photons s−1.18 This energy allows this buried sample to be probed, and showed in particular enhanced arsenic levels (∼147 ppm) in the inclusion as compared to the quartz matrix, with copper and zinc also present. The arsenic was not homogeneous in the inclusion, being absent from a CO2 bubble trapped within the aqueous inclusion.
On the same beamline at the ESRF (ID22), a geological sample from the very large Popigai meteorite impact crater in Russia was also investigated by X-ray fluorescence (using compact refractive lens as focusing element to 2 × 4 μm spot delivering 5 × 109 photons s−1 at 20 keV energy).19 A 70 μm transparent carbonaceous platelet was studied by Raman spectroscopy as well as by X-ray techniques, which also utilised the microfocus beam for X-ray diffraction. A carbon containing grain was identified within a silica host (quartz and cristobalite). Rastering across this platelet with the microbeam located three crystallographic phases. Two are the known carbon forms of graphite and lonsdaleite, a hexagonal form of diamond. But the third phase of hard carbon appears to be a new cubic phase (space group Pm3m), presumably formed under the extreme conditions during the impact some 36 million years ago.
Microfocus diffraction was combined with microfocus XANES (X-ray absorption near edge structure) to analyse particles of nuclear fuel obtained in the vicinity of Chernobyl after the explosion in 1986. X-ray absorption spectroscopy is almost entirely a technique carried out at synchrotron sources, since it requires a tunable X-ray source; the brehmstrahlung from a laboratory X-ray source is not competitive. The position and structure of the near edge region varies with the oxidation state, ligand donor set and coordination geometry. As a spectroscopic technique it may be applied to glassy as well as crystalline samples. While X-ray fluorescence can provide maps of elemental composition, XANES can map chemical speciation (as does IR microspectroscopy for appropriate samples). The uranium L(III) edge (at 17.2 keV, due to the photoionisation of a 2p electron) is sensitive to the oxidation state and so could be used to probe the chemical changes to fuel particles after the explosion and the ensuing fire.20 The wind directions took particles released in the blast to the west of the site, and subsequently deposition during the fire was to the north. The distribution of uranium in the particles is shown in Fig. 4, presented as 3-D microtomographs. The first particle has an even distribution of uranium, with the small voids possibly due to fission gases, however the material deposited after the fire has a much more open structure. Microfocus powder diffraction indicated that the “west” particle gave only weak patterns, mostly of UO2. However the “north” particle appeared to be a mixture of U3O8 and U2O5. The micro-XANES measurements confirmed an increase in the mean oxidation state in the particles deposited after the fire. However, during the explosion the outer layer of the (west) particle appears to have been reduced to an oxidation number of ∼2.5, possibly by the graphite rods in the reactor.
 | ||
| Fig. 4 Exploded 3-D visualisation of the uranium distribution in particles from Chernobyl (a) from the west of the site and (b) from the north of the site. Reprinted from Nucl. Instrum Methods Phys. Res., Sect. A, 467–468, B. Salbu, T. Krekling, O. C. Lind, D. H. Oughton, M. Drakopoulos, A. Simionovici, I. Snigireva, T. Weitkamp, F. Adams, K. Janssens and V. A Kashparov, High energy X-ray microscopy for characterisation of fuel particles, 1249–1252, Copyright 2001, with permission from Elsevier (ref. 20). | ||
The effectiveness of speciation by combining X-ray fluorescence, micro-XANES and IR microspectroscopy is exemplified by a study of microfossils and contemporary microbial filaments.21 With a sub-micron sized beam, the oxidation states of sulfur could be mapped on a sub-cellular scale by comparison with some model compounds (Fig. 5a). The high sensitivity of the sulfur XANES pattern to oxidation state provides a valuable chemical speciation teachnique, and reveals a relatively low level of the high oxidation state sulfur in the microfossil.
 | ||
| Fig. 5 Sulfur K-edges XANES of a microfossil and bacterial filament against the spectra of model compounds (b) XANES intensity maps of a microfossil and bacterial filament at energies typical of S0, SIV and SVI. Reprinted from Geochim. Cosmochim. Acta, 68, J. Foriel, P. Philippot, J. Susini, P. Dumas, A. Somogyi, M. Salomé, H. Khodja, B. Ménez, Y. Fouquet, D. Moreira and P. López-García, High-resolution imaging of sulfur oxidation states, trace elements, and organic molecules distribution in individual microfossils and contemporary microbial filaments, 1561–1569, Copyright 2004, with permission from Elsevier (ref. 21). | ||
3.2 Magnetic properties of materials
The X-ray magnetic circular dichroism (XMCD) effect provides a means of monitoring the magnitude and distribution of magnetic moments. Most typically, it is applied to the photoionisation of the p core electrons, as in the L(III) and L(II) edges. For the 3d transition elements these occur in a soft X-ray range (0.4–1 keV). The L(III) edge creates a 2p53/2 configuration in its excited state, whilst the higher energy L(II) edge is associated with the lower j value, viz. 2p5½. In the XANES region there are transitions from the core to the valence band which, by the dipole selection rule, will be dominated by transitions to 3d orbitals. So for an Fe(II) centre, the excited states will be based around configurations of 2p53d7. Unlike the situation of the ionisation of the 1s electron at the K-edge, these two orbitals interact significantly and the coupling between them must be considered in order to explain the observed spectra.22 The observed spectra are a function of the core and valence spin–orbital coupling constants, the interelectronic interactions (Coulombic and exchange) and also the ligand field. So these L edge spectra are sensitive to the electronic configurations of the 3d ions, and, due to the coupling between the 2p and 3d orbitals, the patterns are different for the L(III) and L(II) edges. As the angular momentum of the photoelectron associated with these two types of transition is coupled to the spin (in opposite senses), right and left hand circularly polarised photons will transfer to states of opposite spin moment in the empty conduction band.23 Hence, when the magnetic degeneracies are lifted by a field, these dichroism effects will become evident. The magnitude of this dichroism can provide a value for the orbital moment in ferro- and ferri-magnetic materials,24 and the ratio of orbital/spin moments in other paramagnetic materials.25 Antiferromagnetic materials can be probed by linearly polarised X-radiation.23,26Since the magnetic features are being sensed by element specific transitions, the moments on each observed element are also distinguished; generally magnetic properties are not disaggregated in this way. An example of this is given in the study of Pd/Fe multilayers using the palladium L(II) and L(III) edges.27 The palladium atoms directly interfaced to iron had an induced moment of 0.4 J T−1, which contained very little orbital contribution. This moment fell away with the number of intervening layers, and was reduced to zero after 4 layers.
Magnetic domains in ferromagnetic materials may also be imaged by monitoring the photoemission on exposure to the circularly polarised X-radiation. This imaging technique uses the electron yield to monitor the X-ray absorption and photoemission microscopy to image the result. An example is a study of a thin layer (10–20 ML) of iron on a Ag(100) surface, also incorporating a sub-monolayer overlayer of manganese.28 The magnetic properties of both the Fe and Mn can be imaged independently using their respective L(II) and L(III) absorption edges (Fig. 6). The manganese pattern can be seen to mirror that of the iron (110) substrate, but with the opposite directions, indicating an antiferromagentic relationship to the iron domain structure.
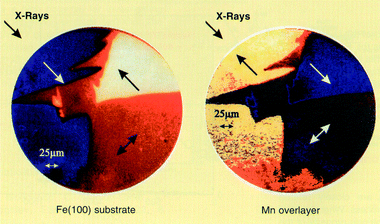 | ||
| Fig. 6 Element specific imaging of magnetic domains of Mn/Fe/Ag(100) using the L(III) edges of Fe (left) and Mn (right). The arrows indicate the direction of magnetisation. Reprinted figure with permission from J. Dresselhaus, D. Spanke, F. U. Hillebrecht, E. Kisker, G. van der Laan, J. B. Goedkoop and N. B. Brookes, Phys. Rev. B, 56, 5461 (1997). Copyright 1997 by the American Physical Society (ref. 28). | ||
In the medium X-ray region (3–10 keV) the normal linear polarisation of synchrotron radiation can be converted into circular polarisation using a diamond phase plate device and this radiation may be used to probe magnetic materials by XMCD or diffraction.29,30 Although diffraction of X-rays is dominated by the lattices of electron charge density, there are also scattering mechanisms from the magnetic moment of the electrons; there are terms which depend upon both the spin and orbital moment.31–33 Normally in a ferromagnetic material the effects are small, but in antiferromagnetics the superlattice peaks are observable due to the high signal–background ratio achievable using a synchrotron source. The tunability of the light source allows diffraction to be studied at the energies of an absorption edge of one of the diffracting elements. The change in scattering factor at the absorption edge (anomalous scattering) is often used to assist in structure determination. However, a large enhancement in the magnetic scattering and a complex polarisation dependence near the L(III) absorption edge of holmium were observed,34 and ascribed to X-ray resonance exchange scattering.35 These enhancements are of the order of 10–100 for the L edges of lanthanides but in the region of 104–106 for the M edges of the actinides.33 Like the XMCD effect, the enhancement is from electronic transitions sensitive to the magnetisation of the partially occupied valence orbitals. In total this allows the separation of spin and orbital contributions to magnetism and also the determination of the spin density distribution. For example in a study of antiferromagnetic materials of the type U(As1−xSex) very large resonant X-ray scattering enhancements were noted around both the As and Se K-edges.36 Even though the magnet moment predominantly resides at the uranium, this effect implies a significant mixing of the uranium 5f and the anions’ 4p orbitals.
3.3 X-Ray coherence effects
As described above, the coherence length in the X-ray region can be larger than the size of the crystallites providing diffraction patterns. So the normal diffraction “spot” from this coherent wave is an interference pattern which contains information about the structure of the crystal planes causing the diffraction. This has been reported for gold nanocrystals that were formed from high temperature treatment of an evaporated polycrystalline film.37 At 1 × 3 μm, this particle was comfortably smaller than the transverse (5 μm) and longitudinal (6 μm) coherence lengths on the beam line at the APS. The 3-D image of the diffracting particle was reconstructed from a series of interference patterns and showed texture inside the crystal that could be ascribed to regions of internal order and defects.In a direct analogue of dynamic light scattering to study colloidal materials, X-ray photon correlation spectroscopy may be used to investigate the dynamics of mesoscopic materials. In one example, the Brownian motion of colloidal gold suspended in glycerol was monitored. The scattering from particles of mean radius 27 nm was monitored and the time constant for their motion estimated.38 Since this report, studies of X-ray speckle patterns have become more common, with the variation in the random interferences providing information about the dynamics of the materials. For example, the dynamic properties of a liquid crystal (8OCB) have been investigated at temperatures near to the nematic-to-smectic A phase transition.39 Gradual formation of smectic layers in the nematic layers could be monitored and the viscosity behaviour of the complex fluid studied.
Atomic resolution imaging by holographic methods is a very appealing target.40 The aim of atomic imaging of a single particle which does not have long range crystallographic order is of widespread significance for characterising functional materials. In this technique, a single energy X-ray fluorescence pattern is monitored over a range of angles. The atom is acting as a coherent light source generating the holographic pattern from scattering from its neighbours. An alternative arrangement, multi-energy X-ray fluorescence holography, uses the fluorescent atom as the detector of monochromatic waves scattered from its neighbours.41 A 2-D image of the atoms in haematite up to a distance of 8.9 Å was achieved in this way. Further developments allowed a 3-D image of the atomic arrangement in a CoO crystal with 0.5 Å resolution to be realised.42 In the quasicrystal alloy Al0.84Pd21Mn8.6, the atomic distribution around the manganese could be imaged by monitoring the Mn Kα fluorescence.43 This showed the icosahedral geometry around manganese and also the first five or six atomic shells (Fig. 7).
 | ||
| Fig. 7 3-D imaging of the quasi crystal Al70.4Pd21Mn8.6 local atomic structure viewed from manganese fluorescence. Top: hologram, bottom: real space image. Reprinted figure with permission from S. Marchesini, F. Schmithüsen, M. Tegze, G. Faigel, Y. Calvayrac, M. Belakhovksy, J. Chevrier and A. S. Simionovici, Phys. Rev. Lett., 85, 4723 (2000). Copyright 2000 by the American Physical Society (ref. 43). | ||
3.4 High resolution and weak effect studies
The high brightness of third generation sources can be used to prise out extra detail from a technique. Increasing the signal/background ratio substantially can increase the reciprocal space range in a diffraction pattern that is analysable and the enhanced collimation can improve the resolution within that range. The combined effect is that larger and more weakly scattering structures can be analysed to a higher spatial resolution. For example, structural detail of a Blue Tongue virus (BTV-10) was obtained from a unit cell of length 1600 Å, and a cell volume of >109 Å3 with only ∼300 unit cells being illuminated.44 A refinement of a polymorph with a smaller unit cell (half of the virus core) was solved to a resolution of 3.5 Å from about 3.2 M unique reflections.45 Although smaller in scale, sub units of the ribosome, complexes of RNA and proteins, still present challenges for crystallisation and structural units of the order of molecular mass 106, and high resolution structures are now feasible.46High resolution diffraction can also be used to show subtle and important effects in less complex molecular entities. The ability to obtain high resolution powder diffraction patterns at high energies (40 keV in this example) means that the residual stresses in a structural unit like a welded aluminium joint can be monitored by observing the changes in cell constant by resolving variations in 2θ of 0.001°.47 At still higher energies (100–300 keV), penetration through heavier metals such as titanium and steel becomes sufficiently high for strain mapping in bulk samples of these materials.48 A sample of 316 stainless steel was mapped using a 0.4 × 0.4 mm beam with counting times of 50 s for each of 800 observations over a 14 × 10 mm area. By total curve fitting, an uncertainty in lattice parameter of 10−5 was also achieved by energy dispersive diffraction. Using hard X-radiation the lattice parameter variation of a silicon crystal under an ultrasonic excitation has also been achieved with a 20 ns time resolution.49 The compression and dilation caused changes in the Bragg reflection angle of 2 arc.seconds.
Inelastic X-ray scattering can provide information about energy levels of various types within a material. In a parallel experiment to the more conventional Raman spectroscopy using visible excitation, inelastic scattering of a hard X-ray may be due to the X-ray absorption spectra of a lower Z element. In one study on water and ice, an exciting radiation of 9.686 keV was employed to derive the oxygen K-edge XAFS pattern.50 In this way the XAFS spectrum from bulk water can be derived (attenuation length ∼1.5 mm), obviating the normal surface selectivity intrinsic to studies using the oxygen K-edge (0.543 keV, attentuation length 500 nm). The inelastic effect is weak, and spectra with 2 eV resolution (using a Si(666) reflection) over a 200 eV range required 24 h collection time, but afforded the O⋯O first neighbour distances (287 pm). With higher order reflections close to a back scattering geometry, higher energy resolution can be achieved. So with 170 meV resolution, inelastic X-ray scattering (IXS) has been employed to probe the plasmon spectra of lithium solutions in ammonia, showing features with energy losses of ∼2 eV.51 Energy resolutions of ∼2 meV (∼16 cm−1) have also been achieved on such solutions, and the vibrational properties of these solutions could be studied, and could be modelled based upon the [Li(NH3)4]+ ion.52
Also, by analogy to resonant Raman spectroscopy using visible light as the excitation method, there is a family of resonant inelastic X-ray scattering (RIXS) techniques based upon photon in and photon out processes. A double spectrometer is employed to delineate the energy of the exciting photon and also to analyse the energies of the emitted photons. This experimental arrangement is a development from the conventional fluorescence method of indirectly measuring an X-ray absorption spectrum. For dilute and/or thin samples, a better signal/background ratio can be achieved by measuring the fluorescence yield from the sample as opposed to transmission through it. This may either be achieved with a detector with little or no energy discrimination, combined with filters, or using energy selective solid state detectors. In practice such detectors have a resolution of ∼200 eV and are principally used to separate the fluorescence from the elastic (Raleigh) and Compton scattering. However, with a crystal analyser, specific fluorescence channels can be identified and monitored. One reason to do so is to improve the resolution of the X-ray absorption near edge features of the excited atom.53 In an early study, the LIII edge of dysprosium (7.790 keV) was monitored for the metal, its oxide and its nitrate. The absorption process creates a core hole in the 2p orbital and the resolution of the XANES features is limited by the Heisenberg uncertainty broadening of this core hole (∼4 eV). The dominant fluorescence process (Lα1) will leave a 3d core hole, with a longer lifetime and smaller atomic shell width (1.4 eV). By monitoring this specific channel, close to the absorption edge, the line width is not limitted by the L shell core hole. The narrower line reveals features near the edge considered to be 2p–4f transitions. Such additional detail greatly adds to the structural discrimination feasible using XANES measurements.
With a fixed incident energy at or above the energy of the absorption edge, the X-ray emission spectrum (XES) of a sample may be measured by scanning the energy of the fluorescence signal with the second spectrometer. As compared with X-ray photoelectron spectroscopy (XPS), which requires energy analysis of the photoelectron, the XES technique has a distinct advantage. It is compatible with a much wider range of representative samples and sampling environments, and the sampling depth is set by the X-ray attenuation length rather than the electron escape depth.
Hence the chemical shifts of the XES lines could provide information about oxidation states. The chemical shifts may be muted since both enegy levels in the transition will undergo shifts. However, these dependencies differ with the source of the electron causing the fluorescence. For a series of manganese compounds the weaker Kβ fluorescence lines involving the 3p orbitals show more significant variations than the Kα (involving the 2p), as a function of ligand, oxidation state and spin state.54
When the energy of the exciting X-radiation passes through the absorption edge region, specific emissions arise in a correlated way, known as resonant inelastic X-ray scattering (RIXS), or X-ray resonance Raman spectroscopy.54,55 The term RIXS is used for different experimental layouts. In the resonant Raman spectroscopy, a series of spherically bent collecting crystals can be used to increase the solid angle collected and thus improve the signal/noise ratio. Alternatively, a single detector can be used at varied scattering angle and this can be used to establish the q vector of the inelastically scattered radiation at a specific photon energy. The results described here are more spectroscopic than scattering in nature. Plots can be presented displaying either the emission energy or the final state (transfer) energy (transfer energy = incident energy − emitted energy) but they depict specific transmissions that can provide still more detailed information about chemical and electronic structure.
The RIXS features of a series of manganese complexes are presented in Fig. 8.56 There is a strong dependence upon oxidation state, with these pre-edge structure moving to higher energies with increasing oxidation state. The spectral shape is highly dependent upon the crystal field splitting, and the features for MnO could be reproduced well using a 10Dq value of 1.1 eV.
 | ||
| Fig. 8 Surface plots of 1s2p RIXS spectra of a series of manganese complexes from scans of the incident X-ray beam near the K absorption edge and the emission of the Kα1 of manganese. Reprinted from J. Phys. Chem. Solids, 66, P. Glatzel, J. Yano, U. Bergmann, H. Visser, J. H. Robblee, W. W. Gu, F. M. F. de Groot, S. P. Cramer and V. K. Yachandra, Resonant inelastic X-ray scattering (RIXS) spectroscopy at the Mn K absorption pre-edge—a direct probe of the 3d orbitals, 2163–2167, Copyright 2005, with permission from Elsevier (ref. 56). | ||
If there are resolvable emissions that may be attributed to a particular chemical environment, then this may overcome one of the tangible difficulties in the use of EXAFS to probe chemical mixtures. Since the scattering curves extend over several 100 eV, they overlap and so the analysis must be framed around the average of all sites of the absorbing element. Site selective EXAFS has been achieved using the different Kβ emissions of the two iron sites in Prussian Blue, Fe4[Fe(CN)6]3·xH2O.57 The energy of the most intense Kβ emission for low spin Fe(II) and high spin Fe(III) were identified as 7.0582 and 7.0614 keV, respectively, using K4Fe(CN)6 and Fe2O3 as reference samples. The emission maximum for Prussian Blue itself at 7.0598 keV is close to the weighted mean of these two contributions. X-Ray absorption spectra were recorded at each of the three energies with a collection time of 75 min each. In this quite favourable case, analysis of the EXAFS curves of the two sites could be separated, but the weightings of the components in the Prussian Blue spectrum implied that the emission band of the Fe(III) site is slightly different from that of Fe2O3, as might be expected. Nevertheless, the data did show the Fe-ligand distances as well as the Fe⋯Fe separation (∼5.1 Å).
The energy of hard X-radiation from a synchrotron source not only matches core to valence transitions, but also some nuclear energy levels. The most utilised transition in Mössbauer spectroscopy, that between I = 1/2 and 3/2 for 57Fe, occurs at 14.4 keV (similar to the K absorption edge for Kr). The radioactive Mössbauer source will emit in all directions, so the high directionality of synchrotron radiation could have experimental advantages since it can be focussed on small samples, such as those at high pressure in diamond anvil cells. Also, since the synchrotron source is tunable, nuclear transitions that do not have viable radioactive sources may also be studied.58 The core synchrotron technique is nuclear resonant forward scattering (NFS) in which synchrotron radiation is used in a pulsed mode, and the quantum beats of the nuclear transitions (the lifetime of the 57Fe excited state is 141 ns) are measured. From these patterns the isomer shift and hyperfine splittings can be extracted. Again, analogous to resonance Raman spectroscopy, there is the phenomenon of nuclear inelastic scattering (NIS), or nuclear resonance vibrational spectroscopy (NRVS), where there is transfer of energy to the vibrational levels associated with the atom undergoing the nuclear transition. This information is detected at 90° to the sample, whereas the NFS signal is in transmission geometry.
In principle this provides isotope selective vibrational information, and thus could be used to identify modes that are shrouded in the complexity of a full infrared spectrum. This technique could therefore be correlated with conventional Raman spectra to identify bands in myoglobin and cytochrome f that involved motion of the iron atoms.59 Hence, the force field for the Fe-porphyrin unit can be refined. The Fe–C and δ(Fe–C–O) modes, previously established by Raman spectroscopy, can be identified at 502 and 572 cm−1 by NIS.60 Low temperature photolysis causes these bands to be lost, and Fe–N stretches to the porphyrin (251 and 267 cm−1) and histidine (234 cm−1) identified. The two porphyrin modes are thought to show the splitting of the in-plane stretches indicating a distortion of the 4-fold symmetry of the porphyrin by the protein chain.
3.5 Time dependent studies
The extra flux on the sample available in a 3rd generation synchrotron source may be used to reduce the acquisition time to allow physical and chemical processes to be monitored. In terms of timescales, there are three regimes that are set by the rotation time of a bunch of electrons in a storage ring (∼10−6 s) and the length of the bunch (∼10−11–10−12 s).The first regime is when the acquisition time of a measurement is significantly longer than the rotation time. The source is then acting as a quasi-continuous one, and the filling mode of the storage becomes relatively unimportant. So multibunch modes may be favoured if they provide higher currents (and hence light fluxes) and stable beams. Even in this mode many chemical processes can be probed with appropriate sampling arrangements.61 For example, the dead-time of a stopped flow cell, of the order of 1 ms, provides a good match for the more rapid experiments that can be performed without the requirement to synchronise the electron bunch to the gating of the experiment. So stopped flow XAFS was demonstrated over 15 years ago, using an energy dispersive technique to provide parallel acquisition of the whole X-ray absorption spectrum of interest.62 This technique was applied to the activation of nickel complexes by aluminium alkyls thus generating homogeneous catalysts for alkene oligomerisation.63 Such processes occur over a timescale of the order of seconds; the new nickel complexes could be identified by XAFS, but no new intermediates could be observed. However, by choosing a very reactive substrate for oxidative addition, an intermediate was observed in the two-step addition of CH3SO3CF3 to [IrI2(CO)2]−. However, the EXAFS features were not well enough defined to derive structural information about the intermediate, this being the added value of the technique. This requires a very flat background and high signal/noise ratio. This was achieved in another iridium system, namely the inner sphere electron transfer between [IrIVCl6]2− and [CoII(CN)5]3−.64 The bridged complex [Cl5IrClCo(CN)5]5− was largely formed by the completion of the first spectrum, but analysis of the suite of time resolved spectra, over a period of ∼6 s, showed there to be two components: the bridged intermediate and the iridium product, mainly [IrIIICl6]3−.65 The environment around the iridium is little changed in this process, and simultaneous monitoring of the reaction by UV-visible spectroscopy was utilised both to correlate with literature data and also to verify the electron transfer steps. The intermediate could be identified by changes in the XANES features and a small but measurable change in the Ir–Cl distance and the associated Debye–Waller factors.
The combined techniques approach has also been employed to monitor the de-activation processes of organopalladium complexes into palladium clusters and, eventually, palladium black, using a stopped flow cell.66 Here a diode array spectrometer was also used to monitor the UV-visible spectrum and this readily allowed palladium dimers and trimers to be identified during the clustering process. While the XAFS spectra alone could directly observe the development of Pd–Pd bonds, establishing the nuclearity within a mixture of species is not clear cut without this second technique.
The concomitant monitoring of the structure of a heterogeneous catalyst with its activity allows a closer marrying of structure and function, since it is clear that the temperature and gas composition over a catalyst bed can rapidly change the constitution of a supported metal, as for Rh/Al2O3 under NO and H2.67 Under conditions of high activity, the rhodium is in a metallic form, and selectivity to the formation of N2 is high. However, to achieve this, an activation temperature is required and the stoichiometry of the gas mixture must not have NO in excess. Even in H2 rich conditions, the rhodium remains oxidised by NO until a threshold temperature, at which point reduction occurs with the evolution of N2O. Similar techniques have been applied to the CO/O2 reaction catalysed by the same material.68 Under CO rich conditions the metal is partially in an oxidised state as Rh(CO)2, whilst the environment is akin to Rh2O3 under an oxygen rich environment. Catalysis can be effected under both composition regimes, but the onset of catalysis occurs at a lower temperature under the oxidising environment. The active phases are considered to be a mixture of small metallic cores with an oxidic shell. Since O2 was found to oxidise the metallic particles within an exposure time of 1 s at room temperature, time resolved studies on a faster timescale than that are necessary to track the structural changes.
Adding additional structurally sensitive techniques will again enhance the identification of components in the catalyst system, thus diffuse reflectance infrared spectroscopy69 and Raman with UV-visible spectroscopies70 have been appended to energy dispersive XAFS. The vibrational data can identify ligand (adsorbate) sites. For example, the mixture of CO and NO were shown to create Rh(CO)2 readily at room temperature.69 Only once a temperature was reached that this complex begins to break down, with the rhodium converting to small metal particles, did the catalysed reaction ensue. In these studies the repetition rate for the 3 techniques was ∼60 ms.
As the timescale of measurement is decreased towards 10 μs, then synchronisation with the electron beam of the sortage ring becomes essential since most filling regimes in the storage ring are non-uniform. At the 1 μs level, the time potential resolution suddenly changes. Synchronisation with the orbiting electron beam to a bunch of electrons then means that the limit on time resolution is the bunch length of the electrons (or positrons), which may last for 10−11–10−10 s. The gap to the next bunch gives the maximum repetition rate of the experiment. For such experiments storage rings operate in single, few (∼4) or hybrid (1 single bunch opposite a multibunch segment) modes.
One approach to time resolved diffraction is to maintian the sample at low temperatures to extend its lifetime and to maintain the transient state by repeated excitation. In one such study, on [{3,5-(CF3)2pyrazolate}Cu]3, a phosphorescent molecule with a lifetime of 53 μs at 17 K, was replenished by pulsed laser operating at 12 kHz repetition rate and sampled by a chopped X-ray pulse of 18 μs duration.71 So synchronisation could maximise the difference between light-on and light-off measurements. The diffraction measurements showed that an intermolecular Cu⋯Cu separation was reduced by 0.56 Å as weakly bonded dimers are formed in the excited state.
The alternative is a pump–probe technique with varying delay times, and this has been applied at the photodissociation of CO from Mb–CO.72 Excitation utilised 7.5 ns pump pulses (630 nm) and the probe was a single X-ray bunch of 150 ps duration with delays of under 1 μs. Between 3 and 30 exposures were required to obtain viable Laue diffraction patterns of the irradiated crystals. The CO was found to migrate to a primary distal site away from the iron atom within 1 ns. Migration to a secondary site gave it a maximum occupancy after 100 ns, that decays with a half life of ∼10 μs. CO molecules then diffuse out of the protein into the solvent prior to a recombination step. These results have been used to create a movie graphic of the CO relocations.
The total scattering from a 60 mM solution of 1,2-C2H2I2 in CH3OH was recorded at 88 keV (0.141 Å) to achieve a high q range (23 Å−1) to maximise the resolution of interatomic distances derived from the scattering pattern.73 The scattering due to the solvent was extracted providing not only the C–I bond length but also the non-bonding C⋯I (3.1 Å) and I⋯I separations. This latter distance (5.1 Å) demonstrated the predominance of the anti conformer. When high stability and reproducibility are achieved, it is possible to derive difference patterns from the overlapping scattering curves of excited and ground state species in solution.73–77
The change in structure of the related molecule, CH2I2, upon irradiation was monitored on a 50 mM solution at 16.22 keV, following excitation by 100 fs laser pulses at 267 nm.75 For both di-iodo-methane and -ethane the time resolved difference scattering patterns for the excited states were discernible over a q range of 8 Å−1.74,75 For CH2I2 the major photochemical pathway is dissociation into the radicals CH2I˙ and I˙, with a minor pathway to form CH2I–I, which has a half life of ∼4 ns.75 Loss of I˙ was also evident from 1,2-di-iodoethane. Calculations indicated that the bridged isomer of CH2I˙ would be more stable than the anti one, with a I–C distance of 3.1 Å, and this provides a better fit of the scattering curve.74 An intermediate, (μ-I–I)(CH2)2 is the dominant species in the 10−10 to 10−6 s time region, before loss of I2 results in ethene formation. The combination of theory73 and experiment74 provides a model for this intermediate with an I–I distance of 2.7 Å and distance from the carbons to the bridging I atom of 3.3 Å. The photo-induced chemistry is depicted in Fig. 9.
 | ||
| Fig. 9 Schematic of the photochemical reactions of 1,2-C2H4I2 in methanol solution from time resolved X-ray scattering. Reprinted with permission from H. Ihee, M. Lorenc, T. K. Kim, Q. Y. Kong, M. Cammarata, J. H. Lee, S. Bratos and M. Wulff, Science, 2005, 309, 1223. Copyright 2005 AAAS (ref. 74). | ||
Thermal expansion of the methanol solvent cage was clearly evident at 100 ns after photolysis, resulting in a warming of ∼5 °C after 1 μs.75 Similar experiments have also been reported on photoexcited iodine in CH2Cl276 and CCl4.77 In the I2 case, the difference pattern between photolysed and non-photolysed solutions shows reduction in scattering due to the I–I separation of 2.7 Å; this reduction reaches a maximum after 200 ps.76,77 Some of the I2 can be observed in excited states (I–I 3.2 Å). The difference in scattering due to the changes in I–I scattering is reduced by 1 ns after excitation and is eliminated by 1 μs.77 The change in scattering is then entirely ascribed to losses of Cl⋯Cl interactions (3.9 and 6.2 Å). In this microsecond time regime, the energy in the hot iodine molecules and atoms that is released on reforming the ground state of I2 has been transferred to the solvent, also resulting in changes in the intermolecular Cl⋯Cl separations. For the solvent to relax will require considerably longer than a microsecond, giving a boundary condition to the repetition rate of some experiments.
Not only in diffraction and scattering is there a drive to derive structural data on short lived transients. The journey for X-ray absorption spectroscopy down from millisecond through to sub-picosecond experimentation has been thoroughly reviewed recently.78 This technique has been used to study the well-established photophysics of [Ru(bipy)3]2+.79 The Ru L(III) edge (2.84 keV) was chosen, which has a prominent white line due to allowed 2p → 4d transitions. However, the relatively soft edge employed does give a high degree of absorption from the solvent (water). Nevertheless, spectra were acquired using 100 ps bunches of 500–1000 photons from a bending magnet source. Using a 1 kHz repetition rate for light-on and light-off (interdigitated) spectra, the XANES features of the phosphorescent transient 3[Ru(bipy)3]2+ could be derived in a 10 min total acquisition time (2500 pump–probe shots) (Fig. 10). The features in the XANES region are very similar in position and magnitude to those of [Ru(bipy)3]3+, consistent with the MLCT nature of this excited state, which approximates to 3[RuIII(bipy)−(bipy)2]2+. This experiment used a relatively high concentration of complex (80 mmol l−1) for a photophysics or photochemistry experiment, but if the experiment were performed using an insertion device the extra flux on the sample could be used to reduce either the concentration of the sample and/or the acquisition time, by sectioning the light within the time span of a single electron bunch.
![(a) Static Ru L(iii) XAFS of aqueous [Ru(bipy)3]n+, (b) the difference spectrum of the excited state 300 ps after the laser pump pulse and (c) the spectrum of the phosphorescent state (solid) and the ground state (dashed). Reprinted figure with permission from M. Saes, C. Bressler, R. Abela, D. Grolimund, S. L. Johnson, P. A. Heimann and M. Chergui, Phys Rev. Lett., 90, 047403 (2003). Copyright 2003 by the American Physical Society (ref. 79).](/image/article/2006/CP/b604369k/b604369k-f10.gif) | ||
| Fig. 10 (a) Static Ru L(III) XAFS of aqueous [Ru(bipy)3]n+, (b) the difference spectrum of the excited state 300 ps after the laser pump pulse and (c) the spectrum of the phosphorescent state (solid) and the ground state (dashed). Reprinted figure with permission from M. Saes, C. Bressler, R. Abela, D. Grolimund, S. L. Johnson, P. A. Heimann and M. Chergui, Phys Rev. Lett., 90, 047403 (2003). Copyright 2003 by the American Physical Society (ref. 79). | ||
One method to probe within the electron bunch envelope has been to use a streak camera which has been triggered by a 100 fs laser pulse timed by the master clock of the electron storage ring.80 A 2 ps slice could be picked out of the 70 ps bunch width from the ALS. The intensity of the diffraction pulse from the bending magnet source indicated ∼1500 diffracted photons (of energy 5 keV) per pulse. A time resolved X-ray diffraction pattern of laser excited InSb crystals has been recorded with this instrumentation.81 A CCD camera captured the output generated by a streak camera. The intensity of diffraction spots near the InSb (111) reflection was measured with a 3 ps time resolution, with each pattern taking 1 minute to acquire (i.e. 60 000 shots). Laser excitation (150 fs pulse, 800 nm) caused an oscillation of the intensity of peaks (∼0.05 THz) displaced from the Bragg reflection of the unexcited material. The laser induced strain in the crystal was observed to propagate with the velocity of sound within the crystal.
Alternatively the source bunch itself may be “sliced” by copropagating a femtosecond laser pulse with a stored electron beam in a resonantly tuned wiggler (Fig. 11).82 The modulated electron slice becomes separated from the rest of the bunch and can be directed towards a beam line while the bulk of the pulse follows the normal track around the storage ring. Hence the bending magnet radiation of the displaced slice may be separated from that of the rest of the bunch. It was estimated that 20% of the electrons received this kick effectively and the photon flux obtained will also be reduced by the ratio of the laser pulse length/electron beam pulse length. Hence relatively few photons per pulse are delivered (∼10–1000).78 Improvements can be made by using an insertion device source, and exploiting the maximum laser repetition rate.
 | ||
| Fig. 11 Bunch slicing arrangement to extract sub-ps X-ray pulses from an electron bunch. Reprinted with permission from R. W. Schoenlein, S. Chattopadhyay, H. H. W. Chong, T. E. Glover, P. A. Heimann, C. V. Shank, A. A. Zholents, M. S. Zolotorev, Science, 2000, 287, 2237. Copyright 2000 AAAS (ref. 82). | ||
Other approaches to enhance the effective time resolution of storage rings are also under consideration. The so-called low-α optics83 could provide 1 ps bunches, but with much reduced beam current (∼1 μA) and larger emittance. Rotation of the electron bunch may also reduce the duration of the light pulse as the long direction of the bunch is moved out of the direction of travel using a pair of (“crab”) RF cavities.84 This has been recently assessed with the APS as the focus, and considered to be a viable means of achieving a light pulse of 1–3 ps with no significant impact on normal APS operation.85 This may thus be a route to a local ultrafast beamline (s) coexisting with the breadth of experiments within a storage ring panoply.
There is much active consideration of the varied options open to develop ultrafast sources in the VUV and X-ray regions.78,86–88 Bench top lasers can provide soft to medium energy X-radiation by higher harmonic generation and plasma formation, respectively.88 Both have the time structure of the source laser, most often a Ti:sapphire with ∼20 fs pulse, but neither can provide the full energy range of a storage ring. The plasma emission has some characteristics of a laboratory source having no directionality, a broad background and X-ray emission lines. HHG methods do have orientational and coherence properties and they are developing rapidly. Their output spectrum can be tuned by control of the spatial structure of the laser pulse,89 and also the intensity and chirp characteristics.90 These source can generate >107 photons per pulse in their higher harmonics. In Fig. 12, some characteristics of the various sources are compared. Many of these boundaries are being expanded, for example by the shrinking of storage ring electron bunches in their direction of travel. The average brilliance of the HHG devices in the VUV region is comparable to a bending magnet output on a storage ring, but is significantly lower than that of an undulator. The peak power, however, is substantially higher.
 | ||
| Fig. 12 Energy and pulse duration properties of different means of creating pulsed radiation between the visible and X-ray regions. Adapted figure with permission from T. Pfeifer, C. Spielman and G. Gerber, Rep. Prog. Phys., 2006, 69, 443. Copyright 2006 Institute of Physics (ref. 88). | ||
Accelerator based light sources are also in rapid development with major projects in free electron lasers (FELs) and energy recovering linacs (ERLs).86,87 These two arrangements relax some of the boundary conditions of a storage ring since they do not attain a steady state. Hence they can provide shorter pulse lengths than a storage ring (Fig. 13). However, at ∼102 fs they are still significantly longer than ultrafast visible light lasers. Their peak brightness is comparable to that of a Ti:sapphire laser, but at much different photon energies. As a rule of thumb, the output per pulse of a FEL is similar to that per second on a storage ring. As yet the jitter and the pulse shapes render them less stable and reproducible sources than storage ring and so experiments will have to be based on single-shot measurements with synchronous characterisation of the pulse profile. That is a challenging task, but the sampled region will not survive to receive averaging pulses.
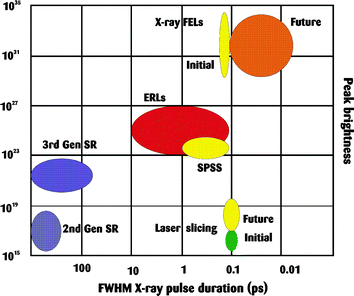 | ||
| Fig. 13 Peak brightness and pulse duration characteristics of accelerator based light sources. Adapted figure with permission from H.-D. Nuhn, J. Phys.: Condens. Matter, 2004, 16, S3413. Copyright 2004 Institute of Physics (ref. 86). | ||
3. Conclusions
The field of light sources is developing extremely rapidly. Storage rings are providing increasing qualities of brightness and stability. These can be exploited to probe far more challenging and realistic samples and processes, using the intensity of the light to shine through sample containment, to probe spatially textured samples, to derive incisive information from weak scattering events that contain chemical connectivities, and also to derive time resolution. Time resolutions are extending to the picosecond regime.There are continuous innovations in the alternative laser and accelerator light sources. These are the alternatives of choice for monitoring processes on a faster timescale (true dynamics rather than kinetics). But for that large tract of science that may be probed outside those timescales, storage rings can be expected to provide the best experimental facility for experiments utilising the X-ray region for many years to come. What delights this writer is the capability of the scientific community to find new ways of exploiting current sources and of developing new ones. That makes the future much more interesting than I can possibly relate.
Acknowledgements
I wish to thank my many colleagues at the Diamond Light Source, the SRS, the ESRF and the Ultrafast Laser X-ray Group in Southampton. It is a privilege to enjoy their imagination and professionalism.References
- See http://www.lightsources.org.
- See http://www.synchrotron-soleil.fr.
- See http://www.diamond.ac.uk.
- See http://www.cells.es.
- See http://www.cat.ernet.in/technology/accel/atdhome.html.
- See http://www.sesame.org.jo.
- See http://www.issp.u-tokyo.ac.jp/labs/sor/project/MENU.html.
- See http://www.synchrotron.vic.gov.au.
- “X-ray data booklet”, ed. A. C. Thompson and D. Vaughan, Lawrence Berkely National Laboratory, University of California, Berkely, CA, USA, 2nd edn, 2001.
- K.-J. Kim, p 2-1ff in ref. 9.
- See http://www.srs.ac.uk.
- ESRF Annual Report 1995-96, ESRF Grenoble.
- See http://www.esrf.fr.
- See http://www.aps.anl.gov.
- W. Chao, B. D. Harteneck, J. A. Liddle, E. H. Anderson and D. T. Atwood, Nature, 2005, 435, 1210 CrossRef CAS.
- P. Dumas, N. Jamin, J. L. Teillaud, L. M. Miller and B. Beccard, Faraday Discuss., 2004, 126, 289 RSC.
- M. Cotte, P. Walter, G. Tsoucaris and P. Dumas, Vib. Spectrosc., 2005, 38, 159 CrossRef CAS.
- P. Philippot, B. Ménez, M. Drakopoulos, A. Simionovici, A. Snigirev and I. Snigireva, Chem. Geol., 2001, 173, 151 CrossRef CAS.
- A. El Goresy, L. S. Dubrovinsky, P. Gillet, S. Mostefaoui, G. Graup, M. Drakopoulos, A. S. Simionovici, V. Swarmy and V. L. Masaitis, C. R. Geosci., 2003, 335, 889 Search PubMed.
- B. Salbu, T. Krekling, O. C. Lind, D. H. Oughton, M. Drakopoulos, A. Simionovici, I. Snigireva, T. Weitkamp, F. Adams, K. Janssens and V. A Kashparov, Nucl. Instrum. Methods Phy. Res. A, 2001, 467–468, 1249 Search PubMed.
- J. Foriel, P. Philippot, J. Susini, P. Dumas, A. Somogyi, M. Salomé, H. Khodja, B. Ménez, Y. Fouquet, D. Moreira and P. López-García, Geochim. Cosmochim. Acta, 2004, 68, 1561 CrossRef CAS.
- F. M. F. de Groot, Coord. Chem. Rev., 2005, 249, 31 CrossRef CAS.
- J. Stöhr and S. Anders, IBM J. Res. Develop., 2000, 44, 535 CrossRef CAS.
- B. T. Thole, P. Carra, F. Sette and G. van der Laan, Phys. Rev. Lett., 1992, 68, 1943 CrossRef CAS.
- P. Carra, B. T. Thole, M. Altarelli and X. Wang, Phys. Rev. Lett., 1993, 70, 694 CrossRef CAS.
- G. van der Laan, B. T. Thole, G. A. Sawatsky, J. B. Goedkoop, J. C. Fuggle, J.-M. Esteva, R. Karnatak, J. P. Remeika and H. A. Dabkowska, Phys. Rev. B, 1986, 34, 6529 CrossRef CAS.
- J. Vogel, A. Fontaine, V. Cros, F. Petroff, J.-P. Kappler, G. Krill, A. Rogalev and J. Goulon, J. Magn. Magn. Mater., 1997, 165, 96 CrossRef CAS.
- J. Dresselhaus, D. Spanke, F. U. Hillebrecht, E. Kisker, G. van der Laan, J. B. Goedkoop and N. B. Brookes, Phys. Rev. B, 1997, 56, 5461 CrossRef CAS.
- S. D. Brown, L. Bouchenoire, D. Bowyer, J. Kervin, D. Laundy, M. J. Longfield, D. Mannix, D. F. Paul, A. Stunault, P. Thompson, M. J. Cooper, C. A. Lucas and W. G. Stirling, J. Synchrotron Radiat., 2001, 8, 1172 CrossRef CAS.
- L. Bouchenoire, S. D. Brown, P. Thompson, J. A. Duffy, J. W. Taylor and M. J. Cooper, J. Synchrotron Radiat., 2003, 10, 172 CrossRef CAS.
- F. de Bergevin and M. Brunel, Acta Crystallogr., Sect. A, 1981, 37, 314 CrossRef.
- S. W. Lovesey and S. P. Collins, X-Ray scattering and absorption by magnetic materials, Oxford University Press, Oxford, 1996 Search PubMed.
- M. J. Cooper and W. G. Stirling, Radiat. Phys. Chem., 1999, 56, 85 CrossRef CAS.
- D. Gibbs, D. R. Harshman, E. D. Isaacs, D. B. McWhan, D. Mills and C. Vettier, Phys. Rev. Lett., 1988, 61, 1241 CrossRef CAS.
- J. P. Hannon, G. T. Tammell, M. Blume and D. Gibbs, Phys. Rev. Lett., 1988, 61, 1245 CrossRef CAS.
- M. J. Longfield, D. Mannix, G. H. Lander and A. Stunault, Phys. Rev. B, 2001, 64, 212407 CrossRef.
- G. J. Williams, M. A. Pfeifer, I. A. Vartanyants and I. K. Robinson, Phys. Rev. Lett., 2003, 90, 175501 CrossRef CAS.
- S. B. Dierker, R. Pindak, R. M. Fleming, I. K. Robinson and L. Berman, Phys. Rev. Lett., 1995, 75, 449 CrossRef CAS.
- A. Madsen, J. Als-Neilsen and G. Grübel, Phys. Rev. Lett., 2003, 90, 85701 CrossRef.
- M. Tegze and G. Faigel, Nature, 1996, 380, 49 CAS.
- T. Gog, P. M. Len, G. Materlik, D. Bahr, C. S. Fadley and C. Sanchez Hanke, Phys. Rev. Lett., 1996, 76, 3132 CrossRef CAS.
- M. Tegze, G. Faisel, S. Marchesini, M. Belakhovsky and A. I. Chumakov, Phys. Rev. Lett., 1999, 82, 4847 CrossRef CAS.
- S. Marchesini, F. Schmithüsen, M. Tegze, G. Faigel, Y. Calvayrac, M. Belakhovksy, J. Chevrier and A. S. Simionovici, Phys. Rev. Lett., 2000, 85, 4723 CrossRef CAS.
- J. M. Grimes and D. I. Stuart, Nat. Struct. Biol., 1998, 5, 630 CrossRef CAS.
- J. M. Grimes, J. N. Burroughs, P. Gouet, J. M. Diprose, R. Malby, S. Ziéntara, P. P. C. Mertens and D. I. Stuart, Nature, 1998, 395, 470 CrossRef CAS.
- M. Gluehmann, R. Zarivach, A. Bashan, J. Harms, F. Schluenzen, H. Bartels, I. Agman, G. Rosenblum, M. Pioletti, T. Auerbach, H. Avila, H. A. S. Hansen, F. Franceschi and A. Yonath, Methods, 2001, 25, 292 Search PubMed.
- M. N. James, D. J. Hughes, D. G. Hattingh, G. R. Bradley, G. Mills and P. J. Webster, Fatique Fract. Eng. Mater. Struct., 2004, 27, 187 Search PubMed.
- A. Steuwer, J. R. Santisteban, M. Turski, P. J. Withers and T. Buslaps, J. Appl. Crystallogr., 2004, 37, 883 CrossRef CAS.
- L. D. Liss, A. Magerl, A. Remhof and R. Hock, Acta Crystallogr., Sect. A, 1997, 53, 181 CrossRef.
- D. T. Bowron, M. H. Krisch, A. C. Barnes, J. L. Finney, A. Kaprolat and M. Lorenzen, Phys. Rev. B, 2000, 62, R9223 CrossRef CAS.
- C. A. Burns, P. Guira, A. Shukla, G. Vankó, M. Teul-Benckendorf, E. D. Isaacs and P. M. Platzman, Phys. Rev. Lett., 2002, 89, 236404 CrossRef CAS.
- C. A. Burns, G. Vankó, H. Sinn, A. Alatas, E. E. Alp and A. Said, J. Chem. Phys., 2006, 124, 024720 CrossRef CAS.
- K. Hämäläinen, D. P. Siddons, J. B. Hastings and L. E. Berman, Phys. Rev. Lett., 1991, 67, 2850 CrossRef CAS.
- P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65 CrossRef CAS.
- P. Glatzel, U. Bergmann, W. Gu, H. Wang, S. Stepanov, B. S. Mandimutsira, C. G. Riodan, C. P. Horwotz, T. Collins and S. P. Cramer, J. Am. Chem. Soc., 2002, 124, 9668 CrossRef CAS.
- P. Glatzel, J. Yano, U. Bergmann, H. Visser, J. H. Robblee, W. W. Gu, F. M. F. de Groot, S. P. Cramer and V. K. Yachandra, J. Phys. Chem. Solids, 2005, 66, 2163 CrossRef CAS.
- P. Glatzel, L. Jacquamet, U. Bergmann, F. M. F. De Groot and S. P. Cramer, Inorg. Chem., 2002, 41, 3121 CrossRef CAS.
- H. Paulsen, V. Schünemann, A. X. Trautwein and H. Winkler, Coord. Chem. Rev., 2005, 249, 255 CrossRef CAS.
- K. L. Adam, S. Tsoi, J. Yan, S. M. Durbin, A. K. Ramdas, W. A. Cramer, W. Sturhahn, E. E. Alp and C. Shultz, J. Phys. Chem. B, 2006, 110, 530 CrossRef.
- J. T. Sage, S. M. Durbin, W. Sturhahn, D. C. Wharton, P. M. Champion, P. Hession, J. Sutter and E. E. Alp, Phys. Rev. Lett., 2001, 86, 4966 CrossRef CAS.
- (a) M. A. Newton, A. J. Dent and J. Evans, Chem. Soc. Rev., 2002, 31, 83 RSC; (b) E. L Heeley, T. Gough, W. Bras, A. J. Gleeson, P. D. Coates and A. J. Ryan, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 238, 21 CrossRef.
- N. Yoshida, T. Matsushita, S. Saigo, H. Oyanagi, H. Hashimoto and M. Fujimoto, J. Chem. Soc., Chem. Commun., 1990, 1, 354 RSC.
- M. B. B. Abdul Rahman, P. R. Bolton, J. Evans, A. J. Dent, I. Harvey and S. Diaz-Moreno, Faraday Discuss., 2002, 122, 211 Search PubMed.
- S. Diaz-Moreno, D. T. Bowron and J. Evans, Dalton Trans., 2005, 3814 Search PubMed.
- D. T. Bowron and S. Diaz-Moreno, Anal. Chem., 2005, 77, 6445 CrossRef CAS.
- M. Tromp, J. R. A. Sietsma, J. A. Van Bokhoven, G. P. F. van Stridonck, R. J. Haaren, A. M. J. van de Eerden, P. W. N. M. van Leeuwen and D. C. Koningsberger, Chem. Commun., 2003, 128 Search PubMed.
- M. A. Newton, A. J. Dent, S. Diaz-Moreno, S. G. Fiddy and J. Evans, Angew. Chem., Int. Ed., 2002, 41, 2002.
- M. A. Newton, A. J. Dent, S. Diaz-Moreno, S. G. Fiddy, B. Jyoti and J. Evans, Chem.-Eur. J., 2006, 12, 1975 CrossRef CAS.
- M. A. Newton, B. Jyoti, A. J. Dent, S. G. Fiddy and J. Evans, Chem. Commun., 2004, 2382 Search PubMed.
- A. M. Beale, A. M. J. van der Eerden, K. Kervinen, M. A. Newton and B. M. Weckhuysen, Chem. Commun., 2005, 3015 Search PubMed.
- I. I. Vorontsov, A. Y. Kovalevsky, Y.-S. Chen, T. Graber, M. Gembicky, I. V. Novozhilova, M. A. Omary and P. Coppens, Phys. Rev. Lett., 2005, 94, 193003 CrossRef.
- V. Šrajer, Z. Ren, T.-Y. Teng, M. Schmidt, T. Ursby, D. Bougeois, C. Pradervand, W. Schildkamp, M. Wulff and K. Moffat, Biochemistry, 2001, 40, 13802 CrossRef CAS.
- Q. Kong, J. Kim, M. Lorenc, T. K. Kim, H. Ihee and M. Wulff, J. Phys. Chem. A, 2005, 109, 10451 CrossRef CAS.
- H. Ihee, M. Lorenc, T. K. Kim, Q. Y. Kong, M. Cammarata, J. H. Lee, S. Bratos and M. Wulff, Science, 2005, 309, 1223 CrossRef CAS.
- J. Davidsson, J. Poulsen, M. Cammarata, P. Georgiou, R. Wouts, G. Katona, F. Jacobson, A. Plech, M. Wulff, G. Nyman and R. Neutze, Phys. Rev. Lett., 2005, 94, 245503 CrossRef.
- R. Nuetze, R. Wouts, S. Techert, J. Davidsson, M. Kocsis, A. Kirrander, F. Schotte and M. Wulff, Phys. Rev. Lett., 2001, 87, 195508 CrossRef.
- A. Plesch, M. Wulff, S. Bratos, F. Mirloup, R. Vuilleumier, F. Schotte and P. A. Anfinrud, Phys. Rev. Lett., 2004, 92, 125505 CrossRef.
- C. Bressler and M. Chergui, Chem. Rev., 2004, 104, 1781 CrossRef CAS.
- M. Saes, C. Bressler, R. Abela, D. Grolimund, S. L. Johnson, P. A. Heimann and M. Chergui, Phys. Rev. Lett., 2003, 90, 47403 CrossRef.
- J. Larsson, Z. Chang, E. Judd, P. J. Schuck, R. W. Falcone, P. A. Heimann, H. A. Padmore, H. C. Kapteyn, P. H. Bucksbaum, N. M. Murnane, R. W. Lee, A. Machacek, J. S. Wark, X. Liu and B. Shan, Opt. Lett., 1997, 22, 1012 Search PubMed.
- A. M. Lindenberg, I. Kang, S. L Johnson, T. Misalla, P. A. Heimann, Z. Chang, J. Larsson, P. H. Bucksbaum, H. C. Kapteyn, H. A Padmore, R. W. Less, J. S. Wark and R. W. Falcone, Phys. Rev. Lett., 2000, 84, 111 CrossRef CAS.
- R. W. Schoenlein, S. Chattopadhyay, H. H. W. Chong, T. E. Glover, P. A. Heimann, C. V. Shank, A. A. Zholents and M. S. Zolotorev, Science, 2000, 287, 2237 CrossRef CAS.
- J. L. Laclare, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 467–468, 1 CrossRef CAS.
- A. Zholents, P. Heimann, M. Zolotorev and J. Byrd, Nucl. Instrum. Methods Phys. Res., Sect. A, 1999, 425, 385 CrossRef CAS.
- M. Borland, Phys. Rev. ST Accel. Beams, 2005, 8, 074001 CrossRef.
- H.-D. Nuhn, J. Phys.: Condens. Matter, 2004, 16, S3413 CrossRef CAS.
- D. H. Bilderback, P. Elleaume and E. Weckert, J. Phys. B: At. Mol. Opt. Phys., 2005, 38, S773 CrossRef CAS.
- T. Pfeifer, C. Spielman and G. Gerber, Rep. Prog. Phys., 2006, 69, 443 CrossRef.
- T. Pfeifer, R. Kemmer, R. Spitzenpfeil, D. Walter, C. Winterfeldt, G. Gerber and C. Spielmann, Opt. Lett., 2005, 30, 1497 CrossRef.
- C. A. Froud, E. T. F. Rogers, D. C. Hanna, W. S. Brocklesby, M. Praeger, A. M. de Paula, J. J. Baumberg and J. G. Frey, Opt. Lett., 2006, 31, 374 CrossRef CAS.
| This journal is © the Owner Societies 2006 |
