Controlled bimolecular collisions allow sub-diffraction limited microscopy of lipid vesicles

Abstract

The concentration and vesicle size-controlled collisions of single molecules with target biological assemblies allow sub-diffraction limited optical images to be obtained that are not subject to the usual photobleaching problems with single molecule experiments. For example, single molecules of the probe Nile Red in aqueous solution emit a burst of fluorescence when they collide with a 50 nm hydrophobic vesicle situated on the surface in the laser focus. The bimolecular kinetics of the bursts is defined by their on- and off-time distribution functions which depend on the concentration and diffusion of the probe and the vesicle size. The mean burst frequency changes much more sharply than does the fluorescence intensity when a vesicle is raster scanned through the laser focus. This sharpness allows the spatial resolution of two objects to be improved and separations less than the diffraction limited resolution of the conventional optical microscope to be measured. The principle of this method of trajectory time distribution optical microscopy (TTDOM) could be used in a far field optical microscopic system with a resolution of several nanometers.

---

Introduction

Two point objects having identical optical properties can be spatially resolved by an optical microscope only if their separation in image space is equal to or larger than 0.61λ/N.A. where λ denotes the detected wavelength of the incoherent fluorescence source and N.A. is the numerical aperture.¹ A confocal microscope using an oil-immersion objective having N.A. of 1.3 at 630 nm achieves a lateral resolution of ∼300 nm. Several optical methods have been developed to achieve resolution beyond the diffraction limit. One is near field scanning optical microscopy (NSOM), in which the size of light source is in the sub-wavelength range.^2,3 There are some difficulties with NSOM including tip manufacture, sample-tip interactions and that in many cases it can only provide surface structures. A 4Pi-confocal microscope and a confocal microscope based on stimulated emission both developed by Hell and coworkers are other approaches to obtain optical images beyond the diffraction limit.^4,5 Recently, high resolution images of single molecules have also been achieved, in which a low noise high quantum yield charge-coupled device (CCD) is coupled to a total internal reflection microscope to record images of individual molecules.⁶ Based on knowledge of the point-spread function, two identical fluorophores separated by distances as small as 10 nm have been resolved. This method is limited to measuring separations between two different fluorophores that are not photobleached simultaneously. Of course a mean location for a source can be measured to any required precision. Many applications take advantage of high precision to make measurements in the region ranging from tens of nanometers down to 1.5 nm.^7–9 There is certainly a great need for new methods of sub-diffraction microscopy that can be applied to biological systems and to living cells.

The probe, Nile Red, has a fluorescence that is very sensitive to its environment. In hydrophilic solvents its quantum yield is much lower than that in nonpolar solvents. Numerous applications have taken advantage of this property to probe polarity in materials or single proteins.^10,11 Single Nile Red molecules become easily detectable when they are bound to a hydrophobic particle that is located near a laser focus. In the present experiments vesicles having a mean radius of 50 nm were used as the hydrophobic objects. The method of microscopy we describe is based on analysis of the concentration controlled bursts of single molecule fluorescence of the probe.

The time record of detectable fluorescence bursts is determined by the frequency of the collisions between a vesicle and a Nile Red molecule and by the lifetime of the vesicle/probe pair. The laser intensity determines what fraction of the bursts are above a detection threshold. This sequence of fluorescence bursts resulting from probes colliding with the vesicle is quite different from that found in fluorescence correlation spectroscopy (FCS),^12,13 where bursts are detected only when single molecules diffuse into the volume defined by the laser beam.

The theory of diffusion controlled reactions predicts that the collision rate τ_R of a small particle with the curved surface of a much larger hemispherical object with radius R_o is given by 1/τ_R = 2πR_oND, where D is the particle diffusion coefficient and N is the particle number density.^14,15 The time record of fluorescence bursts depend only on the distribution functions of the time intervals between the collisions, the so-called off-times, and of the fluorescent periods when the probe is bound to the vesicle, the on-times. In previous work we have shown that these time interval distributions can be measured accurately¹⁶ for bimolecular reactions involving Nile Red and lipid vesicles. We show in this work that the analysis of these controlled collisions can substantially improve the microscope spatial resolution and permit resolution of two vesicles having a spatial separation less than the diffraction limit by means of trajectory time distribution optical microscopy (TTDOM). The on–off character of the signals reported here are analogous to those reported for uncontrolled “blinking” of nanoparticles¹⁷ and for reactions between enzymes and their cofactors at the single molecule level.^18–20 The processing theory and analysis of single molecule on and off trajectories is well established.^21,22

Results

The vesicles are not fluorescent, but at ∼0.1 nM concentration of Nile Red a fluorescence image appears in the form of widely separated (∼1.5 micron) fluorescence bright spots reminiscent of a single molecule image.¹⁶ Clearly the Nile Red probes are locating individual vesicles. These bright spots exhibit no observable photobleaching, however, the fluorescence image appears to be very noisy. Close inspection of a single bright spot shows the fluorescence fluctuations have predictable characteristics: when a vesicle is centered in the laser focus, fluorescence intensity–time records of the type shown in Fig. 1(a) are observed. These records are caused by the collisions of Nile Red molecules with the vesicle: the frequency of the bursts depends on the size of vesicle chosen and on the concentration of the probe in the solution.¹⁶ The time records are characterized by distinctive on-time and off-time distributions (see below) and autocorrelation functions as described in previous work.¹⁶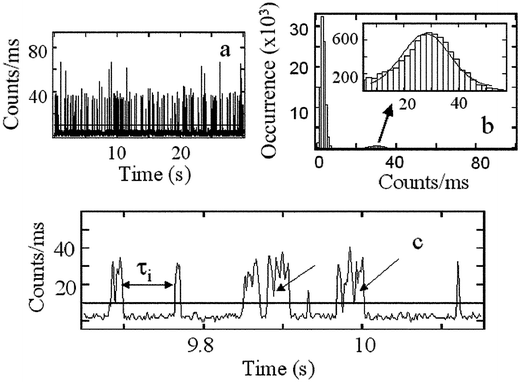

Fig. 1 Typical fluorescence signals: (a) A fluorescence intensity vs. time record over a 30 s period. The few spikes having approximately twice the count rate of the mean correspond to two probe molecules being associated with one vesicle during the binning time of 1 ms. (b) The count rate distribution (number of times a particular photon count rate occurs vs. the photon count rate) at excitation power 30 µW. The inset is a blow up of the 30 counts ms⁻¹ region, which arises from one Nile Red molecule at a time interacting with a vesicle. (c) Expanded view of the intensity–time record near 10 s. The horizontal line is a typical threshold that unequivocally distinguishes fluorescence bursts from background signals. The arrows point to the fast fluctuations occurring during the residence time of the probe on the vesicle: these are caused by shot noise and the fluctuations in the Nile Red locations in the lipid vesicle.

Fig. 1(b) shows the count rate distribution of the intensity–time record shown in Fig. 1(a). The distribution has two Gaussian peaks centered at 3 and 30 counts. The peak at 3 counts is the background signal which is relatively intense because for the majority of time during the record, no bursts are detected. The weaker peak at 30 counts arises from the fluorescence bursts from one Nile Red molecule binding to a vesicle. At higher probe concentration than used here another peak appears near 60 counts corresponding to two Nile Red molecules per vesicle.¹⁶ If the count rate distribution were determined by the profile of the laser beam, Poisson shot noise and background signals, it should exhibit a super-Poissonian behavior.²³ The observed Gaussian distribution shown in Fig. 1(b) confirms that the fluorescence source is confined to a region much smaller than the laser beam confocal volume. Fluorescence bursts are only detected when Nile Red molecules collide with the ca. 50 nm vesicle located in beam focus. The Gaussian width is determined by the laser intensity fluctuations and the size of vesicle. Increasing the size of the vesicle leads to an increase in width. Fig. 1(b) also indicates that the fluorescence signals are accurately separable from background.

To separate the fluorescence bursts from background, a threshold of S +10δ was applied to data sets, where S denotes the mean and δ the standard deviation of the background fluctuations. To be counted as fluorescence, a signal needed to exceed this threshold. The time intervals, or off-times, between sequential fluorescence bursts (illustrated in Fig. 1(c) as τ_i) correspond to the intervals between sequential, successful collisions if the threshold does not alter the burst frequency. In the experiments described here, the mean value of the frequency of fluorescence bursts, defined as 1/〈τ_i〉, was computed from ∼500 off-times. The excellent reproducibility of this method was confirmed from studies of many intensity–time records collected independently from the same vesicle: they yielded a mean deviation of 5% for 1/〈τ_i〉.

The collision rate (1/τ_R) and the mean off-time frequency are related by 1/〈τ_i〉 = β/τ_R, where β represents the probability that a collision results in a fluorescence burst. If β = 1, the slope of the curve of 1/〈τ_i〉 vs. N is given by 2πR_oD if vesicles have hemispherical shape. The collision rate is somewhat dependent on vesicle shape, for example this slope is 4R_oD for a circular disk. With R_o = 50 nm, a number density of 6 × 10¹⁰ cm⁻³ (0.2 nM) and a diffusion coefficient of Nile Red in water of 1.2 × 10⁻⁶ cm² s⁻¹,¹⁶ the mean off-time is expected to be 4 s⁻¹ which is very close to what was observed at the center of the scans shown in Fig. 2. This mean value can be controlled by changing the number density.

Fig. 2 Experimental and expected signals from scans of 1/〈τ_i〉. (a) solid curve: the values of 1/〈τ_i〉 during the raster scanning of a vesicle through a focused laser beam; dashed curves: the squares are the fluorescence intensity recorded during the same raster scanning of the vesicle and the dashed line is a Gaussian fit having 1/e² width of 580 nm. The scan step is 50 nm. (b) simulated 1/〈τ_i〉 curves and gaussian point spread (dashed line) obtained by using thresholds of 10 (outer curve), 15 and 20 (inner curve, all in units of counts ms⁻¹). The off-time distribution was chosen as A exp(−t/τ₁) + B exp(−t/τ₂) with τ₁ = 163 ms, A = 0.11 and with τ₂ = 2 ms, B = 0.89. The on-time distribution was chosen as exp(−t/〈τ_on〉) with a mean on-time of 13 ms. During the on-time, fluorescence signals were assigned gaussian fluctuations about a mean M with full gaussian width of w = 14 counts ms⁻¹ and M = 30 counts ms⁻¹. The radius of the circular disk R = 0.5 nm. The point spacing is 10 nm. (c) Simulated 1/〈τ_i〉 scan obtained by with w = 0 and R = 10 nm, the other parameters are as given in (b).

Fig. 2(a) shows the values of 1/〈τ_i〉 as a function of the location of the vesicle in the laser beam focus. This experiment is quite different from the intensity point spread measurement. When the vesicle was far enough outside the focused laser beam that the detected signals were all below the threshold, the mean value of the off-time was essentially infinite, thus 1/〈τ_i〉 ∼ 0. As it was moved closer to the center of the beam focus, fluorescence bursts above the threshold appeared and the mean off-time became smaller. This is clearly shown in Fig. 2(a), where a sharp increase of 1/〈τ_i〉 was observed when the vesicle was moved into the focus of the laser. Moving the vesicle even closer to the center of the focused laser beam, caused 1/〈τ_i〉 to decrease again as indicated in Fig. 2(a). The dip near the beam center is caused by the fast fluctuation of Nile Red fluorescence during the on-period when the probe is associated with the vesicle¹⁶ as indicated by arrows in Fig. 1(c). When the laser intensity at the vesicle is low, the rapid intensity fluctuations marked by arrows in Fig. 1(c) will be below the threshold and some small off-times are introduced into the statistics of 1/〈τ_i〉, which directly result in an increase of 1/〈τ_i〉. When the vesicle is centered in the focused laser beam, the laser intensity at the vesicle is high so these fast fluorescence fluctuations are above the threshold and their small time intervals will not contribute to 1/〈τ_i〉. This situation causes a dip in the center of the scan shown in Fig. 2(a). This scan is almost symmetric because moving the vesicle into and out of a gaussian profile laser focus presents almost identical conditions for very small vesicles of any shape. The height of the curve in the center should equal β/τ_R which provides an independent measure of the vesicle size which in this case is 48 nm. The controlled collision signal scan shows a much sharper edge than does the fluorescence intensity scan, which is shown for comparison in Fig. 2(a).

Comparisons with simulations

The computer simulations of the experiments were based on stochastic intensity–time records that were synthesized by random selection from off-time and on-time distribution functions with parameters chosen from the experimental results, a gaussian laser beam focus and fluorescent point sources at random locations within circular disks having radii characteristic of vesicles lying flat on the image plane. The intensity of a fluorescence signal spike was assumed to depend on its location relative to the gaussian beam center and on the added shot noise. The parameters are given in the figure captions. The mean value of the fluorescence count rate was set as proportional to the excitation intensity in accordance with the results at 30 μW power.¹⁶Fig. 2(b) shows the scan of 1/〈τ_i〉 for a 1 nm circular disk chosen to represent a point source. The intensity point spread function is shown for comparison. Fig. 2(b) shows two sharp spikes separated by an amount that depends on the threshold that is chosen. The shape degenerates to a rectangle when the shot noise is set at zero, as in Fig. 2(c). As the disk increases in size and becomes larger than the beam diameter the count rate distribution goes over to an exponential similar to what is observed in FCS.²³ The plot of 1/〈τ_i〉 for the small circular disk mimics well what is observed in the experiment: two spikes, which are much sharper than the intensity point spread function, are seen with the signal between them having a dip. The dip was confirmed by simulation to depend on the magnitude of the shot noise and the two sharp peaks are separated approximately by the laser beam width. Fig. 3(a) compares the simulations of 1/〈τ_i〉 for two point-like sources separated by 40, 100 and 250 nm along the scan line. These computed signals are symmetric when very large numbers of off times are incorporated but we chose only 500 for the simulation. Fig. 3(b) presents the corresponding 1/〈τ_i〉 in the absence of shot noise. The corresponding intensity scans and their components are shown in Fig. 3(c). Fig. 4(a) shows a simulation for two circular disks with radii of 50 nm separated by 160 nm from edge to edge with their center-to-center line parallel to the scan direction of the stage. An experimental scan is shown along with a simulation in Fig. 4(b). In this example the intensity scan shows no fine structure. We conclude that the two vesicles, each having a radius of about 50 nm and separated by 160 nm are being spatially resolved by this method. Although we could not prepare pairs of vesicles separated by specific distances, by searching the images we found a few examples that have the appearance of the signals that were simulated for separated pairs. Fig. 4(b) shows a typical experimental result for one such bright spot, where the 1/〈τ_i〉 scan is characteristic of two vesicles. Pairs with smaller separation than ∼160 nm were hard to find since the fluorescence intensity image was used to locate the vesicles: when two vesicles are too close they appear like one in the fluorescence intensity image. From the clarity of the signal in Fig. 3, it is reasonable to predict that we could still distinguish two vesicles at separations much smaller than 160 nm. According to Fig. 3(a), two discernable peaks then appear in the center of the trace, as shown in panels a₂ and a₃. An automatic scanning module will greatly speed up the retrieval of small aggregates of vesicles.

Fig. 3 Simulated 1/〈τ_i〉 results for two circular disks with radii of 0.5 nm. (a) a₁, a₂, a₃: separation of 40, 100 and 250 nm, other parameters as in Fig. 2; (b) b₁, b₂, b₃: as in (a) but w = 0. (c) c₁, c₂, c₃: intensity scans corresponding to (a); dashed lines are contributions from individual disks.

Fig. 4 Simulated (a) and experimental (b) 1/〈τ_i〉 scan for a vesicle aggregate. The experimental scan step is 50 nm. The simulated 〈1/τ_i〉 curve assumes the fluorescence originates from two circular disks (R = 50 nm) separated by 160 nm edge to edge. The other parameters are as given in Fig. 2(b).

The experimental data as well as the simulated results clearly demonstrate that this controlled collision system can distinguish two objects even when the separation between them is smaller than the diffraction limited resolution of the optical microscope. By recording 1/〈τ_i〉 pixel by pixel instead of recording fluorescence intensity as done in conventional fluorescence imaging, high resolution images are obtainable based on the principle reported here. With the present arrangement the scan steps were restricted to 50 nm but obvious improvements are expected when this is reduced.

It was verified by simulation that the off-time distribution does not affect the sharpness of the edge in a 1/〈τ_i〉 scan, but it does determine the magnitude of the maximum signal between the two spikes characteristic of a single particle. The sharpness is determined by the width of the count rate distribution. In general, if the count rate distribution is well separated from the background, as is the case in Fig. 1(b), sharper edges in the 1/〈τ_i〉 scan are obtained with narrower distributions. In the extreme case where all the fluorescence bursts generated by a point-like object have equal intensity, the application of a threshold results in either none or all of the bursts being detected. In this case, two classical objects separated by any distance would be distinguishable by means of a 1/〈τ_i〉 scan, corresponding to a microscope with unlimited resolving power. Of course, this situation does not exist experimentally because of the fluctuations of the fluorescence signals. The simulation assumed that fluorescence events arise at random locations on a circular disk. A slightly different result arises if a hemispheric surface is used to model the vesicle, in which case the normal projection displays a higher density of bright spots closer to the perimeter.

Methods

Materials

Nile Red was purchased from Molecular Probes and used as received. Glass coverslips and cylinders (Fisher) were cleaned by sequential sonication in 2 M sodium hydroxide solution, Methanol, 2 M sodium hydroxide solution, and DI water. The 1,2-Dimyristoyl-sn-Glycero-3-Phosphocholine (DMPC) (Avanti Polar Lipids) was used to prepare large unilamellar vesicles as follows:²⁴ 0.25 ml of 25 mg ml⁻¹ DMPC lipids in CHCl₃ was evaporated in nitrogen to yield a dry phospholipid film on the internal surface of a vial. After 2 h in vacuum the lipid film was hydrated in 4 ml phosphate buffer (20 mM, pH 7.0) with vigorous stirring at 32 °C for 1.5 h. The resulting vesicles were subjected to five freeze/thaw cycles and extruded about 20 times through polycarbonate membranes having 100-nm pore diameter (Avanti Mini-Extruder) and used within two days. The concentration used in the single vesicle experiment is ∼1 pM at which the individual ∼50 nm radius vesicles adsorbed on the glass surface have a mean nearest neighbor separation of ∼1.5 μm.²⁴

The microscope

The scanning confocal microscope, described previously,²⁵ uses a scanning stage (Queensgate), with closed-loop X,Y feedback for accurate sample positioning and location of individual molecules, that is controlled by a modified Nanoscope E Controller (Digital Instruments). The sample and stage were mounted on an inverted, epi-illlumination microscope (Nikon, Diaphot 300). The 514.5 nm argon line was circularly polarized and used for excitation at a power of ∼30 μW. A Nikon FLUOR X40, 1.3 numerical aperture objective was used to produce a nearly diffraction-limited focus on the sample and to collect the fluorescence. Appropriate combinations of notch (Kaiser Optical), band-pass, long-pass and dichroic filters (Chroma Technology) were used to spectrally isolate the fluorescence at 630 nm: the detector was a single-photon counting avalanche diode. The spectra of fluorescence from single vesicles were checked by means of a monochromator (Acton Research) equipped with a back-illumination liquid-nitrogen-cooled CCD camera (Princeton Instruments, Trenton, NJ).

Conclusions

The probe used to effectively transfer collisions into fluorescence bursts has a key role in this kind of experiment. Nile Red, which is non-fluorescent in water and emits strong fluorescence signals in hydrophobic environments, has proven to be useful for acquiring images of hydrophobic objects such as vesicles. The same principles may be applicable to obtain the separations among functional hydrophobic sites within cellular organelles, or to directly measure the hydrophobic sizes of a single protein assemblies or aggregates under various conditions. For such applications, both the excitation wavelength and the chemical properties of the probes will require to be chosen carefully. We have noted that the height of the central portion of the 1/〈τ_i〉 scan is directly proportional to the size of object.¹⁶ Other environment sensitive fluorescent probes could readily be employed in similar counting experiments: all that is required is that the fluorescence yield be changed by collisions with the objects of interest. For example one could use fluorescent dyes that change their fluorescence quantum yield dramatically in different pH and environments,^26–28 or probes that emit strong fluorescence only when both H⁺ and Na⁺ exist nearby.²⁹

We have demonstrated experimentally by means of controlled collision counting that two vesicles with the separation as small as 160 nm can be spatially resolved. Having control of the collisional frequency and off-time distribution function permits the count intervals to be predetermined to be in the most convenient time ranges for measurement and data acquisition. Based on simulations using the experimentally measured distribution functions, two point-like objects with a separation as small as 40 nm should be distinguishable in essentially the same experiment as described here.

Acknowledgements

This work was supported by NIH grants GM48130 and RFA-RM-04-001 using instrumentation developed by the NIH Research Resource grant NIH P41 RR001348.

References

1. M. Born and E. Wolf, Principles of Optics, Pergamon Press, Oxford, UK, 5th edn, 1975.
2. D. W. Pohl, in Advances in Optical and Electron Microscopy, ed. C. J. R. Sheppard, Academic Press, London, 1990, pp. 243–312.
3. E. Betzig, M. Isaacson and A. Lewis, Appl. Phys. Lett., 1987, 51, 2088–2090.
4. P. E. Hanninen, S. W. Hell, J. Salo, E. Soini and C. Cremer, Appl. Phys. Lett., 1995, 66, 1698–1700.
5. T. A. Klar, S. Jakobs, M. Dyba, A. Egner and S. W. Hell, Proceedings of the National Academy of Sciences of the United States of America FIELD Publication Date: 2000 Jul 18, 97, 8206–8210. FIELD Reference Number: FIELD Journal Code: 7505876 FIELD Call Number.
6. M. P. Gordon, T. Ha and P. R. Selvin, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 6462–6465.
7. A. Yildiz and P. R. Selvin, Acc. Chem. Res., 2005, 38, 574–582.
8. M. J. Saxton and K. Jacobson, Annu. Rev. Biophys. Biomol. Struct., 1997, 26, 373–399.
9. E. L. Florin, A. Pralle, J. K. Horber and E. H. Stelzer, J. Struct. Biol., 1997, 119, 202–211.
10. Y. Hou, A. M. Bardo, C. Martinez and D. A. Higgins, J. Phys. Chem. B, 2000, 104, 212–219.
11. J. Tang, E. Mei, J. Kaplan, F. W. DeGrado, A. B. Smith, III and R. M. Hochstrasser, J. Phys. Chem. A, 2004, 108, 15910–15918.
12. D. Magde, E. L. Elson and W. W. Webb, Biopolymers, 1974, 13, 29–61.
13. M. Ehrenberg and R. Rigler, J. Chem. Phys., 1974, 4, 390–401.
14. M. V. Smoluchowski, Phys. Z, 1916, 19, 371.
15. I. V. Gopich and A. Szabo, J. Chem. Phys., 2002, 117, 507–517.
16. F. Gao, E. Mei, M. Lim and R. M. Hochstrasser, J. Am. Chem. Soc. DOI:10.1021/Ja058098a.
17. M. Nirmal, B. O. Dabbousi, M. G. Bawendi, J. J. Macklin, J. K. Trautman, T. D. Harris and L. E. Brus, Nature, 1996, 383, 802–804.
18. Z. Zhang, P. T. R. Rajagopalan, T. Selzer, S. J. Benkovic and G. G. Hammes, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2764–2769.
19. H. P. Lu, L. Xun and S. X. Xie, Science, 1998, 282, 1877–1882.
20. O. Flomenbom, K. Velonia, D. Loos, S. Masuo, M. Cotlet, Y. Engelborghs, J. Hofkens, A. E. Rowan, R. J. M. Nolte, M. Van der Auweraer, F. C. De Schryver and J. Klafter, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 2368–2372.
21. R. Verberk and M. Orrit, J. Chem. Phys., 2003, 119, 2214–2222.
22. O. Flomenbom, J. Klafter and A. Szabo, Biophys. J., 2005, 88, 3780–3783.
23. Y. Chen, J. D. Muller, P. T. C. So and E. Gratton, Biophys. J., 1999, 77, 553–567.
24. J. M. Johnson, T. Ha, S. Chu and S. G. Boxer, Biophys. J., 2002, 83, 3371–3379.
25. M. A. Bopp, A. Sytnik, T. D. Howard, R. J. Cogdell and R. M. Hochstrasser, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 11271–11276.
26. S. Brasselet and W. E. Moerner, Single Mol., 2000, 1, 15–21.
27. Y. Fu, M. M. Collinson and D. A. Higgins, J. Am. Chem. Soc., 2004, 126, 13838–13844.
28. K. A. Willets, P. R. Callis and W. E. Moerner, J. Phys. Chem. B, 2004, 108, 10465–10473.
29. S. Uchiyama, G. D. McClean, K. Iwai and A. P. d. Silva, J. Am. Chem. Soc., 2005, 127, 8920–8921.

---