Gas phase infrared multiple-photon dissociation spectra of methanol, ethanol and propanol proton-bound dimers, protonated propanol and the propanol/water proton-bound dimer
Received
23rd November 2005
, Accepted 11th January 2006
First published on 26th January 2006
Abstract
The infrared multiphoton dissociation (IRMPD) spectra of three homogenous proton-bound dimers are presented and the major features are assigned based on comparisons with the neutral alcohol and with density functional theory calculations. As well, the IRMPD spectra of protonated propanol and the propanol/water proton-bound dimer (or singly hydrated protonated propanol) are presented and analysed. Two primary IRMPD photoproducts were observed for each of the alcohol proton bound dimers and were found to vary with the frequency of the radiation impinging upon the ions. For example, when the proton-bound dimer absorbs weakly a larger amount of SN2 product, protonated ether and water, are observed. When the proton-bound dimer absorbs more strongly, an increase in the simple dissociation product, protonated alcohol and neutral alcohol, is observed. With the aid of RRKM calculations this frequency dependence of the branching ratio is explained by assuming that photon absorption is faster than dissociation for these species and that only a few photons extra are necessary to make the higher-energy dissociation channel (simple cleavage) competitive with the lower energy (SN2) reaction channel.
1. Introduction
Among the many novel bonding features exhibited by gas phase ions, strong hydrogen bonding is perhaps the most interesting and most important. In the formation of an ion–molecule association adduct, the presence of a centre of charge enhances both electrostatic and polarization interactions but, in addition, can also induce changes in the covalent structure of the participants in the association adduct. In the case of hydrogen bonded adducts, this change in covalent structure frequently takes the form of a partial proton transfer in which a proton appears to be shared between two, or more, basic sites of the molecules involved in adduct formation. In the case of adducts involving the same atom or molecule, the proton may be shared equally by the participants. Thus, for example, the protonated water dimer, H5O2+, is predicted to exhibit a structure in which the bridging proton is equidistant from the two oxygen atoms of the participating water molecules.1 This yields the so-called Zundel structure for the protonated water dimer. Similarly, the bifluoride ion, FHF−, which has the strongest known hydrogen bond, has a proton symmetrically disposed between the two fluoride ions in a linear geometry.2 Structures such as these two give rise to a relatively broad potential well for the proton motion which is flatter than a more conventional parabolic potential and thus leads to an anharmonic character of the vibrational motion associated with the proton motion.
Very recently, the advent of the use of tunable, high-power, infrared-output, free-electron lasers (FEL) in conjunction with ion trap mass spectrometers (either FTICR or quadrupole) has permitted the study of the wavelength dependence of photo-dissociation of ion–molecule adducts which, in effect, yields a vibrational signature of the adduct in question. In addition OPO lasers have recently become available with tunability through the common fingerprint range of many molecules in the 600–2000 cm−1 range. Although the power of these OPO lasers is usually insufficient to induce the dissociation of strongly hydrogen bonded adducts, the use of a “messenger” atom or molecule,3 weakly attached to the species of interest, permits a vibrational signature to be obtained through the loss of the messenger species. Both FEL and OPO techniques have recently been applied to the investigation of the vibrational spectrum of the H5O2+ species. The two FEL studies4,5 and the OPO investigation6 all agree on the presence of an intense band in the 1740–1770 cm−1 range corresponding to the bending motion of the terminal water molecules with mixing of the central O–H–O stretch. Based on a fairly low level density functional theory (DFT) calculation of the harmonic frequency of the central O–H–O asymmetric stretch as 1004 cm−1, Fridgen et al.4 assigned the relatively sharp feature in their FEL spectrum at 990 cm−1 to this vibration. Using a more sophisticated quantum 4D model Vener et al.7 calculated a value of 1158 cm−1 for this vibration to which Asmis et al.5 assigned a 1317 cm−1 feature in their FEL spectrum. The OPO-messenger technique of Headrick et al.6 yields much sharper features, although admittedly somewhat blue-shifted in the case of the asymmetric stretch by the perturbation induced by the presence of the Ar or Ne messenger.8 They find this band to be centered at 1080 cm−1 and estimate the blue-shift to be on the order of 60–110 cm−1 which would place the vibration for the isolated H5O2+ species at 970–1020 cm−1, in excellent agreement with the 990 cm−1 experimental assignment of Fridgen et al.4
Protonated dimers of oxygen n-donor bases in general represent an especially interesting class of species for study. The high electronegativity of oxygen results in substantial hydrogen bond energies. For example, Larson and McMahon9 have shown experimentally that symmetric proton bound dimers of oxygen bases, no matter of what functionality, all have hydrogen bond strengths of 30.5 ± 1 kcal mol−1 and quantum chemical calculations suggest that all have a symmetric, single minimum structure associated with the central proton. With the exception of the hydrogen bonds found in the bifluoride ion,10,11 FHF−, and the proton-bound dimer of fluoromethane,12 (CH3F)2H+, these represent the strongest known hydrogen bonds and are thus of considerable interest to study as a class of bonding. Moore et al.13 were the first to investigate the IR spectrum of proton bound dimers of an organic oxygen base using a FEL facility. They obtained the IR photo-dissociation spectra of the proton bound dimers of dimethyl ether and diethyl ether from 600–1800 cm−1. In both cases a well resolved feature was observed between 750 and 825 cm−1 which could be associated with the asymmetric stretch mode of the O–H–O unit. Fridgen et al.14 subsequently obtained spectra of the homogenous-proton bound dimers of dimethyl ether, tetrahydrofuran and 1,4 dioxane. The spectrum for dimethyl ether was in excellent accord with that of Moore et al.13 and they also showed that the two cyclic ethers each exhibited well resolved bands in the same range for the asymmetric stretch at 801 and 753 cm−1, respectively. In addition the IRMPD spectrum of protonated diglyme was also obtained which, in essence is an intramolecular symmetric proton bound dimer.13 It too showed a sharp absorption feature at 760 cm−1 associated with the asymmetric stretch of the intramolecular bonding hydrogen. It is noteworthy that, in the cases of all of the symmetric proton bound dimer of ether species studied, excellent agreement was obtained between hybrid-DFT (B3LYP/6-31+G**) calculated vibrational frequencies for the asymmetric stretching motion and those experimentally observed.14 This was, however, not the case for asymmetric proton bound dimers where considerable differences between calculated and observed frequencies were found.14 This can be attributed to the sensitivity of the calculated frequency to the exact position of the bridging proton in the asymmetric hydrogen bond. While minor displacements have little effect on the hydrogen bond energy, due to the rather flat nature of the potential, such displacements can, in fact, have a considerable influence on the calculated vibrational frequency.
In the present work, the study of the vibrational signature of proton bound dimers of oxygen n-donor bases is extended to alcohols. These species represent an interesting case since they are intermediates in the SN2 reaction between protonated and neutral alcohols from which water elimination may occur to yield protonated ether as the ionic product (see eqn (1) and Scheme 1).
| |  | (1) |
Thus the dissociation of activated
proton bound dimers may proceed either
via simple dissociation to yield the protonated plus neutral
alcohol (
eqn (2)) or
via rearrangement to the S
N2 intermediate to yield protonated
ether plus
water. Fridgen and McMahon have previously examined the potential energy surfaces for these reactions, both experimentally and theoretically, and found that the S
N2 reaction channel is favored enthalpically, although involving a tighter, less entropically favored, transition state.
15,16 In previous IRMPD experiments using a continuous wave CO
2 laser, Bomse and Beauchamp
17 observed exclusive formation of protonated
ether products from the
proton bound dimers of
methanol,
ethanol and
iso-propanol. For
n-propyl and
n-butyl alcohol
proton bound dimers, however, other products were observed. In the
n-propyl case, for example, the major ionic product was protonated
n-propanol from simple bond cleavage (
eqn (2)) with small amounts of protonated di
n-propyl ether (17%) and a protonated propanol–
water adduct (12%,
eqn (3)) being formed.
| |  | (2) |
| |  | (3) |
In addition to the straightforward assignment of the vibrational spectra of
proton bound dimers of
alcohols, the present work shows very interesting trends in branching ratios for the possible dissociation products. These trends provide some considerable insight into the nature of the FEL IR photo-dissociation process.
2. Methods
2.1 Experimental
The coupling of the FTICR and FEL as well as the method for generating the proton bound dimers has been described in detail previously14 and will not be repeated here. All experiments were conducted at the Centre Laser Infrarouge d’Orsay (CLIO),18 which houses a free electron laser (FEL) to which a Mobile Ion Cyclotron Resonance Analyser (MICRA)19 has been coupled. IRMPD Efficiency spectra are obtained by observing IRMPD of an ion of interest and all photoproducts of IRMPD as a function of radiation wavelength. The IRMPD efficiency is defined in eqn (4).| |  | (4) |
The FEL wavelength was scanned by ∼5 cm−1 steps, the laser bandwidth is about 0.3–0.5% of the spectral wavelength. Ions were irradiated for typically 2 s. The laser wavelength and its bandwidth are monitored with a monochromator associated with a spiricon multichannel detector.
2.2 Computational
Geometry optimization and frequency calculations were performed using the hybrid density functional method B3LYP and the 6-31+G** basis set within the Gaussian 0320 suite of programs. These calculations have proven to be quite adequate in predicting the infrared spectrum of the proton-bound dimer of water4 and the complex of H5O2+ with Ar,6 as well as various ether proton-bound dimers.14 Except for protonated propanol the infrared frequencies were used unscaled.
2.3 RRKM calculations
The rate constants for the SN2 reaction and for simple dissociation of the proton-bound alcohol dimers, eqn (1) and (2), respectively were calculated using RRKM theory21 given by,| |  | (5) |
where σ is the symmetry number, h is Planck’s constant. The sum (N≠) and density (ρ) of states were calculated using the Beyer–Swinehart direct count algorithm, E is the internal energy of the reacting proton-bound dimer, and E0 is the activation energy. The vibrational wavenumbers for the proton-bound dimers of methanol, ethanol and propanol as well as the transition states for reactions 1 and 2 used in this RRKM modeling were taken from McCormack and Mayer.22 The activation energies used were 135, 135 and 132 kJ mol−1 for the methanol, ethanol, and propanol proton-bound dimers, respectively,23 for the simple dissociation reaction (eqn (2)) and were 16.9, 16.1 and 15.7 kJ mol−1 less, respectively, for the SN2 reactions (eqn (1)).15,16
3. Results and discussion
3.1 IRMPD of protonated alcohol dimers
Upon resonant infrared irradiation of the alcohol proton-bound dimers with the CLIO FEL dissociation was observed. For all three proton bound dimers the observed products following infrared multiple photon absorption included protonated alcohol, produced by loss of neutral alcohol (eqn (2)), as well as protonated ether formed by dehydration of the proton-bound dimer (eqn (1)). In Fig. 1 is shown the mass spectra recorded without (Fig. 1a) irradiating proton-bound ethanol dimers and after irradiation of proton-bound ethanol dimers with light centred at 760 cm−1 from the CLIO FEL (Fig. 1b), clearly showing both products.
 |
| | Fig. 1 Mass spectra recorded after (a) no irradiation and (b) irradiation of ethanol proton-bound dimers with the CLIO FEL tuned to produce light with a wavenumber value of 760 (±10) cm−1. | |
In previous experiments conducted by irradiating proton-bound alcohol dimers with a low-powered (15–50 W cm−2) CO2 laser (10.6 mm line), Bomse and Beauchamp17 found that only when the alkyl group (R) is n-propyl, i-propyl, and s-butyl, were multiple products observed. When R is methyl or ethyl, the only products were the protonated ethers, eqn (1), as discussed above. For the proton-bound dimer of n-propanol the major ionic product was protonated propanol at 71% (eqn (2)). That multiple products are also observed for R = CH3 and CH2CH3 in the present IRMPD experiments certainly deserves some discussion.
3.1.1 IRMPD of methanol proton-bound dimer.
As already stated, for the present experiments both protonated ether and protonated alcohol were observed for the proton-bound dimers of methanol, ethanol and propanol. In the case of methanol, the major dissociation product was observed at m/z 47, protonated dimethyl ether. Fig. 2 contains a plot of the product signal intensities against the wavenumber of irradiation as well as the IRMPD efficiency spectrum (or infrared spectrum) of protonated methanol (to be discussed in Section 3.2.1). It is interesting to compare these two plots. It should be pointed out first, that over the entire range of the infrared covered in these experiments, the proton-bound dimer dissociates to a small extent indicating that there is at least a small amount of absorption by the proton-bound dimer at all frequencies. Both products increase in intensity upon strong absorption as might be expected for two competing dissociation pathways. What may not be quite apparent from Fig. 2, is that during a strong absorption of the CLIO FEL, m/z 33 increases by a greater amount than m/z 47. This is more clearly shown in Fig. 3 which is a plot of intensity ratios (m/z 47 ∶
m/z 33) against the wavenumber of the light impinging on the ions. Upon irradiation of the ions where absorption is the greatest (858 cm−1) the ratio of products is smaller, meaning that more m/z 33 compared to m/z 47 is produced, however, the ratio does stay above 1. The ratio increases for weaker absorptions (more m/z 47).
 |
| | Fig. 2 Plot of the product ion intensities (m/z 47 circles and m/z 33 squares) vs. wavenumber (ordinate on the left) as well as the IRMPD spectrum of the methanol proton-bound dimer (ordinate on the right). The grey bar indicates the magnitude of background signal intensity for the mass spectra. | |
 |
| | Fig. 3 Plot of the ratio of product ion intensities (m/z 47 ∶
m/z 33) vs. radiation wavenumber. Also shown is the IRMPD efficiency spectrum for protonated methanol. The arrows point toward the ordinate for each plot. The stars at the bottom of the spectra are the points selected for the filled symbols in Fig. 4. | |
Another possibility for the higher energy dissociation (eqn (2)) is subsequent IRMPD of m/z 47, eqn (6). It is necessary to rule out this other pathway for formation of m/z 33 prior to discussing the wavenumber-dependent branching ratio. The reaction in eqn (6) would involve a rearrangement concomitant with or prior to dissociation, and would be expected to have a significant barrier.
| |  | (6) |
This reaction can be ruled out since simple cleavage,
eqn (7), is more thermodynamically favoured by 65 kJ mol
−1 and would not have a significant central energy barrier. If
m/
z 47 were subsequently undergoing IRMPD, CH
3+ (
m/
z 15) would be the expected product which is not observed.
| |  | (7) |
The most convincing evidence for
m/
z 33 being a primary photoproduct of methanol
proton-bound dimer IRMPD, and not sequential IRMPD of protonated dimethyl ether, is that no
m/
z 33 was observed during the IRMPD of the dimethyl ether
proton-bound dimer
14 which produces
m/
z 47 (protonated dimethyl ether) exclusively.
In Fig. 4, the intensity ratio is plotted against the IRMPD efficiency which shows that at higher IRMPD efficiency, the ratio is low and vice versa. In the Bomse and Beauchamp experiments,17 the 10.6 mm line of the CO2 laser (∼945 cm−1) is not where the methanol proton-bound dimer is very strongly absorbing, but in this region, in the present experiments, the m/z 47 ∶
m/z 33 ratio is between 3 and 4. That m/z 33 is still observed in the present experiments likely means that the proton-bound dimers are absorbing more photons than necessary to dissociate by the lowest-energy route (eqn (1)) in the present experiments. The power density of the CLIO FEL has been measured to be on the order of 106 W cm−2 over the infrared range studied here, significantly higher than for a CO2 laser. The enthalpy barrier for the reaction in eqn (1) was experimentally determined to be ∼17 kJ mol−1 below that for the simple dissociation reaction (eqn (2)).15 This energy is less than that contained in two infrared photons (860 cm−1
≈ 10.3 kJ mol−1) in the range of the present experiments. The observation of more of the higher energy dissociation product (protonated methanol) at wavenumber positions where the proton-bound dimer absorbs more strongly suggests that the proton-bound dimer, upon irradiation at these wavenumbers, has an internal energy which is high enough that the dissociation pathway (eqn (2)) has a higher rate constant than the SN2 pathway (eqn (1)). Therefore, when the proton-bound dimer absorbs strongly, absorption competes effectively with the SN2 reaction pathway (eqn (1)), thereby increasing the internal energy of the proton-bound dimer, making the simple dissociation pathway (eqn (2)) more efficient. In Fig. 5 is plotted the RRKM calculated rate constants for the reactions in both eqn (1) and (2) against the number of photons absorbed (bottom axis) or against the internal energy content (top axis) for the methanol proton-bound dimer. It is shown from this figure that after absorption of about 12 photons (at 1000 cm−1) H2O elimination (eqn (1)) is possible. Above 1.94 eV internal energy (or after absorption of ∼16 photons) the simple dissociation mechanism (eqn (2)) becomes the dominant dissociation pathway. This is consistent with our explanation if the rate of photon absorption at the wavelength positions where the proton-bound dimer absorbs very strongly is greater than the rate of reaction in eqn (1).
 |
| | Fig. 4 Plot of the product ion intensity ratio (m/z 47 ∶
m/z 33) vs. IRMPD efficiency. The filled circles are the intensities and efficiencies for the band maxima. | |
 |
| | Fig. 5 RRKM calculated rate constants as a function of internal energy (top axis) and number of 1000 cm−1 photons absorbed (bottom axis) for the methanol proton-bound dimer dissociating according to eqn (1) (solid line) and eqn (2) (dashed line). | |
For completion it should be noted that protonated dimethyl ether was found to be only a minor dissociation product in CO2 laser IRMPD experiments.24 Double-resonance experiments showed that it was not formed via the m/z 33 IRMPD product reacting with background methanol. We can offer no explanation at this time for the fact that m/z 33 is the dominant IRMPD product in Peiris et al.24 experiments.
3.1.2. IRMPD of ethanol and propanol proton-bound dimers.
IRMPD of the proton-bound dimer of ethanol produces predominantly m/z 47 (protonated ethanol) viaeqn (2), with some m/z 75 (protonated diethyl ether). Here as well, there is evidence for some variation in the m/z 75 ∶
m/z 47 ratio as shown in Fig. 6. Note that the ratio only varies by a factor of 2.5 whereas for the proton-bound dimer of methanol, the ratio varies by a factor of about 5. In the case of the ethanol proton-bound dimer some IRMPD of the m/z 75 photoproduct, cannot be completely excluded. Tonner and McMahon25 observed almost complete dissociation of protonated dimethyl ether (eqn (8)) after 30 s irradiation with a CO2 laser operating at 10.6 μm (943 cm−1) and 10 W cm−2.| |  | (8) |
Moore also observed some m/z 47 in their IRMPD experiments on the proton-bound diethyl ether dimer which was presumably due to sequential IRMPD.26
 |
| | Fig. 6 Plot of the ion product intensity ratios (m/z 75 ∶
m/z 47) vs. radiation wavenumber for IRMPD of the ethanol proton-bound dimer. Also shown is the IRMPD efficiency spectrum for proton-bound dimer of ethanol. The arrows point toward the ordinates for each plot. | |
In previous experiments by Solca and Dopfer on the ethanol proton-bound dimer in the 3400–3700 cm−1 range using a Nd/YAG-pumped OPO laser only the m/z 47 photoproduct was monitored.27 That in these experiments using an OPO, the protonated ethanol photoproduct was observed is also evidence that the higher energy photoproducts are observed for high intensity lasers as opposed to the experiments conducted with a low-power CO2 laser.17 The results of the present experiments, however, imply that in order to get an accurate IRMPD spectrum it might be necessary to monitor all photoproducts. Since the variation of the branching ratio with intensity is small for the ethanol proton-bound dimer it is expected that the effects on the spectra produced by Solca and Dopfer27 experiments would be minimal.
Observed IRMPD photoproducts of the propanol proton-bound dimer (m/z 121) include m/z 103 (protonated dipropyl ether), m/z 61 (protonated propanol) and m/z 43 (protonated propene). Protonated propene most likely occurs due to IRMPD of protonated propanol. This was confirmed by isolating protonated propanol and conducting the same IRMPD experiments. The ratio of primary photoproducts of the propanol proton-bound dimer, m/z 103 ∶
m/z 61, is virtually unvaried over the range of infrared shown in Fig. 7, unlike the other proton-bound dimers. As well, the average ratio is about 1 ∶ 10 for these products, showing even less dehydration product (eqn (1)) than the previous two proton-bound dimers, even though the potential energy surfaces are similar, i.e. the enthalpy threshold for dehydration is 15.7 kJ mol−1 less16 than that for dissociation into the neutral and protonated alcohol. Note that the intensity of m/z 43 was included in the intensity of m/z 61 in order to obtain the m/z 103 ∶
m/z 61 ratio (Fig. 7).
 |
| | Fig. 7 Plot of the ion product intensity ratios (m/z 103 ∶
m/z 61) vs. radiation wavenumber for IRMPD of the propanol proton-bound dimer. Also shown is the IRMPD efficiency spectrum for proton-bound dimer of propanol. The arrows point to the corresponding ordinates. | |
For methanol, the rate constants for the two pathways become equal after the proton-bound dimer absorbs 16 photons (1.94 eV internal energy) and have a value of ∼1.3 × 107 s−1. In experiments conducted with a low power CO2 laser,17,28 dissociation must be dominant over net29 IRMP absorption which is why only the product with the lowest energy requirement (SN2 pathway, reaction 1) is observed. In the present experiments on the proton-bound methanol dimer, both products are observed because a very high powered laser is used so that IRMP absorption is competing with the dissociation processes. Furthermore, when the molecule absorbs most strongly, net IRMP absorption is even faster such that enough photons are absorbed to make reaction 2 more competitive with reaction 1. For the ethanol and propanol proton-bound dimers, the rate constants become equal at higher internal energies, 2.10 eV and 2.28 eV, respectively, where the rate constants are 6.3 × 104 and 1.0 × 105 s−1, respectively, two orders of magnitude lower than the rate constants for the proton-bound dimer. Since the IR absorption cross sections for all three proton-bound dimers are predicted to be similar, the rate constant for IRMP absorption is expected to be similar for all three proton-bound dimers. It is therefore easy to postulate that the ethanol and propanol proton-bound dimers will absorb more photons than the methanol proton-bound dimer prior to dissociation, increasing the internal energy to such a level that the rate constant for the higher energy route, eqn (2), is greater making this simple dissociation channel the dominant one. In fact, this explanation is consistent with the observation of both reaction channels for the propanol proton-bound dimer being observed in the CO2 laser IRMPD experiments by Bomse and Beauchamp.17 Even with the low-power CO2 laser, the rate of absorption is competitive with the dissociation rates, especially for the larger proton-bound dimers.
3.2.1 Proton-bound dimer of methanol.
In Fig. 8 and Fig. 9 the IRMPD spectrum of the methanol proton-bound dimer is presented (solid black trace). Also shown in Fig. 9 are the computed infrared spectra for the two lowest energy structures found at the B3LYP/6-31+G** level of theory. The computed spectra shown are unscaled. Conformer MA is lower in energy than MB by only 1.3 kJ mol−1. Both conformers are of C2 symmetry and their geometries are shown in Fig. 10.
 |
| | Fig. 8 RRKM calculated rate constants as a function of internal energy (top axis) and number of 1000 cm−1 photons absorbed (bottom axis) for the ethanol (A) and propanol (B) proton-bound dimer dissociating according to eqn (1) (solid line) and eqn (2) (dashed line) | |
 |
| | Fig. 9 IRMPD efficiency spectrum for the methanol proton-bound dimer (solid trace) as well as the calculated infrared spectrum (B3LYP/6-31+G**, no scaling) for two conformers of the methanol proton-bound dimer. The vertical dashed line shows the position of the C–O stretch for neutral methanol and the arrow indicates the position of an absorption determined using a CO2 laser (see text).24 | |
 |
| | Fig. 10 Structures of two conformers of the methanol proton-bound dimers. | |
The strongest absorption is centred at 866 cm−1 and is attributed to the asymmetric O–H–O stretch. This strong band is in the same vicinity as was observed for the homogenous proton-bound dimers of ether previously.13,14 For both conformers, the O–H–O asymmetric stretch is predicted to occur at 801 cm−1 (796 cm−1 for conformer MA) which is in general agreement. The band observed at 982 cm−1 is most likely the C–O stretching vibration. For conformer MA, the in-phase (ip) and out of phase (op) C–O stretches are both predicted to occur at 969 cm−1, the op stretch is predicted to be of considerable intensity. For the conformer MB, the C–O stretching vibrations are predicted to occur at 953 cm−1 (op) and 991 cm−1 (ip). These predicted values are in good agreement with the observed band. In the gas-phase30 the C–O stretch for neutral methanol is centred at 1033.5 cm−1 (indicated by the vertical dashed line in Fig. 9) and is predicted to occur at 1045.9 cm−1 (unscaled) by the same level of theory as used here for the proton-bound dimers. The red-shift of the C–O stretch for the proton-bound dimer makes sense since the C–O bond length is expected to increase and weaken upon protonation. The calculations predict an increase in C–O bond length in the proton-bound dimer to 1.47 Å from the neutral value of 1.426 Å.
The broad band observed from 1070–1225 cm−1 is assigned to the COH bend. The most intense modes predicted in this region (Fig. 9) are COH bending motions (which are also coupled to O–H–O stretching and CH3 rocking) occurring at 1071 and 1106 cm−1 for conformers MB and MA, respectively. CH3 d-deformation is also predicted to occur in this region, but with insignificant intensity. Neutral methanol also has COH bend and CH3 wagging in this region, but they are significantly weaker than the C–O stretch. That the COH bend is higher in intensity (predicted and observed) for the methanol proton-bound dimer is likely due to its being coupled to the O–H–O asymmetric stretching motion. The next band observed from 1330–1425 cm−1 can also be assigned to CH3 rocking coupled to COH bending, but for this mode the HCO and HOC angles are in phase. Again, there is some O–H–O asymmetric stretching associated with this which may account for its intensity.
Finally, there is a broad feature observed between 1467 and 1634 cm−1. The strongest predicted bands in this region are CH3 s-deformation (umbrella) modes at 1516 and 1543 cm−1, for the conformer MB and MA, respectively, and the HOH bending modes at 1570 and 1638 cm−1 for conformer MB and 1520 and 1639 cm−1 for conformer MA. For neutral methanol, the umbrella mode is predicted to occur at 1484 cm−1 (experimental value, 1455 cm−1) but with insignificant intensity. There is obviously no HOH bend for neutral methanol and these are characteristic solely of the proton-bound alcohol dimers. The observed infrared bands along with those calculated to be the most intense are summarized in Table 1.
Table 1 Summary of observed and B3LYP/6-31+G** predicted infrared bands for the methanol proton-bound dimer
| |
|
Predicteda/cm−1 |
|
| Observed/cm−1 |
Assignment |
Conformer MA |
Conformer MB |
Neutral methanolb (gas-phase/cm−1) |
|
Values in parentheses are calculated intensities in km mol−1.
Ref. 30.
|
| 866 |
O–H–O asym str |
796 (2394) |
801 (2449) |
|
| 982 |
CO str |
969 (196) |
991 (55) |
1033.5 (vs) |
| 1070–1225 |
COH bend/CH3 rock/O–H–O asym str |
1106 (469) |
1071 (766) |
1060 (w) |
| CH3 d-deformation/CH3 rock |
1178 (77) |
1177 (78) |
1165 (w) |
| 1330–1425 |
In phase COH bend/CH3 rock/ O–H–O asym str |
1421 (505) |
1352 (578) |
1345 (s) |
| 1467–1634 |
CH3 s-deformation (umbrella) |
1543 (760) |
1516 (263) |
1455 (m) |
| HOH bend |
1520 (346) |
1570 (73) |
|
| |
1639 (69) |
1638 (741) |
|
In previous experiments24 using a CO2 laser, and based on the extent of dissociation, a sharp feature was found to occur at 1039.36 cm−1 (arrow in Fig. 9). This band actually occurs at a position which is a minimum in IRMPD efficiency in the present experiments. We do not have an explanation for this.
3.2.2 Proton-bound dimer of ethanol.
The IRMPD efficiency spectrum of the ethanol proton-bound dimer is shown in Fig. 11. Also shown are calculated spectra of the three lowest energy conformers identified. The lowest energy conformer (EA) is of C2 symmetry as is the second lowest energy conformer (EB). The third lowest energy conformer (EC) is of C1 symmetry. In all, seven distinct conformers were found, all within 7.1 kJ mol−1, and more may exist. In fact, nine conformers of the neutral ethanol dimer were determined computationally in a recent publication.31 In Fig. 12, only the structures of the three lowest energy conformers mentioned above are outlined as a full study of the possible conformers is beyond the scope of this work.
 |
| | Fig. 11 IRMPD efficiency spectrum for the ethanol proton-bound dimer (solid trace) as well as the calculated infrared spectrum (B3LYP/6-31+G**, no scaling) for three conformers of the ethanol proton-bound dimer. | |
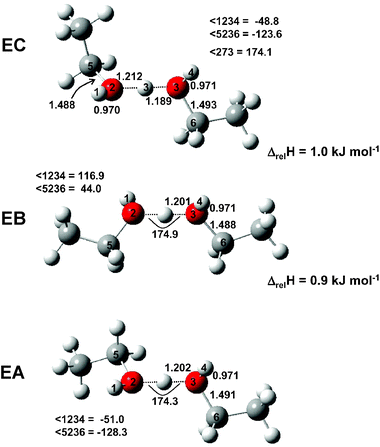 |
| | Fig. 12 Structures of the three lowest-energy conformers found for the ethanol proton-bound dimer. | |
The O–H–O asymmetric stretch of the ethanol proton-bound dimer is found at a somewhat lower wavenumber position, 760 cm−1, than for the methanol proton-bound dimer, 866 cm−1, a difference of 106 cm−1. The calculations also predict a significant shift, 82 cm−1, which is in good agreement with experiment (compare Fig. 9 and 11, as well as Tables 1 and 2).
Table 2 Summary of observed and B3LYP/6-31+G** predicted infrared bands for the ethanol proton-bound dimer
| |
Predicteda/cm−1 |
|
| Observed/cm−1 |
Assignment |
Conformer EA |
Conformer EB |
Conformer EC |
Neutral ethanolb |
|
Values in parentheses are calculated intensities in km mol−1.
Ref. 32.. In CD3CH2OH. |
| 760 |
O–H–O asym str |
714 (2638) |
714 (2788) |
725 (211) |
|
| 956 |
CCO sym str/O–H–O str |
867 (583) |
870 (509) |
874 (512) |
884.6 |
| 1078 |
CCO asym str |
1073 (173) |
1059 (347) |
1081 (209) |
1089.2 |
| 1137 |
CH2 rocking |
1164 (249) |
1163 (301) |
1156 (194) |
Not observed |
| 1238–1660 |
OH bend/CH2 twist |
1293 (198) |
1283 (542) |
1289 (183) |
1241.3 |
| |
1341 (676) |
|
|
| HOH bend |
1427 (1201) |
1565 (89) |
1447 (1191) |
|
| 1636 (91) |
1630 (668) |
1645 (82) |
|
| CH2 wag/CH3 umbrella |
1435 (311) |
1435 (6) |
1431 (88) |
1393.7 |
| |
|
1434 (36) |
|
| CH3 asym def |
1501 (1.1) |
1500 (10) |
1503 (115) |
1451.6 |
| CH2 deformation |
1535 (201) |
1523 (27) |
1526 (160) |
1490c |
The CCO symmetric stretch is predicted to be coupled to motion of the proton between the two monomers motion and is seen to occur at 956 cm−1 based on comparison with the predicted position and intensities as well as comparison with the methanol proton-bound dimer spectrum. For comparison, the symmetric C–C–O stretch of gas-phase neutral ethanol32 (also coupled to HCC bending) occurs at 884.6 cm−1. It is difficult to compare the modes observed in neutral ethanol and the proton-bound dimer due to the coupling of motion of the central proton which obviously cannot be the case for neutral ethanol.
The next band is seen to be somewhat resolved showing two features centred at 1078 and 1137 cm−1 which are assigned to asymmetric C–C–O stretching and CH2 rocking, respectively. The asymmetric C–C–O stretch in gas-phase neutral ethanol occurs at a similar position, 1089.2 cm−1. The next feature is abroad, perhaps with some resolved features occurring between 1238–1660 cm−1. Rather than assigning any of the resolved features, a number of modes predicted to be fairly intense are listed in Table 2. This broad feature is most likely due to CH2 and CH3 motions and quite obviously, HOH bending as it is the strongest predicted absorption.
3.2.3 Proton-bound dimer of propanol.
In Fig. 13 two IRMPD spectra of the propanol proton-bound dimer (solid line). For the less intense spectrum, an attenuator was used to decrease the intensity of light impinging on the ions from the CLIO FEL by a factor of three. That the relative intensities of the bands remains similar in both spectra suggests that IRMPD is not saturated at full laser power. The spectrum of the propanol proton-bound dimer may, at first glance, seem different from the methanol and ethanol proton-bound dimers (see Fig. 14). The band(s) around 750 cm−1 are not nearly as intense as observed for the other alcohols and there are more bands resolved in the rest of the spectrum. Clearly the spectrum of the propanol proton-bound dimer is more complex and will prove to be more difficult to interpret, which might be expected since there are significantly more vibrational modes compared to the ethanol and methanol proton-bound dimers. There are also, however, many similarities between the three spectra. While the methanol proton-bound dimer O–H–O asymmetric stretch is significantly red-shifted, for the ethanol and propanol proton-bound dimers this mode occurs in the same vicinity, an observation which is reproduced by theory (see Fig. 13 and Table 3). The bands observed with maxima at 737, 758(shoulder), and 802 cm−1 are likely all O–H–O asymmetric stretching modes of different conformers. As well, the band centred at 982 cm−1 is most likely the C–O stretching vibration based on comparing the bands observed for the other dimers and the calculated spectra (see Table 3 and Fig. 13). Finally the broad band between 1300 and 1600 cm−1, perhaps with resolved features, is similar in shape and position to the one observed for the ethanol proton bound dimer and the two bands at higher wavenumber for the methanol proton-bound dimer. In Table 3 the most intense bands predicted by theory are presented for the three lowest-energy structures (shown in Fig. 15).
 |
| | Fig. 13 IRMPD efficiency spectrum for the ethanol proton-bound dimer (black trace) as well as the calculated infrared spectrum (B3LYP/6-31+G**, no scaling) for three conformers of the propanol proton-bound dimer. The colours of the calculated spectra correspond to the coloured dots in Fig. 13. | |
 |
| | Fig. 14 Comparison of the IRMPD efficiency spectrum for the methanol, ethanol and propanol proton-bound dimers. | |
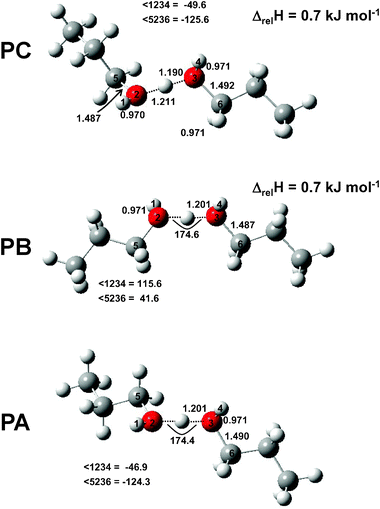 |
| | Fig. 15 Structures of the three lowest-energy conformers found for the propanol proton-bound dimer. | |
Table 3 Summary of B3LYP/6-31+G** predicted infrared bands for the propanol proton-bound dimer
| |
|
Predicteda/cm−1 |
| Observed/cm−1 |
Assignment |
Conformer PA |
Conformer PB |
Conformer PC |
|
Values in parentheses are calculated intensities in km mol−1.
|
| 737 |
O–H–O asym str |
710 (3160) |
708 (3419) |
734 (2444) |
| 758sh |
| 802 |
| 852 |
CH2/CH3 twisting and rocking |
904 (101) |
906 (97) |
901 (65) |
| 903 |
| 982 |
CO str |
968 (298) |
958 (101) |
972 (276) |
| 1030–1140 |
CH2/CH3 wagging |
1106 (224) |
1088 (579) |
1110 (249) |
| 1150–1280 |
CH2 twisting |
1172 (229) |
1170 (286) |
1166 (186) |
| 1256 (216) |
1250 (529) |
1256 (216) |
| 1290–1650 |
CH2 wagging |
1324 (75) |
1312 (460) |
1326 (26) |
| |
1351 (228) |
|
| CH3 umbrella |
1415 (484) |
1423 (87) |
1409 (132) |
| |
|
1418 (92) |
| COH bend/CH2 scissors |
1442 (733) |
|
1450 (1195) |
| CH2 wag |
1432 (347) |
|
|
| CH3 scissors |
1495 (125) |
|
1503 (154) |
| CH2 scissors |
1511 (64) |
|
1511 (59) |
| 1523 (70) |
|
1524 (95) |
| HOH bend |
1449 (94) |
1573 (72) |
1642 (82) |
| |
1620 (728) |
|
3.2.4. Protonated propanol.
Fig. 16 shows the experimental spectrum for protonated propanol (dark solid line). Also displayed in Fig. 16 are calculated spectra of four conformers of protonated propanol whose wavenumber positions have been scaled by 0.96. It was considered to be fair to use a scaling factor in the case of protonated propanol since the modes in this species are not unlike those for which scaling factors were derived. This is not the case for the proton-bound dimers with weaker hydrogen bonding which do not have enough data to assign a scaling factor with confidence. The agreement between the experimental and calculated spectra is very good.
 |
| | Fig. 16 IRMPD efficiency spectrum of protonated propanol as well as computed infrared spectra (B3LYP/6-31+G**, scale factor = 0.96) of four conformers of protonated propanol. | |
The assignments in Fig. 16 are based on comparing the experimental and computed spectra. The strongest band observed, centred at 1591 cm−1, is the HOH bend which is in almost exactly the same position as the bend for gas-phase water, 1595 cm−1.33 Obviously, in neutral ethanol this mode does not exist and there is no absorption in this region of neutral ethanol’s infrared spectrum.34 The C–O stretch of neutral propanol occurs at 971 cm−1 in the gas phase.34 This band is significantly shifted to a lower wavenumber, predicted to occur at ∼650 cm−1 based on the calculated spectrum and is not observed in these experiments due to the use of ZnSe windows. The red shift of the C–O stretch upon protonation is most likely to be due to the change in the C–O bond length which is 1.57 Å in protonated propanol and 1.43 Å in neutral propanol. A weaker band observed at 743 cm−1 is assigned to the CO stretch/OH2 wag.
3.2.5. Heterogeneous propanol/H2O proton-bound dimer.
The observed IRMPD fragments for m/z 79, the mixed propanol/H2O proton-bound dimer, are m/z 61 (major product), 43, 37 and 19. Presumably the primary IRMPD product ions are protonated propanol, m/z 61, and the proton-bound water dimer, m/z 37, which both have very similar reaction enthalpies, differing by only 1 kJ mol−1, based on heats of formation for H5O2+, H2O, protonated propanol and propene of 213, −242, 476 and 20.2 kJ mol−1, respectively.23 As discussed above, m/z 43 is a product of subsequent IRMPD of protonated propanol and m/z 19 is formed from subsequent IRMPD of m/z 37. Both m/z 43 and m/z 19 were observed in only very small amounts.
The IRMPD efficiency spectrum is shown in Fig. 17 along with the computed spectrum (dashed line) of the lowest-energy isomer found for the proton-bound propanol/water dimer. It is fairly obvious that the experimental and calculated spectra are not in nearly as good agreement as for the homogenous proton-bound dimers presented above and previously.4,14 The C–O bond of this mixed dimer is predicted to be 1.52 Å, shorter than in protonated propanol, due to the “sharing” of the proton between the two monomers. The C–O bond length is also predicted to be longer than in the proton-bound dimer of propanol since in the mixed proton-bound dimer, the proton is bound more strongly to the oxygen than in the homogeneous dimer. It is expected then, that the C–O stretch would be to the blue of that observed in protonated propanol. The band centred at 821 cm−1 is most likely the C–O stretch which is predicted to occur at 823 cm−1. The broad band centred at 1775 cm−1 is assigned to the HOH bending modes (in phase and out of phase) of the two H2O moieties. The HOH bend of the protonated water dimer was found to occur at 1756 cm−1,4 in the same vicinity as that observed here for the proton-bound propanol/water dimer. The calculated bands are predicted to occur at 1615 and 1682 cm−1 in disagreement by some 100 cm−1. A similar disagreement between the level of theory used here and the experimental spectra of homogenous proton bound dimers was seen previously.14 The O–H–O stretch is predicted to occur at 2357 cm−1, well outside the present observation window.
 |
| | Fig. 17 IRMPD efficiency spectrum of the protonated propanol/water dimer (solid trace) and the B3LYP/6-31+G** spectrum (unscaled, dashed trace). | |
4. Conclusions
The infrared spectra of three homogeneous proton bound dimers (methanol, ethanol, and propanol) were recorded and bands were assigned based upon comparisons with the neutral alcohol infrared spectra and computed infrared spectra. Similarities in the three spectra, such as the position of the O–H–O asymmetric stretch and the C–O stretch as well as the COH bend are noted. The position of the O–H–O asymmetric stretch for these proton-bound dimers is also similar in position and prominence as for the ether proton-bound dimers reported previously. The B3LYP/6-31+G** calculations presented are shown to adequately compare with the experimental spectra. For the mixed water/propanol proton-bound dimer assignments were made to the C–O stretch as well as the HOH bend based on comparisons with the other spectra and that for the water proton-bound dimer where the HOH bend was previously assigned. Protonated propanol’s IRMPD spectrum was also assigned.
Two primary IRMPD photoproducts were observed for each of the alcohol proton bound dimers. These dissociation routes differ in that the simple dissociation pathway, forming protonated alcohol, is of higher energy but the entropy requirement is lower compared with the SN2 process. The ratio of these photoproducts were found to vary with the frequency of the radiation impinging upon the ions. For example, when the proton-bound dimer absorbs weakly a larger amount of SN2 product, protonated ether and water, are observed. When the proton-bound dimer absorbs more strongly an increase in the simple dissociation product, protonated alcohol and neutral alcohol, is observed. With the aid of RRKM calculations this frequency dependence of the branching ratio is explained assuming that photon absorption is faster than dissociation for these species and that only a few photons extra are necessary to make the higher-energy dissociation channel (simple cleavage) competitive with the lower energy (SN2) reaction channel.
Acknowledgements
The CLIO team, especially J. M. Ortega and F. Glotin, is gratefully acknowledged for their technical help. We also thank the CNRS and the Université de Paris XI for financial support. The Natural Sciences and Engineering Research Council of Canada is also acknowledged for financial support. The Atlantic Computational Excellence Network (ACENet) and the Memorial University of Newfoundland Advanced Computation and Visualization Centre is gratefully acknowledged for free computational resources. We would also like to thank the referees for their helpful comments.
References
- E. F. Valeev and H. F. Schaefer III, J. Chem. Phys., 1998, 108, 7197 CrossRef CAS.
- C. L. Janssen, W. D. Allen, H. F. Schaefer III and J. M. Bowman, Chem. Phys. Lett., 1986, 131, 352 CrossRef CAS.
- L. I. Yeh, M. Okumura, J. D. Myers, J. M. Price and Y. T. Lee, J. Chem. Phys., 1989, 91, 7319 CrossRef CAS.
- T. D. Fridgen, T. B. McMahon, L. MacAleese, J. Lemaire and P. Maitre, J. Phys. Chem. A, 2004, 108, 9008 CrossRef CAS.
- K. R. Asmis, N. L. Pivonka, G. Santambrogio, M. Brummer, C. Kaposta, D. M. Neumark and L. Woste, Science, 2003, 299, 1375 CrossRef CAS.
- J. M. Headrick, J. C. Bopp and M. A. Johnson, J. Chem. Phys., 2004, 108, 11523 CrossRef.
- M. V. Vener, O. Kuhn and J. Sauer, J. Chem. Phys., 2004, 114, 1462.
- N. I. Hammer, E. G. Diken, J. R. Roscioli, M. A. Johnson, E. M. Myshakin, K. Jordan, A. B. McCoy, X. Huang, J. M. Bowman and S. Carter, J. Chem. Phys., 2005, 122, 244301 CrossRef.
- J. W. Larson and T. B. McMahon, J. Am. Chem. Soc., 1982, 104, 6255 CrossRef CAS.
- T. B. McMahon and P. Kebarle, J. Am. Chem. Soc., 1983, 105, 2944 CrossRef CAS.
- P. G. Wenthold and R. R. Squires, J. Phys. Chem., 1995, 99, 2002 CrossRef.
- T. B. McMahon and P. Kebarle, J. Phys. Chem., 1986, 108, 6502 CAS.
- D. T. Moore, J. Oomens, L. van der Meer, G. von Helden, G. Meijer, J. Valle, A. G. Marshall and J. R. Eyler, ChemPhysChem, 2004, 5, 740 CrossRef CAS.
- T. D. Fridgen, L. MacAleese, P. Maitre, T. B. McMahon, P. Boissel and J. Lemaire, Phys. Chem. Chem. Phys., 2005, 7, 2747 RSC.
- T. D. Fridgen, J. D. Keller and T. B. McMahon, J. Phys. Chem. A, 2001, 105, 3816 CrossRef CAS.
- T. D. Fridgen and T. B. McMahon, J. Phys. Chem. A, 2002, 106, 9648 CrossRef CAS.
- D. S. Bomse and J. L. Beauchamp, J. Am. Chem. Soc., 1981, 103, 3292 CrossRef CAS.
- R. Prazeres, F. Glotin, C. Insa, D. A. Jaroszynski and J. M. Ortega, Eur. Phys. J. D, 1998, 3, 87 CrossRef CAS.
- G. Mauclaire, J. Lemaire, P. Boissel, G. Bellec and M. Heninger, Eur. J. Mass Spectrom., 2004, 10, 155 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, GAUSSIAN 03, (Revision B.04), Gaussian, Inc., Pittsburgh PA, 2003 Search PubMed.
-
T. Baer and W. L. Hase, Unimolecular Reaction Dynamics, Theory and Experiments, Oxford University Press, New York, 1996 Search PubMed.
- J. A. D. McCormack and P. M. Mayer, Int. J. Mass Spectrom., 2001, 207, 183 CrossRef CAS.
-
NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, June 2005, National Institute of Standards and Technology, Gaithersburg MD, 20899, (http://webbook.nist.gov) Search PubMed.
- D. M. Peiris, J. M. Riveros and J. R. Eyler, Int. J. Mass Spectrom. Ion Processes, 1996, 159, 169 CrossRef CAS.
- D. S. Tonner and T. B. McMahon, Anal. Chem., 1997, 69, 4735 CrossRef CAS.
-
D. T. Moore, personal communication, June 23rd, 2005.
- N. Solca and O. Dopfer, J. Am. Chem. Soc., 2004, 126, 9520 CrossRef CAS.
- G. Wu and A. Stace, Chem. Phys. Lett., 2005, 412, 1 CrossRef CAS.
- There are of course photon emission process in effect such as stimulated emission and the slower spontaneous emission which is why we say “net” absorption.
- A. Serrallach, R. Meyer and Hs. H. Günthard, J. Mol. Spectrosc., 1974, 52, 94 CrossRef.
- C. Emmeluth, V. Dyczmons, T. Kinzel, P. Botschwina, M. A. Suhm and M. Yáñez, Phys. Chem. Chem. Phys., 2005, 7, 991 RSC.
- J. P. Perchard and M. L. Josien, J. Chem. Phys., 1968, 65, 1834 CAS.
-
J.-M. Flaud, C. Camy-Peyret and R. A. Toth, Water Vapour Line Parameters from Microwave to Medium Infrared, Pergamon Press, London, 1981 Search PubMed.
- K. Fukushima and B. J. Zwolinski, J. Mol. Spectrosc., 1968, 26, 368 CrossRef CAS.
|
| This journal is © the Owner Societies 2006 |
Click here to see how this site uses Cookies. View our privacy policy here. 

























