A structural analysis of lead hydroxyvanadinite
Received
7th November 2005
, Accepted 16th February 2006
First published on 7th March 2006
Abstract
Hydroxyvanadinite, Pb10(VO4)6(OH)2, was prepared by the co-precipitation method and analyzed by X-ray absorption spectroscopy (XANES, EXAFS), infrared spectroscopy, Raman scattering and X-ray diffraction (XRD). The results showed that the structure is very similar to that of vanadinite, Pb10(VO4)6Cl2, with space group P63/m (176) and cell parameters a = 10.2242(3) Å and c = 7.4537(2) Å. A Rietveld refinement of the structure was performed using vanadinite as the starting model and fixing the geometry of the vanadate ion as a rigid body. First-principles Density Functional embedded cluster models are developed to analyze electronic structures, bonding, and densities of states. Interaction of Pb with the OH channel anion is examined in detail, as an important structural feature. A periodic band structure approach was used to obtain a further estimate of relaxed atomic coordinates.
1. Introduction
Apatites are generally described in the hexagonal symmetry group P63/m and expressed as M102+ (XO4)63− Z2−. These apatites can easily accommodate a great variety of substitutions, both anionic and cationic. For example, the M2+ sites can be occupied by cations like Ca2+, Sr2+, and Pb2+ among others, while the XO43− and the monovalent Z− ions are anions such as PO43−, VO43−, and OH−, Cl−, and F−, respectively. Interest in apatite compounds has grown in recent years due to their biological relevancy and their medical applications. Hydroxyapatite, Ca10(PO4)6(OH)2, containing several substitution ions such as CO32−, K+, Na+, Mg2+, Cl−, and F− is the main inorganic compound of calcified tissue (bone and teeth) and one of the most promising bioceramics for bone substitution and bone regeneration.1,2 In environmental applications, apatite compounds and apatitic phosphate rocks are proposed for heavy metal removal from contaminated soils and waste water.3,4 For this reason, several studies concerning the substitution mechanisms of calcium and phosphate by metals and metal complexes have been performed.5,6 Apatites with M = Pb2+, Sr2+ or Co2+ have also been proposed as catalysts.7,8 In a recent paper we suggested that a complete or partial substitution of the phosphate by the vanadate group in hydroxyapatite, Ca10(PO4)6(OH)2, could provide new redox properties to this material.8 It has been shown that the vanadate group can be reduced at high temperature when the sample is treated with hydrogen, inducing strong modification in the VO44− local chemical environment. Evidently, the reduction mechanism involves the formation of vanadate oxyapatite Ca10(VO4)6O as an intermediate compound.
Pursuant to our investigation on the M10(VO4)6(OH)2 compounds, we have synthesized hydroxyvanadinite (OH-VA), Pb10(VO4)6(OH)2, a compound that evidenced unexpected redox properties.9 This paper is thus devoted to an analysis of the geometric and electronic structure of this material. Its crystallographic structure was characterized using Rietveld refinement of XRD patterns. The local structure of vanadium sites is studied by XAS and Raman spectroscopies. The crystallographic structure of OH-VA obtained from Rietveld refinements is used to model this structure for the first time, employing a first-principles density functional (DF) method to understand the local electronic properties. These properties are compared to similar calculations on the well-established vanadinite (VA), Pb10(VO4)6Cl2, used as a structural prototype. The suggestion reported in the literature that Pb 6s electrons can play a significant role in the anisotropic variation of Pb10(PO4)6(Z)2, Z = OH−, F−, Cl−, Br−, cell parameters is also discussed. In particular, we examine the interaction of Pb with OH as a function of the anion position within the c-axis channel. Periodic band structure calculations are used to provide a further estimate of atomic positions.
The remainder of the paper is organized as follows: In Sections 2, 3 and 4 we describe experimental and theoretical procedures, in Section 5 we present and discuss the results obtained, and in Section 6 we summarize our main conclusions.
2. Experimental
Hydroxyvanadinite was prepared by precipitation of ammonium vanadate with lead nitrate in aqueous solution, following the method described by Nadir et al.10
The X-ray powder diffraction (XRD) pattern was recorded with a HZG diffractometer, using monochromatic Cu Kα radiation. The pattern was scanned in steps of 2θ = 0.05°, in the range 5–100° at a counting time of 2 s step−1. The data were analyzed using the Rietveld method with the FullProf program.11
The Fourier Transform infrared spectrum was recorded on a Nicolet FTIR 760 spectrometer in the 400–4000 cm−1 range. The sample was pressed with KBr (0.5% mass) into a thin wafer. Raman spectra were recorded in the range 100 to 1600 cm−1 with a Raman LabRAM Infinity microprobe (Jobin Yvon) equipped with a liquid nitrogen-cooled detector and a frequency-doubled Nd:YAG laser supplying the excitation line at 532 nm. The power was less than 5 mW at the sample.
X-Ray absorption spectra (EXAFS and XANES) were acquired at the vanadium K-edge (5.465 keV) using the facilities of the LNLS storage ring (Campinas, Brazil), operated at an energy of 1.37 GeV with a maximum beam current of 120 mA. Monochromatization of the incident beam was made using a double Si (111) crystal. No harmonic rejection method was necessary due to the low energy of the ring. Energy calibration of the beam was performed using metal foils. Three scans were recorded in transmission mode for each sample. Data were collected typically out to k = 13 Å−1 beyond the absorption edge, at ambient temperature. The intensities of the incident and transmitted beams were monitored by air-filled ionization chambers. The resultant EXAFS spectra were averaged and analyzed by a standard procedure of data reduction using the IFEFFIT code. Structural parameters were obtained from least squares fitting in R-space, using theoretical phase and amplitude functions obtained from the FEFF8 program.12 Standard parameters are reported here with the same names as they are defined in the FEFFIT code.13
3. Crystal structure and cluster models
The focus of the present study is the hydroxyl analogue of the rare mineral vanadinite (VA), Pb10(VO4)Cl2, called hydroxyvanadinite (OH-VA), Pb10(VO4)(OH)2, where the Cl anions are replaced by OH groups. Considering the different sites at which the Pb2+ and O2− atoms are found, the structure can be written as| | | Pb(1)4Pb(2)6 [VO(1)O(2)O(3)2]6 (OHH)2, | (1) |
where the [VO(1)O(2)O(3)2] tetrahedra form robust fundamental units of the structure. The hydroxyls and the Pb ions at the fourfold lattice positions, Pb(1), lie along columns parallel to the c-axis (referred to hereafter as the OH axis) in the ratio of 1 to 2 throughout the crystal. The Pb ions at the sixfold lattice position, Pb(2), are closely associated with the OH groups, forming triangles centered on, and perpendicular to, the OH axis. Repetition of this pattern along the OH axis defines a channel in OH-VA, labeled hereafter as the OH channel. Both Pb sites may be considered sixfold coordinated to O atoms presenting, however, distinguishable characteristics. The anion coordination of the Pb(1) site is a Pb(1)O(1)3O(2)3 metaprismatic arrangement with the basis formed by O(1) and O(2) triangles twisted by an angle of 0° < φ < 60°, while the anion coordination of the Pb(2) site is a distorted Pb(2)O(2)O(3)4OH octahedron, with one pair of O(3) closer to Pb(2) than the other one. The main difference between the OH-VA and VA apatites consists of the anion positions inside channels: OH and Cl are at (0,0,0.37) and (0,0,1/2) positions, respectively. Consequently, in VA, the Pb(2) site is sevenfold coordinated to five oxygens, as in OH-VA, and two Cl anions, instead of one channel anion as found in OH-VA. The crystal structures of such apatites have been extensively discussed and further information can be found in ref. 14 and 15.
In the present work, we adopt an embedded cluster model to represent VA and OH-VA electronic structures. The 44 atomic positions in the unit cell used to define the cluster environment were derived from our Rietveld refinement, with twist angle φ = 17.36°. Since the OH group is not fully resolved in XRD, it was necessary to estimate positions for the hydrogen atoms. Based on the neutron diffraction results in calcium hydroxyapatite,16 Ca10(PO4)6OH2, we have considered protons aligned with the OH axis and at a distance of 1 Å from OH. The main purpose here is to investigate the environment of Pb and OH sites in OH-VA in comparison with VA, and modelled in the light of our characterization by XRD, XAS and Raman scattering. To this end, the electronic structure of the well-established crystallographic structure of VA was also studied and used as a structural prototype. The 42 atomic positions in the VA unit cell are those determined by Dai and Hughes:17a = b = 10.317 Å, c = 7.338 Å and φ = 17.63°. We defined ten clusters of 93/84, 87/85, 84/82, 96/99, and 90/86 atoms centered, respectively at Pb(1), Pb(2), V, OH/Cl sites and at the center of the Pb(2) triangle to represent the OH-VA/VA local environments. Such a procedure allows the chemical environment for Pb, V, O, and Cl to be appropriately described to determine the atomic configuration (i.e., effective atomic orbital occupation numbers) and bonding structure, since all its bonding and coordination capacity is fulfilled as it is in the bulk. The coordination of oxygens at the O(1), O(2), and O(3) sites is completely represented within both OH-VA and VA vanadium-centered clusters.
4. Embedded-cluster density functional scheme
Embedded-Cluster Density Functional (ECDF) models embody the self-consistent calculation of localized molecular orbitals within a finite cluster that is coupled to an environment, typically an infinite crystal medium. Our theoretical investigations employed a first-principles real-space Linear Combination of Atomic Orbitals (LCAO) Discrete Variational Method18 (DVM) based on density functional theory and the Local Density Approximation18 (LDA) to calculate the electronic structure for clusters of varying sizes representing OH-VA and VA. DVM has been well documented elsewhere; in the following, we only give a short account of its features specific to the present calculation.
We obtain approximate solutions of the one-electron DF Kohn–Sham equations,20 using the Vosko et al.21 formulation to the exchange and correlation potential. The cluster potentials are functionals of the electron density ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = ∑ni|ϕi(
) = ∑ni|ϕi(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )|2, where the summation runs over the cluster orbitals ϕi, and ni are Fermi–Dirac occupation numbers. In order to solve the Poisson equation for the Coulomb potential efficiently, a model potential is found by least-squares fitting the “true” charge density to a multipolar expansion22 to within any desired level of precision. In the present work, guided by previous DVM studies on substituted apatites, only spherical terms are included in the expansion. This is adequate for describing the approximately spherical Pb cations, as well as the localized σ-electron structure of the VO4 tetrahedral units.
)|2, where the summation runs over the cluster orbitals ϕi, and ni are Fermi–Dirac occupation numbers. In order to solve the Poisson equation for the Coulomb potential efficiently, a model potential is found by least-squares fitting the “true” charge density to a multipolar expansion22 to within any desired level of precision. In the present work, guided by previous DVM studies on substituted apatites, only spherical terms are included in the expansion. This is adequate for describing the approximately spherical Pb cations, as well as the localized σ-electron structure of the VO4 tetrahedral units.
The DVM linear secular equations are solved self-consistently on a three-dimensional numerical grid. This grid is chosen to be regular (polynomial in angle, logarithmic in radius) inside a sphere of radius 2.0 and 1.2 a.u. around the central Pb (and Pb of the Pb(2) triangle, whose center is the origin of two clusters) and V atoms, respectively. Outside these spheres and around other atoms in all ten clusters, a pseudo-random diophantine scheme is used to define the points. The total number of points employed is in the range 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–155
000–155![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Optimized atomic basis functions were defined as solutions of nonrelativistic numerical self-consistent atomic DF calculations, with configurations determined in turn self-consistently from the VA embedded clusters. The omission of relativistic effects is expected to cause only small deviations in the valence electron distributions; these effects are however included in the lattice relaxation study (vide infra). The atomic basis set of the OH-VA embedded clusters included the oxygen (OH) and hydrogen (H) atoms associated to hydroxyl in place of Cl. These optimized basis functions were obtained from the OH-VA embedded cluster centered at OH. The variational basis functions used are: Pb {5spd, 6s, 6p}, V {3d, 4s, 4p}, O{2s, 2p}, Cl {3s, 3p}, and H {1s}. The deep-lying atomic orbitals are treated in the frozen-core approximation; i.e., the valence basis functions are orthogonalized against the frozen-core basis in the first iteration and orbitals not included in the variational basis are subsequently kept frozen.
000. Optimized atomic basis functions were defined as solutions of nonrelativistic numerical self-consistent atomic DF calculations, with configurations determined in turn self-consistently from the VA embedded clusters. The omission of relativistic effects is expected to cause only small deviations in the valence electron distributions; these effects are however included in the lattice relaxation study (vide infra). The atomic basis set of the OH-VA embedded clusters included the oxygen (OH) and hydrogen (H) atoms associated to hydroxyl in place of Cl. These optimized basis functions were obtained from the OH-VA embedded cluster centered at OH. The variational basis functions used are: Pb {5spd, 6s, 6p}, V {3d, 4s, 4p}, O{2s, 2p}, Cl {3s, 3p}, and H {1s}. The deep-lying atomic orbitals are treated in the frozen-core approximation; i.e., the valence basis functions are orthogonalized against the frozen-core basis in the first iteration and orbitals not included in the variational basis are subsequently kept frozen.
A Mulliken-type atomic orbital population analysis is used and effective atomic configurations and charges determined. Partial densities of states (DOS) are defined by
| |  | (2) |
where
Pqnl,i are the Mulliken populations of orbital nl of atom q in the cluster orbital
ϕi with energy
ξi. “L” is a line-shape function chosen as a Lorentzian of width
δ = 0.005 eV. By summing over n, l, and q, the total DOS is obtained.
5. Results and discussion
The XANES spectrum at the vanadium K-edge of OH-VA (Fig. 1) clearly indicates tetrahedral coordination of the metal, with the characteristic intense pre-edge peak appearing at about 5.470 keV. Fig. 2 shows the experimental EXAFS oscillations at the V K-edge, and the simulated spectrum obtained from the Artemis program using a coordination sphere of four oxygen atoms at a single distance. The results suggest a vanadium–oxygen distance, d(V–O) = 171 ± 1 pm (σ2 = 0.003 Å2). The corresponding experimental and simulated Fourier Transforms are given in Fig. 3. The spectrum does not provide any evidence relative to other coordination spheres about vanadium.
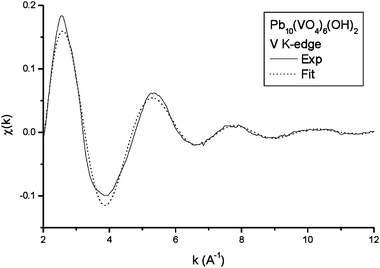 |
| | Fig. 2 Experimental and simulated EXAFS oscillations at the vanadium K-edge. | |
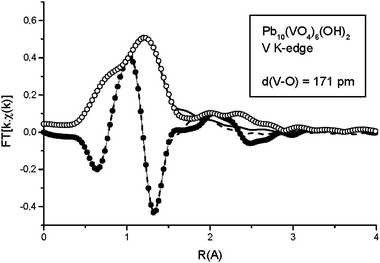 |
| | Fig. 3 Fourier Transform of the experimental (Mag = ○, Im = ●) and simulated (Mag = ![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) , Im = , Im = ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ) EXAFS oscillations at the vanadium K-edge. ) EXAFS oscillations at the vanadium K-edge. | |
5.2 Raman spectroscopy
The Raman spectrum of OH-VA is in agreement with the spectra reported in the literature for VA. The band attributed to the symmetric and asymmetric stretching of the VO4 group is shown in Fig. 4, and was fitted with four Lorentzian bands, whose parameters are shown in Table 1. A model proposed by Hardcastle23 was applied to the corresponding vibration frequencies and allowed a fair estimation of the V–O bond lengths and electrostatic bond strengths as reported in Table 2. Considering the very weak intensity of the first band at 736.9 cm−1, this was not included in the model. Three different V–O bonds are then obtained with average distances in good agreement with the EXAFS data and very similar to the corresponding values in vanadinite (Table 3).
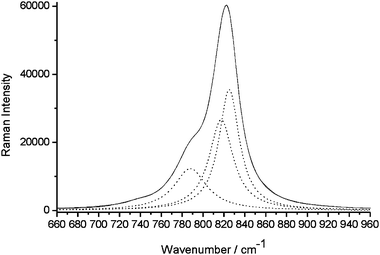 |
| | Fig. 4 Raman spectra of VO4 stretching bands: experimental (![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) ) and three fitted (⋯). ) and three fitted (⋯). | |
Table 1 Lorentzian parameters for V–O stretching band in hydroxyvanadinite
| Center/cm−1 |
Width/cm−1 |
Area/cps cm−1 |
| 736.9 |
19.6 |
18 724 |
| 787.9 |
37.9 |
732 860 |
| 817.3 |
27.9 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166 166![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 549 549 |
| 825.0 |
23.7 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324 324![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238 238 |
Table 2 V–O bond lengths and bond strengths associated to each component of the vibration band
| Center/cm−1 |
Distance/pm |
Bond strength |
| 787.9 |
172.1 |
1.227 |
| 817.3 |
170.1 |
1.299 |
| 825.0 |
169.7 |
1.318 |
Table 3 Characteristic distances in Pb10(VO4)6(OH)2 adopted from vanadinite for Rietveld refinement
| |
Distance/pm |
| V–O1 |
170.5 |
| V–O2 |
169.3 |
| V–O3 |
170.4 |
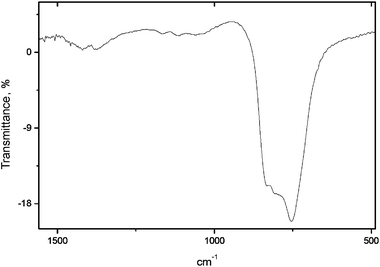
The experimental X-ray diffraction pattern of OH-VA is given in Fig. 5. The data are compatible with space group P63/m (176); the cell parameters were refined to a = 10.2242(3) Å and c = 7.4537(2) Å, values that are consistent with data from previous work (a = 10.1938 Å and c = 7.4499 Å). The atomic parameters, however, could not be found in the literature; therefore, an objective of the present paper is to propose a cell structure obtained by Rietveld refinement of the XRD pattern. Comparison of spectroscopic data of OH-VA and VA suggests that the geometry of the vanadate group can be transferred to hydroxyvanadinite. The structure of vanadinite was thus used as a starting model for the refinement. Fig. 5 shows the difference between the experimental and simulated patterns using the structure parameters listed in Table 4, where the vanadate group was defined as a rigid body as defined from the structure of VA. The corresponding R-Bragg factor (= 4.65), indicated that the refinement was reasonable. It is worth noting the low occupation factor of the OH site as well as its shifted position along the main channel of the apatite structure. This fact might be correlated with the infrared spectrum shown in Fig. 6, which does not show any evidence of the libration band of the hydroxyl group.
 |
| | Fig. 5 Experimental X-ray diffraction pattern of Pb10(VO4)6(OH)2 and difference (line at bottom of figure) with simulated pattern. | |
| Site |
x
|
y
|
z
|
Occupation |
B |
| Pb(1) |
0.3333 |
0.6667 |
0.0071(5) |
0.943(4) |
0.2000 |
| Pb(2) |
0.2495(2) |
0.0004(3) |
0.2500 |
0.915(4) |
0.2000 |
| V |
0.4098 |
0.3836 |
0.2500 |
1 |
0.2000 |
| O(1) |
0.3326 |
0.4978 |
0.2500 |
1 |
0.2000 |
| O(2) |
0.6008 |
0.4853 |
0.2500 |
1 |
0.2000 |
| O(3) |
0.3585 |
0.2675 |
0.0679 |
1 |
0.2000 |
| OH |
0.0000 |
0.0000 |
0.370(4) |
0.35(2) |
0.2000 |
5.4 Electronic structure
We carried out ECDF calculations on ten clusters centered at both Pb sites, and at V, OH and Cl selected to represent OH-VA (taking atomic coordinates from the Rietveld refinements given in Table 4) and VA apatites. The results of Mulliken-type charge and atomic orbital populations for selected ions near the cluster center, with complete chemical coordination, are summarized in Table 5. It may be observed that configurations and charges related to Pb are similar in both apatites and deviate only slightly from the so-called “inert pair “ Pb2+ 6s2 6p0 configuration. The closeness of the charges on Pb to the formal charge +2 reflects the strong ionic character of the chemical Pb–O bonding and confirms the expected divalent nature of Pb in these compounds. It is worth mentioning that previous ECDF calculations on calcium hydroxyapatite,14 Ca10(PO4)6(OH)2, showed a less ionic character for the corresponding Ca(1)–O and Ca(2)–O bonding. There, we obtained effective charges on Ca(1) and Ca(2) of 1.85e and 1.82e, respectively.
Table 5 Mulliken atomic orbital populations and net charges of atoms in the clusters representing the OH-VA and VA apatites, as described in the text
| |
|
OH-VA |
VA |
| Pb(1) |
5s |
1.99 |
1.99 |
| 5p |
5.99 |
5.99 |
| 5d |
9.99 |
9.99 |
| 6s |
1.76 |
1.72 |
| 6p |
0.19 |
0.23 |
| Charge |
+2.08 |
+2.08 |
| Pb(2) |
5s |
1.99 |
1.99 |
| 5p |
5.99 |
5.99 |
| 5d |
9.99 |
9.99 |
| 6s |
1.70 |
1.62 |
| 6p |
0.33 |
0.43 |
| Charge |
+2.00 |
+1.98 |
| V |
3d |
2.56 |
2.56 |
| 4s |
0.07 |
0.07 |
| 4p |
0.04 |
0.04 |
| Charge |
+2.33 |
+2.33 |
| O(1) |
2s |
1.98 |
1.98 |
| 2p |
5.33 |
5.31 |
| Charge |
−1.31 |
−1.29 |
| O(2) |
2s |
1.96 |
1.96 |
| 2p |
5.33 |
5.31 |
| Charge |
−1.29 |
−1.27 |
| O(3) |
2s |
1.97 |
1.98 |
| 2p |
5.30 |
5.30 |
| Charge |
−1.27 |
−1.28 |
| OH, Cl |
2s, 3s |
1.88 |
1.96 |
| 2p, 3p |
5.59 |
5.72 |
| Charge |
−1.47 |
−0.68 |
| H |
1s |
0.38 |
— |
| Charge |
+0.62 |
— |
| VO4 charge |
−2.81 |
−2.79 |
| OH charge |
−0.85 |
— |
Similarities between OH-VA and VA are also observed in the VO4 group. In both apatites, vanadium and oxygen ions are far from their “ideal” pentavalent and divalent states respectively, attaining equal effective configuration of V2.33+ 3d2.564s0.074p0.04 in both apatites and comparable effective configurations for oxygens. Such configurations evidence the expected strong V–O covalency and indicate insensitivity of the vanadate to neighbouring OH− and Cl− species in the OH channel. The resultant charge on VO4 of −2.81e and −2.79e in OH-VA, and VA, respectively, are not far from the formal charge −3e. Finally, the effective charges on the OH and Cl ions related to the channel sites are −0.85e and −0.68e, arising from the OH 2s1.882p5.59, H 1s0.38 and Cl 3s1.963p5.72 configurations. The charge on the OH radical is thus reasonably close to the formal monovalent charge, while that on Cl is rather far from it.
The partial densities of states (PDOS) of Pb(2) and its ligands derived from the Pb(2)-centered cluster representing OH-VA are shown in Fig. 7. The orbital projections are expected to be distinctly different for oxygens in inequivalent sites in the distorted Pb(2)O(2)Of(3)2Oc(3)2(OHH) octahedron. The superscripts f (for far) and c (for close) identify the O(3) pairs in relation to the Pb(2)–O(3) interatomic distances: Pb(2)–Of(3) = 2.74 Å and Pb(2)–Oc(3) = 2.59 Å. The other Pb(2)–O distances are: Pb(2)–O(2) = 2.35 Å and Pb(2)–OH = 2.70 Å. The lowest-energy band, ranging from −22 to −14 eV below the Fermi level, is predominantly O 2s in character; there is a very small Pb(2) 5d participation in this band and such a mixture takes place with O(2), which is closer to Pb(2) than the others. The upper valence band is separated from the O 2s band by a sizable gap of approximately 8 eV and it is dominated by O 2p levels, with practically no O 2s, 2p hybridization. The O 2p band presents a set of distributions which extends approximately from 8 eV below to 8 eV above the Fermi level for oxygens positioned at O(2) and O(3) sites, while it spreads from −10 to +12 eV for OH. Contributions from Pb(2) 6s take place at higher energies of the O 2p bands, and a very small participation from Pb(2) 6p is also predicted. The semi-core Pb(2) 5s, 5p, and 5d states are represented by isolated narrow distributions centered respectively at −110, −75 and −20 eV. They were included in the variational space principally to avoid any possible distortion due to imperfect orthogonalization and to allow for the possible slight (resonant) mixing of Pb 5d and ligand O 2s states. The higher-energy Pb(2) valence bands straddling the Fermi level are primarily the Pb(2) 6s band with small mixtures with Pb(2) 6p. The conduction band unoccupied levels are predominantly Pb(2) 6p, where a very small mixture of Pb(2) 6s is observed. The PDOS of Pb(2) and their ligands (not shown) present similar characteristics in VA, giving support to our structural model. Strong similarities are also observed in PDOS of Pb(1) and their coordinated oxygens in both apatites.
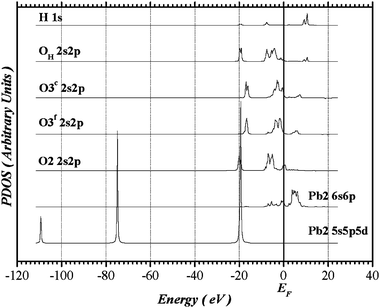 |
| | Fig. 7 Partial density of states of Pb(2) and its ligands in OH-VA derived from the Pb(2)-centered cluster. | |
Studies of synthetic calcium and lead apatites24 with the channel anionic sites occupied by OH−, F−, Cl−, or Br− have related the anisotropic variation in the cell parameters to the different locations of the halide ions in the two systems. By Rietveld refinements, halide ions were determined to be distributed along the OH axis according to their ionic radius for calcium compounds while they are forced to the z = 0.5 position for lead compounds. It is suggested that such behaviour may be caused by the Pb 6s electrons, which could be filling the void at the center of the Pb(2) triangle, generating electrostatic repulsions not found in the Ca compounds. That hypothesis would be further strengthened by evidence for “stereochemically active” lone pairs consisting of hybridized Pb 6s, p orbitals with directional character. We can draw a parallel to divalent tin, where it is a common characteristic of all Sn(II) compounds that a lone pair is invoked, which is accommodated in a void space in the crystal where a bond with an anion is missing.25 In a “cluster-orbital” picture such as the present one, this lone pair on Pb(2) would be detected as one (or more) orbitals with significant Pb(2) 6s–6p mixing. However, as discussed above and seen in Fig. 7, the degree of mixing between the Pb(2) 6s and 6p levels found here is insignificant, therefore precluding any occupied orbitals to be identified as lone-pairs. This may be clearly visualized in the calculated charge contour plots for a plane centered at the center of the Pb(2) triangle shown in Fig. 8. We can see some aspherical contributions in the Pb(2) triangle; however, they are very small compared to any expected directed lone-pair distributions. The contour lines in the middle of the triangle are contributions related to the OH radical, which is on-axis, and 0.89 Å away from the center of the Pb(2) triangle. We also observe the extremely strong covalent character of the V–O bonds, and the lack of significant charge density outside the VO4 ions, further indicating the dominant ionic character of the Pb–O bonds. We obtain similar contour maps for VA, showing again the high degree of compatibility of the electronic structure with OH-VA.
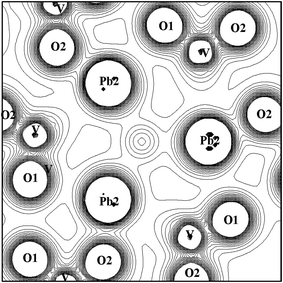 |
| | Fig. 8 Contour plot of charge density on the plane of the Pb(2)-triangle. Contours are from 0.0 to 0.2 e/a.u.3 with intervals of 0.01 e/a.u.3 The Pb(2)–Pb(2) distance is 4.41 Å. | |
In order to make an independent test of the experimentally derived atomic coordinates, we carried out periodic band structure calculations in which the unit cell parameters were held fixed and all atomic positions were allowed to relax. In this way, the restrictive assumption of space group P63/m was lifted, and shifts away from the symmetry-related sites could lower the cohesive energy and give information about the stability of the structure. Calculations were carried out in the plane-wave pseudopotential formalism using the program VASP,26–29 with Projector-Augmented Wave potentials30 in the Generalized Gradient Approximation,31 a 450 eV cutoff in the wavefunction expansion, and a 2 × 2 × 2 k-space integration mesh. This procedure was found to be quite satisfactory in previous calculations on hydroxyapatite, fluorapatite, and on Pb-substituted HA.32 Starting from the symmetry-restricted coordinates given in Table 4, we find that unconstrained relaxation leads to an energy lowering of ∼5 eV to 307.11 eV cell−1 with an estimated uncertainty of <0.1 eV in energy and <0.1 Å in position. The most significant change observed is a displacement of the OH group along the c-axis from the experimentally-derived position of 0.37 to the optimized value of 0.31, with OH lying 0.43 Å above the Pb(2) plane, with distance R(Pb–OH) of 2.58 Å. The complete set of relaxed coordinates is given in Table 6.
Table 6 Optimized unit cell coordinates for hydroxyvanadinite, starting from P63/m space group and experimentally derived values
| Site |
Crystallographic Coord: x, y, z |
Site |
x, y, z |
| General |
x, y, z and inversion |
|
|
|
x
−
y, x, 1/2 + z |
|
|
| −y, x
−
y, z |
|
|
| −x, −y, 1/2 + z |
|
|
| −x + y, −x, z |
|
|
|
y, −x + y, 1/2+z |
|
|
| Pb(1) |
0.333 0.666 0.498 |
P |
0.398 0.369 0.744 |
| 0.666 0.333 0.484 |
|
0.630 0.028 0.744 |
| 0.666 0.333 −0.002 |
|
0.971 0.601 0.744 |
| 0.333 0.666 −0.016 |
|
0.601 0.630 0.244 |
| Pb(2) |
0.253 0.009 0.750 |
|
0.369 0.971 0.244 |
| 0.990 0.243 0.750 |
|
0.028 0.398 0.244 |
| 0.756 0.746 0.750 |
O(3) |
0.335 0.246 0.563 |
| 0.746 0.990 0.250 |
|
0.753 0.089 0.563 |
| 0.009 0.756 0.250 |
|
0.910 0.664 0.563 |
| 0.243 0.253 0.250 |
|
0.654 0.753 0.424 |
| O(1) |
0.326 0.491 0.747 |
|
0.246 0.900 0.424 |
| 0.508 0.835 0.747 |
|
0.099 0.346 0.424 |
| 0.164 0.673 0.747 |
|
0.664 0.753 0.063 |
| 0.673 0.508 0.247 |
|
0.246 0.910 0.063 |
| 0.491 0.164 0.247 |
|
0.089 0.335 0.063 |
| 0.835 0.326 0.247 |
|
0.345 0.246 −0.076 |
| O(2) |
0.595 0.470 0.741 |
|
0.753 0.099 −0.076 |
| 0.529 0.125 0.741 |
|
0.900 0.653 −0.076 |
| 0.874 0.404 0.741 |
OH |
0.000 0.000 0.808 |
| 0.404 0.529 0.241 |
|
0.000 0.000 0.308 |
| 0.470 0.874 0.241 |
H |
0.000 0.000 −0.061 |
| 0.125 0.595 0.241 |
|
0.999 0.000 0.439 |
6. Conclusions
Application of XAS and Raman spectroscopies confirm the tetrahedral geometry of the vanadate ion in hydroxyvanadinite Pb10(VO4)6(OH)2. The structure is isomorphic to that of vanadinite, in agreement with the X-ray diffraction pattern. The atomic positions obtained from Rietveld refinement were used to model the OH-VA structure, using a first-principles embedded-cluster density functional approach. The electronic structure calculations reveal the ionic–covalent interaction of Pb with its oxygen ligands at both Pb(1) and Pb(2) sites in OH-VA as well as in VA. Pb is confirmed to be essentially divalent at both sites, with only a weak covalent component, and very little 6s,p hybridization. Although some aspherical contributions can be seen in the Pb(2)-triangle plane, they are small compared to the “lone-pair” distribution proposed in some previous works as a mechanism to explain displacement of anions along the channel by Pb(2). The vanadate group reveals expected strong covalent V–O interaction, with net Mulliken charge (VO4)Q, Q = −2.81e in OH-VA and −2.79e in VA. This shows the insensitivity of the vanadate to OH− and Cl− species in the OH channel. Observed differences between hydroxyvanadinite and calcium vanadate apatite in their redox behavior under hydrogen should probably be attributed to the nature of the substituting cation or to electronic exchanges occurring between the two kinds of metal centers; this discussion will be the subject of future work.9 The OH charge of −0.85e is close to the formal charge of −1e. First-principles band structure calculations were performed to confirm the stability of experimentally derived atomic coordinates, and to remove symmetry constraints imposed on the fitting model. Small symmetry-breaking deviations were found to increase the cohesive energy by 1.5% and the OH groups move a little closer to the Pb(2) plane. Overall, agreement between experimentally derived coordinates and the band structure results is excellent. It would certainly be interesting to obtain neutron diffraction measurements to obtain a further confirmation of the OH position, and to verify the degree of (dis)order in the orientation in the microcrystalline material.
Acknowledgements
The authors would like to thank CNPq (Conselho de desenvolvimento Científico e Tecnológico of Brazil), CNRS (Centre National de la Recherche Scientifique of France) and more particularly the Laboratoire de Catalyse (Lille, France) for Raman data and the LNLS (Laboratoire Nacional de Luz Sincrotron/Campinas, Brazil), which supported this work. This work was supported in part by the National Science Foundation, through the Latin American Materials Inititiative, Grant DMR-0303491. Electronic structure calculations were performed in part on a Cray T94 at the Supercomputing Center of the Federal University of Rio Grande do Sul.
References
- K. J. L. Burg, S. Porter and J. F. Kellam, Biomaterials, 2000, 21, 2347 CrossRef CAS.
- R. Z. Legeros, Clin. Orthop. Rel. Res., 2002, 395, 81 Search PubMed.
- E. Mavropoulus, A. M. Rossi, C. A. Peres, J. C. Moreira and M. Saldanha, Environ. Sci. Technol., 2002, 36, 1630 CrossRef.
- A. M. Rossi and T. Moure, Environ. Sci. Technol., 2002, 36, 1625 CrossRef CAS.
- Ming Jiang, J. Terra, A. M. Rossi, M. A. Morales, E. M. B. Saitovitch and D. E. Ellis, Phys. Rev. B, 2002, 66, 224107 CrossRef.
- Xinde Cao, Lena. Q. Ma, Dean. R. Rhue and Chip. S. Appel, Environ. Pollut., 2004, 131, 435 CrossRef CAS.
- C. B. Boechat, J. G. Eon, A. M. Rossi, C. A. C. Perez and R. A. S. San Gil, Phys. Chem. Chem. Phys., 2000, 2, 4225 RSC.
- C. B. Boechat, J. Terra, J. G. Eon, D. E. Ellis and A. M. Rossi, Phys. Chem. Chem. Phys., 2003, 5, 4290 RSC.
-
M. Ikram
et al., in preparation.
- S. Nadir, J. L. Lacout, G. Montel and J. C. Trombe, Ann. Chim., 1983, 8, 463 CAS.
-
J. Rodriguez-Carvajal, FULLPROF program for Rietveld, Profile Matching and Integrated Intensities Refinement of X-ray and/or Neutron Data, Satellite Meeting on Powder Diffraction of the XVth Congress of IUCr, Toulouse, France, 1990 Search PubMed.
- J. J. Rehr, J. Mustre de Leon, S. I. Zabinsky and R. C. Albers, J. Am. Chem. Soc., 1991, 113, 5135 CrossRef CAS.
- M. Newville, B. Ravel, D. Haskel, J. Rehr, A. Stern and Y. Yacoby, Physica B, 1995, 208 & 209 Search PubMed.
- J. Terra, M. Jiang and D. E. Ellis, Philos. Mag. A, 2002, 82, 2357 CrossRef CAS.
- T. J. White and D. Zhili, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 1 CrossRef CAS.
- M. I. Kay, R. A. Young and A. S. Posner, Nature, 1964, 204, 1050 CAS.
- Y. Dai and J. M. Hughes, Can. Mineral., 1989, 27, 189 CAS.
-
(a) D. E. Ellis, Int. J. Quantum Chem., 1968, 25, 35;
(b) D. E. Ellis and G. Painter, Phys. Rev. B, 1970, 2, 2887 CrossRef;
(c) D. E. Ellis and D. Guenzburger, Adv. Quantum Chem., 1999, 34, 51 CAS.
-
(a) P. Hohenberg and W. Kohn, Phys. Rev. Sect. B, 1964, 136, 864 Search PubMed;
(b) J. Callway and N. H. March, Solid State Phys., 1984, 38, 135 Search PubMed.
- W. Kohn and L. J. Sham, Phys. Rev. Sect. A, 1965, 140, 1133 Search PubMed.
- H. Vosko, L. Wilk and M. Nussair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- B. Delley and D. E. Ellis, J. Chem. Phys., 1982, 76, 1949 CrossRef.
- F. D. Hardcastle and I. E. Wachs, J. Phys. Chem., 1991, 95, 5031 CrossRef CAS.
- J. Y. Kim, R. R. Fenton, B. A. Hunter and B. J. Kennedy, Aust. J. Chem., 2000, 53, 679 CrossRef CAS.
- J. Terra and D. Guenzburger, Phys. Rev. B, 1991, 44, 8584 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B, 1994, 49, 14251 CrossRef CAS.
- G. Kresse and J. Furtmuller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furtmuller, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and D. Fiolhais, Phys. Rev. B, 1992, 46, 6671 CrossRef CAS.
- D. E. Ellis, J. Terra, O. Warschkow, M. Jiang, G. Gonzalez, J. Okasinski, M. Bedzyk, A. M. Rossi and J.-G. Eon, Phys. Chem. Chem. Phys., 2006, 8, 967 RSC.
|
| This journal is © the Owner Societies 2006 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = ∑ni|ϕi(
) = ∑ni|ϕi(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )|2, where the summation runs over the cluster orbitals ϕi, and ni are Fermi–Dirac occupation numbers. In order to solve the Poisson equation for the Coulomb potential efficiently, a model potential is found by least-squares fitting the “true” charge density to a multipolar expansion22 to within any desired level of precision. In the present work, guided by previous DVM studies on substituted apatites, only spherical terms are included in the expansion. This is adequate for describing the approximately spherical Pb cations, as well as the localized σ-electron structure of the VO4 tetrahedral units.
)|2, where the summation runs over the cluster orbitals ϕi, and ni are Fermi–Dirac occupation numbers. In order to solve the Poisson equation for the Coulomb potential efficiently, a model potential is found by least-squares fitting the “true” charge density to a multipolar expansion22 to within any desired level of precision. In the present work, guided by previous DVM studies on substituted apatites, only spherical terms are included in the expansion. This is adequate for describing the approximately spherical Pb cations, as well as the localized σ-electron structure of the VO4 tetrahedral units.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–155
000–155![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Optimized atomic basis functions were defined as solutions of nonrelativistic numerical self-consistent atomic DF calculations, with configurations determined in turn self-consistently from the VA embedded clusters. The omission of relativistic effects is expected to cause only small deviations in the valence electron distributions; these effects are however included in the lattice relaxation study (vide infra). The atomic basis set of the OH-VA embedded clusters included the oxygen (OH) and hydrogen (H) atoms associated to hydroxyl in place of Cl. These optimized basis functions were obtained from the OH-VA embedded cluster centered at OH. The variational basis functions used are: Pb {5spd, 6s, 6p}, V {3d, 4s, 4p}, O{2s, 2p}, Cl {3s, 3p}, and H {1s}. The deep-lying atomic orbitals are treated in the frozen-core approximation; i.e., the valence basis functions are orthogonalized against the frozen-core basis in the first iteration and orbitals not included in the variational basis are subsequently kept frozen.
000. Optimized atomic basis functions were defined as solutions of nonrelativistic numerical self-consistent atomic DF calculations, with configurations determined in turn self-consistently from the VA embedded clusters. The omission of relativistic effects is expected to cause only small deviations in the valence electron distributions; these effects are however included in the lattice relaxation study (vide infra). The atomic basis set of the OH-VA embedded clusters included the oxygen (OH) and hydrogen (H) atoms associated to hydroxyl in place of Cl. These optimized basis functions were obtained from the OH-VA embedded cluster centered at OH. The variational basis functions used are: Pb {5spd, 6s, 6p}, V {3d, 4s, 4p}, O{2s, 2p}, Cl {3s, 3p}, and H {1s}. The deep-lying atomic orbitals are treated in the frozen-core approximation; i.e., the valence basis functions are orthogonalized against the frozen-core basis in the first iteration and orbitals not included in the variational basis are subsequently kept frozen.



![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) , Im =
, Im = ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ) EXAFS oscillations at the vanadium K-edge.
) EXAFS oscillations at the vanadium K-edge.
![[thick line, graph caption]](https://www.rsc.org/images/entities/char_e117.gif) ) and three fitted (⋯).
) and three fitted (⋯).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166
166![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 549
549![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324
324![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238
238