View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/B515409J (Invited Article) Phys. Chem. Chem. Phys., 2006, 8, 1357-1370

Computational studies of molecular hydrogen binding affinities: The role of dispersion forces, electrostatics, and orbital interactions†

Rohini C. Lochan and Martin Head-Gordon
Department of Chemistry, University of California and Chemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley CA, 94720, USA

Received 31st October 2005, Accepted 20th January 2006

First published on 13th February 2006

Abstract

Intermolecular interactions between H2 and ligands, metals, and metal–ligand complexes determine the binding affinities of potential hydrogen storage materials (HSM), and thus their extent of potential for practical use. A brief survey of current activity on HSM is given. The key issue of binding strengths is examined from a basic perspective by surveying the distinct classes of interactions (dispersion, electrostatics, orbital interactions) in first a general way, and then in the context of calculated binding affinities for a range of model systems.

Introduction

Molecular hydrogen is considered to be a clean, renewable replacement for the world’s fast diminishing fossil fuel resources that are non-renewable and a major source of environmental pollution and possibly also contribute to global warming. However, a conversion to a hydrogen-based economy, especially for mobile applications, is far from realization in the near future as present day technology is not yet fully capable of dealing with issues of economical production and effective fuel storage.1–3 Conventional hydrogen storage methods include compression and liquefaction of H2. However, efficiency, safety and economic issues appear likely to limit the viability of these methods as practical storage options in the future.4–6

Another approach to hydrogen storage is to let H2 interact (physically/chemically) with a host material. Developing viable hydrogen storage materials (HSM), as measured, for example, against the US Department of Energy (DOE) targets,7 has emerged as a challenge for an interdisciplinary scientific community. Metallic hydrides, complex hydrides, carbon nano-structures, metal–organic frameworks (MOF), zeolites and other microporous solids constitute the main classes of materials investigated to date for their hydrogen sorption properties.4–6 The 2010 DOE target for a promising HSM is that it should be able to contain a gravimetric density of about 6 wt% hydrogen, volumetric capacity of 0.045 kg H2 L−1 and should be able to reversibly absorb/desorb H2 in the temperature range of −20 to 50 °C and moderate pressures (max. 100 atm).7

Although many novel HSM show promising characteristics, none of them yet meet all these specifications, and therefore research into this problem is continuing at an intense pace. At a basic level, the nature and strength of the fundamental interaction of H2 with the HSM plays a decisive role in determining both sorption properties as well as reversibility under ambient conditions. A very weak interaction would lead to lower H2 sorption at reasonable temperatures while a very strong interaction might be irreversible or require extreme conditions to release H2. Therefore, achievement of improved HSM depends upon first understanding the nature and mechanism of H2 storage, and second, designing materials that possess desired H2-HSM interactions.

This paper has the goal of discussing the range of attainable molecular hydrogen binding affinities with HSM, with emphasis on the inextricable connections between the strengths of the interactions and their physical and chemical nature. We employ a computational approach, with use of a broad range of simple model systems. The model systems used are not representative of real-world solid state materials themselves. Rather, they are chosen to allow straightforward identification of physical and chemical interactions with H2. In this way the objective is to gain some insight into the factors controlling the strength of molecular hydrogen binding interactions. Such insight can possibly be applied in the future to the design of new HSM with favorable properties.

The outline of the paper is as follows. First, we give a short overview of recent efforts to develop HSM, starting with materials that store hydrogen based on dissociative chemisorption, such as metallic and chemical hydrides, and followed by a somewhat more detailed discussion of materials where H2 is molecularly adsorbed, which is our main focus. This overview provides motivation and context for the calculations we present in subsequent sections, after first discussing general requirements for reliable theoretical modeling of H2 binding. Our calculations are then summarized in three sections, which move from the weak interaction regime, dominated by van der Waals forces, to an intermediate regime where stronger electrostatic effects are controlling, to a stronger regime where electrostatic effects and orbital interaction effects are operative. Finally we close with some conclusions, and comment on the outlook for this area.

2. Brief overview of hydrogen storage materials

H2 can interact with a material in its molecular form (either via physisorption or chemisorption) or dissociate to chemically interact with the material (dissociative chemisorption). The latter mechanism involves a chemical (often covalent/ionic) absorption of dissociated hydrogen atoms on the material that requires subsequent breaking (and making) of chemical bonds to allow the release of H2. The use of metallic hydrides and chemical hydrides as HSM falls into this category.4–6,8–10 Storage through chemisorption leads to two possible problems, particularly, for ionic hydrides and alanates: (i) the release of H2 might render the material unstable or incapable of re-absorption of H2 if its chemical nature is altered; (ii) the interaction of H2 with the material can be very strong, which might then require extreme conditions for the release of H2. Some metal hydrides have been shown to reversibly absorb/desorb H2 at ambient conditions but are often too heavy to attain the targeted wt% H2, while other lighter metal hydrides like MgH2 require very high temperatures (∼573 K) to release H2 as the hydride bond is very strong (∼75 kJ mol−1) and in many cases, such processes are often irreversible.6,8

Complex hydrides like NaAlH4 show promising features (∼4 wt% H2 at 333 K and 2 bar) but are prone to slow kinetics and high desorption temperature.9 Studies indicate that there is a good correlation between the standard enthalpy of decomposition of the hydride to release H2 and the thermal temperature of decomposition. The standard enthalpy of decomposition per hydride bond is estimated to be about −20 kJ per mol of hydrogen atom in order to achieve thermodynamic equilibrium at 300 K and 1 bar. As these metal and complex hydrides show a wide range of enthalpy of formations, it was suggested that the thermal decomposition temperature of new HSM can be controlled by varying the metal and/or other chemical constituents.8

‘Combined systems’ are yet another newly emerging class of hydrides that are a combination of metal and complex hydrides.6 For example, LiNH2 + LiH is considered a potentially interesting HSM that exhibits a theoretical sorption capacity ∼6.5 wt% H2 and also possess features like good kinetics and reversibility. However these types of material often operate at temperatures higher than ∼150 °C.6,11–14 Also, there are other hydrogen rich nitrogen boron compounds such as ammonia borane (NH3BH3), which have been demonstrated to generate H2 by thermolysis through nearly thermoneutral steps. While reversibility, kinetics and undesirable by-products pose potential problems, recent efforts indicate that these issues can be considerably ameliorated by using external mesoporous substrates.15–18

As described above, there are several promising materials that store hydrogen through dissociative chemisorption, and there is intensive effort being devoted to obtaining further improvements. However, one of the main challenges for this class of materials continues to be achieving and maintaining reversible absorption/desorption of H2. Fast, effective reversible hydrogen sorption can be conveniently achieved if forces that dictate the mechanism of H2 interaction with the material allow molecular hydrogen to be adsorbed on the material (without dissociating the H–H bond). Carbon nanostructures,19 metal–organic frameworks (MOF)20 and zeolites21–23 are HSM that fall under this category. In these cases, in addition to critical physical characteristics such as surface area and porosity of the material, the binding affinity of H2 plays a crucial role in determining the sorption capacity of the material under ambient conditions. This is in contrast to the hydrides discussed above, where the strength of the M–H bonds directly affects the H2 discharging process. It is therefore important to analyze and understand the nature and strength of molecular hydrogen binding in order to understand and improve H2 sorption properties of candidate materials.

As discussed in more detail in the following section, molecular hydrogen interactions with any system range from weak dispersive or van der Waals forces, to electrostatic interactions, to orbital interactions and non-classical sigma bonding (metal–dihydrogen complexes).24 The van der Waals interactions involving H2 are typically of the order of a few kJ mol−1 and HSM that rely solely on this interaction cannot achieve significant adsorption capacity at reasonable temperatures. Theoretical investigations suggest that the DOE target at ambient conditions cannot be achieved by HSM like pure carbon nanostructures, which interact with H2 by van der Waals interactions.6,25 Indeed, the potential of carbon nanostructures as a HSM has been a controversial topic since the first reported H2 uptake in 199726 due to inconsistent experimental results, and lack of agreement with theoretical studies which themselves have not always employed reliable methods.4–6,19,27–32

Electrostatic interactions between hydrogen and charged sites are typically stronger than van der Waals forces, depending upon the nature of the charged site, such as the extent of localization and polarizability. Strategies to improve adsorption energies can take advantage of this interaction by making charged metal sites available within the material. For instance, alkali-doped carbon nanotubes were found to exhibit higher H2 uptakes (∼2–14 wt% H2 under ambient conditions).33–35 From theoretical investigations,36–39 it was concluded that the doped element transfers charge to the nanosurface, which enables adsorption of H2 on the alkali atom through charge-induced dipole interactions that improve the H2 binding affinity from about 5–6 kJ mol (on plain graphene surfaces)40–42 to about 8–12 kJ mol−1.37,38 The possibility of direct chemisorption with the doped metal was ruled out. It was also suggested that the adsorption energy decreases rapidly with temperature and hence, uptake due to adsorption on the alkali metal centers is unlikely at room temperature.36,39 Recently, Deng et al. have used computational methods to design and propose a new class of Li-doped pillared carbon nanomaterials that can theoretically meet the DOE target.36 These observations suggest that enhanced electrostatic interactions can improve adsorption energies, but careful consideration of the electronic structure of the modified materials is necessary for reliable prediction and understanding.

Sigma bonded H2 complexes are now common in transition metal chemistry where forward donation of the H–H electron density into low-lying vacant metal d-orbitals and back-donation from the metal (M) to the anti-bonding σ* H2 orbital, synergistically stabilize the M–H2 bond. Isolation of the Kubas complex in the mid 1980s is considered a landmark event in the field of coordination chemistry as the idea that molecular hydrogen could act as a σ-donating ligand instead of forming hydridic complexes was groundbreaking.43 Hundreds of dihydrogen transition metal complexes have been isolated and characterized since then. From the perspective of hydrogen storage, these transition metal–hydrogen complexes (M–H2) can reversibly bind H2 and the magnitude of the M–H2 bond strength can be varied between 20–160 kJ mol−1 depending upon the valence configuration of the metal and the coordinating ability of the ligands attached to the metal.24,44,45 While the heavy masses of the transition metals are not favorable for achieving high gravimetric density, it is possible that strong σ-bonded H2 complexes can be exploited as part of the design of novel HSM.46–48 For example, a recent computational study proposed attaching simple transition metal complexes on fullerenes as a strategy to enhance the H2 binding affinity (∼30–40 kJ mol−1) and offer H2 uptake as high as ∼9 wt% H2 at ambient conditions.48

Nonetheless, it is desirable to avoid heavy transition metal centers, and thus it is of great interest to explore the interactions of H2 with lighter main group metal ions/complexes. Numerous theoretical studies (and a few experiments) have been conducted on these simple systems in order to compare and contrast the bonding picture against transition metal–dihydrogen complexes.49–59Ab initio investigations revealed that non-transition metal ions like Li+, Na+, Be2+, Mg2+, Al+ and simple compounds like BeO, MgF2, AlF3, BeS, MgS form stable molecular hydrogen complexes. Intriguingly, from the viewpoint of tuning the interaction strength, the magnitude of H2 binding energy exhibits a very wide range of between ∼4–200 kJ mol−1.49–59 These studies suggest that electrostatic effects play a dominant role, especially in alkali metal ions, and forward σ donation of H2 also contributes to the stabilization of the M–H2 bond of the other relatively heavier and smaller main group metal ions. Some studies also showed that the bare alkali metal ions could interact with multiple hydrogen molecules with a small loss in each binding energy increment owing primarily to increased repulsions.50–53 It is only in the recent past that the potential/importance of these lightweight metal ion/complex–H2 interactions was realized in the context of hydrogen fuel storage.59–63

Microporous metal–organic frameworks (MOF) are made up of inorganic metal-oxide clusters linked together by organic units, such as (Zn4O(BDC)3; BDC = 1,4-benzenedicarboxylate). They have received considerable attention as a new class of promising HSM since the first reported H2 uptake by Yaghi and co-workers.20,64,65 The H2 uptake at room temperature and 20 bar of the isoreticular metal–organic framework (IRMOF-1) is reported to be ∼1 wt%.64 Although this is far from the 6 wt% H2 target of DOE, the sorption properties of these easily synthesized, pure, crystalline, highly porous structures with a large surface area can be potentially improved. In particular, the building blocks, namely, the metal oxide clusters and organic linkers can be systematically replaced (without disrupting the framework) to explore possible enhancement of H2 sorption properties. Both experimental64,66 and theoretical studies67–72 have recently started exploring this option although no significant breakthroughs have yet been reported.20

Inelastic neutron scattering (INS) experiment and grand canonical Monte Carlo (GCMC) simulations suggest that the zinc-oxide clusters within the MOF’s are the preferred molecular hydrogen binding sites at low pressures while the organic linkers (BDC) play a more crucial role at higher pressures.64–,67,70,72 This is because the metal-oxide sites bind H2 more strongly (∼7–8 kJ mol−1) than the organic linker sites (∼4–5 kJ mol−1) but as only a few metal-oxide sites are available, they tend to get saturated quickly. The stronger H2 binding observed at the metal-oxide site can be attributed to electrostatic and possibly orbital donation interactions, while it is likely that van der Waals forces dominate the interaction at the organic linkers. In a separate study of H2 adsorbed on a model benzene system, Hamel et al. theoretically confirmed the assignment of the rotational peaks observed in the INS experiment64 that correspond to binding sites close to the aromatic system.68

It is evident from the above observations that molecular hydrogen binding energetics plays a crucial role in designing and evaluating potential HSM like microporous materials. The mode of H2 binding can be used as a tool to tune the H2 sorption properties of candidate HSM. A rough estimate of the ideal binding energy range can be determined from simple entropic arguments.73,67 In order to achieve saturation at targeted conditions (−20 to 50 °C and pressure varying between ∼1–100 bar), the enthalpy of H2 adsorption, ΔH = TΔS at equilibrium, assuming that there is no activation barrier to H2 adsorption. Considering reference entropy values of H2 at 100 bar and 1 bar,74 the range of ΔH values at ∼−20 °C varies between ∼21–32 kJ mol−1; at ∼0 °C, ΔH ∼24–34 kJ mol−1; at room temperature, ΔH ∼28–40 kJ mol−1 and at ∼50 °C, ΔH ∼30–42 kJ mol−1. Therefore based on these simple estimates, the magnitude of ideal H2 binding affinity should roughly be in the range of ∼20 to 40 kJ mol−1 (∼5 to 10 kcal mol−1). Binding energies that are weaker than 20 kJ mol−1 correspond to complexes that are not likely to survive at ambient condition, which directly affects the H2 uptake. This is the primary reason for the low uptakes observed in MOF, and pure and alkali doped carbon nanostructures. Also interactions that are stronger than 40 kJ mol−1 are likely to require temperatures (or pressures) that do not conform to the target conditions to discharge H2, as is probably the case with most of the transition metal–H2 complexes.

In the remainder of this paper, we report a systematic ab initio computational study of the range of H2 binding affinities that are possible, and the physical features that are responsible for larger or smaller binding energies. We will consider strategies that would enable the H2 adsorption energy to fall in the above-described ideal binding energy range. Microporous frameworks and solids form the ideal candidates for such an investigation, as it is an emerging field whose materials are capable of displaying all three binding modes of molecular hydrogen. Thus there is great scope to design novel materials that might display improved sorption properties. The first strategy reported to improve H2 adsorption energies in MOF was to replace BDC with other similar aromatic systems that had larger surface areas or functional groups. However, both experimental64,65,75,76 and theoretical67–72 studies suggest that only marginal improvements are possible. We revisit this question in section 4 by analyzing the extent of change and trend observed in the H2 binding affinities when different functional groups (both electron withdrawing and electron releasing) are introduced in the ortho position of BDC.

Recent reports77,78 have demonstrated that dehydrated Prussian blue analogues (DPBA) M3[Co(CN)6]2 (M = Mn, Fe, Co, Ni, Cu, Zn, Cd) can be a potential HSM (about 1.8 wt% H2 uptake observed for M = Cu at 77 K and 890 Torr).77 The nature of H2 interactions in these frameworks is not very clear. It is believed that the coordinatively-unsaturated metal centers77,78 and the electron rich environment of the bridging cyanide ligands can act as the possible binding sites of H2.77,79 It may also be possible to introduce alternative ligands with greater H2 affinity into the framework. To explore these possibilities we have systematically studied a series of simple, uncomplexed ligands to analyze the fundamental nature and strength of H2 interaction in section 5. The ligands considered are NC−, CN−, CO, NO+, Cp− (cyclopentadienyl anion), F− and SO2−4.

The last part of our study involves adsorption of molecular hydrogen on bare lightweight metal ions and complexes. This is motivated by the fact that the coordinatively unsaturated metal binding sites in MOF and other microporous solids like DPBA77,78 show stronger interaction with H2 than the organic linkers.20 Additional open metal sites can be made available in the framework by incorporating coordinatively unsaturated metal sites within the linker to promote hydrogen interaction.80 The framework density can also be reduced by simply replacing the heavier transition metal ions with lighter main group metal ions like Li+, Na+, Mg2+ and Al3+.20,73,81 Dinca et al. have recently succeeded in synthesizing a microporous coordination solid with Mg2+ ions incorporated in the framework that displays a low sorption of ∼0.5 wt% H2 at 77 K and 880 Torr but their H2 adsorption isotherm indicates a relatively strong binding of H2 (∼7–10 kJ mol−1), which is encouraging.73 In section 6, we examine the binding interaction of H2 with Li+, Na+, Mg2+ and Al3+ and also explore the possibility of multiple H2 molecules interacting with the metal centers. To study the effect of environment, we have considered simple complexes of the form [M(L)n − (H2)]m+ (Mm+ = Li+, Mg2+, Al3+; L = CN−, CO; n = 1–3).

3. Computational modeling of hydrogen binding

3A. Elementary physical considerations

The different types of interactions between H2 and host materials can in principle be grouped into three broad categories, which we summarize below. We emphasize that in physical systems usually all are operative at once; just to greatly varying extents. To set the stage, recall that free H2 has a single occupied molecular orbital of σg symmetry, with an energy level of about −11.7 eV. There is a very large gap to the energy of the corresponding antibonding σu* orbital, whose position can be estimated as roughly +2 eV, and which will play a role in any charge transfer to H2 (see orbital interactions, below). A continuum of other empty levels ranging from very diffuse and free-electron like (near 0 eV) through to very high energy high angular momentum states (e.g. constructed from atomic p,d,f… functions) surround the σu* level, and collectively play a role in electron correlation effects, as we shall see.
Dispersion (van der Waals) interactions. There are always weak attractions between electron clouds that do not overlap, arising from instantaneous transition dipoles (where an electron transiently fluctuates from a filled level to an empty level) on each system that couple to each other. These dispersion interactions are a quantum mechanical electron correlation effect that is completely absent when considering the classical interactions of separate charge distributions. Their strength can readily be shown to decrease as 1/R6 with the separation, R, of the two systems in the non-overlapping regime. When the charge distributions overlap, electron correlation effects continue to increase in strength, but are usually still far smaller than strong orbital repulsions between filled levels (see below) that prevent the systems from approaching closer than their typical van der Waals radius. For H2 in contact with larger molecules this net binding interaction is on the order of a few kJ mol−1, as will be discussed in more detail later.
Electrostatic interactions. With no charge and no dipole, the leading permanent multipole moment in H2 is its small quadrupole moment, which can weakly couple to other charges (decaying as 1/R3). Given that the quadrupole moment of H2 is 2.21 × 10−40 C m2,82,83 we can estimate that its interaction with a point charge at 3 Å separation is ∼3.5 kJ mol−1. H2 is also moderately polarizable, which is to say that a dipole moment can be induced by distorting (polarizing) the bonding σ orbital towards one end or the other of the molecule in the presence of other charges. In orbital terms, the perturbing charges cause some admixture of the empty orbitals, particularly σu*, with the original σg orbital, to lower the symmetry, and the energy in this environment. Charge-induced dipole interactions decay as 1/R4 with distance. Given that the polarizability of H2 is 8.79 × 10−41 C2 m2 J−1,82 we can estimate that the magnitude of this interaction with a unit charge at 3 Å separation is ∼6.8 kJ mol−1.
Orbital interactions. According to perturbation theory, the interaction between filled orbitals of two systems (see Fig. 1a) is overall repulsive, decreasing as their overlap decreases, which is to say as the exponential, exp(−kR), of their separation, R. The balance between this strong repulsion and weak long-range attractions (van der Waals and electrostatics) determines non-bonding contact distances. More interesting is the interaction of filled orbitals of one system with empty orbitals of another (see Fig. 1b), which can lead to overall stabilization, partial charge transfer, and a donor–acceptor bonding interaction. The matrix element W controlling this interaction also usually depends on the overlap of the interacting orbitals, and thus decays exponentially with R. From second order perturbation theory, the interaction energy depends on W2 and the inverse of the energy difference, Δ, between the orbitals, according to δE ∼ −W2/Δ. This simple analysis tells us that when we encounter L–H2 distances, which are significantly smaller than the expected van der Waals contact distance, this is likely a consequence of contributions to the interaction from donor–acceptor orbital interactions of this type (rather than electrostatics or dispersion). However, H2 is a poor charge donor because the deep energy of its bonding orbital means it will tend to couple weakly to empty orbitals on the other system. Likewise, it is also a poor charge acceptor, because of the relatively high value of its antibonding σu* orbital. Thus, while orbital interactions are crucial to obtaining substantial interaction energies with host materials, H2 is an intrinsically reluctant participant in such interactions.
Schematic representation of orbital interactions: (a) filled–filled interaction. (b) filled–empty interaction.
Fig. 1 Schematic representation of orbital interactions: (a) filled–filled interaction. (b) filled–empty interaction.

3B. Computational considerations

In realistic systems, all of the individual interactions discussed above will be collectively operative to varying extents. The job of a reliable first principles computational quantum mechanical calculation is to capture the net effect of those interactions, because of the impossibility of making useful back-of-the-envelope predictions. One must first choose an electronic structure method, and then select an appropriate atomic orbital (AO) basis set within which the calculation will be performed. The most widely used electronic structure method is density functional theory (DFT), which with the best functionals presently available, can do a good job of capturing all of the interactions discussed above except for the long-range dispersion interactions.84 Therefore we instead employ the simplest wave-function based method that is capable of describing dispersion, which is second order Mϕller–Plesset perturbation theory (MP2).85 Briefly, MP2 theory corrects a mean-field (Hartree–Fock) molecular orbital calculation for the effects of electron correlation, including dispersion. MP2 calculations are known to yield generally reliable descriptions of intermolecular interactions, although in some cases such as π stacking complexes, it is known to overestimate the binding affinity.86

We turn next to the question of the atomic orbital basis set. Working with a limited AO basis leads to potential artifacts in calculations of intermolecular interaction energies, whose relative importance is largest for the smallest interaction energies. This basis set superposition error (BSSE)87 is a consequence of electrons on one fragment borrowing basis functions from the other fragment to lower their energy and partially compensate for limitations of their own basis functions. As a result the intermolecular interaction energy may be overestimated, and will converge from below. To compensate, it is usual to calculate intermolecular interaction energies not as a simple difference, but rather as a difference relative to fragments, which are treated with ghost basis functions of the missing partner present. We will apply this counterpoise correction to all calculated binding affinities. Optimized geometries are determined without such corrections.

Dispensing with generalities, we turn now to the specifics of our calculations. All calculations were performed using a developmental version of the Q-Chem program.88 For the systems considered in section 4, geometry optimizations were carried out at the second order Mϕller–Plesset perturbation theory (MP2) level with the 6-31G* basis and further single point calculations were calculated with the computationally efficient, resolution-of-the-identity (RI) approximation MP2 method (RIMP2)89 using Dunning’s correlated consistent basis sets cc-pVXZ (X = T, Q)90,91 and the corresponding optimized set of auxiliary basis functions.92 Approximate values for interaction energies at the complete basis set limit (CBS) were estimated by performing a simple two-point extrapolation.93 All the remaining systems were optimized at the MP2/6-31G** level. Single point calculations were then evaluated at RIMP2/cc-pVTZ. In a few cases, the binding affinities were estimated using the highly correlated and extremely expensive method, coupled-cluster singles and doubles with perturbative triples correction (CCSD(T))94 with cc-pVTZ basis in order to evaluate the performance of RIMP2. Only valence electrons were correlated for all systems except those that involve metal ions.

In all the H2 complexes investigated, the H–H bond length is sensitive to the mode of H2 binding. Complexation of H2 to any system would undoubtedly perturb the H–H bond but a significant lengthening of the H–H bond relative to the unbound H295 case is indicative of strong interactions like charge transfer to and from the system resulting in a σ bonded complex. Systems that display H–H bond distances greater than 1.6 Å are considered to be hydrides.24 The distance of H2 from the system (evaluated based on binding geometry of H2 with the substrate) can be directly correlated with the strength of H2 interaction. These parameters are used as tools for analyzing the nature and strength of molecular hydrogen binding. Additionally, while atomic charges are not observable quantities, and thus are not uniquely defined, we shall sometimes employ natural bond orbital (NBO) and the associated natural population analysis as useful measures of the extent of charge transfer between substrates and H2.96,97

4. Interactions with benzene dicarboxylic acid (BDC) derivatives

With regard to metal oxide frameworks (MOF’s), considerable efforts have already gone into trying to improve H2 uptake at ambient conditions by systematically replacing the organic linkers to enable flexible pore size and for possible improvement in hydrogen sorption properties.20 Theoretical studies suggested that H2 prefers to bind head-on above the center of the aromatic ring (∼3 Å) with its axes perpendicular to the plane.67–72 The binding energy is characterized by relatively weak van der Waals interactions, yielding affinities in the range of 4–5 kJ mol−1, which are well below the desired range to meet the 2010 DOE targeted uptake at ambient conditions. Using a simple energetic model, Garberoglio et al. conclude that none of the MOF that they studied are capable of meeting the target.67

Hübner et al.69 studied the interaction of H2 with singly substituted benzenes and BDC at the RIMP2/TZVPP level. They found that the presence of electron-donating groups (like –NH2) on the benzene ring and moving to larger aromatic systems (like coronene) helps to improve the H2 binding affinity by about 0.6–1.5 kJ mol−1 more than the binding energy obtained with benzene (∼3.9 kJ mol−1). The H2 interaction energy with BDC was found to be ∼3.6 kJ mol−1. Sagara et al.70 carried out MP2 calculations on IRMOF-1 (also called MOF-5) to evaluate the H2 binding energy with both metal-oxide cluster and BDC (both carboxylic groups terminated by Li atoms). They estimate the binding energies to be 6.9 and 5.4 kJ mol−1, respectively. In a recent second report, they have computationally studied the H2 binding interaction with a series of IRMOF materials at the RIMP2/QZVPP level of theory with no correction for BSSE and give a best estimate of the respective binding energies that range between 4.2–5.5 kJ mol−1 for the various IRMOF. They also concluded that adding electron-donating groups to the organic systems improves the binding energy.71

To further explore the extent to which the H2 binding affinities can be perturbed by the presence of nearby functional groups, we have systematically studied the effect of adding a single substituent at the ortho position of BDC (represented as BDC-X; X = H, F, CH3, NH2, OH). For simplicity, we have not replaced the acidic hydrogen of the carboxylic groups with lithium or any metal. The MP2/6-31G* optimized geometries of the two H2 binding configurations considered (perpendicular and parallel) for BDC-H2 complex are shown in Fig. 2. The presence of an ortho substituent did not seem to affect the geometry of H2 adsorption for the perpendicular configuration, which was found to be the most favorable structure for all BDC-X considered and the distance between H2 (measured from the hydrogen atom closest to the ring) and the center of the aromatic ring was around 3 Å (see Table 1), in agreement with all the previous theoretical studies.69–71


Top and side view of the MP2/6-31G* optimized BDC-H2 complex. (a) Perpendicular configuration. (b) Parallel configuration. M–H2 distances indicated in Å.
Fig. 2 Top and side view of the MP2/6-31G* optimized BDC-H2 complex. (a) Perpendicular configuration. (b) Parallel configuration. M–H2 distances indicated in Å.
Table 1 Geometrical parameters (in Å) and BSSE corrected hydrogen binding affinity (in kJ mol−1) of BDC-X—H2 complexes evaluated at the RIMP2/CBS//MP2/6-31G* level
XPerpendicularaParallela
M–HbH–H−BEcM–HdH–H−BEc
a See Fig. 2.b Distance measured from center of the aromatic plane to that H atom of the H2 molecule that is closer to the ring.c BE: binding energy.d Distance measured from center of the aromatic ring to the center of mass of the H2 molecule.e Unbound H–H bond length optimized at MP2/6-31G* level.
  0.737e  0.737e 
H3.0440.7384.0293.4470.7383.396
F3.0150.7383.7743.4450.7383.416
CH33.0110.7384.3253.4540.7383.347
NH23.0300.7384.2973.4320.7383.543
OH3.0120.7384.1633.4310.7383.551

The counterpoise-corrected binding energies calculated at RIMP2/CBS level are listed in Table 1. The H2 binding energies obtained for the parallel configurations are smaller by ∼0.4–1 kJ mol−1 than the corresponding energies for the perpendicular configurations. Substitution in the parallel binding configuration (except X = CH3) uniformly increases the magnitude of the binding energy and correlates well with decreasing M–H distance. In case of X = CH3 (relative to X = H), repulsion between methyl hydrogens and H2 is probably responsible for the longer M–H distance ∼3.454 Å and correspondingly weaker binding energy.

For the perpendicular configurations, the electron-releasing CH3 and NH2 substituted BDCs show the highest binding affinity ∼4.3 kJ mol−1, closely followed by the OH group with ∼4.2 kJ mol−1. The binding energy of H2 with BDC-F is about 0.2 kJ mol−1 smaller than regular BDC-H indicating the effect of an electron-withdrawing group. While it is satisfying to confirm the expected trend, it should be noted that the difference in the binding energies due to different substituents is not substantial. The key point is that the nature of the H2 interaction with the organic linkers is inherently weak as it is a van der Waals/dispersion interaction. Adding simple electron-donating substituents or increasing the size of the aromatic system will not help to dramatically improve the H2 binding strength from the current 4–5 kJ mol−1 to the targeted 20–40 kJ mol−1, at least not without additional assistance from direct electrostatic or donor–acceptor interactions, which we investigate with case studies in the following two sections.

5. Interaction of hydrogen with simple charged ligands

Kaye et al. recently reported that dehydrated Prussian blue analogs (DPBA’s) display modest hydrogen adsorption.77 They further suspect that the electron rich cyanide bridging ligands can act as a potential binding site similar to the role played by the BDC linkers in MOF’s. In order to investigate this possibility, we have studied the possible interaction of H2 with a series of uncomplexed (free) ligands NC−, CN−, CO, NO+, Cp−, F− and SO2−4. The first question that we seek to answer is, can H2 interact with these ligands without dissociating? If yes, then how strong is the interaction and what forces are responsible for stabilizing the ligand–H2 bond? Intuitively, we expect H2 to form a complex stabilized by charge-induced dipole and charge–quadrupole interactions with the charged ligands. We also need to investigate the possibility of orbital interactions, and compare against the case of neutral CO, where no substantial electrostatic effects are possible.

We first consider the interaction of one hydrogen molecule with each ligand. The MP2/6-31G** optimized structures are shown in Fig. 3, 4a and 5a. Every structure was verified to be a valid minimum with no imaginary frequencies. Perhaps in order to maximize charge–quadrupole interactions, H2 adopts a distorted parallel configuration (see Fig. 3d) over the positively charged NO+ ligand and the strength of this interaction is about ∼7 kJ mol−1. The importance of electrostatic effects in strengthening the molecular hydrogen binding interaction is clear when we consider the iso-electronic neutral CO ligand. H2 binds very weakly with both CO (∼0.4 kJ mol−1) and OC (∼0.6 kJ mol−1). The fact that the uncorrelated Hartree–Fock model does not bind H2 and CO indicates that dispersive van der Waals forces are primarily responsible for this weak interaction (see section 3). This is supported by the long distance between the ligand and H2 (∼2.8–3.0 Å) and the almost unperturbed H–H bond length (see Fig. 3e and 3f). The magnitude of the natural charge on the H atoms of H2 is ∼0.004–0.008 e for CO and NO+ suggesting that the H–H bond is not sufficiently polarized for charge-induced dipole interactions to play a dominant role.


MP2/6-31G** optimized structures of various ligand–H2 complexes: (a) CN−–H2 (b) NC−–H2 (c) Cp−–H2 (d) NO+–H2 (e) CO–H2. All distances (H–H and L–H) are given in Å.
Fig. 3 MP2/6-31G** optimized structures of various ligand–H2 complexes: (a) CN−–H2 (b) NC−–H2 (c) Cp−–H2 (d) NO+–H2 (e) CO–H2. All distances (H–H and L–H) are given in Å.

MP2/6-31G** optimized structures of the complexes F−–(H2)n: (a) n = 1 (b) n = 2 (c) n = 3 (d) n = 4. All distances (H–H and F–H) are given in Å.
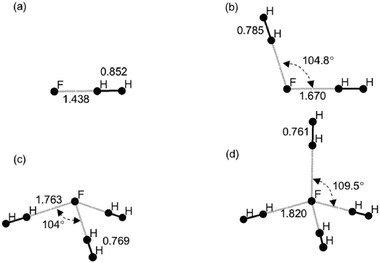Fig. 4 MP2/6-31G** optimized structures of the complexes F−–(H2)n: (a) n = 1 (b) n = 2 (c) n = 3 (d) n = 4. All distances (H–H and F–H) are given in Å.

A few representative MP2/6-31G** optimized structures of the complex SO2−4–(H2)n: (a) n = 1 (b) n = 4 (c) n = 5 (d) n = 8. All distances (H–H and O–H) are given in Å.
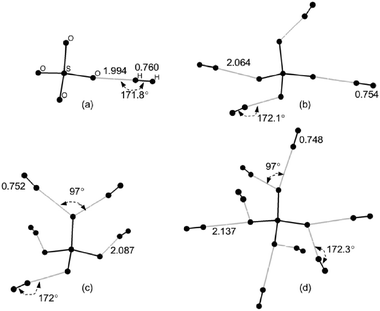Fig. 5 A few representative MP2/6-31G** optimized structures of the complex SO2−4–(H2)n: (a) n = 1 (b) n = 4 (c) n = 5 (d) n = 8. All distances (H–H and O–H) are given in Å.

Molecular hydrogen binds in an “end-on” fashion (see Fig. 3a–c, 4a and 5a), with the negatively charged ligands, which induces a dipole on H2 and results in a charge-induced dipole dominant interaction. Table 2 gives a summary of the structural features of the optimized geometries and the binding energies obtained at different levels of theory. Table 3 highlights the natural charges obtained on the ligating atom and H atoms of H2 in the various complexes, the σ* H–H bond occupancy calculated from natural bond orbital (NBO) analysis and the ionization potential of the ligands considered. Table 2 reflects that the interaction energies obtained at the RIMP2 level are quite satisfactory as they are comparable to energies obtained at a higher level of theory like CCSD(T). There is significant difference between the binding energies predicted by the uncorrelated Hartree–Fock method and the two correlated methods indicating that correlation effects are important in addition to electrostatic effects.

Table 2 Geometrical features (in Å) and BSSE corrected hydrogen binding energies (in kJ mol−1) with the ligands considered optimized at MP2/6-31G** level
LigandL–HaH–H−BEb
HFRIMP2CCSD(T)
a Distance of H2 from ligand, see Fig. 3, 4a and 5a.b BE: Binding energy evaluated with cc-pVTZ basis.c Unbound H–H bond length optimized at MP2/6-31G** level.d Ligating atom is C. See Fig. 3f.
  0.734c   
NC−2.3850.7503.137.817.90
CN−2.2860.7476.259.639.69
SO2−41.9940.76014.9121.3321.66
F−1.4380.85220.6434.1934.70
Cp−2.5320.7415.5213.3412.40
CO2.8080.734−0.400.360.41
OCd3.0020.734−0.750.560.52
NO+2.8040.7365.516.666.63

Table 3 Natural charges (Q) on ligating atom (L) and H atoms of H2, natural bond orbital occupancy (n) of the σ* orbital of H2 in units of e− and ionization potential of the ligands
LigandaQnσ*(H–H)IP/eV
LH1bH2b
a Ligating atom given in paranthesis.b H1 ≡ H atom of H2 that interacts with ligating atom L. H2 ≡ the other H atom of H2.c Charge on N.
NC− (C)−0.17600.0919−0.12310.03124.63
CN− (N)−0.84340.1040−0.11720.01444.63
SO2−4 (O)−1.18850.1575−0.18530.02800.11
F− (F)−0.89040.2526−0.36230.10493.54
Cp− 0.0887−0.09170.00271.71
CO (O)−0.61850.0075−0.00810.000515.13
OC (C)+0.61430.0044−0.00720.002615.13
NO++0.8796c0.0081−0.00440.000130.59

The binding affinities range between 8–34 kJ mol−1 for the negatively charged ligands under consideration and indicate that the affinity has a large dependence on the interacting ligand. These interactions are almost an order of magnitude stronger than the van der Waals forces of interaction. Table 2 indicates that the H2 binding affinity amongst the negatively charged ligands increases in the order NC− < CN−< Cp−< SO2−4< F−. With the exception of Cp−, there is good correlation between the L–H1 distance, H–H bond length, effective atomic charge on H1 and the trend observed in the binding affinity. For instance, F−–H2 displays the highest binding energy (∼34 kJ mol−1), shortest L–H distance (∼1.438 Å), longest H–H bond (∼0.852 Å) and highest natural charge (∼0.25 e) on H1.

As discussed in section 3, a combination of electrostatic induction and charge transfer orbital interaction is responsible for these observed trends. The extent of inductive effects is expected to be largest for ligands with the most localized charges. The estimated magnitude of the effective charge on the ligating atom (L) in the anionic ligands decreases in the order SO2−4 > F− > CN− > NC− while the natural charge on the H1 atom follows F− > SO2−4 > CN− > NC− > Cp−. The shorter L–H distance in the case of F−–H2 suggests a greater inductive contribution to the interaction energy relative to SO2−4. In the case of the ligand Cp−, the π-electron cloud of the five-membered ring is responsible for inducing a dipole on H2 and results in a binding configuration reminiscent of the BDC-H2 picture seen in the previous section. However, the interaction observed here is about three times stronger than the BDC case and falls in the binding range between CN− and SO2−4.

The noticeable perturbation of the H–H bond length in these systems indicates decreased occupation of the σ orbital and/or increased occupation of the σ* orbital, in the simplest molecular orbital (MO) picture. The back-donation can occur as the end result of two successive interactions. First, mixing of the unperturbed σ and σ* orbitals of H2 under the influence of the neighboring charge, followed by coupling between the highest occupied MO (HOMO) of the anion with the perturbed σ* orbital to effect partial charge transfer. The extent of charge-transfer binding is expected to be strongest for systems with HOMO of appropriate symmetry and highest energy (i.e. lowest ionization potential). For example, NO+ does not bind in a linear geometry because its HOMO is of π symmetry, which cannot couple to the σ* level of H2 in that geometry, but can in the off-center geometry that is favored. The ionization potential of the ligands under study increases in the order SO2−4 < Cp− < F− < CN− < CO < NO+. Natural bond orbital (NBO) analysis (refer Table 3) suggests that the σ* orbital occupancy decreases in the order F− > NC− > SO2−4 > CN− > Cp− > OC > CO > NO+. This trend is a result of considering both ionization potential and favorable symmetry of the HOMO criteria and it is also indicative of the extent to which orbital interactions contribute to the interaction energy.

A combination of these electrostatic induction and covalent charge-transfer effects therefore determines the trend observed in the strength of H2 interactions with ligands. The relative importance of the two effects largely depends upon the properties of the ligand. For instance, in case of Cp−–H2 system, the relatively long L–H distance (∼2.53 Å), weakly perturbed H–H bond length (∼0.74 Å) and low σ* occupancy suggests that inductive effects are stronger than charge transfer interactions whereas in the F−–H2 complex, both effects are of comparable magnitude.

The binding affinities of molecular hydrogen with F− and SO2−4 alone fall within our definition of ideal binding range for H2 storage. Can these ligands adsorb more than one H2 molecule with reasonably strong binding strengths? Potentially, the free sulfate dianion SO2−4 has 4 equivalent binding sites and so we should expect at least 3 more H2 molecules to bind with an affinity close to 20 kJ mol−1. The binding energies are expected to decrease owing to the increased electron density of the Lm−–(H2)n−1 complex when the nth H2 is added. We were able to locate valid minimum energy structures for F−–(H2)n (n = 1–4) and SO2−4–(H2)n (n = 1–8). Fig. 4 and 5 show the optimized structures obtained at MP2/6-31G** level for F− and a few representative SO2−4 complexes. Table 4 gives a summary of the structures and incremental binding energies that correspond to the reaction, Lm− − (H2)n−1 + H2 → Lm− − (H2)n. As Table 1 suggests that RIMP2 binding energies are close to those predicted by higher-level correlated methods like CCSD(T), we have only computed the RIMP2 interaction energies to save on computational effort.

Table 4 Geometrical parameters (in Å) and BSSE corrected hydrogen binding affinities (in kJ mol−1) for L–(H2)n complexes optimized at MP2/6-31G** level
LigandnL–HaH–H−BEb
HFRIMP2
a Distance of H2 from ligand, see Fig. 3 and 4.b Incremental binding energy calculated with cc-pTVZ basis as BE = E[L–(H2)n] − E[L–(H2)n−1] − E[H2] and further corrected for BSSE.c Unbound H–H bond length optimized at MP2/6-31G** level.
   0.734c  
F−11.4380.85220.6434.19
 21.6700.78516.2716.41
 31.7630.76913.5614.62
 41.8200.76112.5413.08
      
SO2−411.9940.76014.9121.33
 22.0200.75814.4819.78
 32.0410.75615.2519.50
 42.0640.75414.2617.47
 52.0870.75212.8516.60
 62.1050.75112.4316.07
 72.1230.75011.9615.03
 82.1370.74811.3614.30

The addition of a second H2 molecule to the F− complex decreases the RIMP2 binding energy by about 50% and reflecting the weaker interactions, the H–H bond length is shortened by about ∼0.07 Å relative to the n = 1 complex. Subsequent addition of H2 results in a small additional decrease (∼1 kJ mol−1) in binding affinity. The close correspondence between the HF and RIMP2 results for the clusters n = 2–4 indicates that the covalent effects operating in the F−–H2 complex are redistributed and additional stability comes largely from inductive and electrostatic effects.

As expected, the energy released upon successive adsorption of the next three H2 molecules onto the remaining O sites of SO2−4–H2 (see Fig. 5 and Table 4) varies between ∼17–20 kJ mol−1. It is also possible to adsorb another set of H2 molecules (n = 5–8) on each of the O binding sites. The incremental binding energy for this adsorption decreases by ∼1 kJ mol−1 with each successive adsorption. The complexes n = 1–8 show a systematic shortening of ∼0.001–0.002 Å of the H–H bond distance with each additional H2 molecule reflecting decreased binding energy, perhaps associated with greater charge delocalization as the complex size increases.

This study of ligand–H2 interactions emphasizes the importance of charge-induced dipole and charge-quadrupole interactions in strengthening the H2 binding affinity. One should bear in mind that it is experimentally very difficult to achieve bare sites like F− or SO2−4 in real systems. Therefore, binding affinities that have been calculated with these bare ligands would be considerably reduced when the ligands are complexed to some metal center as the full charge would no longer be available, which is likely to result in weaker electrostatic and orbital interaction forces. This aspect will be investigated further in the following section.

6. Interactions with lightweight metal ions/complexes

Adsorption of molecular hydrogen on metal centers/complexes is another important mode of H2 interaction, which is receiving considerable attention as it is inherently stronger than the weak van der Waals interactions and can be crucial to improving H2 sorption properties under ambient conditions. To explore the range of bonding affinities that are possible for such systems, as well as to understand the origin of this kind of hydrogen binding, we analyze the interaction of H2 with bare lightweight metal ions and some of their simple complexes, in the following two subsections.

6A. Bare metal ions

We have systematically studied the interaction of H2 with a few lightweight non-transition metal ions (Li+, Na+, Mg2+, Al3+) with two goals in mind. First, to assess the role played by the magnitude of ionic charge on the H2 binding affinity. Second, to examine the possibility of clustering more than one H2 around these bare metal centers. It is now well known that the first H2 binds in a side-on fashion (C2v symmetry) with the metal ion, which is likely to maximize charge-quadrupole coupling. The additional hydrogen molecules would then tend to take up those optimal positions around the metal center that would minimize the repulsive H2–H2 interaction and maximize the attractive interaction. The MP2/6-31G** optimized structures of Mg2+–(H2)n (n = 1, 6) systems are shown in Fig. 6. The other metal ion–H2 clusters also adopt similar structures. However, the average H–H bond length and the average distance between the metal ion and the center of mass of H2 (M–H2 distance) depend significantly on the metal center, as shown in Table 5. The average M–H2 distance increases as the ionic charge decreases and size of the ion increases, Al3+<Mg2+ < Li+< Na+. The H–H bond distance increases in the reverse order. This trend will be discussed in more detail shortly.
MP2/6-31G** optimized structures of Mg2+–(H2)n (n = 1–6). Dashed lines represent the distance from metal to center of mass of H2 (M–H2). All distances (H–H and M–H2) are given in Å.
Fig. 6 MP2/6-31G** optimized structures of Mg2+–(H2)n (n = 1–6). Dashed lines represent the distance from metal to center of mass of H2 (M–H2). All distances (H–H and M–H2) are given in Å.
Table 5 Geometrical parameters (in Å) and BSSE corrected binding energies (in kJ mol−1) of various lightweight metal ion–dihydrogen [M(H2)n]m+ complexes optimized at MP2/6-31G** level
Mm+nM–H2aH–H−BEb
HFRIMP2CCSD(T)
a Distance measured from metal ion to center of mass of H2 (see Fig. 6).b Incremental binding energy calculated with cc-pTVZ basis as BE = E[L–(H2)n] − E[L–(H2)n−1] − E[H2] and further corrected for BSSE.c Unbound H–H bond length optimized at MP2/6-31G** level.
   0.734c   
Li+12.0890.74123.8924.0624.06
 22.0830.74122.8023.2223.26
 32.0930.74120.2121.3021.63
 42.1010.74117.4519.8719.96
 52.1370.7408.2812.4312.93
 62.1710.7399.2913.7714.23
       
Na+12.4710.73912.5512.7612.80
 22.4710.73912.1812.4712.51
 32.4750.73811.3010.6310.63
 42.4770.73810.5911.6711.84
 52.4910.7388.4911.6312.01
 62.5000.7388.2011.0011.34
       
Mg2+12.0340.76490.3791.7192.34
 22.0370.76283.8185.4886.06
 32.0510.75971.5972.9373.47
 42.0630.75662.0165.9466.53
 52.0940.75240.4247.5348.24
 62.1120.75040.3847.7448.45
       
Al3+11.8390.878346.64350.45354.13
 21.8290.844291.50296.10298.07
 31.8330.817218.15222.97224.05
 41.8400.800175.77184.35185.27
 51.8730.784100.83113.68114.68
 61.8880.77599.91115.60115.94

Table 5 also gives the BSSE corrected binding energies calculated at different levels of theory with Dunning’s cc-pVTZ basis for the different metal ion–H2 clusters (n = 1,2… 6). The difference between the HF and post-HF results becomes steadily more significant as the number of H2 molecules bound to the metal center increases. Fortunately, correlation introduced at the level of RIMP2/cc-pVTZ theory seems sufficient to describe binding energies that are as accurate as more sophisticated methods like CCSD(T). The results obtained agree well with previous studies on molecular hydrogen interaction with Li+ and Na+ clusters.51–53,59 It is noteworthy that the binding energies vary over a tremendously wide range of ∼12–340 kJ mol−1!

As expected, the magnitude of the interaction energy (per H2 that is bound) decreases systematically as the cluster size is increased from n = 1 to 6 (overall decrease ⇒ Li+: ∼10.3 kJ mol−1; Na+: ∼1.8 kJ mol−1; Mg2+: ∼44 kJ mol−1; Al3+: ∼234.9 kJ mol−1). There is a relatively significant drop in the binding energy as the cluster size is increased from n = 2 to 3 for all ions (Li+: ∼2 kJ mol−1; Na+: ∼1.8 kJ mol−1; Mg2+: ∼12.6 kJ mol−1; Al3+: ∼73.1 kJ mol−1) and a similar drop is observed as size is increased from n = 4 to 5, except for Na+ (Li+: ∼7.4 kJ mol−1; Mg2+: ∼18.4 kJ mol−1; Al3+: ∼70.7 kJ mol−1). This behavior of the odd-numbered clusters seems to arise from the fact that the centers of masses of three H2 are forced to almost lie in a triangular plane (see Fig. 6) and the H2–H2 repulsions are relatively increased compared to the even-numbered clusters where the H2 molecules are alternately perpendicular to each other. Barbatti et al. have also noticed a similar feature in their Li+–(H2)n clusters.51

What are the underlying forces of interaction that are responsible for this wide range of binding energies? It is now quite well understood that the forces binding the hydrogen molecules in the alkali metal ion clusters are predominantly electrostatic charge-quadrupole and charge-induced dipole interactions.49,51–53,59 The smaller size of Li+ enables a better charge to size ratio than Na+ and hence H2 sticks to the former more strongly than the latter. Charge-transfer effects have been ruled out and this is evident from the not-so-significant lengthening of the H–H bond (<0.005 Å) relative to the free H–H bond. Nevertheless, the simple electrostatic interaction of Li+ and molecular hydrogen (∼20–24 kJ mol−1 for n = 1–4) is just strong enough to fall into our range of ideal H2 binding affinities.

If electrostatics alone dominates the Mg2+–H2 cluster interactions then the binding strength of the first H2 with Mg2+ should be roughly twice that of Li+, owing to their similar sizes. However, the binding energy of Mg2+–H2 is about four times stronger than that of Li+–H2 and the H–H bond is lengthened by ∼0.03 Å relative to the free H–H bond. This clearly indicates that there are other important effects present apart from electrostatic forces. This is true for the Al3+ clusters too, which shows a phenomenally strong binding of ∼350.5 kJ mol−1 with the first H2 molecule. Even though the H–H bond is elongated to ∼0.878 Å, this is still considered a molecular H2 complex.24 Both Mg2+ and Al3+ have low lying vacant valence orbitals of favorable symmetry that can mix with the σ bonding orbital of H2, permitting a forward donation of the H2 σ electron density into the vacant orbitals. Donor interactions are strongest for Al3+ because its empty valence orbitals are lower in energy than those of Mg2+ and as a result couple more strongly to H2 leading to a stronger complex with a shorter Mm+–H2 distance (∼1.839 Å). As a result of the σ donation, the H–H bond is lengthened considerably. By contrast, σ donation is not significant for the alkali metal ions as their unoccupied valence orbitals lie much higher in energy than Mg2+ and Al3+. Back-donation from the filled metal ion orbitals to σ* antibonding orbital of H2 is also insignificant.

The magnitude of charge transfer is decreased when additional H2 are adsorbed onto the complex Mm+–(H2)n−1, which in turn weakens the binding interactions of the subsequent H2 molecules and is also responsible for the H–H bond distance to asymptotically decrease towards the free H–H bond length.95 The electrostatic charge-quadrupole effects are also affected as the cluster size increases as the forward σ donation from the multiple H2 molecules decreases the effective charge on the metal center. To summarize, the H2 molecule can act as a strong σ donor when low lying vacant metal orbitals are available. This charge transfer effect augmented with the electrostatic and inductive effects are responsible for the strong binding of H2 to bare metal ions like Mg2+ and Al3+. These metal ions can also interact with several H2 molecules with significantly strong bonds. However, the incremental binding energies decrease with increase in cluster size owing to: (i) decreased charge transfer; (ii) reduced effective charge of the metal core and (iii) increased H2–H2 repulsions.

6B. Metal complexes

From the hydrogen storage perspective, Mg2+ ions and Al3+ form extremely strong molecular hydrogen bonds, which are too strong for our ideal H2 binding range of 20–40 kJ mol−1. However, it is important to bear in mind that these are bare metal ions and they are experimentally very difficult to realize in real systems. The bonding picture will be quite different when the metals are complexed with only part of the charge available to interact with the H2 molecules. This raises the question of whether lightweight complexes of Al3+, Mg2+ and Li+ can still bind molecular hydrogen effectively? Nicolaides et al. found that MgF2 and AlF3 form very weak molecular H2 complexes with binding energies, ∼11.8 kJ mol−1 and 11.3 kJ mol−1, respectively.55 They also reported that BeO, BeS and MgS form stable H2 complexes with the best calculated binding energies of ∼72.4 kJ mol−1, 64.9 kJ mol−1 and 5 kJ mol−1, respectively. The high binding affinity shown by BeS and BeO motivated further theoretical studies to explore the use of BeO and BeS as HSM.60,61 It was suggested that the isomeric hydrides, HBeOH and HBeSH, could serve as HSM, although the energy barrier to release the products, H2 and corresponding beryllium oxide/sulfide, is quite high (∼322 and 205 kJ mol−1, respectively).60,61 Davy et al. reported that LiH+ and LiH also form molecular hydrogen complexes with ∼24.3 kJ and 10.5 kJ mol−1 binding energies, repectively.53

There have been a couple of experimental studies too. A recent infrared absorption study of association of molecular hydrogen with alkali-halide ion-pairs in rare-gas matrices revealed that H2 could interact with both cation and anion, however, the heat of complex formation could not be estimated from the experiment.98 A recent FTIR study on MgO in a hydrogen gas environment at 20 K disclosed that dihydrogen could adsorb on various MgII sites to form a complex with an interaction energy ranging between 4–8 kJ mol−1 but the molecular hydrogen dissociates to form hydrides at higher temperatures.99 All these studies and observations underline the important role played by charged or electron-deficient centers in strengthening the H2 interaction. Therefore, we focus on lightweight metal ions complexed to ligands that can stabilize the charge on the metal. A few gas-phase studies (both experimental and theoretical) on stabilizing the charge on Al3+ and Mg2+ using ligands has been recently reported.100,101

In order to investigate the effect of ligand environment, we have considered the binding of H2 to metal complexes of the form MLn (M = Al3+, Mg2+, Li+; L = CN−, CO; n = 1,3). CN− is a better σ donor but poorer π acceptor than its isoelectronic counterpart CO, which is known to be a strong, well-balanced σ donor and π acceptor making it a popular ligand in organometallic chemistry, where the ability of a ligand to accept the metal back-donation is often deemed important for the stability of the complex. Particularly, in transition metal–dihydrogen complexes, a good π-accepting ligand positioned trans to H2 is able to increase the electrophilicity of the metal center and thereby, improve the H2 binding affinity.24,102

In the case of main-group metal cations, the extent of back donation is much less significant than the transition metal complexes and therefore, they are less likely to gain from the π accepting ability of the ligand. Nevertheless, being good σ donors, the ligands will be able to partially populate the valence orbitals of the metal core, which would result in the decreasing the extent of H2 interaction with the metal ion. This is due to two reasons: (i) the local positive charge on the metal is decreased and (ii) the σ electron density of H2 would face repulsion as it approaches the partly populated valence orbitals. As CN− is negatively charged and also a better σ donor than CO, the H2 binding affinity to the former metal complexes will exhibit a more pronounced decrease than the latter. Obviously, as the number of the ligands complexed to the metal center increases, the strength of H2 interaction with the corresponding complexes is expected to decrease due to the aforementioned reasons.

The MP2/6-31G** optimized structures of [AlLn(H2)]m+ are shown in Fig. 7a. The Li+ and Mg2+ complexes have the same skeleton structure as the Al3+ complexes with H2 bound in a side-on fashion close to the metal core. Valid local minima were also found for structures [M(CN)(H2)]m+ (M = Mg2+, Al3+) where H2 interacts with the cyanide ligand and is bound similar to the corresponding uncomplexed ligand case, however, the interaction is very weak ∼1 kJ mol−1 (L–H distance ∼2.7–2.8 Å) as suspected in Section 5. This suggests that the speculation of Kaye et al.77 that the bridging cyanide ligands could act as potential binding sites for hydrogen sorption in DPBA could be true at very low temperatures but certainly not at ambient conditions. The important geometrical features and binding properties (RIMP2/cc-pVTZ) of the studied complexes are summarized in Table 6.


MP2/6-31G** optimized structures of: (a) [Al(L)n –(H2)]3+ (L = CN−, CO; n = 1–3). (b) [Al(CO)3 –(H2)2]3+. Dashed lines represent the distance from metal to center of mass of H2 (M–H2). All distances (H–H and M–H2) are given in Å.
Fig. 7 MP2/6-31G** optimized structures of: (a) [Al(L)n –(H2)]3+ (L = CN−, CO; n = 1–3). (b) [Al(CO)3 –(H2)2]3+. Dashed lines represent the distance from metal to center of mass of H2 (M–H2). All distances (H–H and M–H2) are given in Å.
Table 6 Geometrical features (in Å) and BSSE corrected dihydrogen binding energy (in kJ mol−1) of lightweight metal complexes optimized at MP2/6-31G** level
SystemM–H2aH–H−BEb
a Distance measured from metal ion to center of mass of H2 (See Fig. 7a).b Incremental binding energy calculated at RIMP2/cc-pTVZ level as BE = E[L–(H2)n] − E[L–(H2)n−1] − E[H2] and further corrected for BSSE.c Unbound H–H bond length optimized at MP2/6-31G** level.
  0.734c 
Li+2.0890.74124.06
    
[Li(CN)]2.1050.73811.58
    
[Li(CO)]+2.0680.74121.99
[Li(CO)2]+2.1310.73915.72
[Li(CO)3]+2.1670.73912.34
    
Mg2+2.0340.76491.71
    
[Mg(CN)]+2.1050.75049.04
[Mg(CN)2]2.3630.74012.38
    
[Mg(CO)]2+2.0510.76079.24
[Mg(CO)2]2+2.0760.75352.76
[Mg(CO)3]2+2.1150.74944.48
    
Al3+1.8390.878350.45
    
[Al(CN)]2+1.8420.791169.12
[Al(CN)2]+1.9490.75546.19
[Al(CN)3]2.1170.74318.54
    
[Al(CO)]3+1.8280.829267.69
[Al(CO)2]3+1.8430.793160.50
[Al(CO)3]3+1.8670.776118.53

In general, the M–H2 distance is increased while the bound H–H bond distance contracts to approach the free H–H bond length,95 indicating a weaker interaction with the metal complex. As expected, the effect is more pronounced in case of the CN− complexed systems. The interaction of H2 with the neutral complexes LiCN, Mg(CN)2, Al(CN)3 decreases by about 52, 87 and 95%, respectively, relative to the bare metal ion cases and with the partially neutralized complexes, [Mg(CN)]+, [Al(CN)]2+ and [Al(CN)2]+, the binding energy reduces by ∼47, 43 and 87%, respectively. This indicates that there is systematic loss in H2 binding energy (relative to the bare metal ion case) when the overall positive charge of the complex is decreased by one unit charge at a time.

It is interesting to note that the binding energy of H2 with the three neutral metal–cyanide complexes is roughly around 12–19 kJ mol−1 and the corresponding H–H bond lengths vary between 0.740 ± 0.003 Å. This indicates that the charge transfer effects operative in the bare metal ion cases are insignificant in the neutral complexes and the dominant mode of binding is an electrostatic interaction with the local charge on the metal core increasing in the order Al > Mg > Li. The partially neutralized complexes, [Mg(CN)]+, [Al(CN)]2+ and [Al(CN)2]+ exhibit features of strong σ donation by H2, characterized by relatively elongated H–H bonds and strong binding energies ∼49, 169 and 46 kJ mol−1, respectively. Note that the singly charged complexes [Mg(CN)]+ and [Al(CN)2]+ show similar H2 binding energies and H–H bond elongations. In fact, their binding energies are roughly about twice that of the Li+–H2 complex, reflecting again that the covalent charge-transfer type effects are very important.

The [M(CO)n(H2)]m+ complexes (Mm+ = Mg2+, Al3+; n = 1–3) all show significantly strong H2 binding affinities ranging between (44–268 kJ mol−1). The observed M–H2 and H–H bond distances correlate well with the trend in binding energy and indicate that charge-transfer interactions are present, although to a lower extent. The binding energies of the [Li(CO)n(H2)]+ decrease with increasing ‘n’ purely because of the fact that the effective positive charge on the metal core is stabilized by the strong σ donating CO ligands, thereby affecting the magnitude of the electrostatic interactions, which is modestly strong even at n = 3 (∼12.3 kJ mol−1).

Overall, a reasonably controlled decrement in the H2 binding affinity is observed as the number of carbonyl groups in the metal complex is increased. The percentage reduction in binding energy relative to the corresponding bare metal ion energy is as follows, [M(CO)–H2]m+: ∼10–20%; [M(CO)2–H2]m+: ∼30–50%; [M(CO)3–H2]m+: ∼50–70%. For instance, the binding energy of Mg2+–H2 complex is reduced from ∼92 kJ mol−1 to ∼45 kJ mol−1 when three carbonyl groups are bound to the metal core, whereas, in the case of Al3+, the binding energy decreases from ∼351 kJ mol−1 to ∼119 kJ mol−1. It might be possible to further tune the H2 binding energy with AlIII-complex by either increasing the number of CO ligands attached or replacing CO with a stronger σ donating, neutral ligand. It is an example of how one might be able to control the H2 binding strengths to fall into the ideal range of binding affinities.

To further investigate if these simple metal complexes have the ability to bind more H2 molecules, we consider metal complexes of the form [M(CO)3–(H2)2]m+ for Li+, Mg2+ and Al3+. The MP2/6-31G** optimized structure of [Al(CO)3–(H2)2]3+ is shown in Fig. 7b and the corresponding Li+ and Mg2+ complexes bear the same skeleton structure. The main structural features and BSSE corrected incremental binding energy computed at RIMP2/cc-pVTZ level are listed in Table 7. The binding energy of all three complexes decreases by about ∼40–60% relative to the parent complex (with only one bound H2 molecule) accompanied by increase in the average M–H2 distance and approach of the average H–H bond length in the complex towards the unbound H–H distance.95 The strong binding displayed by H2 with the Mg2+ and Al3+ complexes (∼27.2 and 62.8 kJ mol−1, respectively) reiterates the importance of charged centers in enhancing the H2 binding affinity.

Table 7 Geometrical features (in Å) and BSSE corrected dihydrogen binding energies (in kJ mol−1) of lightweight metal complexes [M(CO)3–(H2)2]n+
Mn+M–H2aH–H−BEb
a Distance measured from metal ion to center of mass of H2 (See Fig. 7b).b Incremental binding energy calculated at RIMP2/cc-pTVZ level as BE = E[L–(H2)n] − E[L–(H2)n−1] − E[H2] and further corrected for BSSE.c Unbound H–H bond length optimized at MP2/6-31G** level.
  0.734c 
Li+2.3490.7365.02
Mg2+2.1910.74527.15
Al3+1.9510.76062.80

7. Conclusions

Molecular hydrogen binding affinities play a very important role in determining the hydrogen sorption capacities of novel HSM. In order to achieve the DOE target at ambient conditions, the ideal H2 binding energy should be in the range of ∼20–40 kJ mol−1 (∼5–10 kcal mol−1). We have shown that H2 adsorption energies can display a wide range of energies depending upon the mode of interaction. The weakest mode is van der Waals interactions (∼4–5 kJ mol−1). HSM that rely solely on this type of interaction are unlikely to achieve the DOE target. Efforts to improve the organic linker binding site by introducing functional groups will only bring about a very modest change. The intermediate range of interactions that are likely to help achieve the ideal H2 binding energy range is a combination of electrostatic, inductive and covalent charge transfer effects. These interactions are limited by the nature of the interacting charge and its environment.

Binding of H2 to ligands like cyanide that are present within the framework of the material like DPBA is very weak and unlikely to survive at high temperatures. However, uncomplexed ligands like F− and SO2−4 can bind molecular hydrogen with reasonably strong affinity (∼34 and 20 kJ mol−1, respectively, compared to CN−: ∼10 kJ mol−1) and are characterized by charge-induced dipole interactions and covalent effects. When these ligands are complexed, it is possible that they might still be able to bind H2 with moderately strong affinity. Also, ligands like SO2−4 provide multiple binding sites, which can help to increase the H2 uptake. Therefore, more efforts are required to identify and analyze ligands that can exhibit the above characteristics, as well as modes of coordination that preserve significant local charge.

The H2 binding affinity can be enhanced by allowing H2 to interact with a coordinatively unsaturated or partially charged lightweight metal centers that are characterized by electrostatic charge-quadrupole, charge-induced dipole interactions and sometimes, charge transfer effects like forward donation of the σ electron density of H2 to the metal. The strength of these interactions depends critically on the metal center and its charge. Amongst the alkali metal ions, Li+ shows a reasonable strong affinity for H2 (∼24 kJ mol−1) but upon complexation, this is reduced ∼12 kJ mol−1. More highly charged metal ions like Mg2+ and Al3+ bind H2 too strongly to fall within the ideal binding range. However, their H2 binding energy can be tuned with reasonable control upon complexation with ligands like CO. For instance, the H2 binding energy for the [Mg(CO)3]2+ complex was found to be ∼44 kJ mol−1 and moreover, we found that a second H2 molecule could be adsorbed with ∼27 kJ mol−1. Future strategies to improve hydrogen uptake in these types of novel HSM should definitely try to incorporate lightweight metal ions like Mg2+ and Al3+ as they can bind H2 quite strongly and can also decrease the gravimetric density.

Due to the critical role of the detailed environment, it is also clear that the scope for further model computational studies is somewhat limited. This work, as well as others, clearly shows that detailed tuning of the H2 binding affinity is possible based on clear physical and chemical considerations. Incorporating these considerations into the intelligent design of next-generation HSM is the open challenge, which is made difficult by the fact that the properties of model binding sites depend so strongly upon their solid state environment. Therefore, moving towards direct modeling of the systems that are potential targets for synthesis (or at least modeling their proposed binding sites in full detail) is clearly the direction that future computational efforts must increasingly take.

Acknowledgements

This work was funded by the Department of Energy grant no. DE-FG36-05GO15002 and additional indirect support from a grant through the Computational Nanosciences program for the development of relevant methodology. We thank Jeffrey R. Long, Steven S. Kaye and Mircea Dinca for useful discussions.

References

  1. R. Coontz and B. Hanson, Science, 2004, 305, 957–957 CrossRef .
  2. L. Schlapbach, MRS Bull., 2002, 27, 675 CAS .
  3. L. Schlapbach and A. Zuttel, Nature, 2001, 414, 353–358 CrossRef .
  4. L. Zhou, Renew. Sust. Energ. Rev., 2005, 9, 395–408 Search PubMed .
  5. A. Zuttel, Naturwissenschaften, 2004, 91, 157–172 CrossRef .
  6. M. Fichtner, Adv. Eng. Mater., 2005, 7, 443–455 CrossRef CAS .
  7. Explanations of FreedomCAR/DOE hydrogen storage technical targets, http://www.eere.energy.gov/hydrogenandfuelcells/pdfs/freedomcar_targets_explanations.pdf, Jan 2005.
  8. W. Grochala and P. P. Edwards, Chem. Rev., 2004, 104, 1283–1315 CrossRef CAS .
  9. F. Schuth, B. Bogdanovic and M. Felderhoff, Chem. Commun., 2004, 2249–2258 RSC .
  10. L. Gagliardi and P. Pyykko, J. Am. Chem. Soc., 2004, 126, 15014–15015 CrossRef CAS .
  11. P. Chen, Z. T. Xiong, J. Z. Luo, J. Y. Lin and K. L. Tan, Nature, 2002, 420, 302–304 CrossRef CAS .
  12. P. Chen, Z. T. Xiong, J. Z. Luo, J. Y. Lin and K. L. Tan, J. Phys. Chem. B, 2003, 107, 10967–10970 CrossRef CAS .
  13. J. F. Herbst and L. G. Hector, Phys. Rev. B, 2005, 72 Search PubMed .
  14. T. Ichikawa, N. Hanada, S. Isobe, H. Y. Leng and H. Fujii, J. Phys. Chem. B, 2004, 108, 7887–7892 CrossRef CAS .
  15. J. Baumann, E. Baitalow and G. Wolf, Thermochim. Acta, 2005, 430, 9–14 CrossRef CAS .
  16. A. Gutowska, L. Y. Li, Y. S. Shin, C. M. M. Wang, X. H. S. Li, J. C. Linehan, R. S. Smith, B. D. Kay, B. Schmid, W. Shaw, M. Gutowski and T. Autrey, Angew. Chem., Int. Ed., 2005, 44, 3578–3582 CrossRef CAS .
  17. M. Gutowski and T. Autrey, Prepr. Pap.-Am. Chem. Soc., Div. Fuel Chem., 2004, 49, 275–276 Search PubMed .
  18. G. Wolf, J. Baumann, F. Baitalow and F. P. Hoffmann, Thermochim. Acta, 2000, 343, 19–25 CrossRef CAS .
  19. C. Liu and H. M. Cheng, J. Phys. D: Appl. Phys., 2005, 38, R231–R252 CrossRef CAS .
  20. J. L. C. Rowsell and O. M. Yaghi, Angew. Chem., Int. Ed., 2005, 44, 4670–4679 CrossRef CAS .
  21. V. B. Kazansky, V. Y. Borokov, A. I. Serykh, R. A. van Santen and P. J. Stobbelaar, Phys. Chem. Chem. Phys., 1999, 1, 2881–2886 RSC .
  22. H. W. Langmi, A. Walton, M. M. Al-Mamouri, S. R. Johnson, D. Book, J. D. Speight, P. P. Edwards, I. Gameson, P. A. Anderson and I. R. Harris, J. Alloys Compd., 2003, 356, 710–715 CrossRef .
  23. J. Weitkamp, M. Fritz and S. Ernst, Int. J. Hydrogen Energy, 1995, 20, 967–970 CrossRef CAS .
  24. G. J. Kubas, Metal Dihydrogen and σ-bond Complexes: Structure, Theory, and Reactivity, Kluwer Academic/Plenum Publishers, New York, 2001 Search PubMed .
  25. Q. Y. Wang and J. K. Johnson, J. Phys. Chem. B, 1999, 103, 277–281 CrossRef CAS .
  26. A. C. Dillon, K. M. Jones, T. A. Bekkedahl, C. H. Kiang, D. S. Bethune and M. J. Heben, Nature, 1997, 386, 377–379 CrossRef CAS .
  27. M. Becher, M. Haluska, M. Hirscher, A. Quintel, V. Skakalova, U. Dettlaff-Weglikovska, X. Chen, M. Hulman, Y. Choi, S. Roth, V. Meregalli, M. Parrinello, R. Strobel, L. Jorissen, M. M. Kappes, J. Fink, A. Zuttel, I. Stepanek and P. Bernierg, C. R. Phys., 2003, 4, 1055–1062 Search PubMed .
  28. H. M. Cheng, Q. H. Yang and C. Liu, Carbon, 2001, 39, 1447–1454 CrossRef CAS .
  29. M. Conte, P. Prosini and S. Passerini, Mater. Sci. Eng., B, 2004, 108, 2–8 CrossRef .
  30. G. E. Froudakis, J. Phys.: Condens. Matter, 2002, 14, R453–R465 CrossRef CAS .
  31. M. Hirscher and M. Becher, J. Nanosci. Nanotechnol., 2003, 3, 3–17 Search PubMed .
  32. V. Meregalli and M. Parrinello, Appl. Phys. A: Mater. Sci. Process., 2001, 72, 143–146 Search PubMed .
  33. P. Chen, X. Wu, J. Lin and K. L. Tan, Science, 1999, 285, 91–93 CrossRef CAS .
  34. F. E. Pinkerton, B. G. Wicke, C. H. Olk, G. G. Tibbetts, G. P. Meisner, M. S. Meyer and J. F. Herbst, J. Phys. Chem. B, 2000, 104, 9460–9467 CrossRef CAS .
  35. R. T. Yang, Carbon, 2000, 38, 623–626 CrossRef CAS .
  36. W. Q. Deng, X. Xu and W. A. Goddard, Phys. Rev. Lett., 2004, 92, 166103 CrossRef .
  37. G. E. Froudakis, Nano Lett., 2001, 1, 531–533 CrossRef CAS .
  38. Y. L. Zhao, R. Q. Zhang and R. S. Wang, Chem. Phys. Lett., 2004, 398, 62–67 CrossRef CAS .
  39. Z. H. Zhu, G. Q. Lu and S. C. Smith, Carbon, 2004, 42, 2509–2514 CrossRef CAS .
  40. A. Ferre-Vilaplana, J. Chem. Phys., 2005, 122, 214724 CrossRef CAS .
  41. A. Ferre-Vilaplana, J. Chem. Phys., 2005, 122, 104709 CrossRef CAS .
  42. T. Heine, L. Zhechkov and G. Seifert, Phys. Chem. Chem. Phys., 2004, 6, 980–984 RSC .
  43. G. J. Kubas, R. R. Ryan, B. I. Swanson, P. J. Vergamini and H. J. Wasserman, J. Am. Chem. Soc., 1984, 106, 451–452 CrossRef CAS .
  44. A. W. Ehlers, S. Dapprich, S. F. Vyboishchikov and G. Frenking, Organometallics, 1996, 15, 105–117 CrossRef CAS .
  45. D. S. Nemcsok, A. Kovacs, V. M. Rayon and G. Frenking, Organometallics, 2002, 21, 5803–5809 CrossRef .
  46. T. Yildirim and S. Ciraci, Phys. Rev. Lett., 2005, 94, 175501 CrossRef CAS .
  47. T. Yildirim, J. Iniguez and S. Ciraci, Phys. Rev. B, 2005, 72, 153403 CrossRef .
  48. Y. F. Zhao, Y. H. Kim, A. C. Dillon, M. J. Heben and S. B. Zhang, Phys. Rev. Lett., 2005, 94, 155504 CrossRef .
  49. M. Barbatti, G. Jalbert and M. A. C. Nascimento, J. Phys. Chem. A, 2002, 106, 551–555 CrossRef CAS .
  50. M. Barbatti, G. Jalbert and M. A. C. Nascimento, J. Chem. Phys., 2001, 114, 7066–7072 CrossRef CAS .
  51. M. Barbatti, G. Jalbert and M. A. C. Nascimento, J. Chem. Phys., 2001, 114, 2213–2218 CrossRef CAS .
  52. J. E. Bushnell, P. R. Kemper and M. T. Bowers, J. Phys. Chem., 1994, 98, 2044–2049 CrossRef CAS .
  53. R. Davy, E. Skoumbourdis and T. Kompanchenko, Mol. Phys., 1999, 97, 1263–1271 CrossRef CAS .
  54. C. A. Nicolaides and E. D. Simandiras, Comments Inorg. Chem., 1996, 18, 65–75 CrossRef CAS .
  55. C. A. Nicolaides and E. D. Simandiras, Chem. Phys. Lett., 1992, 196, 213–219 CrossRef CAS .
  56. J. Niu, B. K. Rao, P. Jena and M. Manninen, Phys. Rev. B, 1995, 51, 4475–4484 CrossRef CAS .
  57. E. D. Simandiras and C. A. Nicolaides, Chem. Phys. Lett., 1994, 223, 233–239 CrossRef CAS .
  58. E. D. Simandiras and C. A. Nicolaides, Chem. Phys. Lett., 1991, 185, 529–534 CrossRef CAS .
  59. J. G. Vitillo, A. Damin, A. Zecchina and G. Ricchiardi, J. Chem. Phys., 2005, 122, 114311 CrossRef .
  60. D. Y. Hwang and A. M. Mebel, J. Am. Chem. Soc., 2000, 122, 11406–11410 CrossRef CAS .
  61. D. Y. Hwang and A. M. Mebel, Chem. Phys. Lett., 2000, 321, 95–100 CrossRef CAS .
  62. L. Turker, J. Mol. Struct. (THEOCHEM), 2005, 723, 105–110 CrossRef .
  63. L. Turker and S. Gumus, J. Mol. Struct. (THEOCHEM), 2005, 719, 103–107 CrossRef .
  64. N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O'Keeffe and O. M. Yaghi, Science, 2003, 300, 1127–1129 CrossRef CAS .
  65. J. L. C. Rowsell, A. R. Millward, K. S. Park and O. M. Yaghi, J. Am. Chem. Soc., 2004, 126, 5666–5667 CrossRef CAS .
  66. Y. Kubota, M. Takata, R. Matsuda, R. Kitaura, S. Kitagawa, K. Kato, M. Sakata and T. C. Kobayashi, Angew. Chem., Int. Ed., 2005, 44, 920–923 CrossRef CAS .
  67. G. Garberoglio, A. I. Skoulidas and J. K. Johnson, J. Phys. Chem. B, 2005, 109, 13094–13103 CrossRef CAS .
  68. S. Hamel and M. Cote, J. Chem. Phys., 2004, 121, 12618–12625 CrossRef CAS .
  69. O. Hübner, A. Gloss, M. Fichtner and W. Klopper, J. Phys. Chem. A, 2004, 108, 3019–3023 CrossRef .
  70. T. Sagara, J. Klassen and E. Ganz, J. Chem. Phys., 2004, 121, 12543–12547 CrossRef CAS .
  71. T. Sagara, J. Klassen, J. Ortony and E. Ganz, J. Chem. Phys., 2005, 123, 014701 CrossRef .
  72. Q. Y. Yang and C. L. Zhong, J. Phys. Chem. B, 2005, 109, 11862–11864 CrossRef CAS .
  73. M. Dinca and J. R. Long, J. Am. Chem. Soc., 2005, 127, 9376–9377 CrossRef CAS .
  74. CRC Handbook of Chemistry and Physics, Chemical Rubber Publishing House, Boca Raton, 76th edn, 1995 Search PubMed .
  75. B. Kesanli, Y. Cui, M. R. Smith, E. W. Bittner, B. C. Bockrath and W. B. Lin, Angew. Chem., Int. Ed., 2005, 44, 72–75 CrossRef CAS .
  76. L. Pan, M. B. Sander, X. Y. Huang, J. Li, M. Smith, E. Bittner, B. Bockrath and J. K. Johnson, J. Am. Chem. Soc., 2004, 126, 1308–1309 CrossRef CAS .
  77. S. S. Kaye and J. R. Long, J. Am. Chem. Soc., 2005, 127, 6506–6507 CrossRef .
  78. K. W. Chapman, P. D. Southon, C. L. Weeks and C. J. Kepert, Chem. Commun., 2005, 3322–3324 RSC .
  79. K. Chenoweth and C. E. Dykstra, Chem. Phys. Lett., 2004, 400, 153–157 CrossRef CAS .
  80. R. Kitaura, G. Onoyama, H. Sakamoto, R. Matsuda, S. Noro and S. Kitagawa, Angew. Chem., Int. Ed., 2004, 43, 2684–2687 CrossRef CAS .
  81. G. Ferey, M. Latroche, C. Serre, F. Millange, T. Loiseau and A. Percheron-Guegan, Chem. Commun., 2003, 2976–2977 RSC .
  82. P. Hobza and R. Zahradnik, Intermolecular Complexes: The role of van der Waals systems in physical chemistry and in the biodisciplines, Elsevier, New York, 1988 Search PubMed .
  83. D. E. Stogryn and A. P. Stogryn, Mol. Phys., 1966, 11, 371 CAS .
  84. S. Kristyan and P. Pulay, Chem. Phys. Lett., 1994, 229, 175 CrossRef CAS .
  85. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef CAS .
  86. M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2004, 108, 10200 CrossRef CAS .
  87. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 .
  88. J. Kong, C. A. White, A. I. Krylov, C. D. Sherrill, R. D. Adamson, T. R. Furlani, M. S. Lee, A. M. Lee, S. R. Gwaltney, T. R. Adams, C. Ochsenfeld, A. T. B. Gilbert, G. S. Kedziora, V. A. Rassolov, D. R. Maurice, N. Nair, Y. Shao, N. A. Besley, P. E. Maslen, J. P. Dombroski, H. Daschel, W. Zhang, P. P. Korambath, J. Baker, E. F. C. Byrd, T. V. Voorhis, M. Oumi, S. Hirata, C. P. Hsu, N. Ishikawa, J. Florian, A. Warshel, B. G. Johnson, P. M. W. Gill, M. Head-Gordon and J. A. Pople, J. Comput. Chem., 2000, 21, 1532 CrossRef CAS .
  89. F. Weigend, M. Haser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143 CrossRef CAS .
  90. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS .
  91. R. A. Kendall, T. H. Dunning Jr and R. J. Harris, J. Chem. Phys., 1992, 96, 6796 CrossRef CAS .
  92. F. Weigend, A. Kohn and C. Hattig, J. Chem. Phys., 2002, 116, 3175 CrossRef CAS .
  93. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Oslen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243 CrossRef CAS .
  94. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS .
  95. ‘Free’ H–H bond length optimized at: (i) MP2/6-31G** level = 0.734 Å; (ii) MP2/6-31G* level = 0.737 Å.
  96. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS .
  97. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS .
  98. R. L. Sweany, L. Vuong and J. Bishara, J. Phys. Chem. A, 2002, 106, 11440–11445 CrossRef CAS .
  99. E. N. Gribov, S. Bertarione, D. Scarano, C. Lamberti, G. Spoto and A. Zecchina, J. Phys. Chem. B, 2004, 108, 16174–16186 CrossRef CAS .
  100. L. Puskar, K. Tomlins, B. Duncombe, H. Cox and A. J. Stace, J. Am. Chem. Soc., 2005, 127, 7559–7569 CrossRef CAS .
  101. N. Walker, M. P. Dobson, R. R. Wright, P. E. Barran, J. N. Murrell and A. J. Stace, J. Am. Chem. Soc., 2000, 122, 11138–11145 CrossRef CAS .
  102. B. J. Coe and S. J. Glenwright, Coord. Chem. Rev., 2000, 203, 5–80 CrossRef CAS .

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of all reported optimized structures and their raw energies calculated at different levels of theory. See DOI: 10.1039/b515409j
This journal is © the Owner Societies 2006
Click here to see how this site uses Cookies. View our privacy policy here.