Plasma–surface interaction in the context of ITER

Abstract

The decreasing availability of energy and concern about climate change necessitate the development of novel sustainable energy sources. Fusion energy is such a source. Although it will take several decades to develop it into routinely operated power sources, the ultimate potential of fusion energy is very high and badly needed. A major step forward in the development of fusion energy is the decision to construct the experimental test reactor ITER. ITER will stimulate research in many areas of science. This article serves as an introduction to some of those areas. In particular, we discuss research opportunities in the context of plasma–surface interactions. The fusion plasma, with a typical temperature of 10 keV, has to be brought into contact with a physical wall in order to remove the helium produced and drain the excess energy in the fusion plasma. The fusion plasma is far too hot to be brought into direct contact with a physical wall. It would degrade the wall and the debris from the wall would extinguish the plasma. Therefore, schemes are developed to cool down the plasma locally before it impacts on a physical surface. The resulting plasma–surface interaction in ITER is facing several challenges including surface erosion, material redeposition and tritium retention. In this article we introduce how the plasma–surface interaction relevant for ITER can be studied in small scale experiments. The various requirements for such experiments are introduced and examples of present and future experiments will be given. The emphasis in this article will be on the experimental studies of plasma–surface interactions.

---

1. Introduction

On June 28th 2005, the ITER partners China, the European Union, Japan, the Russian Federation, South Korea and the USA agreed to construct ITER in Cadarache, France. ITER is the large international fusion reactor and a major step on the way (ITER is Latin for ‘the way’) to commercial exploitation of nuclear fusion for the production of electricity. ITER is a fusion reactor of the ‘tokamak’-type, in which a hydrogen plasma is confined in a torus by means of strong magnetic fields. ITER must demonstrate tenfold power multiplication in a controlled fusion process, at a power level in excess of 500 MW and during pulses of 10 min or longer. Experiments with ITER should lead to the solution of the remaining physics problems on the way to fusion. It will be used to address a number of technological issues that will be important in the construction of commercial reactors.^1–4

Obviously, the construction and scientific and technological exploitation of ITER itself will be the main focus of the ITER programme. But in addition, a large accompanying research effort is needed to resolve issues that are relevant for ITER and fusion, but can best be carried out using other research tools. This article will focus on research efforts in an area that has been identified as one of the most critical in the ITER research and is close to the heart of the readership of Phys. Chem. Chem. Phys.: plasma–surface interactions (PSI).

In order to do this, we will introduce some aspects of ITER and fusion energy, lay out some of the exciting physics and chemistry that takes place in the extreme conditions at the periphery of the burning fusion plasma, and indicate where Phys. Chem. Chem. Phys. readers can contribute to the success of fusion. With the focus on plasma–surface interactions the discussion will end with the characteristics and design of a new, large plasma generator that is presently under construction at the FOM Institute for Plasma Physics: Magnum-psi.⁵ This device has been conceived to mimic the ITER PSI conditions, and in this respect will be unique world-wide.

2. ITER and fusion energy

2.1. Fusion reactions and reactor design

Nuclear fusion is the energy source of the stars; it is a major source of energy in the universe. When plotting the stability of nuclei against atomic number we find a maximum about halfway across the periodic system around nuclei such as Fe. As a consequence of this and Einstein’s famous formula, E = mc², the fission of heavy nuclei like ²³⁵U yields fragment nuclei and neutrons with excess (translational) energy. Likewise, the fusion of light nuclei yields heavier ones with excess energy.

However, because of the Coulomb repulsion of the nuclei concerned, fusion reactions proceed only at temperatures which are roughly 6 orders of magnitude higher than regular chemical reactions. The least activated reaction is the one between deuterium and tritium. This is the reaction of choice in ITER:

²D⁺ + ³T⁺ → n + ⁴He⁺⁺ + 17.6 MeV.

For comparison we list the energetics of carbon monoxide combustion:

2CO + O₂ → 2CO₂ + 10 eV.

The six orders of difference in magnitude of the barrier is reflected in the exothermicity of the two reactions. Per unit of mass of the ‘fuel’, the energy release of the fusion reaction is even 7 orders of magnitude larger than that of the chemical reaction.

Most (80%) of the energy of the DT fusion is carried away by the neutron. It is captured in a blanket containing Li, in a reaction in which tritium is also regenerated:

⁶Li + n → ³T + ⁴He + 4.78 MeV

This yields the overall reaction equation for a fusion reactor,

²D + ⁶Li → 2 ⁴He + 22.4 MeV.

This reaction shows that ²D and ⁶Li constitute the fuel for fusion. ²D is abundant in seawater and ⁶Li is present in many common minerals. 250 g of typical Li-containing rock and 2 L of regular water are equivalent to 1000 L of oil, and would provide a family with electricity for a year. The exhaust of a 1 GW fusion plant is only 250 kg of benign He per year. The latter is to be compared to 7.2 × 10⁹ kg of CO₂, which is released by a 1 GW coal fired power plant, not to mention the tons of ash and cinders. To put this number in the global perspective, the otherwise very fortunate rapid economic progress in China requires this country to open a 1 GW coal fired power plant every month. The need for fusion energy is obvious in view of the current debates on climate change.

The DT fusion reaction is not a chain reaction; a fusion reactor cannot have an energetic runaway. A fusion reactor is thus inherently safe from nuclear explosion. Some components inside the fusion reactor become activated during the operational lifetime, but the total radiotoxicity decays rapidly, dropping by 4 orders of magnitude within the first 100 years, to a level that allows recycling of the material. In addition, operation of a fusion plant does not require transport of radioactive fuel or waste. The fuel is abundant, practically unlimited, very cheap, and available to everyone, which could greatly reduce political tension. Fusion is one of the few options for large scale power generation. In summary, a fusion plant would be a very desirable addition to the world’s capabilities of generating energy in a sustainable fashion.

The rate coefficient 〈σv〉 for the DT reaction peaks at a value of 10⁻²¹ m⁻³ s⁻¹. The peak occurs at a Maxwellian temperature of 70 keV. For the fusion power output the ion density also plays an important role. For a given product of density and temperature (pressure) we find that the maximum output of fusion power is given around a fusion reactor operation temperature of 10 keV or 110 000 000 K! At those temperatures all light atoms are fully stripped of their electrons; light atom containing matter transforms into in a highly ionized plasma. Obviously, the contact of the hot plasma with a material wall has to be avoided, because the wall will be evaporated, the evaporated matter will be ejected into the hot plasma, and the plasma will be extinguished by the resulting fast cooling of the plasma. In ITER, and other so-called tokamak reactors this is done by confining the plasma in a doughnut-shaped magnetic field. In the picture of ITER in Fig. 1, the doughnut-shaped plasma chamber, surrounded by magnets, can be seen clearly. The magnetic field is so strong that the ions and electrons can only move along the field lines, reducing the plasma transport perpendicular to the magnetic field lines by 14 orders of magnitude. This lowers the thermal conduction of the hot plasma to the wall so much that a temperature difference of 100 million K over a distance of about a meter can be sustained. The magnetic field is produced by superconducting coils, which implies that the hottest volume on earth is placed inside the world’s largest liquid He cryostat.

Fig. 1 Artist’s view of ITER. The toroidal plasma chamber is clearly visible. Some parameters are: major radius, 6.2 m; minor radius, 2 m; vertical elongation, 1.86 m; plasma current, 15 MA; magnetic field, 5.3 T; plasma volume, 850 m³; fusion power, 500 MW; power multiplication Q, 10. Published with permission from ITER, http://www.iter.org.¹.

2.2. Scientific issues of ITER

It is obvious that this is not the place to discuss the scientific issues of ITER in any detail. The reader is referred to other sources, notably also on the web.^1,3 However, roughly three issues can be discerned. Moving from the core of the reactor to the outside world, these are:

(1) The stable and efficient confinement of the hot plasma.

(2) The development of materials for the reactor that can withstand the high neutron flux.

(3) The exhaust of the power and associated plasma–surface interaction.

2.2.1. Physics of the burning plasma. The confinement of the hot plasma has for a long time been the focus of the fusion plasma community. Without magnetic confinement the required temperatures cannot even be obtained, which is the first step to a continuously burning plasma. The magnificent results of the three major tokamaks: JET (Culham, UK), JT60 (Naka, Japan) and TFTR (formerly at Princeton, USA) have demonstrated that stable confinement could be achieved at temperatures well in excess of the required 10 keV (40 keV and more have been achieved) during pulses of tens of seconds. In addition, JET and TFTR have demonstrated that DT fusion can be achieved in a tokamak,⁶ producing fusion power of up to 16 MW. It is interesting to note that the Royal Society of Chemistry declared the generation of 1 MW of neutron power in JET to be the chemistry landmark for the year 1991. The achievement of break-even for the fusion reaction—released fusion power comparable to the power needed to maintain the operation of the reactor—is even more remarkable if one realises how difficult it is to sustain such a plasma. These results obtained on JET together with data from smaller devices now provide a very reliable data base from which we can extrapolate to a fusion machine which will be significantly beyond break-even; in ITER, 10 times more fusion power will be generated than is needed for the external heating of the plasma and device operation. This extrapolation implies that for an improvement of the heat insulation and energy confinement, a larger plasma volume than that in JET is needed, among other parameters. This results in the dimensions of ITER used in its design.

The understanding of confinement has strongly evolved over the past decades. Initially, the emphasis was on achieving a global steady state between the plasma and the confining fields; i.e., keeping the plasma suspended in the intended position. The next step is to maintain a local steady state as well, which implies suppression of local, small perturbations of the magnetic field structure, that could grow out and lead to rapid decay of the high temperature. This means an optimization of thermal confinement by active reduction of turbulence: in a strongly driven system such as the fusion plasma, with very steep gradients of pressure and temperature, turbulence can naturally form. Turbulence leads to enhanced thermal losses and hence reduced performance of the reactor. The fusion community has successfully developed ways to actively suppress or avoid the development of turbulence, so that the experimentally achieved thermal confinement can be brought close to the theoretical optimum. This achievement is built on an extensive basis of both theoretical and experimental work.

Although for ITER it is expected that the same physical models used for smaller tokamaks apply, the ITER plasma will enter an essentially new parameter domain. This means that the extrapolations that lie at the basis of the ITER design must be put to the experimental test, and the theoretical description must be extended. Completely new in ITER will be the physics of a ‘burning’ plasma, a plasma that is sustained by the power released by He⁺⁺ produced in the fusion reaction and carrying an energy of 3.5 MeV. The confinement of the alpha particles and the transfer of their energy, through collisional processes, to the plasma is uncharted water. As the neutrons are not confined in the magnetic field, their fusion power is transferred to the lithium blanket surrounding the plasma.

Thus, while the fusion community is confident that ITER will achieve its design goals for confinement, ITER does constitute an essential step beyond the presently known physics, and in this respect should be regarded as a true, and exciting, physics experiment. The proof of the pudding remains in the eating!

2.2.2. Construction materials. ITER will generate significant fusion power, at the 500 MW level, and as most of this energy is in the neutrons that are produced in the DT fusion reaction, ITER will be exposed to a large dose of 14 MeV neutrons and thus get activated. This is in particular true for the ‘first wall’, and the components that are most exposed to the plasma, such as the vacuum vessel and the Li-containing blanket. ITER is by far the most intense source of such neutrons on earth, so the development of materials that can withstand this neutron flux is required. Analysis shows that the radiotoxicity of the activated parts of a fusion reactor—mainly the ‘first wall’ as seen by the neutrons—will be reduced to safe levels in 50–100 y. A lot of information regarding this can be found in EFDA reports such as ‘EU Power Plant Conceptual Study, Annex 10: Safety and Environment Assessment’ and the ‘Safety and Environmental Impact of Fusion (SEIF report)’, which can be downloaded from http://www.efda.org. Work is being done on materials such as vanadium containing alloys that have low activation and fast decay of activated compounds. Silicon carbide also seems an interesting option.

The behaviour of matter under prolonged neutron irradiation requires further study. Therefore, as part of the so-called broader approach to fusion energy, a special test facility IFMIF is to be constructed to carry out the irradiation tests of materials to be used in fusion reactors.⁷ This is obviously a task for materials scientists, and will not be discussed further here.

2.2.3. Plasma–surface interaction. Plasma–surface interaction is an area of very exciting research, where ITER will be radically different from its predecessors. A typical plasma pulse in a contemporary, non-superconducting tokamak lasts for at most tens of seconds. An ITER pulse will last at least 500 s and continuous operation is foreseen. While the electron, ion and power fluxes to the wall in ITER will be only a factor of 2–3 higher, the accumulated particle and energy loads of the surfaces concerned in ITER will be up to 4 orders of magnitude higher than for the earlier machines. In terms of wall-load, a single ITER pulse is comparable to at least a year of operation of JET, which is presently the largest fusion device in the world.

It is very challenging to construct walls that can sustain the loads expected in ITER. It is an interdisciplinary problem to be tackled by, for instance, fusion scientists, low temperature plasma physicists, surface scientists, surface chemists, atomic and molecular physicists, with respect to theory and experiment. This is the main topic of the present article and will be developed in the following sections.

3. Plasma–surface interaction in fusion devices

The first questions to be addressed here are: Where does the plasma hit the surface and why?^3,8–14 The primary wall is supposed to be completely protected from impact of the plasma by the confining magnetic field. Diffusion across this field is strongly suppressed, but some diffusion across the field always occurs. Delicate equipment inside the toroidal plasma chamber is protected from plasma impact by so-called limiters. Impact on these devices is also unlikely under normal conditions, but they are designed to take a large power load in exceptional cases. In the so-called divertor the plasma is deliberately brought in contact with the wall. The reason for this is simple: in a burning DT plasma, He is produced. If the He remains in the core of the plasma, it will gradually dilute the burning DT mixture, and eventually extinguish the nuclear fire. In addition, the heating power released into the plasma volume by the He⁺⁺ formed and the initial external heating has to be exhausted via the wall.

3.1 Divertor physics

The He removal and plasma power exhaust occurs in modern tokamaks in the divertor. In Fig. 2 a view inside the vacuum vessel is shown with the divertor at the bottom, and in Fig. 3 a cross section perpendicular to the toroidal field is shown. The magnetic field surrounding the plasma core is designed to block any transport across it to the wall. The field lines form nested flux surfaces as shown, on which the particles run around the torus according to their thermal speed. The outermost of such magnetic flux surfaces is called the ‘last closed flux surface’ (LCFS). Below the LCFS the so-called X-point is shown; the magnetic field lines below it are designed to intersect the wall in the divertor region. Plasma that has moved by diffusion below the X-point will eventually hit the divertor surface. The angle between magnetic field lines and divertor surface is very small, only a few degrees, to reduce the specific heat load.

Fig. 2 Detailed cross section of ITER, showing the divertor at the bottom. The target plates of the divertor are made of carbon, the dome structure of tungsten and the primary wall of beryllium. Published with permission from ITER.

Fig. 3 Poloidal cross section of a tokamak, showing the regions of the plasma and the boundary walls, where the important plasma–surface interaction takes place. Important regions are: the plasma core, the edge region just inside the separatrix, the scrape off layer outside the separatrix and the divertor region, which is an extension of the scrape off layer plasma along field lines into the divertor chamber. The divertor structure is designed to prevent neutral atoms and molecules from leaving the divertor. In the magnetic flux region below the X-point, the magnetic surfaces are spiralling downward to interact with the wall at the vertical divertor target plates and are isolated from the rest of the plasma. From ref. 10. Published with permission from IAEA.

At the divertor plate, the ions from the plasma are neutralised on the surface. The neutralization step will result in electron or photon emission and surface heating. The neutral molecules formed on the surface leave the divertor plates as atoms or molecules and are re-ionized when entering the plasma. Once ionized the magnetic field guides the ions and the plasma flow forces them to return to the surface, where neutralisation occurs again. In addition, (resonant) charge transfer reactions with the neutral gas produce hot neutral atoms, which exhaust a significant fraction of plasma energy onto the entire divertor wall when leaving the plasma. In addition, neutral molecules and impurity ions are excited by electron impact which leads to a significant electromagnetic radiation. Electrons and ions originating from the core plasma are thus effectively cooled by radiation and charge exchange processes from the keV range to preferably below 1 eV.^8,15 The plasma ions can undergo many neutralization–reionization cycles before they leave the plasma regions as neutral molecules towards the vacuum pumps under the divertor. Inside the divertor, at plasma temperatures around a few eV, the plasma is in a so-called detached state.¹⁶ The surface is thus protected by a dense plasma with a low degree of ionization. In Fig. 4 vertical cross sections through the ASDEX-Upgrade and JET tokamaks are shown, with a measurement of the total emission of electromagnetic radiation (as detected by bolometry) from the plasma.¹⁷ This radiation is concentrated in the cooler regions of the tokamak, where the mainly singly charged ions provide the main part of radiation via electron impact excitation. It is clear that the entire divertor area below the X-point is filled with radiation. In this way a large fraction of the power entering the divertor region as plasma flow along the magnetic field is radiated into the entire tokamak, thus avoiding the overheating of small areas where the magnetic field lines intersect the divertor plates.

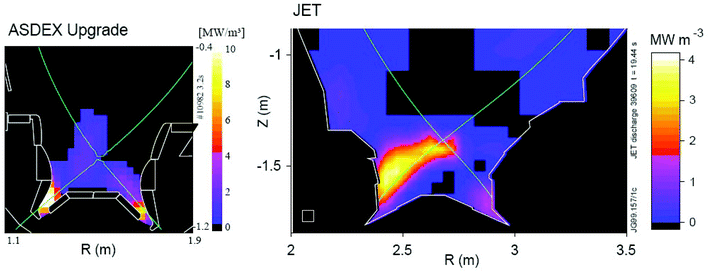Fig. 4 Vertical cross sections through the ASDEX Upgrade and JET tokamaks, with a measurement of the emission from the plasma. From ref. 17. Published with permission from IOP.

3.2 Strong coupling and synergy

In the detached regime the plasma is strongly coupled to the surface. By this we mean that the mean free path for plasma ions, molecules and dust particles eroded from the surfaces is small with respect to the plasma size. Most species will undergo many collisions in the divertor area before eventually disappearing in the vacuum pump, making the plasma physics of this multicomponent system very complex. This does not imply that the interaction in the weakly coupled limit is simple. Here the mean free path for constituents of the plasma is larger than the size of the interaction region. Winters and Coburn have demonstrated the existence of so-called synergistic effects in plasma etching of silicon.¹⁸ Roughly speaking this means that two components of the plasma, e.g. Ar⁺ ions and XeF₂ molecules individually hardly etch the surface, but together they realize significant etching. These synergistic effects make plasma chemistry particularly rich, non-linear, and again very complex. This effect is also present in the H⁽⁺⁾ and CH₃⁽⁺⁾ system, as demonstrated by von Keudell and Jacob.¹⁹ Synergistic effects have been discovered for weakly coupled plasmas.²⁰ It is to be expected that for strongly coupled plasmas the effects will be even stronger. It is clear that in this strongly coupled cooling process in the divertor region an enormous amount of atomic and molecular collision physics, surface science and cluster science is involved.

3.3 Wall materials and lifetime

The materials of the various walls are of critical importance, because they might be emitted in some form into the divertor plasma, contributing to the plasma chemistry and to the radiation level in the plasma. The role of the divertor surface and its material composition require much more study. Requirements for divertor materials are:

• good thermal and electrical conductivity,

• low probability of ending up in the core plasma, and

• if ending up in the core plasma: low Z.

The low Z requirement follows from the fact that ions which are not fully stripped act as a heat sink in the plasma, due to continuous excitation–de-excitation cycles of inner shell electrons by plasma electrons. For ITER the provisional choice of materials is:

• W for limiters,

• Be for the primary wall, and

• C for the divertor target plates.

The argument in general for this choice is beyond the scope of the present paper, and the reader is referred to other literature sources.^3,10,11 Some arguments will be touched on later in this article.

Control of the plasma–surface interaction has always been very important for the optimisation of the fusion plasma performance in present day devices. In the past, most PSI research has concentrated on plasma performance and optimal confinement, aiming at maximum flexibility with respect to different plasma scenarios. The plasma–surface interaction was approached with plasma performance in mind rather than surface science. However, in future, research activity in this field should concentrate on topics arising from long pulse operations with high duty cycles. Here, the most important information required concerns the lifetime expectations of the divertor target plates.

The expectations for ITER, which are based on knowledge obtained from present devices, suffer from large uncertainties. Therefore, the ITER design foresees an exchangeable system of divertor cassettes, which can be entirely remotely controlled.²¹

The details of this first design are still under investigation and need to be agreed upon in about 3–4 years from 2006. At this moment the surface materials have to be decided upon. The first operation of ITER is planned to be in 2015. After a few years of operation with the first set of divertor cassettes the exchange of the whole divertor with a further optimised design will be possible.

3.4 Tritium retention

Because tritium is radioactive the amount allowed within the ITER installation is quite restricted. It is desirable that most of the tritium is in the plasma volume or in the gas processing plant, but not retained or trapped elsewhere. Hydrogen and its heavier isotopes deuterium and tritium can be adsorbed with a long residence time in deep pores in the walls. In addition, they readily form compounds with carbon. In these compounds the deuterium and tritium present in a fusion reactor are not available for the fusion reactions in the plasma, but are retained somewhere in the vacuum vessel or walls. For hydrogen and deuterium this is only an operational problem, because there is no upper limit to the amount of hydrogen in a tokamak. For tritium, the retention in the walls is a serious problem because the amount of tritium allowed in the reactor is small.

From present tokamak experience it is definitely concluded that the overwhelming majority of the long term tritium retention is due to co-deposition of tritium along with eroded carbon forming tritium saturated carbon co-deposits. Like H and D, T is very reactive with carbon and can form a variety of molecules. To evaluate the scientific basis of this process and to improve our predictions for future devices a comprehensive study is needed. The reactivity of D and T will be considered to be similar, so that the majority of studies can be carried out with D. Issues that must be addressed include:

• The evaluation of the intensity and the location of the physical and chemical erosion sources in the main chamber and divertor

• The impurity transport behaviour in the edge plasma

• The local carbon transport in the divertor along the target plates

• The sticking probability of plasma constituents such as D⁰, D⁺, neutral and ionized hydrocarbons etc.

Other important issues are the re-erosion of deposits, the relationship between plasma conditions and properties, such as hardness, of the deposited layers, and the migration of carbon in gaps in castellated tiles or between tiles.

While the database and experiences with present day tokamaks operating with a full carbon wall indicate that the amount of long term tritium retention in a future device like ITER might quickly reach its limit (350 g),²² it is very important to study whether an ITER-like choice of wall materials with a beryllium metal first wall, tungsten baffles and graphite in the lower divertor region leads to a material composition by which the carbon erosion and the tritium co-deposition with carbon is largely reduced. Whereas mixed materials are the present proposal for ITER, very little is known about the effect of the presence of these mixed species on the PSI, erosion and re-deposition. For metal surfaces, erosion is also an important issue to study, and additionally the resilience of the surface under high and varying heat loads is of great importance.

Of similar importance is to investigate whether the choice of surface temperatures in the divertor region would allow the majority of the co-deposited tritium to be concentrated on special areas from which it can be recovered easily. The control of the properties and patterns of the deposits will also be studied.

This is closely related to the task of developing methods to remove retained tritium from co-deposited films in an effective way which is also compatible with plasma operation. One obvious way is to study the hydrogen isotope exchange behaviour in various plasma-facing components, others are to investigate thermal outgassing or the chemical reactions of hydrogen-rich carbon layers with reactive species like oxygen.

3.5 Dust formation

As long as carbon is considered for use as a wall material in any part of the device, dust formation is a crucial element of the problem. Therefore, this is receiving more attention. Dust particles—cauliflower-like particles of hydrocarbons in various compositions—in the critical size range of 1–10 nm are thought to play an essential role in the formation of re-deposits.^23–25 Such particles may be confined in the high magnetic fields found in the divertor, so their concentration can be high. In this size range, their growth rate scales approximately quadratically with their concentration. The fundamental processes leading to the formation and growth of such dust particles are of prime importance for divertor performance and tritium retention. It is interesting to note that dust particles also play an essential role in astrochemical systems and silicon etching.²⁴ Many molecules identified in interstellar space are formed on the surfaces of dust particles in interstellar clouds, but the reaction temperatures here are orders of magnitude lower, a few K, than the eV temperatures in ITER.²⁶

3.6 Research on ITER-relevant plasma–surface interaction

ITER itself will serve as an important test bed for the divertor design. However, supporting experiments in smaller devices are indispensable for approaching a deeper understanding of the processes. The issue of PSI and wall materials in reactor conditions is far from settled. ITER itself will provide essential new experimental data in this field and the integrated research programme, including the development of theoretical models and experiments in both ITER and dedicated experiments, should provide the basis for the choice of materials for reactors beyond ITER.

Tokamaks are needed to study the complex interplay of main chamber plasma and divertor plasma in toroidal geometry. The most important large scale experiment in this context is planned to be conducted on JET by modifying the JET wall with an ITER-like mix of materials (for more details, see http://www.JET.org). On a smaller scale, but addressing the processes in more detail with specialised diagnostics, experiments on plasma–wall interactions will be performed on other tokamaks, such as e.g. on TEXTOR in Jülich. TEXTOR is operated by the Trilateral Euregio Cluster collaboration (TEC: FOM Institute for Plasma Physics, Rijnhuizen, The Netherlands; Institute for Plasma Physics Forschungszentrum, Jülich, Germany; Royal Military School, Brussels, Belgium). However, most tokamaks are at present short-pulsed compared to ITER. Their rather small duty cycle and lack of easy access for PSI diagnosis give rise to uncertainties with respect to long term erosion and deposition processes. For this problem the need for steady state experiments with the relevant PSI parameters will be obvious. Such experiments should allow addressing the issues discussed above in an open and easily accessible, steady state flexible laboratory environment. The open laboratory environment has the advantage of much better accessibility and greater flexibility than an actual tokamak divertor. The accessibility allows the use of in situ real time plasma and surface diagnostics, so that processes can be studied while they happen, with the plasma on. Samples should be transferable, if necessary under vacuum, to surface analysis facilities. Modifications, changes to materials etc. should be introduced relatively quickly. Thus, smaller scale laboratory experiments, with steady state capability and heavily equipped with diagnostic tools, will complement the studies of the plasma–wall interaction in tokamaks.

4. Devices to study the plasma–surface interaction

Plasma–surface interactions have been studied in a number of devices. Obviously, tokamaks are among them, as already discussed, but in other fields, such as plasma processing of materials, many experiments have also been built. Dry or plasma etching of silicon is such a field.²⁷ Many experiments in the context of fusion have also been built. Experiments currently in operation include NAGDIS at Nagoya, Japan,^28,29 PISCES at San Diego, USA,^30–33 Pilot-PSI at the FOM Institute, Rijnhuizen, The Netherlands,^34,35 and PS2 at Berlin, Germany.^36,37 The feature that all of these devices have in common is that plasma production is clearly separated from the region where the plasma–surface interaction is studied. This allows adequate tailoring of the plasma without unwanted feedback from the surface region. This is a major advantage with respect to tokamaks, where the plasma–surface interaction can sometimes directly couple to the performance of the core plasma. The same holds with respect to, for instance, RF plasma etchers, where a change in surface conditions feeds back to plasma conditions. In the four devices mentioned this decoupling of plasma generation and surface interaction is realized by using a remote plasma generator that is connected to the surface region by a straight and long transport section. This long section gives space for modification and diagnosis of the plasma streaming to the surface. This surface section allows direct surface analysis. A schematic diagram of one linear device, PISCES-B is reproduced in Fig. 5.

Fig. 5 Schematic diagram of the linear device, PISCES, used to study plasma–surface interactions. The various components are clearly marked in the figure. Private communication by Dr M. Baldwin, see also refs. 32 and 33.

However, all kinds of equipment can be used to study plasma–surface interactions in the context of ITER. For instance, if one is interested in the interaction of atomic or molecular radicals and ITER-relevant surfaces, molecular beam machines could be used. Different aspects of the issue can be studied by different types of equipment often used by very different scientific communities. Therefore, we will discuss below a number of requirements that need to be met to mimic the plasma–surface interaction in ITER as well as possible without using a tokamak.

When sacrificing certain requirements, experiments of very modest size and cost can be designed, which can still do many relevant studies on plasma–surface interactions for ITER, whilst focusing on a specific aspect of the overall problems.

The authors are closely involved in the building of a machine meeting most demands, called Magnum-PSI, at the FOM-Institute for Plasma Physics Rijnhuizen, as part of the TEC and the Euratom Association.^5,38

4.1 Pulse duration

The issues that must be addressed for which the pulse duration is an essential parameter are: erosion rates, dust formation, pattern formation, and possible saturation of the substrate. The system must have the time to establish a steady state, which as far as the temperature is concerned already requires minutes. The surface processes themselves, the ‘conditioning’ of the surface, also typically takes many minutes, determined by diffusion times. Quantitative studies on layer formation and dust production call for pulse durations of several hours before commencing steady state experiments.

4.2 Flux

The ion flux to the surface is a very important parameter. At fluxes above roughly 10²³ ions m⁻² s⁻¹, the frequency with which a site at the surface is visited can exceed the typical inverse residence time for weakly chemisorbed species. Hence, the surface becomes strongly modified, and could be completely metastable when the plasma is on. Where deposition occurs, surface roughness with a typical scale of tens or hundreds of microns is found (see e.g.Fig. 6).

Fig. 6 Carbon deposits in the TEXTOR tokamak.

When the flux is above 10²² ions m⁻² s⁻¹ the chemical erosion rate apparently starts to decrease, reaching a ten-fold reduction at fluxes of 10²³–10²⁴ ions m⁻² s⁻¹ (see Fig. 7). It has also been recently observed in tokamaks and plasma generators that high fluence may reduce chemical erosion of graphite materials.³⁹ These arguments call for the capability of reaching a flux in the ITER divertor range, i.e. exceeding 10²³ ions m⁻² s⁻¹.

Fig. 7 Erosion rates for carbon surfaces by low temperature plasma. From ref. 39. Reprinted from J. Nucl. Mater., 2005, 970 by Roth et al., with permission from Elsevier.

Reaching such a flux density is far from trivial. This can be seen, for instance, in Fig. 7, where the high flux data is obtained from tokamaks. The flux density reaching the surface is, in the end, determined by the plasma sheath. The sheath region maintains the charge neutrality of the plasma by allowing equal positive ion and electron fluxes to the solid surface. Because electrons at the same temperature as ions are much more mobile, an electrostatic potential is dynamically established over the sheath that retards the electrons and accelerates the ions. The sheath potential is proportional to the electron temperature, and will be on the order of a few eV. The sheath thickness is on the order of the Debye screening length over which the overall charge neutrality of the plasma is maintained. The Debye length is of the order of a fraction of a millimetre. The sheath is often described by the Bohm criterion that describes the ion velocity upon entering the sheath as a function of the local electron temperature.⁴⁰

In the linear plasma generator, the Bohm criterion translates into some special requirements on, firstly, the power transported by the plasma beam (as this determines the electron temperature—see section 4.3) and, secondly, on the ion and electron fluxes in the beam.

Experimentally it is very difficult to create such a plasma flux over a macroscopic surface area, say at least 1 cm². Most of the current experiments cannot reach a flux of 10²³ ions m⁻² s⁻¹. Perhaps experiments with focused low energy ion beams could come close to the requirements presented here, but presumably at a very small surface area.

It is much more difficult to retain a hydrogen plasma than a noble gas plasma. In the latter the only neutralization possibility is electron capture in the presence of a third body. This is only probable at high density. For H⁺, resonant charge transfer in a collision with H₂ leads to the formation of H₂⁺, which can capture an electron with high probability leading to dissociative neutralization (H₂⁺ + e⁻ → H^* + H) with one of the H atoms in an excited, radiative state. Hydrogen plasma is only stable against charge recombination if the degree of ionization of the plasma is close to unity and the temperature is high. If the temperature is above about 2 eV the plasma can ionize the remaining neutral gas fairly easily. Only in tokamaks is the degree of ionization close to unity, because of the very high temperature. In a small laboratory plasma the degree of ionization is usually smaller than 0.1. For hydrogen this results in fast extinction of the plasma. The best remedy against this is to confine the hydrogen plasma in a magnetic field. This reduces the number of collisions with residual gas, keeps the temperature higher and thus keeps the plasma ionizing. Experiments in the Pilot-PSI device at the FOM Institute, Rijnhuizen, have provided a dramatic demonstration of the influence of the magnetic confinement of the plasma on the flux. The study has shown that at the relevant temperature of the order of 1 eV, the application of a magnetic field of the order of 1 T enhances the flux by several orders of magnitude. (see Fig. 8).³⁵ Therefore, an axial magnetic field of several T is essential to bring the flux in the required range, i.e. well in excess of 10²³ ions m⁻² s⁻¹. The field is also required to ensure that the redeposition mechanism is in the parameter range of the divertor. Finally, as will be shown below, a magnetic field of B > 3 T has a dramatic impact on the confinement of hydrocarbons and dust particles up to some 10 nm radius.

Fig. 8 Plasma density in Pilot-PSI as a function of applied magnetic field. Data for both Ar and H plasmas are shown. The density has been determined using Langmuir probes. From ref. 35. Reprinted from Fusion Eng. Des., 2003, 66–68, 413 by de Groot et al., with permission from Elsevier.

To keep the plasma density over a length of more than a meter in order to decouple the source and plasma–surface interaction, it is essential that the plasma is ionizing, not recombining. This calls for an electron temperature of well above 1 eV. Moreover, to carry the required power flux, a temperature in excess of 3 eV is required (see section 4.3). Hence, the requirements related to particle flux and energy flux are strongly linked.

4.3 Plasma temperature

The temperature of the plasma in front of the surface is a dominant parameter determining a variety of processes, such as

• The flux to the target, which through the Bohm criterion for the sheath (introduced earlier) is determined by the values of the density n_e and the electron temperature T_e in front of the surface. This in turn determines the sheath potential and hence the impact energy on the surface.

• The ionization degree. The nature of the incoming plasma, i.e. whether it is recombining or ionizing, is connected to this. The re-ionization of species that come off the surface is important and the plasma should be hot enough to allow it.

• The charging of dust particles, and thus their confinement and growth rate.

• The Larmor radius and mean free path of the various species, and thus their confinement. This determines the so-called Hall factor of the plasma.

For a plasma in local equilibrium the electron temperature T_e and the ion temperature T_ion are equal and in this case also called the plasma temperature. Experiments should aim at simulating the detached divertor regime, with its typical temperature of 1–3 eV. This is non-trivial because very high fluxes are needed to release enough surface material to effectively cool the plasma. However, it can be done at lower fluxes with tricks. A very hot, low flux plasma can reach a detached regime by injecting or ‘puffing in’ neutral gas near the divertor, as is demonstrated by the NAGDIS experiment. In such regimes the Larmor radii will be typically at most a few cm, and the mean free path will be around 1 mm.

To cover the wide variation of temperature that can occur in a divertor, and, more generally, to study the effect of the temperature on the PSI processes including the transition from chemical erosion to physical sputtering, the experiment must be able to vary the plasma temperature in a range of 0.5–30 eV.

The temperature determines the sheath potential, and hence the impact energy of ions hitting the surface. A rule of thumb is that the effective ion energy is about 3–4 times T_e. To do relevant experiments on erosion mechanisms, the plasma generator must provide plasma with a temperature in the relevant range of 1–3 eV, and the means to control and vary it. This calls for auxiliary heating of the beam and gas injection near the target to cool the plasma. Cooling must be done very close to the surface, as at low T_e the plasma is strongly recombining and loses charge density quickly. For T_e < 1 eV the plasma is recombining and electron heat conduction is too low to sustain the temperature over lengths of more than tens of cm. Hence, the plasma temperature and degree of ionization decay quickly along the beam path, and the plasma extinguishes. However, for T_e > 3 eV the electron heat conduction will sustain the plasma temperature over a length exceeding 1 m, and at that temperature the plasma is ionizing.

For plasma beam heating, Ohmic heating can be employed by inducing a parallel current in the plasma beam through electrodes. As well as this, RF-heating can be considered, for which a special differential pumping stage with low neutral density is needed. NAGDIS has a special section for this.

The impact energy can be further controlled by the application of a bias to the substrate, by which the sheath potential can be enhanced from an order of 10 eV to hundreds of eV. However, in this case there is no longer charge neutrality near the surface, and the equilibrium plasma is effectively turned into an ion beam, a situation which is dissimilar from the divertor plasma in ITER. Nevertheless, biasing may allow experiments with large fluxes of low energy ions that are otherwise impossible.

Finally, the plasma temperature determines the Larmor radii as well as the charging of small dust particles.

In conclusion, the plasma temperature is such an important parameter that it is essential to be able to control it in the relevant range for the ITER divertor.

4.4 System size and plasma beam diameter

The system size is of importance when species coming off the surface become ionized, or in the case of dust particles, charge up, and are trapped in the plasma–surface system before eventually returning to the surface. The key parameter is the mean free path of the neutral particles produced at the surface. In most of the linear devices and plasma etchers available today, the mean free path for reionization in the plasma is larger than the system size. These devices work in the weakly coupled limit of the plasma–surface interaction. Therefore, the very important phenomenon of recycling which occurs in tokamaks is missed in most smaller devices. This is an important shortcoming, because the atoms and molecules emitted by the surface in a tokamak may be re-excited or ionized, and their reactivity, both with gas phase species and a surface, can be completely different. It is hard to reach the strongly coupled limit for hydrogen, because of its high velocity and small cross sections, and in particular for charged heavy clusters because they are not easily deflected in a magnetic field. The Larmor radius for nanometer sized and multiply charged carbon clusters has been computed to be on the order of several cm.⁴¹ Obviously, to reach the strongly coupled limit and to be able to study phenomena of surface diffusion over macroscopic distances, the plasma beam diameter should be at least 10 cm at ITER-relevant plasma densities.

In the operational density and temperature range of ITER, the ionization length of molecules such as CH₄ is typically a fraction of 1 cm. CH₄ is taken here as a typical representative of a molecule that can come off the surface. The dominant process is charge exchange (which is practically independent of temperature), but for plasma temperatures well in excess of 3 eV electron impact ionization becomes dominant.

The requirement that simple molecules leaving the surface must be trapped in the plasma implies that the system dimension should be several cm at least. For hydrogen atoms, the size has to be even larger.

For carbon dust particles, with a typical size of several nm, two criteria should be satisfied: i) their Larmor radius should be much smaller than the system size, and ii) their Hall or reionization factor should be well in excess of unity to ensure trapping in the magnetic field (and so reach the same conditions that are present in the ITER divertor). These two criteria necessitate both a magnetic field of several tesla and a linear system dimension of the order of 10 cm.

4.5 Neutral pressure

The neutral pressure is important in a variety of processes. The pressure and heating power determine the degree of ionization and other plasma parameters. It is important to note that the neutral gas does not necessarily have to be in full equilibrium with the wall. Association of H atoms at the wall can lead to creation of excited H₂ and other molecules. Also, the neutralization of the plasma beam at the surface and the neutral molecules that come off the surface, mostly with high translational and ro-vibrational temperatures, are essential players in PSI processes. If the neutral gas density were dominated by a large thermal component, the results of such an experiment may be very unlike those observed in ITER, because in ITER all neutral gas is produced by neutralization reactions in the plasma or at the surfaces.

Hence, the system must have the capability to vary the neutral density, and to get as close as possible to the situation in a detached divertor, where the plasma and neutral density are comparable. Interference by a large density of thermal gas, which will not be present in the ITER divertor, should be avoided. The neutral pressure is almost entirely due to the recombining plasma beam; the influx of cold neutral molecules should be negligible. Vacuum systems should be designed for a neutral pressure in the interaction region below 3 Pa during plasma operation at maximum flux. Secondly, when the plasma is off, the base pressure in the target compartment must be low enough to conserve the surface for analysis.

4.6 Heat flux to target and target temperature

The heat flux to the target is not a fundamental parameter, but it determines the surface temperature, especially in the case of peak heat load. The surface temperature is the critical parameter here, as it determines the residence times of intermediate states at the surface, and of course when it rises too high, gives rise to melting or ablation. The material of the target is, of course, a prime parameter of the model system.

Experiments should aim to handle target heat fluxes in the realm of the ITER divertor i.e. ∼10 MW m⁻². This should be consistent with the electron density and temperature expected in ITER, i.e. >10²⁰ m⁻³ at ∼3 eV. The targets have to be equipped with multi kW cooling capability to control the temperature.

4.7 ELM simulation and pulsed heat flow

An important issue is the behaviour of plasma-facing components under pulsed heat load such as that occurring in the so-called edge localised modes (ELM) in tokamaks on time scales close to ms (in JET: 0.1–0.4 ms, in Asdex Upgrade: 0.5–1.0 ms).⁴²

Concerning the physics, the essential processes to study are the melting, the formation and stability of the melt layer, the movement of the melt layer under j·B forces, and sublimation of the target surface and the ensuing ionization and redeposition of material. Here j is the current flowing in the molten material and B the applied magnetic field.

The technical possibilities to achieve an energy burst are:

1. Pulsed operation of the plasma source.

2. Modulation of the additional heating power.

3. Direct additional heating of the surface by e.g. a powerful laser pulse. This technique is easy to implement, because often the required lasers will be available and are also used for optical detection methods.

Such experiments, focused on transient heat loads, will give access to fundamental processes such as melting and sublimation under plasma impact.

4.8 Angle of incidence on target plate

The angle of incidence is a very important parameter. It comes about in rather trivial ways, such as the reduction of the flux density for grazing incidence. However, when the surface roughness comes into the realm of the Larmor radii of the ions and the Debye length, the sheath physics and deposition processes essentially change. Of particular importance, especially in the case of carbon targets, is the migration of material: where the erosion occur, the mechanism by which the eroded material travels, and where it travels to. For castellated target plates, the migration or deposition of dust in the slits between the plates is an important and urgent problem, for which the small angle geometry is essential.

4.9 Plasma diagnostics

To allow a detailed study of the underlying processes in plasma–surface interactions a detailed diagnosis of the plasma is essential. One needs to know the composition of the plasma, its ion temperature T_ion, its electron temperature T_e, the density, the degree of ionization, the neutral gas temperature, the internal temperatures of molecular species and the atom or molecule velocities, to name just the most important parameters. In addition, the plasma close to the surface is a system very far from local thermal equilibrium, and the energy content for different degrees of freedom can be very dissimilar and needs to be individually measured.

Passive emission spectroscopy is a very good and easy to implement tool to characterize excited species in a plasma, see e.g.ref. 43. A caveat is that it is hard to fully interpret the data if the excitation mechanism is not fully understood.

Active or laser induced spectroscopy does not have this problem, but needs an excitation laser of some sort. Methods used are laser induced fluorescence, and cavity ring down spectroscopy. Thomson scattering (of photons) on the plasma electrons gives the absolute electron densities and temperatures.

Mass spectrometry can provide the plasma composition. However, the implementation of mass spectrometry is very complex if the plasma is confined in a strong magnetic field.

In all cases a number of methods need to be used in order to characterize multicomponent systems, and a plasma interacting with a surface is certainly such a system.

4.10. Surface diagnostics

Proper characterization of the surface is essential for a detailed study of the plasma–surface interaction. The methods used are well established in the fields concerned and will not be introduced further. Some reports in the relevant literature includeref. 44–47. Characterization can be carried out at three levels:

• In situ characterization, preferably with the plasma on. This is needed because in the strongly coupled limit the plasma and surface are in a dynamic equilibrium, but this could be changed as soon as the plasma is switched off. Optical methods are preferred, as they can operate in the harsh plasma environment. Ellipsometry is one available method, but it is difficult to interpret its information content properly. The same holds to a certain extent for second harmonic generation. More specific information can be obtained from sum frequency generation, which essentially measures the infrared absorption spectrum of the surface on the femtosecond timescale.⁴⁸ Due to the very high peak photon fluxes used, the technique is not very sensitive to light produced by the plasma.

• In vacuo characterization, but without the presence of a plasma. In this case all methods of modern surface science can, in principle, be applied. However, the surface treated by the plasma has to be brought to these tools, which in the case of a large, heavily cooled target is not trivial. Various kinds of sample transfer systems can be used, including vacuum suitcases. Methods that can be relatively easily implemented are laser ablation mass spectrometry and thermal desorption spectroscopy.

• Ex situ characterization, including a transfer through air. This method has mainly been used for the analysis of tokamak surfaces. In the case where one is interested in such things as depth profiles of contaminants or the lateral structures built, ex situ studies can be excellent, because little change is expected. Obviously, such analysis will fail to show reactive structures of the surface while it interacts with the plasma.

4.11 An experiment under development: Magnum-psi

As part of the TEC collaboration and within the framework of Euratom, the FOM Institute is building a new machine that meets all of the requirements listed in sections 4.1–4.10. This apparatus, Magnum-psi, will be unique and provides an important new experimental facility for the range of experiments that are available to PSI research for ITER and reactors beyond ITER.^5,38 Magnum-psi will be described in detail elsewhere; an overview of the current design is shown in Fig. 9. The uniqueness of Magnum-psi lies first in its ability to access simultaneously several aspects of PSI, the combination of which results in the difference between ITER and present day experiments:

(1) Large ion fluence and continuous operation, which leads to ‘macroscopic’ modification of plasma-facing surfaces.

(2) High power density (5–10 MW m⁻²) with low plasma temperatures (<5 eV) such that materials are close to, or at the energy threshold for, sputtering, but have high surface temperature and are therefore near their materials limits for stress/strain, etc.

(3) Strong plasma–surface coupling: the high plasma density leads to short mean free paths for dissociation/ionization of eroded atoms or molecules in comparison to the linear dimensions of the plasma.

(4) Access to plasma diagnostics and in situ surface analysis.

Fig. 9 Schematic diagram of the new linear device Magnum-psi. In the overview drawings the superconducting magnet (yellow) surrounding the vacuum vessel can be seen. At one end of the magnet the roots pumps for the plasma sources can be seen. At the other end a special vacuum vessel is projected into which the target can be retracted for in vacuo surface analysis. To the sides, large tubes lead to two roots pumps for the evacuation of the plasma heating chamber.

The steady state high flux of up to 10²⁴ ions m⁻² s⁻¹ at a plasma temperature in the eV range, a magnetic field of 3 T, and a large beam diameter make Magnum-psi a unique experiment, bringing the relevant parameters to typically an order of magnitude beyond what is presently available in linear plasma devices, and into the realm of the ITER divertor. It will be the only device so far to enter the strongly coupled regime, in which molecules and dust particles that come off the surface are trapped and remain part of the plasma–surface interaction system, and thus will allow relevant studies of dust formation, redeposition, migration and hydrogen retention. The steady state and high flux capability, combined with the large flexibility and easy access, allow frequent post-mortem analysis, which in present devices normally occurs only every 1–2 y.

Magnum-psi is not a nuclear device, and cannot be operated with tritium. However, by carefully studying the uptake and exchange of H and D with various surfaces, the tritium retention problem can be studied, albeit indirectly. Through modelling H and D experiments information about the behaviour of T can be obtained.

The 3 T magnetic field is a unique feature, which is essential both to achieve the required fluxes and to reach the strongly coupled regime. Moreover, it allows investigation of those phenomena in which the magnetic field is directly involved in the physics, such as the j·B movement of melt layers.

The comprehensive diagnostics and the flexible target geometry, the possibility of varying target materials and the in-house ability to prepare target samples with a complex layered structure further add to the uniqueness of Magnum-psi.

Linear plasma generators—and Magnum-psi—can never fully model the physics of a tokamak divertor, due to the differences in geometry and energy spectrum of the constituents of the plasma that impact on the surface. Also, the conditions that occur during an ELM or a disruption are much more complex in a tokamak than in any experiment foreseen to mimic these in a linear device. However, as part of an integral research program on PSI, the value of Magnum-psi will especially lie in the exploration of the basic physics of PSI in conditions that are ITER- relevant, and in the development and testing of theoretical models for PSI and material damage under intense plasma fluxes, again in conditions that approach those which will occur in ITER. Magnum-psi will provide a new window on PSI in these extreme conditions, and complement PSI research at tokamaks, other plasma generators and theoretical studies.

5. Scientific challenges in the study of plasma–surface interactions

The major challenge for studies of plasma–surface interactions in the context of ITER is to find material surfaces that:

• have a sufficient lifetime under the steady state atom or molecule and power load of ITER

• are resistant against short bursts of excessive power load

• retain tritium at a sufficiently low rate and

• are compatible with the general plasma performance (radiation, impurity contamination).

It is obvious that attempts to reach these goals will occur along different simultaneous routes. Research on the topic in tokamaks will continue vigorously in a very mission oriented fashion. Research in dedicated devices such as Magnum-PSI will contribute to a better understanding of the processes at stake and point to new solutions. Research concerning many basic issues can be carried out in smaller machines, and can elucidate the elementary mechanisms that dominate the overall processes. Obviously, modelling at various levels of complexity, from basic quantum mechanics to empirical descriptions using rate equations, will have to unify the results from all studies and determine their implications for plasma surface interaction in ITER.

Here we list a number of issues on which further study at essentially all of the levels discussed is necessary.

(1) The mechanism of physical sputtering, sticking, desorption, evaporation and recombination at the surfaces and the low energies concerned.

(2) The role of diffusion, both lateral and into the bulk. The study of diffusion barriers.

(3) The role of surface morphology, both at the atomic scale (faces, steps, kinks etc.) and at the mesoscopic scale.

(4) The role of surface materials and use of mixed materials (e.g. Be, C, W) on all processes mentioned.

(5) The nature of the chemical reactions at the surface. Besides Langmuir–Hinschelwood reactions, Eley–Rideal (or direct impact) reactions are expected to be very relevant in hydrogen dominated systems. What is the role of metastable intermediates at the surfaces? Chemical reactions of molecules in the gas phase are also highly relevant.

(6) Plasma physics of plasma–surface interactions, such as sheath formation at surfaces in a strong magnetic field.

(7) Growth, charging and dynamics of clusters.

(8) Novel spectroscopic methods to study all of these features.

(9) Atomic collision physics in the strongly coupled region, of gases with a high degree of internal excitation.

All of these topics and presumably many more need further study. Obviously, in several areas there is a large number of reports available in the literature, but it needs to be assessed to determine whether the extent of this knowledge is sufficiently pertinent for the present conditions.

As stated before, only modelling will be capable of combining all the available information and adapting it to the needs of ITER.

Conclusions

Plasma–surface interaction will be one of the areas determining the success of ITER and the ultimate viability of generating fusion power under steady state conditions. Erosion and redeposition, handling the steady state power and intermittent peak powers, and preventing tritium retention on the reactor walls are issues to be solved for and by ITER. Although a lot is currently known about these issues, an extension of our knowledge base at all levels is necessary for the ultimate success of ITER. Mimicking the ITER divertor closely in an independent experiment will still require a very large experiment, such as the one under construction at the FOM Institute. However, many aspects of the underlying physical chemistry and chemical physics can be explored in dedicated experiments of a smaller scale. A large effort, including contributions from the readership of Phys. Chem. Chem. Phys., can contribute to making ITER a success, and ultimately enable a new way to generate an almost unlimited amount of energy in a sustainable fashion.

Acknowledgements

Dr Wim Koppers is thanked for his careful reading of the manuscript. This work, supported by the European Communities under the contract of association between EURATOM and FOM, was carried out within the framework of the European Fusion Programme with financial support from NWO.

References

1. ITER, http://www.iter.org.
2. J. Ongena and G. Van Oost, Trans. Fusion Sci. Technol., 2002, 41, 3–14.
3. U. Samm, Contemp. Phys., 2003, 44, 203–217.
4. J. Lister and H. Weisen, Europhys. News, 2005, 36, 48–51.
5. B. de Groot, G. J. van Rooij, V. Veremiyenko, M. G. von Hellermann, H. J. N. van Eck, C. J. Barth, G. L. Kruijtzer, J. C. Wolff, W. J. Goedheer, N. J. Lopes Cardozo, A. W. Kleyn, P. H. M. Smeets, S. Brezinsek, A. Pospieszczyk, R. A. H. Engeln and R. P. Dahiya, Fusion Eng. Des., 2005, 74, 155–159.
6. C. M. Braams and P. E. Stott, Nuclear Fusion: Half a Century of Magnetic Confinement Fusion Research, Institute of Physics Publishing, Bristol, 2002.
7. IFMIF, http://insdell.tokai.jaeri.go.jp/IFMIFHOME/if_download_site.html.
8. U. Samm, Fusion Sci. Technol., 2002, 41, 352–358.
9. U. Samm, Fusion Sci. Technol., 2005, 47, 73–75.
10. G. Federici, C. H. Skinner, J. N. Brooks, J. P. Coad, C. Grisolia, A. A. Haasz, A. Hassanein, V. Philipps, C. S. Pitcher, J. Roth, W. R. Wampler and D. G. Whyte, Nucl. Fusion, 2001, 41, 1967–2137.
11. G. Federici, P. Andrew, P. Barabaschi, J. Brooks, R. Doerner, A. Geier, A. Herrmann, G. Janeschitz, K. Krieger, A. Kukushkin, A. Loarte, R. Neu, G. Saibene, M. Shimada, G. Strohmayer and M. Sugihara, J. Nucl. Mater., 2003, 313–316, 11–22.
12. V. Philipps, J. Roth and A. Loarte, Plasma Phys. Controlled Fusion, 2003, 45, A17–A30.
13. V. Philipps, Fusion Sci. Technol., 2002, 41, 319–329.
14. V. Philipps, Fusion Sci. Technol., 2005, 47, 119–125.
15. U. Samm, G. Bertschinger, P. Bogen, J. D. Hey, E. Hintz, L. Konen, Y. T. Lie, A. Pospieszczyk, D. Rusbuldt, R. P. Schorn, B. Schweer, M. Tokar and B. Unterberg, Plasma Phys. Controlled Fusion, 1993, 35, B167.
16. P. C. Stageby, The Plasma Boundary of Magnetic Fusion Devices, Institute of Physics Publishing, Bristol, 2000.
17. A. Kallenbach, D. Coster, J. C. Fuchs, H. Y. Guo, G. Haas, A. Herrmann, L. D. Horton, L. C. Ingesson, C. F. Maggi, G. F. Matthews, R. D. Monk, J. Neuhauser, F. Ryter, J. Schweinzer, J. Stober, W. Suttrop, A. U. Team and J. Team, Plasma Phys. Controlled Fusion, 1999, 41, B177–B189.
18. H. F. Winters and J. W. Coburn, Surf. Sci. Rep., 1992, 14, 162–269.
19. A. von Keudell and W. Jacob, Prog. Surf. Sci., 2004, 76, 21–54.
20. D. C. Schram, Nucl. Instrum. Methods Phys. Res., Sect. B, 1998, 139, 136–144.
21. G. Janeschitz, A. Antipenkov, G. Federici, C. Ibbott, A. Kukushkin, P. Ladd, E. Martin and R. Tivey, Nucl. Fusion, 2002, 42, 14–20.
22. A. Kirschner, A. Huber, V. Philipps, A. Pospieszczyk, P. Wienhold and J. Winter, J. Nucl. Mater., 2001, 290–293, 238–244.
23. J. Winter, Phys. Plasmas, 2000, 7, 3862–3866.
24. C. Hollenstein, W. Schwarzenbach, A. A. Howling, C. Courteille, J.-L. Dorier and L. Sansonnens, J. Vac. Sci. Technol., A, 1996, 14, 535–539.
25. C. Hollenstein, Plasma Phys. Controlled Fusion, 2000, 42, R93–R104.
26. E. F. van Dishoeck, in The Molecular Astrophysics of Stars and Galaxies, ed. T. W. Hartquist and D. A. Williams, Clarendon Press, Oxford, 1998, p. 53.
27. D. B. Graves and D. Humbird, Appl. Surf. Sci., 2002, 192, 72–87.
28. D. Nishijima, M. Y. Ye, N. Ohno and S. Takamura, J. Nucl. Mater., 2003, 313–316, 97–101.
29. N. Ohno, M. Tanaka, N. Ezumi, D. Nishijima, S. Takamura, S. I. Krasheninnikov, A. Y. Pigarov and J. Park, Phys. Plasmas, 1999, 6, 2486–2494.
30. Y. Hirooka, R. W. Conn, T. Sketchley, W. K. Leung, G. Chevalier, R. P. Doerner, J. Elverum, D. M. Goebel, G. Gunner, M. Khandagle, B. Labombard, R. Lehmer, P. Luong, Y. Ra, L. Schmitz and G. R. Tynan, J. Vac. Sci. Technol., A, 2001, 8, 1790–1797.
31. R. P. Doerner, D. G. Whyte and D. M. Goebel, J. Appl. Phys., 2003, 93, 5816–5823.
32. R. P. Doerner, M. J. Baldwin, S. I. Krasheninnikov and K. Schmid, J. Nucl. Mater., 2005, 337–39, 877–881.
33. K. Schmid, M. Baldwin and R. Doerner, J. Nucl. Mater., 2005, 337–39, 862–866.
34. W. J. Goedheer, G. J. van Rooij, V. Veremiyenko, Z. Ahmad, C. J. Barth, S. Brezinsek, R. P. Dahiya, H. J. N. van Eck, R. A. H. Engeln, U. Fantz, B. de Groot, M. G. von Hellermann, A. W. Kleyn, G. L. Kruijtzer, N. J. Lopes Cardozo, V. Philipps, A. Pospieszczyk, U. Samm, D. C. Schram and J. C. Wolff, High Temp. Mater. Processes, 2004, 8, 627–633.
35. B. de Groot, Z. Ahmad, R. P. Dahiya, R. Engeln, W. J. Goedheer, N. J. Lopes Cardozo and V. Veremiyenko, Fusion Eng. Des., 2003, 66–8, 413–417.
36. H. Meyer, S. Klose, E. Pash and G. Fussmann, Phys. Rev. E, 2000, 61, 4347–4355.
37. B. Koch, W. Bohmeyer and G. Fussmann, J. Nucl. Mater., 2003, 313–316, 1114–1118.
38. H. J. N. van Eck, A. den Ouden, G. J. van Rooij, W. J. Goedheer, B. de Groot, N. J. L. Cardozo and A. W. Kleyn, IEEE Trans. Appl. Supercond., 2005, 15, 1303–1306.
39. J. Roth, A. Kirschner, W. Bohmeyer, S. Brezinsek, A. Cambe, E. Casarotto, R. Doerner, E. Gauthier, G. Federici, S. Higashijima, J. Hogan, A. Kallenbach, H. Kubo, J. M. Layet, T. Nakano, V. Philipps, A. Pospieszczyk, R. Preuss, R. Pugno, R. Ruggieri, B. Schweer, G. Sergienko and M. Stamp, J. Nucl. Mater., 2005, 337–39, 970–974.
40. F. F. Chen, Introduction to Plasma Physics, Plenum Press, New York, 1974.
41. W. J. Goedheer, unpublished results.
42. A. Loarte, G. Saibenal, R. Sartoril, D. Campbell, M. Becoulet, L. Horton, T. Eich, A. Herrmann, G. Matthews, N. Askura, A. Chankin, A. Leonard, G. Porter, G. Federici, G. Janeschitz, M. Shimada and M. Sugihara, Plasma Phys. Controlled Fusion, 2003, 45, 1549–1569.
43. V. M. Lelevkin, D. K. Otorbaev and D. C. Schram, Physics of Non-equilibrium Plasmas, North-Holland, Amsterdam, 1992.
44. K. W. Kolasinski, Surface Science: Foundations of Catalysis and Nanoscience, John Wiley and Sons, Chichester, 2002.
45. M. Bonn, A. W. Kleyn and G. J. Kroes, Surf. Sci., 2002, 500, 475–499.
46. M. Bonn, H. Ueba and M. Wolf, J. Phys.: Condens. Matter, 2005, 17, S201–S220.
47. D. P. Woodruff and T. A. Delchar, Modern Techniques of Surface Science, Cambridge University Press, Cambridge, 1986.
48. S. Roke, A. W. Kleyn and M. Bonn, Surf. Sci., 2005, 593, 79–88.

---