Knowledge-based approaches to crystal design†
James
Chisholm
,
Elna
Pidcock
,
Jacco
van de Streek
,
Lourdes
Infantes
,
Sam
Motherwell
and
Frank H.
Allen
*
Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge, UK CB2 1EZ
First published on 27th January 2006
Abstract
The 365![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 crystal structures recorded so far in the Cambridge Structural Database (CSD) have already been used extensively in the study of intermolecular interactions and crystal packing, providing fundamental knowledge that can be applied in crystal engineering and crystal design. However, as the scientific problems posed to the CSD become more sophisticated, there is a need to develop more extensive software facilities for database searching and for analysing search results. In this Highlight, we review a number of novel informatics approaches to the CSD, including derivative databases and new research software, and exemplify their use in providing further knowledge that is important in the design of novel crystalline materials.
000 crystal structures recorded so far in the Cambridge Structural Database (CSD) have already been used extensively in the study of intermolecular interactions and crystal packing, providing fundamental knowledge that can be applied in crystal engineering and crystal design. However, as the scientific problems posed to the CSD become more sophisticated, there is a need to develop more extensive software facilities for database searching and for analysing search results. In this Highlight, we review a number of novel informatics approaches to the CSD, including derivative databases and new research software, and exemplify their use in providing further knowledge that is important in the design of novel crystalline materials.
 James Chisholm | James Chisholm received an M.Sci. in theoretical physics from the University of St. Andrews, Scotland in 1996 and a Ph.D. in materials science from the University of Cambridge in 2000. Since 2002 he has been a Scientific Software Engineer at the CCDC, having previously worked as a computer consultant for Tessella Support Services. James' interests lie in the development of efficient software for the search and analysis of crystal structures. |
 Elna Pidcock | Elna Pidcock received a B.Sc. from Nottingham in 1992, and a Ph.D. from the University of Manchester in 1995. She then undertook postdoctoral work in resonance Raman spectroscopy at Stanford University, California, and moved to the University of East Anglia in 1999 where she studied single molecule magnets using magnetic circular dichroism. She joined the CCDC in 2001 and has developed interests in the interplay of molecular and crystallographic symmetry, chirality and fundamental aspects of molecular crystal packing. |
 Jacco van de Streek | Jacco van de Streek studied chemistry at Utrecht University in The Netherlands and received a Ph.D. in physical chemistry from the University of Nijmegen in 2001. Since then he has been a Research Scientist at the CCDC, where his main interests are in polymorphism, isostructurality and powder X-ray diffraction. |
 Lourdes Infantes | Lourdes Infantes received a B.A. in Chemistry in 1995 and a Ph.D. in 2000 from Autonoma University of Madrid (UAM). She moved to the CCDC in 2001 to work with Sam Motherwell on supramolecular chemistry and the analysis and prediction of hydrogen bond patterns. She returned to Spain in 2003 and is currently working in the Department of Crystallography at the Rocasolano Institute (CSIC) in Madrid, and maintains a collaboration with the CCDC. Her research interests include molecular recognition, pattern prediction and water clusters. |
 Sam Motherwell | Sam Motherwell graduated from St Andrews with a B.Sc. in chemistry and Ph.D. in X-ray crystallography and joined the CCDC in 1968. In 1978 he became Head of Automation at Cambridge University Library. Sam rejoined the CCDC in 1992 as Research Manager and has also been the CCDC's representative on the Board of the Pfizer Institute for Pharmaceutical Materials Science since 2002. His group carries out CSD-based research both internally and in collaboration with external groups. His particular interest is to promote the use of the CSD in crystal structure prediction and crystal engineering. |
 Frank Allen | Frank Allen studied chemistry at Imperial College, receiving a B.Sc. in 1965 and a Ph.D. in 1968. Following postdoctoral work at the University of British Columbia, Vancouver, he joined the CCDC in 1970. He has been involved in most major developments, with a strong accent on research applications of the CSD. He received the RSC Prize for Structural Chemistry in1994 and the Herman Skolnik Award of the ACS Division of Chemical Information in 2003. He is now Executive Director of the CCDC and a Visiting Professor of Chemistry at the University of Bristol. |
Introduction
“Crystals are windows on the world of atoms”:1 crystal structures reveal how atoms form molecules, and how molecules interact to form regular repeating patterns in crystals. Thus, crystals are also windows on the world of crystals, and any understanding of how crystals may be designed requires that we continue to extend our knowledge of supramolecular organisation and crystal packing.2 Self-evidently the study of existing crystal structures—an informatics approach—must play a key role in this design process. Thus, systematic studies of molecular packing must be allied to, and combined with, a knowledge of the strong intermolecular interactions that are often involved in crystal formation. This latter includes studies of interaction geometries, together with a knowledge of the higher-order motifs that form the supramolecular scaffolds which stabilise extended structures. All of this knowledge is encapsulated in the rapidly growing archives of existing crystal structure data in the crystallographic databases.3In this Highlight, we review some recent advances in the use of crystal structure data retrieved from the Cambridge Structural Database (CSD), and show how these applications are requiring the development of more advanced methods for database searching. We begin, however, with a short overview of the current distributed CSD System.
The Cambridge Structural Database (CSD) System
The CSD is the principal source of crystal structure data on molecular organic and metal–organic compounds,4 and is the core product of the Cambridge Crystallographic Data Centre. This year, 2005, is the 40th anniversary of the inception of the CCDC, and its developmental history has recently been summarised.5 The CSD was created to record the primary structural results of diffraction analyses: cell dimensions and atomic coordinates. However, to make this data accessible and searchable by the scientific community, it includes important value-added information, such as the formal 2D chemical representations of molecules and ions, chemical name(s) and formulae, bibliographic citations, and text and numerical information relating to the experiment. All of this information is fully validated and cross-checked during database creation. Full details of the information content of the CSD are documented elsewhere,4 and are maintained on the CCDC website at http://www.ccdc.cam.ac.uk, which also contains general statistical information on the 365![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures recorded in the CSD in November 2005.
000 structures recorded in the CSD in November 2005.
The CCDC has always been active in software development to provide code for data validation and database creation and, most importantly, to provide user access to the database itself.4,6,7,9 Three programs form the core of the current CSD System:
ConQuest 6—for searching text, numerical data and chemical information, and the retrieval of user specified information. 2D and 3D substructure searches can be entered via a chemical sketcher, including the ability to locate intermolecular interactions using geometrical constraints. ConQuest will retrieve user-defined geometrical data for substructural queries.
Mercury 6—for visualising 3D structures, either directly from the CSD, or from other data representations, such as the CIF or PDB formats. Mercury has all the expected standard chemical and crystallographic visualisation features, together with facilities for locating H-bonds and other short contacts, and for rapidly building and visualising networks generated by these interactions. Mercury has many other features, including ADP-ellipsoid display, structure superposition, visualisation of slices through crystals relative to least-squares or Miller planes, etc. A version of Mercury is available for free download from the CCDC website.
Vista—reads geometrical and other numerical information retrieved by ConQuest into a spreadsheet, and displays parameter distributions as histograms or scattergrams on Cartesian or polar axes together with descriptive statistics. Vista will also carry out more advanced statistical functions, such as linear regression and principal components analysis.
The CCDC also provides two software applications related to data checking and database creation:
enCIFer—provides facilities for checking the syntax and format compliance of CIF files prior to their submission for publication, or storage in a database or in laboratory archives. The program is available for free download from the CCDC website.
PreQuest—creates crystal structure databases in CSD search format. This is the same software used by the CCDC in database creation, with facilities for structure validation, and entering chemical diagrams and other CSD-compliant information.
Two further software products have recently been added to the CSD System. These are knowledge-based libraries designed to provide instant access to a wide variety of chemically classified geometrical information.
Mogul 7—a library of chemically classified intramolecular geometry containing more than 20 million bond lengths, valence angles and acyclic torsions. Complete molecules or substructural queries can be imported or built in the graphical interface, a bond, angle or torsion identified, and the distribution of the CSD values obtained (Fig. 1). Fast searching is accomplished by use of a tree indexed on chemical keys that classify bonds, angles and torsions and their chemical environments. If there are few examples of an environment in the CSD, Mogul will add values to the distribution that arise from chemically similar environments, where the similarity level can be chosen by the user. Mogul also has the ability to generate distributions for all bonds, angles and acyclic torsions in a query molecule. Mogul can be used, e.g., for predicting conformational preferences during model building, or for carrying out reality checks on geometrical parameters in computational models or during the determination and refinement of novel small molecule crystal structures,8 as embodied in the programs CRYSTALS and DASH. The possibility of using Mogul to set up ligand dictionaries for refinement of protein-ligand crystal structures is an obvious extension of this philosophy.
 | ||
| Fig. 1 The Mogul library of intramolecular geometry: Results of a search for a C–S–S–C torsion angle. (a) Selecting the atoms that identify the torsion angle in the query molecule. (b) Mogul distribution of C–S–S–C torsion angles in the CSD. The value in the 3D query molecule (a) is shown in red on the histogram. | ||
IsoStar
9—a library of intermolecular interactions between pairs of groups A⋯B. By superimposing crystallographically-observed contacts between A and B so that the A moieties are overlaid, a three-dimensional scatterplot can be produced showing the experimental distribution of B (the “contact” or “probe” group) around A (the “central group”), as shown in Fig. 2a. The scatterplot can be converted to a contoured surface (Fig. 2b) showing the density of contact groups around the central group. IsoStar contains over 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 scatterplots of this type, 20
000 scatterplots of this type, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 are derived from the CSD, and a further 5000 are derived from protein-ligand complexes in the Protein Data Bank (PDB).10 IsoStar also contains about 1500 energy minima computed using distributed multipole analysis and intermolecular perturbation theory.11 IsoStar not only provides an instant view of group⋯group interactions, as shown for the interaction of carbonyl groups with a central phenyl moiety (Fig. 2c), but is also valuable as an ideas generator and in answering simple questions, for example which acceptor in isoxazole, the N or the O, is most likely to form H-bonds? The answer (Fig. 2d) is clearly the N atom, which forms stronger H-bonds than the O atoms.12 IsoStar is hyperlinked to both the CSD and the PDB so that individual interactions in any scatterplot can be observed in their original structural environments.
000 are derived from the CSD, and a further 5000 are derived from protein-ligand complexes in the Protein Data Bank (PDB).10 IsoStar also contains about 1500 energy minima computed using distributed multipole analysis and intermolecular perturbation theory.11 IsoStar not only provides an instant view of group⋯group interactions, as shown for the interaction of carbonyl groups with a central phenyl moiety (Fig. 2c), but is also valuable as an ideas generator and in answering simple questions, for example which acceptor in isoxazole, the N or the O, is most likely to form H-bonds? The answer (Fig. 2d) is clearly the N atom, which forms stronger H-bonds than the O atoms.12 IsoStar is hyperlinked to both the CSD and the PDB so that individual interactions in any scatterplot can be observed in their original structural environments.
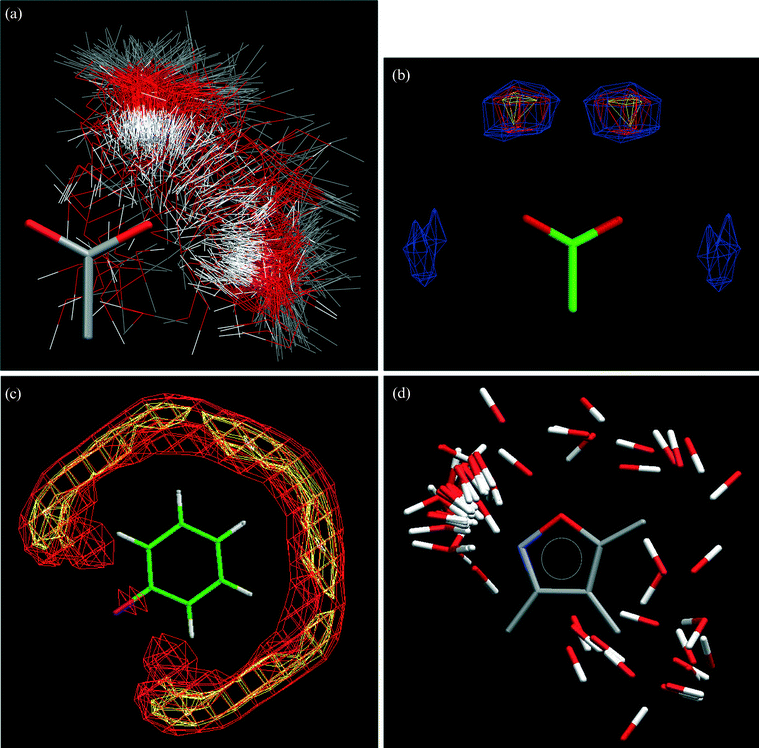 | ||
Fig. 2 The IsoStar library of intermolecular interactions. (a) Scatterplot (symmetry-reduced) of an OH contact group around a charged carboxylate central group. (b) Contoured and symmetry-expanded version of the scatterplot in Fig. 2(a). (c) IsoStar scatterplot of a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O contact group around a phenyl central group, contoured on the carbonyl-O atoms. (d) IsoStar scatterplot of O–H donor contact groups around an isoxazole ring, showing the preference for H-bonding to the ring N atom. O contact group around a phenyl central group, contoured on the carbonyl-O atoms. (d) IsoStar scatterplot of O–H donor contact groups around an isoxazole ring, showing the preference for H-bonding to the ring N atom. | ||
Scientific applications of the CSD System: history, reviews and recent work
More than 1200 research applications of the CSD System and other CCDC products have been published over the past 25 years. These have been collected in a classified and freely searchable database called WebCite13 maintained by the CCDC. WebCite contains literature references, including article titles and a short synopsis of each application prepared by CCDC staff. In recent years also, reviews have been published summarising applications of the CSD in crystal engineering,14,15 rational drug design16,17 and molecular inorganic chemistry.18 These reviews cover the available literature up to the beginning of 2002. In that year, the CCDC began a major collaboration with Pfizer Inc. and the Departments of Chemistry and Materials Science of Cambridge University to form the Pfizer Institute for Pharmaceutical Materials Science. The objective of the Institute is to use a variety of techniques, including CSD analysis, to answer important questions relevant to the formulation and delivery of pharmaceutically active ingredients. The CSD-based research projects of the Pfizer Institute are closely allied to crystal engineering objectives, and have also integrated well with established research projects at the CCDC itself. Results from both the internal and collaborative research programmes will be discussed in this Highlight. Apart from generating novel science, both of these programmes have also suggested new ‘enabling technologies’ for CSD analysis, and specialised derivative databases and new algorithms are beginning to answer CSD queries that are more complex than those which can be handled by the current CSD System.Specialised databases and specialist data subsets derived from the CSD
The master CSD contains many basic data items which enable a very wide range of searches to be performed rapidly via a single pass mechanism. However, more complex data items, derived from several basic data items, are sometimes required in order to satisfy more complex queries, and generation of these derived data items is often cpu-intensive—thus prohibiting their calculation ‘on the fly’ during a normal single-pass search. To address these specific problems, some or all CSD entries must be pre-processed to form a derivative database which can itself be searched rapidly to obtain the desired results.CSDSymmetry
Information within the CSD is primarily concerned with recording molecular structures within three dimensional crystal structures. However, the CSD is also a unique source of information about relationships between molecular and crystallographic symmetry. Statistics detailing the coincidence of molecular and crystallographic symmetry are, potentially, of interest to those endeavouring to engineer or predict crystal structures. In previous studies of symmetry in crystal structures, much use has been made of the number of molecules in the asymmetric unit, Z′.19 There is only a loose correlation between Z′ and molecular symmetry so, for example, Z′ cannot be used to distinguish between the occupancy of an inversion centre or a 2-fold axis in C2/c. Recently, Cole et al.20 described a molecular symmetry perception algorithm and its implementation in RPluto.21 Symmetry elements are detected within specified geometrical tolerances and the collection of symmetry elements returned for each molecule is used to assign the point group. The detection of molecular symmetry is performed using only atomic coordinates and hence information about the crystallographic environment is not included in the analysis. The application of this algorithm to thousands of molecules, in conjunction with the ability to detect the symmetry of occupied Wyckoff positions in crystal structures22 has led to the creation of a relational database, CSDSymmetry,23 constructed using Microsoft Access. It contains information such as space group, point group, Z, Z′, and symmetry of Wyckoff positions for each of the 273![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 291 entries extracted from the CSD (V5.23, November 2003 release). Auxiliary tables, linked to the main table, list the symmetry elements which belong to 38 common point groups, the symmetry operators, and Wyckoff positions of the 230 space groups. These tables allow selection of molecules by the symmetry elements that characterise them or by their membership of a space group with a particular symmetry operator.
291 entries extracted from the CSD (V5.23, November 2003 release). Auxiliary tables, linked to the main table, list the symmetry elements which belong to 38 common point groups, the symmetry operators, and Wyckoff positions of the 230 space groups. These tables allow selection of molecules by the symmetry elements that characterise them or by their membership of a space group with a particular symmetry operator.
The unambiguous assignment of the symmetry of the molecule and the Wyckoff position, permits large scale surveys of the coincidence of molecular and crystallographic symmetry. A survey of occupied Wyckoff positions was performed24 using CSDSymmetry by extracting a subset of 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 836 structures having only a single chemical residue. The distribution of molecules over the common point groups was examined and the distribution of crystal structures over the common space groups was determined. To probe the point of contact of molecular and crystallographic symmetry, statistics detailing the occupancy of Wyckoff positions by molecules of a particular symmetry, and the occupancy of Wyckoff positions in the common space groups, were collated. Finally, the most common locations (Wyckoff position and space group) for molecules of a particular symmetry were presented. From this study it was found24 that “point acting” molecular symmetry was commonly retained in crystal structures. Thus molecules with an inversion centre (Ci (S2) or
836 structures having only a single chemical residue. The distribution of molecules over the common point groups was examined and the distribution of crystal structures over the common space groups was determined. To probe the point of contact of molecular and crystallographic symmetry, statistics detailing the occupancy of Wyckoff positions by molecules of a particular symmetry, and the occupancy of Wyckoff positions in the common space groups, were collated. Finally, the most common locations (Wyckoff position and space group) for molecules of a particular symmetry were presented. From this study it was found24 that “point acting” molecular symmetry was commonly retained in crystal structures. Thus molecules with an inversion centre (Ci (S2) or ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) or molecules containing the S4 (
) or molecules containing the S4 (![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) ) or S6 (
) or S6 (![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ) symmetry elements had a high probability (68–99%) of retaining this symmetry in crystal structures. Conversely, molecular mirror symmetry was retained in crystal structures in only 30% of cases, and the most common location for mirror symmetric molecules was found to be a general position in P21/c. Examination of the statistics of occupied Wyckoff positions in space groups showed that inversion centres were occupied in approximately 20% of cases. In stark contrast, mirror planes were found to be occupied in almost all cases. Thus, it may be concluded that inversion centres in space groups are effective mediators of good close-packing hence the high occurrence of unoccupied inversion centres.
) symmetry elements had a high probability (68–99%) of retaining this symmetry in crystal structures. Conversely, molecular mirror symmetry was retained in crystal structures in only 30% of cases, and the most common location for mirror symmetric molecules was found to be a general position in P21/c. Examination of the statistics of occupied Wyckoff positions in space groups showed that inversion centres were occupied in approximately 20% of cases. In stark contrast, mirror planes were found to be occupied in almost all cases. Thus, it may be concluded that inversion centres in space groups are effective mediators of good close-packing hence the high occurrence of unoccupied inversion centres.
However, it must be the case that good close-packing is not mediated by crystal inversion centres for molecules with molecular inversion symmetry. Inversion operators in space groups are rarely used to relate molecules of Ci (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) symmetry to one another, perhaps because the action of an inversion operator on a molecule with inversion symmetry is equivalent to a translation. Hence, molecules with inversion symmetry retain this symmetry in crystal structures and reside on Wyckoff positions of
) symmetry to one another, perhaps because the action of an inversion operator on a molecule with inversion symmetry is equivalent to a translation. Hence, molecules with inversion symmetry retain this symmetry in crystal structures and reside on Wyckoff positions of ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry. Again, in contrast, space groups containing mirror planes are not popular, and do not offer good close-packing conditions to molecules in general positions. Thus, only molecules which are able to “neutralise” the poor packing resulting from mirror planes are found in mirror containing space groups, so molecules with mirror symmetry are found in Pnma and P21/m occupying the crystal mirror plane. However, it is much more common for mirror symmetric molecules to “discard” the mirror symmetry and crystallise on general positions in the common space groups.
symmetry. Again, in contrast, space groups containing mirror planes are not popular, and do not offer good close-packing conditions to molecules in general positions. Thus, only molecules which are able to “neutralise” the poor packing resulting from mirror planes are found in mirror containing space groups, so molecules with mirror symmetry are found in Pnma and P21/m occupying the crystal mirror plane. However, it is much more common for mirror symmetric molecules to “discard” the mirror symmetry and crystallise on general positions in the common space groups.
CSDSymmetry is both simple and versatile. It can be used to address questions on the nature of close-packing and can answer specific questions regarding occurrences of particular symmetry combinations in crystal structures. It is available for free download at http://www.ccdc.cam.ac.uk/free_services/csdsymmetry.
CSDContact
Within the distributed CSD System, ConQuest and IsoStar provide excellent facilities for studying and analysing data for individual non-bonded contacts. However, it is either very difficult or impossible to carry out searches that provide information about, e.g., the chemical environment and the number of H-bonds formed at a given acceptor atom, the numbers of donors and acceptors in each structure, etc. Such information is vital in studies of H-bond competition, and hence in predicting the most likely H-bonding options for a given molecule. These predictions are important in pharmaceutical materials development, particularly in evaluating possible differences between polymorphic forms, and in filtering the results of computational polymorph predictions, as discussed in a later section.To enable such studies a specialised database, CSDContact, has been derived25 from organic structures in the CSD that have: R < 0.10, no residual validation errors, no disorder and no catena bonding. CSDContact records all potential intermolecular H-bonds involving donor and acceptor O, N, and S atoms, with the donors having up to 3 (for O), 4 (N), and 1 (S) hydrogen substituents, and using a distance cutoff (∑vdW + 0.1Å), where ∑vdW is the sum of the appropriate van der Waals radii. Additionally, CSDContact records: (a) chemical environment codes for donors and acceptors, (b) the number of contacts at each acceptor, (c) a steric accessibility measure for each acceptor, and (d) the donor/acceptor ratio in each structure. Initial results25 show, for example, that the numbers of contacts formed appears (a) to be minimally affected by increasing steric accessibility, but (b) to have a high dependence on the donor/acceptor ratio. CSDContact will not include structures for which a later and more precise determination has revealed disorder, but it will include the earlier ‘non-disordered’ structure. Such structures represent a very small proportion of the content, and will not materially affect statistical conclusions drawn from the database. We are currently working on automated techniques for choosing structure(s) from a family of determinations of the same compound that are best suited for the purpose of the analysis.
The use of CSDContact to study the effects of competition for available donors and acceptors26 is summarised in Table 1, in which Part (a) shows the very high propensity for self-association exhibited by functional groups that contain both donors and acceptors. In some cases, e.g.
–COOH and –CONH this propensity is 100%, while in other cases, the propensity increases with increasing numbers of the target functional group in a structure. Table 1, Part (b) shows the effect of introducing a second group B into structures containing the –COOH or –CONH functions, denoted here as A-groups. The propensity of the A groups to self-associate is disrupted to very different degrees depending on the nature of B. A strong ability to disrupt each other's self-association is found when B = –COOH or –CONH, while the Csp3–OH group has a high ability to disrupt both –COOH and –CONH self-association. By contrast, the etheric C–O–C B-group has little effect on self-association, while the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group disrupts –COOH self-association more than it does for –CONH.
O group disrupts –COOH self-association more than it does for –CONH.
| (a) Group self-association in structures containing only a single type of functional group. N(grp) is the number of occurrences of the group in a structure; obs is the number of observed self-associations; poss is the number of possible self-associations; % is the ratio obs/poss expressed as a percentage. | |||
|---|---|---|---|
| Group | N(grp) | obs ∶ poss | % |
| COOH | 1 | 146 ∶ 146 | 100 |
| 2 | 164 ∶ 164 | 100 | |
| 3 | 14 ∶ 14 | 100 | |
| CONH | 1 | 117 ∶ 120 | 98 |
| 2 | 131 ∶ 132 | 99 | |
| 3 | 29 ∶ 29 | 100 | |
| Csp3OH | 1 | 58 ∶ 79 | 60 |
| 2 | 317 ∶ 341 | 93 | |
| 3 | 66 ∶ 66 | 100 | |
| Csp2OH | 1 | 16 ∶ 28 | 57 |
| 2 | 38 ∶ 47 | 81 | |
| 3 | 10 ∶ 11 | 91 | |
| (b) Disruption of self-association of functional group A through addition of a functional group B. A⋯A, A⋯B and B⋯B are the percentages of group–group associations of the three possible types, N(str) is the number of CSD structures contributing to the analysis. These data are for structures containing only groups A and B. | |||||
|---|---|---|---|---|---|
| A group | B group | A⋯A (%) | A⋯B (%) | B⋯B (%) | N(str) |
| COOH | 100 | ||||
| COOH | Csp3–OH | 12 | 88 | 0 | 49 |
| COOH | CONH | 14 | 58 | 28 | 40 |
| COOH | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (keto) O (keto) |
62 | 38 | 0 | 86 |
| COOH | C–O–C | 92 | 8 | 1 | 26 |
| CONH | 100 | ||||
| CONH | Csp3–OH | 35 | 60 | 5 | 30 |
| CONH | COOH | 28 | 58 | 14 | 40 |
| CONH | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (keto) O (keto) |
89 | 11 | 0 | 26 |
| CONH | C–O–C | 97 | 3 | 0 | 35 |
Detecting ‘hidden’ polymorphic forms in the CSD
Polymorphism is a phenomenon that is often crucial in drug development and delivery,27 since the physical properties of polymorphs are usually different, particularly their solubilities and bioavailabilities. The extensive coverage of the CSD makes it ideal for studying polymorphism in organic and metal–organic compounds. However, if the crystal structures of two polymorphs are determined by different sets of authors, then it is sometimes not until both have been archived to the database that their polymorphic relationship becomes apparent. Until recently, the identification and flagging of polymorphs in the CSD depended principally on this fact being mentioned in the original publication, and as a result an unknown number of polymorphs remained ‘undiscovered’. Searching for polymorphs requires comparison of more than one CSD entry at a time, a type of search that is not possible with existing software. In 2004, a project was started to develop software that would locate as many of these unflagged polymorphs as possible.28CSD entries are grouped by chemical compound, each compound sharing the same six-letter section of its CSD reference code (refcode) which is assigned by compound registration when each new structure is archived to the database. Thus, the task of locating hidden polymorphs reduces to a cross-comparison of pairs of entries in a refcode family and establishing if there are structural differences for each pair. The problems that arise when comparing crystal structures are well known: the same crystal structure may have been determined using different space-group settings (e.g.P21/n and P21/c), with different choices of origin (e.g.P212121) or in a space group of too low symmetry (e.g.Cc instead of C2/c). All of these problems can be overcome by transforming the published crystal structures to their simulated powder diffraction patterns (XRPDs).
However, this process is not straightforward. A few older CSD entries (before the CIF-format was widely adopted) contain residual errors in the atomic coordinates, or there may be confusions over non-standard space-group settings, e.g. for P212121. As a result, two crystal structures may appear to be different even though they are in fact the same. Because unit-cell parameters are generally correct, comparing only the unit cells rather than the complete crystal structures gives less false positives (at the expense of a handful of false negatives for pairs of polymorphs with very similar unit cells). It is possible to eliminate the contribution of the atoms and space group to a powder diffraction pattern by setting the magnitudes of all the structure factors, including the systematic absences, to a constant value. One problem of crystal structure comparison that cannot be solved by simulating XRPDs is that of unit-cell differences due to differences in temperature and/or pressure. The influence of differences in unit-cell volumes can, however, be reduced by an additional step in which the volumes are normalised to their expected values, calculated by summing average atomic volumes29 for every element. After volume normalisation and transformation to simulated XRPDs, pairwise crystal structure similarities are calculated using the similarity measure for powder diffraction patterns of De Gelder et al.,30 based on weighted cross-correlation functions. The measure is normalised and is not as sensitive to peak shifts caused by unit-cell volume differences as point-by-point similarity measures. For full details we refer to the original paper.30 The volume normalisation, powder pattern simulation and calculation of similarities were implemented via an in-house C++ library and used to write a stand-alone program that finds all chemical compounds having more than one crystal structure in the CSD, and outputs all of the cross-comparisons within those refcode families.
The similarity measure spans all values between 0 and 1, and there is no obvious cut-off value between polymorphs and re-determinations of the same structure. Assuming that the relative number of possible polymorphs in the CSD is independent of the similarity, then a plot of the relative number of possible polymorphs as a function of similarity will show a plateau for low similarity values, indicative of true polymorphism. As the similarity approaches unity more and more of the potential polymorphs are in fact re-determinations and the relative number of true polymorphs decreases. The onset of a steady rise in the plot (Fig. 3) was therefore used to determine a cut-off below which two crystal structures were judged to be polymorphic. The list of similarity measures for all pairs of crystal structures of the same chemical compound can now be combined with the cut-off criterion to arrive at a list of all pairs of potential polymorphs in the CSD.28 Structural pairs that were not already flagged as polymorphs were examined manually, and 154 new pairs of polymorphs were ‘discovered’ and flagged in the CSD. The coverage of the polymorph flag is estimated to be approximately 99% comprehensive.
 | ||
| Fig. 3 Detecting the similarity cut-off for polymorph identification using simulated powder diffraction patterns. The number of unidentified polymorphs per 100 CSD entries (y-axis) as a function of similarity cut-off (x-axis). The background level is around 4% for similarities below 0.960 that unambiguously point to polymorphism, with more and more false positives being added as the similarity cut-off approaches 1.000. | ||
There are also good reasons to apply the procedure outlined here to CSD entries that are already known to be polymorphic. First, the presence of the polymorph flag does not guarantee that more than one crystal structure of the compound has been determined, e.g. because the existence of a second polymorph was established using powder diffraction or DSC, and its crystal structure was not determined. Secondly, the polymorph flag is applied to the compound as a whole, and does not currently contain information about which CSD entries relate to which polymorph, and this again makes it impossible to distinguish polymorphs from re-determinations.
Processing all pairs of polymorphs in the CSD, both previously known and previously unknown, therefore allows us to: (a) distinguish re-determinations of polymorphs from real polymorphs, and (b) remove crystal structures of compounds that are known to be polymorphic but for which the crystal structure of only one polymorph is known. Applied to paracetamol, the results are as follows: there are 21 crystal structures in the CSD—2 entries for the first polymorph and 19 entries for the second. These generate 2 × 19 = 38 pairs of polymorphs, of which only one pair is unique, the other pairs are duplicates caused by re-determinations. When applied to the whole CSD, the resultant list contains 7300 pairs, including duplicates. Work is in progress to further reduce this list to provide the number of unique polymorph pairs.
Software to extend the searchability of the CSD
A common feature of most existing CSD applications is that they use ConQuest to search the CSD. This section describes novel research software that is being developed to address two shortcomings in ConQuest search facilities. First, we note that ConQuest searches for extended intermolecular motifs can be very slow. ConQuest searches for bonded 2D chemical substructures are optimised using a set of heuristics, and these searches remain acceptably fast despite significant annual increases in database size. The beneficial effects of the heuristics persist to intermolecular searches involving single interactions between chemical groups. It is the introduction into the query of additional non-bonded interactions involving several substructures that nullifies the existing heuristics and leads to excessive search times. The study of extended intermolecular motifs has become increasingly important, and the CCDC has begun to develop software that will locate these motifs systematically and with much shorter cpu-times.Secondly, there are interesting properties of compounds that only become apparent when their structures are considered in pairs, and here the single-pass sequential search mechanisms of ConQuest are inappropriate. The polymorph detection software discussed above is one example in which pairs of related compounds are located, in this case within a CSD refcode family. Recently, software has been written to address two other typical and more general search problems where pairwise relationships are located within the complete database: (a) the location of compounds that exist in both unsolvated and solvated forms, and (b) the location of structures that differ only by the exchange of a single functional group.
Software for locating general extended motifs
The importance of robust bimolecular structural motifs (synthons) in crystal engineering has long been recognised.31 The CSD has previously been used32 to identify and classify the most commonly occurring cyclic motifs in terms of their probabilities of occurrence, using specially written software. However, the need for more general software for locating extended structural motifs in the CSD was exemplified during the work on hydration and salt formation discussed below and a research program, 3DSEARCH,33 has been coded.3DSEARCH generalises a query motif in terms of a collection of bonded chemical substructures and ‘connections’ between them. These connections can be defined relative to ∑vdW, and can therefore be constrained such that a specified connection is either: (a) a non-bonded contact (normally < ∑vdW), or (b) is not a close contact (normally > ∑vdW). The 3DSEARCH program combines both substructure and distance searching into a depth-first backtracking algorithm33 to locate the complete query in the CSD. The operation of the program is illustrated in Fig. 4 by a search for a tape motif comprising eight water molecules (W) and six atoms (X ≠ C, H). Two types of connections were specified to enforce the regularity of the hexagons: (a) those corresponding to the dotted lines in Fig. 4 which should be H-bonds and are constrained to be <∑vdW, and (b) cross-ring distances that must not be H-bonds, and are constrained to be >(∑vdW + 0.35 Å). The complete query, having 14 substructures (W and X), and a total of 44 connections, yielded 116 CSD entries in an elapsed time of 30 min on a modern PC (e.g. a 2.60 GHz Pentium 4). Further examples are shown elsewhere,33 and work is now in progress to fully test and implement the 3DSEARCH code in a distributable form.
 | ||
| Fig. 4 Locating extended non-bonded motifs in the CSD using 3DSEARCH. (a) A T6(2) tape motif comprising a specific arrangement of water molecules (W) and general atoms (X ≠ C, H); dotted lines indicate hydrogen bonds. (b) The CSD entry AMIMZC10 illustrating the T6(2) motif located, and the query connections described in the text. | ||
Software for filtering crystal structure prediction results
The computational prediction of molecular crystal structures has huge potential. Within the pharmaceutical industry, for example, it is vital to identify and characterise all possible polymorphic forms of a drug product, and particularly those that might be accessible under normal conditions. In some cases, the ability to predict the most thermodynamically stable form could provide a valuable warning that the form developed is not the most stable and that phase transformations during manufacture or storage are a distinct possibility. Unfortunately, crystal structures cannot yet be predicted with the necessary level of confidence.35 A typical approach is to use empirical force fields to rank large lists of generated candidate structures in terms of minimised lattice energy or minimised free energy. The difficulty is that, typically, very many plausible structures are generated whose calculated lattice energies are similar to, or lower than, the lattice energy of the experimentally observed structure(s). One is always conscious that predictions can suffer from limitations in the computational methodology and progress in crystal structure prediction will certainly come from the application of criteria other than relative energies to reduce the number of possible candidates.One approach to the refinement of these energy-based lists is to use information derived from the CSD: given a particular molecule, can we determine the hydrogen bonding pattern(s) that are most likely to be exhibited in its crystal structure by analysing how similar molecules have behaved in existing crystal structures? We are investigating a scheme for automatically assigning hydrogen bond scores to predicted structures in order to determine whether such an approach can improve on predictions. The intention is to promote those structures in the prediction list that display frequently observed motifs and demote structures that display motifs that are seen less frequently.
The first step is to compile a list of molecules that are similar to the prediction molecule. Special attention is paid to similarity of hydrogen bonding functionality. For example, given a prediction molecule with a single amide group, say fluorobenzamide, a ConQuest search is performed to find all other CSD molecules that also contain a single amide group and no other strongly competing hydrogen bonding functionality. There are some difficulties to consider. First the notion of similarity can be subjective and the CSD may not contain a sufficient number of ‘similar’ molecules. For example, the ‘single amide search’ finds only 18 structures. Secondly, such similar molecules may display a wide range of different hydrogen bonded motifs and our analysis of CSD structures may not uncover any consensus of behaviour.
Once a list has been compiled, searches can be performed to find the frequency of occurrence of various types of ring and chain motif. Searches are performed using 3DSEARCH,33 described above. Generation of the 3DSEARCH queries (rings and chains) has been automated to avoid manual sketching. Fig. 5a shows the three most commonly observed motifs for molecules that contain a single amide group, and their frequencies can be used to derive hydrogen bond scores for each predicted structure. One method is simply to sum the motif frequencies. Alternatively, scores can be normalised by dividing by the number of motifs observed. Thus, if a predicted structure displays the motifs described by the graph sets34 R2,2(8) and R4,6(16) then a hydrogen bond score of (88 + 55)/2 = 71 can be assigned.
 | ||
| Fig. 5 Use of CSD information to filter crystal structure prediction results. (a) The three most commonly observed H-bonded motifs in structures that contain a single amide group. (b) Hydrogen bond scores determined for the 100 lowest energy predicted structures of fluorobenzamide. (c) Ranking of observed structures in an energy ranked prediction list. Red values indicate the original rank, blue values indicate the rank following removal of predicted structures that receive low hydrogen bond scores. | ||
Fig. 5b shows motif scores derived for the 100 lowest energy structures obtained from a force field crystal structure prediction for fluorobenzamide. Many structures receive high scores indicating the presence of motifs that are commonly observed in the CSD (mainly the motifs shown in Fig. 5a). No attempt is made to promote one structure above all others as the expected observed structure. Instead hydrogen bond scores are used to identify structures that are unlikely to form, i.e. the low scoring structures that display motifs not commonly seen in the CSD. One approach is to simply remove from the list those predicted structures that score less than half the maximum hydrogen bond score. This procedure has been carried out for a range of force field predictions carried out by Day et al.36 The results of re-ranking the predictions are shown in Fig. 5c. The use of hydrogen bond scores improves the ranking of the observed structure for 12 out of 29 predictions. For 15 predictions the ranking is left unaltered, and for 2 predictions (acetic acid and tetrolic acid) the use of hydrogen bond scores actually removes the observed structures from the prediction list altogether, since both structures display the catemer motif, while the dimer motif dominates mutual COOH interactions in the CSD. Also, we find that hydrogen bond scores perform best where force fields perform poorly: indicating perhaps that the H-bond scores are simply acting as a correction factor for poorly computed energies.
Pairwise relationships: locating solvated and unsolvated compounds
While screening for polymorphs, new crystal structures are often prepared that turn out to be a solvated form of the molecule of interest. While these structures may be regarded as ‘just another solvate’, they also have the additional and important property that they are known to exist in both solvated and unsolvated forms. While it is relatively simple to locate all solvates in the CSD using a self-constructed solvent list,37 it is non-trivial to locate compounds for which both the unsolvated and solvated forms co-exist in the database and a special program is required.38The 2D connectivity of a solvent of interest can be sketched into ConQuest and saved to a file which serves as input for the new program. In a first pass through the CSD, all entries that contain the solvent are located. In the second pass, the solvent is removed from entries in this list, and the CSD is searched for entries that match the resulting desolvated structure. If a match is found in this second pass, then a pair of crystal structures has been identified that satisfy the search problem. If no match is found, the solvated form is recorded in a separate list of compounds for which only a solvated crystal structure is present in the CSD.
Although conceptually simple, the total number of comparisons involved in this type of search can be very large: for water, the most abundant solvent in the CSD, the search requires 10 billion pairwise entry comparisons. Using the full 2D connectivity would be prohibitively slow, and a fast screening step is carried out using a topological index:39,40 a close to unique single number that summarises the entire 2D connectivity. Thus, the topological index for water is 560 and the CSD is first searched for all entries containing a molecule having that index. A full confirmatory 2D connectivity search is only required for those entries that pass the screening step. In version 5.26 (November 2004) of the CSD, 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 550 entries contain water, and screening reduces the 10 billion potential comparisons to 8845 possible matched pairs of structures, of which 1448 pairs are genuine examples of hydrated and non-hydrated forms. This leaves 30
550 entries contain water, and screening reduces the 10 billion potential comparisons to 8845 possible matched pairs of structures, of which 1448 pairs are genuine examples of hydrated and non-hydrated forms. This leaves 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 102 hydrates without a non-hydrated counterpart in the CSD. The topological screening takes ∼15 minutes, and the entire process takes ∼30 minutes, on a modern PC (e.g. a 2.60 GHz Pentium 4). The program must, of course, be run for every solvent of interest, and a comprehensive survey37 of solvates in the CSD provides a valuable starting point.
102 hydrates without a non-hydrated counterpart in the CSD. The topological screening takes ∼15 minutes, and the entire process takes ∼30 minutes, on a modern PC (e.g. a 2.60 GHz Pentium 4). The program must, of course, be run for every solvent of interest, and a comprehensive survey37 of solvates in the CSD provides a valuable starting point.
Pairwise relationships: functional group exchanges
It is observed that if a methyl group on a molecule is substituted by bromine, the crystal structures of the two compounds are commonly isostructural. In order to quantify “commonly”, it is necessary to find all occurrences of such functional group replacements in the CSD. Again, this type of search cannot be done in a single pass through the database, and a computer program to perform these searches (GRX, for GRoup eXchange)41 has been written. GRX first locates all occurrences of the first of the two functional groups in the CSD. When the functional group is found, it is removed from the molecule, leaving a ‘radical’ fragment. The same is done for the second functional group and the ‘radical’ fragments are then compared: if they are the same, the two compounds are related by a ‘functional group exchange’. Hydrogen, because it is so abundant in the CSD, is treated as a special case.We can now determine, for example, if Cl- or Br-substitution of a methyl group is more likely to result in an isostructural crystal structure. Here, GRX is used to find all crystal structures related by a methyl–chlorine substitution and likewise for methyl–bromine substitution. The pairs of crystal structures are then compared to establish if they are isostructural, by comparison of their simulated powder patterns. The answers are 26% and 25% for chlorine and bromine respectively, indicating that both halogens are equally effective at replacing a methyl group without changing the crystal structure. GRX is not restricted to single atoms, and allows searching for fragments of arbitrary size. Fig. 6a shows the replacement of a phenyl substituent by cyclohexadienyl; the similarity of simulated powder diffraction patterns of the two crystal structures is 0.991. GRX is not restricted to monovalent functional groups, but also allows searching for the exchange of, for example, –CH2– by –S– (Fig. 6b).
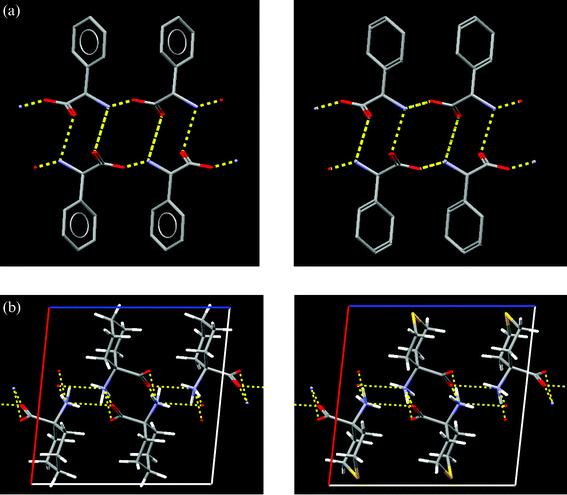 | ||
| Fig. 6 Functional group exchanges and isostructurality located by the GRX program. (a) Isostructural pair of crystal structures obtained by substituting a phenyl group (CSD refcode FIVGEW) by a cyclohexadienyl group (CSD refcode CHEDGL10). Hydrogen bonds are shown in yellow. (b) Isostructural pair of crystal structures obtained by substituting a –CH2– group (CSD refcode ACYHXA) by a sulfur atom –S– (CSD refcode ACXTPY). Hydrogen bonds are shown in yellow. | ||
Extending CSD-based research
CSD System software can be combined with both new and existing research code to extend the scientific scope and value of chemoinformatics studies using the CSD. In this section, we summarise three different studies which each contribute knowledge about how crystal structures are built, and how molecules prefer to pack in those structures.Studies of hydration
Compounds that exist as anhydrous crystals below a certain level of relative humidity, may convert to a hydrated form at higher humidity levels. Such lack of stability in the presence of atmospheric moisture is a significant concern in pharmaceutical development, since it has serious implications for the processing, formulation, packaging and storage of the product. The CSD has recently been used to study water affinity42 in organic crystal structures in an attempt to indicate possibilities in generating stable formulations for a variety of pharmaceutical compound types. A subset of 121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 345 CSD structures was analysed in terms of 36 chemical functional groups. Fig. 7a shows a plot of the water affinity of those groups, expressed as the ratio of the number of hydrated structures containing the group divided by the total number of structures containing the group. It can be seen that the highest affinities are exhibited by compounds containing charged species, while the lowest affinities are exhibited by compounds having terminally bound halogens. It is notable that the most popular donor/acceptor groups in organic molecules have rather moderate hydrate affinities.
345 CSD structures was analysed in terms of 36 chemical functional groups. Fig. 7a shows a plot of the water affinity of those groups, expressed as the ratio of the number of hydrated structures containing the group divided by the total number of structures containing the group. It can be seen that the highest affinities are exhibited by compounds containing charged species, while the lowest affinities are exhibited by compounds having terminally bound halogens. It is notable that the most popular donor/acceptor groups in organic molecules have rather moderate hydrate affinities.
 | ||
Fig. 7 CSD studies of water affinity. (a) Water affinity (frequency of hydrate formation) for various chemical groups. Affinity is defined as Nobs/Nposs, where Nobs is the number of structures containing the group and a water molecule, and Nposs is the total number of structures containing the group within a CSD sample of 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 803 structures. (b) Variation of water affinity with the number of chemical groups present in the structure: top left: COO−, top right: –OH, bottom left: –O–, bottom right: C–Cl. 803 structures. (b) Variation of water affinity with the number of chemical groups present in the structure: top left: COO−, top right: –OH, bottom left: –O–, bottom right: C–Cl. | ||
A further factor42 that appears to affect hydrate formation is the number of acceptor groups available in any structure. In general, water affinity appears to increase as the number of functional groups increases. However, the nature of the groups under study is also important, as indicated in Fig. 7b, which shows the variation of water affinity with the numbers of donors/acceptors for four common functional groups. Two points can be made:
• The water affinity of strongly polar groups increases quite significantly with increasing numbers of these groups, and the slope of the plot is higher for groups that have a higher basic affinity value. Thus the affinity of COO− (Fig. 7b, basic affinity 35%) increases much more rapidly with an increasing number of groups than does the plot for –OH (Fig. 7b, basic affinity 15%).
• For non-polar groups, e.g. –O– and C–Cl, the water affinity is essentially unaffected by increasing the number of groups (Fig. 7b).
While it is true that increasing the number of functional groups increases molecular size, and that larger molecules may have an increased propensity to form hydrates and other solvates, the results above are derived from the complete range of molecular sizes available in the CSD, and quite small molecules can exhibit significant numbers of functional groups. However, further work that takes account of molecular size is being undertaken. The studies of water affinity have also involved studies of extended motifs involving water clusters alone43 and water combined with other functional groups.42 These studies have made extensive use of the 3DSEARCH algorithm33 noted above and exemplified in Fig. 4. Work to compare hydrated and non-hydrated structures, using software described above, is also progressing.
Investigating suitable counterions for use in pharmaceutical salt formation
Another concern in the development of novel pharmaceutical materials is the frequent need to form a suitable salt of a drug molecule, in order to (a) increase or decrease its solubility, (b) fine tune its bioavailability, and (c) generate formulations which are crystalline, stable, and exhibit long shelf life.44 Here, it is important that any counterions used in salt formation must themselves be designated as safe, and several lists of approved counterions are available.45,46 The potential value of the CSD in suggesting potential counterions has been examined47 by searching the database for occurrences of a wide range (69 acids, 21 bases) of these pharmaceutically approved components. The CSD was then used to determine the percentages of crystal structures that existed in hydrated and polymorphic forms.The type of detailed information that can be obtained from the CSD is exemplified by a study of one of these approved counterion types: sulfonate groups in R–SO3− derivatives48 for which the CSD contains 1069 examples. It was found that 594 of these structures (56%) contained N–H donors, and this subset was investigated in terms of the observed H-bonded motifs. A wide variety of motifs was identified and those cyclic motifs with an occurrence of >10% in the sample are illustrated in Fig. 8a. The bidentate motif is particularly robust: 192 structures in the 594-structure subset have the chemical group components required to form the motif, and it actually occurs in 151 of these structures—a probability of occurrence of 78.6%. It was also noted that 122 structures in the subset were guanidinium salts, with the sulfonate group often attached to an aromatic ring. These structures are remarkably consistent: 121 of them contain the bidentate motif, and 119 contain ribbons of bidentate motifs. Overall, there is a 92% probability of sulfonate salt formation with guanidinium cations via the bifurcated motif, hence R–SO3− is an extremely favourable counterion for use with guanidinium-containing pharmaceutical compounds, as shown in Fig. 8b, because the motif is highly reproducible.
 | ||
| Fig. 8 Investigating suitable counterions for use in pharmaceutical salt formation. (a) Robust N–H⋯O(sulfonate) hydrogen bonded motifs located via a CSD search: top left: R2,2(8) bidentate motif (26.4%), top right: R4,4(10) 13.6%, bottom left: R4,4(12) 17.9%, bottom right: R6,6(18) 12.6%. (b) CSD entry UBESAV, illustrating H-bonding between a guanidinium cation and a sulfonate anion. | ||
The Box Model of crystal packing
Following Kitaigorodskii,49 it is generally accepted that molecular crystal structures are close-packed, i.e. molecules make the most efficient use of space as possible, unless engineered to be otherwise. Kitaigorodskii's predictions of space group populations, based on how well the symmetry operators of the space groups were able to fit molecules together, have been shown to be remarkably accurate by the advent of hundreds of thousands of new test cases. As noted above, much effort has been devoted to employing intermolecular motifs and synthons to “engineer” and “design” crystal structures.31 These strategies are not infallible, however, indicating other factors need to be considered. Little attention has been paid to the role of close-packing in crystal structure design and few attempts are made to “engineer” structures from molecules with no hydrogen bonding capabilities. In an attempt to establish whether the notion of close-packing has any utility in the design of crystal structures we have examined the parameters of molecular crystal structures. If close-packing is truly a tenet underpinning crystal nucleation and crystal growth it must be reflected in the basic metrics of crystal structures.To assess the spatial arrangements of molecules in crystal structures, cell lengths of thousands of molecules extracted from the CSD were described in terms of multiples of the constituent molecular dimensions.50 By reducing the description of a molecule to three dimensions, long, L, medium, M, and short, S (hence L > M > S) and describing each cell length in terms of a multiple of a molecular dimension, unit cells are revealed to be of similar construction. The histograms of Fig. 9 arise from plotting the values of the three ratios of cell length to molecular dimension, calculated for thousands of structures belonging to the same space group.51 Histograms of ratios calculated for structures belonging to different space groups, but having the same Z-value, are almost identical. Comparison of the histograms calculated for structures of different Z show different numbers of peaks, but exhibit similarities in peak positions. Thus unit cells containing 2, 4 or 8 molecules can frequently have a cell length described by 0.87 × (molecular dimension: L, M or S) as evidenced by the presence of a peak at ∼0.87 in all histograms. The similar peak positions observed in the histograms indicate that cell lengths are related to molecular dimensions in a systematic way, irrespective of space group or Z. Thus, the histograms “demonstrate” close-packing.
 | ||
Fig. 9 Histograms of pattern coefficients calculated for structures belonging to a) P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , Z = 2; b) P21/c, Z = 4; c) C2/c, Z = 8. The pattern coefficients were calculated by dividing each cell length by the molecular dimension most closely aligned with the cell axis, thus orientation of the molecule is taken into consideration. , Z = 2; b) P21/c, Z = 4; c) C2/c, Z = 8. The pattern coefficients were calculated by dividing each cell length by the molecular dimension most closely aligned with the cell axis, thus orientation of the molecule is taken into consideration. | ||
To explain the variations in the form of the histograms for structures of different Z, a model of crystal packing was required. A three dimensional object, a box, was chosen to represent the molecule in the model. The box has three unequal dimensions, L, M and S, and for a given number of boxes there is a limited number of arrangements which have faces touching and edges aligned. For two boxes there are only three “close-packed” arrangements, or packing patterns (Fig. 10), and there are six possible arrangements of four boxes (Fig. 11). Since the box represents a molecule in the model, the close-packed arrangements of boxes represent “unit cells” whose overall dimensions can be described in terms of the box dimensions. The three packing patterns of two boxes are described as 1L × 1M × 2S (112S), 1L × 1S × 2M (112M) and 1M × 1S × 2L (112L). Using this nomenclature, the descriptions of the arrays of four boxes fall into two families, the 221 family (221L, 221M and 221S) and the 114 family (114L, 114M and 114S). In the Box Model, the boxes are aligned perfectly with the “cell” axes, and the faces of the boxes touch but do not interpenetrate, leading to “cell” dimensions described by integer multiples of the box dimensions.
 | ||
| Fig. 10 For a box of three unequal dimensions, L, M and S where L > M > S, there are only three ways of “close-packing” two boxes with faces touching and edges aligned. The packing pattern names are included to the right. | ||
 | ||
| Fig. 11 The six possible close-packed arrangements of four boxes. The packing pattern names are shown within each packing pattern. | ||
Histograms of Box Model ratios, or pattern coefficients, Fig. 12 show that the model reproduces the key features of the histograms calculated from experimental data. Thus, only two peaks are expected in the histogram calculated from Z = 2 structures (ideal pattern coefficients from the Box Model are 1,1,2), and the height of the first peak is expected to be twice that of the second peak. The three peaks observed in the histograms calculated from Z = 4 structures indicate that there are experimental structures belonging to both the 221 family and the 114 family. Three peaks are also expected in the Z = 8 histogram due to contributions from the 421 packing pattern family as well as the 222 family.
 | ||
| Fig. 12 Histograms of pattern coefficients of the Box Model for the packing patterns for 2 and 4 boxes. Ideal pattern coefficients for the a) 112 packing pattern (2 boxes) and b) the 221 family (left) and 114 family (right), four boxes. | ||
The good agreement between the experimental and Box-Model histograms led to the assignment of thousands of Z = 2, Z = 4 and Z = 8 crystal structures to the Box-Model packing patterns50 by comparing calculated pattern coefficients to target pattern coefficients of the Box Model, and choosing the packing pattern which gave the best agreement with the calculated coefficients. Examination of the distribution of structures with the same Z, over the packing patterns, showed that the lower surface area packing patterns were more popular. Within the Box Model, it can be seen that the arrangements of two boxes (Fig. 10) have the same volume, but differ in total exterior surface area. In the 112 packing pattern family, when the largest faces of the boxes are placed in contact the surface area is the smallest, but when the smallest faces of the boxes are placed in contact the surface area is the greatest. For Z = 2 structures belonging to P21 and P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , the proportion of structures found in the lowest surface area packing pattern, 112S, was 52.1% and the proportion of structures found in the greatest surface area packing pattern, 112L, was 15.6%. Similarly, for Z = 4 structures, the lowest surface area packing pattern, 221L, represented 36.5% of the 23
, the proportion of structures found in the lowest surface area packing pattern, 112S, was 52.1% and the proportion of structures found in the greatest surface area packing pattern, 112L, was 15.6%. Similarly, for Z = 4 structures, the lowest surface area packing pattern, 221L, represented 36.5% of the 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 859 structures belonging to P21/c, P212121 and C2/c, whereas the packing pattern with the greatest surface area, 114L, represented only 1.6% of these structures. This observation of a preference for low surface area packing patterns has led to the reiteration of one of Kitaigorodskii's assertions, namely, molecular shape is of primary importance in crystal packing. There certainly appears to be a driving force to minimise surface area for a given volume, resulting in unit cells of low surface area. This observed distribution of structures over the packing patterns is potentially helpful in a crystal engineering context. High surface area packing patterns are unusual and common unit cells are those where the repeats of the longest molecular dimension are minimised and repeats of the shorter molecular dimensions are maximised.
859 structures belonging to P21/c, P212121 and C2/c, whereas the packing pattern with the greatest surface area, 114L, represented only 1.6% of these structures. This observation of a preference for low surface area packing patterns has led to the reiteration of one of Kitaigorodskii's assertions, namely, molecular shape is of primary importance in crystal packing. There certainly appears to be a driving force to minimise surface area for a given volume, resulting in unit cells of low surface area. This observed distribution of structures over the packing patterns is potentially helpful in a crystal engineering context. High surface area packing patterns are unusual and common unit cells are those where the repeats of the longest molecular dimension are minimised and repeats of the shorter molecular dimensions are maximised.
The preference exhibited by experimental structures for unit cells described by low surface area packing patterns indicates a desire to minimise surface area for a given volume. To examine whether there is an energetic argument to support this preference, calculations were performed52 to identify the two strongest energetic interactions in the structure, using Gavezzotti's potentials34 as implemented in RPluto.21 These calculations are crude but fast, and a dataset of approximately 2400 structures was processed which belonged to P21/c, had Z′ = 1, and for which packing patterns were assigned. From a consideration of molecular orientation in the cell, in conjunction with the identification of the symmetry operator that mediated the strong energetic interactions, it was possible to determine which faces of the molecule were interacting most strongly. It was found that, irrespective of molecular orientation, the inversion operator most often mediated the strongest interaction, but that the second strongest interaction was frequently mediated by a symmetry operator that related the largest faces of the molecule. For example, in structures where the largest face of the molecule was oriented perpendicular to b, it was found that the 21 operator (parallel to b) mediated strong interactions more often than the glide plane or unit-cell translations. For structures having the 221S packing pattern, strong interactions were found between translationally related molecules: translation relates the largest faces of the molecule in this packing pattern (see Fig. 11). It is not surprising that strong interactions are found between the large faces of molecules: when these are in contact, we expect a large number of atom-pair contacts near the minimum of the van der Waals potential curve, and a higher energy sum than for two small faces in contact. Thus, minimising surface area for a given volume, by placing the large faces of the molecules together, is energetically fruitful. The occurrence of low surface area packing patterns indicates that symmetry operators (as opposed to unit cell translations) are more likely to mediate these “large-face” interactions between molecules.
We then examined whether strong H-bonds, e.g. those between carboxylic acids or amide groups, would perturb the preference for low surface area patterns or compete with the large-face interactions. A dataset of 241 structures containing the carboxylic acid dimer was extracted from P21/c structures for which a packing pattern had been assigned. The structures were processed to identify the strong energetic interactions and the inversion centre, which is responsible for building the majority of dimer motifs, was found to be a very common mediator of the strong interactions. Translation was also utilised more frequently than expected in the generation of strong interactions. This preference for inversion and translation operators appeared to yield a greater than expected population of the 221S and 114S packing patterns. In a second dataset, containing structures with a trans-amide chain motif, it was found that the glide plane was used most frequently in chain propagation. The glide plane was well represented in the symmetry operators of strong energetic interactions. However, the population of the packing patterns was very much as expected from previous work. It was proposed52 that the differences observed in packing pattern populations between the amide and the carboxylic acid datasets could be rationalised in terms of the position of the functional group within the molecule. For the majority of the carboxylic acids, the group was positioned on the smallest face of the molecule, but in the CONH-chain dataset the amide group was most commonly located on the largest face of the molecule. Therefore, in the crystal packing of the carboxylic acids, two important and opposing “structure-directing” interactions need to be satisfied: the interaction between the large faces of the molecules and the carboxylic acid dimer interaction. The greater than expected population of 221S and 114S packing patterns (higher surface area packing patterns), may reflect a compromise between two energetically important but geometrically conflicting interactions. In contrast, the CONH chain motif propagates by placing the large molecular faces together, so there is no conflict between motif building and the large-face interaction. The population of the packing patterns is approximately as expected with a slightly increased population of the lowest surface area packing patterns, 221L and 221M.
Thus the Box Model provides a fundamental framework within which we may increase our understanding of crystal packing. It has been shown that molecular crystal structures are fundamentally very similar and that structures are well represented by only a small number of packing patterns. Cell dimensions are related to molecular dimensions in a systematic way. The preference for low surface area packing patterns demonstrates that molecular shape is an important “structure-directing” factor. We hope a consideration of the geometry of intermolecular interactions in conjunction with molecular shape will provide further useful insights into the packing compromises inherent in molecular crystal structures.
Conclusion—and challenges for the future
In this article, we have highlighted recent computational and scientific research at the CCDC, and illustrated new ways in which CSD data can be accessed and analysed. The key objective has been to use the CSD to address problems of intrinsic scientific interest, but in so doing we have also explored the limits of existing distributed software6,7,9 and begun to develop new tools for CSD analysis23,25,33,38,41 and for improving the information content of the database.28 It is our aim to further extend and systematise this new analysis code, and make it more widely available in due course.The problems discussed in this Highlight are ones for which CSD data are uniquely able to provide scientific insights. However, the value and credibility of these insights depends crucially on the accuracy and completeness of the underlying crystal-structure data: as with all CSD-based research, the work is only as good as the data upon which it is based. At present, the CSD is a major component in a set of comprehensive crystal structure databases,3 whose contents are trusted by their users, and whose creation: (a) is financed through Government grants or through subscription income and (b) is carried out by subject experts—modern-day electronic librarians. Elsewhere,5 we have commented on the scientific and financial aspects of the CCDC's operations, and noted some significant challenges to be faced in maintaining the CSD.
Principal amongst these challenges is to ensure that the CSD remains as accurate, up to date and comprehensive as possible. To do this, the CCDC must keep pace with the ever-increasing number of novel crystal structures being generated by modern technology, but maintaining acceptable cost levels. It is inevitable that the CSD's current annual input, currently ca. 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 published structures, will accelerate faster than hitherto, and that the CSD's historical doubling period of 8–9 years is likely to reduce. So, while part of the available software development resource must be directed towards bringing better tools to the desks of CSD users, another part must be directed towards bringing increased automation to CSD creation and maintenance. Novel algorithms and computational procedures, which also embody many years of chemical and crystallographic experience, are already beginning to make an impact on data processing. The ultimate aim is to automate much of the routine information processing, enhancing CSD data content wherever possible, but to identify those difficult, erroneous or highly novel structures which will always require the detailed attention of skilled scientific editors.
000 published structures, will accelerate faster than hitherto, and that the CSD's historical doubling period of 8–9 years is likely to reduce. So, while part of the available software development resource must be directed towards bringing better tools to the desks of CSD users, another part must be directed towards bringing increased automation to CSD creation and maintenance. Novel algorithms and computational procedures, which also embody many years of chemical and crystallographic experience, are already beginning to make an impact on data processing. The ultimate aim is to automate much of the routine information processing, enhancing CSD data content wherever possible, but to identify those difficult, erroneous or highly novel structures which will always require the detailed attention of skilled scientific editors.
A second challenge is to ensure that as many structures as possible, published and unpublished, enter the CSD. It has been realised for some time that the era of high-throughput crystallography has created its own problems in terms of data availability.53,54 Thus, decreasing percentages of the structures determined, perhaps as low as 20–25%, are now made available through formal publication, due to the time required to prepare manuscripts and for other reasons.54 Furthermore, increasing numbers of structures ‘fit for the purpose’ are being determined using rapid data collections to reveal gross structural features—thus requiring improved flagging in a crystal structure database. These factors, combined with the development of e-science approaches,55 and calls by government agencies for the establishment of open archives of data and results arising from their funding,56 will have significant impact on increasing data availability to the CSD in ensuing years, thus increasing the ability of the database to provide answers to challenging scientific questions.
References
- C. Raymo, The Virgin and the Mousetrap: Essays in search of the soul of science, Viking-Penguin, New York, 1991 Search PubMed.
- D. Braga, L. Brammer and N. Champness, CrystEngComm, 2005, 7, 1–19 RSC.
- F. H. Allen and J. P. Glusker, Preface to Acta Crystallogr., Sect. B, 2002, 58, Issue 3, Part 1, available at: http://journals.iucr.org/b/issues/2002/03/01/me0172/index.html. Search PubMed.
- F. H. Allen, Acta Crystallogr., Sect. B, 2002, 58, 380–388 CrossRef.
- F. H. Allen and R. Taylor, Chem. Commun., 2005, 5135–5140 RSC ; see also: F. H. Allen, International Union of Crystallography Newsletter, 2005, 13, 23–24 Search PubMed (http://www.iucr.org/).
- I. J. Bruno, J. C. Cole, P. R. Edgington, M. Kessler, C. F. Macrae, P. McCabe, J. Pearson and R. Taylor, Acta Crystallogr., Sect. B, 2002, 58, 389–397 CrossRef; C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr. Search PubMed , submitted for publication.
- I. J. Bruno, J. C. Cole, M. Kessler, Jie Luo, W. D. S. Motherwell, L. H. Purkis, B. R. Smith, R. Taylor, R. I. Cooper, S. E. Harris and A. G. Orpen, J. Chem. Inf. Comput. Sci., 2004, 44, 2133–2144 CrossRef CAS.
- e.g. CRYSTALS: R. I. Cooper and D. J. Watkin, Acta Crystallogr., Sect. A, 2002, 58(Supplement), C58 Search PubMed [See also: http://www.xtl.ox.ac.uk/crystals.html]; DASH: W. I. F. David, K. Shankland, J. van de Streek, E. Pidcock and S. Motherwell, DASH version 3.0, Cambridge Crystallographic Data Centre, Cambridge, UK, 2004.
- I. J. Bruno, J. C. Cole, J. P. M. Lommerse, R. S. Rowland, R. Taylor and M. L. Verdonk, J. Comput. Aided Mol. Des., 1997, 11, 525–537 CrossRef CAS.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS.
- I. C. Hayes and A. J. Stone, Mol. Phys., 1984, 53, 83–105 CAS.
- I. Nobeli, S. L. Price, J. P. M. Lommerse and R. Taylor, J. Comput. Chem., 1997, 18, 2060–2074 CrossRef CAS.
- CCDC WebCite database: http://www.ccdc.cam.ac.uk/free_services/webcite.
- A. Nangia, CrystEngComm, 2002, 4, 93–101 RSC.
- F. H. Allen and W. D. S. Motherwell, Acta Crystallogr., Sect. B, 2002, 58, 407–422 CrossRef.
- R. Taylor, Acta Crystallogr., Sect. D, 2002, 58, 879–888 CrossRef.
- F. H. Allen and R. Taylor, Chem. Soc. Rev., 2004, 33, 463–475 RSC.
- A. G. Orpen, Acta Crystallogr., Sect. B, 2002, 58, 398–406 CrossRef.
- C. P. Brock and J. D. Dunitz, Chem. Mater., 1994, 6, 1307–1312 CrossRef CAS and refs. therein.
- J. C. Cole, J. W. Yao, G. P. Shields, W. D. S. Motherwell, F. H. Allen and J. A. K. Howard, Acta Crystallogr., Sect. B, 2001, 57, 88–94 CrossRef CAS.
- W. D. S. Motherwell, G. P. Shields and F. H. Allen, Acta Crystallogr., Sect. B, 1999, 55, 1044–1056 CrossRef.
- J. C. Cole, PhD Thesis, University of Durham, UK, 1995 Search PubMed.
- J. W. Yao, J. C. Cole, E. Pidcock, F. H. Allen, J. A. K. Howard and W. D. S. Motherwell, Acta Crystallogr., Sect. B, 2002, 58, 640–646 CrossRef.
- E. Pidcock, W. D. S. Motherwell and J. C. Cole, Acta Crystallogr., Sect. B, 2003, 59, 634–640 CrossRef.
- L. Infantes and W. D. S. Motherwell, Chem. Commun., 2004, 1166–1167 RSC.
- L. Infantes and W. D. S. Motherwell, Z. Kristallogr., 2005, 220, 333–339 CrossRef CAS.
- J. Bernstein, Polymorphism in Molecular Crystals, IUCr Monographs on Crystallography, Clarendon Press, Oxford, 2002, vol. 14 Search PubMed.
- J. van de Streek and S. Motherwell, Acta Crystallogr., Sect. B, 2005, 61, 504–510 CrossRef.
- D. W. M. Hofmann, Acta Crystallogr., Sect. B, 2002, 58, 489–493 CrossRef.
- R. De Gelder, R. Wehrens and J. A. Hageman, J. Comput. Chem., 2001, 22, 273–289 CrossRef CAS.
- G. R. Desiraju, Angew. Chem., Int. Ed. Engl., 1995, 34, 2311–2327 CrossRef CAS.
- F. H. Allen, P. R. Raithby, G. P. Shields and R. Taylor, Chem. Commun., 1998, 1043–1044 RSC; F. H. Allen, W. D. S. Motherwell, P. R. Raithby, G. P. Shields and R. Taylor, New J. Chem., 1999, 23, 25–34 RSC.
- J. A. Chisholm and W. D. S. Motherwell, J. Appl. Crystallogr., 2004, 37, 331–334 CrossRef CAS.
- M. C. Etter, Acc. Chem. Res., 1990, 23, 120–126 CrossRef CAS; J. Bernstein, R. E. Davis, L. Shimoni and N.-L. Chang, Angew. Chem., Int. Ed., 1999, 38, 3440–3451 CrossRef.
- A. Gavezzotti, Acc. Chem. Res., 1994, 27, 309–314 CrossRef CAS; J. D. Dunitz, Chem. Commun., 2003, 545–548 RSC; G. M. Day, W. D. S. Motherwell, H. Ammon, S. X. M. Boerrigter, R. G. Della Valle, E. Venuti, J. Dunitz, A. Dzyabchenko, B. P. van Eijck, P. Erk, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, F. J. J. Leusen, C. Liang, C. C. Pantelides, P. G. Karamertzanis, S. L. Price, T. C. Lewis, A. Torrissi, H. Nowell, H. Scheraga, Y. Arnautova, M. U. Schmidt, B. Schweizer and P. Verwer, Acta Crystallogr., Sect. B, 2005, 61, 511–527 CrossRef CAS and refs. therein.
- G. M. Day, J. Chisholm, N. Shan, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2004, 4, 1327–1340 CrossRef CAS.
- C. H. Görbitz and H.-P. Hersleth, Acta Crystallogr., Sect. B, 2000, 56, 526–534 CrossRef.
- J. van de Streek and W. D. S. Motherwell, in preparation.
- L. A. Evans, M. F. Lynch and P. Willett, J. Chem. Inf. Comput. Sci., 1978, 18, 146–149 CAS.
- D. Bawden, J. T. Catlow, T. K. Devon, J. M. Dalton, M. F. Lynch and P. Willett, J. Chem. Inf. Comput. Sci., 1981, 21, 83–86 CrossRef CAS.
- J. van de Streek and W. D. S. Motherwell, J. Appl. Crystallogr., 2005, 38, 694–696 CrossRef CAS.
- L. Infantes, J. Chisholm and S. Motherwell, CrystEngComm, 2003, 5, 480–486 RSC.
- L. Infantes and S. Motherwell, CrystEngComm, 2002, 4, 454–461 RSC.
- P. J. Gould, Int. J. Pharm., 1986, 33, 201–217 CrossRef CAS.
- P. H. Stahl and C. G. Wermuth (Editors), Handbook of pharmaceutical salts: properties, selection and use, Wiley-VCH/VHCA, Weinhiem, Zurich, 2002 Search PubMed.
- L. D. Bighley, S. M. Berge and D. C. Monkhouse, in Encyclopaedia of pharmaceutical technology, ed. J. Swarbrick and J. C. Boylan, Marcel Dekker, New York, 1996, vol. 13, pp. 453–499 Search PubMed.
- D. A. Haynes, W. Jones and W. D. S. Motherwell, J. Pharm. Sci., 2005, 94, 2111–2120 CrossRef CAS.
- D. A. Haynes, J. A. Chisholm, W. Jones and W. D. S. Motherwell, CrystEngComm, 2004, 6, 584–588 RSC.
- A. I. Kitaigorodskii, Organic Chemical Crystallography, Consultants Bureau, New York, 1961 Search PubMed.
- E. Pidcock and W. D. S. Motherwell, Cryst. Growth Des., 2004, 4, 611–620 CrossRef CAS.
- E. Pidcock and W. D. S. Motherwell, Acta Crystallogr., Sect. B, 2004, 60, 725–733 CrossRef.
- E. Pidcock and W. D. S. Motherwell, Cryst. Growth Des., 2005, 5, 2322–2330 CrossRef CAS.
- A. D. Bond and J. E. Davies, Chem. Br., 2003, 39, 44 Search PubMed.
- F. H. Allen, Crystallogr. Rev., 2004, 10, 3–15 CrossRef CAS.
- M. B. Hurtshouse, Crystallogr. Rev., 2004, 10, 85–96 CrossRef; S. J. Coles, J. G. Frey, M. B. Hursthouse, M. E. Light, L. A. Carr, D. De Roure, C. J. Gutteridge, H. R. Mills, K. E. Meacham, M. Surridge, E. Lyon, R. Heery, M. Duke and M. Day, J. Chem. Inf. Model., submitted Search PubMed.
- See, e.g.: http://www.rcuk.ac.uk/access/ and http://publicaccess.nih.gov/.
Footnote |
| † This article is partly based on a presentation which was given by FHA at the European Research Conference (EURESCO) on Molecular Crystal Engineering - EuroConference on Evaluations and Predictions of Solid State Materials Properties (Helsinki, Finland, 17–22 June 2005) organised by the European Science Foundation and supported by the European Commission, Research DG, Human Potential Programme, High-Level Scientific Conferences (Contract No: HPCF-CT-2002-00270). Information in this article is the sole responsibility of the authors and does not reflect the ESF or Community’s opinion. The ESF and the Community are not responsible for any use that might be made of data appearing in this publication. |
| This journal is © The Royal Society of Chemistry 2006 |
