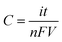Selective coulometric release of ions from ion selective polymeric membranes for calibration-free titrations

Abstract

Coulometry belongs to one of the few known calibration-free techniques and is therefore highly attractive for chemical analysis. Titrations performed by the coulometric generation of reactants is a well-known approach in electrochemistry, but suffers from limited selectivity and is therefore not generally suited for samples of varying or unknown composition. Here, the selective coulometric release of ionic reagents from ion-selective polymeric membrane materials ordinarily used for the fabrication of ion-selective electrodes is described. The selectivity of such membranes can be tuned to a significant extent by the type and concentration of ionophore and lipophilic ion-exchanger and is today well understood. An anodic current of fixed magnitude and duration may be imposed across such a membrane to release a defined quantity of ions with high selectivity and precision. Since the applied current relates to a defined ion flux, a variety of non-redox active ions may be accurately released with this technique. In this work, the released titrant's activity was measured with a second ionophore-based ion-selective electrode and corresponded well with expected dosage levels on the basis of Faraday's law of electrolysis. Initial examples of coulometric titrations explored here include the release of calcium ions for complexometric titrations, including back titrations, and the release of barium ions to determine sulfate.

---

Introduction

Coulometry in chemical analysis has always been a highly attractive approach because it offers the promise of calibration-free measurements. For instance, calibration-free enzyme-based glucose biosensors for blood measurements have been realized by exhaustively converting all available glucose in a confined sample.¹ The coulometric detection of ions has recently been reported by Kihara et al., by selectively and quantitatively extracting them under potential control into an organic phase doped with a selective receptor for that ion.² Coulometry is also very attractive for reagent generation and delivery, especially in chemical titrations. Traditional volumetric titrations require standardized stock solutions, and the accuracy of the volumetric delivery becomes difficult to achieve with decreasing sample volume. Recent efforts in miniaturizing fluidic delivery of reagents include the use of fused silica capillaries and mechanically driven syringes,^3,4 and a diffusional titration approach, with reagent delivery from a plug of a gelled membrane backfilled with reagent into drop sized samples.⁵ The coulometric electro-generation of reagents is an elegant, calibration free alternative to miniature titrators. A coulometric nano-titrator with fast response integrated into a flow-through automatic analyzer consisted of two coulometric metal-based electrodes for reagent generation and a potentiometric detection electrode.⁶ This type of work resulted in a commercial product, including the so-called Orion FLASH titrator^™ by Thermo Electron.⁷ Potentiometric titration using dual microband electrodes in generator-collector mode has been reported very recently.⁸ The main advantage of the above method is the electrogeneration of titrant to determine the endpoint by a single scan with the ramp current method. Another area where calibration free coulometric titrators have been of interest is for the determination of drugs in pharmaceutical preparations by galvanostatic bromine generation, for instance.⁹

There are two key challenges associated with coulometric reagent delivery: a limited selectivity and a limited choice of reagents that can be released in such a manner. Redox reactions at metal electrodes are normally not perfectly selective, especially in complex and unknown samples. Besides acid–based titrations,¹⁰ such principles have also been used for the generation of chemically reactive reagents such as bromine,⁹ but the possibilities are limited.¹¹

Besides the triggering of a direct redox reaction by applying suitable potentials or currents, coulometry can also be applied for non-redoxactive processes as long as the reagents carry a well defined charge. In such cases, a suitable applied current generates a flux of such ions whose magnitude can be accurately calculated. Of course, the selectivity of this process depends on the materials from which the ions are released. Simple hydrophilic ion-exchange membranes have been used for such purposes,^12,13 but the selectivity of such materials is normally not well controlled and spontaneous exchange with competing ions may occur in contact with complex samples. Ion conductors such as silver sulfide deposited onto silver wires were used to generate silver ions.¹⁴ Although this principle still relies on a redox process of the silver/silver(I) couple, the selectivity is largely dictated by the sulfide solubility of the involved salt and therefore uniquely different from simpler redox systems. More recently, lead(II) ions were released coulometrically from chalcogenide glasses for the purpose of determining sulfate ions.¹⁵ The selectivity of the process was dictated by the properties of the glass membrane, and the lead ions were released without involving a direct redox process for these ions itself.

When coulometric reagent generation was first starting to emerge, ionophore-based ion-selective membranes were not yet a mature technology. Today, they are widely established for the selective chemical detection of ionic analytes, and a chemical receptor (ionophore) in the membrane is normally used to tune the selectivity to a wide extent. Such membranes contain a lipophilic ion-exchanger and their counterions are the analyte ions to be determined. In recent years, the selectivity of such sensors has been more fully understood;¹⁶ protocols determining unbiased selectivity coefficients have been introduced, shown to be extremely high in some cases;¹⁷ and their detection limits have been lowered to ultra-trace levels for a number of examples by carefully minimizing undesired zero-current ion-fluxes across the membrane.^18,19

To our knowledge, we report here for the first time on the selective coulometric release of ionic reagents from ionophore-based solvent polymeric ion-selective membranes for the purpose of conducting calibration-free titrations. If a suitable current pulse of fixed duration and amplitude across such an ion-selective membrane is applied, a well-defined flux of ions in the direction of the sample may be observed (see Fig. 1). So far, such types of experiments have already been performed, for instance, to counter undesired spontaneous ion fluxes and to lower the detection limit of the electrode.²⁰ More recently, applied current pulses leading to defined ion fluxes into and from the membrane have been used to develop the concept of instrumentally controlled ion-selective electrodes.²¹ This has brought ion-selective electrodes closer to the realm of voltammetric sensors.

Fig. 1 A constant current pulse applied across a calcium-selective polymeric membrane results in the injection of a fixed amount of calcium into the sample. This is here used for chemically selective coulometry.

In this paper, calcium-selective membrane electrodes are explored as an initial model system for the coulometric release of calcium and barium ions, coupled with potentiometric detection using ion-selective membranes with nanomolar detection limits.

Experimental

Reagents

High molecular weight poly(vinyl chloride) (PVC), the plasticizers 2-nitrophenyl-octyl ether (o-NPOE) and bis(2-ethylhexyl) sebacate (DOS), the ionophore calcium(IV) N,N-dicyclohexyl-N’,N’-dioctadecyl-3-oxapentanediamide (ETH 5234), the lipophilic cation-exchanger salt sodium-tetrakis[3,5-bis(trifluoromethyl)phenyl]borate (NaTFPB), the inert lipophilic salt tetradodecylammonium-tetrakis(4-chlorophenyl)borate (ETH 500), tetrahydrofuran (THF) and all salts were purchased from Fluka Chemical Corp. (Milwaukee, WI) in Selectophore quality or puriss quality. Aqueous solutions were prepared by dissolving the appropriate salts in nanopure-deionized water (18.2 MΩ cm).

Ion selective membrane preparation

The calcium selective membrane components consisted of 13 mmol kg⁻¹ Ca(IV) ionophore, 4.5 mmol kg⁻¹ NaTFPB and 10 mmol kg⁻¹ of inert lipophilic salt ETH 500 together with o-NPOE and PVC (in a 2 ∶ 1 mass ratio) with a total mass of 140 mg, dissolved in 1.5 mL of THF and pouring into a glass ring (22 mm id) affixed to a microscope glass slide. The solvent THF was allowed to evaporate overnight to give a membrane of 200 µm approximate thickness.

Electrodes

Ion-selective electrodes for the detection of the released calcium ions were prepared by punching a series of 3 mm discs from the parent membrane and gluing to a plasticized PVC tube with PVC glue, which was mechanically affixed to a 1000 µL pipette tip. The detecting calcium electrodes were conditioned for 1 day in 10⁻³ M CaCl₂ followed by conditioning in 10⁻⁵ M of NaCl and HNO₃ each for one additional day. The inner filling solution contained CaCl₂ 10⁻³ M with 0.05 M Na₂EDTA at a pH of 5.8 adjusted by 0.01 M NaOH to give a calculated calcium activity of 3 × 10⁻⁸ M. The calcium selective coulometric electrodes were prepared by punching a series of 9 mm discs from the parent membrane and gluing to a wide plasticized PVC tube with PVC glue, which was mechanically attached to a rigid Teflon tube. These electrodes were conditioned in 10⁻² M CaCl₂ overnight. The inner filling solution was identical to that of the conditioning solution. The barium selective coulometric electrodes were conditioned in 10⁻² M BaCl₂ overnight with an identical inner filling solution. The barium selective sensors were conditioned in 10⁻³ M BaCl_2. The calcium selective electrodes characterized for the selectivity were conditioned in a 0.01 M NaCl solution identical to the inner filling solution overnight. Selectivity characterization required no prior exposure to the primary ion calcium before the measurement. Standard deviations were obtained based on the measurements of sets of at least three replicate membrane disks from the same parent membrane.

Experimental setup for coulometry

Due to the simplicity of instrumentation for constant current coulometry, we built the apparatus from a galvanostat as the constant current source and the electrolysis cell, including endpoint detection system. Traditional constant current coulometry consists of a 2-electrode set-up with the coulometric electrode as the anode in the case of cations. A high surface area coiled Pt wire was used as a counter electrode. The experiments were performed with an AFCBP1 Bipotentiostat (Pine Inst., Grove City, PA). The detection circuit consisted of an ISE and a reference electrode isolated from the current generating galvanostat ground loop. In our setup ISE potentials were recorded with a battery-powered high impedance amplifier (AD820, Analog Devices) connected to the data acquisition system (AduC824, Analog Devices) controlled by a handheld computer (Palm III) at room temperature. The external reference electrode consisted of a double-junction Ag/AgCl electrode with a 1 M LiOAc bridge electrolyte and 3 M KCl as reference electrolyte. All EMF values were corrected for the liquid junction potential using the Henderson equation. The activity coefficients were calculated according to Debye–Hückel approximations.²²

Coulometric cell

The electrochemical cell was made out of Teflon. The cell was separated into two compartments by a flexible polypropylene separator. It contained a wide opening on the top to fit all four electrodes and included ISE and reference electrodes on one side with ion selective membrane based generating and Pt wire counter electrode on the other side (see Fig. 2). The electrolysis cell was fitted with a solution inlet and outlet for the replacement of the sample with fresh solution by means of a syringe when calibration of the sensor was carried out. The volume of 1 mL was measured exactly by pipetting out the sample into the cell after arranging the electrodes and closing the inlet and outlet valves.

Fig. 2 Schematic representation of the coulometric cell with the generating ion-selective membrane anode (G.E.), a Pt counter electrode (C.E.) separated by a polypropylene separator (p) from the calcium ion-selective electrode (ISE) and a reference electrode (R.E.). S is a stirring bar; In is the solution inlet and Out the outlet, each with 0.5 cm id. The wide opening on the top has a 3 cm diameter; the total height of the cell was 1.8 cm. The diameter of the flat bottom of the cell was 1.2 cm.

Calculations

The concentration of the electro-generated reagent was calculated according to Faraday's law:
where C is the concentration of reagent, i is the magnitude of the constant current pulse used to generate the reagent, t is the duration of current applied pulse, n is the valency of the reagent (here, n = 2), F is the Faraday constant and V is the volume of the sample into which the reagent is released.

Titration curves were calculated according to established procedures, taking into account the following EDTA complex formation constants for the considered metal ions: log K_f(Ca–EDTA) = 10.69, log K_f(Ni–EDTA) = 18.62.²³ The sample pH of 10 and 11.6 for the two experiments was used to calculate the effective complex formation constant with α_y⁴⁻ = 0.36 and α_y⁴⁻ = 0.93.²³ The precipitation reaction titration curve was calculated with the solubility product K_sp = 1.1 × 10⁻¹⁰. End points were obtained according to established procedures from the second derivative plot of [Δ(ΔpM²⁺/Δt)]/Δtversust. The endpoint is the t value when the curve crosses the abscissa.

Results and discussion

The coulometric release of calcium ions was here explored with an ionophore-based polymeric membrane calcium-selective electrode. In addition to a high concentration of inert lipophilic electrolyte to reduce the membrane resistance to about 7 kΩ, the membrane was formulated according to standard procedures with the ionophore ETH 5234 and an appropriate cation-exchanger, and backfilled with a relatively concentrated calcium chloride solution. The ionophore ETH 5234 is known to be very selective to calcium.²⁴ So-called unbiased selectivity coefficients¹⁷ of ETH 5234 based coulometric electrodes towards discriminated ions were measured and are reported in Table 1. These were obtained from three identical Ca²⁺ selective electrodes conditioned overnight in 0.01 M NaCl. The obtained response slopes were all near-Nernstian, suggesting that the selectivity coefficients shown are close to their unbiased values. From the small values of log K_Ca,J^pot obtained for all the discriminated ions, it is evident that the membranes exhibited a high selectivity over all these potential interferences. If the membrane is not selective to the ion it releases, an interfering ion from the sample may spontaneously ion-exchange into the membrane and limit the accuracy of the method.

Table 1 Experimental selectivity coefficients log K_Ca,J^pot for the PVC/o-NPOE releasing membrane containing Ca(IV) ionophore

Ion J	Slopes of ion J/mV decade^−1	log KCa,J^pot
Na^+	46.1 ± 2	−7.13 ± 0.1
K^+	43.8 ± 3	−9.32 ± 0.2
Mg^2+	29. 9 ± 1	−9.47 ± 0.1
Ba^2+	27.4 ± 3	−3.54 ± 0.1
Ca^2+	29.7 ± 1	0

---

In order to facilitate the potentiometric detection of the sample calcium activity with an ion-selective electrode, cross-talk between the two electrochemical cells needed to be eliminated. The ion-selective electrode and reference electrode formed a circuit that was physically isolated from the ground loop of the galvanostat. Yet, initial experiments revealed that cross-talk between the two circuits was an important problem because even minute currents flowing through the common ground loop seriously affected the measured open circuit potential. Consequently, the two circuits needed to be operationally isolated from each other (see Experimental). Ions were released from the membrane during a discrete current pulse, followed by an open circuit measuring period during which time the galvanostat circuitry was disconnected. Typical current pulse durations were 120 s, followed by open circuit measuring pulses of 180 s. This allowed the calcium gradients within the releasing membrane to re-establish to some extent, and hence relatively large current densities on the order of 31 × 10⁻⁶ A cm⁻² could be applied. In the setup tested here, the sample volume and the releasing electrode area were 1 mL and 0.65 cm², respectively, and hence did not yet constitute a miniaturized setup.

Basic characterizaton of coulometric calcium release

Equi-duration steps of constant current were applied to coulometric electrodes in order to electro-release calcium into an electrolyte solution, the activity of which was observed with a calcium-selective electrode after each release step. The calcium sensing membrane was calibrated before the release experiment. It showed a typical response curve of the calcium electrode and an improved lower detection limit relative to classical ISEs.²⁵ The calibration was carried out in a sample solution containing 10⁻⁵ M NaCl as a background electrolyte. The potentiometric response of the sensor was found to be linear over the range of 10⁻⁹ to 10⁻⁵ M of calcium activity with a Nernstian electrode slope of 30 mV decade⁻¹. The potential response of these sensors was stable in the measured concentration range and exhibited high reproducibility.

Fig. 3 shows a plot of calcium concentration increase from the calcium selective coulometric membrane electrode at constant currents of 1 and 2 µA, respectively, in a background of 5 × 10⁻⁷ M calcium chloride in a 1 mL sample volume. This calcium background was chosen here to avoid the occurrence of a sub-Nernstian slope for the potentiometric sensor calibration curve at low calcium activities. Individual release step durations were chosen as 120 s. The solid lines in Fig. 3 are theoretical predictions calculated using Faraday's first law of electrolysis. The experimental points were in good agreement with theoretical predictions. A release experiment of calcium in a higher background concentration of 0.01 M KCl gave the same results (data not shown). Fig. 4 presents data on the coulometric release of calcium from ion selective coulometric membrane electrode with sequentially increasing current amplitudes into a background of 5 × 10⁻⁷ M calcium chloride in a 1 mL sample volume. Again, experimental data corresponded very well with theory, indicating that the applied current densities did not diminish coulometric efficiency under these conditions.

Fig. 3 Typical concentration, in moles of calcium, observed by coulometric release from the inner filling solution into the sample across the membrane by passing constant current pulses of 1 and 2 µA, respectively. Individual release step durations were 120 s in a background of 5 × 10⁻⁷ M calcium chloride. The solid lines are theoretical predictions calculated with Faraday's law.

Fig. 4 Coulometric release of calcium at increasing anodic current amplitudes. An individual release step duration of 120 s in a background of 5 × 10⁻⁷ M calcium chloride was used. The solid line is the theoretical prediction calculated with Faraday's law.

Direct EDTA titrations

The titration of EDTA with calcium was chosen as a typical example for a coulometric complexometric titration. Shown in Fig. 5 are data from complexometric titrations of three different concentrations of EDTA with calcium. The coulometric titrations were carried out by the electro-generation of calcium ions through a 0.65 cm² area calcium ion selective membrane into a 1 mL sample volume containing 1, 5, and 10 µM of Na₂EDTA buffered at pH 10, respectively. The titration rates were sufficiently high for these sample concentrations to be practically useful. Titration times totaled 24, 120, and 240 s, respectively, with release step durations of 3, 10, and 30 s. Here, however, step durations were shortened near the equivalence point to obtain a sharper endpoint. The observed endpoints showed good reproducibility, with a relative standard deviation on the order of less than 3%. All the titrations were carried out at 10 µA constant current pulses. The theoretical titration curves shown in Fig. 5 were constructed from calculating pCa values from effective complex formation constants, as established.²³ Overall, the experimental titration curves were in excellent agreement with theoretical predictions.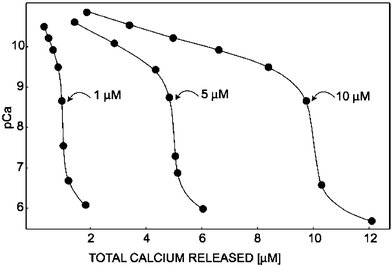

Fig. 5 Coulometric titrations of 1, 5, and 10 µM EDTA with calcium. The endpoints shift to the right with increasing concentrations of EDTA. The sample was buffered to pH 10 and titrations were carried out at a constant current of 10 µA. Solid lines are the theoretically predicted titration curves.

EDTA back titrations

As a second application for coulometric calcium release, an EDTA back titration was explored. A remaining excess of EDTA was titrated with coulometrically generated calcium to determine nickel(II) in a solution containing a large excess of iron(III) in a weakly acidic solution in the presence of triethanolamine, following established volumetric protocols.²⁶ The titration was carried out at a constant current of 20 µA in a 1 mL sample volume with the sample solution buffered to pH 11.6. The resulting titration curve is shown in Fig. 6. In this present setup, total titration times were on the order of 5 min. The excess EDTA was titrated with coulometrically released calcium and the amount of nickel was estimated as 6.84 ± 0.16 × 10⁻⁵ M. It corresponds well with initial added concentration of 7.0 × 10⁻⁵ M nickel in the solution. Again, the experimental data corresponded well with the theory. This is a strong indication that many other classical direct and back titrations may be performed coulometrically by the use of ion-releasing ion-selective membranes.

Fig. 6 Estimation of nickel by coulometric back titration of EDTA with calcium at a sample pH of 11.6. The titration was carried out at a constant current of 20 µA. Solid line: theoretical titration curve.

Precipitation titrations to estimate sulfate

The indirect determination of sulfate as barium sulfate by precipitation titration was also explored. In the selectivity data shown in Table 1, the calcium-releasing membrane was found to be moderately selective for barium ions. They are less preferred than calcium ions by 3.5 orders of magnitude, but if calcium is absent, the other tested ions are still reasonably discriminated, even when compared to the commercially available barium ionophore I.²⁷ A fresh releasing membrane was conditioned in and backfilled with barium chloride solutions for the purpose of releasing barium ions. The electro-release of barium into the sample containing sodium sulfate was achieved at 20 µA current pulses, as shown in Fig. 7. For the current setup and with a 100 µM sulfate concentration, the endpoint was observed after 485 ± 6 s. The sensors used for barium detection also were calcium-selective membranes of the same type as used in the above experiments, but conditioned in barium chloride solutions. The experimental titration curves corresponded well with the theory, which was obtained from the solubility product after calculating the released barium concentration using Faraday's law.

Fig. 7 Coulometric precipitation titration to estimate 1 × 10⁻⁴ M sodium sulfate with coulometrically released barium from an ion-selective membrane. The titration was carried out at a constant current of 20 µA. Solid line: theoretical titration curve.

Conclusions

An attractive semi-automatic coulometric method employing an ionophore-based ion-selective membrane as a coulometric electrode is reported here for the first time. Various types of titrations such as precipitation and complex formation were carried out using ion-selective membrane based coulometric electrodes, demonstrating its wide applicability. The use of ion-selective polymeric membranes for coulometric release broadens the spectrum of reagents that can be electro-released. Attractive applications include the generation and detection of various metals ions, including magnesium, and important non-electroactive reagents such as protamine for the detection of heparin via heparin–protamine titration. Further work in this direction is in progress.

Acknowledgements

The authors would like to acknowledge the National Institutes of Health through grant GM07178 and EB002189 for financial support of this research.

References

1. T. Tanaka, E. Shutto, T. Mizoguchi and K. Fukushima, Anal. Sci., 2001, 17, 277–280.
2. N. Kurauchi, Y. Yoshida, N. Ichieda, H. Ohde, O. Shirai, K. Maeda and S. Kihara, J. Electroanal. Chem., 2001, 496, 118–123.
3. L. Alerm and J. Bartroli, Anal. Chem., 1996, 68, 1394–1400.
4. F. Sagara, T. Kobayashi, T. Tajima, H. Ijyuin, I. Yoshida, D. Ishii and K. Ueno, Anal. Chim. Acta, 1992, 261, 505–508.
5. M. Gratzl and C. Yi, Anal. Chem., 1993, 65, 2085–2088.
6. O. T. Guenat, W. E. Morf, B. H. van der Schoot and N. F. de Rooij, Anal. Chim. Acta, 1998, 361, 261–272.
7. B. van der Schoot, P. van der Wal, N. de Rooij and S. West, Sens. Actuators, B, 2005, 105, 88–95.
8. H. Rajantie and D. E. Williams, Analyst, 2001, 126, 1882–1887.
9. I. F. Abdullin, N. N. Chernysheva and G. K. Budnikov, J. Anal. Chem., 2002, 57, 629–631.
10. W. Olthuis, J. Luo, B. H. Van der Schoot, J. G. Bomer and P. Bergveld, Sens. Actuators, B, 1990, 1, 416–420.
11. A. J. Bard, Anal. Chem., 1966, 38, 88R–98R.
12. R. B. Hanselman and L. B. Rogers, Anal. Chem., 1960, 32, 1240–1245.
13. P. P. L. Ho and M. M. Marsh, Anal. Chem., 1963, 35, 618–620.
14. K. S. Fletcher III and R. F. Mannion, Anal. Chem., 1970, 42, 285–287.
15. E. Schumacher and B. Hackmann, Fresenius' J. Anal. Chem., 1980, 304, 350–357.
16. E. Bakker, P. Buehlmann and E. Pretsch, Anal. Chem., 2000, 72, 1127–1133.
17. E. Bakker, Anal. Chem., 1997, 69, 1061–1069.
18. T. Sokalski, T. Zwickl, E. Bakker and E. Pretsch, Anal. Chem., 1999, 71, 1204–1209.
19. A. Ceresa, A. Radu, S. Peper, E. Bakker and E. Pretsch, Anal. Chem., 2002, 74, 4027–4036.
20. E. Pergel, R. E. Gyurcsanyi, K. Toth and E. Lindner, Anal. Chem., 2001, 73, 4249–4253.
21. A. Shvarev and E. Bakker, Anal. Chem., 2003, 75, 4541–4550.
22. P. C. Meier, Anal. Chim. Acta, 1982, 136, 363–368.
23. D. C. Harris, Quantitative Chemical Analysis, Freeman Publishers, 6th edn, 2002.
24. Y. Qin, Y. Mi and E. Bakker, Anal. Chim. Acta, 2000, 421, 207–220.
25. E. Bakker, P. Buehlmann and E. Pretsch, Chem. Rev., 1997, 97, 3083–3132.
26. A. I. Vogel, A Text-Book of Quantitative Inorganic Analysis, John Wiley and Sons Inc., New York, 3rd edn., 1961.
27. M. W. Laeubli, O. Dinten, E. Pretsch, W. Simon, F. Voegtle, F. Bongardt and T. Kleiner, Anal. Chem., 1985, 57, 2756–2758.

---